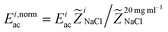Acoustic radiation forces at liquid interfaces impact the performance of acoustophoresis

Abstract

Acoustophoresis is a method well suited for cell and microbead separation or concentration for downstream analysis in microfluidic settings. One of the main limitations that acoustophoresis share with other microfluidic techniques is that the separation efficiency is poor for particle-rich suspensions. We report that flow laminated liquids can be relocated in a microchannel when exposed to a resonant acoustic field. Differences in acoustic impedance between two liquids cause migration of the high-impedance liquid towards an acoustic pressure node. In a set of experiments we charted this phenomenon and show herein that it can be used to either relocate liquids with respect to each other, or to stabilize the interface between them. This resulted in decreased medium carry-over when transferring microbeads (4% by volume) between suspending liquids using acoustophoresis. Furthermore we demonstrate that acoustic relocation of liquids occurs for impedance differences as low as 0.1%.

---

Introduction

Microchannel acoustophoresis has been shown to be a promising tool in applications involving cells and microbeads in suspension.¹

Previous work on washing of beads and cells by acoustophoretic transport across a liquid–liquid interface into a clean buffer have shown that for some samples the washing efficiency is very low. The two main categories of troublesome configurations are transfer of particles or cells from a liquid of high mass density (e.g. blood plasma) into a liquid of lower mass density (e.g. isotone solutions such as PBS or cell culture medium)² and the transfer of particles of high number concentration.^3–5

In this work we report that liquids of different acoustic properties can relocate inside a microchannel when exposed to an acoustic standing wave field directed perpendicular to the interface between the liquids. The experiments show that by altering the acoustic properties of one of the two liquids the performance of acoustophoretic washing of beads or cells can be substantially improved.

The phenomenon of a traveling sound beam deforming the interface between liquids of different acoustic properties was first investigated by Hertz and Mende in 1939.⁶ By directing an ultrasonic beam across the interface between two immiscible liquids of different acoustic properties they showed that the direction of the deformation caused by acoustic radiation pressure was independent of the direction of propagation of the sound.

For travelling plane wave incidence on a plane interface between liquids the phenomenon is well charted. In the regime where density and speed of sound of the two liquids are of comparable magnitude the direction and magnitude of the acoustic radiation pressure will be primarily dictated by the relative difference in speed of sound.⁷

The effect has been largely overlooked for resonant acoustophoretic microsystems until Johansson et al. reported the potential usefulness of such modalities for mixing of liquids in the laminar regime,⁸ in a constellation where a standing wave propagates parallel to the interface between two miscible liquids. An analytical expression was derived for the force on the interface that could be successfully fitted to experimental data for increasing density difference between mixtures of glycerol and water. It was concluded that the relative difference in density governs the deformation of the interface between the liquids.

Experiments reported herein indicate that, for a setting where a standing wave is directed perpendicular to an interface between two liquids of similar but different acoustic properties, neither density nor speed of sound can solely account for the deformation of the interface and the subsequent relocation of liquids. Rather, the experiments support a hypothesis that the radiation pressure on the interface is proportional to the relative difference in acoustic impedance between the two liquids.

Experimental

Sample preparation

Aqueous solutions of sodium chloride (NaCl) (GPR Rectapur, VWR, BDH Prolabo) were prepared of concentrations in the range from 0 mg mL⁻¹ to 20 mg mL⁻¹. Whenever fluorescein sodium dye (BDH Merck KgaA, Poole England) or Evans Blue dye (Merck, Darmstadt, Germany) was used in the experiments, 0.1 mg ml⁻¹ of the dye was added and the concentration of NaCl was adjusted so as to preserve the overall mass of solute per volume. Samples of Histopaque®-1077 (Cat # 10771, Sigma, Saint Louis, MO, USA) density gradient medium were prepared by diluting a stock solution with de-ionized and filtered (0.22 μm pore size) water. Samples containing microbeads were prepared by spinning them to a pellet in a centrifuge, aspiration of original suspending liquid, and re-suspending the beads in NaCl fluorescein solution to a final bead concentration of 5 mg mL⁻¹ for the acoustic energy density measurements and to 40 mg mL⁻¹ for the washing experiments.

Measuring mass density and speed of sound

A standard curve of density versus concentration was measured for solutions of NaCl and Histopaque using a pycnometer (5 mL nominal volume) and a weighing scale. The speed of sound of the solutions was measured by the pulse echo method where an ultrasound pulse is sent through the liquid which is contained in a cavity of known length. The speed of sound was then calculated from the time points of the pulse entering the cavity and the echo from the far wall.

Acoustophoresis chip

The acoustophoresis chip, shown in Fig. 1(a), used in this study is a longer version of a device for cell sorting based on acoustophoretic mobility of cells, previously reported in Augustsson et al.⁹ The channel structure consists of a 20 mm long particle pre-alignment channel, 300 μm wide and 150 μm high, which is bifurcated and routed to the side branches of a trifurcation inlet of a sorting channel (20 mm × 375 μm × 150 μm). Particle free liquid can be injected through the central branch of the trifurcation to enable flow lamination of the particle suspension near the walls of the sorting channel. At the end of the sorting channel the flow is split in a trifurcation outlet where the side branches leads to a common side outlet and the central branch leads to a central outlet. Two piezoceramic transducers (PZT 26, Ferroperm Piezoceramics, Kvistgard, Denmark) resonant at 5 MHz (5 mm × 5 mm) and 2 MHz (15 mm × 5 mm), were glued to the back side of the pre-alignment channel and the sorting channel, respectively.

Fig. 1 (a) A photograph of the chip which is temperature controlled to 25 °C by a Peltier element and a Pt-1000 RTD temperature sensor. Piezoceramic transducers resonant at 2 and 5 MHz are glued to the underside of the chip. Reprinted with permission from Augustsson et al.⁹ Copyright 2012 American Chemical Society. (b–g) A schematic of the flow configuration for the acoustophoresis washing experiments. The pressure driven system comprises a pressure terminal (b) attached to sample reservoirs at inlets (c and d) and at the outlets (e–f). When pressurized, aqueous suspension from (c) flows through the pre-alignment channel of the chip (a). (g) Flow sensors are used to measure the flow rate within the chip.

Throughout this work the pre-alignment channel has not been utilized except for when measuring the acoustic energy density (ESI,† Fig. S1).

Ultrasound actuation

The signals to the piezoceramic actuators were generated by two waveform generators (Agilent 33120A, Agilent Technologies Inc., Santa Clara, CA, USA) connected via an amplifier circuits based on a high power operational amplifier (LT1012, Linear Technology Corp., Milpitas, CA, USA). An oscilloscope (TDS 1002, Tektronix, UK Ltd., Bracknell, UK) was used for measuring the peak-to-peak voltage over the transducers.

A Peltier element and a Pt1000 resistance temperature detector (RTD) were used in a control loop to maintain a constant temperature of 25 °C.

Flow system

The microchannel pressure control system as shown schematically in Fig. 1, assembled in-house, is based on an 8-port proportional pressure control valve-terminal (VEMA, FESTO, Germany) within a pressure range of 0–1 bar and liquid thermal flow sensors (SLI-1000, Sensirion AG, Staefa ZH, Switzerland) having a maximum calibrated flow of 1 mL min⁻¹ for water. Briefly, sample and wash buffer containers held on an air-sealed sample manifold are pressurized to inject liquids through the pre-alignment channel and the central inlet respectively. The pressures in the outlet containers were controlled in a closed feedback loop based on readings from the flow sensors. The total volumetric flow rate in the combined side inlet was set to 100 μL min⁻¹, the flow rate in the central inlet was set to 400 μL min⁻¹, the flow rate in the central outlet was set to 100 μL min⁻¹ and the flow rate in the side outlet was set to 400 μL min⁻¹, using in-house developed flow control software, code written in LabView (Version 2012, National Instruments Corporation, Austin, Texas, USA), unless otherwise stated.

Image acquisition and analysis

A microscope equipped with a digital color camera (Dino-Lite Pro, AnMo Electronics Corporation, Hsinchu, Taiwan) was used for capturing images for image analysis. Confocal microscopy was performed using Olympus microscope (BX51WI, Olympus Corporation, Tokyo, Japan) and the Fluoview 300 software was used to generate the confocal image data taken at different depths in the channel on the chip using an automated microscope stage with a step size of 1 μm. Fluorescence images were acquired using a 20× objective and the fluorescence was quantified using MATLAB version 2013a.

Fluorescein green emitted light profiles were extracted from a region near the outlet of the chip by analyzing the green channel in the images and Evans blue dye bright field absorption was evaluated by evaluating the relative intensity drop in the red channel compared to background images.

Results and discussion

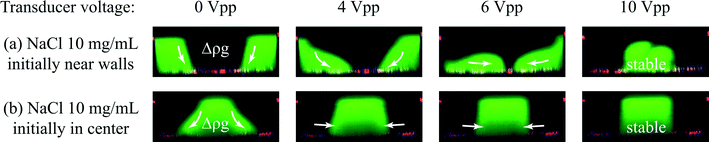
The work presented in this paper is based on the finding, shown in Fig. 2(a and b), that flow laminated liquids can be manipulated using ultrasonic resonances in microfluidic channels. In the experiment, NaCl-solution of concentration 11 mg mL⁻¹ was injected along both sides of an acoustophoretic microchannel and NaCl 10 mg mL⁻¹ was injected through a central inlet. Fluorescein salt was added to the side liquid. When an acoustic resonance is present across the width of the channel the two liquids relocate with respect to each other so that the liquid injected at the sides exit through the central outlet and vice versa.

Fig. 2 Microscope images of the trifurcation outlet of an acoustophoresis microchannel. When the ultrasound is (a) off the two liquids follow their flow laminated paths, whereas when the ultrasound is (b) on they relocate with respect to each other. The flow rate was 500 μL min⁻¹ in this experiment corresponding to an average residence time in the channel of 0.2 s. (c) A schematic of the channel indicating the outlet region of the chip.

Relocation was not observed when the liquids were initially arranged with a higher NaCl concentration in the center of the channel. This implies that the phenomenon cannot be explained by acoustic streaming which could also render a similar pattern of relocation.^10,11 To avoid diffusion of dye molecules to obscure the effect of acoustic relocation the flow rate was set to 500 μL min⁻¹ in all experiments unless otherwise stated yielding a sufficiently short retention time in the microchannel not to be influenced by diffusion (ESI,† Fig. S2).

The phenomenon is important to investigate since it is present even for very subtle differences in the properties of the two liquids. E.g. the density difference between the two liquids shown in Fig. 2 is only 0.1%. Furthermore the phenomenon occurs at acoustic energies and flow rates that are comparable to those used when handling microbeads and cells in acoustophoretic systems.^9,12–14

Throughout the rest of the text the word mismatch will be used to refer to constellations where a property of the liquid injected in the center of the trifurcated inlet differs from that of the liquid injected at each side of the main channel. Positive mismatch indicates that the property of the side streams has a higher value than the corresponding property of the central stream. The abovementioned constellation of salt solutions can therefore be said to be positively mismatched regarding salt concentration.

Relocation and stabilization

To find out how liquids of positive mismatch in concentration can relocate with respect to each other inside the microchannel, two experiments were carried out in a confocal microscope. Fluorescence intensity was recorded in the vertical cross section of the channel near the trifurcation outlet for a constant flow of the liquids. The cross sectional fluorescence profile was recorded for actuator voltages ranging from 0 to 10 V peak to peak.

Fig. 3(a) shows the behavior of the two liquids for 10 mg mL⁻¹ NaCl initially injected near the sides (green) and water initially in the center of the channel as viewed within the observation zone shown in Fig. 2. At 0 V_pp-actuation the interfaces between the two liquids are observed to be slanted due to gravity acting on the density difference between the liquids. The gravity effect on a vertical interface for the relevant timescale could also be confirmed in a simulation (ESI,† Fig. S3). When the sound intensity was increased through 4 V_pp and 6 V_pp the NaCl solutions migrated towards the center along the bottom of the channel while the water follows the ceiling towards the side walls. At 10 V_pp the liquids were completely relocated.

Fig. 3 Confocal vertical scans near the end of the channel. Fluorescent liquid (green) of NaCl-concentration 10 mg mL⁻¹ was laminated (a) near the side walls of the channel or (b) in the center of the channel. Pure water occupied the remaining parts of the flow (dark areas). The images show (a) acoustic relocation of liquid for increasing actuator voltages for positive mismatch in concentration. (b) For negative mismatch the onset of the acoustic resonance does not cause any relocation of the liquids and counteracts the inclination of the interfaces which is caused by gravity and the density difference between the liquids.

Fig. 3(b) shows the behavior of the same two liquids for negative concentration mismatch. At 0 V_pp the interfaces between the liquids display a substantial tilt. When increasing the actuator voltage through 4 V_pp and 6 V_pp up to 10 V_pp the interfaces are gradually pushed to a vertical orientation.

The origin of the phenomenon

To find the underlying acoustic property that governs the relocation of liquids a set of experiments was carried out using solutions of Histopaque gradient density media and NaCl. For the two solutions the density and speed of sound vs. concentration was measured using a pycnometer and pulse echo timing, respectively.

Three candidate acoustic properties, speed of sound (c), density (ρ) and acoustic impedance (Z = ρc), were compared. For each candidate property, a solution of Histopaque was prepared so as to be perfectly matched with a corresponding solution of NaCl. Since the concentration dependency of density and speed of sound is different in the two solutions, the other two candidate properties will be mismatched whenever one of them is perfectly matched.

Images of the outlet region were analyzed, compare Fig. 2(a and b), and the broadening of the bands of fluorescein dye was estimated in the images for a range of acoustic energy densities (E_ac). The relationship between the ultrasound transducer voltage amplitude and E_ac inside the microchannel was determined by analyzing trajectories of 5 μm beads. This method was adopted from Augustsson et al.⁹ (ESI,† Fig. S1).

For each combination of liquids the acoustic energy density at which the dye band relocation exceeded ~50 μm was estimated. This was performed by comparing images side by side that had been acquired near the outlet of the channel. One of the images was chosen as a reference for 50 μm relocation and was thereafter compared to all other images to find the best match for each of the configurations. No relocation implicates either the currently matched candidate was indeed governing the relocation and therefore there was no force on the liquid interface or that the true candidate was negatively mismatched so that net force at the interface pushes the side liquid towards the walls. If no relocation was observed the recording of acoustic energy density was assigned an arbitrary high value.

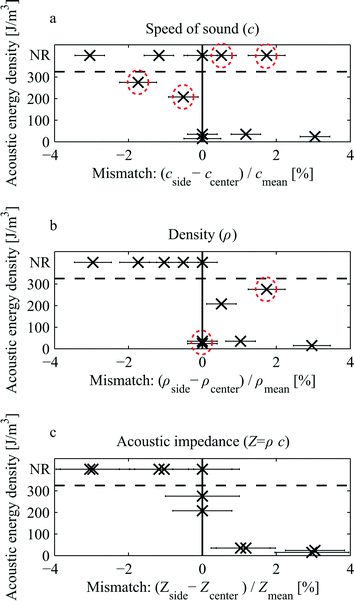
Fig. 4(a–c) shows scatter plots of the acoustic energy density required to produce a 50 μm relocation of the side liquid. The horizontal axis indicates the relative mismatch for the three candidates. The scatters show that speed of sound alone does not appear to govern the relocation since the experimental observations of relocation are found for both positive and negative mismatch, Fig. 4(a). Furthermore, Fig. 4(b) indicates that density alone cannot govern the relocation because of the two observations of relocation occurring at very low acoustic energy for perfectly matched densities. Also, very high relocation energy was observed for a 1.7% density mismatch while the neighboring data points on either side display relocation at much lower energies. The data is tabulated in ESI,† Table S1.

Fig. 4 Relocation energy plotted against the relative mismatch for the three candidate acoustic properties, speed of sound, density, and acoustic impedance. Configurations that did not lead to relocation within the assessment range of the acoustic energy density were assigned an arbitrary energy density of 400 J m⁻³ indicated by the dashed line. NR = no relocation. Red dashed circles indicate data points that are not consistent with the hypotheses of relocation being solely a function of speed of sound or density, respectively. Bars indicate error estimates derived from a 1% uncertainty in the volumetric measurement when preparing the solutions.

The scatter for acoustic impedance shown in Fig. 4(c) is consistent with the fundamental hypothesis that a high positive mismatch shall lead to relocation at low acoustic energies, a zero mismatch shall require very high acoustic energy (infinite) for relocation, and negative mismatch shall never lead to relocation of the two liquids.

The interpretation of the data requires some caution since the acoustic amplitude is likely to vary for different constellations of liquids. The resonance peak width in these systems is typically on the order of 10 kHz for a 2 MHz resonance.^12,14 For a mismatch in e.g. speed of sound of a few percent, the amplitude is likely not the same as for zero mismatch. Therefore the vertical axes in the scatters can only be regarded as semi quantitative. Furthermore, perfect matching of acoustic properties is difficult to achieve and therefore an error estimate was derived for the mismatch assuming a 1% uncertainty for the volume measurements when preparing the samples.

Agreeable, the lack of a theoretical explanation to the hypothesis that the impedance difference causes the relocation is dissatisfying. Nevertheless, this is perhaps the simplest expression that fulfills the most fundamental requirements. Deeper understanding of the impact of acoustic standing waves on stratified liquids would benefit from analytical derivation or numerical simulation of the acoustic field inside the acoustic cavity.

Acoustic mobility of liquids

To investigate the sensitivity in acoustic mobility of the liquid–liquid interface for changes in acoustic impedance, solutions of NaCl at different concentrations were introduced through the combined side inlet of the chip. NaCl-solution of concentration 10 mg mL⁻¹ was infused in the central inlet in all experiments. The relative mismatch in impedance is by definition (Z̃_NaCl ≡ (Z^side_NaCl − Z^center_NaCl)/Z^mean_NaCl) fluorescein 0.1 mg mL⁻¹ was added to the side inlet liquid to visualize the motion of two liquids.

The images were analyzed in terms of the broadening (δ) of the fluorescent dye band on either side of the flow. From each image the fluorescence intensity profile was recorded across the width of the channel near the trifurcation outlet. From the profiles the width of the dye band was measured at the intensity level of 50% after which the dye band width for no actuation was subtracted to compute the broadening.

From Fig. 5(a) it is evident that whenever the concentration of NaCl is higher in the side liquid than in the central liquid, the broadening of the fluorescing dye band increases with acoustic energy density until the liquids are relocated. For the opposite configuration, i.e. for negative impedance mismatch, no broadening of the band occurs. Rather, the dye band narrows slightly compared to perfectly matched concentrations. This suggests that in this constellation the liquid is experiencing a force outwards the side walls, counteracting any broadening induced by acoustic streaming, gravity and imperfect lamination at the trifurcation inlet.

Fig. 5 (a) Relocation rate of NaCl solutions vs. acoustic energy density as measured by the dye band broadening (δ) near the channel outlet. Legend shows the relative mismatch in acoustic impedance (Z̃_NaCl = (Z^side_NaCl − Z^center_NaCl)/Z^mean_NaCl) for the side inlet relative to the central inlet. (b) To test the hypothesis (δ ∝ E_acZ̃) that the acoustic relocation is proportional to the acoustic energy and to the relative impedance mismatch, the streaming-corrected dye band broadening was plotted as a function of the rescaled horizontal axis for each of the i configurations.

The dye band broadening is a measure of the rate u_relocation of which the acoustic relocation occurs relative to the average flow velocity <u_x> in the channel such that where L is the length of the channel. The following assumption was made: the relocation rate is proportional to acoustic energy density and to the impedance mismatch, i.e. δ ∝ E^a_acZ̃^a = E^b_acZ̃^b. To test this, the dye band broadening from Fig. 5(a) was plotted versus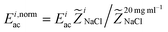 for each of the i configurations. Fig. 5(b) shows that for this rescaling of the horizontal axis the data collapses onto the curve of the largest mismatch with an exception for the smallest mismatch where Z̃_NaCl = 0.015%. In this plot the broadening has been adjusted for the contribution by diffusion, trifurcation inlet lamination imperfections and acoustic streaming by subtracting the broadening for perfectly matched solutions (i.e. Z̃_NaCl = 0).

Improving washing efficiency

The ability to confine a liquid close to the walls of a microchannel can be useful for instance to increase the washing efficiency in acoustophoresis for cell and particle handling applications. Fig. 6(a–c) show the trifurcation outlet of the acoustophoresis chip where a 4%_vol suspension of 5 μm beads in fluorescent liquid is laminated on both sides of particle free solution of NaCl 10 mg mL⁻¹. In Fig. 6(a) the sound is off and the beads remain in their flow laminated path. When the sound is increased to 350 J m⁻³ (9 V_pp) the beads are pushed to the center of the channel by the acoustic radiation force^15,16 and exit through the central outlet. If the two liquids are matched in terms of NaCl-concentration as is the case in Fig. 6(b) the drag from the microbeads tend to transfer some of the initial suspending liquid towards the center of the flow. The higher the concentration of beads, the more dramatic is this effect.^3–5

Fig. 6 Images and intensity profiles at the trifurcation outlet. (a) For zero acoustic actuation the microbeads (white) remain in the initial suspending liquid (green). When the ultrasound is active (b and c), beads move towards the center of the channel and are separated from the initial suspending liquid. The intensity profile (e) reveal a drag-induced broadening of the suspending liquid when (b) the acoustic properties of the initial suspending liquid is matched to the properties of the central liquid (clear). For (c) negative NaCl-concentration mismatch between the central liquid relative to the injected suspension the intensity profile (f) reveals that the ultrasound reduces the drag-induced transfer of dye molecules. For reference the intensity profile of the matched liquid is overlaid (dashed grey).

Fig. 6(d–f) shows that the drag-induced carry-over of dye molecules can be substantially suppressed when introducing a negative acoustic impedance mismatch. This was achieved by reducing the NaCl concentration to 5 mg mL⁻¹ in the side liquid while maintaining a concentration of 10 mg mL⁻¹ in the central liquid stream.

The question arises how the bead associated dye transfer occur in this configuration. Two potential effects are proposed in the following and most likely they both contribute in part to the carry-over. For either of the two effects the dye broadening will be reduced by properly adjusting the acoustic impedance mismatch.

First, as beads move through the liquid the acoustic radiation force is counteracted by drag force from the liquid.¹⁷ When the number of beads is high the net volume force on the liquid becomes substantial and if the interface between the liquids is perturbed the liquids can relocate.

Second, the carry-over may be caused by an average increase in acoustic impedance in the side suspension due to the addition of microbeads of higher density and speed of sound. Especially in the light of the experiments reported herein that liquids can relocate based on differences in acoustic impedance it is reasonable to believe that below some critical particle size the particles will contribute to the relocation.

It is not trivial to discriminate between the two effects in experiments but for an experimental platform of high sensitivity and a sensible set of experiments it is undoubtedly possible to achieve.

Conclusions

The acoustic properties of liquids are key elements for understanding the behavior of acoustofluidic microsystems. For a standing wave oriented perpendicular to the flow direction acoustic relocation of liquids was demonstrated within a microchannel of width 375 μm and height 150 μm. This was achieved for acoustic impedance differences between the flow laminated liquids as low as 0.1%.

Confocal imaging revealed that the relocation is a rotational motion that is promoted by an initial inclination of the interface that in this case was caused by the effect of gravity and the density difference between the liquids.

By comparing liquids of different densities, speed of sound and acoustic impedance we managed to cancel out the effect for constellations only where the difference in acoustic impedance was zero. This contrasts to, but does not contradict, previous work for perpendicular incidence of travelling waves on a liquid–liquid interface^6,7 and for a standing wave parallel to the interface.⁸ The understanding of acoustic relocation of liquids would greatly benefit for a theoretical model of the sound field in stratified liquids. From this model the acoustic radiation pressure on the liquid interface can be derived.

As an application example of the sensitivity and potential of this phenomenon an experiment was carried out where microbeads were separated from dye molecules. By altering the acoustic impedance of the initial suspending liquid, the drag associated carry-over of minute species was substantially reduced.

Acknowledgements

Our best thanks are due to M.Sc. P.B. Muller and Dr. R. Barnkob and Dr. P. Ohlsson, who have been good enough to examine this work. The results are thus put forward with greater confidence than we could otherwise have felt. The authors are grateful for financial support from the Swedish governmental agency for innovation systems, VINNOVA, CellCARE, grant no. 2009-00236, the Swedish Research Council grant no. 2012-6708, and the MPD program of Foundation for Polish Science, co-financed from European Union.

References

1. A. Lenshof, C. Magnusson and T. Laurell, Lab Chip, 2012, 12, 1210–1223.
2. P. Augustsson and T. Laurell, Lab Chip, 2012, 12, 1742–1752.
3. J. J. Hawkes, R. W. Barber, D. R. Emerson and W. T. Coakley, Lab Chip, 2004, 4, 446–452.
4. F. Petersson, A. Nilsson, H. Jönsson and T. Laurell, Anal. Chem., 2005, 77, 1216–1221.
5. P. Augustsson, J. Persson, S. Ekström, M. Ohlin and T. Laurell, Lab Chip, 2009, 9, 810–818.
6. G. Hertz and H. Mende, Z. Phys., 1939, 114, 354–367.
7. F. Borgnis, Rev. Mod. Phys., 1953, 25, 653–664.
8. L. Johansson, S. Johansson, F. Nikolajeff and S. Thorslund, Lab Chip, 2009, 9, 297–304.
9. P. Augustsson, C. Magnusson, M. Nordin, H. Lilja and T. Laurell, Anal. Chem., 2012, 84, 7954–7962.
10. R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056307.
11. P. B. Muller, M. Rossi, Á. G. Marín, R. Barnkob, P. Augustsson, T. Laurell, C. J. Kähler and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 023006.
12. P. Augustsson, R. Barnkob, S. T. Wereley, H. Bruus and T. Laurell, Lab Chip, 2011, 11, 4152–4164.
13. R. Barnkob, I. Iranmanesh, M. Wiklund and H. Bruus, Lab Chip, 2012, 12, 2337–2344.
14. R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Lab Chip, 2010, 10, 563–570.
15. H. Bruus, Lab Chip, 2012, 12, 1014–1021.
16. L. P. Gor'kov, Sov. Phys. Dokl., 1962, 6, 773–775.
17. C. Mikkelsen and H. Bruus, Lab Chip, 2005, 5, 1293–1297.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4lc00572d

---