Time lapse investigation of antibiotic susceptibility using a microfluidic linear gradient 3D culture device†
Zining
Hou‡
ab,
Yu
An‡
ab,
Karin
Hjort
c,
Klas
Hjort
a,
Linus
Sandegren
c and
Zhigang
Wu
*a
aMicrosystem Technology, Department of Engineering Sciences, Uppsala University, The Angstrom Laboratory, Box 534, SE-751 21, Uppsala, Sweden. E-mail: Zhigang.Wu@angstrom.uu.se
bSchool of Life Science, Fudan University, 200433, Shanghai, China
cDepartment of Medical Biochemistry and Microbiology, Uppsala University, SE-751 23, Uppsala, Sweden
First published on 24th June 2014
Abstract
This study reports a novel approach to quantitatively investigate the antibacterial effect of antibiotics on bacteria using a three-dimensional microfluidic culture device. In particular, our approach is suitable for studying the pharmacodynamics effects of antibiotics on bacterial cells temporally and with a continuous range of concentrations in a single experiment. The responses of bacterial cells to a linear concentration gradient of antibiotics were observed using time-lapse photography, by encapsulating bacterial cells in an agarose-based gel located in a commercially available microfluidics chamber. This approach generates dynamic information with high resolution, in a single operation, e.g., growth curves and antibiotic pharmacodynamics, in a well-controlled environment. No pre-labelling of the cells is needed and therefore any bacterial sample can be tested in this setup. It also provides static information comparable to that of standard techniques for measuring minimum inhibitory concentration (MIC). Five antibiotics with different mechanisms were analysed against wild-type Escherichia coli, Staphylococcus aureus and Salmonella Typhimurium. The entire process, including data analysis, took 2.5–4 h and from the same analysis, high-resolution growth curves were obtained. As a proof of principle, a pharmacodynamic model of streptomycin against Salmonella Typhimurium was built based on the maximal effect model, which agreed well with the experimental results. Our approach has the potential to be a simple and flexible solution to study responding behaviours of microbial cells under different selection pressures both temporally and in a range of concentrations.
1 Introduction
In recent years, microfluidics has gained significant advances in mammalian cell studies due to its similar size range as the cells.1 However, compared to mammalian cell studies, the use of microfluidics to analyse bacteria is less common.2,3 Bacterial cells strongly impact our daily life and are, in human bodies, estimated to be around ten times more frequent than “our” (mammalian) cells.4 An interesting and important growing global problem is antibiotic resistant bacteria,5 causing intractable infections with increasing personal suffering and medical costs.6The traditional antibiotic susceptibility testing, as recommended by the Clinical and Laboratory Standard Institute (CLSI), has mainly been limited to Mueller-Hinton agar plates containing predefined concentrations of antibiotics or dilution series in liquid Mueller-Hinton broth.7 An alternative technique is the Etest,8 consisting of a rectangular strip with a set of pre-defined antibiotic concentrations within a certain concentration range. The Etest eases practical operation significantly but it still needs a long incubation time and only records the final time point of the bacterial response, the minimum inhibitory concentration as measured by no visible growth after 18–20 h of incubation. For more in-depth pharmacodynamics studies of the response of bacterial cells to antibiotics, time-kill experiments, where the fraction of surviving cells is measured at intervals during treatment with fixed concentrations of a drug, are conventionally used. In general, these methods are time-consuming and laborious, especially when a larger number of antibiotic concentrations are required for testing. Microtiter plate-based assays, using multiple wells with different antibiotic concentrations, provide temporal data and increase the number of tested concentrations but basically have the same shortcomings as the previous methods.7,9
Besides smaller amounts of sample and reagent volumes, microfluidics offers faster procedures and significantly decreases the time for analysis to only a few hours due to a shorter diffusion distance in the channel.3,10–19 Several microfluidics approaches have been tested for bacterial studies. A droplet-based digital device was first used to investigate bacterial susceptibility by mixing nutrient, a viability indicator, bacterial cells and antibiotics.3 Later, magnetic beads were introduced to enhance its performance,10 and recent work aimed to make this digital-based approach automated.11 Another approach was to use micro-fabricated micro-wells to capture droplets with bacteria inside.12 However, these droplet-based approaches can only test a single antibiotic concentration. Testing numerous concentrations will make the device too complex to implement. A polydimethylsiloxane (PDMS) device with a simple straight channel was shown to have similar performance to traditional liquid and solid methods owing to the excellent gas permeability of PDMS.13 Furthermore, by fixating the bacteria on the channel surface, mechanical stress as well as chemical (antibiotic) stress was studied in a similar design.14 Recently, the principle of the Etest was applied to a microfluidic device with a limited set of drug reservoirs connected to a straight channel.15 Studies have also been focused on single-cell assays via various trapping strategies such as DEP16 (dielectrophoretic) or agarose-based encapsulation.17 In addition, the straight channel approach was further extended to analyse the antibiotic susceptibility of bacterial biofilms.18 However, their microfluidic system required 24 h of incubation and the tested bacteria contained a green fluorescent protein (GFP) expressed from a plasmid, limiting the approach to molecularly engineered lab strains. Recently, a microfluidic device was developed to determine MIC by a 3D fluorescence visualization technique.19
There are several limitations to previous approaches. First, they can only analyse a single antibiotic concentration or a set of a few selected antibiotic concentrations. Second, they only offer static results and provide no information on how bacterial cells respond to the antibiotics during the incubation. Third, most approaches require the bacteria to be studied to be internally labelled by, for example, green fluorescent protein and can therefore only be used with genetically modifiable lab strains and not with clinical isolates. Instead of static values, pharmacodynamics, which investigates the concentration-dependent effects of a drug on the targeted microorganism over time, can provide a link between the antimicrobial activity and the susceptibility of a bacterial strain.20 A recent study demonstrated a microfluidic device for pharmacokinetics–pharmacodynamics modelling, which requires a few days for analysis.21 Further, mathematical models based on chemical kinetics have been built according to the mechanism of the antimicrobial and the population evolution of the strain.22 These models are the quantitative frameworks for interpreting the results of antimicrobial susceptibility testing and for the generation of novel hypotheses on the mechanism of antimicrobials targeting bacterial strains.21 This type of information is very important to evaluate the antibacterial effects of novel drugs and guide the usage of antibiotics.20 There is a need for fast methods and systems that could overcome the disadvantages of previous studies.
One promising solution is to use a microfluidic 2D gradient system.23 It is similar to the technology used in this work but a 2D cell culture in a small area reduces the cell numbers and, hence, gives less statistics. Still, this system complements ours well and is especially useful when studying single cells and their cell growth.
In this work, our aim was to develop a rapid and simple way to investigate antibiotic susceptibility temporally and at different concentrations and to offer high-resolution readouts with numerous concentrations and dynamic information on bacterial response under these concentrations. To achieve this, a continuous linear antibiotic gradient with gel-encapsulated bacteria was used to generate high-resolution readouts, which in principle can produce unlimited numbers of concentrations in a given range, and time-lapse microscopy was used to obtain dynamic information. Finally, the greyscale intensity in the micrographs is assumed as linear to the local cell concentration and continuous data analyses are made in regard to time and antibiotic concentration. A schematic representation of the procedure is shown in Fig. 1. In our tests, five antibiotics with different mechanisms against three common wild-type strains of Gram-positive and Gram-negative bacteria were investigated. Static measurements (minimum inhibitory concentration24) using the traditional methods were used as references, and we systematically investigated the bacterial growth curves at various drug concentrations. Finally, a pharmacodynamics model of streptomycin against Salmonella Typhimurium LT2 was generated and validated.
2 Materials and methods
2.1 Preparation and experiments using microfluidics
With a linear distribution of the antibiotic concentration, a specific concentration could be mapped to a certain location of the chip's length. With this information the relationship between the cell growth and the antibiotic concentration could be determined. Series of arrays were constructed into a matrix, where the time is determined along the columns while the width location–concentration was along the rows (Fig. 1C). Each column indicates the growth of the cells under a certain concentration of the antibiotics, and each row indicates the cell concentration of the whole chip at a certain time. Cell growth under nine concentrations were picked evenly and were plotted as continuous growth curves. These curves show a temporal distribution of cell growth (Fig. 1D, left panel). Also, the column value could be used and plotted as a growth distribution curve of cells at different concentrations, e.g., for MIC determination (Fig. 1D, middle panel).
2.2 Reference studies by traditional methods
2.3 Pharmacodynamics modelling
The change of concentration (growth) of the bacterial cells in the chamber without antibiotics over time can be described by, | (1) |
 | (2) |
 | (3) |
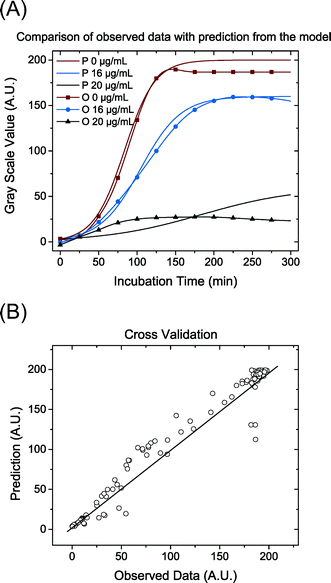
The data were analysed with a non-linear model fit algorithm using Mathematica (version 9.0.0.0). All data from the streptomycin experiment with S. Typhimurium LT2 and the control test (without antibiotics) were included in the data analysis. The cross-validation was used to perform model validation. One hundred concentration values were randomly chosen and the trials with these concentration values were excluded from the estimation of parameters. Then these excluded concentrations values were predicted by the model. Data from the test and the prediction from the model with the same concentration were plotted and presented graphically (Pharmacodynamics, Fig. 1D).
3 Results and discussion
3.1 Cell growth under an antibiotic gradient and MIC determination
Control experiments were performed to validate the growth of E. coli and S. Typhimurium in the microfluidic device without antibiotic addition. Both species showed logarithmic growth during the majority of the incubation time. The cell growth was uniform, showing that the growth of the bacteria was not influenced by their position in the chamber (Fig. S4 in the ESI†). We tested the microfluidics gradient setup with four different classes of mechanistically different antibiotics on three different bacterial species. Fig. 2 shows growth curves of S. Typhimurium and E. coli cells in the presence of three translation-inhibiting antibiotics. Similar shapes of growth curves were obtained for S. Typhimurium LT2 with addition of streptomycin (A) or tetracycline (B) and for E. coli with addition of spectinomycin (C). All three antibiotics inhibit bacterial growth by binding to the ribosome, thereby inhibiting bacterial protein synthesis.From the growth curves, there are indications on the uncertainty of the optical readout. There are no indications as to why the greyscale should change at very high concentrations of antibiotic. Hence, the uncertainty is approximately ±10 a.u. greyscale.
The output, cell growth against the antibiotic concentration gradient over time (Fig. 2A–C), indicates the relationship of the concentration effect between the antibiotic and the growth of the bacterial cells, where the steeper the drop in the cell growth, the higher the concentration effect is, i.e. the so-called all-or-nothing effect.29 From these curves, we can extract several parameters that are important for studies of the antimicrobial action of antibiotics. First, the bacterial growth rate at every concentration of drug within the gradient can be extracted from the plot of growth versus time (Fig. 2). Second, the minimum inhibitory concentration can be determined from the breakpoint where 90% of the growth is inhibited. Third, any effect of antibiotic on the bacterial growth at concentrations below the MIC can easily be assessed and monitored over time. All translation inhibiting antibiotics gave nice curves with the expected shape. The reduction of growth was directly dependent on the concentration of the drug with marked drops in growth around the MIC. The effect of antibiotic concentration on growth was already evident after 120 min.
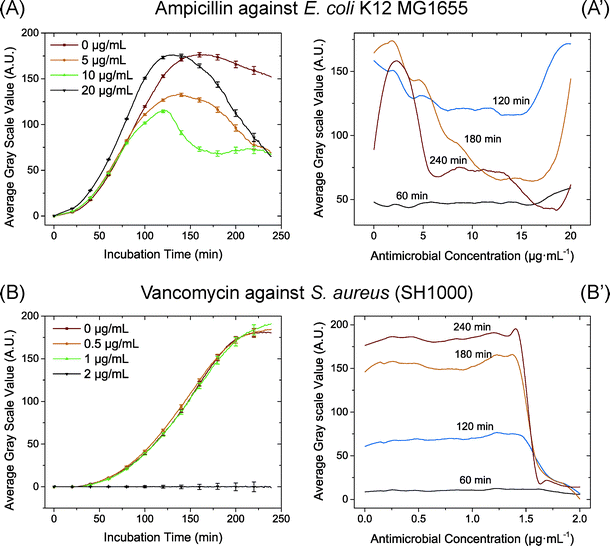
We also used antibiotics with a different mode of action, inhibition of the bacterial cell wall: ampicillin against E. coli and vancomycin against S. aureus (Fig. 3). These antibiotics have different targets; vancomycin binds the terminal D-alanyl-D-alanine residue of peptidoglycan, blocking its elongation,30 while beta-lactams like ampicillin bind as irreversible inhibitors of the penicillin binding proteins (transpeptidases) and inhibit cross-linking of the peptidoglycan forming a weaker cell wall.31,32 For S. aureus with the addition of vancomycin there was a clear threshold effect of growth inhibition as seen previously.33 For E. coli with the addition of ampicillin we observed a marked difference in the growth curves, reflecting the different mode of action of this antibiotic. Before 100 min, there was no significant difference in growth between cells at different ampicillin concentrations. Cells subjected to higher ampicillin concentrations even showed slightly increased growth (Fig. 3 (A)). However, after 120 min, cells growing at concentrations higher than 5 μg mL−1 began to decrease in number (due to cell disruption), thus yielding a decrease in the average greyscale value. At 240 min there was a clear breakpoint at which the bacteria most probably lysed. This breakpoint coincides very well with the MIC measured on plates by standard methods. This variation in growth curves is an example of the mechanistic difference between ampicillin that still allows growth until the cells lyse and the protein synthesis inhibiting antibiotics where the growth rate is directly affected by the inhibition of translation. In our study, the optical intensity is used to present the growth of the bacteria, which will reflect increased cell size or cell number indiscriminately. In previous studies with flow cytometry, it was found that the bacteria increased in cell size when treated with high concentrations of ampicillin.33–35 We believe that an enlarged cell size was the dominant reason for the increased optical intensity early in the experiment.
The growth to concentration distribution may also have potential in determining the MIC value. For instance, from Fig. 3 (B′), it is easy to determine the S. aureus MIC for vancomycin to 1.5 by finding the breakpoint at the antibiotic concentration where inhibition was observed in the growth curve. When using the same relative greyscale value of 75 of 255 at 240 min as an indicator for MIC at the different chips, each MIC value determined by the chip is between the values for MIC determined by broth dilution and Etest (Table 1). Not surprisingly, most of the MIC values determined by our method are more in agreement with Etest than with broth dilution, given the slight differences in bacterial growth in liquid (broth dilution) and on solid media (Etest and our chip). Compared to other microfluidic approaches to determine MIC such as that in ref. 19, our approach requires significantly less time, without introducing any fluorescence labelling and dedicated fluorescence microscopy.
| E. coli | S. Typhimurium LT2 | ||||||
|---|---|---|---|---|---|---|---|
| Antibiotic | CLSI | Etest | Chip | Antibiotic | CLSI | Etest | Chip |
| Ampicillin | 4–8 | 4 | 5 | Streptomycin | 16–32 | 16 | 18 |
| Spectinomycin | 16–32 | 16 | 18 | Tetracycline | 1–2 | 0.5 | 0.5 |
| S. aureus | |||
|---|---|---|---|
| a Unit: μg mL−1. | |||
| Antibiotic | CLSI | Etest | Chip |
| Vancomycin | 1–2 | 1.5 | 1.5 |
By comparing the time-cost of our microfluidic approach and traditional analysis, it is possible for significant savings in time in our microfluidic approach. Noticeable differences in cell growth were observed already after 2 h incubation. To determine the MIC break points, our approach may give a result with incubation as short as 2 h 30 min when streptomycin and tetracycline were used for S. Typhimurium LT2 and vancomycin was used for S. aureus. For measuring the MIC of ampicillin for E. coli a longer incubation time was needed but still only 4 h. The data analysis is fast and only a few seconds are needed to provide the full data from the images. However, both the broth dilution method and the Etests need overnight incubation for at least 18 h.
As mentioned above, a continuous concentration gradient offers higher resolution readouts than traditional approaches. Furthermore, with a continuous concentration and temporal observation, a significantly larger amount of information was obtained as compared to the standard methods (Fig. 2). For instance, in traditional approaches, the concentrations are predefined, and to decrease the large amount of laborious operations a limited set of concentrations are used, which somewhat decrease the details observed. This is especially true when a steep concentration–effect curve is obtained. Replacing the traditional 2-fold-dilution based concentration series by a linear concentration gradient will generate a more detailed picture of growth inhibition. With the high resolution of the data we can extract from a single group of experiments, we created 3D diagrams of bacterial growth curves as shown in Fig. 4. This helps in finding more detailed information without redoing the experiments. For instance, when comparing Fig. 4 (A) and (B), we will find an intuitive and detailed description of the growth difference between antibiotics with different mechanisms. With our camera, the resolution of this method can reach the highest antibiotic concentration present on one of the sides of the linear gradient divided by 1500. In Fig. 4, each pixel step on the Y-axis represents a step of 13.3 ng mL−1.
In summary, besides giving researchers a more detailed and faster method to look at the interaction between antibiotic and bacteria, our proposed approach has potential in offering fast high-resolution static results.
3.2 Pharmacodynamics study
As a demonstration, a pharmacodynamics model for the impact of streptomycin on S. Typhimurium LT2 growth was built and also cross-validated to experimental data (Fig. 5). The parameters used are listed in Tables 2 and 3. The concentration–effect curve of streptomycin against S. Typhimurium LT2 has a steep sigmoid shape according to the parameters and with a p value of 6.97, i.e. significantly greater than 1. This steep relationship can also be revealed from the concentration of the cell growth distribution (Fig. 5 (A)). The EC50 value estimated from the model gives us the efficiency of the antibiotic, and for streptomycin against S. Typhimurium LT2 it is estimated to be 16 μg mL−1 (Table 3). The value for EC50 is close to the MIC value of 18 μg mL−1 as determined by three different methods, indicating that with the addition of a small amount of streptomycin the level of cell death can move from 50% to close to 100% efficiency. This also confirms that the concentration–efficiency curve has a sigmoid-like shape, indicating that streptomycin and the target ribosome molecules have a cooperative binding effect. With this simple device, we demonstrate the possibility of utilizing the large amount of dynamic data provided to estimate and validate the mathematical model and obtain growth and pharmacodynamics parameters that are important for evaluation of the antibacterial effect on an antibiotic.| Parameters | Estimated value | Standard error (%) |
|---|---|---|
| r | 0.025 | 0.059 |
| N max | 202.003 | 3.84 |
| Parameters | Estimated value | Standard error (%) |
|---|---|---|
| p | 6.97 | 4.26 |
| EC50 | 16.00 | 2.89 |
| E max | 1.33 | 0.72 |
4 Conclusions
Time-lapse microscopy using a microfluidic linear gradient 3D culture device with bacterial cells was proposed for investigating antibiotic susceptibility. A large amount of dynamic data on the bacterial behaviour was obtained in this process, e.g. growth curves and cell behaviours in the range of concentrations of the antibiotics gradient at any given time point. The presented results show that this approach can rapidly obtain MIC values and the total yield of bacterial growth. We also show that the produced data could be used for pharmacodynamics studies that are important to evaluate an antibiotic candidate or further study the effect of antibiotics on bacteria. In addition, this approach is flexible and can easily be extended to any kind of bacterial strain and to studies such as antimicrobial combination therapy or multi-resistant bacteria with minor revision of the device.Acknowledgements
The authors thank Dr. Sara Thorslund, Gradientech AB, for discussions and the generous donation of microfluidic culture devices used in this work. Z. G. Wu holds a junior researcher position funded by the Swedish Research Council (contract no. 621-2010-5443).References
- J. El-Ali, P. K. Songer and K. F. Jensen, Nature, 2006, 442, 403 CrossRef CAS PubMed.
- Z. G. Wu, B. Willing, J. Bjerketorp, J. K. Jansson and K. Hjort, Lab Chip, 2009, 9, 1193 RSC.
- J. Q. Boedicher, L. Li, T. R. Kline and R. F. Ismailov, Lab Chip, 2008, 8, 1265 RSC.
- D. C. Savage, Annu. Rev. Microbiol., 1977, 31, 107 CrossRef CAS PubMed.
- D. I. Andersson, Curr. Opin. Microbiol., 2003, 6, 452 CrossRef CAS PubMed.
- H. C. Neu, Science, 1992, 257, 1064 CAS.
- J. H. Jorgensen and M. J. Ferraro, Clin. Infect. Dis., 2009, 49, 1749 CrossRef CAS PubMed.
- L. F. Joyce, J. Downes, K. Stockman and J. H. Andrew, J. Clin. Microbiol., 1992, 30, 2709 CAS.
- G. V. Doern, J. Clin. Microbiol., 2011, 49, S4 CrossRef PubMed.
- I. Sinn, P. Kinnunen, T. Albertson, B. H. McNaughton, D. W. Newton, M. A. Burns and R. Kopelman, Lab Chip, 2011, 11, 2604 RSC.
- K. Churski, T. S. Kaminski, S. Jakiela, W. Kamysz, W. Baranska-Rybak, D. B. Weibel and P. Garstecki, Lab Chip, 2012, 12, 1629 RSC.
- R. Iino, K. Hayama, H. Amezawa, S. Sakakihara, S. H. Kim, Y. Matsumono, K. Nishino, A. Yamaguchi and H. Noji, Lab Chip, 2012, 12, 3923 RSC.
- C. H. Chen, Y. Lu, L. Y. Sin, K. E. Mach, D. Zhang, V. Gau, J. C. Liao and P. K. Wong, Anal. Chem., 2010, 82, 1012 CrossRef CAS PubMed.
- M. Kalashnikov, J. C. Lee, J. Campbell, A. Sharon and A. F. Sauer-Budge, Lab Chip, 2012, 12, 4523 RSC.
- N. J. Cira, J. Y. Ho, M. E. Dueck and D. B. Weibel, Lab Chip, 2012, 12, 1052 RSC.
- I. Peitz and R. van Leeuwen, Lab Chip, 2010, 10, 2944 RSC.
- J. Choi, Y. G. Jung, J. Kim, S. Kim, Y. Jung, H. Na and S. Kwon, Lab Chip, 2013, 13, 280 RSC.
- K. P. Kim, Y.-G. Kim, C.-H. Choi, H.-E. Kim, S.-H. Lee, W.-S. Chang and C.-S. Lee, Lab Chip, 2010, 10, 3296 RSC.
- R. Takagi, J. Fukuda, K. Nagata, Y. Yawata, N. Nomura and H. Suzuki, Lab Chip, 2013, 138, 1000 CAS.
- G. L. Drusano, Nat. Rev. Microbiol., 2004, 2, 289 CrossRef CAS PubMed.
- J. H. Sung, C. Kam and M. L. Shuler, Lab Chip, 2010, 10, 446 RSC.
- B. R. Levin and K. I. Udekwu, Antimicrob. Agents Chemother., 2010, 54, 3414 CrossRef CAS PubMed.
- B. Li, Y. Qiu, A. Glidle, D. Mcllvenna, Q. Luo, J. Cooper, H.-C. Shi and H. Yin, Anal. Chem., 2014, 86, 3131 CrossRef CAS PubMed.
- J. M. Andrews, J. Antimicrob. Chemother., 2001, 48(suppl. S1), 5–16 CrossRef CAS PubMed.
- J. H. Humphrey and J. W. Lightbown, J. Gen. Microbiol., 1952, 7, 129 CrossRef CAS PubMed.
- W. Derbyshire and I. D. Duff, Faraday Discuss. Chem. Soc., 1974, 57, 243 RSC.
- J. H. Wang, J. Am. Chem. Soc., 1954, 76, 4755 CrossRef CAS.
- N. L. Dayneka, V. Garg and W. J. Jusko, J. Pharmacokinet. Biopharm., 1993, 21, 457 CrossRef CAS.
- E. I. Nielsen, A. Viberg, E. Löwdin, O. Cars, M. O. Karlsson and M. Sandström, Antimicrob. Agents Chemother., 2007, 51, 128 CrossRef CAS PubMed.
- B. Kasten and R. Reski, J. Plant Physiol., 1997, 150, 137 CrossRef CAS.
- K. Izaki, M. Matsuhashi and J. L. Strominger, Proc. Natl. Acad. Sci. U. S. A., 1966, 55, 656 CrossRef CAS.
- E. Löwdin, I. Odenholt and O. Cars, Antimicrob. Agents Chemother., 1998, 42(10), 2739–2744 Search PubMed.
- O. V. Martinez, H. G. Gratzner, T. I. Malinin and M. Ingram, Cytometry, 1982, 3, 129 CrossRef CAS PubMed.
- V. A. Gant, G. Warnes, I. Philips and G. F. Savidge, J. Med. Microbiol., 1993, 39, 147 CrossRef CAS PubMed.
- M. Walberg, P. Gaustad and H. B. Steen, J. Antimicrob. Chemother., 1996, 37, 1063 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4lc00451e |
| ‡ Who contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2014 |