Cell patterning with a heptagon acoustic tweezer – application in neurite guidance

Abstract

Accurate control over positioning of cells is a highly desirable feature in tissue engineering applications since it allows, for example, population of substrates in a controlled fashion, rather than relying on random seeding. Current methods to achieve a differential distribution of cells mostly use passive patterning methods to change chemical, mechanical or topographic properties of surfaces, making areas differentially permissive to the adhesion of cells. However, these methods have no ad hoc control over the actual deposition of cells. Direct patterning methods like bioprinting offer good control over cell position, but require sophisticated instrumentation and are often cost- and time-intensive. Here, we present a novel electronically controlled method of generating dynamic cell patterns by acoustic trapping of cells at a user-determined position, with a heptagonal acoustic tweezer device. We demonstrate the capability of the device to create complex patterns of cells using the device's ability to re-position acoustic traps by using a phase shift in the acoustic wave, and by switching the configuration of active piezoelectric transducers. Furthermore, we show that by arranging Schwann cells from neonatal rats in a linear pattern we are able to create Bands of Büngner-like structures on a non-structured surface and demonstrate that these features are able to guide neurite outgrowth from neonatal rat dorsal root ganglia.

---

Introduction

Spatial control of cell positions is of particular importance in the field of tissue engineering. In complex tissues, cells rely on a variety of cues from their environment, such as cell–cell contacts (homo- or heterotypic), substrate adhesion and mechanical forces or extracellular stimuli such as signalling molecules (auto- or paracrine).¹ These factors are dependent on accurate positioning of cells in their microenvironment, which remains a major challenge for replication of a functional histoarchitecture in tissue engineering.

A variety of microscale methods for patterning cells on a substrate with μm accuracy have been developed in recent years. They are based either on the direct patterning of cells, or indirect patterning via chemical,² topographic,³ or mechanical^4,5 modification of surfaces to direct differential cell adhesion. Direct cell patterning has been demonstrated with inkjet or laser assisted cell printing,^6,7 as well as electrical force (dielectrophoresis^8,9), optical force (laser guided direct writing¹⁰ and laser guided micropatterning¹¹) and magnetic forces using iron oxide-labelled cells.¹² Indirect patterning by selective surface modification is mostly done by microcontact printing (μCP) using poly-di-methyl-siloxane (PDMS) stamps fabricated from a master made using photolithography.¹³ The PDMS stamp is then used to print self-assembling monolayers of derivatized alkanethiols, on to a solid substrate, that promote matrix protein and thus cell adhesion. Alternatively, extracellular matrix proteins can also be printed directly on a substrate to permit cell adhesion.¹⁴ PDMS stamps have also been used to create microfluidic devices for cell and protein patterning.¹⁵ Other approaches use dynamic substrates, i.e. “switchable surfaces”, whose cell adhesiveness can be modified by light,¹⁶ temperature¹⁷ or voltage.¹⁸

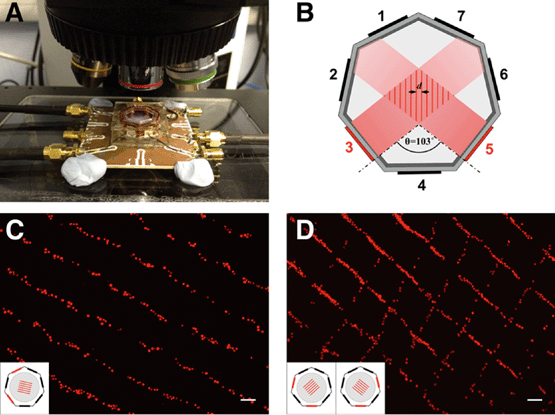
While these methods have been successfully employed to create cell patterns and co-cultures of varying complexity, they often require specialized equipment, and can be cost- and time intensive. Furthermore, many of these methods are inflexible and do not offer dynamic ad hoc geometric control over the pattern; in the case of PDMS stamps, for example, the pattern is limited to that of the lithographic mask used to create the stamp. To address some of these shortcomings we have recently developed a portable device based on acoustic force for spatial manipulation of cells and particles¹⁹ (Fig. 1A). The use of acoustic force for immobilization of cells is well established, employing either bulk or surface acoustic waves in a resonant structure that produces a fixed standing wave pattern.^20–22 Cells or dense particles agglomerate at nodes with lowest acoustic pressure. The position of these pressure nodes is determined by the geometry of the device and the frequency at which piezoelectric transducers generating the standing acoustic wave are operated. Control over the position of the pressure nodes in conventional transducer-reflector devices is therefore limited. Our device overcomes this limitation by using a heptagonal geometry with transducers that generate travelling waves. The interference pattern produced at the intersection of two or more forward travelling waves creates a nodal pattern that is capable of trapping cells²³ (Fig. 1B). Waves are either absorbed at the vertex opposing the transducer, or scattered away from the central region of the device. Because the device operation relies on the use of travelling waves, the precise interference pattern, hence the acoustic pressure nodes, may be electronically controlled by adjusting the phase of the excitation to each transducer.¹⁹ The distance between two adjacent pressure nodes is given by d = θ/2 sin(λ/2), where θ is the angle formed between the normals to the planes of the active transducers. In a regular heptagonal device with sides numbered 1–7, when transducers placed on two adjacent odd, or equivalently even-numbered, sides and activated at a frequency of 4 MHz (λ = 375 μm in water), θ = 103°. The separation distance between nodes is therefore d = 240 μm. Using the phase shifting capabilities of the device, linear acoustic pressure nodes can then be moved linearly to any desired position in the range d.¹⁹

Fig. 1 Device setup and simple cell patterning. (A) Setup of the heptagon acoustic tweezer on a microscope stage (Olympus BX51). The device is connected to a wave generator on three connectors, allowing each of the connected transducers (1, 3 and 5) to be addressed individually. A 4× objective is used to observe the experiment. (B) Principle of device operation. Acoustic waves emanating from two activated non-adjacent transducers (3 and 5, highlighted in red) interfere at the center of the device, combining to form a standing wave pattern where nodes of minimal acoustic energy act as acoustic traps (schematically depicted as vertical red lines). 1–7, piezoelectric transducers, black – inactive, red – active; dashed lines, normals to the plane of active transducers; d, distance between two neighbouring acoustic traps determined by the angle θ. (C) Pattern of MitoTracker Red labelled C2C12 cells aligned in parallel using a 1–3 transducer configuration (see inset). (D) “Lattice” pattern of C2C12 cells generated by two successive patterning steps (see inset). Scale bars – 100 μm.

Our aim in this study was to investigate successive patterning of cells and using acoustic tweezers for an application in tissue engineering. We have previously shown that acoustic tweezers are capable of trapping micron-scale particles, and cells at nodes of minimal acoustic pressure.²³ Here, we demonstrate complex multistep cell patterning using phase shifting and varying transducer configurations to arrange cells in six different successive patterns. Furthermore, we show the usefulness of a pattern generated by the device for tissue engineering. In response to peripheral nerve injury, a natural aligned structure termed “Bands of Büngner” develops during peripheral nerve repair.²⁴ These Bands of Büngner consist of aligned Schwann cells and are the natural substrate that regenerating neurons follow and use to reconnect to their peripheral targets. A variety of methods have been developed to create aligned structures that guide Schwann cells in vitro and in vivo with the aim to create an environment conducive to optimal nerve regeneration. Apart from mechanically aligning Schwann cells by directional tension within a collagen gel²⁵ most techniques rely on indirect patterning of cells by proxy of their interaction with a patterned substrate. Substrate features that align neuronal regeneration can be linear chemical micropatterns,^26,27 microtopographies,²⁸ and static electrical fields.²⁹ So far direct cell patterning, e.g. with cell printing, optical trapping or magnetic guidance, has not been used to create replicates of Bands of Büngner to the best of our knowledge. Therefore we decided to explore the capability of the heptagon acoustic tweezer device for direct patterning of Schwann cells, obviating the need for prior treatment of the substrate. We show that ultrasonically patterned Schwann cells form linear arrangements resembling Bands of Büngner that serve to guide neurite outgrowth from rat dorsal root ganglia (DRG), in an in vitro model for peripheral nerve regeneration.

Experimental

Sample preparation including cell culture and fluorescent labelling, magnetic labelling and separation of Schwann cells, and image analysis of neurite outgrowth are described in the ESI.†

Acoustic tweezer operation

The design and construction of the heptagon acoustic tweezer is described in detail elsewhere.¹⁹ The transducers were driven by a 4 MHz sine wave (corresponding to a wavelength of 375 μm in water) at an amplitude of 8 Vpp, generated from an arbitrary waveform generator (TGA12104, Thurlby Thandar Instruments Ltd, UK). The waveform generator enabled synchronisation between channels and independent control of frequency, phase and amplitude to each transducer. Signals were amplified and electronically matched using high-speed buffers (BUF634T, Texas Instruments UK).

Prior to the patterning experiments, a layer of 1.5% agar in phosphate buffered saline (PBS) was deposited inside the heptagon cell, filling the cavity up to approximately halfway (~1.2 mL) in order to reduce acoustic streaming that can occur in liquid medium.³⁰

Cell patterning

A 13 mm glass cover slip coated with poly-L-lysine (Sigma-Aldrich) or laminin (AMS Biotechnology, UK), to facilitate cell adhesion, was placed at the centre of the cavity and covered with 0.5 mL of DMEM. The differently labelled cells were introduced to the cavity in successive stages, with different patterns of acoustic excitation for each. 50–100 μl of cells (25–50 000 cells) were carefully added to the centre of the device and left to adhere under the influence of the acoustic field for 30–60 min before altering the acoustic excitation for the next round of cell patterning. After patterning was complete and cells had adhered sufficiently strong, the coverslips were transferred to a tissue culture plate for further incubation if required.

Patterning of Schwann cells for DRG neurite outgrowth

Schwann cells at P0 or P1 were detached from tissue culture flasks with Trypsin/EDTA and resuspended at a concentration of 5 × 10⁵ cells mL⁻¹ in DMEM/F12. 5 × 10⁴ cells were patterned in the heptagon acoustic tweezer using two active transducers for 30 min to generate a linear pattern as described in the main text. After letting the patterned cells adhere for at least another hour, the 13 mm coverslip was carefully removed with forceps from the device, transferred to a 24 well plate and 500 μl of culture medium added, taking care to prevent dislodging of cells. Patterned Schwann cells and randomly seeded controls were incubated for 24 h at 37 °C (5% CO₂, 100% humidity) before initiating co-culture with DRGs.

Co-culture of DRG and Schwann cells

Thoracic DRGs were isolated from 2 day-old neonatal Sprague-Dawley rats. Rats were euthanized by a Euthatal® injection and then dissected in accordance with Home Office regulation. After removal of muscle and bones dorsally around the spinal cord, the DRGs were extracted with surgical tweezers and processed to remove remaining nerve tissue.

The freshly isolated rat neonatal DRGs were placed onto the patterned area at the center of the coverslip in SCGM supplemented with 10 ng mL⁻¹ NGF 2.5S (Life Technologies, UK). The media level was reduced to 250 μl in order to permit attachment of DRGs and incubation continued for 4 days. One half of the media was exchanged daily.

DRGs placed at the center of coverslips with randomly seeded Schwann cells and treated identically throughout served as controls.

Immunofluorescence

Cells were fixed in 4% formaldehyde, permeabilized (10.3 g sucrose, 0.292 g NaCl, 0.06 g MgCl₂, 0.476 g HEPES 0.5 ml Triton X-100 in 100 ml PBS) and blocked using 1% bovine serum albumin (BSA) in PBS. Neurons were immunostained with a βIII-tubulin antibody (mouse anti-TU-20, Santa Cruz Biotechnologies, USA), followed by biotinylated anti-mouse IgG and Fluorescein-labelled streptavidin (Vector Laboratories Ltd, UK). All antibodies were diluted 1 : 100 in PBS/1% BSA.

Microscopy & image analysis

For microscopic observation the device was placed on the stage of an upright epifluorescence microscope (Olympus BX51, Olympus UK; Fig. 1A) equipped with a tri-pass filter cube (U-M61002, DAPI/FITC/TexasRed) and a motorized stage (H1P1BX, Prior Scientific UK). Micrographs were taken using a 4 or 5× objective with a cooled CCD camera (QImaging) and the ImagePro Plus 7.0 software package (Media Cybernetics, USA). Tiled images of neurite outgrowth from DRGs were taken with the StagePro module of the ImagePro Plus software; the scan area was manually defined to encompass the entire area of interest and images stitched automatically. Image analysis for measuring distances and angles was performed using the corresponding tools in ImageJ 1.44.³¹ Qualitative and quantitative analysis of the directionality of neurite outgrowth was performed using the ImageJ plug-in OrientationJ³² (see ESI† for more details). A chi-square test was performed to compare the frequency distributions obtained for neurite outgrowth on patterned and randomly seeded Schwann cells.

Results

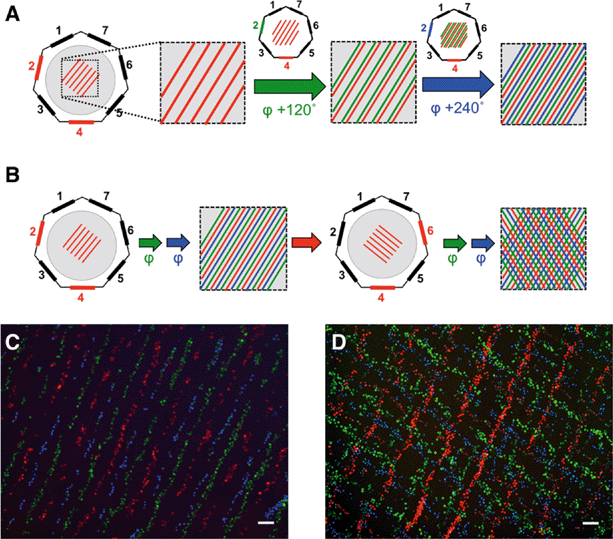
Initial experiments to demonstrate the feasibility of the approach were conducted using fluorescently labelled C2C12 cells (ATCC CRL 1772). Three sets of C2C12 stained with different fluorescent dyes (MitoTracker Green, MitoTracker Red and Hoechst 33342) were used in order to visualize successive patterning events. Once we had demonstrated to our satisfaction that acoustic tweezing could be used to manipulate multiple batches of cells in successive cycles, we went on to demonstrate that manipulated cells could be used to in turn align neurite outgrowth in a peripheral nerve injury model.

Acoustic trapping

It was first necessary to show that lines of cells could be formed using the acoustic tweezer, and that they would adhere and begin to culture on a planar surface as determined by the user. The surface was a 13 mm PLL-coated glass coverslip inserted into the centre of the acoustic tweezer device. The cell alignment is illustrated in Fig. 1C where C2C12 that were stained with MitoTracker (MT) red were patterned using transducer pair 2–4.

Patterning with transducer switching. Complex cell patterns can be generated using the heptagon device by operating different sets of transducers in succession. C2C12 cells stained with CellTracker (CT) Orange dye were initially patterned on a PLL-coated coverslip in parallel lines using transducers 2 and 4 as in the previous experiment (Fig. 1C). After cells had adhered to the substrate for 30 min, the active transducers were switched from a 2–4 to a 4–6 configuration. The pattern of acoustic pressure nodes was rotated by 2 × 360°/7 = 102.9° by this action. Fig. 1D shows the result of a patterning experiment after addition of a second aliquot of CT Orange stained C2C12 cells to the initially patterned lines and left for at least a further 30 min, up to 60 min. Consequently, the combination of the two successive additions of cells formed a lattice pattern at the centre of the device. Measurement of the obtuse angle formed by the patterned cells with ImageJ confirmed that the lines intersected at 102 ± 4° (n = 10). We conclude that switching the transducer configuration could be used to create lattice patterns at angles defined in accordance with the geometry of the heptagon.

Patterning with phase shift. Next, we explored the capability of the device to dynamically create complex cell patterns using phase shifts to re-position acoustic pressure nodes. As before, C2C12 cells stained with MT Red were patterned in lines on a PLL-coated coverslip using a 2–4 transducer configuration. After a period of 45 min the cells had adhered to the substrate and the phase of the acoustic wave emanating from transducer 2 was shifted by 120° (for a schematic depiction see Fig. 2A). This change in phase resulted in a shift of acoustic pressure nodes by 80 μm at the centre of the device (60 μm per 90° shift, i.e. 80 μm for 120° shift). Adherent cells were not moved by this shift of the position of the pressure nodes of the acoustic pattern. A fresh batch of cells, this time labelled with MitoTracker Green dye, was added to the device and left to adhere for 45 min, as before. Finally, another phase shift of transducer 2, again by 120° (for a total of 240°) was performed and C2C12 cells labelled with Hoechst 33342 (blue) were added to the device. Fig. 2C shows the final result of this patterning experiment. Cells had adhered in a pattern of parallel lines with a spacing of ~80 μm between neighbouring ones. Detailed evaluation showed the separations to be 86 ± 6 μm between red and green, 76 ± 10 μm between green and blue, 82 ± 7 μm between blue and red for n ≥ 21. The separation between cells of the same colour should ideally be 240 μm was experimentally found to be 239 ± 8 μm, 237 ± 8 μm and 241 ± 7 μm for red, green and blue labelled cells, respectively, for n ≥ 15. The error between the experimentally obtained values and expectation is attributed to slight deviations in the geometry of the device from that of a perfect heptagon.

Fig. 2 Complex cell patterning by phase shift and transducer switching. (A) Cartoon depicting the generation of a complex striped pattern by applying successive phase shifts of an acoustic wave at one transducer. Differently colored lines (red, green and blue) represent successive patterning events. Active transducers are highlighted, with the colour indicating the phase φ of the acoustic wave emanating from the transducer: red – 0°, blue – 120°, green – 240°. (B) Schematic representation of phase shifts and transducer switches used to pattern cells in a “tartan”-like pattern. Active transducers are highlighted in red, coloured arrows indicate successive phase shifts (green 120°, blue 240°), red arrow indicates a transducer switch. Shown are schematic representations of the pattern obtained before the transducer switch and the final pattern. (C) Composite of fluorescent micrographs taken after patterning fluorescently labelled C2C12 cells as depicted in (A). (D) Composite of fluorescent micrographs taken after patterning fluorescently labelled C2C12 cells as depicted in (B). Cells in (C) and (D) stained with MitoTracker Red, MitoTracker Green and Hoechst 33342, scale bar 100 μm.

Although 90% of cells remained attached where they had initially settled, some (~10%) were moved to the new position of the pressure node when the phase was shifted, as evident by the presence of green (11.4%) and red cells (9.1%) mixed with the blue cells, which had been patterned last (Fig. 2C).

Patterning with transducer switching and phase shift. To complete our initial patterning study, we investigated whether or not a combination of phase-shifts and transducer switching could be employed to create an even more elaborate cellular pattern. We started out by creating a striped cell pattern using MT Red, MT Green and Hoechst 33342 stained C2C12 cells and used two successive 120° phase shifts (+120°, +240°) of the acoustic wave at a 2–4 transducer configuration. After patterning the three sets of labelled cells in this direction, we switched to a 4–6 active transducer setup to pattern cells in a second direction (at an ~103° angle to the first). This was followed again by two successive 120° phase shifts of the acoustic wave, in order to pattern all three labelled cell types in a parallel fashion at the new angle (see Fig. 2B for a schematic). In this manner, we were able to dynamically build up the complex pattern of cell tissue seen in Fig. 2D – a “tartan-like” arrangement of the cells, essentially a superposition of two successively derived striped patterns at an angle of 103° to one another. From these experiments we concluded that a high degree of control over cell position and orientation could be achieved using this acoustic tweezer.

Schwann cell patterning for neurite guidance

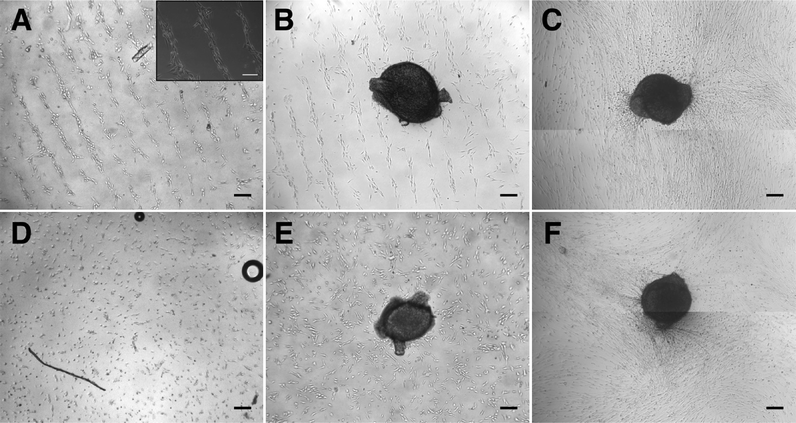
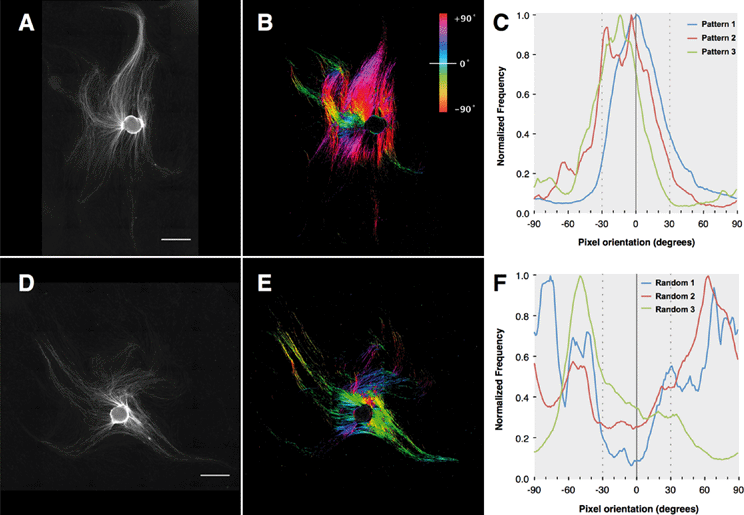
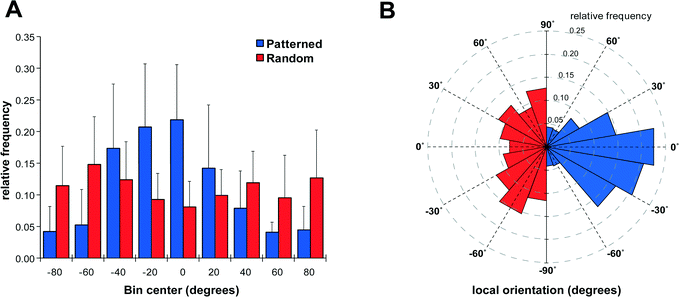
After establishing the capability of the acoustic tweezer for cell patterning, we aimed to test its usefulness in a model system for tissue engineering, specifically in peripheral nerve regeneration. To this end we deposited Schwann cells isolated from neonatal rat sciatic nerves in a linear pattern on PLL-coated cover slips using the heptagon acoustic tweezer device for 30 min, in a 1–3 transducer configuration. After 24 h incubation the cells largely retained the linear pattern and partially arranged in a columnar fashion reminiscent of bands of Büngner (Fig. 3A + inset), formed by denervated Schwann cells during peripheral nerve regeneration. In contrast, randomly seeded Schwann cells displayed no preferential orientation after overnight incubation (Fig. 3D). There was no difference in the number of rounded – non-proliferating cells between the two groups (e.g. in Fig. 3A, D), indicating that acoustic tweezing did not affect cell survival. Neonatal rat DRGs placed on patterned and randomly seeded Schwann cells (Fig. 3B and E, respectively) both had substantial neurite outgrowth after 4 days in culture (Fig. 3C and F).

Fig. 3 Seeding of DRGs on acoustically patterned Schwann cells. Schwann cells patterned in lines have formed columnar structures 18 h after seeding (A), while randomly seeded cells have not (D). Explanted neonatal rat DRGs are positioned at the center of the coverslip (D, E) and neurite outgrowth from DRGs is assessed after 4 days (C, F). Top panels – patterned Schwann cells, lower panels – randomly seeded Schwann cells. Scale bars 200 μm. Inset shows Bands of Büngner-like structures at higher magnification using a phase contrast objective, scale bar 100 μm.

In order to visualize the direction of outgrowing neurites, cells were stained for βIII-tubulin, which revealed an extensive network of neurites on patterned as well as non-patterned Schwann cells (Fig. 4). Neurites growing on a patterned Schwann cell layer exhibited an orientation along a pattern axis, while those on randomly seeded Schwann cells projected networks in several directions (Fig. 4A and D). We used the ImageJ plug-in OrientationJ³² to obtain a qualitative and quantitative measure of neurite orientations. OrientationJ derives the local orientation and isotropic values (coherency and energy) of every pixel in an image and outputs a color-coded representation of local angles and isotropy of features. Fig. 4B and E show the output generated for the images in Fig. 4A and D respectively. For those neurites outgrowing on patterned Schwann cells (Fig. 4B) a clear preference for directions around +90 and −90 degrees, which is in good accordance with the original Schwann cell pattern (Fig. 3B) is evident. The neurites on randomly seeded Schwann cells appear to show a set of two preferential orientations as well, which could be due to a bias e.g. by the position of the nerve stumps, and maybe some neurite associated self-organization of the underlying Schwann cell layer (see difference in cell pattern between 3E and 3F). However, compared to the axon network on patterned Schwann cells, other local angles are just as strongly represented, indicating a more random pathfinding of the axon network. This becomes even more evident when comparing the local angle histograms from three separate experiments (Fig. 4C and F). The local angles of neurites growing on patterned Schwann cells display a preferred direction around the initial angle of the respective Schwann cell pattern (defined as zero degrees) compared to the random controls (where zero denotes the horizontal axis of the image), indicating that patterned Schwann cells provide an efficient guidance cue for neurites growing out from the DRGs. A second analysis using OrientationJ's Measure function, which determines the dominant orientation (as well as coherency and energy) of features within a user defined ROI, allowed us to include faintly stained areas, that were excluded from the measurement of pixel orientation due to the detection threshold being set for the whole image. Using a custom-written macro each image was divided into adjoining 250 × 250 pixel ROIs that were individually analyzed, if their integrated density value exceeded a user-defined threshold. In this way we were able to include even faintly stained neurites in our analysis (Fig. S1†). The relative frequency distributions of local directions, obtained with this analysis are shown in Fig. 5, using 20 degree bins centered on zero degrees (Fig. 5A). Despite experimental variability, neurites growing on patterned Schwann cells show a clustering around the zero degree orientation, with ~60% of the analyzed areas oriented within ±30 degrees of the initial Schwann cell pattern, and angles >50 degrees relative to the pattern clearly underrepresented. In contrast the neurite outgrowth on randomly seeded Schwann cells shows no preferred direction (Fig. 5B). A chi-square test showed a highly significant difference between the two frequency distributions (p ≪ 0.001), indicating that the initial patterning of Schwann cells by acoustic force had a significant influence on the subsequent outgrowth of neurites from explanted DRGs.

Fig. 4 Analysis of neurite outgrowth on patterned and non-patterned Schwann cells. Representative images of a β3-tubulin stain of neurites outgrowing from DRGs on patterned (A) and randomly seeded Schwann cells (D) after 4 days and false-color representation of pixel orientations computed using the ImageJ plug-in OrientationJ (B, E). Scale bars 1 mm. (C) and (F): normalized frequencies of pixel orientations obtained with OrientationJ for three different patterned (C) and randomly seeded cover slips (F). Pixel orientation in (C) relative to the initial angle of patterned Schwann cells.

Fig. 5 Direction of neurite outgrowth on patterned and non-patterned Schwann cells. (A) Histogram of neurite orientations on patterned and randomly seeded Schwann cells as determined with OrientationJ's Measure function. Zero degrees is defined as either the initial angle of Schwann cell patterning (patterned) or the horizontal axis (random). Bin size is 20 degrees centred on zero, error bars represent standard deviation from n = 6 different patterning events. (B) Wind rose plot of the data in (A) illustrating bias introduced to neurite outgrowth by patterning Schwann cells. Note that the dataset for neurites on random seeding have been mirrored in order to prevent overlap.

Discussion

In the present study we have shown that the acoustic tweezer is capable of trapping cells at predetermined positions and, by using the ability to switch phase, and operate different sets of transducers, we can generate complex cellular patterns. Compared to other methods such as laser guided direct writing, the new device has the advantage of being small, electronically controlled, flexible in the patterning and can be easily integrated with standard microscopy equipment. The device can handle high cell densities and consequently has a relatively good throughput, which is very beneficial for applications in tissue engineering. Additionally it allows handling of different cell types sequentially; if an initially patterned cell type is left to adhere for a sufficient amount of time (usually 30 min) these cells stay in position when the position of the acoustic traps is shifted. Another cell type can then be seeded at the newly positioned pressure nodes, as exemplified by the patterning experiments with fluorescently labelled cells. The technique is made possible because cells, once adhered to a surface, are sufficiently firmly bound that the acoustic forces exerted by the tweezing device cannot move them. Therefore, successive additions of cells can be manipulated independently from previous aliquots of cells. The forces exerted onto individual cells by this acoustic tweezer is in the range 2–10 pN, or 71 kPa.³⁰ However, the forces needed to detach individual cells are of the order of tens, to several hundreds of nN.^33–35 Even individual integrin/fibronectin binding events can reach rupture strengths of around 90 pN,³⁶ which exceeds the maximal forces applied by the acoustic tweezer by a factor of about 10–20.

While the topologies of the patterns that can be generated with the acoustic tweezer are set by the device geometry, it is possible to actively control the position of any further cell types by adjusting the position of the acoustic pressure nodes by phase shifts, or transducer switching with an accuracy of less than 10 μm, which is smaller than a tissue cell diameter. It should be noted that no treatment of either the cells or the surfaces is necessary to achieve a patterned cell layer. The number of different cell types that can be patterned in this fashion is only limited by space available between the pressure nodes. Using a 1–3 transducer configuration, operated at 4 MHz, results in a spacing of ~240 μm between the nodes, taking the size of cells into account (10–30 μm) this limits side-by-side patterning to 90° phase shifts (~60 μm spacing) and thus four different cell types. Space permitting, cells can then be patterned at an angle to the initial pattern as evidenced by the “cell tartan” (Fig. 2D). Available space being the main limitation, for C2C12 cells, some cells were inevitably stacked on top of previously patterned cells, which prevented them from adhering to the substrate. The other possible transducer combinations (1–2, 1–3–5) were not considered here because of extreme streaming (1–2),³⁰ or because the position of the phase shifted node pattern would in parts overlap with the initial pattern (1–3–5).¹⁹ The “cell tartan” shows clearly the versatility of the acoustic tweezer device for complex cell patterning on any flat substrate with any adhesive cell type in normal media, making this technology compatible with a wide array of cell culture techniques.

After demonstrating the versatility of the acoustic tweezer for manipulating cells, we tested its usefulness in a model system for tissue engineering, specifically in peripheral nerve regeneration. Although peripheral nerves have good regenerative properties, the outcome is often less than optimal, highlighting the importance of supporting strategies in nerve repair.³⁷ Schwann cells are instrumental in supporting the repair process, first by initiating clearance of axonal and myelin debris at the injury site and subsequently supporting regrowth of axons sprouting from the proximal stump.³⁸ However, functional outcomes are often suboptimal, limited by misdirection of outgrowing neurites and a slow regeneration rate, leading to chronic denervation of Schwann cells distal to the injury site.³⁹ This in turn causes those Schwann cells to lose their growth supporting phenotype, ultimately leading to a failure to re-innervate the target organ.⁴⁰ While autologous nerve grafts still represent the gold standards in peripheral nerve repair, tissue engineering approaches to improve the functional outcome have received increasing attention in recent years.⁴¹ Several studies utilized Schwann cells to generate a repair-permissive environment in in vitro or animal models of nerve repair.^{27,28,42–45} While these approaches used micropatterned or microstructured surfaces or polymer scaffolds our goal was to investigate whether it is possible to align Schwann cells for nerve repair without underlying guidance cues in a self-organizing, scaffold-free approach.

A simple, linear pattern of Schwann cells was chosen to assess if we can influence the direction of neurite outgrowth from explanted DRGs in this manner. Interestingly, once patterned, the Schwann cells maintained their linear orientation and formed columnar structures similar to Bands of Büngner in regenerating peripheral nerves (Fig. 3A), a phenomena that has also been observed previously in scaffold based Schwann cell alignment.⁴² Outgrowth of neurites on the layer of Schwann cells was obvious after 4 days when observed through brightfield microscopy, but directional information could not be extracted due to the background of cells and high density of neurites growing on top of them. We utilized βIII-tubulin staining to visualize the neurites and analyzed area scans taken with a motorized stage. Due to the high density of neurites a tracing of single neurites was not feasible. We therefore used the ImageJ plug-in OrientationJ to obtain quantitative data on directionality. Analyses on a single pixel level (Fig. 4) using the Distribution function of OritentationJ showed that the outgrowth of neurites largely followed the orientation of the initial Schwann cell pattern. While the analysis of pixel orientations provided useful information on the direction of neurite outgrowth, it also had some limitations. In order to restrict the analysis to actual features (i.e. neurites) and omit isotropic areas, the threshold for analysis parameters – coherency and energy – had to be chosen accordingly. Invariably, in some of the images this caused some of the more faintly stained neurites to be omitted from analysis (compare Fig. 4A + B and D + E). In addition, the fact that the distribution histogram is weighted by the coherency parameter makes it difficult to compare the results from different experiments, even after normalization. Analysis of 250 × 250 ROIs (Fig. 5 and S1†) with OrientationJ's Measure function confirmed that the majority of neurites growing on patterned Schwann cells were oriented within ±30° of the pre-patterned direction. This is in good agreement with other studies, which aligned Schwann cells using micropatterned laminin⁴⁴ or a stretched collagen matrix.⁴⁶ The fact that in our experimental setup, the Schwann cells had no external guidance cues after the initial patterning by the acoustic stencil suggests that there was a significant degree of self-organization involved. A study by Parrinello et al. found that after peripheral nerve injury, fibroblast are instrumental in organizing Schwann cells into cords, in a cell-sorting process mediated by Sox-2.⁴⁷ It appears that the acoustic alignment was sufficient to promote a similar process just with Schwann cells. The extending neurites maintain the alignment of their associated Schwann cells, thus stabilizing the patterns⁴⁸ (Fig. 3C & F). Further studies using the phase-shift capabilities of our acoustic tweezer device could explore if including fibroblasts in the patterning process would improve the neurite guiding properties of the patterned cells.

Conclusions

The engineering of tissues for regenerative medicine sometimes requires accurate positioning of cells. Here we demonstrate the usability of a novel method manipulating cells, using acoustic radiation forces, for the creation of complex, tartan-like patterns of cells. This relies on the fact that the forces acting on the cells are very low, in the pico-Newton range, and that the pattern in which cells are deposited can be switched easily. We test the usefulness of such a cellular pattern, on a model of peripheral nerve injury. In peripheral nerve injury bands of Schwann cells guide axonal regeneration, we create such bands using the acoustic tweezer, and show that outgrowth is guided even though the acoustic forces are no longer present.

Acknowledgements

The authors would like to acknowledge support by the Engineering and Physical Sciences Research Council in the UK under the “Sonotweezers” grant (EPSRC ref.: EP/G011494/1), the University of Glasgow for a Lord Kelvin Adam Smith Fellowship in Sensor Systems (AB), and the Stephen Forrest Charitable Trust for funding TD. We also thank the staff of the James Watt Nanofabrication Centre for support in the cleanroom (http://www.jwnc.gla.ac.uk).

Notes and references

1. Principles of Tissue Engineering, ed. R. Lanza, R. Langer and J. P. Vacanti, Academic Press, Burlington, 2007.
2. C. S. Chen, M. Mrksich, S. Huang, G. M. Whitesides and D. E. Ingber, Science, 1997, 276, 1425–1428.
3. L. Csaderova, E. Martines, K. Seunarine, N. Gadegaard, C. D. Wilkinson and M. O. Riehle, Small, 2010, 6, 2755–2761.
4. C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Biophys. J., 2000, 79, 144–152.
5. B. Cortese, G. Gigli and M. Riehle, Adv. Funct. Mater., 2009, 19, 2961–2968.
6. J. A. Barron, P. Wu, H. D. Ladouceur and B. R. Ringeisen, Biomed. Microdevices, 2004, 6, 139–147.
7. T. Xu, J. Jin, C. Gregory, J. J. Hickman and T. Boland, Biomaterials, 2005, 26, 93–99.
8. M. Suzuki, T. Yasukawa, H. Shiku and T. Matsue, Biosens. Bioelectron., 2008, 24, 1049–1053.
9. J. Voldman, Annu. Rev. Biomed. Eng., 2006, 8, 425–454.
10. Y. Nahmias, R. E. Schwartz, C. M. Verfaillie and D. J. Odde, Biotechnol. Bioeng., 2005, 92, 129–136.
11. R. K. Pirlo, Z. Ma, A. Sweeney, H. Liu, J. X. Yun, X. Peng, X. Yuan, G. X. Guo and B. Z. Gao, Rev. Sci. Instrum., 2011, 82, 013708.
12. S. P. Grogan, C. Pauli, P. Chen, J. Du, C. B. Chung, S. D. Kong, C. W. Colwell Jr., M. K. Lotz, S. Jin and D. D. D'Lima, Tissue Eng., Part C, 2012, 18, 496–506.
13. R. Singhvi, A. Kumar, G. P. Lopez, G. N. Stephanopoulos, D. I. Wang, G. M. Whitesides and D. E. Ingber, Science, 1994, 264, 696–698.
14. J. L. Tan, W. Liu, C. M. Nelson, S. Raghavan and C. S. Chen, Tissue Eng., 2004, 10, 865–872.
15. D. T. Chiu, N. L. Jeon, S. Huang, R. S. Kane, C. J. Wargo, I. S. Choi, D. E. Ingber and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 2408–2413.
16. Y. Nakayama, A. Furumoto, S. Kidoaki and T. Matsuda, Photochem. Photobiol., 2003, 77, 480–486.
17. M. Yamato, O. H. Kwon, M. Hirose, A. Kikuchi and T. Okano, J. Biomed. Mater. Res., 2001, 55, 137–140.
18. M. N. Yousaf, B. T. Houseman and M. Mrksich, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5992–5996.
19. A. L. Bernassau, C. K. Ong, Y. Ma, P. G. MacPherson, C. R. Courtney, M. Riehle, B. W. Drinkwater and D. R. Cumming, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 2011, 58, 2132–2138.
20. K. A. Garvin, D. C. Hocking and D. Dalecki, Ultrasound Med. Biol., 2010, 36, 1919–1932.
21. L. Gherardini, S. Radel, S. Sielemann, O. Doblhoff-Dier, M. Groschl, E. Benes and A. J. McLoughlin, Bioseparation, 2001, 10, 153–162.
22. J. Shi, D. Ahmed, X. Mao, S. C. Lin, A. Lawit and T. J. Huang, Lab Chip, 2009, 9, 2890–2895.
23. A. L. Bernassau, F. Gesellchen, P. G. Macpherson, M. Riehle and D. R. Cumming, Biomed. Microdevices, 2012, 14, 559–564.
24. M. D. Binder, N. Hirokawa and U. Windhorst, Encyclopedia of neuroscience, Springer, Berlin, New York, 2009.
25. V. T. Ribeiro-Resende, B. Koenig, S. Nichterwitz, S. Oberhoffner and B. Schlosshauer, Biomaterials, 2009, 30, 5251–5259.
26. D. M. Thompson and H. M. Buettner, Tissue Eng., 2001, 7, 247–265.
27. K. E. Schmalenberg and K. E. Uhrich, Biomaterials, 2005, 26, 1423–1430.
28. C. Miller, S. Jeftinija and S. Mallapragada, Tissue Eng., 2001, 7, 705–715.
29. J. K. Alexander, B. Fuss and R. J. Colello, Neuron Glia Biology, 2006, 2, 93–103.
30. A. L. Bernassau, P. Glynne-Jones, F. Gesellchen, M. Riehle, M. Hill and D. R. Cumming, Ultrasonics, 2014, 54, 268–274.
31. C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675.
32. R. Rezakhaniha, A. Agianniotis, J. T. Schrauwen, A. Griffa, D. Sage, C. V. Bouten, F. N. van de Vosse, M. Unser and N. Stergiopulos, Biomech. Model. Mechanobiol., 2012, 11, 461–473.
33. E. Lamers, J. te Riet, M. Domanski, R. Luttge, C. G. Figdor, J. G. Gardeniers, X. F. Walboomers and J. A. Jansen, Eur. Cells Mater., 2012, 23, 182–193 ; discussion 184–193.
34. E. Potthoff, O. Guillaume-Gentil, D. Ossola, J. Polesel-Maris, S. LeibundGut-Landmann, T. Zambelli and J. A. Vorholt, PLoS One, 2012, 7, e52712.
35. G. Weder, N. Blondiaux, M. Giazzon, N. Matthey, M. Klein, R. Pugin, H. Heinzelmann and M. Liley, Langmuir, 2010, 26, 8180–8186.
36. R. I. Litvinov, H. Shuman, J. S. Bennett and J. W. Weisel, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7426–7431.
37. H. T. Khuong and R. Midha, Curr. Neurol. Neurosci. Rep., 2013, 13, 322.
38. Y. J. Son and W. J. Thompson, Neuron, 1995, 14, 125–132.
39. S. M. Hall, Ann. N. Y. Acad. Sci., 1999, 883, 215–233.
40. S. Y. Fu and T. Gordon, J. Neurosci., 1995, 15, 3886–3895.
41. R. Deumens, A. Bozkurt, M. F. Meek, M. A. Marcus, E. A. Joosten, J. Weis and G. A. Brook, Prog. Neurobiol., 2010, 92, 245–276.
42. A. Bozkurt, R. Deumens, C. Beckmann, L. Olde Damink, F. Schugner, I. Heschel, B. Sellhaus, J. Weis, W. Jahnen-Dechent, G. A. Brook and N. Pallua, Biomaterials, 2009, 30, 169–179.
43. J. B. Phillips, S. C. Bunting, S. M. Hall and R. A. Brown, Tissue Eng., 2005, 11, 1611–1617.
44. D. M. Thompson and H. M. Buettner, Ann. Biomed. Eng., 2004, 32, 1120–1130.
45. Y. G. Zhang, Q. S. Sheng, F. Y. Qi, X. Y. Hu, W. Zhao, Y. Q. Wang, L. F. Lan, J. H. Huang and Z. J. Luo, J. Mater. Sci.: Mater. Med., 2013, 24, 1767–1780.
46. M. Georgiou, S. C. Bunting, H. A. Davies, A. J. Loughlin, J. P. Golding and J. B. Phillips, Biomaterials, 2013, 34, 7335–7343.
47. S. Parrinello, I. Napoli, S. Ribeiro, P. Wingfield Digby, M. Fedorova, D. B. Parkinson, R. D. Doddrell, M. Nakayama, R. H. Adams and A. C. Lloyd, Cell, 2010, 143, 145–155.
48. C. Fernandez-Valle, D. Gorman, A. M. Gomez and M. B. Bunge, J. Neurosci., 1997, 17, 241–250.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4lc00436a

---