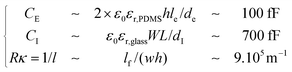Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic flow-focusing in ac electric fields
Say Hwa
Tan
,
Benoît
Semin
and
Jean-Christophe
Baret
*
Droplets, Membranes and Interfaces; MPI for Dynamics and Self-organization, Am Fassberg 17, 37077 Goettingen, Germany. E-mail: jean-christophe.baret@ds.mpg.de; Web: http://dmi.ds.mpg.de
First published on 9th January 2014
Abstract
We demonstrate the control of droplet sizes by an ac voltage applied across microelectrodes patterned around a flow-focusing junction. The electrodes do not come in contact with the fluids to avoid electrochemical effects. We found several regimes of droplet production in electric fields, controlled by the connection of the chip, the conductivity of the dispersed phase and the frequency of the applied field. A simple electrical modelling of the chip reveals that the effective voltage at the tip of the liquid to be dispersed controls the production mechanism. At low voltages (≲ 600 V), droplets are produced in dripping regime; the droplet size is a function of the ac electric field. The introduction of an effective capillary number that takes into account the Maxwell stress can explain the dependance of droplet size with the applied voltage. At higher voltages (≳ 600 V), jets are observed. The stability of droplet production is a function of the fluid conductivity and applied field frequency reported in a set of flow diagrams.
Introduction
Droplet-based microfluidics is a powerful high-throughput method that is used in a wide range of applications, including single cell analysis, next generation sequencing systems, molecular diagnostics and drug screening.1–5 The technology uses the controlled production of droplets and their subsequent manipulation in microfluidic channels.6 Series of operations are then integrated to follow complex biological protocols.7 The modules assembled together very often function in different regimes of flows. As an example, the droplet production mechanism is predetermined by the channel geometry and the flow rates.8,9 Therefore, increasing the chip complexity requires additional external controls. A few methods provide such additional degrees of freedom using, for example, thermal or magnetic responsive systems,6,10–13 which have strong limitations in biological applications. Electric actuation offers a promising alternative. First, the integration of electrodes on chip has been demonstrated using a technology that is easily accessible,14 providing simpler systems compared to surface acoustic wave based systems15 or valve-based systems.16 Various microfluidic devices have been developed making use of these techniques to integrate the concepts of electric actuation, using ac fields,17,18 electrocapillarity,19 electrowetting13 or dielectrophoretic actuation20 (for example, for droplet sorting21 and coalescence22,23). Second, the response of the fluids to electric actuation is fast21 and parallelisable, providing interesting engineering capabilities. The first step in a typical droplet-based microfluidics experiment is the encapsulation through droplet production, which can be influenced by electric fields. Electric fields at soft interfaces display a very rich variety of behaviours (for example, droplet deformation and tip streaming or Taylor cone formation and electrospinning) when coupled with flow.24–27 The geometry of the electrodes and the fluid conductivity usually have a strong influence on the field distribution and on the flow of electrical charges,26,27 making the system sensitive to experimental details. In addition, electrochemical effects represent a major limitation in the devices when the electrodes come in direct contact with the fluids (such as flow instabilities, degradation of the electrodes, generation of reactive species). Engineering reliable devices to control multiphase flow is therefore challenging, but microfabrication techniques enable today the production of electrodes with well defined geometries that are compatible with large ac electric fields.14In this article, we present and study a microfluidic device that uses an electric field to actively control droplet sizes at a flow-focusing junction. The field is applied directly at the flow-focusing junction using electrodes which are not connected to the fluids. We demonstrate that this applied electric field leads to a versatile and reliable modulation of droplet size in the dripping regime of production. Jetting may be induced when applying high electric fields. The stability of the droplet production depends on the conductivity of the dispersed phase and the field frequency. Our system therefore provides an additional level of control over droplet production, independent of the flow and usable in a wide range of electrical conductivities for fluids of practical interest.
Materials and methods
Microfluidic device
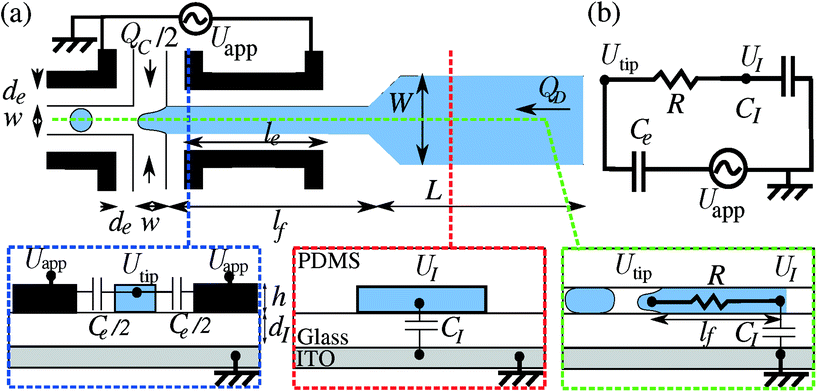
We use standard soft lithography techniques28 to manufacture a flow-focusing junction of lateral width w = 100 μm and height h = 35 μm8,29 in poly(dimethylsiloxane) PDMS (Dow Corning, relative permittivity εr,PDMS = 2.5) (Fig. 1). Electrodes are patterned around the junction as microfluidic channels and produced using the microsolidics technique.14 The fluidic and electrode channels are therefore within the same plane and positioned within a micron accuracy. The spacing between the electrodes and the fluidic channel is de = 35 μm over a length le = 2.2 mm around the junction (lf = 3 mm). The channels widen to W = 1 mm to connect to the inlets and outlets at a distance L = 11 mm.Emulsification system
Water-in-oil (W/O) droplets are formed by focusing an aqueous stream (dispersed phase; D) with two side oil streams (continuous phase; C). The volumetric flow rates (QD and QC) are controlled using syringe pumps (neMESYS, Cetoni). The dispersed phase is NaCl aqueous solution in Milli-Q water with an electrical conductivity κ between ~3 × 10−5 (Milli-Q water) and 3 S m−1. The continuous phase is mineral oil (M5904, Sigma Aldrich; viscosity η = 0.03 Pa s; εr = 2.1) with 5%w/w non-ionic surfactant (SPAN 80, Sigma Aldrich) to prevent droplet coalescence. Equilibrium interfacial tensions are about 4–5 mN m−1 independent of NaCl concentrations. Droplet production is imaged using an inverted microscope (IX81, Olympus) with a high speed camera (V210, Phantom; 5000 frames s−1). The apparent diameter d of at least 100 successive droplets is measured via image processing (Matlab, Mathworks).Electrical system
A sinusoidal voltage at frequencies from 1 kHz to 50 kHz (33210A, Agilent) is amplified from 0 to ~1 kV (623B, Trek). In the following discussion, all voltages are peak to peak (unless otherwise stated). With three sets of electrodes (upstream pairs, downstream pairs and ITO counter electrodes), three configurations are possible: the high-voltage is applied to the upstream pair of electrodes while the others are grounded (configuration 1); the high-voltage is applied to the downstream pair of electrodes while the others are grounded (configuration 2); or the high-voltage is applied to the ITO counter electrode while the others are grounded. All other configurations are symmetrical cases of these configurations (or of the trivial case where no field is applied). For practical convenience, configuration 3 is defined as the case where ITO is grounded and both the downstream and the upstream pairs of electrodes are connected to the high-voltage. Therefore, the ITO (Indium-Tin Oxide) counter electrode at the bottom of the glass plate (thickness dI = 1 mm, εr,glass = 7.5) is systematically grounded to prevent electrocoalescence downstream of the nozzle and to shield the field.Experimental results
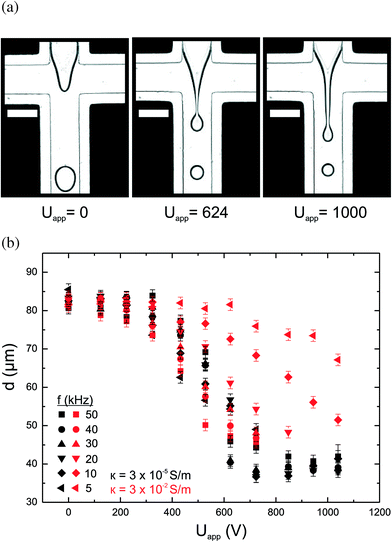
In a first series of experiments, we used Milli-Q water (Fig. 2(a) and the black symbols in 2(b)). We measured droplet size as a function of applied voltage at fixed QD = 50 μL hr−1 and QC = 400 μL hr−1 and fixed frequency f = 50 kHz, much larger than the droplet production frequency (100–500 Hz). When the applied voltage is increased from 0 to about 600 V, the droplet size shows a non-linear decrease (Fig. 2(b)). The continuous decrease is similar to previous experiments in unconfined geometry where a DC field is applied.30–32 This behaviour is quantitatively reproduced for all frequencies down to 5 kHz. Beyond 600–650 V, a dripping-to-jetting transition is observed above 5 kHz. The droplet size is constant, but the increase in the field leads to an increase in the jet length (up to a factor of 2). Below 5 kHz, the droplet production becomes unstable with polydisperse droplets and satellites. Inverting the connection of the electrodes (switching the downstream and upstream pairs) did not modify the observed behaviour for Milli-Q water. The droplet size is constant when the upstream and downstream pairs are at high voltage, indicating that electrowetting of the backplate does not occur13 and that the relevant field to consider is the one in the plane of the chip and not the one in the perpendicular direction.We consider the case where the high voltage is applied to the upstream pair of electrodes, the downstream pair of electrodes and the ITO counter electrode are grounded. We repeated our analysis at higher conductivities. At κ = 3 × 10−2 S m−1 and f = 50 kHz, below 600 V, the droplet size decreases as for Milli-Q water, with no significant deviation (red square symbols in Fig. 2(b)). Above ~600 V, the droplet production becomes unstable, leading to polydisperse droplets; no stable jets are formed (Fig. 3(a)). When the frequency is decreased below 20 kHz, the applied voltage has less of an effect on the droplet size and no dripping-to-jetting transition is observed.
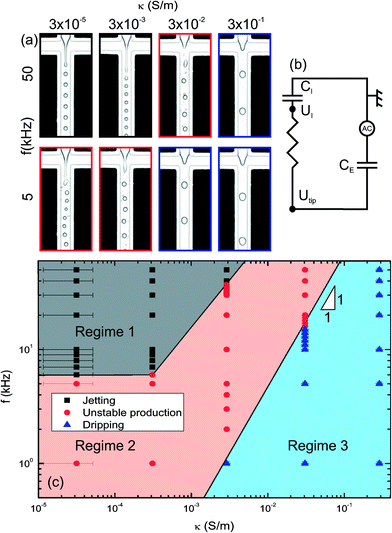 | ||
| Fig. 3 Flow diagram of the production at 1 kV in the conductivity–frequency space (QD = 50 μL hr−1 and QC = 400 μL hr−1) in configuration 1 (upstream pair of electrodes at high-voltage, downstream pair of electrodes and ITO counter electrode are grounded). (a) Snapshots of the droplet production. (b) Equivalent electrical circuit (see Fig. 1 for the definition of the electrical parameters). (c) Complete flow diagram: three regimes are observed (jetting, unstable production and dripping). | ||
We investigated systematically the droplet production mechanism at a fixed applied voltage (Uapp = 1 kV), as reported in a flow diagram displayed in Fig. 3(c) in the plane (κ, f). The flow diagram displays three regimes. In regime 1 (large f; small κ), jets are stable. In regime 2 (intermediate values of f and κ), jets are unstable. These two regimes correspond to the two cases described above. In regime 3 (small f; large κ), the droplets are produced in the dripping regime (also at lower applied voltages); the droplet size is a function of the electrical parameters (κ, f). The transition between regimes 2 and 3 is linear in the flow diagram (κ, f). Experimentally, all the data collected in the dripping regime collapse on a single master curve, provided that the applied voltage is rescaled by a constant dependent on the ratio f/κ, with the rescaling factor G(f/κ) being a sigmoidal function (Fig. 4). We present an electrical model to interpret this rescaling in the next section.
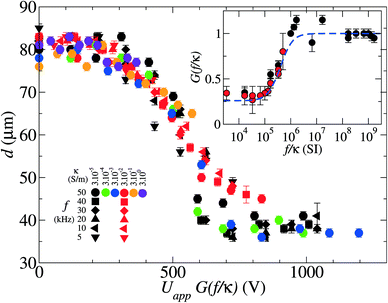 | ||
| Fig. 4 Droplet diameter as a function of the rescaled voltage. The rescaling factor G is chosen for each couple (f, κ) so that the curve collapses on the curve measured (f = 50 kHz, κ = 3 × 10−5 S m−1). Inset: the rescaling factor G is displayed as a function of f/κ. The black points are obtained from regime 1, and red points from regime 3. The blue dashed line is a fit to eqn (1) (QD = 50 μL hr−1 and QC = 400 μL hr−1). | ||
Electrical model
One of the keys to understanding the difference between regimes 2 and 3 is the difference between the applied voltage Uapp and the voltage at the tip of the dispersed fluid Utip. This difference is attributable to the absence of contact between the dispersed fluid and the upstream electrodes (Fig. 1(a)). The dispersed fluid and the upstream electrodes are separated by a dielectric PDMS layer acting as a capacitor CE. The fluid is modeled as a resistor R = 1/(lκ) (where l is a length determined by the geometry). We neglect here the dielectric properties since the corresponding charge relaxation time scale τ = ε/κ is, under most of our experimental conditions, much shorter than the field frequency. The fluid is separated from the ITO backplate through the glass plate modelled as capacitance CI. We neglect the connection to the downstream electrodes, which can be justified by the low value of the associated capacitance. Within this electrokinetic model, the voltage at the tip is given by the voltage divider formula: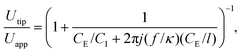 | (1) |
Using CE/CI = 0.35 and CE/l = 4 × 10−7 F m−1, the model fits the factor G(f/κ) = Utip/Uapp obtained experimentally. Although we cannot extract the exact values of these electrical parameters from our complex geometry, we estimate the capacitances using parallel plate approximation and the resistance of the liquid finger (dominated by the smallest dimensions), leading to:
We obtain CE/CI ~ 0.14 and CE/l ~ 0.9 × 10−17 F m−1, which are in reasonable agreement with the values obtained by the fit, considering the very crude approximations made. Our model gives the correct behaviour, a high-pass filter for Utip with a cutoff:
| f/κ ∼ l/(2πCE) ∼ 4 × 105 m/F |
Above the cutoff, Utip ≈ Uapp, and below the cutoff, Utip = Uapp, CE/(CE + CI) ≪ Uapp (~ 25% based on eqn (1)). Interestingly, the line of the flow diagram separating regimes 2 and 3 corresponds to f/κ ~ 5 × 105 m F−1, close to the cutoff condition: in regime 3, Utip < 600 V (Fig. 4(a), inset) and the droplet production is therefore found in the dripping regime. A modification of the size of the electrodes or of the thickness of the glass slide significantly impacts this behaviour, as observed experimentally: regime 3 disappears when the ITO is removed (CI = 0; Utip = Uapp), although additional stray capacitance in the setup might still have an impact.
To further assess the relevance of our electrical model, we studied two additional configurations. In configuration 2, the high-voltage is applied to the downstream pair of electrodes, the upstream pair of electrodes and the ITO counter electrode are grounded. In configuration 3, the high-voltage is applied to the upstream and downstream pairs of electrodes, while the ITO counter electrode is still grounded. The corresponding flow diagrams at 1 kV are displayed in Fig. 5. We obtain the same types of behaviours (namely jetting, unstable production and dripping) but they are differently arranged as compared to configuration 1. Regime 3 vanishes when the connections between the upstream electrodes and the downstream electrodes are interchanged, and regime 1 vanishes when both electrode pairs are at high voltage.
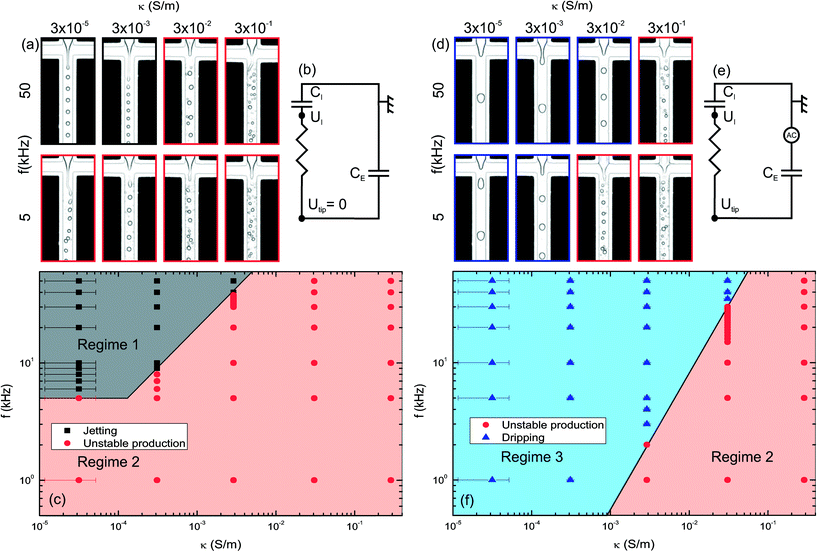 | ||
| Fig. 5 Flow diagram of the production at 1 kV in the conductivity–frequency space (QD = 50 μL hr−1 and QC = 400 mL hr−1) using the two other possible connection configurations. (a, b, c) Configuration 2: the high-voltage is applied to the downstream pair of electrodes while the upstream pair of electrodes and the ITO counter electrode are grounded; regime 3 vanishes compared to Fig. 3. (a) Snapshots of the droplet production. (b) Equivalent electrical circuit (see Fig. 1 for the definition of the electrical parameters). (c) Complete flow diagram. (d, e, f) Configuration 3: the high-voltage is applied to the downstream and upstream pairs of electrodes while the ITO counter electrode is grounded; regime 1 vanishes, and regimes 2 and 3 are reversed compared to Fig. 3. (d) Snapshots of the droplet production. (e) Equivalent electrical circuit (see Fig. 1 for the definition of the electrical parameters). (f) Complete flow diagram. | ||
The electrical model explains these behaviours using the proper electrical connections. The key point to consider is the difference in voltage between the tip of the fluid and the downstream electrodes. In configuration 2, the voltage at the tip of the fluid is always 0, while the voltage at the downstream electrodes is always Uapp. The condition for the existence of regime 3 is never fulfilled, and regime 3 does not appear. The rest of the flow diagram is not affected by the choice of the connection, and we observe the same transition between unstable production and jets, consistent with the statement that this transition is triggered by the conductivity of the liquid jet. For configuration 3, the voltage at the tip has the same variation as the first case. The same expression, eqn (1), can be used to derive the voltage at the tip. But in the present case, this voltage has to be compared to the voltage Uapp at the downstream electrodes. We expect therefore a behaviour complementary to configuration 1. We indeed observe that regimes 2 and 3 are interchanged with a transition at the same position as for configuration 1 given by:
| f/κ ∼ l/(2πCE) ∼ 5 × 105 m F−1 |
Regime 1 cannot be observed because when Utip is equal to the applied voltage, there is no voltage difference from the voltage of the downstream electrodes. These experiments confirm the importance of the voltage difference between the tip and the downstream electrodes and the absence of electrowetting due to the voltage difference between the ITO counter electrodes and the tip.
Electrohydrodynamic model
In order to understand the effects of the applied field on the droplet production in the dripping regime, we focus on regimes 1 and 2 of configuration 1, where the voltage at the tip is equal to the applied voltage. Since each fluid is homogeneous, the electric field has a mechanical effect only at the interface between the fluids where the Maxwell stress is non-zero.33 One of the components of this Maxwell stress is an electrical pressure normal to the interface, opposing to the Laplace pressure associated with the surface tension. The simplest way to take this effect into account is to introduce an effective capillary number Caeff defined as: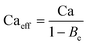 | (2) |
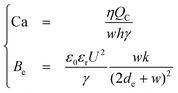 | (3) |
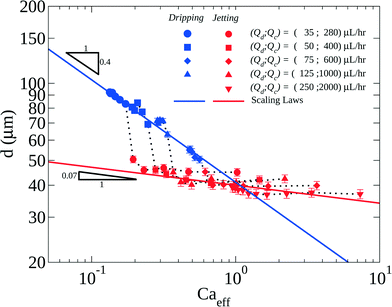 | ||
| Fig. 6 Droplet diameter as a function of the effective capillary number which takes into account the Maxwell stress as a contribution to the surface tension (eqn (2)). Data are obtained for typical voltages ranging from 0 to 1000 V in the jetting regime (Milli-Q water, f = 50 kHz). | ||
We investigate now the dripping-to-jetting transition. In the absence of the field, we observe a dripping-to-jetting transition for Ca ~1, as described for capillaries.9,34 When the field is applied, the Ca*eff at the transition depends on the flow conditions (see Fig. 6): Caeff is not the relevant parameter for capturing the transition. Considering that the effective surface tension impacts the inner Weber number, We is also not reasonable as We ≪ 1 for all our flow conditions. The jet is rather stabilised by the axial field in the direction of the flow, as already observed during capillary breakup in electrowetting35 or in electrospinning,26,27,33 which would suggest that the electrical Bond number is one of the parameters controlling the transition. In our experiments, the voltage at the transition is approximatively the same (~600–650 V) irrespective of the total flow rate, which leads indeed to an approximately constant electrical Bond number at the transition 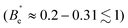 . Since we did not vary the other parameters (surface tension, geometrical parameters w) of the electrical Bond number, we cannot however conclude on the relevance of this number to the jetting-to-dripping transition.
. Since we did not vary the other parameters (surface tension, geometrical parameters w) of the electrical Bond number, we cannot however conclude on the relevance of this number to the jetting-to-dripping transition.
Discussion
Our expression for Caeff does not account for the fluid conductivities and therefore cannot describe the destabilisation of the jet at high conductivities observed in the flow diagrams. Here we argue that the destabilisation of conducting jets occurs in whipping mode.26,27,36,37 Indeed, Fig. 3(a) and 5 show a non axisymmetric droplet production in the jet, and we propose the whipping instability of a conducting jet as the stability limit. The second mechanism occurring at low frequency (close to 1 kHz) is the interplay between droplet production frequency and field frequency, which can lead to charging of the droplet, thereby influencing the jet stability.35,38 Further analysis of these instabilities is of interest but is beyond the scope of the present manuscript.We used surfactants in the experiments because they are often used in practical applications to avoid droplet coalescence. Moreover, they decrease the surface tension, making the system more sensitive to the Maxwell stress. Unfortunately, they introduce a level of complexity in the analysis and an unknown parameter, namely the dynamic interfacial tension at the scale of droplet production.39,40 In our analysis, this uncertainty is not detrimental as it can be regarded as an additional contribution to the geometrical fitting factor k. To gain quantitative insights into the mechanisms of dripping-to-jetting transition and the destabilisation of the jet, further experiments have to be carried out without surfactants.
Because the concept of actuation of droplet size by electric fields can be used in a wide range of conductivities, flow rates and interfacial tension, we believe that it will be useful as a tool to control droplet sizes independently of the flow conditions. This is a useful aspect in the integration of complex protocols for droplet manipulation when the flow conditions for the droplet modules are not compatible with those for other modules. Besides this integration aspect, the interest in the actuation of droplet size by electric fields lies in the fast response of the system's electrical actuation. Response times on the order of 1 ms and below are classically obtained in sorting experiments21 or in electrocoalescence.19 The analysis of the response time of the system is beyond the scope of the present manuscript and will be presented elsewhere.41 The system responds at the subsecond time-scale, which will be of interest for applications requiring active control or for designing feedback loops on droplet sizes during production (for example, to compensate for pulsating flow due to pumps or pressure cross-talks between channels).
Conclusion
In conclusion, we developed and characterized an electro-flow-focusing junction that is usable for droplet-based microfluidics. The flow diagrams of the droplet production regime as a function of the aqueous dispersed phase conductivity and of the applied electric voltage frequency revealed regions in this parameter space where the electric fields do not have any effects. We presented a model which assumes that only the voltage difference between the dispersed liquid tip and the downstream electrodes matters. The difference between the liquid tip voltage and the applied voltage, due to the absence of connection between the fluid and the electrodes, is the other key ingredient of our model. This simple model allowed us to explain all the possible electrode configurations. In the regimes where the electric field actually plays a role, the droplet size decreases with increasing electric fields. For a high-enough electric field, a dripping-to-jetting transition is induced, and for liquids of high conductivity or low applied voltage frequency, the droplet production becomes unstable. In the dripping regime, the mechanism of production is in good agreement with the modulation of surface tension by the Maxwell stress, and a power law can be used to relate the size of the droplets formed as a function of an effective capillary number that takes into account this Maxwell stress. The dripping-to-jetting transition is not described by this unified electrocapillary number, as well as the stability of the jet which depends on electrical parameters such as conductivity and field frequency. The electric actuation finally provides an additional degree of freedom on the production of droplets: droplet size can be tuned independently of hydrodynamic conditions which – we believe – will be of interest for the fine control of droplets in channels.Acknowledgements
The authors thank Dr. V. Taly, Dr. K. Hantke, Dr. M. Brinkmann, Prof. S. Herminghaus, Prof J. Enderlein and Prof. N.T. Nguyen for insightful discussions. We acknowledge the financial support of the Max-Planck Society. S.H.T. also acknowledges the support from the GGNB doctoral school. B.S. acknowledges the financial support from BP. A patent application with priority date March 31st 2012 has been filed for the control of droplet production in electric fields.References
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J.-C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed.
- J.-C. Baret, Y. Beck, I. Billas-Massobrio, D. Moras and A. D. Griffiths, Chem. Biol., 2010, 17, 528–536 CrossRef CAS PubMed.
- D. Pekin, Y. Skhiri, J.-C. Baret, D. L. Corre, L. Mazutis, C. B. Salem, F. Millot, A. E. Harrak, J. B. Hutchison, J. W. Larson, D. R. Link, P. Laurent-Puig, A. D. Griffiths and V. Taly, Lab Chip, 2011, 11, 2156–2166 RSC.
- O. J. Miller, A. E. Harrak, T. Mangeat, J.-C. Baret, L. Frenz, B. E. Debs, E. Mayot, M. L. Samuels, E. K. Rooney, P. Dieu, M. Galvan, D. R. Link and A. D. Griffiths, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 378–383 CrossRef CAS PubMed.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601 CrossRef PubMed.
- A. Fallah-Araghi, J.-C. Baret, M. Ryckelynck and A. D. Griffiths, Lab Chip, 2012, 12, 882–891 RSC.
- T. Cubaud and T. G. Mason, Phys. Fluids, 2008, 20, 053302 CrossRef PubMed.
- A. S. Utada, A. Fernandez-Nieves, J. M. Gordillo and D. A. Weitz, Phys. Rev. Lett., 2008, 100, 014502 CrossRef.
- S.-H. Tan, S. M. Sohel Murshed, N.-T. Nguyen, T. N. Wong and L. Yobas, J. Phys. D: Appl. Phys., 2008, 41, 165501 CrossRef.
- S.-H. Tan, N.-T. Nguyen, L. Yobas and T. G. Kang, J. Micromech. Microeng., 2010, 20, 045004 CrossRef.
- A. Abate and D. A. Weitz, Appl. Phys. Lett., 2008, 92, 243509 CrossRef PubMed.
- F. Malloggi, H. Gu, A. G. Banpurkar, S. A. Vanapalli and F. Mugele, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 91–96 CrossRef CAS PubMed.
- A. C. Siegel, S. S. Shevkoplyas, D. B. Weibel, D. A. Bruzewicz, A. W. Martinez and G. M. Whitesides, Angew. Chem., 2006, 118, 7031 ( Angew. Chem., Int. Ed. , 2006 , 45 , 6877 ) CrossRef.
- L. Schmid and T. Franke, Lab Chip, 2013, 13, 1691–1694 RSC.
- A. Abate, M. B. Romanowsky, J. Agresti and D. A. Weitz, Appl. Phys. Lett., 2009, 94, 023503 CrossRef PubMed.
- H. Kim, D. Luo, D. Link, D. A. Weitz, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2007, 91, 3 Search PubMed.
- P. He, H. Kim, D. Luo, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2010, 96, 3 Search PubMed.
- A. R. Abate, T. Hung, P. Mary, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19163–19166 CrossRef CAS PubMed.
- D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. D. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556–2560 CrossRef CAS PubMed.
- J.-C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak, L. Frenz, C. Rick, M. L. Samuels, J. B. Hutchison, J. J. Agresti, D. R. Link, D. A. Weitz and A. D. Griffiths, Lab Chip, 2009, 9, 1850–1858 RSC.
- C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 89, 3 CrossRef PubMed.
- A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2009, 102, 188304 CrossRef.
- J. Zeleny, Phys. Rev., 1917, 10, 1–6 CrossRef.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1964, 280, 383–397 CrossRef.
- M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2201–2220 CrossRef CAS PubMed.
- M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2221–2236 CrossRef CAS PubMed.
- Y. N. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184 CrossRef CAS.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366 CrossRef CAS PubMed.
- T. Takamatsu, Y. Hashimoto, M. Yamaguchi and T. Katayama, J. Chem. Eng. Jpn., 1981, 14, 178–182 CrossRef CAS.
- C. Byers and J. Perona, AIChE J., 1988, 34, 1577–1580 CrossRef CAS.
- X. Zhang and O. A. Basaran, J. Fluid Mech., 1996, 326, 239–263 CrossRef CAS.
- D. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64 CrossRef.
- A. S. Utada, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 094502 CrossRef.
- J.-C. Baret, M. M. J. Decré and F. Mugele, Langmuir, 2007, 23, 5173–5179 CrossRef CAS PubMed.
- H.-H. Kim, J.-H. Kim and A. Ogata, J. Aerosol Sci., 2011, 42, 249–263 CrossRef CAS PubMed.
- G. Riboux, A. Marin, I. Loscerrtales and A. Barrero, J. Fluid Mech., 2011, 671, 226–253 CrossRef.
- F. Malloggi, D. van den Ende and F. Mugele, Langmuir, 2008, 24, 11847–11850 CrossRef CAS PubMed.
- S. L. Anna and H. C. Mayer, Phys. Fluids , 2006, 18, 121512 Search PubMed.
- J.-C. Baret, F. Kleinschmidt, A. E. Harrak and A. D. Griffiths, Langmuir, 2009, 25, 6088–6093 Search PubMed.
- S.-H. Tan, F. Maes, B. Semin, J. Vrignon and J.-C. Baret, 2013, submitted.
| This journal is © The Royal Society of Chemistry 2014 |