Fluid inclusion measurements by laser ablation sector-field ICP-MS

Abstract

A state-of-the-art, highly sensitive sector-field inductively coupled plasma mass spectrometer (SF-ICP-MS) was evaluated for analyzing fluid inclusions in combination with a 193 nm excimer laser ablation, with the aim of expanding the technique to smaller inclusions and/or lower element concentrations. A well-defined assemblage of numerous co-genetic fluid inclusions and thin layers (50 nm) of chromium and copper containing traces of gold were studied regarding reproducibility and detection limits. For comparison, aliquots were analyzed with a quadrupole (Elan 6100 DRC) and the SF-ICP-MS instrument (Element XR). While using an element menu of 21 elements covering the mass range from lithium (7 amu) to lead (208 amu), approximately ten times lower detection limits were found for the SF-ICP-MS, whereby the cycle time increased by only 20% compared with the quadrupole instrument. An absolute detection limit for e.g. gold of 1 femtogram (10⁻¹⁵ g) was found for fluid inclusions analysis. Detection efficiencies of 2.6 × 10⁻⁵ counts per ablated atom for copper and 3.1 × 10⁻⁵ for chromium were determined by ablating the thin layers. The detection efficiency for sodium in the fluid inclusions was 2 × 10⁻⁷, about five times lower than that expected from the sensitivity obtained on NIST SRM 610 glass.

---

Introduction

The determination of elemental concentrations in fluid inclusions has greatly advanced the understanding of mass transfer by fluids in the earth's crust and the formation of ore deposits.^1–8 Given the importance of textural control and local features within minerals, notably multiple generations of different fluid inclusions that may be trapped successively in a single mineral grain, laser ablation (LA) was recognized by early authors^9–13 as a powerful sample introduction device for inductively coupled plasma (ICP) based spectrometry for these kinds of samples. Laser ablation was coupled to ICP atomic emission spectrometers (AES) in the early 1980s by several authors^14–16 and first coupled to ICP mass spectrometry (ICP-MS) by Gray¹⁷ in 1985. Around 1990, laser ablation was recognized as a preferred sampling tool for fluid inclusion analysis by coupling it to ICP-AES^9–11,18 or to ICP-MS.^12,13,19 With well-controlled ablation of quartz using UV lasers²⁰ and the development of quantification strategies for transient inclusion signals by combination of LA-ICP-MS with microthermometry,^21–24 LA-quadrupole (Q-)ICP-MS has become the established method for major and trace elemental analyses of natural fluid inclusions, as summarized in several application reviews.^25,26 In experimental studies of mineral solubility at high pressures and temperatures, synthetic fluid inclusions can be used to trap solutions under run conditions without disturbing the equilibrium system, followed by LA-ICP-MS analysis after cooling of the mineral host.^27–30

The small size of natural as well as synthetic fluid inclusions, typically ranging from a few microns up to a few tens of microns in most samples, remains an ongoing challenge in many applications. The smaller inclusion size affects LA-ICP-MS in two ways: it reduces the absolute mass of any element to be detected, but it also leads to shorter signals that are more difficult to quantify in a representative manner.

Absolute detection limits, largely determined by inclusion mass and the concentration of the elements of interest contained in an inclusion, are the first-order limitations in applying fluid inclusion microanalysis to resolve important geochemical questions in hydrothermal ore formation as well as metamorphic and magmatic petrology. Small inclusions of dilute fluids forming in low-temperature geological environments have been largely inaccessible to microanalytical studies, which is regrettable because smaller fluid inclusions occur in far greater numbers and may commonly be better preserved than larger ones. However, going to smaller inclusions means lowering the total mass available for an analysis. This is particularly critical for economically interesting trace elements such as gold, which is commonly present in concentrations below 1 μg g⁻¹ and therefore close to or below the detection limit in a wide range of inclusions. Reducing the absolute amount in an inclusion by going down to the smallest possible size in LA-ICP-MS primarily requires maximizing the sensitivity of the ICP-MS,³¹ although for some elements the background intensity is the limiting factor (e.g., anion components like S, Cl, and Br (ref. 32)).

The duration of small and highly transient signals, typically showing an almost instantaneous rise in intensity after the inclusion is breached and a more gradual decline depending on ablation progress, is the second limiting factor in LA-ICP-MS microanalysis of fluid inclusions. Representative signal quantification of multiple elements across a wide range of atomic masses requires an adequate definition of this time-dependent signal. Simultaneous detection using a multi-collector ICP-MS is limited by the small mass range of these magnetic-field based spectrometers and the need to include Na as an internal standard for quantifying natural fluid inclusion compositions.²¹ The recently introduced Mattauch-Herzog ICP-MS³³ using a detector plane and a time of flight ICP-MS³⁴ both allow simultaneous detection across the entire mass range. Although, recent applications show a similar sensitivity to Q-ICP-MS instruments,³⁴ their dynamic range, from major (e.g. percents of Na) to trace elements (e.g., ng g⁻¹ Au) present in single inclusions, so far precludes useful applications to this type of microanalysis.

With sequential detection of elements, a compromise must be achieved between shortening the signal (leading to a greater chance of detection of a given total mass of an element above the instrumental background) and a representative sampling of all elements of interest (requiring an adequate number of significant readings of all elements that are counted successively during each acquisition cycle). The use of short peaks in a single collector ICP-MS using a sequential acquisition method raises the risk of spectral skew.³⁵ Such non-representative sampling may lead to systematic errors in individual inclusion analyses and can only be corrected by analyzing and averaging numerous inclusions considered to have identical compositions. Thanks to its rapid element scanning through the entire mass range, quadrupole mass spectrometry (Q-ICP-MS) has been the detection method of choice for many years of fluid inclusion research. Today, state-of-the-art single-collector sector-field ICP-MSs have comparably fast-scanning magnets, but considerably higher sensitivities compared to Q-ICP-MS, especially with sample introduction by liquid nebulization but also in combination with laser ablation^36,37 and electrothermal vaporization (ETV).³⁸ ETV signals have a similar duration to LA signals from fluid inclusions, so that ETV experiments³⁸ also show the suitability of the Element XR to record fast changing transient signals. According to Resano et al.³⁸ about 20 different masses can be reliably measured in a few second long ETV signal using a SF-ICP-MS. However, spectral skew is less of an issue in these analyses because measurements are easy to replicate, in contrast to fluid inclusions where each microsample has a finite mass.

In this study, we explore the suitability of a state-of-the-art SF-ICP-MS for quantifying low short transient signals of multiple elements across a wide mass range, by the ablation of thin layers of known analyte density and of a well-defined assemblage of numerous compositionally identical fluid inclusions. A Q-ICP-MS (Elan 6100 DRC) was used for direct comparison using the same ablation optics and aerosol transport system, using He as the sample-chamber gas merged with Ar (± minor H₂) downstream from the sample cell.

Experimental

ETH Zurich's ArF excimer laser system, which is described in more detail by Günther et al.²⁰ as the prototype of the commercial GeoLas system (Coherent, Germany), was used for all ablation experiments, in combination with a fast wash-out rhomb-shaped ablation cell having a volume of 1 cm³. The SF-ICP-MS was an Element XR (Thermo Scientific, Bremen, Germany), standing next to an Elan 6100 DRC (PerkinElmer, Canada). Both instruments were tuned to high sensitivity and low oxide formation ratio (ThO/Th). The Element XR was furthermore optimized and successfully tested for low settling times, reducing the cycle time by about a factor of two compared to the software settings by the manufacturer for the chosen element menu. The detailed parameters are listed in Table 1. To ensure the same laser ablation conditions, measurements with both mass spectrometers were performed on the same days without changing the laser conditions, moving the sample in the chamber or modifying the transport conditions except for the transfer tube from the ablation cell. The tube length was about 0.6 m to the Elan 6100 DRC, and about 3 m to the Element XR. The longer tube spread out the signal time by about 20%, which roughly compensates for the 20% longer cycle time on the Element XR. Hydrogen was added to the carrier gas for the measurements with the Elan 6100 DRC only, to enhance its sensitivity for heavier elements including gold.³⁹ A typical set of 21 elements was measured, on isotopes which had the highest signal to noise ratio for the Elan 6100 DRC setup. The LA-ICP-MS signals were evaluated with SILLS⁴⁰ and the limits of detection (LODs) were calculated according to eqn (1) (eqn (6) in Pettke et al. 2012 (ref. 26)) were Bg_i stands for the background intensity of element i, DT_i stands for the dwell time, N_sg stands for the number of cycles in the signal window, N_bg stands for the number of cycles in the background window and S_i stands for the sensitivity.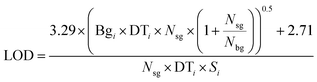

Table 1 ICP-MS parameter used for the fluid inclusion measurements

	Elan 6100 DRC	Element XR
Carrier gas	1.1 L min^−1 He + 5 mL min^−1 H2	1.0 L min^−1 He
Nebulizer gas flow	0.8–0.82 L min^−1 Ar	0.946–0.950 L min^−1 Ar
Auxiliary gas flow	0.85 L min^−1 Ar	0.95 L min^−1 Ar
Cooling gas flow	15.5 L min^−1 Ar	15 L min^−1 Ar
Plasma power	1550 W	1350 W
Dwell times	10 ms (Au: 80 ms)	10 ms (Au: 80 ms) 5 samples per peak
Cycle time	343 ms	418 ms
Isotopes (for fluid inclusions):	^7Li, ^11B, ^23Na, ^24Mg, ^27Al, ^29Si, ^39K, ^44Ca, ^55Mn, ^57Fe, ^65Cu, ^66Zn, ^75As, ^85Rb, ^88Sr, ^107Ag, ^121Sb, ^133Cs, ^137Ba, ^197Au, ^208Pb
Oxide ratio (ThO^+/Th^+)	∼0.5%	∼0.3%

---

Thin layers (50 nm) of chromium and copper on a glass slide were produced by physical vapor deposition. A microscope cover glass (thickness ∼ 0.2 mm) was glued on top of these layers to allow controlled ablation and to avoid erratic flaking off the crater rim. These sandwiched layers were ablated with a 90 μm spot which (due to the high numerical aperture of the imaging objective and the resulting conical ablation pit²⁰) sampled a 80 μm circle of the layer, as determined by optical microscopy after ablation. Trace concentrations of ∼2 ppm Au in chromium and ∼40 ppm Au in gold were found by LA-ICP-MS measurements. These transient gold signals are close to the detection limit of the Elan 6100 DRC instrument. They resemble transient signals from fluid inclusion but are more reproducible in terms of absolute gold mass, thus allowing a direct comparison of the sensitivities of both instruments.

The ablation rate on NIST SRM 610 was determined by ablating three craters (40 μm) for 30 s with a repetition rate of 10 Hz, i.e. 300 laser shots each. We ablated the side of a thin slice of doubly polished NIST SRM 610, using the same fluence (5.5 J cm⁻²) as for the standard measurements for fluid inclusion analysis. Afterwards the depth of the crater was measured with a microscope placed perpendicular to the craters. The measured depth of the flat-bottomed craters was 48 μm resulting in an ablation rate of 0.16 μm per laser pulse.

We used an assemblage of numerous fluid inclusions on a single healed microfracture in a quartz crystal from an Alpine fissure vein found near Thusis, Switzerland,⁴¹ ranging in size from a few microns to ∼200 μm. All fluid inclusions have an identical salinity of 4.0 ± 0.1 wt% NaCl equivalent and contain an aqueous liquid and a small vapor bubble homogenizing at 130 ± 5 °C, but no daughter crystals.⁴¹ The average diameter of each inclusion was measured in a microscope before ablation and a spherical symmetry was assumed to estimate the inclusion volume.

Results

The gold concentration in the thin chromium layer was determined with NIST SRM 610 as the external standard and using ⁵³Cr as the internal standard (concentration 100%). Identical gold concentrations of 1.7 ± 0.5 and 1.7 ± 0.2 μg g⁻¹ from five individual measurements were obtained using the Elan 6100 DRC and the Element XR, respectively. The corresponding LODs were 0.7 and 0.15 μg g⁻¹, i.e., approximately 5× lower using the Element XR. Total integrated gold counts (over ∼18 s) were 1330 ± 150 counts for the Element XR, after subtracting from the signal on mass 197 the instrument background (15 cps) and the 50 cps contributed by the host (i.e., cover glass). For the Elan 6100 DRC measurements, the 197 amu intensity was <10 cps for the background and the cover glass, while the gold integral from the chromium layer was 166 ± 35 counts. The observed intensity of the Element XR measurement in the cover glass would correspond to a gold concentration of 5 ppb. However, the ¹⁹⁷Au to ¹⁸¹Ta cps-ratio was about 0.5% and therefore a significant contribution of TaO⁺ to the signal on mass 197 cannot be excluded. From results on both metal layers and then the total mass of ablated metals, detection efficiencies (counts per ablated atom) were calculated for chromium, copper and gold. Detection efficiencies obtained with the Elan 6100 DRC were in agreement with the values published by Wälle et al.,³¹ whereas detection efficiencies of the Element XR were about ten times higher (see Table 2).

Table 2 Detection efficiencies determined by ablation of thin layers

Sample	Isotope	Elan 6100 DRC [counts per ablated atom]	Element XR [counts per ablated atom]
Copper layer (50 nm)	^65Cu	3.7 × 10^−6	2.6 × 10^−5
	^197Au	1.3 × 10^−5	1.1 × 10^−4
Chromium layer (50 nm)	^53Cr	2.7 × 10^−6	3.1 × 10^−5
	^197Au	9.8 × 10^−6	1.0 × 10^−4
Fluid inclusions	^23Na	8 × 10^−9	2 × 10^−7

---

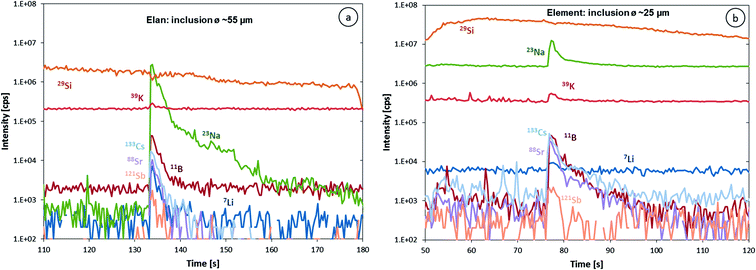
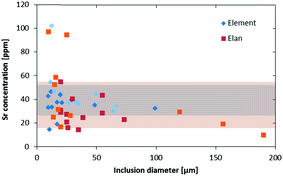
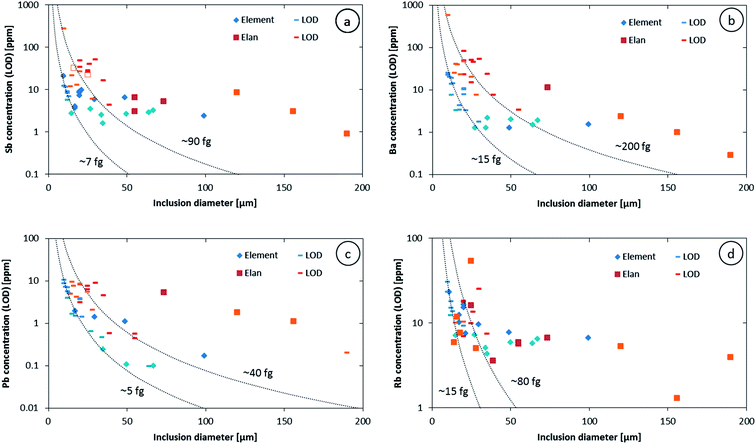
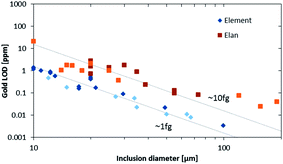
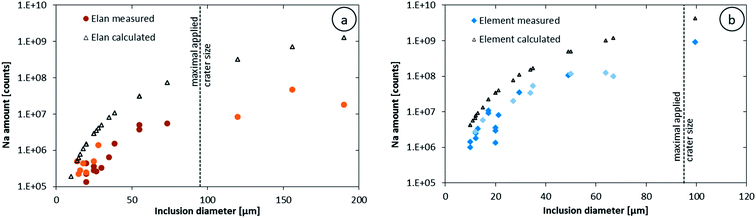
The higher sensitivity and suitable time resolution of the transient signal of the Element XR is demonstrated in Fig. 1. Two otherwise identical fluid inclusions of ∼55 μm and ∼25 μm in diameter were analyzed with the Elan 6100 DRC and the Element XR respectively; the first inclusion is about ∼10 times larger by volume and contained mass. Backgrounds are generally higher on the Element XR than on the Elan 6100 DRC. This is especially pronounced for sodium and to a smaller extent for lithium backgrounds. The potassium background is similar due to the ³⁸ArH⁺ interference on the Elan 6100 DRC, caused by the hydrogen addition to the carrier gas. Strontium, cesium and boron were consistently detected as major signals by both instruments and in all inclusions, besides Na. Their average concentrations (± one standard deviation) determined with the Element XR and the Elan 6100 DRC, respectively, were 39 ± 16 and 35 ± 22 μg g⁻¹ (Sr), 46 ± 17 and 50 ± 36 μg g⁻¹ (Cs), and 670 ± 155 and 720 ± 295 μg g⁻¹ (B). This indicates no significant difference between the measurements from the two instruments. The distribution of the obtained strontium concentrations in relation to the inclusion size is shown in Fig. 2. Other elements like antimony, barium, lead and rubidium (Fig. 3) also show consistent concentrations or limits of detection in the smaller inclusions. The measurements of those elements clearly demonstrate the advantage of the Element XR for quantifying trace element concentrations in smaller inclusions. Detection limits for gold concentrations as a function of inclusion size are shown in Fig. 4 and indicate that the detection limit is about one order of magnitude lower for the Element XR compared to the Elan 6100 DRC. The trend lines indicate the expected correlation of a homogenous assemblage with the volume of near-spherical inclusions, indicating an absolute limit of detection of 1 fg (10⁻¹⁵ g) gold for the Element XR and about 10 fg (10⁻¹⁴ g) gold for the Elan 6100 DRC under optimized conditions. These trend lines are calculated from the LOD and the inclusions size, assuming a bulk density of 0.95 g cm⁻³ of the inclusions corresponding to 5 volume% vapor bubbles. Both datasets of individual inclusions follow such a trend, except for inclusions with diameters greater than 100 μm, which have only been measured with the Elan 6100 DRC and may not have been completely ablated at the maximum available crater size of 90 μm. Also, minimum detected concentrations (LOD) for very large inclusions do not further improve, because signals become longer and are increasingly affected by background intensities on minor elements, as already discussed by Günther et al.²¹

Fig. 1 Transient LA-ICP-MS signals of (a) a ∼55 μm fluid inclusion measured with an Elan 6100 DRC and (b) a ∼25 μm inclusion of likely identical composition measured using an Element XR. Note that the difference in the inclusion diameter corresponds to a 10× lower mass.

Fig. 2 Strontium concentration in fluid inclusions from an assemblage with 4 wt% salinity, measured on two different days on both instruments (indicated by the lighter and darker colors). The bands indicate the average ±1σ concentrations from the Element XR (darker) and the Elan 6100 DRC (lighter). All measurements were above the LOD.

Fig. 3 Antimony (a), barium (b), lead (c) and rubidium (d) concentrations and LODs from an assemblage with a 4 wt% salinity measured on two different days on both instruments (indicated by the lighter and darker colors). Empty symbols indicate questionable signals. Dashed lines represent the estimated absolute LOD for the two instruments. The labels indicate the minimum mass of each element that can be reliably recorded in a short transient signal.

Fig. 4 Gold LODs from an assemblage with a 4 wt% salinity measured on two different days on both instruments (indicated by the lighter and darker colors). The lines indicate the theoretical slope assuming a constant gold concentration in the assemblage and an absolute LOD of ∼1 fg and ∼10 fg.

Our data further allow an estimate of detection efficiency for Na in fluid inclusions compared to solid standard materials. Knowing the size of an inclusion allows estimating the amount of liquid it contains. With the estimated density and the salinity determined by microthermometry, the absolute amount of sodium in each inclusion can be calculated. Relating the calculated masses of Na to the integrated signal intensities gives a detection efficiency (see Table 2), which is considerably lower than the ones reported earlier using NIST SRM 610, 612 and 614 based on determining the ablated volume by profilometry.³¹ Calculating the expected sodium intensities from the ablation rate of NIST SRM 610, its sodium concentration and the crater volume, the inclusion size and sodium content lead to higher sodium intensities than the actual measured ones as shown in Fig. 5. The measured integrated sodium intensities represent just 14% (Elan 6100 DRC) and 22% (Element XR), on average for medium sized inclusions (25 to 90 μm), of the intensities expected from NIST glass ablation. A minor offset in the calculated values may originate from the different sensitivities obtained on different days, which were not resolvable by the tuning procedure. The scatter in the measured sodium counts in the smaller inclusions is likely related to asymmetric inclusions shapes and a resulting spherical asymmetry. Nevertheless, the detection efficiency from fluid inclusions is significantly lower than that obtained by ablating homogeneous solids. This signal deficiency may either be due to a less efficient transport of the ablated liquid from the inclusion, compared to the aerosol ablated from a solid material, a less efficient ionization in the ICP or a less efficient ion extraction from the ICP.

Fig. 5 Sodium intensities integrated over the entire inclusion signals compared to the expected count numbers if the detection efficiency was as good as for NIST SRM 610; data from the Elan 6100 DRC (a) and the Element XR (b). The darker and fainter symbols represent data two different days of measurement. The dashed line shows the biggest crater that was applied for these measurements; inclusions larger than this maximum crater size may have not been completely ablated.

Conclusions

We have shown that a state-of-art SF-ICP-MS (Element XR) can record transient signals from fluid inclusions, even though these signals change the intensity over many orders of magnitude within a few seconds. The signals can be accurately quantified to a geochemically useful precision, provided that a restricted set of less than ∼20 elements is measured. The cycling time is about 20% longer for such an element menu, compared with a quadrupole ICP-MS. With ∼10× higher sensitivity of the Element XR compared with the H₂-boosted Elan 6100 DRC, ∼10× lower detection limits were achieved. This expands the accessible fluid inclusion size range to two or three times smaller inclusions or 10× lower concentrations in larger inclusions. The significantly poorer detection efficiency in fluid inclusions compared to the detection efficiency on solid samples such as NIST SRM 610 is not fully explained but implies the open potential to further improve the LOD of LA-ICP-MS analysis of fluid inclusions.

Acknowledgements

Financial support by the Swiss National Science Foundation (SNF/project 200021_146651) is gratefully acknowledged.

References

1. A. Audétat, D. Günther and C. A. Heinrich, Science, 1998, 279, 2091–2094.
2. T. Ulrich, D. Günther and C. A. Heinrich, Econ. Geol., 2001, 96, 1743–1774.
3. T. Baker, E. Van Achterberg, C. G. Ryan and J. R. Lang, Geology, 2004, 32, 117–120.
4. M. M. Allan, G. W. Morrison and B. W. D. Yardley, Econ. Geol., 2011, 106, 413–436.
5. J. J. Wilkinson, B. Stoffell, C. C. Wilkinson, T. E. Jeffries and M. S. Appold, Science, 2009, 323, 764–767.
6. M. Scambelluri, O. Muntener, L. Ottolini, T. T. Pettke and R. Vannucci, Earth Planet. Sci. Lett., 2004, 222, 217–234.
7. A. E. Williams-Jones, I. M. Samson, K. M. Ault, J. E. Gagnon and B. J. Fryer, Econ. Geol., 2010, 105, 1411–1440.
8. S. E. Kesler, R. J. Bodnar and T. P. Mernagh, Geofluids, 2013, 13, 398–404.
9. S. R. N. Chenery and A. H. Rankin, ECROFI, X Symp., London, 6–8 April 1989, p. 21.
10. M. H. Ramsey, B. J. Coles, J. J. Wilkinson and A. H. Rankin, J. Anal. At. Spectrom., 1992, 7, 587–593.
11. A. H. Rankin, M. H. Ramsey, B. Coles, F. Vanlangevelde and C. R. Thomas, Geochim. Cosmochim. Acta, 1992, 56, 67–79.
12. N. Imai, Anal. Chim. Acta, 1990, 235, 381–391.
13. E. E. Horn and C. T. Tye, PACROFI Prog. Abstr., VA, 4–7 January 1989, vol. 2, p. 32.
14. M. Thompson, J. E. Goulter and F. Sieper, Analyst, 1981, 106, 32–39.
15. J. W. Carr and G. Horlick, Spectrochim. Acta, Part B, 1982, 37, 1–15.
16. T. Ishizuka and Y. Uwamino, Spectrochim. Acta, Part B, 1983, 38, 519–527.
17. A. L. Gray, Analyst, 1985, 110, 551–556.
18. J. J. Wilkinson, A. H. Rankin, S. C. Mulshaw, J. Nolan and M. H. Ramsey, Geochim. Cosmochim. Acta, 1994, 58, 1133–1146.
19. T. J. Shepherd, C. Ayora, D. I. Cendon, S. R. Chenery and A. Moissette, Eur. J. Mineral., 1998, 10, 1097–1108.
20. D. Günther, R. Frischknecht, C. A. Heinrich and H. J. Kahlert, J. Anal. At. Spectrom., 1997, 12, 939–944.
21. D. Günther, A. Audétat, R. Frischknecht and C. A. Heinrich, J. Anal. At. Spectrom., 1998, 13, 263–270.
22. M. M. Allan, B. W. D. Yardley, L. J. Forbes, K. I. Shmulovich, D. A. Banks and T. J. Shepherd, Am. Mineral., 2005, 90, 1767–1775.
23. T. U. Schlegel, M. Waelle, M. Steele-MacInnis and C. A. Heinrich, Chem. Geol., 2012, 334, 144–153.
24. M. Leisen, J. Dubessy, M.-C. Boiron and P. Lach, Geochim. Cosmochim. Acta, 2012, 90, 110–125.
25. C. A. Heinrich, T. Pettke, W. E. Halter, M. Aigner-Torres, A. Audétat, D. Günther, B. Hattendorf, D. Bleiner, M. Guillong and I. Horn, Geochim. Cosmochim. Acta, 2003, 67, 3473–3497.
26. T. Pettke, F. Oberli, A. Audétat, M. Guillong, A. C. Simon, J. J. Hanley and L. M. Klemm, Ore Geol. Rev., 2012, 44, 10–38.
27. R. R. Loucks and J. A. Mavrogenes, Science, 1999, 284, 2159–2163.
28. L. Zhang, A. Audétat and D. Dolejš, Geochim. Cosmochim. Acta, 2012, 77, 175–185.
29. C. Spandler, J. Mavrogenes and J. Hermann, Chem. Geol., 2007, 239, 228–249.
30. A. C. Hack and J. A. Mavrogenes, Geochim. Cosmochim. Acta, 2006, 70, 3970–3985.
31. M. Wälle, J. Koch, L. Flamigni, S. Heiroth, T. Lippert, W. Hartung and D. Günther, Spectrochim. Acta, Part B, 2009, 64, 109–112.
32. M. Guillong, C. Latkoczy, J. H. Seo, D. Günther and C. A. Heinrich, J. Anal. At. Spectrom., 2008, 23, 1581–1589.
33. M. Resano, K. S. McIntosh and F. Vanhaecke, J. Anal. At. Spectrom., 2012, 27, 165–173.
34. O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, J. Anal. At. Spectrom., 2013, 28, 226–233.
35. T. Pettke, C. A. Heinrich, A. C. Ciocan and D. Günther, J. Anal. At. Spectrom., 2000, 15, 1149–1155.
36. R. Thomas, Spectroscopy, 2001, 16, 22–27.
37. C. Latkoczy and D. Günther, J. Anal. At. Spectrom., 2002, 17, 1264–1270.
38. M. Resano, M. Aramendia and F. Vanhaecke, J. Anal. At. Spectrom., 2009, 24, 484–493.
39. M. Guillong and C. A. Heinrich, J. Anal. At. Spectrom., 2007, 22, 1488–1494.
40. M. Guillong, D. L. Meier, M. M. Allan, C. A. Heinrich and B. W. D. Yardley, Mineralogical Association of Canada Short Course, 2008, vol. 40, pp. 328–333.
41. G. D. Miron, T. Wagner, M. Wälle and C. A. Heinrich, Contrib. Mineral. Petrol., 2013, 165, 981–1008.

---