Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
LA-ICP-MS Pb–U dating of young zircons from the Kos–Nisyros volcanic centre, SE Aegean arc†
M.
Guillong
*a,
A.
von Quadt
a,
S.
Sakata
b,
I.
Peytcheva
a and
O.
Bachmann
a
aDepartment of Earth Sciences, ETH Zurich, 8092 Zurich, Switzerland. E-mail: guillong@erdw.ethz.ch
bDepartment of Geology and Mineralogy, Kyoto University, Kyoto 606-8502, Japan
First published on 4th April 2014
Abstract
Zircon Pb–U dating has become a key technique for answering many important questions in geosciences. This paper describes a new LA-ICP-MS approach. We show, using previously dated samples of a large quaternary rhyolitic eruption in the Kos–Nisyros volcanic centre (the 161 ka Kos Plateau Tuff), that the precision of our LA-ICP-MS method is as good as via SHRIMP, while ID-TIMS measurements confirm the accuracy. Gradational age distribution over >140 ka of the Kos zircons and the near-absence of inherited cores indicate near-continuous crystallisation in a growing magma reservoir with little input from wall rocks. Previously undated silicic eruptions from Nisyros volcano (Lower Pumice, Nikia Flow, Upper Pumice), which are stratigraphically constrained to have happened after the Kos Plateau Tuff, are dated to be younger than respectively 124 ± 35 ka, 111 ± 42 ka and 70 ± 24 ka. Samples younger than 1 Ma were corrected for initial thorium disequilibrium using a new formula that also accounts for disequilibrium in 230Th decay.
Introduction
Laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) is a relatively cheap and fast method to obtain age information from zircons.1 Recent improvements in instrumentation and methods,2–5 standard reference materials,6–9 and data processing10–12 have made this method very popular.13–16 A better understanding of elemental fractionation processes,17–19 which previously were a limitation on accuracy, has produced improved results.11 Alternative methods, like sensitive high resolution ion microprobe (SHRIMP) and isotope dilution thermal ionisation mass spectrometry (ID-TIMS), still benefit, respectively, from lower sample consumption and better precision and accuracy, but are more expensive and slower than LA-ICP-MS, limiting the amount of samples that can be analysed for a given project.Due to the complexity17,18 of LA-ICP-MS for U–Pb zircon dating, the method requires care and results must be validated. However, it can now be shown that it is possible to generate accurate results with a good precision over extended periods of time using matrix matched standard reference materials and secondary standards.4,6,7,9,14,19–21
As dating techniques improve, young samples are of increasing interest; they allow (1) improved stratigraphic constraints on active volcanoes, (2) investigation of magma chamber processes that occur over timescales less than a few 100 ka, and (3) inter-comparison of different dating methods at high resolution. The analysis of young zircons in the range of 50 ka to 10 Ma is challenging due to the low radiogenic Pb content, problems with common Pb contamination and the necessity to correct for the initial Th disequilibrium.22 However, new results presented in this paper on young zircons (in the range of 50 to 500 ka) from the Kos–Nisyros volcanic centre (Aegean arc) show that we can reproduce SHRIMP precision and accuracy, while analysing a lot more zircons with relative ease. We also show that the LA-ICP-MS technique can provide a powerful means of finding the youngest zircon within a population to estimate the eruption age of silicic units that would not be easily dateable otherwise. We stress, however, that this youngest zircon within a population can still be much older than the true eruption age.
Samples
Five samples from the active Kos–Nisyros volcanic center (Eastern Aegean Arc) were chosen for this study (KPT04-24, KPT04-36, NS07, NS24 and NISP2(1), Table 1). The two samples from the Kos Plateau Tuff (a > 60 km3 rhyolite ignimbrite, erupted at 161 ± 1 ka,23 KPT04-24 and KPT04-36), studied petrologically24 and already dated by SHRIMP,24 were used to compare the LA-ICP-MS results to those from the SHRIMP and ID-TIMS. The last three samples (NS07, NS24, and NISP2(1)) are from (1) the Lower Pumice (NISP2(1)), (2) the Nikia Flow (NS24), and (3) the Upper Pumice (NS07), all erupted on Nisyros Island25 after the Kos Plateau Tuff. However, at present, these rhyo-dacitic to rhyolitic units, all with volumes of a few km3, are poorly dated26 to undated. As the youngest of tens of Pb–U zircon analyses typically overlap with the Ar/Ar ages when both methods have been applied,27,28 we used the youngest zircons to give an estimate of the maximum eruption age.| Sample | Coordinates | Th/U magma ± 2SEa (30%) | Sourceb | Th/U zircons ± 2SE | f (Th/U) ± 2SE |
|---|---|---|---|---|---|
| a Analytical uncertainty: for disequilibrium correction a minimum of 30% uncertainty is assumed for error propagation. b WR = whole rock analysis. | |||||
| NS07 | N36°36.728 E 27°09.407 | 4.0 ± 0.1 (1.2) | WR analysis | 0.95 ± 0.11 | 0.236 ± 0.028 |
| NS24 | N36°34.630 E 27°10.560 | 3.85 ± 0.43 (1.15) | WR analysis (= NISP2) | 0.89 ± 0.16 | 0.231 ± 0.041 |
| NISP2(1) | N36°36.986 E 27°09.814 | 3.85 ± 0.43 (1.15) | WR analysis | 0.95 ± 0.22 | 0.246 ± 0.057 |
| KPT04-36 | N36°46.097 E 27°06.990 | 3.3 ± 0.3 (1) | WR analysis | 0.83 ± 0.18 | 0.252 ± 0.056 |
| KPT04-24 | N36°57.791 E 26°57.294 | 3.3 ± 0.3 (1) | WR analysis | 0.59 ± 0.05 | 0.181 ± 0.016 |
Instrumentation
The LA-ICP-MS system used for this work was a Resonetics Resolution 155 laser ablation system coupled to a Thermo Element XR Sector-field ICP-MS. The LA system is equipped with some improvements compared to similar systems previously described.3,29–31 The design of the 2 volume constant geometry ablation cell has changed: the stage movement mechanism is now within the larger volume ablation cell making the ball joint and arm that moves through the ball joint in and out redundant. Cell volume and gas flow thus remain truly constant while moving the samples in the sample holder. The small volume ablation cell (funnel) is fixed on the large cell and the argon make-up gas is mixed with the helium aerosol within the funnel, decreasing the effective ablation volume where the ablated material is dispersed to less than 1 cm3. This improves the wash out and decreases the transport time from the ablation cell to ICP. The sample holder can take up to 15 one inch mounts. Due to the implementation of a z-stage, small changes in the height of a sample relative to the objective can be corrected. A backlash correction is implemented in the Geostar software that controls the stage movement pushing the precision and reproducibility of the stage in the range of 3 micrometres. The only drawback compared to the original HelEx3,29–31 ablation cell is a longer purge process to remove the air after sample exchange (15 min.). Parameters of the system are summarized in Table 2 following the guidelines presented by the Earthtime initiative.32 The laser-ablated aerosols are introduced into a Thermo element XR mass spectrometer. Coupled to the LA system, the spectrometer is used in the fast scan mode with 5 pre-scans. A separate set of cones is used for zircon analysis to minimize cross-contamination. A jet-sampling cone in combination with an H skimmer cone is used for best sensitivity with the guard electrode off. Neither N2 nor H2 addition33 generally enhanced sensitivity with or without the use of the guard electrode with this ICP-MS. Instrument parameters are daily optimized after instrument warm-up, and for quality control the sensitivity of selected elements as well as the signal stability and the gas blank intensities for most masses are recorded. The instrument is optimized ablating NIST 612 with a 43-micron crater at 10 Hz and 3.5 J cm−2 energy density in scanning mode (3 μm s−1). Typical sensitivity for 238U is 1.5 M cps. Typical gas bank levels are 0–3 CPS for 238U, 5–10 cps for 206Pb and 2000–3000 cps for 202Hg although all gases pass a mercury trap. ID-TIMS measurements of 7 zircons from the Kos Plateau Tuff were performed on a Thermo Triton instrument. Details of the instrument settings and the method can be found elsewhere.34| Laboratory & sample preparation | |
| Laboratory name | Dept. of Earth Science, ETH Zurich |
| Sample type/mineral | Zircons |
| Sample preparation | Conventional mineral separation, 1 inch resin mount, 1 μm polish to finish |
| Laser ablation system | |
| Make, model & type | Resonetics resolution 155 |
| Ablation cell & volume | Laurin Technics 155, constant geometry, aerosol dispersion volume <1 cm3 |
| Laser wavelength | 193 nm |
| Pulse width | 25 ns |
| Energy density/fluence | ∼2.0 J cm−2 |
| Repetition rate | 5 Hz |
| Spot size | 30 μm |
| Ablation rate | ∼75 nm per pulse |
| Sampling mode/pattern | Single hole drilling, 5 cleaning pulses |
| Carrier gas and flow | 100% He, 0.7 l min−1 |
| Ablation duration | 40 seconds |
| ICP-MS Instrument | |
| Make, model & type | Thermo Element XR SF-ICP-MS |
| Sample introduction | Ablation aerosol only, squid aerosol homogenisation device |
| RF power | 1500 W |
| Make-up gas flow | ∼0.95 l min−1 Ar (mixed with He inside ablation cell funnel) |
| Detection system | Single detector triple mode SEM, analog, Faraday |
| Masses measured | 202, 204, 206, 207, 208, 232, 235, 238 amu |
| Integration time per peak | 12 ms (masses 202, 204), 20 ms (masses 208, 232, 235, 238), 40 ms (masses 206, 207) |
| Total integration time per reading | 0.202 seconds |
| Dead time (ns) | 8 ns |
| Typical oxide rate (ThO/Th) | 0.18% |
| Typical doubly charged rate (Ba++/Ba+) | 3.5% |
| Data processing | |
| Gas blank | 10 second prior to each ablation spot |
| Calibration strategy | GJ-1 used as a primary reference material, Plesovice, 91500 & Temora used as secondary's for quality control |
| Reference material information | GJ-1 206Pb/238U 0.09761 ± 0.0002 (Wtd mean of TIMS analysis)35 |
| Data processing package used | Iolite 2.5 with VizualAge |
| Mass discrimination | Mass bias correction for all ratios normalized to the primary reference material |
| Common-Pb correction | No common-Pb correction applied |
| Uncertainty level & propagation | Ages are quoted at 2 SE absolute, propagation is by quadratic addition. Reproducibility of reference material uncertainty is propagated10 |
| Quality control/validation | Plesovice: Wtd ave. 206Pb/238U age = 338.3 ± 1.7 (2 SE, MSWD = 3.1, n = 16 in 3 sessions), Temora: Wtd ave. 206Pb/238U age = 421.6 ± 2.0 (2 SE, MSWD = 3.4, n = 18 in 3 sessions), 91500: Wtd ave. 206Pb/238U age = 1064.8 ± 3.3 (2 SE, MSWD = 0.44, n = 8 in 1 session) |
| Th disequilibrium correction and error propagation | 206Pb/238U ages of the samples were corrected using eqn (3). Errors from (206/238) measured, f(Th/U), λ238 (1.55125 × 10−10, 0.11% 2δ),36 and λ230 (9.17055 × 10−06, 0.15% 2δ)37 are propagated |
Methods
All samples were mounted in 1 inch epoxy mounts and polished, and prior to analysis, cathode luminescence (CL) images were acquired to identify possible inherited cores. Laser analysis spots on the zircon grains were programmed using the Geostar software with a precision of 3 microns in the x and y directions. Each spot consists of: (1) movement of the stage to the location; (2) surface cleaning with 5 laser pulses; (3) wash out of the aerosol from cleaning over 17 seconds; (4) triggering the ICP-MS to start the next measurement; (5) acquiring a gas blank signal for 10 seconds; (6) ablating the sample for 40 seconds (30 microns crater, 5 Hz repetition rate, 2 J cm−2 energy density). The primary standard reference sample GJ-1 was measured 3 times at the beginning and end of each sequence and also 3 times after 15–20 samples. Total numbers of primary SRM were >15. Between the primary SRM measurements at least 2 secondary SRM (Plesovice, Temora, 91500) were included for quality control. Raw data were imported into Iolite10,11 and with the use of the VizualAge12 data reduction scheme reduced to obtain ages and ratios corrected for instrumental drift and down hole fractionation. Downhole fractionation was found to be very similar between SRM, secondary SRM and the samples.Zircon ages can be corrected for common Pb contamination using different methods. The most commonly used approach is via measuring 204Pb and using common Pb isotope ratios to subtract the common Pb component from the radiogenic Pb isotopes. It is also widely used to calculate the intercept of the measured ratios with the concordia curve assuming a common Pb composition38 or applying the routine proposed by Andersen.39 These common Pb corrections were considered, but due to the very low 204 counts and the isobaric interference from 204Hg, it was not possible to measure the 204Pb counts with sufficient precision. The 207Pb signal was also very low and therefore not precise enough to reliably correct for common Pb. All age results presented in this work are therefore not common Pb corrected. With the help of VizualAge and a live Concordia diagram common Pb contaminated signals are easily recognised as a shift of the data point ellipse away from the Concordia towards common Pb composition as shown in the ESI, Fig. 1–7.† Integration intervals are, where possible, set to exclude any common Pb. As few as 1 analysis (KPT samples) to up to 50% of analyses (NS07) with remaining common Pb were discarded based on live Concordia diagrams and the offset to the Concordia as is shown for all samples in the ESI, Fig. 1–7.† These Concordia plots show results prior to the Th disequilibrium correction and are therefore expected to be discordant.40 Although all masses were measured, only the 206Pb/238U age is considered precise and accurate enough. The other ratios (207Pb/235U, 208Pb/232Th and 207Pb/206Pb) could not be measured with sufficient precision and accuracy, partly due to the influence of common Pb on these ratios and the low abundance in such young zircons.
Thorium disequilibrium correction
The U/Pb age of zircons can be calculated using the following equation, originally suggested by Schärer (1984).22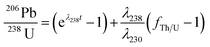 | (1) |
As zircon grows from a melt, Th gets fractionated from U, imparting a disequilibrium in 230Th (an intermediate product in the 238U decay series) that has to be corrected to get an accurate age. The initial Th disequilibrium correction has been described in detail in several papers.22,40–43 This fractionation is described by f(Th/U) (eqn (2)) that needs to be determined.
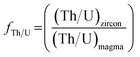 | (2) |
There are several approaches to quantify the fractionation factor f(Th/U). With LA-ICP-MS and SHRIMP, Th/U in the mineral is directly measured. Th/U in the magma is typically considered as a constant and can be estimated by whole rock or volcanic glass analysis. However, the assumption of a homogeneous magma with constant Th/U is questionable. Instead of assuming a constant Th/U in the magma, it is possible to assume a constant fractionation and variations in Th/U in the magma. An investigation of these two approaches43 found larger scatter in the data using the constant fractionation compared to the constant magma value. A constant magma value implies varying fractionation, while a constant fractionation would imply variations in the Th/U ratio within the magma. Reality might be in-between and the assumption of a constant Th/U in the magma was weighted more43 and this approach was also used in this work. The uncertainty on Th/U in the magma was found to be 14% estimated from isotope dilution Th/U measurements.43 Another approach to overcome the problem of unknown Th/U in the magma uses the difference between the measured 208Pb/232Th age which is not affected by disequilibrium and the 206Pb/238U age to get f(Th/U).44 Our data did not allow this approach as the 208Pb/232Th age has too high uncertainty and variability possibly due to common Pb contamination.
The influence on the corrected age of changing the Th/U values in the magma from 2 to 4 has been found to be 1.4% for 1 Ma old zircons, decreasing for older zircons.40 This is a problem for high precision TIMS dating with uncertainties of 0.1% but not for LA-ICP-MS where the uncertainty for such young samples is ∼1–10%. The typical Th disequilibrium correction for zircons is in the range of 50 to 110 ka.41 The correction usually is accurate to ±15 ka due to the above mentioned uncertainties in the Th/U ratio determination in the magma.41
The growth of the 206Pb/238U ratio can be calculated correctly with this eqn (1) only after 230Th reaches radioactive equilibrium. This equation does not accurately correct when 230Th is still in disequilibrium which is the case up to about 300 ka. In fact, the isotopic growth curve defined from eqn (1) does not pass the origin point when t = 0 and 206Pb = 0. Therefore, for the chronology of the zircon crystals with ages below 1 Ma, a more accurate correction must be applied as shown in eqn (3). The initial assumptions and the derivation of eqn (3) can be found in the ESI† and in the study of Sakata et al., 2013.44
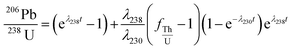 | (3) |
As the ages measured in this work are between 70 ka and 400 ka, eqn (3) was used to get accurate results. A comparison of ages determined using both equations is discussed below. Th/U whole rock data available on the Kos Plateau Tuff are limited and the precision based on few samples and bulk chemistry analysis is likely overestimating the uncertainty on Th/U in the magma itself. Therefore we assume an uncertainty on Th/U in the magma of 30% and propagate this uncertainty to the corrected age.
Results
Only 206Pb/238U ages are considered for the interpretation of the young samples from Kos and Nisyros, because of the low intensities of 207Pb and 208Pb and the larger influence from small amounts of common Pb on the 208Pb/232Th and 207Pb/235U ages. The accuracy of the method in general is shown using secondary standards. Unfortunately no suitable young secondary SRM was available at the time of measurements. Resulting ages are compared with accepted (ID-TIMS) ages. All three secondary standards (Plesovice: measured 338.3 ± 1.7 Ma, ref.: 337.13 ± 0.37 ma;8 Temora: 421.6 ± 2.0 Ma, ref.: 416.8 ± 1.1 ma;45 91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1064.8 ± 3.3 Ma, ref.: 1065 ± 2 ma (ref. 46)) agree reasonably well with ID-TIMS reference values. The precision of these secondary SRMs was found to be between 0.5% and 1%, 2 standard errors for 8–18 replicate analyses and about 1% (2 SE) on individual point analysis. The MSWDs obtained for the secondary standards (Table 1) are as high as 3.4 which could either be due to standard heterogeneity or an overestimated precision. All data can be found in the ESI† following the guidelines suggested by the Earthtime initiative.32
1064.8 ± 3.3 Ma, ref.: 1065 ± 2 ma (ref. 46)) agree reasonably well with ID-TIMS reference values. The precision of these secondary SRMs was found to be between 0.5% and 1%, 2 standard errors for 8–18 replicate analyses and about 1% (2 SE) on individual point analysis. The MSWDs obtained for the secondary standards (Table 1) are as high as 3.4 which could either be due to standard heterogeneity or an overestimated precision. All data can be found in the ESI† following the guidelines suggested by the Earthtime initiative.32
The approach of using an old SRM to quantify these very young zircons might be affected by small differences in the ablation behaviour between the SRM and the samples, especially the downhole fractionation. Parameters that can have and influence include the amount of radiation damage, trace element composition, transparency, crystal orientation and carrier gas composition and are currently under investigation and discussion.47,48 The individual contributions to the uncertainty on the final age were calculated. The most important one (∼65% of the total error) is the uncertainty from the measured 206Pb/238U ratio. The remaining 35% comes in approximately even parts from the uncertainty on the decay constants λ232 and λ238 and the uncertainty of the fractionation factor f(Th/U).
The comparison between age data acquired using LA-ICP-MS in this study with the published data using SHRIMP27 shows remarkable agreement. Zircon ages cover the same range between the eruption age of 161 ka (40Ar/39Ar sanidine dating23) and approximately 350 ka (Fig. 1), with very similar uncertainties (although errors on Th-corrections were not propagated in the SHRIMP results27). Ages are evenly distributed in this range, with no major gaps in crystallization that can be seen within the precision of the method (ESI, Fig. 8 and 9†). It reinforces previous interpretations that zircons have been crystallizing over an extended period of time (>140 ka), recording the growth and maturation of the silicic magma reservoir in the upper crust.27 Based on the precision we obtain, it is not possible to distinguish between several discrete crystallisation events and a real continuous crystallisation in the given time frame.
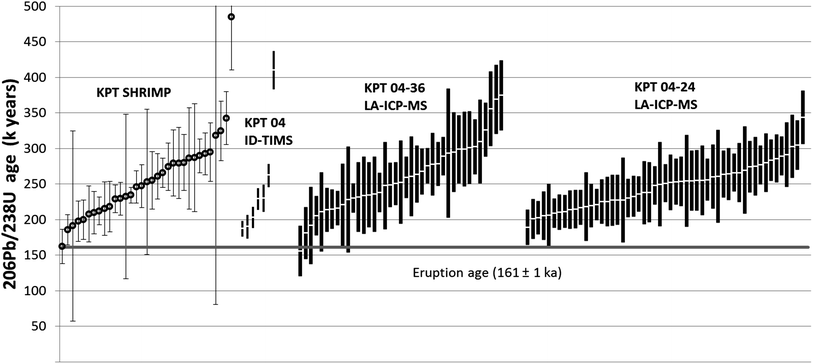 | ||
| Fig. 1 206Pb/238U age results for SHRIMP27 (narrow error bars), ID-TIMS (medium error bars) and LA-ICP-MS (wide error bars) for Kos Plateau Tuff samples including 2 standard errors. Only LA-ICP-MS and ID-TIMS results have the errors from the Th disequilibrium correction propagated. 2 old cores found with LA-ICP-MS and integrations with common Pb are not plotted. | ||
ID-TIMS measurements on 7 selected grains (ESI Table 2†) show again a remarkable overlap with SHRIMP and LA-ICP-MS ages. The age of 6 grains falls well within the range of all SHRIMP and LA-ICP-MS data. One zircon with an age of 410 ± 27 ka can be treated as an outlier. The distribution of ID-TIMS ages from 187 ± 15 ka to 262 ± 16 ka supports both the accuracy of the LA-ICP-MS measurements and the interpretation of zircon crystallization over an extended time. All details on the ID-TIMS method and measurements are given in the study of von Quadt et al., 2014.34
Although no old grains were found using SHRIMP, two inherited cores stand out in the LA-ICP-MS analyses. Precise ages on those cores cannot be given, as they are a mixture of young overgrowth and an old core, but they are very old, with ages in the range of 1 to 2 Ga (see ESI, Table 1†). In general, LA-ICP-MS is much more sensitive in finding inherited cores as LA removes about 10 times more material per analysis than SHRIMP (crater depth for LA is 10–15 microns while SHRIMP craters are only 1–2 microns deep).
As our LA-ICP-MS method has shown its high degree of accuracy and precision especially in comparison to ID-TIMS data, we dated 3 younger, hitherto undated samples from the nearby Nisyros volcano. Using the youngest zircons as the best estimate of the eruption age, results yield (1) 124 ± 35 ka for the Lower Pumice (NISP2(1)), (2) 111 ± 42 ka for the Nikia Flow (NS24), and 70 ± 24 ka for the Upper Pumice (NS07) as shown in Fig. 2. All errors are given as 2 SE. Only a limited number of zircons could be separated from these samples, especially NS24, as they may have been zircon-undersaturated prior to eruption.25,26,49 By analysing more zircon grains from these samples it is likely that the spread increases, therefore the youngest zircon found can only be interpreted as maximum ages.
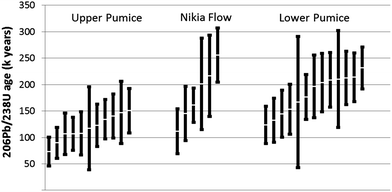 | ||
| Fig. 2 U–Pb age results for Nisyros samples including 2SE. Eruption ages for these units are assumed to be at the youngest zircon age or younger. | ||
Impact of data reduction on final ages
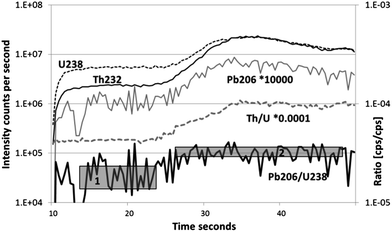
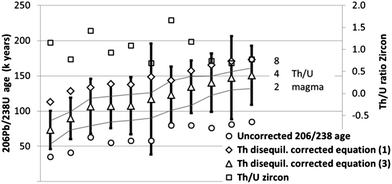
We investigated the effects of data reduction on final ages. The selection of integration intervals in U/Pb dating appears to be a critical aspect of the data reduction process. Modern data reduction software can give instant feedback on the resulting age while selecting integration intervals. These instant feedback tools can be used to recognize heterogeneities, inclusions and inherited cores when drilling with the laser through a zircon grain. Fig. 3 provides an example of such a procedure (with full dataset in the ESI†). The ablation consisted of two parts: the first integration of 10 seconds has a resulting age of 210 ± 31 ka with a corresponding Th/U ratio of 0.440 ± 0.003, while the second integration interval is 260 ± 29 ka old with a Th/U ratio of 0.93 ± 0.03. Based on the variable Th/U ratio, we assume that this zircon grain was growing over an extended period, during which the composition and/or the fractionation f(Th/U) changed. Several zircon grains showed similar characteristics and were similarly treated in the data reduction process. All ages that do not show enhanced common Pb were taken into account for Fig. 1 and 2 and are listed in the ESI† with a comment. A detailed description of a universal data reduction protocol is beyond the focus of this work.The different Th disequilibrium corrections (eqn (1) and (3)) also have a significant impact on the final age for young samples. Using sample NS07, we show that the higher the measured Th/U, the less is the correction (Fig. 4). The correction is as previously reported in the range of 70–110 ka (ref. 41) towards older age compared with the uncorrected age. For ages above 300 ka, the correction model of either eqn (1) or eqn (3) has limited influence on the final age. For ages younger than 300 ka, the correction model becomes important. A zircon with an age as young as 70 ka calculated using eqn (3) is more than 50% older (110 ka) when using eqn (1), which is outside the error bar in that case.
The Th/U ratio in the magma measured by whole rock data or assumed influences in a limited way the final age as was investigated and is shown in Fig. 4. The grey lines represent the corrected ages using two different Th/U ratios for the magma. The measured Th/U ratio was found to be 4 for this sample (whole rock analysis, Table 1). Changing Th/U in the magma to either 8 or 2, instead of 4, changes the corrected age by about +10 or −20 ka respectively, which is always within the uncertainty. As the variation of Th/U in the zircons is lower than a factor of 4, all corrected ages assuming a constant fractionation factor f(Th/U) and varying Th/U ratios in the magma would fall between the two grey lines. Based on these findings, the method including the Th disequilibrium correction gives accurate results for the LA-ICPMS technique. However, more precise and accurate Th/U ratios in the magma are needed for high precision ID-TIMS dating. A possibility might be analysing melt inclusions in zircons that represent the local magma composition and fractionation factors can be determined for individual zircons.
Conclusions
This work shows that the in situ LA-ICP-MS method is well suited to date zircons as young as 50 ka. Applying our improved initial thorium disequilibrium correction, results are accurate based on the comparison between three different methods: SHRIMP, ID-TIMS and LA-ICP-MS applied to zircons from KPT. Precision of ages acquired via LA-ICP-MS for zircons in the range of 70–500 ka is comparable with data collected with SHRIMP. ID-TIMS results for such young zircons are a factor of 2–3 more precise. We stress, however, that as more material is consumed with LA-ICP-MS, much more information is acquired which obviously can also be a drawback when analyses of very small features like thin rims are required. In addition, running costs are low, and hundreds of zircons can easily be analysed per day. The limiting step becomes sample preparation as well as data reduction and interpretation of the results after analysis. Due to the large sample consumption (about 75 nm per laser pulse), zircons with inclusions not detected by CL images can lead to common Pb contamination. Hence, we recommend, when possible, to measure additional elements (31P, 27Al, 56Fe) to recognize the presence of these inclusions.To further improve the method, a reliable common Pb correction is necessary. Possibilities include better detection of 207Pb and the 207Pb/206Pb ratio by increasing the repetition rate and/or crater size and increasing the dwell time on mass 207, keeping 238U in the pulse counting mode to avoid detector cross-calibration problems. Due to the low count rate on Pb isotopes, a bias in calculated ratios is possible as the mean-of-ratios can be different from the ratio-of-means. A simple comparison between the two calculations showed an average bias of the 206Pb/238U ratio smaller than 3% for all 11 good analyses of sample NS07 well below the precision of these measurements and without down-hole fractionation correction.
Th disequilibrium correction is essential for zircons younger than 10 Ma and the improved equation (3) should be used for zircons younger 0.5 Ma. The influence from the uncertainty of f(Th/U) is relatively small in comparison to the overall uncertainty for analysis with LA-ICP-MS. Nevertheless errors from the correction should be propagated.
The evenly spread age distribution of the Kos Plateau Tuff samples (from 320 ka to 180 ka) is interpreted as recording near-continuous crystallisation of zircons in a persistent magma chamber. A probability density plot (ESI Fig. 8†) does not show a normal distribution of the KPT ages that would be expected from a sharp single crystallisation age. Therefore the calculation of a weighted mean of all the 132 zircons from all 3 techniques (SHRIMP, ID-TIMS and LA-ICP-MS, ESI Fig. 9†) is meaningless in this case, as it results in an weighted mean age of 238.3 ± 7.1 ka with a MSWD of 7.8 (see also previous discussion50).
The fact that only 2 inherited cores were found, despite the very large number of analyses, suggests that the silicic magma reservoir was mostly isolated from its upper crustal wall rocks. Such a near closed-system fractionation is confirmed by the unradiogenic isotopic ratios of the Kos Plateau Tuff25,27,51 and is consistent with thermal models of upper crustal reservoirs that interacted in a limited way with their wall rocks.27,50,52,53 The fact that only very few zircons were found with ages in the range of 20 ka before eruption is also consistent with the interpretation that the magma was rejuvenated prior to eruption by fresh recharge,24 reducing the growth and even causing resorption of zircons.
The ages of the youngest zircons found in the Nisyros samples agree with previously determined stratigraphy25,54 and provide the first direct geochronological estimates of the eruption ages for the following three deposits: (1) Lower Pumice, (2) Nikia Flow, and (3) Upper Pumice. We stress that these are maximum ages, as they may all be zircon-undersaturated prior to eruption.26 It is demonstrated that the Kos–Nisyros system took at least several tens of thousands of years (from 160 ka, eruption of KPT to ∼120–130 ka, maximum eruption age of the Lower Pumices on Nisyros) to generate another explosive silicic eruption after the caldera-forming Kos Plateau Tuff. All three units also display an extended range of zircon ages, suggesting similar crystal recycling to that observed for the Kos Plateau Tuff27 and many other eruptions (e.g., see reviews by Costa, 2008 and Simon et al., 2008).41,55 A comparison between zircons with and without chemical abrasion using LA-ICP-MS is an ongoing project with the Kos Plateau Tuff and related units.34
Acknowledgements
We would like to thank Tilman Jeske for the preparation of the Nisyros samples. Critical reading by Ben Ellis helped to improve the manuscript. Comments especially on the common Pb correction by two unknown referees further helped improve the work. This work was in part supported by Swiss SNF grant 200021_146268 (to OB).Notes and references
- B. J. Fryer, S. E. Jackson and H. P. Longerich, Chem. Geol., 1993, 109, 1–8, DOI:10.1016/0009-2541(93)90058-q.
- S. Johnston, G. Gehrels, V. Valencia and J. Ruiz, Chem. Geol., 2009, 259, 218–229, DOI:10.1016/j.chemgeo.2008.11.004.
- W. Muller, M. Shelley, P. Miller and S. Broude, J. Anal. At. Spectrom., 2009, 24, 209–214, 10.1039/b805995k.
- D. Frei and A. Gerdes, Chem. Geol., 2009, 261, 261–270, DOI:10.1016/j.chemgeo.2008.07.025.
- B. Shaulis, T. J. Lapen and A. Toms, Geochem., Geophys., Geosyst., 2010, 11, Q0AA11 CrossRef.
- U. Kloetzli, E. Kloetzli, Z. Guenes and J. Kosler, Geochim. Cosmochim. Acta, 2007, 71, A495 Search PubMed.
- Y. Orihashi, S. i. Nakai and T. Hirata, Resour. Geol., 2008, 58, 101–123, DOI:10.1111/j.1751-3928.2008.00052.x.
- J. Slama, J. Kosler, D. J. Condon, J. L. Crowley, A. Gerdes, J. M. Hanchar, M. S. A. Horstwood, G. A. Morris, L. Nasdala, N. Norberg, U. Schaltegger, B. Schoene, M. N. Tubrett and M. J. Whitehouse, Chem. Geol., 2008, 249, 1–35, DOI:10.1016/j.chemgeo.2007.11.005.
- U. Kloetzli, E. Kloetzli, Z. Guenes and J. Koslar, Geostand. Geoanal. Res., 2009, 33, 5–15, DOI:10.1111/j.1751-908x.2009.00921.x.
- C. Paton, J. Hellstrom, B. Paul, J. Woodhead and J. Hergt, J. Anal. At. Spectrom., 2011, 26, 2508–2518, 10.1039/c1ja10172b.
- C. Paton, J. D. Woodhead, J. C. Hellstrom, J. M. Hergt, A. Greig and R. Maas, Geochem., Geophys., Geosyst., 2010, 11, Q0AA06 CrossRef.
- J. A. Petrus and B. S. Kamber, Geostand. Geoanal. Res., 2012, 36, 247–270, DOI:10.1111/j.1751-908x.2012.00158.x.
- E. Butler, W. Winkler and M. Guillong, Swiss J. Geosci., 2011, 104, 225–236, DOI:10.1007/s00015-011-0065-1.
- J. Kosler, J. Slama, E. Belousova, F. Corfu, G. E. Gehrels, A. Gerdes, M. S. A. Horstwood, K. N. Sircombe, P. J. Sylvester, M. Tiepolo, M. J. Whitehouse and J. D. Woodhead, Geostand. Geoanal. Res., 2013, 37, 243–259, DOI:10.1111/j.1751-908x.2013.00245.x.
- E. Buetler, W. Winkler and M. Guillong, Swiss J. Geosci., 2011, 104, 225–236, DOI:10.1007/s00015-011-0065-1.
- T. D. Yokoyama, T. Suzuki, Y. Kon and T. Hirata, Anal. Chem., 2011, 83, 8892–8899, DOI:10.1021/ac2012448.
- J. Kosler, M. Wiedenbeck, R. Wirth, J. Hovorka, P. Sylvester and J. Mikova, J. Anal. At. Spectrom., 2005, 20, 402–409, 10.1039/b41629b.
- B. K. Kuhn, K. Birbaum, Y. Luo and D. Guenther, J. Anal. At. Spectrom., 2010, 25, 21–27, 10.1039/b917261k.
- G. E. Gehrels, V. A. Valencia and J. Ruiz, Geochem., Geophys., Geosyst., 2008, 9, Q03017 CrossRef.
- L. A. Solari, A. Gomez-Tuena, J. Pablo Bernal, O. Perez-Arvizu and M. Tanner, Geostand. Geoanal. Res., 2010, 34, 5–18 CrossRef CAS.
- E. Kooijman, J. Berndt and K. Mezger, Eur. J. Mineral., 2012, 24, 5–21, DOI:10.1127/0935-1221/2012/0024-2170.
- U. Schärer, Earth Planet. Sci. Lett., 1984, 67, 191–204, DOI:10.1016/0012-821x(84)90114-6.
- P. E. Smith, D. York, Y. Chen and N. M. Evensen, Geophys. Res. Lett., 1996, 23, 3047–3050, DOI:10.1029/96gl02759.
- O. Bachmann, B. Schoene, C. Schnyder and R. Spikings, Geochem., Geophys., Geosyst., 2010, 11, Q0AA08 CrossRef.
- L. Francalanci, J. C. Varekamp, G. Vougioukalakis, M. J. Defant, F. Innocenti and P. Manetti, Bull. Volcanol., 1995, 56, 601–620 CrossRef.
- O. Bachmann, C. D. Deering, J. S. Ruprecht, C. Huber, A. Skopelitis and C. Schnyder, Contrib. Mineral. Petrol., 2012, 163, 151–166, DOI:10.1007/s00410-011-0663-y.
- O. Bachmann, B. L. A. Charlier and J. B. Lowenstern, Geology, 2007, 35, 73–76, DOI:10.1130/g23151a.1.
- S. J. A. Brown and I. R. Fletcher, Geology, 1999, 27, 1035–1038, DOI:10.1130/0091-7613(1999)027<1035:supdot>2.3.co;2.
- S. Eggins, R. Grun, A. W. G. Pike, M. Shelley and L. Taylor, Quat. Sci. Rev., 2003, 22, 1373–1382, DOI:10.1016/s0277-3791(03)00064-7.
- W. Muller, J. M. G. Shelley and S. O. Rasmussen, J. Anal. At. Spectrom., 2011, 26, 2391–2395, 10.1039/c1ja10242g.
- J. Woodhead, J. Hergt, M. Shelley, S. Eggins and R. Kemp, Chem. Geol., 2004, 209, 121–135, DOI:10.1016/j.chemgeo.2004.04.026.
- ed. M. S. A. Horstwood, J. Kosler, S. Jackson, N. Pearson and P. Sylvester, 2013, http://www.cirdles.org/LA-ICP_MS_Data_Handling.
- M. Guillong and C. A. Heinrich, J. Anal. At. Spectrom., 2007, 22, 1488–1494, 10.1039/b709489b.
- A. von Quadt, D. Gallhofer, M. Guillong, I. Peytcheva, M. Waelle and S. Shuhei, J. Anal. At. Spectrom., 2014 Search PubMed , in review, this volume.
- S. E. Jackson, N. J. Pearson, W. L. Griffin and E. A. Belousova, Chem. Geol., 2004, 211, 47–69, DOI:10.1016/j.chemgeo.2004.06.017.
- A. H. Jaffey, K. F. Flynn, L. Glendeni, W. C. Bentley and A. M. Essling, Phys. Rev. C: Nucl. Phys., 1971, 4, 1889–1906, DOI:10.1103/physrevc.4.1889.
- H. Cheng, R. L. Edwards, C. C. Shen, V. J. Polyak, Y. Asmerom, J. Woodhead, J. Hellstrom, Y. J. Wang, X. G. Kong, C. Spotl, X. F. Wang and E. C. Alexander, Earth Planet. Sci. Lett., 2013, 371, 82–91, DOI:10.1016/j.epsl.2013.04.006.
- A. Cocherie, C. M. Fanning, P. Jezequel and M. Roberta, Geochim. Cosmochim. Acta, 2009, 73, 1095–1108, DOI:10.1016/j.gca.2008.11.028.
- T. Andersen, Chem. Geol., 2002, 192, 59–79, DOI:10.1016/s0009-2541(02)00195-x.
- M. Chiaradia, U. Schaltegger, R. Spikings, J. F. Wotzlaw and M. Ovtcharova, Econ. Geol., 2013, 108, 565–584 CrossRef CAS.
- J. I. Simon, P. R. Renne and R. Mundil, Earth Planet. Sci. Lett., 2008, 266, 182–194, DOI:10.1016/j.epsl.2007.11.014.
- N. M. McLean, J. F. Bowring and S. A. Bowring, Geochem., Geophys., Geosyst., 2011, 12, Q0AA18 CrossRef.
- M. Rioux, C. J. Lissenberg, N. M. McLean, S. A. Bowring, C. J. MacLeod, E. Hellebrand and N. Shimizu, Nat. Geosci., 2012, 5, 275–278, DOI:10.1038/ngeo1378.
- S. Sakata, S. Hirakawa, H. Iwano, T. Danahara and T. Hirata, Mineral. Mag., 2013, 77, 2116, DOI:10.1180/minmag.2013.077.5.19.
- L. P. Black, S. L. Kamo, C. M. Allen, J. N. Aleinikoff, D. W. Davis, R. J. Korsch and C. Foudoulis, Chem. Geol., 2003, 200, 155–170, DOI:10.1016/s0009-2541(03)00165-7.
- M. Wiedenbeck, P. Alle, F. Corfu, W. L. Griffin, M. Meier, F. Oberli, A. Vonquadt, J. C. Roddick and W. Speigel, Geostand. Newsl., 1995, 19, 1–23, DOI:10.1111/j.1751-908x.1995.tb00147.x.
- E. Marillo Sialer, J. Woodhead, J. M. Hergt, A. Greig, M. Guillong, A. Gleadow, N. Evans and C. Paton, J. Anal. At. Spectrom., 2014 10.1039/c4ja00008k.
- J. Kosler, S. Jackson, Z. Yang and R. Wirth, J. Anal. At. Spectrom., 2014 10.1039/c3ja50386k.
- L. Vanderkluysen, A. Volentik, C. Principe, J. C. Hunziker and J. Hernandez, in The petrology and geochemistry of lavas and tephras of Nisyros Volcano (Greece), ed. J. C.Hunziker and L. Marini, Lausanne, 2006, vol. 44, pp. 100–106 Search PubMed.
- O. Bachmann, F. Oberli, M. A. Dungan, M. Meier, R. Mundil and H. Fischer, Chem. Geol., 2007, 236, 134–166, DOI:10.1016/j.chemgeo.2006.09.005.
- A. Buettner, I. C. Kleinhanns, D. Rufer, J. C. Hunziker and I. M. Villa, Lithos, 2005, 83, 29–46, DOI:10.1016/j.lithos.2005.01.001.
- J. Dufek and G. W. Bergantz, J. Petrol., 2005, 46, 2167–2195, DOI:10.1093/petrology/egi049.
- S. E. Gelman, F. J. Gutierrez and O. Bachmann, Geology, 2013, 41, 759–762, DOI:10.1130/g34241.1.
- A. Volentik, L. Vanderkluysen and C. Principe, Eclogae Geol. Helv., 2002, 95, 223–235 Search PubMed.
- F. Costa, R. Dohmen and S. Chakraborty, in Minerals, Inclusions and Volcanic Processes, ed. K. D. Putirka and F. J. Tepley, 2008, vol. 69, pp. 545–594 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Table with all results of LA-ICP-MS and ID-TIMS analyses, ESI Fig. 1–9, derivation of the Th disequilibrium correction. See DOI: 10.1039/c4ja00009a |
| This journal is © The Royal Society of Chemistry 2014 |