Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determination of stability constants of strong metal–ligand complexes using anion or cation exchange chromatography and atomic spectrometry detection†
M.
Wacker
and
A.
Seubert
*
Philipps Universitaet Marburg, Chemistry Department, Analytical Chemistry, D-35043 Marburg, Germany. E-mail: seubert@staff.uni-marburg.de; Tel: +49-6421-28-25661
First published on 21st January 2014
Abstract
A method for the determination of stability constants of polyaminocarboxylic acid ligands with trivalent metal ions based on the addition of a second metal ion as a competitor has been developed. However, the absolute values of these stability constants are too high for an accurate direct determination. A competition approach delivers the ratio of the stability constants of the two competing metal ions. The different species were separated via anion and cation ion exchange chromatography and their metal content was quantitatively detected online utilizing inductively coupled plasma atomic emission spectrometry. The model ligand used was N,N,N′,N′-ethylenediaminetetraacetic acid as a most prominent polyaminocarboxylic acid ligand. The trivalent ions of chromium, iron, gallium, indium, and scandium were successfully investigated using this approach.
Introduction
The first synthetic and still most abundant chelator from the family of polyaminocarboxylic acids is edta, which was patented by F. Münz in 1935.1 The field of application of polyaminocarboxylic acids is wide spread. The most deployed chelators are edta, dtpa (diethylentriaminepentaacetic acid) and nta (nitrilotriacetic acid). The majority of these chelators are used as laundry detergents or in the textile and paper industries. They bind to catalytically active metal ions like iron, manganese or copper, so the metals are not able to destroy bleachers or they are used as water softeners. Other applications are in the medical domain, where chelators are applied as detoxificators to cure metal poisoning or as markers for special examinations. Commonly strong lanthanoid complexes are used to enhance the contrast of magnetic resonance measurement. Another application is their use as tracers in groundwater studies. Therefore the complexes must fulfill some requirements such as water solubility, thermodynamic stability and kinetic inertness. Furthermore, the complexes should not be absorbed into soil and the chelated metal ion should be insoluble in its non-complexed form to gain low limits of detection. Some lanthanoid polyaminocarboxylic acid complexes are quite suitable for this purpose.2–4Due to their poor biodegradability and high potential of remobilisation of heavy metals from soil a substitution of them is advisable. If new chelators should be used it will be very helpful to have information about their important chemical properties. One of these properties is the stability constant of the metal ligand complex. Among the most accomplished techniques are complex formation titrations or electrophoretic or chromatographic separations to measure these thermodynamic values.5–10
The stability constant can be deduced from the law of mass action. Eqn (1) shows the reaction between one trivalent metal ion (Me) and edta (Y) with the resulting stability constant K1.
| Me3+ + Y4− ⇔ MeY− |
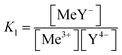 | (1) |
The known stability constants of Y with metal ions are very high, the decadic logarithms of them are between 20 and 30 depending on the metal ion. Y can form very stable complexes such as a hexadentate ligand because of the entropy accession compared to monodentate ligands.
However, you should have in mind that Y will only be four times deprotonated if the pH value suits. The pKA-values of Y are pKa1 = 0.92, pKa2 = 1.62, pKa3 = 2.00, pKa4 = 2.71, pKa5 = 6.16, and pKa6 = 10.23. The measurements were done at pH 3, so in most of the Y all four carboxylic acids are deprotonated and the metal ions are free and not in their hydroxide complexes.11,12
When determining the stability constants of a complex, the medium in which the measurements are made, must be taken into account. The temperature, ionic strength and the pH value of the solution are vital to the success of the determination. Literature values are often extrapolated to the standard conditions at 25 °C and an ionic strength of I = 0 mol l−1. Extrapolation to an ionic strength of I = 0 mol l−1 is usually done using the Davies equation (eqn (2)). This equation was first published in 1938 as an empirical extension of the Debye–Hückel theory. It calculates the activity coefficient γi of analytes in solution with ionic strength I′ not equal to zero. Limitations of the equation are highly concentrated solutions and highly diluted solutions. When solutions are very diluted the Debye–Hückel equation should be used.13,14
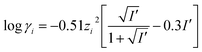 | (2) |
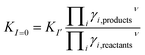 | (3) |
The integrated van't Hoff equation (if the standard reaction enthalpy ΔH0 is known and constant in the temperature range of the measurement) is used for temperature correction, cf.eqn (4).16
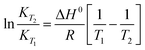 | (4) |
The pH value has a great influence on the form of metal and ligand ions. In a basic medium, metal hydroxides occur and in an acidic medium not all carboxylic acid functions are deprotonated. This influence on the hexadentate ligand edta is particularly pronounced, since four carboxylic acid functions are present. For correction the factor βY is introduced which calculates the proportion of the active species of the ligand Y.
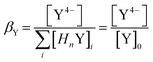 | (5) |
β Y can be approximately calculated from the acidity constants of the individual carboxylic acids of the ligand. An example of a ligand with four carboxylic acid and two amine functions is shown below.
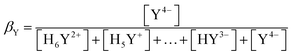 | (6) |
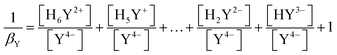 | (7) |
From the law of mass action the fractions can be replaced by the ratio between [H+] and Kn (the numbering of the constants is analogous to that of the pKa values).
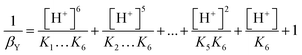 | (8) |
This process is carried out analogously for the metal ions.
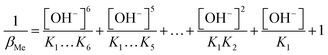 | (9) |
In Table 1 the stability constants of the pH relevant species for the ligand edta and the metal ion In3+ are listed. Since all measurements are carried out at a pH value of 3, the βY and βMe values are calculated exemplarily for this pH. When calculating the value of βMe only the last four terms are considered, since the other constants are very low and do not matter at this pH.
| Y | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
In species | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|---|
| pKa1 | −0.92 | InOH2+ | −3.9 |
| pKa2 | −1.62 | In(OH)2+ | −7.8 |
| pKa3 | −2.0 | In(OH)3aq | −12.39 |
| pKa4 | −2.71 | In(OH)4− | −22.1 |
| pKa5 | −6.16 | ||
| pKa6 | −10.23 | ||
| β Y | 2.65 × 10−11 | β In | 0.999999919 |
| log(βY) | −10.58 | log(βIn) | −3.5 × 10−8 |
The influence of pH on the ligand is immense, whereas the influence on the metal is very small. For the remaining metal ions the βMe values are in the same range. Using the β values, the conditional constants Kc are calculated as shown in eqn (10).
Kc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KβYβMe KβYβMe | (10) |
In Table 2 the stability and conditional constants of all analyzed metal ions are combined.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc Kc |
|
|---|---|---|
| CrY− | 23.40 | 12.82 |
| FeY− | 25.10 | 14.52 |
| GaY− | 24.26 | 13.68 |
| InY− | 27.46 | 16.88 |
| ScY− | 25.66 | 15.08 |
Examples of Beauchemin et al. show the ability of the coupling of IEC and ICP-MS to determine the conditional stability constants of divalent metal ions with Y. The complexes of ZnY− and CoY− are measured. The law of mass is rewritten and the data are plotted. Out of the intercept of the regression line the condition stability constant is calculated. For this method the complex concentration and the free metal ion concentration have to be detectable.17–19 In the case of trivalent metal ions and Y the stability constants are so strong that in many cases no free metal ion signal is detectable. Therefore and keeping the above mentioned points in mind a method is developed in which competing reactions in solution are used. Both reactions have the same temperature, ionic strength, and βY value. The only value that is different is βMe and this is (depending on pH) usually negligible. The ratio of the stability constants is determined therefore no adjustment of the conditional constants needs to be considered.
The theoretical calculation of the stability constants can be deduced from the law of mass action. Therefore the following competing reaction eqn (11) is shown as an example.
Me1Y− + Me23+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⇔ Me2Y− ⇔ Me2Y−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + Me13+ + Me13+ |
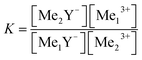 | (11) |
The stability constant K is a combination of the stability constants of both reactions.
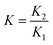 | (12) |
Wu et al. have used a similar approach successfully.20,21 The concentration of free metal ions is not easily determined as shown in the “challenges” section. This is the reason why this parameter should be eliminated. Eqn (13), (14) and (15a) are needed to simplify eqn (11). [Me03+] is equal for both metals because in the models they had the same initial concentration.
| [Me23+] = [Me03+] − [Me2Y−] | (13) |
| [Me13+] = [Me03+] − [Me1Y−] | (14) |
| [Y04−] = [Me1Y−] + [Me2Y−] + [Y4−] | (15) |
Since the ligand is present in a substoichiometric amount, the concentration of the free ligand can be neglected. This simplifies eqn (15) to eqn (15a).
| [Me2Y−] = [Y04−] − [Me1Y−] | (15a) |
Eqn (13)–(15) are inserted into eqn (11), resulting eqn (16) only consists of the initial concentrations of metal ions and the ligand, the stability constants of both reaction and the metal complex with the unknown stability constant.
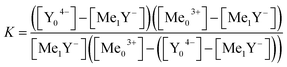 | (16) |
Eqn (16) is solved for [Me1Y−].
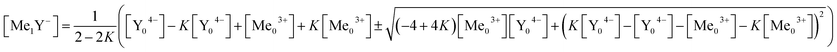 | (17) |
The solution with the positive square root leads to negative concentration and therefore makes no sense. Using eqn (17) the measured complex concentrations can be simulated. This requires only the initial concentrations of the metal ion and the ligand as well as the complex concentration. These can be easily obtained from chromatographic separations using ICP-AES as a quantitative detector.
Experimental
Instrumental conditions and columns
A Dionex DX500 ion chromatograph with LC20 and GP40 gradient pumps (Idstein, Germany), an injection valve and a 100 μl sample loop was used. The columns (anion and cation exchange columns) were self-made via a grafting reaction adopted from patent EP 1 842 592 A1.22 A monodisperse polystyrene–divinylbenzene polymer with 55% crosslinkage and approx. 1000 m2 g−1 surface area and an average diameter of 5 μm was used for the grafting reaction. The anion exchange column contained a trimethyl amine functional group with a dynamic capacity of 48 mmol per column measured for Cl−. The cation exchange column contained a sulfonic acid functional group with a dynamic capacity of 0.07 mmol per column measured for H+. The column dimensions were 100 × 4 mm for both columns. The eluent flow was 0.8–1.0 ml min−1 and dependent on the backpressure of the column. All tubing and fittings were made of polyether ether ketone (PEEK). The column temperature was controlled by a cryostat and set to 0 °C. The column outlet was directly connected to the nebulizer of the ICP-AES.The element specific detection was utilized by a Spectro ICP-AES M120 S (Spectro Analytical Instruments GmbH, Kleve, Germany) with a cross-flow nebulizer and a Scott spray chamber. The RF power was set to 1200 W and a sequential monochromator with a focal length of 750 mm was used. The emission lines were 239.204 nm (iron), 283.563 nm (chromium), 325.609 nm (indium), 357.253 nm (scandium) and 403.298 nm (gallium). Data acquisition was done in a time resolved transient scan mode. The data rate was one point per second.
Reagents
The commercial calibration standards were an indium(III) ICP/AAS standard solution 1000 mg l−1 in 0.5 mol l−1 nitric acid (Bernd Kraft GmbH, Duisburg, Germany) and a scandium(III) atomic spectroscopy standard solution 1000 mg l−1 in 0.5 mol l−1 nitric acid (Fluka, Germany).The remaining reagents were obtained in the solid form and 1000 mg l−1 standard solutions in 0.7 mol l−1 nitric acid were self-prepared. Chromium(III) nitrate nonahydrate 99% was obtained from ABCR (Karlsruhe, Germany), iron(III) nitrate nonahydrate p.a was obtained from Fluka (Germany) and gallium(III) nitrate x-hydrate was generated from Ga(s). Concentrated nitric acid min 65% p.a. was obtained from Honeywell (Seelze, Germany) and concentrated ammonium hydroxide 25% for analytical purposes from Grüssing GmbH (Filsum, Germany). The ligand solutions were prepared from ethylenediaminetetraacetic acid disodium salt dihydrate p.a. grade (Fluka, Germany).
Ultrapure water (Milli-Q, Millipore) was used for sample preparation as well as for eluents and rinsing of the system. All reagents were used without further purification.
Procedure
The samples were prepared by mixing the two metals and the ligand. Out of every metal stock solution (1000 mg l−1) the adequate value was taken, so that after a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 dilution the metal concentration was 0.19 mmol l−1. The concentration of Y was varied in the range from 0.024 to 0.95 mmol l−1 (1
100 dilution the metal concentration was 0.19 mmol l−1. The concentration of Y was varied in the range from 0.024 to 0.95 mmol l−1 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.125–5 molar ratio Me
0.125–5 molar ratio Me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Me
Me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y). The pH value was adjusted to 3 with the help of diluted ammonium hydroxide or nitric acid. Before measurement the samples were stored at 65 °C for one week to allow full equilibration, because of the slow equilibrium adjustment of chromium. Its water exchange rate is 2.4 × 10−6 s−1.23
Y). The pH value was adjusted to 3 with the help of diluted ammonium hydroxide or nitric acid. Before measurement the samples were stored at 65 °C for one week to allow full equilibration, because of the slow equilibrium adjustment of chromium. Its water exchange rate is 2.4 × 10−6 s−1.23
The eluent was prepared from concentrated nitric acid and ammonium hydroxide, resulting in a final concentration of 300 mmol l−1 nitrate with pH 3. No calibration needs to be done because the metal ion concentration in every model solution is 0.019 mmol l−1. The total peak area (integral) of a chromatograph corresponds to this concentration. In the case of minor total integral (see section “Determination of the total integral”) an acid reference standard with the same concentration was measured.
Data processing
Raw data were collected using the Smart Analyser Software for ICP-Spectrometer version 2.25, Spectro A.I. GmbH, Kleve, Germany, the integration was done after data export by IC Net 2.3 from Metrohm, Switzerland. For the illustration of the data QTI Plot 0.9.8.9 and for calculation of the species distribution Visual MINTEQ ver. 2.61 was used. For fitting of the measured data the solver macro from MS Excel 2003 was used.Results and discussion
Chromatographic data
Ion exchange chromatography is a very useful tool to separate charged species. In this case, the free trivalent metal ions and the metal ligand complexes are separated and determined by the element specific detector ICP-AES. The cation separation needs about 15 minutes using the elution program from Table 3 while the isocratic separation of anions is finished after 5 minutes.| Time [min] | 300 mmol l−1 NH4NO3 [%] | HNO3 pH 3 [%] |
|---|---|---|
| 0.0 | 0 | 100 |
| 4.5 | 100 | 0 |
| 10.5 | 100 | 0 |
| 10.51 | 0 | 100 |
| 15.0 | 0 | 100 |
In Fig. 1 the measurements of the chromium line of the anion and cation IEC are shown. In the cationic separation the complex signal corresponds to the first signal, since the anionic complexes undergo no retention. The second signal corresponds with the free metal ion. In separations with the anion exchange column, the elution order is vice versa. For both types of measurements a significant rise of the complex signal can be seen with the increasing content of the ligand.
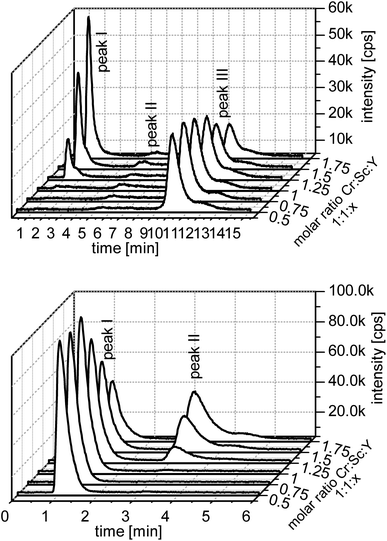 | ||
| Fig. 1 Measurement of the chromium line and competing ion scandium. Upper figure: cation IEC and lower figure: anion IEC. | ||
Regarding all model systems some differences can be seen. Especially in the cationic measurements the free metal ions are not detectable or the peak is very small. The same applies to gallium, indium, scandium, and iron. Only the chromium model shows a larger amount of free metal ions. In this model the free metal ions are represented by peak III.
Peak II in the chromium model is an artefact of the evaluation program and can be seen in every cationic measurement. In most measurements it is only a little rising of the base intensity.
In the anionic measurement the first peak is the free metal ion and the second is the complex peak. Like in the cationic measurements the free metal peak is well detectable only in the chromium model. Indium and scandium show a third peak, which is probably a higher charged hydroxo species. The chromatographs of the other ions are provided in the ESI.†
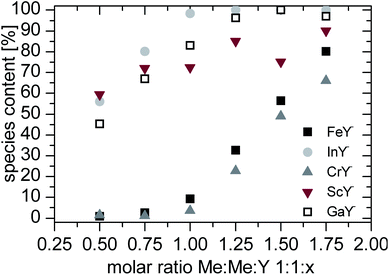
In Fig. 2 the species content of the complex signals are summarized. Depending on the counter ion the data show different distributions. The metal ion with the higher stability constant (in this case indium, scandium and gallium) shows from the lowest ligand concentrations a complex signal. At a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 the complex value reaches a maximum. In contrast to that, the two metal ions with the lower stability constant (iron and chromium) have a kind of mirrored complex content. Under the molar ratio of 1
1 the complex value reaches a maximum. In contrast to that, the two metal ions with the lower stability constant (iron and chromium) have a kind of mirrored complex content. Under the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 almost no complex peak is found. After almost complete complexation of the counter ions the metal ions with lower stability constants are also complexated.
1 almost no complex peak is found. After almost complete complexation of the counter ions the metal ions with lower stability constants are also complexated.
Stoichiometry and effective charge of the complexes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (Me
1 (Me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Me
Me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y). Therefore the stoichiometry of the GaY− complex is 1 to 1.24,25
Y). Therefore the stoichiometry of the GaY− complex is 1 to 1.24,25
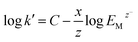 | (18) |
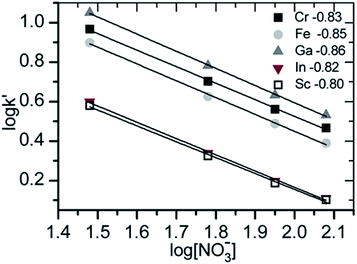
This method can be applied to both anionic and cationic ions. Since anionic complexes are obtained only the consideration of the anionic separation makes sense. Therefore the concentration of the eluent was varied and the capacity factors of the signals were calculated. Both values were logarithmically plotted and from the slope of the regression line the effective charge was determined. As an eluent ammonium nitrate was used, the charge of the eluent is –1.
In Fig. 4 the results of the effective charge determination with anionic separation of the model solutions are shown. The obtained values (from −0.80 to −0.86) correspond with the reference value of −0.89 for chloride.
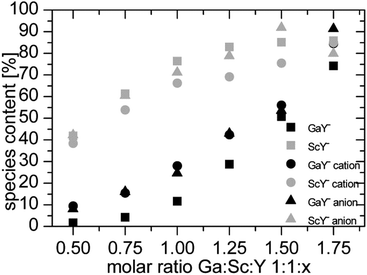
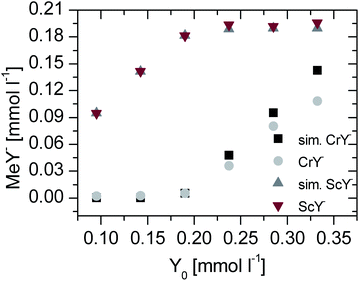
The comparison of the experimental data (Fig. 5) corresponds to simulated data, especially the scandium data. The gallium data have deviations to the calculated data. The higher than expected complex species could be due to lower total integrals. This problem is discussed in the next section.
Challenges
(1) The total integral increases if more ligands are present in the solution.
(2) This effect is significantly influenced by the second metal ion in the solution.
(3) It makes a difference if the total integral is measured with or without a separation column.
The less ligand present in the solution, the lower the total integral is. The pH value has no significant influence. At pH 2 the increase of the total integral is as strong as at pH 3. It is described that metal ions are adsorbed onto PE surfaces. The adsorption takes place on unreacted additives in the preparation of the PEs. The older the material, the faster the adsorption occurs.27,28
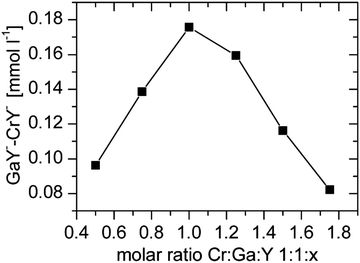
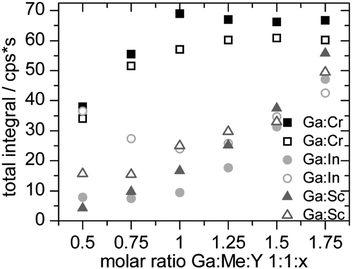
Depending on the metal complex stability the variation of the total integrals is differently pronounced. The GaY− complex is more stable than CrY− therefore the total integral reaches its maximum value at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In contrast, InY− and ScY− are more stable and the total integral of gallium only reached the maximum value at the highest concentration of the ligand.
1. In contrast, InY− and ScY− are more stable and the total integral of gallium only reached the maximum value at the highest concentration of the ligand.
In the measurements with and without the column it is striking that there is no clear tendency regarding the total integral. In the Ga/In models the total integrals without the column are lower and higher in the other two model systems (see Fig. 6). For example hydroxo species are formed, which are so strongly retained on the column that they do not elute during a measurement. The ligand Y helps to reduce the amount of these species, so the effect is stronger the less ligand is available for the metal ions.
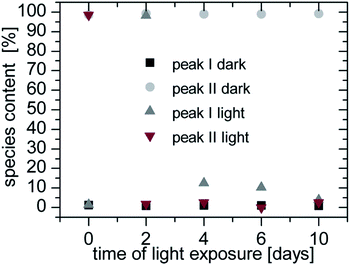
The photolysis of FeY− was determined by the storage of samples for a definite time under irradiation. An Atlas XI Sun-Tester was used as the irradiation source. In Fig. 7 the species content of Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Y 1
Y 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is shown. On the day of preparation, peak II is nearly 100%. The samples that were not irradiated have no changes in species distribution but the irradiated samples have very strong changes in their species distribution over the measured period of time.
1 is shown. On the day of preparation, peak II is nearly 100%. The samples that were not irradiated have no changes in species distribution but the irradiated samples have very strong changes in their species distribution over the measured period of time.
After two days of exposure peak I was almost 100%. This degeneration behaviour was described in Lambert29 and Lockhart.30 Because of redox reactions the acetate groups are degenerated. Since one group was degenerated the complex (FeED3A ethylene diamine, triacetate ferrum(III)) had no charge and eluted in the void volume. After the next two days of irradiation the next acetate groups were degenerated and the complexes FeEDDA+ (ethylene diamine diacetato ferrum(III) ion) and FeEDMA2+ (ethylene diamine monoacetato ferrum(III) ion) were formed. The longer the irradiation took place the stronger the degeneration was until no complex could be detected. Finally the iron ions were precipitated as iron hydroxides.
The other metal complexes showed no or only minor photolysis (max. 15% CrY−) during the irradiation time of 10 days.
Determination of the stability constants via modelling of the measured data
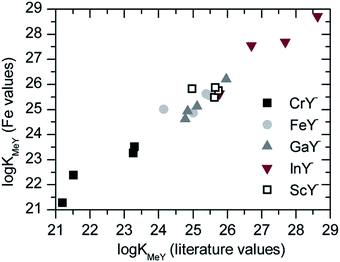
The adaptation of the simulated complex concentrations was done with MS Excel with the macro solver. It minimizes the sum of deviations by varying the unknown stability constants. Eqn (17) is used as a basis. Fig. 8 shows the adjustment of the simulated data to the measured ones. As example the Cr:Sc:Y system is presented.The simulations were performed for all permutations of combinations of metal ions and were compared with the literature values. In Table 4 the results are summarized. For the simulation the second stability constant was given and thus the first one could be calculated.
| Cr3+ | Fe3+ | Ga3+ | In3+ | Sc3+ | Cr3+ | Fe3+ | Ga3+ | In3+ | Sc3+ | |
|---|---|---|---|---|---|---|---|---|---|---|
Literature log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
23.40 | 25.10 | 24.26 | 27.46 | 25.66 | 23.40 | 25.10 | 24.26 | 27.46 | 25.66 |
| Competing ion | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K by cation separation K by cation separation |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K by anion separation K by anion separation |
||||||||
| Cr3+ | 25.01 | 24.78 | 25.77 | 25.62 | 25.24 | 25.9 | 25.57 | 25.38 | ||
| Fe3+ | 23.26 | 25.12 | 27.69 | 25.74 | 24.82 | 24.56 | 26.16 | 25.1 | ||
| Ga3+ | 21.52 | 24.15 | 26.7 | 24.97 | 20.98 | 25.28 | 27.75 | 25.33 | ||
| In3+ | 23.29 | 25.39 | 25.97 | 25.65 | 23.09 | 26.56 | 26.69 | 25.77 | ||
| Sc3+ | 21.2 | 25.48 | 24.85 | 28.63 | 20.28 | 25.82 | 24.76 | 27.24 | ||
| Average | 22.32 | 25.01 | 25.18 | 27.20 | 25.50 | 22.29 | 25.73 | 25.48 | 26.68 | 25.40 |
As in the literature the stability constants often had different values. A second calculation was done. The Fe:Y-system was determined very often and therefore the stability constant should be reliable. For the calculation the iron complex literature value was used as mentioned above. The resulting values for the other ions were used for further calculations. The obtained stability constants are summarized in Table 5.
| Cr3+ | Fe3+ | Ga3+ | In3+ | Sc3+ | Cr3+ | Fe3+ | Ga3+ | In3+ | Sc3+ | |
|---|---|---|---|---|---|---|---|---|---|---|
Literature log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
23.40 | 25.10 | 24.26 | 27.46 | 25.66 | 23.40 | 25.10 | 24.26 | 27.46 | 25.66 |
| Competing ion | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K by cation separation K by cation separation |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K by anion separation K by anion separation |
||||||||
| Cr3+ | 24.87 | 24.64 | 25.63 | 25.48 | 26.66 | 27.32 | 26.99 | 26.80 | ||
| Fe3+ | 23.26 | 25.12 | 27.69 | 25.74 | 24.82 | 24.56 | 26.16 | 25.10 | ||
| Ga3+ | 22.38 | 25.01 | 27.56 | 25.83 | 21.28 | 25.58 | 28.05 | 25.63 | ||
| In3+ | 23.52 | 25.62 | 26.20 | 25.88 | 21.79 | 25.26 | 25.39 | 24.47 | ||
| Sc3+ | 21.28 | 25.56 | 24.93 | 28.71 | 19.72 | 25.26 | 24.20 | 26.68 | ||
| Average | 22.61 | 25.27 | 25.22 | 27.40 | 25.73 | 21.90 | 25.69 | 25.37 | 26.97 | 25.50 |
The comparison of both calculations is shown in Fig. 9. The slope of the regression line of all data from the cation separation was 0.96. The values of the iron calculation were slightly lower than the calculation with the literature values.
Conclusions
The method was useful for the determination of stability constants of very strong polyaminocarboxylic acid complexes that were hardly detectable with any known methods. Due to the use of a competing second complexation reaction the effect of the solution parameters such as pH or ionic strength, could be neglected for calculation of stability constant ratios. The use of ICP-AES as an element specific and quantitative tool for the measurement of complex concentration ratios made it even more convenient. Furthermore it could be shown that the dark storage of samples was crucial for the achievement of useful results.Notes and references
- F. Münz, Verfahren zum Unschädlichmachen der Härtebildner des Wassers, DE Patent, 718981, 1935.
- C. K. Schmidt and H.-J. Brauch, Aminocarbonsäuren in der aquatischen Umwelt, Quellen, Vorkommen, Umweltverhalten, Toxizität und Beseitigung, DVGW-Technologiezentrum Wasser (TZW), Karlsruhe, Germany, 2003, vol. 20 Search PubMed.
- V. Alexander, Chem. Rev., 1995, 95, 273 CrossRef CAS.
- J. Byegård, G. Skarnemark and M. Skålberg, J. Radioanal. Nucl. Chem., 1999, 241(2), 281–290 CrossRef.
- A. E. Martell and L. G. Sillén, Stability constants of metal-ion complexes, The Chemical society, 1964, vol. 2 Search PubMed.
- V. V. Nikonorov, J. Anal. Chem., 2010, 65(4), 359–365 CrossRef CAS.
- Z. Y. Tao, Zh. J. Guo and W. M. Dong, J. Radioanal. Nucl. Chem., 2003, 256(3), 575–580 CrossRef CAS.
- P. Janoš, J. Chromatogr. A, 2004, 1037, 15–28 CrossRef.
- C. Y. Li, J. Z. Gao, G. H. Zhao, J. W. Kang and H. H. He, Chromatographia, 1997, 46(9/10), 489–494 CAS.
- E. Sato, S. Miya, K. Saitoh, S. Saito and M. Shibukawa, J. Chromatogr. A, 2011, 1218, 922–928 CrossRef CAS PubMed.
- G. Schwarzenbach and G. Anderegg, Helv. Chim. Acta, 1957, 40, 1773 CrossRef CAS.
- M. T. Beck and S. Görög, Acta Chim. Acad. Sci. Hung., 1960, 22, 159 Search PubMed.
- C. W. Davies, J. Chem. Soc., 1938, 2093–2098 RSC.
- I. Grenthe, H. Wanner and E. Östhols, Guidelines for the extrapolation to zero ionic strength, OECD Nuclear Energy Agency, Issy-les-Moulineaux, France, http://www.oecd-nea.org/dbtdb/guidelines/tdb2.pdf, 14 October 2011 Search PubMed.
- Usermanual Visual MINTEQ, http://www2.lwr.kth.se/English/OurSoftware/vminteq/index.html, 29 September 2013.
- G. Wedler, Lehrbuch der Physikalischen Chemie, Wiley-VCH, Weinheim, 4th edn, 1997 Search PubMed.
- C. Huang and D. Beauchemin, J. Anal. At. Spectrom., 2006, 21, 317–320 RSC.
- C. Huang and D. Beauchemin, J. Anal. At. Spectrom., 2006, 21, 1419–1422 RSC.
- L. Xing and D. Beauchemin, J. Anal. At. Spectrom., 2009, 24, 336–339 RSC.
- S. L. Wu and W. D. Horrocks Jr, Anal. Chem., 1996, 68, 394–401 CrossRef CAS.
- S. L. Wu and W. D. Horrocks Jr, J. Chem. Soc., Dalton Trans., 1997, 1497–1502 RSC.
- M. Raskop, A. Seubert and A. Grimm, Patent EP 1 842 592 A1, 2007.
- E. Riedel, R. Alsfasser, C. Janiak, T. M. Klapötke and H.-J. Meyer, Moderne Anorganische Chemie, Walter de Gruyter, Berlin, New York, 3rd edn, 2007 Search PubMed.
- P. Job, Ann. Chim., 1928, 9, 113 CAS.
- E. Olson and P. Bühlmann, J. Org. Chem., 2011, 76, 8406–8412 CrossRef CAS PubMed.
- D. T. Gjerde, G. Schmuckler and J. S. Fritz, J. Chromatogr., 1980, 187, 35–45 CrossRef CAS.
- H.-J. Hoffmann and J. Bosholm, Acta Hydrochim. Hydrobiol., 1986, 14, 395–405 CrossRef CAS.
- L. A. Holmes, A. Turner and R. C. Thompson, Environ. Pollut., 2012, 160, 42–48 CrossRef CAS PubMed.
- J. L. Lambert, C. E. Godsey and L. M. Seitz, Inorg. Chem., 1963, 2, 127–129 CrossRef CAS.
- H. B. Lockhart Jr and R. V. Blakeley, Environ.Sci. Techol., 1975, 12, 1035–1038 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ja50358e |
| This journal is © The Royal Society of Chemistry 2014 |