Open Access Article
Open Access ArticlePredicting essential genes in prokaryotic genomes using a linear method: ZUPLS†‡
Kai
Song
*,
Tuopong
Tong
and
Fang
Wu
School of Chemical Engineering and Technology, Tianjin University, 92 Weijin Road, Nankai district, Tianjin, 300072, China. E-mail: ksong@tju.edu.cn; tptong@tju.edu.cn; wufang@tju.edu.cn; Tel: +86-2227408399
First published on 14th February 2014
Abstract
An effective linear method, ZUPLS, was developed to improve the accuracy and speed of prokaryotic essential gene identification. ZUPLS only uses the Z-curve and other sequence-based features. Such features can be calculated readily from the DNA/amino acid sequences. Therefore, no well-studied biological network knowledge is required for using ZUPLS. This significantly simplifies essential gene identification, especially for newly sequenced species. ZUPLS can also select necessary features automatically by embedding the uninformative variable elimination tool into the partial least squares classifier. No optimized modelling parameters are needed. ZUPLS has been used, herein, to predict essential genes of 12 remotely related prokaryotes to test its performance. The cross-organism predictions yielded AUC (Area Under the Curve) scores between 0.8042 and 0.9319 by using E. coli genes as the training samples. Similarly, ZUPLS achieved AUC scores between 0.8111 and 0.9371 by using B. subtilis genes as the training samples. We also compared it with the best available results of the existing approaches for further testing. The improvement of the AUC score in predicting B. subtilis essential genes using E. coli genes was 0.13. Additionally, in predicting E. coli essential genes using P. aeruginosa genes, the significant improvement was 0.10. Similarly, the exceptional improvement of the average accuracy of M. pulmonis using M. genitalium and M. pulmonis genes was 14.7%. The combined superior feature extraction and selection power of ZUPLS enable it to give reliable prediction of essential genes for both Gram-positive/negative organisms and rich/poor culture media.
Insight, innovation, integrationAn effective linear method, ZUPLS, was developed to improve the accuracy and speed of prokaryotic essential gene identification. ZUPLS only uses the Z-curve and other sequence-based features. Such features can be calculated readily from the DNA/amino acid sequences. Therefore, no well-studied biological network knowledge is required for using ZUPLS. This significantly simplifies essential gene identification, especially for newly sequenced species. ZUPLS can also select necessary features automatically by embedding the uninformative variable elimination tool into the partial least squares classifier. No optimized modelling parameters are needed. ZUPLS has been used, herein, to predict essential genes of 12 remotely related prokaryotes to test its performance. Comparing our method with the best existing approaches, the improvements were quite significant. The combined superior feature extraction and selection power of ZUPLS enable it to give reliable prediction of essential genes for both Gram-positive/negative organisms and rich/poor culture media. |
Introduction
Essential genes (EGs) are genes that are indispensable for supporting an organism and therefore constitute a minimal gene set. They encode foundational functions required for a living cell under certain conditions.1 The identification of EGs in bacteria allows us to understand the underlying mechanism of cellular life, identify potential targets for antimicrobial drug development,2 reveal bacterial relationships during evolution3 and provide simplified ‘chassis’ for biological engineering purposes.4To circumvent the expense and difficulty in experimentally identifying EGs, researchers attempt to use in silico methods to resolve the problem. Saha and Heber used a modified simulated annealing algorithm for feature selection and variable weighting. Then they used the weighted KNN (k-nearest neighbour) and SVM (support vector machine) algorithms in the EG classification for bacteria, fungi, Ascomycota, plants, and mammals. In the case of fungi, Ascomycota was excluded, and in the case of Ascomycota, Saccharomyces cerevisiae was excluded.5 Seringhaus et al. identified 14 features of the genome and measured the relationships between them and the essentiality of genes. They used S. cerevisiae as an example. Their 14 features included localization signals, codon adaptation, GC content, and overall hydrophobicity.6 Gustafson et al. assessed the relationships of some features with genes' essentiality. Experimental and genomic features such as phyletic retention, protein interaction degree, protein size and codon bias were included. They subsequently utilized a machine learning method to construct an integrated classifier of EGs in both S. cerevisiae and E. coli.7 Hwang et al. developed an approach combining the protein–protein interaction network and sequence information to predict EGs in both genomes.8 Plaimas et al. used a broad variety of metabolic network features and sequence characteristics. They trained hundreds of SVM classifiers to identify 35 EGs in Salmonella typhimurium. They assumed the enzymes encoded by these genes to be the potential drug targets.9
Deng et al. focused on four bacterial species (E. coli, B. subtilis, Acinetobacter baylyi and Pseudomonas aeruginosa) and tested the accuracy of the EG predicting models among them. They achieved cross-organism prediction AUC (Area Under the Curve) scores between 69% and 89%. Their approach proved that gene essentiality can be reliably predicted using models trained and tested in a remotely related organism.10 Lin and Zhang developed an algorithm integrating the information of biased distribution and homology of genes. In predicting EGs, their algorithm performed a self-consistence test which resulted in an average sensitivity and specificity of 80.8% for the Mycoplasma pulmonis genome. They also performed cross-validation tests showing an average accuracy of 78.9% and 78.1% for Staphylococcus aureus and Bacillus subtilis genomes respectively. Accordingly, they predicted 5880 putative EGs of 16 Mycoplasma organisms.11
Although these attempts sometimes offered increased accuracy, the improvements may not justify the heavy computational requirements they impose for training classifiers. More importantly, experimental genome-wide data or metabolic networks are often limited for newly sequenced or under-studied genomes. This precludes the application of the above-mentioned methods in the issue of identifying EGs.
The ability to recognize EGs for newly sequenced genomes lacking in genetic or metabolic network information is of added importance. To accomplish this recognition, we developed a simple but useful linear method, named ZUPLS. Our study is the first to use the 93′ Z-curve features to resolve the EG recognition problem.12 ZUPLS also combined several other easily obtained sequence-based features. These included gene size, the frequencies of amino acids, codon adaptation index, etc. ZUPLS can identify necessary features according to their stabilities and contributions by utilizing the uninformative variable elimination (UVE) technique.13 We then used the selected features as input variables to the partial least squares (PLS) classifier for further classification. ZUPLS does not require well-studied biological characteristics or optimized modelling parameters. For example, it does not require information about genome annotation or genetic or metabolic networks. Thus, ZUPLS has an advantage over other existing approaches in predicting newly-sequenced species EGs.
We used ZUPLS to predict EGs of 12 remotely related prokaryotic organisms to test its prediction performance. The tests yielded AUC scores of the cross-organism predictions between 0.8042 and 0.9319 (E. coli scenario) and 0.8111 and 0.9371 (B. subtilis scenario) depending on the superiority of ZUPLS in feature extraction and selection.
We also compared it with other existing methods for further testing:
• Compared with the results obtained by the method presented by Deng et al.,10 ZUPLS improved the AUC scores maximally by 0.13 in predicting B. subtilis EGs using E. coli genes. The precision of the prediction values in this case was also improved by 19%.
• Comparing our results with those obtained by the approach proposed by Lin and Zhang (2011),11 the average of specificity and sensitivity (AVE) in predicting M. pulmonis EGs was improved by 14.7%. Similarly, the AVE of predicting E. coli EGs was improved by 6.1% and the AUC score was improved from 0.813 to 0.896. In addition, the AVE of predicting S. aureus EGs was improved from 78.9% to 83.0% and the AUC score was improved from 0.778 to 0.904. In this comparison, we used the M. genitalium and M. pulmonis genes as the training samples as Lin and Zhang did.
• The accuracy of predicting EGs of P. aeruginosa using E. coli genes when compared with the methods developed by Plaimas et al. (2010)9 was improved by 7%. The accuracy of predicting EGs of E. coli using P. aeruginosa genes was improved by 8%.
This is the first study to report that gene essentiality can be reliably predicted by only using sequence-based features and a linear model trained and tested in remotely related organisms.
Results and discussion
Cross-organism EG prediction results using the E. coli and B. subtilis genomes as the training samples
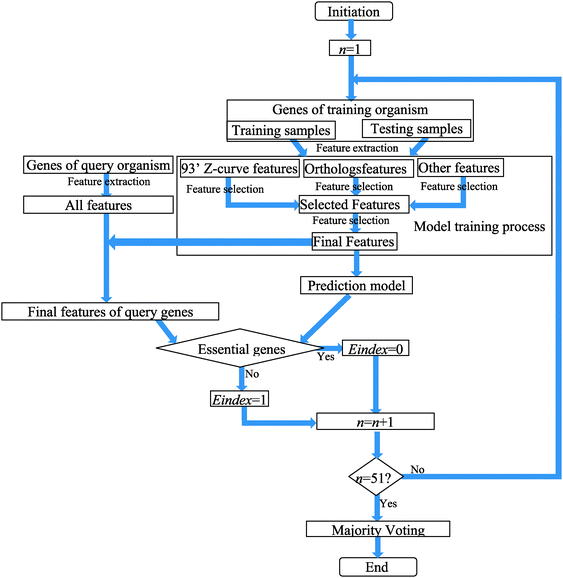
It is acknowledged that E. coli (EC) and B. subtilis (BS) represent Gram negative and Gram positive bacteria, respectively. These well-studied genomes are often used to demonstrate the performance of in silico methods. The EGs of EC and BS were identified by single gene knockout/inactivation experiments.1a,14 Such experiments can identify EGs with comparatively higher accuracy. We chose EC and BS as the basic training genomes to test the hypothesis that EG annotations can be cross-predicted between distantly related organisms. For brevity, we denoted the studies in which the EC genome was used as the training set in the EC scenario. Additionally, the BS genome was used as the training set in the BS scenario.The self-consistence test could not assess the generalization ability of a model for new genomes. Therefore, we selected the cross-organism tests on ZUPLS. We also used 10 other prokaryotic genomes as testing samples to do verifications. The details of these data are shown in Table S1 in the ESI.‡ For brevity, we introduced the symbol “→” used by Deng et al.10 For example: EC → AB is intended to predict EGs of AB using the classifier trained by the known essential/non-essential genes in EC. The AVE, PPV and ACC measurements used to determine the accuracy of the prediction of EGs for these 10 genomes are shown in Tables 1 and 2, respectively.
| No. | Genome | Gram | Ratio (%) | Sn (%) | Sp (%) | AVE (%) | DIF (%) | AUC | ACC (%) | PPV (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| a DIF: the absolute value of the difference between Sn and Sp; ‘−’: gram-negative bacterium; ‘+’: Gram-positive bacterium; ratio: the percentage of the EGs in common between the training and target genomes. b Although mycoplasmas lack cell walls, they are phylogenetically related to Gram-positive bacteria with genomes of low G + C content.18 | ||||||||||
| 1 | AB | − | 44 | 77.51 | 85.05 | 81.28 | 7.54 | 0.8595 | 89.99 | 79.37 |
| 2 | CC | − | 42 | 77.08 | 87.43 | 82.26 | 10.35 | 0.8936 | 91.80 | 77.95 |
| 3 | FN | − | 53 | 73.08 | 84.12 | 78.60 | 11.04 | 0.8068 | 84.18 | 66.86 |
| 4 | PA14 | − | 44 | 60.90 | 90.08 | 75.49 | 29.18 | 0.8133 | 93.92 | 46.55 |
| 5 | SE | − | 73 | 86.93 | 92.63 | 89.78 | 5.70 | 0.9113 | 92.60 | 52.97 |
| 6 | BS | + | 62 | 86.14 | 87.08 | 86.61 | 0.94 | 0.9319 | 96.02 | 73.49 |
| 7 | MPb | + | 42 | 70.55 | 87.53 | 79.04 | 16.98 | 0.8596 | 81.33 | 94.19 |
| 8 | SA315 | + | 46 | 79.80 | 83.82 | 81.81 | 4.02 | 0.8800 | 91.91 | 73.85 |
| 9 | SA8325 | + | 48 | 68.95 | 90.55 | 79.75 | 21.60 | 0.8636 | 92.04 | 78.05 |
| 10 | SS | + | 65 | 86.24 | 87.43 | 86.83 | 1.19 | 0.9008 | 92.47 | 59.44 |
| 11 | MT | N | 27 | 69.19 | 77.83 | 73.51 | 8.64 | 0.8042 | 87.68 | 77.45 |
| No. | Genome | Gram | Ratio (%) | Sn (%) | Sp (%) | AVE (%) | DIF (%) | AUC | ACC (%) | PPV (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| a DIF: the absolute value of the difference between Sn and Sp; ‘−’: Gram-negative bacterium; ‘+’: Gram-positive bacterium; ratio: the percentage of the EGs in common between the training and target genomes. b Although mycoplasmas lack cell walls, they are phylogenetically related to Gram-positive bacteria with genomes of low G + C content.18 | ||||||||||
| 1 | AB | − | 39 | 78.11 | 84.44 | 81.28 | 6.33 | 0.8545 | 89.72 | 73.67 |
| 2 | CC | − | 39 | 82.50 | 86.22 | 84.36 | 3.72 | 0.8983 | 91.33 | 69.89 |
| 3 | EC | − | 56 | 84.46 | 91.43 | 87.94 | 6.97 | 0.9052 | 94.84 | 63.67 |
| 4 | FN | − | 46 | 76.41 | 80.66 | 78.54 | 4.25 | 0.8124 | 84.00 | 70.04 |
| 5 | PA14 | − | 36 | 67.76 | 83.14 | 75.45 | 15.38 | 0.8143 | 93.70 | 43.48 |
| 6 | SE | − | 51 | 85.51 | 91.09 | 88.30 | 5.58 | 0.9371 | 95.11 | 73.42 |
| 7 | MPb | + | 53 | 73.14 | 90.27 | 81.71 | 17.13 | 0.8782 | 83.50 | 93.55 |
| 8 | SA315 | + | 56 | 84.77 | 81.81 | 83.29 | 2.96 | 0.8825 | 91.60 | 65.45 |
| 9 | SA8325 | + | 61 | 80.06 | 86.50 | 83.28 | 6.46 | 0.8592 | 90.49 | 59.60 |
| 10 | SS | + | 75 | 90.37 | 86.50 | 88.43 | 3.87 | 0.9106 | 91.98 | 55.96 |
| 11 | MT | N | 27 | 67.71 | 81.65 | 74.68 | 13.94 | 0.8111 | 87.53 | 71.23 |
The influence of the numbers of common EGs on cross-organism prediction performance of ZUPLS
For cross-organism prediction, high accuracy may be due to the large number of common EGs between the training genome and the query genome rather than the performance of the prediction model. The ratios between the number of common EGs and the number of query EGs are listed in Tables 1 and 2, respectively. Accordingly, we were able to evaluate the influence of the numbers of the common EGs on the cross-organism prediction results.Only about 27% of the EGs of MT are common to the EGs of BS. Even with this low ratio, the AUC score was still as high as 0.8111. The scores of AVE, ACC and PPV were 74.68%, 87.53% and 71.23%, respectively. These results sufficiently prove that the prediction accuracy was due to the performance of our method.
The influence of different kinds of culture media on prediction performance
The genes essentially required for a given prokaryote to grow on a minimal medium should be more than that required on a rich medium. In our study, the EGs of training organisms, BS and EC, were both restricted to genes required for viability under favorable conditions (rich media). Therefore it is necessary to test whether ZUPLS could accurately predict EGs required on a minimal medium.The EGs of the candidate AB were obtained under a minimal medium.15
– In the case of EC → AB, the AUC score was as high as 0.8595, the ACC was 89.99%, the PPV was 79.37%, and the trade-off between Sn and Sp was 7.54%.
– In the case of BS → AB, the AUC score was as high as 0.8972, the ACC was 89.72%, the PPV was 73.67%, and the trade-off between Sn and Sp was 6.33%.
The results support the proposed method as a reliable model for prediction of EGs required for different kinds of culture media. This model is convenient for researchers to use in either minimal or rich medium conditions.
The influence of the Gram staining properties on cross-organism prediction performance
Gram-negative bacteria and Gram-positive bacteria have many distinguishable properties. Gram-positive bacteria have a thick mesh-like cell wall made of peptidoglycan (50–90% of cell envelope) which is stained purple by crystal violet. In contrast, Gram-negative bacteria have a thinner layer (10% of the cell envelope) which is stained pink by the counter-stain.16,17 Consequently, it is very hard to predict the EGs of a Gram-positive bacterium using the EGs of a Gram-negative bacterium as the training samples. The same is true for using a Gram-negative bacterium to predict a Gram-positive bacterium.Notwithstanding the difficulty mentioned above, using our method, the AUC score of EC → BS yielded a result as high as 96.02%. BS → SE also possessed the highest AUC score (0.9371) and the highest ACC value (95.11%).
Additionally, the minimum AUC score of predicting the Gram-positive genomes in EC scenario is still as high as 0.8596 (EC → MP§). The minimum AUC score of predicting the Gram-negative genomes in BS scenario is also as high as 0.8124 (BS → FN).
MT has an unusual waxy coating on its cell surface, which makes the cells impervious to Gram staining. There are different opinions about MT's Gram-staining property.19 No matter whether MT is a Gram-positive bacterium or a Gram-negative one, the AUC score is still as high as 0.8042 (EC → MT) and 0.8111 (BS → MT), respectively.
Comparisons with other existing methods
Evaluating the performance of the proposed method requires comparisons with other available methods. Because different methods use different sample sets and different features, only rough comparisons are possible. We therefore compared ZUPLS to the methods with the best available results. We also used the same measurements that the chosen methods used. The comparison results are shown in Tables 3–5, respectively.| Genome | ZUPLS | Deng et al. (2011)10 | ||
|---|---|---|---|---|
| AUC | PPV | AUC | PPV | |
| a Deng et al. also predicted EGs of P. aeruginosa PAO1. Now it's impossible for us to get the same data set of P. aeruginosa PAO1 as that of Deng et al. 2011,10 we only gave the prediction result comparisons of other three prokaryotic organisms. | ||||
| EC → AB | 0.86 | 0.79 | 0.80 | 0.81 |
| EC → BS | 0.93 | 0.73 | 0.80 | 0.54 |
| BS → EC | 0.91 | 0.64 | 0.86 | 0.48 |
| AB → EC | 0.91 | 0.64 | 0.89 | 0.43 |
| ZUPLS | Lin and Zhang (2011)11 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sn (%) | Sp (%) | AVE | AUC | PPV (%) | Sn (%) | Sp (%) | AVE | AUC | PPV (%) | |
| a “/”: the corresponding measurements were not given by Lin and Zhang (2011),11 therefore we did not calculate it. | ||||||||||
| MG + MP → EC | 79.4 | 89.0 | 84.2 | 0.896 | / | 67.5 | 88.7 | 78.1 | 0.813 | / |
| MG + MP → SA315 | 78.5 | 87.5 | 83.0 | 0.904 | / | 70.2 | 87.6 | 78.9 | 0.778 | / |
| MG + MP → MP | 93.0 | 98.1 | 95.5 | 0.967 | 97.0 | 78.4 | 83.3 | 80.8 | 0.812 | 75.5 |
| ZUPLS | Plaimas et al. (2010)9 | |||||||
|---|---|---|---|---|---|---|---|---|
| Sn | AUC | ACC | PPV | Sn | AUC | ACC | PPV | |
| a Plaimas et al. used two data sets of PA (paeJ and paeL) and two data sets of EC (ecoB and ecoG). We only compared the prediction results for paeL and ecoB in consideration of the fact that Plaimas et al. (2010) obtained the best results for them. | ||||||||
| PA → EC | 0.72 | 0.91 | 0.95 | 0.62 | 0.27 | 0.81 | 0.87 | 0.61 |
| EC → PA | 0.47 | 0.81 | 0.94 | 0.47 | 0.07 | 0.80 | 0.87 | 0.67 |
There was only one exception to improved PPV values. In the case of EC → AB, our calculated PPV was 0.79 compared to Deng et al. 0.81, a negligible difference.
Contrarily, there were significant improvements in other cases obtained by ZUPLS. The PPV value was improved by 0.21 in AB → EC, 0.19 in EC → BS and 0.16 in BS → EC.
Such comparison results consequently confirmed the significantly improved performance utilizing our proposed method.
The case MG + MP → MP is a kind of self-consistence test whose accuracy represents the highest prediction accuracy that an algorithm can reach. In this case, ZUPLS yielded an exceptional AVE of 95.5% and PPV of 97.0%. Both the values of Sn and Sp were higher than 90%. Even the tradeoff between Sn and Sp was only 5.1%. The minimum improvement of the Sn measurement was a significant 14.6%. Sn obtained by our method was 93.0% while that of Lin and Zhang was only 78.4%. Additionally, the improvement of the AUC score reached 0.155.
Using ZUPLS, the AVE score for MG + MP → EC improved from 78.1% to 84.2%, while the AUC score improved from 0.813 to 0.896. The difference in value between Sn and Sp was 9.6%, much smaller than the 21.2% obtained by Lin and Zhang.
Using ZUPLS, the AVE score for MG + MP → SA315 improved from 78.9% to 83.0%, while the AUC score improved from 0.778 to 0.904. The trade-off between Sn and Sp in our study was only 9.0%, which was much smaller than the 17.4% obtained by Lin and Zhang.
These two cross-genome tests confirmed that our method is superior in both the prediction accuracy and the trade-off between Sn and Sp in comparison with the method proposed by Lin and Zhang.
Using ZUPLS, in the case of PA → EC, the AUC score was improved by as much as 0.1, the ACC was improved by 8% and the Sn was surprisingly improved from 0.27 to 0.72.
In the case of EC → PA, the Sn obtained by Plaimas et al. was only 0.07 while the Sn obtained by ZUPLS was 0.47. Although the PPV value of 47% obtained by using ZUPLS was smaller than the 67% obtained by Plaimas et al., PPV is not recognized as a comprehensive measurement. Accordingly, most researchers use ACC or AUC to quantify the prediction performance of their proposed methods. Our application of ZUPLS improved ACC by 7% in this case. This demonstrates the superiority of our method in comparison with that of Plaimas et al.
Materials and methods
Databases
We obtained the information of the essential protein-coding genes of 12 prokaryotic genomes from the DEG 6.5 database¶ and the corresponding references. All of the protein-coding gene sequences of the genomes were retrieved from NCBI GenBank.20 Since these two databases had been updated asynchronously, a protein-coding gene was taken as a positive sample so long as it met at least one of the following conditions:(a) The sequence of a protein-coding gene given by DEG 6.5 was identical with that given by NCBI GenBank;
(b) The start location of a protein-coding gene given by DEG 6.5 was identical to that given by NCBI;
(c) The end location of a protein-coding gene given by DEG 6.5 was identical to that given by NCBI.
The remaining protein-coding genes were then taken as negative samples.
Several EGs may be incorrectly treated as being non-essential; similarly, others may be incorrectly treated as essential. Such incorrectly classified genes were purposely used as noise to test the robustness of our method. We showed the details of the 12 organism datasets in Table S1 in the ESI.‡
The training and predicting step of each pair of training and query genomes was run 51 times to alleviate the effect of local optima. Each time it was started by randomly re-arranging training samples. The outputs of the 51 rounds were used as a voting score that represented the propensity of a gene to be essential for the query genome. A high number of instances of essentiality led to a high specificity, ACC and PPV, while a low number of instances led to a high sensitivity. In our Matlab codes, we used “Propensity” as the score to qualify the propensity of a gene to be essential for the query genome. If Propensity (i) = 1, then the possibility of gene i to be an essential gene is 100%. In contrast, if Propensity (i) = 0, then the possibility of gene i to be an essential gene is 0%. The corresponding programs in Matlab Codes are available in the ESI‡ and our lab website (http://www.csssk.net). The BS → EC case was used as an example and the demo file was named as: testbsecoli_for_demo.m.
The flow chart of training and predicting procedures is shown in Fig. 1.
Measurements for evaluating the performance of EG prediction
To evaluate the performance of the classifier exhaustively, we included AVE, ACC, PPV and AUC as the measurements. Their definitions are:Sensitivity:
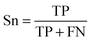 | (1) |
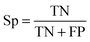 | (2) |
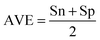 | (3) |
 | (4) |
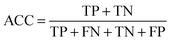 | (5) |
A receiver operator characteristics curve (ROC-curve) is used to measure the performance for a classifier system with various thresholds. In the ROC-curve, the sensitivity is plotted against 1-specificity. The area under the curve (AUC) yields a performance estimate across the entire range of thresholds.
Features
The features used in our study can be broadly classified into three categories, i.e. the 93′ Z-curve features, orthologs, and other DNA or amino acid sequence based features.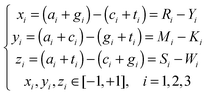 | (6) |
A DNA sequence therefore can be represented by a selective combination of n (n ∈ [1 252]) variables derived from the Z-curve methods in the n-dimensional space V.
Genes with a high number of thymine at the third codon positions were found more likely to be essential for cell viability. Base compositions at such positions are therefore used as features in EG recognition problems. They are denoted as T3s, C3s, A3s and G3s, respectively.9 From eqn (6), it can be seen that the Z-curve parameters at the third codon positions (i = 3) are linear combinations of T3s, C3s, A3s and G3s.
GC-content and other sequence-based features were also used as features in EG recognition6 and promoter analyses.23Z-curve parameters were also used to calculate the GC-content and display its distribution.24
Accordingly, eqn (6) clearly illustrates that Z-curve parameters can evaluate a given DNA sequence from three main components, i.e. distributions of purine/pyrimidine, amino/keto and strong/weak H-bonds.25
Z-curve parameters can consequently extract useful information as effectively as possible and therefore allow the prediction of EGs with a high degree of accuracy.
Unfortunately, there is strong multi-collinearity among Z-curve variables. In our previous study to recognize short coding sequences of human genes, we selected 93′ Z-curve variables from all 252 Z-curve variables to eliminate the multi-collinearity. We thereby successfully improved the performance of ordinary data-driven techniques.12
93′ Z-curve variables were used here considering their proved superiority in both feature extraction and time consumption. This is the first time that 93′ Z-curve variables have been used in prokaryotic EG recognition problems. The descriptions of the 93′ Z-curve variables are shown in Table S2 (ESI‡).
– Orthologs: orthologs are genes of different species that evolved from a common ancestral gene by speciation. Previous studies have proven that EGs tend to be evolutionarily more conserved than NEGs in bacterial species.3b,7,26 Therefore, we used orthologs between the query genome and the other 183 control genomes as features. In addition, we also used the mean values and their standard deviations as features. We introduced a Reciprocal Best Hit (RBH)10 method to identify the orthologs between training and target genomes.
– Gene size: there is a trend for proteins to become larger throughout evolution.7
– Strand bias: EGs are more likely to be encoded on the leading strand of the circular chromosomes.11,27 The strand information of genes was used as a feature in our study.
– Codon Adaptation Index (CAI): a measurement of the relative adaptability of the codon usage of a given gene towards the codon usage of highly expressed genes.28
– Frequency of optimal codons (Fop): the ratio of optimal codons to synonymous codons (genetic code dependent).7
– Frequency of all encoded amino acids: Lin et al. found that rather than all essential genes, only those with the COG functional category of information storage and process (J, K and L), and subcategories D, M, O, C, G, E and F were preferentially situated at the leading strand,11 where:
• D is cell cycle control
• M is cell wall biogenesis
• O is posttranslational modification
• C is energy production and conversion
• G is carbohydrate transport and metabolism
• E is amino acid transport and metabolism
• F is nucleotide transport and metabolism
Therefore, we used the frequency of encoded amino acids as features.
– Close_stop_ratio: the number of codons that are one-third of base mutation removed from a stop codon6,8 is used as a feature.
– Paralogs: paralogs are genes related by duplication within a genome.
– DES (Domain enrichment score): the domain enrichment score reflects the conservation of the local sequence rather than the entire gene.10
The ZUPLS method
The methodology of the used features indicates that there are strong multi-collinear relationships among them. For example, the frequencies of all kinds of amino acids are definitely strongly related to Z-curve features. Although PLS could exclude the multi-collinearity among features to some extent by itself, the prediction results were far from satisfactory. Hence, we introduced the uninformative variable elimination (UVE) method to further improve the recognition performance.Accordingly, we named our proposed method ZUPLS, using the 93′ Z-curve features while embedding UVE as the feature selection method and executing PLS as the classifier.
In linear models, the reliability (or score) of each variable j can be quantitatively measured by the stability, which is defined as:
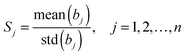 | (7) |
In our case, the recognition of essential genes is a typical two-class supervised pattern analysis problem. The two-class supervised pattern analysis can be handled as a univariate regression problem in which the dependent variables are defined as l ∈ {−1, +1}. For univariate regression problems, the absolute value of the regression coefficient of each variable is a reasonable measurement of its contribution. To consider the stability of each variable, we introduced the reliability to quantify its importance. Generally, the absolute value of the coefficient bj represents the contribution of the feature j to the established model and std(bj) indicates the stability of such a contribution in each round of cross-validation or the voting procedure. It is clear that the larger the mean(bj) and the smaller the std(bj) are, the larger and more stable the contribution of variable j is to the model. The variable j is therefore more important. So the reliability can be used as the score or the prioritization of the features. The variables having too small stability values should be eliminated as the uninformative noises thus improving the performance of the model.
In the ZUPLS method, considering the large number of variables, the iterative feature elimination should be processed to identify the real key features. That is to say, in each round of ZUPLS:
(1) Getting an initial PLS prediction model using all features.
(2) Sorting variables in descending order according to their stability values calculated from eqn (7).
(3) Eliminating given number of features with the minimum stability values.
(4) Using a cross-validation procedure to assess the prediction performance of the model.
(5) Repeating steps 2–4 until the prediction average accuracy converges.
We used the ZUPLS method to select important features from 93′ Z-curve features, orthologs and other sequence-based features separately to avoid the cross interferences among them. We then exploited the ZUPLS on the selected features to get the final prediction models. The corresponding programs in Matlab Codes are available in the ESI‡ and our lab website, http://www.csssk.net.
We used BS → EC case as an example and named the demo file as: testbsecoli_for_demo.m. In this case, there are 4146 genes in the BS genome and 4176 genes in the EC genome. Except for feature extraction procedures, the whole training and predicting procedure took 870.84 seconds. The parameters of the computer properties are DELL Optiplex, Intel Core I7-3770, 3.4 GHz, 16 GB memory and 64-bit Operation System.
Conclusions
Our study identified an effective linear method, named ZUPLS, to recognize prokaryotic EGs. Only Z-curve features and other easily obtained sequence-based features were used in ZUPLS. ZUPLS can also successfully eliminate unimportant features by embedding the uninformative variable elimination tool into the partial least squares classifier. Much more accurate predicting results can be obtained thereby. ZUPLS is very practical for predicting EGs of newly-sequenced species because neither well-studied biological features nor optimization modelling parameters are needed. ZUPLS was utilized to predict EGs of 12 remotely related prokaryotic organisms. Regardless of the gram staining properties of the organisms, ZUPLS can yield cross-organism prediction with a significantly high accuracy. Whichever kinds of EGs are required by different types of culture media, ZUPLS can predict them accurately. Our analysis also compared ZUPLS with the best available results of other existing methods. The AUC score in predicting B. subtilis essential genes using E. coli genes was improved by 0.13. Additionally, for predicting E. coli essential genes using P. aeruginosa genes, the AUC score was improved by 0.10. The average accuracy of M. pulmonis using M. genitalium and M. pulmonis genes was also improved by 14.7%. These results confirmed the significant improvement of utilizing ZUPLS.Acknowledgements
The authors are very grateful to Prof. Chun-Ting Zhang, the Department of Physics, Tianjin University, China, for instructing the methodology of the Z-curve method. The authors are also very grateful to Dr. Yan Lin, the Department of Physics, Tianjin University, China, for providing the important EG data of E. coli. The authors are also very grateful to Mr J. L. Jackson, Dallas, Texas, USA, for helping us improve our written English. This work was supported by the National Natural Science Foundation of China [31271351] and [31000592].References
- (a) K. Kobayashi, S. D. Ehrlich, A. Albertini, G. Amati, K. K. Andersen, M. Arnaud, K. Asai, S. Ashikaga, S. Aymerich, P. Bessieres, F. Boland, S. C. Brignell, S. Bron, K. Bunai, J. Chapuis, L. C. Christiansen, A. Danchin, M. Debarbouille, E. Dervyn, E. Deuerling, K. Devine, S. K. Devine, O. Dreesen, J. Errington, S. Fillinger, S. J. Foster, Y. Fujita, A. Galizzi, R. Gardan, C. Eschevins, T. Fukushima, K. Haga, C. R. Harwood, M. Hecker, D. Hosoya, M. F. Hullo, H. Kakeshita, D. Karamata, Y. Kasahara, F. Kawamura, K. Koga, P. Koski, R. Kuwana, D. Imamura, M. Ishimaru, S. Ishikawa, I. Ishio, D. Le Coq, A. Masson, C. Mauel, R. Meima, R. P. Mellado, A. Moir, S. Moriya, E. Nagakawa, H. Nanamiya, S. Nakai, P. Nygaard, M. Ogura, T. Ohanan, M. O'Reilly, M. O'Rourke, Z. Pragai, H. M. Pooley, G. Rapoport, J. P. Rawlins, L. A. Rivas, C. Rivolta, A. Sadaie, Y. Sadaie, M. Sarvas, T. Sato, H. H. Saxild, E. Scanlan, W. Schumann, J. F. Seegers, J. Sekiguchi, A. Sekowska, S. J. Seror, M. Simon, P. Stragier, R. Studer, H. Takamatsu, T. Tanaka, M. Takeuchi, H. B. Thomaides, V. Vagner, J. M. van Dijl, K. Watabe, A. Wipat, H. Yamamoto, M. Yamamoto, Y. Yamamoto, K. Yamane, K. Yata, K. Yoshida, H. Yoshikawa, U. Zuber and N. Ogasawara, Essential Bacillus subtilis genes, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 4678–4683, DOI:10.1073/pnas.0730515100; (b) M. Itaya, An estimation of minimal genome size required for life, FEBS Lett., 1995, 362, 257–260 CrossRef CAS.
- S. Y. Gerdes, M. D. Scholle, M. D'Souza, A. Bernal, M. V. Baev, M. Farrell, O. V. Kurnasov, M. D. Daugherty, F. Mseeh, B. M. Polanuyer, J. W. Campbell, S. Anantha, K. Y. Shatalin, S. A. Chowdhury, M. Y. Fonstein and A. L. Osterman, From genetic footprinting to antimicrobial drug targets: examples in cofactor biosynthetic pathways, J. Bacteriol., 2002, 184, 4555–4572 CrossRef CAS.
- (a) B. Y. Liao, N. M. Scott and J. Zhang, Impacts of gene essentiality, expression pattern, and gene compactness on the evolutionary rate of mammalian proteins, Mol. Biol. Evol., 2006, 23, 2072–2080, DOI:10.1093/molbev/msl076; (b) I. K. Jordan, I. B. Rogozin, Y. I. Wolf and E. V. Koonin, Essential Genes Are More Evolutionarily Conserved Than Are Nonessential Genes in Bacteria, Genome Res., 2002, 12, 962–968, DOI:10.1101/gr.87702.
- P. E. M. Purnick and R. Weiss, The second wave of synthetic biology: from modules to systems, Nat. Rev. Mol. Cell Biol., 2009, 10, 410–422 CrossRef CAS PubMed.
- S. Saha and S. Heber, In silico prediction of yeast deletion phenotypes, GMR, Genet. Mol. Res., 2006, 5, 224–232 CAS.
- M. Seringhaus, A. Paccanaro, A. Borneman, M. Snyder and M. Gerstein, Predicting essential genes in fungal genomes, Genome Res., 2006, 16, 1126–1135, DOI:10.1101/gr.5144106.
- A. Gustafson, E. Snitkin, S. Parker, C. DeLisi and S. Kasif, Towards the identification of essential genes using targeted genome sequencing and comparative analysis, BMC Genomics, 2006, 7, 265 CrossRef PubMed.
- Y. C. Hwang, C. C. Lin, J. Y. Chang, H. Mori, H. F. Juan and H. C. Huang, Predicting essential genes based on network and sequence analysis, Mol. BioSyst., 2009, 5, 1672–1678, 10.1039/B900611G.
- K. Plaimas, R. Eils and R. Konig, Identifying essential genes in bacterial metabolic networks with machine learning methods, BMC Syst. Biol., 2010, 4, 56, DOI:10.1186/1752-0509-4-56.
- J. Deng, L. Deng, S. Su, M. Zhang, X. Lin, L. Wei, A. A. Minai, D. J. Hassett and L. J. Lu, Investigating the predictability of essential genes across distantly related organisms using an integrative approach, Nucleic Acids Res., 2011, 39, 795–807, DOI:10.1093/nar/gkq784.
- Y. Lin and R. R. Zhang, Putative essential and core-essential genes in Mycoplasma genomes, Sci. Rep., 2011, 1, 53, DOI:10.1038/srep00053.
- K. Song, Z. Zhang, T. P. Tong and F. Wu, Classifier assessment and feature selection for recognizing short coding sequences of human genes, J. Comput. Biol., 2012, 19, 251–260, DOI:10.1089/cmb.2011.0078.
- (a) W. Cai, Y. Li and X. Shao, A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra, Chemom. Intell. Lab. Syst., 2008, 90, 188–194, DOI:10.1016/j.chemolab.2007.10.001; (b) S. Ye, D. Wang and S. Min, Successive projections algorithm combined with uninformative variable elimination for spectral variable selection, Chemom. Intell. Lab. Syst., 2008, 91, 194–199, DOI:10.1016/j.chemolab.2007.11.005.
- T. Baba, T. Ara, M. Hasegawa, Y. Takai, Y. Okumura, M. Baba, K. A. Datsenko, M. Tomita, B. L. Wanner and H. Mori, Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection, Mol. Syst. Biol., 2006, 2, 2006 0008, DOI:10.1038/msb4100050.
- V. de Berardinis, D. Vallenet, V. Castelli, M. Besnard, A. Pinet, C. Cruaud, S. Samair, C. Lechaplais, G. Gyapay, C. Richez, M. Durot, A. Kreimeyer, F. Le Fevre, V. Schachter, V. Pezo, V. Doring, C. Scarpelli, C. Medigue, G. N. Cohen, P. Marliere, M. Salanoubat and J. Weissenbach, A complete collection of single-gene deletion mutants of Acinetobacter baylyi ADP1, Mol. Syst. Biol., 2008, 4, 174, DOI:10.1038/msb.2008.10.
- R. Austrian, The Gram stain and the etiology of lobar pneumonia, an historical note, Bacteriol. Rev., 1960, 24, 261–265 CAS.
- T. Beveridge, Use of the Gram stain in microbiology, Biotech. Histochem., 2001, 76, 111–118, DOI:10.1080/bih.76.3.111.118.
- C. T. French, P. Lao, A. E. Loraine, B. T. Matthews, H. Yu and K. Dybvig, Large-scale transposon mutagenesis of Mycoplasma pulmonis, Mol. Microbiol., 2008, 69, 67–76, DOI:10.1111/j.1365-2958.2008.06262.x.
- (a) S. T. Cole, R. Brosch, J. Parkhill, T. Garnier, C. Churcher, D. Harris, S. V. Gordon, K. Eiglmeier, S. Gas, C. E. Barry, 3rd, F. Tekaia, K. Badcock, D. Basham, D. Brown, T. Chillingworth, R. Connor, R. Davies, K. Devlin, T. Feltwell, S. Gentles, N. Hamlin, S. Holroyd, T. Hornsby, K. Jagels, A. Krogh, J. McLean, S. Moule, L. Murphy, K. Oliver, J. Osborne, M. A. Quail, M. A. Rajandream, J. Rogers, S. Rutter, K. Seeger, J. Skelton, R. Squares, S. Squares, J. E. Sulston, K. Taylor, S. Whitehead and B. G. Barrell, Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence, Nature, 1998, 393, 537–544, DOI:10.1038/31159; (b) L. M. Fu and C. S. Fu-Liu, Is Mycobacterium tuberculosis a closer relative to Gram-positive or Gram-negative bacterial pathogens?, Tuberculosis, 2002, 82, 85–90 CrossRef CAS.
- D. A. Benson, I. Karsch-Mizrachi, D. J. Lipman, J. Ostell and E. W. Sayers, GenBank, Nucleic Acids Res., 2010, 38, D46–D51, DOI:10.1093/nar/gkp1024.
- (a) C. T. Zhang, A symmetrical theory of DNA sequences and its applications, J. Theor. Biol., 1997, 187, 297–306, DOI:10.1006/jtbi.1997.0401; (b) C. T. Zhang, R. Zhang and H. Y. Ou, The Z curve database: a graphic representation of genome sequences, Bioinformatics, 2003, 19, 593–599 CrossRef CAS PubMed.
- F. Gao and C. T. Zhang, Comparison of various algorithms for recognizing short coding sequences of human genes, Bioinformatics, 2004, 20, 673–681, DOI:10.1093/bioinformatics/btg467.
- P. Gagniuc and C. Ionescu-Tirgoviste, Eukaryotic genomes may exhibit up to 10 generic classes of gene promoters, BMC Genomics, 2012, 13, 512 CrossRef CAS PubMed.
- (a) K. Song, Recognition of prokaryotic promoters based on a novel variable-window Z-curve method, Nucleic Acids Res., 2012, 40, 963–971, DOI:10.1093/nar/gkr795; (b) J. Y. Yang, Y. Zhou, Z. G. Yu, V. Anh and L. Q. Zhou, Human Pol II promoter recognition based on primary sequences and free energy of dinucleotides, BMC Bioinf., 2008, 9, 113 CrossRef PubMed.
- R. Zhang and C. T. Zhang, Z curves, an intutive tool for visualizing and analyzing the DNA sequences, J. Biomol. Struct. Dyn., 1994, 11, 767–782 CAS.
- G. Giaever, A. M. Chu, L. Ni, C. Connelly, L. Riles, S. Veronneau, S. Dow, A. Lucau-Danila, K. Anderson, B. Andre, A. P. Arkin, A. Astromoff, M. El-Bakkoury, R. Bangham, R. Benito, S. Brachat, S. Campanaro, M. Curtiss, K. Davis, A. Deutschbauer, K. D. Entian, P. Flaherty, F. Foury, D. J. Garfinkel, M. Gerstein, D. Gotte, U. Guldener, J. H. Hegemann, S. Hempel, Z. Herman, D. F. Jaramillo, D. E. Kelly, S. L. Kelly, P. Kotter, D. LaBonte, D. C. Lamb, N. Lan, H. Liang, H. Liao, L. Liu, C. Luo, M. Lussier, R. Mao, P. Menard, S. L. Ooi, J. L. Revuelta, C. J. Roberts, M. Rose, P. Ross-Macdonald, B. Scherens, G. Schimmack, B. Shafer, D. D. Shoemaker, S. Sookhai-Mahadeo, R. K. Storms, J. N. Strathern, G. Valle, M. Voet, G. Volckaert, C. Y. Wang, T. R. Ward, J. Wilhelmy, E. A. Winzeler, Y. Yang, G. Yen, E. Youngman, K. Yu, H. Bussey, J. D. Boeke, M. Snyder, P. Philippsen, R. W. Davis and M. Johnston, Functional profiling of the Saccharomyces cerevisiae genome, Nature, 2002, 418, 387–391, DOI:10.1038/nature00935.
- E. P. C. Rocha and A. Danchin, Essentiality, not expressiveness, drives gene-strand bias in bacteria, Nat. Genet., 2003, 34, 377–378 CrossRef CAS PubMed http://www.nature.com/ng/journal/v34/n4/suppinfo/ng1209_S1.html .
- P. M. Sharp and W. H. Li, The codon Adaptation Index–a measure of directional synonymous codon usage bias, and its potential applications, Nucleic Acids Res., 1987, 15, 1281–1295 CrossRef CAS PubMed.
- (a) A. J. Burnham, J. F. MacGregor and R. Viveros, Latent variable multivariate regression modeling, Chemom. Intell. Lab. Syst., 1999, 48, 167–180, DOI:10.1016/s0169-7439(99)00018-0; (b) O. M. Kvalheim, The latent variable, Chemom. Intell. Lab. Syst., 1992, 14, 1–3, DOI:10.1016/0169-7439(92)80088-l.
- W. Wu, Q. Guo, D. Jouan-Rimbaud and D. L. Massart, Using contrasts as data pretreatment method in pattern recognition of multivariate data, Chemom. Intell. Lab. Syst., 1999, 45, 39–53, DOI:10.1016/s0169-7439(98)00088-4.
Footnotes |
| † KS conceived of the study, participated in its design, performed the statistical analysis and coordination and drafted the manuscript. FW and TPT performed the statistical analysis. All authors read and approved the final manuscript. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c3ib40241j |
| § Although mycoplasmas (MP) lack cell walls, they are phylogenetically related to gram-positive bacteria with genomes of low GC-content, from French, Lao, Loraine, Matthews, Yu and Dybvig, Large-scale transposon mutagenesis of Mycoplasma pulmonis. In Molecular Microbiology, 2008, vol. 69, pp. 67–76. |
| ¶ http://tubic.tju.edu.cn/deg/ |
| This journal is © The Royal Society of Chemistry 2014 |