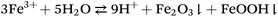Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanistic and kinetic aspects of pentose dehydration towards furfural in aqueous media employing homogeneous catalysis
Bart
Danon
a,
Gianluca
Marcotullio
b and
Wiebren
de Jong
*a
aEnergy Technology, Delft University of Technology, Leeghwaterstraat 44, 2628CA, Delft, The Netherlands. E-mail: wiebren.dejong@tudelft.nl; Tel: +31 (0)152789476
bSEA Servizi Energia Ambiente srl, Via Miraflores 2, 67100, L'Aquila, Italy
First published on 15th October 2013
Abstract
In this paper both the mechanistic and kinetic aspects of furfural formation from pentoses in aqueous acidic media have been reviewed. Based on the reviewed literature, a comprehensive reaction mechanism has been proposed consisting of more than one route, all starting from acyclic xylose, and involving alternately 1,2-enolization, β-elimination or isomerization via 1,2-hydride shift as key steps. Those studies that employ combined acid–base catalysts, soluble halide salts and trivalent cations in aqueous solutions appear to be most promising. Next, a detailed overview is presented of the results of kinetic studies on furfural formation from pentoses and furfural disappearance in aqueous acidic media. Although these results span over a very wide range of both experimental conditions and different kinetic models employed, an attempt has been made to present the published kinetic data in such a manner that it allows a global comparison. Since even in those cases where the reaction conditions seemed to be comparable, the reported kinetic constants often agree merely in the order of magnitude, thus, the validity of most of the data presented here is restricted to the specific conditions as used by each author. Additionally, a very concise overview is included of research on direct furfural production from lignocellulosic materials. In conclusion, the intricate set of reactions accompanying furfural formation from pentoses, although appearing well established in some aspects, is yet to be fully unraveled, especially with regard to the complex set of side and loss reactions seemingly involving largely unknown reaction intermediates. Such uncertainties are reflected in the contradictory kinetic models exploited and kinetic data presented in the literature, which still prevent a common and coherent interpretation.
1 Introduction
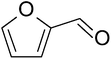
Nowadays, biomass as a renewable and potentially sustainable resource is seriously considered to contribute to the production of green chemicals, products and biofuels via the oil refinery analogue of a biorefinery.1–6 Second and higher generation biomasses, based on (co-)processing of non-edible plant parts to generate such products, are attractive in this respect as they do not cause unacceptable interferences with the food and feed production chain. In a biorefinery, fractionation of the biomass’ main organic constituents, the polymeric carbohydrates (hemicellulose and cellulose) and lignin, can be performed in different ways.2,7 Many studies have been performed concerning the conversion of non-first generation biomass carbohydrates to ethanol using hydrolytic pre-treatment and subsequent fermentation.8 Lignin is usually converted to produce steam via combustion, but studies towards valorization of this major biomass constituent are also accumulating,9 though up to now only ligno-sulphonate production in the context of the pulp and paper industry has been commercialized.10 However, the valorization of the hemicellulose derived pentose sugars to higher value added chemicals than ethanol has been subjected to substantially fewer studies. Furfural is one such chemical. It consists of a furan-ring with an aldehyde side group, see also Fig. 1.Its formation was discovered by Döbereiner back in 1821, but it only reached the stage of the first industrial production processes after about one century when in 1922 Quaker Oats started industrial production in the USA (Cedar Rapids, Iowa) based on the agricultural food residue oat husk.1,11,12 Furfural is considered to be an attractive platform chemical,13,14 and therefore it is suitable in a biorefinery context for the production of a myriad of product types, e.g. solvents (tetrahydrofuran, THF), plastics (in particular, polyamides), resins via furfuryl alcohol (already in current practice) and fuel additives (e.g. methyl-tetrahydrofuran used in novel fuel formulations,15 or rather methylfuran that can be blended into petrol as has been demonstrated by road testing16) with huge market potential. Current production levels are of the order of 300 ktons per year globally with a major production capacity in China17 and furfural production is mainly targeted at furfuryl alcohol production which is used to produce foundry resins.18 Furfural itself finds application in the oil refining sector for the selective extraction of butadiene and lube oils19 and in novel applications such as pesticides and nematicides in agricultural practice.
The production of furfural based on biomass, mainly nonfood residues of food crops and wood, is already an old practice. Furfural is one of the few chemicals that are not manufactured by a petro-chemical route as biomass chemical processing is cheaper. A substantial number of processes that were and are still operated have been described well by Zeitsch.12 Recently, an updated overview of current furfural production processes was presented.20 Acid catalysed hydrolysis and dehydration of the pentosan derived sugars forms the basis of such industry. Most processes use sulphuric acid as the mineral acid, but hydrochloric acid has also been used in different low to high concentrations. The product recovery is conventionally accomplished via steam stripping with a relatively high steam and thus energy consumption, in the range of 25–35 tons per ton of furfural produced.21 Industrial furfural production today thus still largely relies on the batch dehydration of pentosan-rich biomass using sulphuric acid, with yields typically hovering around 50%.18 Such reactor configurations cause the furfural once formed to stay too long in the acid aqueous medium so that follow-up degradation reactions take place. A crucial key to furfural production optimization lies in understanding the mechanism and related kinetics of its formation from the hemicellulose derived sugars, like xylose and arabinose to name the most prevalent, and in particular in the minimization of side and loss reactions. This paper will therefore review studies that have been performed about C5 sugar conversion to furfural and furfural loss reactions under homogeneously acid catalysed aqueous reaction conditions. Heterogeneous catalysis is not addressed in this work; a recent overview was given by Dashtban et al.22 First, the mechanisms of the formation of furfural from pentoses that have been described in the literature will be critically reviewed. Then, studies concerning the kinetics of furfural formation and degradation reactions to solid humins will be summarized and discussed, including an outlook on the application to the formation from biomasses.
2 Mechanistic aspects
2.1 Mechanisms of furfural formation
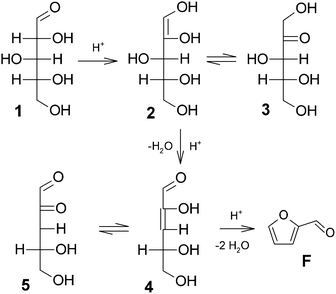
The discussion around the mechanistic aspects of furfural formation might seem of only academic interest, although a deeper understanding of such a mechanism is also crucial for planning an appropriate catalytic strategy in the furfural industry.More than one reaction mechanism has been proposed in different studies based on different techniques, and under disparate reaction conditions. Firstly, the reaction was believed to start from the acyclic form of the pentoses, either via a 1,2-enediol intermediate 2 and subsequent dehydration (see Fig. 2)23,24 or directly via a 2,3-(α,β-)unsaturated aldehyde 4, see Fig. 3.25,26 More recently, other authors believed the reaction to take place starting from the pyranose form of the pentoses, by the action of H+ on the O-2 of the pyranose ring, leading to the 2,5-anhydroxylose furanose intermediate 7 which is subsequently dehydrated to furfural, see Fig. 4.27–30
 | ||
| Fig. 2 Xylose dehydration mechanism via enolization.23,24 | ||
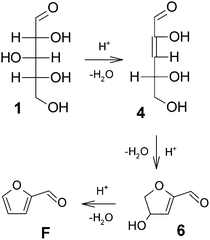 | ||
| Fig. 3 Xylose dehydration mechanism via β-elimination.25,26 | ||
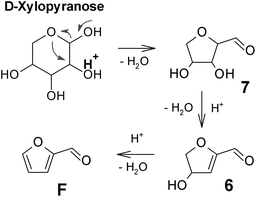 | ||
| Fig. 4 Xylose dehydration mechanism via cyclic intermediates.27–30 | ||
Published experimental evidence exists, mainly based on the reaction of labeled model compounds and on isotope exchange techniques, which is decisive in elucidating some aspects of this discussion. In the first place it has been shown that when reacting xylose-1-14C in 12% aqueous HCl, the carbon at the C-1 position is found nearly completely at the ‘aldehydic’ carbon of the final product, 2-furaldehyde-14C.26 In fact all the mechanisms proposed so far adhere to this evidence. Using similar isotope-exchange techniques, in more than one work it has been proven that, under strongly acid conditions, and in the presence of deuterated/tritiated water, nearly no carbon-bound tritium/deuterium is found in the furfural generated.23,31,32 This suggests that no solvent hydrogen is exchanged during the course of the reaction, contrary to the well-known mechanism of aldose–ketose isomerization under alkaline conditions.33,34 In this perspective, Harris and Feather31 provided evidence for the intramolecular hydrogen transfer reaction, i.e. the direct conversion of D-glucose-2-3H into D-fructose-1-3H in 1 M aqueous H2SO4, although such transfer was only partial at lower acidity (pH 3). More recently, Binder et al. reported similar results,32 showing 48% deuterium incorporation at the furfural C-1 position when xylose-2-2H was converted in the presence of water, concluding that 1,2-enediol 2 is not involved in intramolecular hydrogen-transfer, and aldose dehydration might always take place via the intermediate isomerization to the ketose 3. This is supported by the fact that ketopentoses react much faster in water,23,35–37 in analogy with the lower reactivity of glucose compared to fructose.38
Ahmad et al. reported similar evidence,23 showing a decreasing deuterium content at the furfural aldehydic carbon when reacting pentoses in deuterated water at 96 °C at decreasing pD from 4.5 to 1.5, although explaining the only partial deuterium exchange at C-1 at higher pD using the fact that the 1,2-enediol 2 is faster tautomerizing to the ketose 3 than dehydrating. The authors confirmed this interpretation with the gradual exchange of H-la and H-lb in the ketose. Importantly, in the same work it was remarked that no hydrogen was exchanged in the aldoses; hence these were converted irreversibly to 1,2-enediol. Such an indication is in agreement with the general aldose reluctance to isomerization under acidic conditions,31 and leads to the conclusion that, since enolization reactions are normally reversible, enolization or isomerization can be considered the rate limiting step in the formation of furfural.39
Remarkably, the original mechanism proposed by Hurd et al. in 1932 is also consistent with the foregoing experimental evidence.25 In this case the β-elimination forming a 2,3-unsaturated aldehyde intermediate 4 conforms to the absence of solvent hydrogen in furfural, and resembles a well-known reaction in organic chemistry whereby β-hydroxyaldehydes readily lose water in acidic solution. On the other hand this theory fails to explain intramolecular hydrogen-transfer.
As far as the furanose 2,5-anhydroxylose intermediate is concerned (Fig. 4), this mechanism presents more than one weak point compared to the others. Notably, it cannot explain the observed intramolecular hydrogen-transfer, as well as the partial deuterium exchange at C-1 and C-3 reported at lower acidity.23 Moreover, it is not straightforward to extend this mechanism to the pentuloses, at the same time explaining their significantly higher reactivity compared to the corresponding pentoses.
In conclusion, on the one hand it seems reasonable that pentoses react with furfural via their acyclic form. In fact ketopentoses, which present a significantly higher proportion of acyclic form in water solution when compared to aldopentoses,40,41 react much faster in water yielding furfural in proportion to the acidity of the solution.23,35–37 This is in agreement with the explanation normally given for the higher reactivity of fructose compared to glucose in acidic solution.38 Furthermore, the same authors putting forward the theory of the 2,5-anhydroxylose intermediate to furfural29 showed a very low energy of activation related to protonation at O-5 and subsequent ring opening.
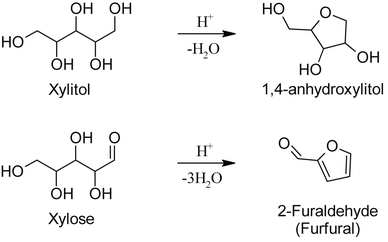
Reasonably, the presence of an electron-rich carbonyl group in the acyclic sugars is crucial for dehydration, as enols are very good electron donors favoring the elimination of water. In fact, the dehydration of sorbitol and xylitol requires much more severe conditions to take place compared to glucose and xylose, and they do not yield the corresponding furfuryl-alcohols as one could wrongly expect. In analogy furan cannot be formed from erythritol.25 The reaction of sugar alcohols in acid solution leads to 1,4-cyclization, yielding rather stable compounds such as 1,4-anhydroxylitol,42–46 see Fig. 5. The incomplete dehydration of sugar alcohols, and their relative reluctance to undergo such a reaction, is indicative of the importance of the enol functions in the intermediate dehydrations to furfural. Lastly, recent kinetic studies from our group47 have shown a positive entropy of activation during acid-catalyzed dehydration of xylose, indicating increasing degrees of freedom across the activated state, imputed to protonation and ring opening.
On the other hand, although glucose–fructose31,38,48 and xylose–xylulose32,35–37 isomerizations have been often reported to take place in the course of aldoses conversion into furfurals, there is no common agreement on the key intermediate of the reaction, this being the ketose sugar 3, the 1,2-enediol 2, or the 2,3-unsaturated aldehyde 4. From the foregoing evidence, when sugars are reacted under acidic conditions it seems reasonable to accept the mechanism proposed by Feather and Ahmad et al.,23,24 although neither direct aldose–ketose isomerization nor β-elimination can be ruled out. It is difficult to select one prevailing mechanism; the mechanisms rather seem to coexist, gaining importance one over the other according to the different reaction conditions and the nature of the solvent/catalyst system.
In Fig. 6 an attempt is made to group the mechanisms proposed. At lower acidities, enolization and subsequent isomerization is favored, although the formation of furfurals is retarded and there are more options for side reactions (via3e). Under these conditions ketoses may be detected,31 and enol intermediates such as 2 and 4 generally tautomerize respectively to 3 and 5 faster than they are dehydrated.23 Further enolization to 3e has been reported to be irreversible,23 seemingly leading to side reactions. Also β-elimination cannot be excluded under these conditions, offering a direct path to 4, hence reducing the possibilities for side reactions via3e.
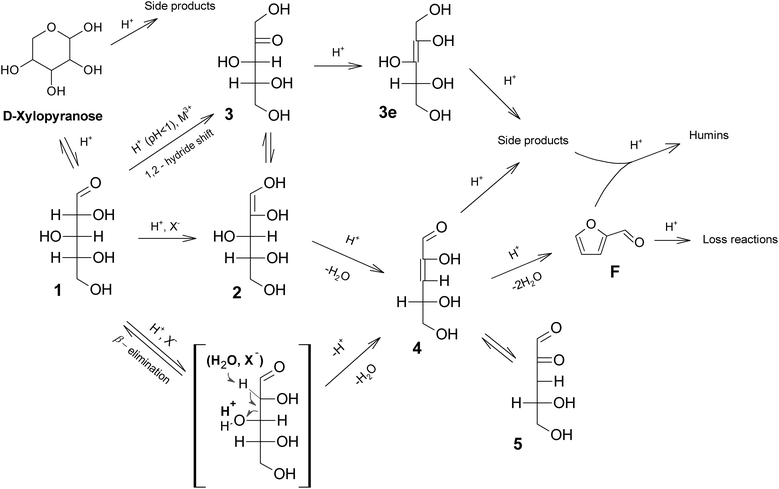 | ||
| Fig. 6 Plausible mechanism of xylose reaction to furfural in acid media. X− indicates halides ions, and M3+ indicates metal cations. | ||
At lower pH (especially pH < 1) direct isomerization via intramolecular hydrogen-transfer takes place, and the ketose is readily dehydrated, likely via an enol intermediate 2.
2.2 Catalytic strategies emerging from the observation of the reaction mechanism
Based on similar reasoning, Takagaki et al.59,60 attempted to promote the isomerization of aldoses and subsequent dehydration to furfurals by using a combination of acid and basic heterogeneous catalysts in one-pot reactions. When a combination of hydrotalcite (base) and Amberlyst-15 (acid) were used, results showed significant improvements both in terms of furfural selectivity and xylose conversion compared to only solid acid or homogeneous acid catalysis. In particular, good results are achieved especially at lower temperatures and in polar aprotic solvents such as dimethylformamide. A similar approach has been adopted for pentoses by Choudhary et al.35,36 although making use of Sn-beta zeolites or a Lewis acid as isomerization catalysts and conducting the reaction in aqueous solution. Interestingly, a significant drop in activation energy was observed36 in the reaction sequence involving xylose–xylulose isomerization (96.7 kJ mol−1 in aqueous CrCl3), and xylulose dehydration (64.9 kJ mol−1 in aqueous HCl), compared to the known acid-catalyzed xylose dehydration (133 kJ mol−1).36,39,47 Overall a significantly improved yield was reported (76%) at 413 K when a biphasic system water–toluene was employed.
It is known that aqueous solutions of FeCl3 present a Brønsted acid character due to the hydrolysis of Fe3+ resulting in the formation of different kinds of complexes:75
| [Fe(H2O)6]3+ ⇄ H+ + [Fe(OH)(H2O)5]2+ 2[Fe(OH)(H2O)5]2+ ⇄ [(H2O)5FeOFe(H2O)5]4+ + H2O |
The H+ molar concentration of a 100 mM FeCl3 aqueous solution under ambient conditions is about 17 mM, i.e. 17% of an equimolar HCl solution. On the other hand, it has been noticed76 that the pH of such solutions drops significantly after heating, forming a dark precipitate consisting of iron oxides such as –Fe2O3 and –FeOOH.77 Consequently the H+ concentration of the FeCl3 liquid solution increases according to the simplified reaction:
For these reasons aqueous FeCl3, already at 100 °C, can be regarded as a source of HCl and iron oxides, lowering accordingly the pH of the solution. With similar reasoning the pH drop of CrCl3 solutions after heating has been justified,36 and a similar behavior may be expected from similar trivalent metal chlorides. In this way the peculiar catalytic effect of metal chlorides may be partly justified by HCl formation, although other aspects are also involved.
When xylose reacted in N,N-dimethylacetamide in the presence of CrCl3, isomerization into xylulose (3) via 1,2-hydrogen transfer has been observed, with further dehydration into furfural, see Fig. 7.32 Evidence of xylose isomerization to xylulose and lyxose in the presence of CrCl3 and AlCl3 in aqueous solutions has also been shown.36,37 Hence bi- and trivalent metal ions such as Cr2+, Cr3+, Fe3+, and Al3+ have been proven to be appealing isomerization catalysts, already at very low concentration (e.g. 6 mM). When suitably combined with Brønsted acids they strongly favor furfural formation, although side reactions are not always easy to control limiting the overall furfural yields.
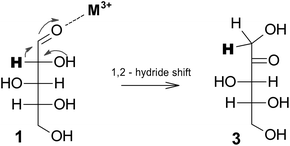 | ||
| Fig. 7 Proposed isomerization of xylose via 1,2-hydride shift.32 | ||
3 Kinetic aspects
In this section kinetic studies on furfural loss reactions and furfural formation from pentoses will be subsequently discussed. The focus is on studies in water and with homogeneous catalysts. At the end of the section, a short overview of studies on furfural production from biomass is also presented. These papers are not discussed in detail, but merely mentioned for further reference. Heterogeneous catalysis and reaction in ionic liquids are not included in this review.3.1 Furfural loss reactions
Firstly, the kinetic studies on furfural degradation in aqueous dilute acidic solutions are reviewed. Most studies follow a reaction mechanism including a single degradation reaction, which is presented in Fig. 8. Unless indicated otherwise, this reaction is assumed to follow first-order kinetics. In Table 1 the reported Arrhenius parameters are summarized for this reaction, following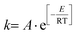 | (1) |
| Ref. | Solvent | [F]o (mM) | Catalyst (mM) | Temperature (°C) | ln(A) (s−1) | E (kJ mol−1) |
|---|---|---|---|---|---|---|
| 53 | H2O | 10–20 | H2SO4 (50) | 150–210 | 12.36 | 83.6 |
| 78 | H2O | 47.8 | H2SO4 (3.1–400) | 160–240 | [H+]·17.15 | 92.3 |
| 54 | H2O | 10 | HCl (100) | 150–169 | 3.07 | 48.1 |
| 52 | H2O | 60.4–72.5 | H2SO4 (36.4–145.5) | 150–200 | a H+·26.64 | 125.1 |
| 79 | H2O | 50 | HCOOH (50–80) | 160–200 | (Uncatalyzed) 13.82 | 75.5 |
| (Acid-catalyzed) [H+]·31.44 | 135.0 | |||||
| 80 | H2O | 160 | HCl (100) | 140–160 | 8.43 | 67.6 |
| 81 | H2O | 34 | None | 180–220 | 7.59 | 58.8 |
| 56 | H2O | 50 | HCl (50) + NaCl (500) | 160–200 | 16.84 | 102.1 |
Williams and Dunlop quantitatively investigated the loss reactions of furfural in dilute aqueous solutions.53 Both sulphuric acid and hydrochloric acid have been used as the catalyst, but only for the experiments with H2SO4 the Arrhenius parameters have been determined. The rate of degradation showed a proportional correlation with the hydrogen ion concentration. Moreover, the loss reaction showed dependency not only on the hydrogen ion concentration and the temperature, but also on the furfural concentration (which indicates a higher reaction order). However, the experimental results still followed an (apparent) first-order behavior and were therefore perceived as pseudo-unimolecular. Two different degradation products were identified: formic acid and a resinous tar. The formic acid is assumed to be formed via the hydrolytic fission of the aldehyde group of furfural. For the formation of the resins, condensation polymerization reactions were postulated. Root et al. performed a more extensive kinetic study on the furfural loss reactions.78 Experiments starting with aqueous furfural solutions with various concentrations of sulphuric acid and at various temperatures were performed in order to calculate the kinetic parameters. The measured furfural concentrations showed an apparent first-order disappearance rate. The calculated pre-exponential factor was defined as a function of the hydrogen ion concentration (mol L−1) and was [H+]·exp(17.15) s−1. The corresponding activation energy was calculated to be 92.36 kJ mol−1. However, it was also observed that the initial furfural concentration had a significant influence on the disappearance reaction rate; at higher initial furfural concentrations the degradation reactions were faster. A mechanism was proposed that could explain these observations. In this mechanism (following the work of Schoenemann et al., see the next section82) it was postulated that the furfural was degraded both via (self-)degradation (with first-order kinetics) and via a reaction of furfural with some kind of degradation intermediate (with second-order kinetics). It was shown that for the proposed mechanism, incorporating these two routes for furfural disappearance, at low furfural concentrations the reactions showed apparent first-order behavior. Moreover, Zeitsch compared the furfural resinification reaction rates with the disappearance rate of xylose obtained by Root et al., and showed that at higher temperatures (above 200 °C) resinification plays a minor role.12,78
At the turn of the millennium, Rose et al. have determined the Arrhenius parameters for furfural decomposition in dilute hydrochloric acid solutions.54 The kinetic results were compared with the results of Williams and Dunlop with sulphuric acid; the calculated activation energy with HCl was lower, which was attributed to the fact that H2SO4 was not fully dissociated under these conditions.
Subsequently, Marcotullio et al. elaborated the assumption of partially dissociated H2SO4 by substituting the hydrogen ion concentration with the hydrogen ion activity (aH+) in the equation for the reaction rate constant.52 For this purpose an extensive study on the kinetics of furfural degradation in dilute sulphuric acid solutions (36–145 mM) at temperatures between 150 and 200 °C has been performed. From these experiments the activation energy (125.1 kJ mol−1) and pre-exponential factor (exp(26.64) s−1) were derived. Moreover, the authors did not observe any formic acid formation during the destruction of the furfural.
Lamminpää et al. determined the kinetics of furfural degradation in aqueous solutions as a part of a study on furfural production from xylose with formic acid as the catalyst.79 First order reaction kinetics were assumed, based on a relatively few measurements. Both the temperature and pH were varied, and because it was observed that the pH had a larger influence on the furfural destruction rate at higher temperature, this rate was divided into an uncatalyzed and an acid-catalyzed part. For both parts, an activation energy and a pre-exponential factor have been determined. The activation energy of the uncatalyzed reaction is in good agreement with the value found by Jing et al. (see below).81 In the case of the acid-catalyzed reaction the activation energy is higher than that in most of the other studies. This could be due to the fact that in the other studies only one (acid-catalyzed) reaction was assumed. Therefore, this single reaction also includes the uncatalyzed reaction, resulting in a lower activation energy.
Also, Weingarten et al. determined the kinetics of furfural degradation as part of a study on furfural production from xylose, but then in a biphasic reactor.80 It was assumed that the furfural only degraded in the aqueous phase and not in the organic phase. Furfural degradation experiments were performed with 160 mM furfural in a 100 mM HCl aqueous solution at temperatures between 140 and 160 °C. The experimental data were assumed to follow first-order kinetics and the activation energy and pre-exponential factor were estimated to be 67.58 kJ mol−1 and exp(8.43) s−1, respectively.
Jing et al. have investigated the degradation of furfural in high temperature liquid water (without the addition of any catalyst).81 The kinetics were determined based on experiments in the temperature range of 180 to 220 °C and at a constant pressure of 10 MPa and were assumed to be first-order. The estimated value for the activation energy was 58.8 kJ mol−1 and that for the pre-exponential factor was exp(7.59) s−1.
Danon et al. have performed a study on the influence of glucose on the degradation of furfural.56 Furfural (50 mM) degradation experiments have been performed in a 50 mM HCl and a 500 mM NaCl solution at temperatures between 160 and 200 °C. Experiments with and without glucose present in the reaction mixture have been performed. Both a first- and a second-order kinetic model could reasonably well predict the experimental results for pure furfural degradation. For comparison purposes, only the first-order model is included in Table 1. When glucose was present in the reaction mixture, clear second-order reaction kinetics were observed for the degradation of furfural. A Diels–Alder reaction was propounded for this second-order behavior.
Finally, the paper published by Curtis and Hatt in 1948 needs to be included in this discussion.83 The main added value of this paper is the liquid–vapor equilibrium data presented in the first two parts. However, in the last part, the reaction rates of loss reactions of furfural in pure water and in sulphuric acid solutions are presented. The reaction rates were only determined at 180 °C and the analysis methodology might seem outdated by twenty-first century standards. However, their conclusions, such as the observation of first-order reaction kinetics and the proportionality of the disappearance rate to the acid concentration, clearly anticipated the results obtained in later studies.
It can be concluded that the degradation of furfural has not been studied extensively; however, the presented results do allow for some important observations. First, many authors note that the reaction order of the degradation reaction(s) might be different from unity; however, the majority conclude that the experimental data are well represented by a first-order kinetic model. Then, a comparison of the activation energies (excluding the saline case) indicates that the highest values are obtained in studies where H2SO4 was used as the catalyst. The activation energies predicted for the uncatalyzed reaction and with HCl as the catalyst are in the same range, and they are lower than those with H2SO4.
3.2 Furfural formation from pentoses
In this section, the kinetic studies on the dehydration of monomeric pentoses to furfural are presented. Since most studies assume a reaction mechanism with two first-order reactions (R1 and R2) for the disappearance of pentose (see Fig. 9), the values of the reaction rate constants for these types of reactions are presented in Table 2, following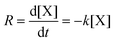 | (2) |
| Ref. | Pentose (mM) | Solvent | Catalyst (mM) | Temp. (°C) | k 1 (s−1) | k 2 (s−1) | Max. yield (%) |
|---|---|---|---|---|---|---|---|
| 81 | Xylose (72) | H2O | None | 200 | 1.98 × 10−4 | 2.05 × 10−4 | ∼50 |
| 84 | Xylose (200) | H2O | None | 200 | 4.30 × 10−6 | [X]·7.73 × 10−9 (k2a) | ∼52 |
| 6.39 × 10−6 (k2b) | |||||||
| 85 | Xylose (50) | H2O | None | 350 | 2.8 × 10−1 | 9.7 × 10−1 | 6 |
| 85 | Xylose (50) | H2O | None | 400 | 9.7 × 10−1 | 6.88 | 8 |
| 86 | Arabinose (14–350) | H2O | None | 200 | 1.56 × 10−4 | 1.74 × 10−4 | 8 |
| 87 | Arabinose (33) | H2O | None | 170 | 5.81 × 10−3 (k1 + k2) | n.d. | |
| 87 | Arabinose (33) | H2O | FA (50) | 170 | 4.52 × 10−3 (k1 + k2) | n.d. | |
| 87 | Arabinose (33) | H2O | MA (50) | 170 | 5.81 × 10−3 (k1 + k2) | n.d. | |
| 87 | Arabinose (33) | H2O | H2SO4 (50) | 170 | 1.56 × 10−2 (k1 + k2) | n.d. | |
| 25 | Xylose (3) | H2O | HCl (5200) | 107 | 3.2 × 10−2 (k1 + k2) | 93 | |
| 25 | Xylose (3) | H2O | H2SO4 (3750) | 109 | 1.1 × 10−2 (k1 + k2) | 69 | |
| 82 | Xylose (84–350) | H2O | HCl (277) | 150 | 3.8 × 10−4 | [X] 0.16·[F]0.5 3.0 × 10−5 | ∼46 |
| 78 | Xylose (667) | H2O | H2SO4 (50) | 200 | 4.17 × 10−3 | n.d. | ∼48 |
| 30 | Ribose (0.1–1.0) | H2O | HCl (1000) | 80 | 1.67 × 10−6 | 5.45 × 10−7 | 48 |
| 30 | Xylose (0.1–1.0) | H2O | HCl (1000) | 80 | 6.99 × 10−7 | 1.12 × 10−7 | 38 |
| 30 | Lyxose (0.1–1.0) | H2O | HCl (1000) | 80 | 6.77 × 10−7 | 2.92 × 10−7 | 35 |
| 30 | Arabinose (0.1–1.0) | H2O | HCl (1000) | 80 | 3.12 × 10−7 | 0.28 × 10−7 | 26 |
| 27 | Xylose (50) | H2O | H2SO4 (20) | 250 | n.d. | n.d. | 64 |
| 50 | Xylose (67) | H2O | None | 190 | 2.75 × 10−4 (k1 + k2) | ∼13 | |
| 50 | Xylose (67) | H2O | H2SO4 (50) | 190 | 4.05 × 10−4 (k1 + k2) | ∼52 | |
| 50 | Xylose (67) | H2O | NaOH (100) | 220 | 1.03 (k1 + k2) | ∼49 | |
| 39 | Xylose (35) | H2O | HCl (50) + KCl (340) | 200 | 5.49 × 10−3 | 1.24 × 10−3 | 74 |
| 39 | Xylose (35) | H2O | HCl (50) + NaCl (340) | 200 | 5.28 × 10−3 | 1.17 × 10−3 | 73 |
| 39 | Xylose (35) | H2O | HCl (50) + CaCl2 (170) | 200 | 5.10 × 10−3 | 1.20 × 10−3 | 72 |
| 39 | Xylose (35) | H2O | HCl (50) + FeCl3 (113) | 200 | >6.00 × 10−2 | >4.00 × 10−2 | 62 |
| 39 | Xylose (35) | H2O | HCl (50) + NaCl (856) | 200 | 1.19 × 10−2 | 1.07 × 10−2 | 81 |
| 69 | Xylose (35) | H2O | H2SO4 (50) + KCl (500) | 200 | 6.28 × 10−3 | 1.11 × 10−3 | 77 |
| 69 | Xylose (35) | H2O | H2SO4 (50) + KBr (500) | 200 | 5.54 × 10−3 | 7.7 × 10−4 | 80 |
| 69 | Xylose (35) | H2O | H2SO4 (50) + KI (500) | 200 | 5.36 × 10−3 | 6.5 × 10−4 | 81 |
| 69 | Xylose (35) | H2O | H2SO4 (50) + KCl/KI (500/250) | 200 | 7.46 × 10−3 | 3.7 × 10−4 | 87 |
| 79 | Xylose (20–80) | H2O | HCOOH (50) | 200 | 6.85 × 10−4 | 2.28 × 10−4 | ∼65 |
| 68 | Xylose (13) | H2O | FeCl3 (49) | 180 | 2.05 × 10−3 (k1 + k2) | ∼23 | |
| 68 | Xylotriose (11) | H2O | FeCl3 (49) | 180 | 3.72 × 10−2 (k1 + k2) | ∼24 | |
| 80 | Xylose (740) | H2O | HCl (100) | 170 | 6.11 × 10−4 | [F]·2.04 × 10−3 | 30 |
| 80 | Xylose (740) | H2O–MIBK (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
HCl (100) | 170 | 6.11 × 10−4 | [F]·2.04 × 10−3 | 85 |
| 37 | Xylose (266) | H2O | HCOOH (326) | 180 | n.d. | n.d. | 74 |
| 67 | Xylose (667) | H2O–toluene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15) 15) |
H2SO4 (1019) + NaCl (2.4 g) | b.p. | n.d. | n.d. | 83 |
| 88 | Xylose (740) | H2O–CPME (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.33) 2.33) |
H2SO4 (105) | 180 | n.d. | n.d. | ∼59 |
| 89 | Xylose (33) | H2O | HCl (100) | 180 | n.d. | n.d. | 60 |
For those studies that only present the Arrhenius constants, the values of the kinetic rate parameters at specific temperatures have been calculated for comparison purposes.
The order in which the studies are discussed is roughly chronological. However, first, those studies where no additional catalysts were employed are presented. Then, the studies with homogeneous catalysts are discussed. The overview will conclude with several studies in biphasic media (with an aqueous and an organic phase) and some papers that do not include a proper kinetic study, but still seem relevant for the present review.
Jing et al. have concisely investigated furfural formation from xylose in an aqueous system.81 Over a temperature range between 180 and 200 °C and at 10 MPa, experiments were performed with 72 mM xylose as the initial concentration. Reasonable yields were obtained with values between 30 and 50%. Additionally, Arrhenius parameters were estimated for the reactions using Arrhenius plots. The kinetic parameters estimated for the degradation of furfural (as discussed in the previous section) were used for the estimation of the kinetic parameters of the dehydration reactions.
Kim et al. performed a similar study on xylose dehydration in high temperature water.84 At temperatures between 140 and 240 °C feed streams with 200 mM xylose in water have been investigated in a continuous tubular reactor. The assumed reaction mechanism is comparable to that presented in Fig. 9, although reaction R2 is assumed to consist of two reactions, one following first-order and the other following second-order kinetics, k2b and k2a, respectively. The highest furfural yields were obtained between 200 and 220 °C. In additional experiments various feed flows (which result in a variation of the residence time) and various initial xylose concentrations were employed. It is shown that lower feed flow (0.016 mL min−1 which coincides with a residence time of 3.7 h) and lower initial xylose concentrations result in higher furfural yields.
Also Aida et al. have investigated the reaction kinetics of xylose in sub- and supercritical water without any catalysts.85 Xylose degradation was investigated at 350 and 400 °C and at pressures between 40 and 100 MPa. Based on the identified products in the experiments a complex reaction mechanism was proposed including the Lobry de Bruyn–Alberta van Ekenstein transformations (LBET) and retro-aldol reactions. However, no furfural degradation reactions were included in the reaction mechanism. The method of chemical analysis was extensive, including a total organic carbon detector, two HPLC systems and a GC-MS analysis. The LBET reactions mainly led to the formation of xylulose and the retro-aldol reactions cover the otherwise termed xylose loss reactions. In all experiments the majority of the retrieved products were from retro-aldol reactions. The highest furfural yields were obtained at the highest pressures (100 MPa), although these yields were still relatively low: 6 and 8% at 350 and 400 °C, respectively. For comparison with the other studies reported in this overview the kinetic rate parameters of the retro-aldol reactions are summed to form k2. Finally, the authors have also included a sensitivity analysis of the estimated kinetic parameters.
Gairola et al. have kinetically modeled the hydrothermal dehydration of arabinose (as the second most abundant pentose in hemicellulose) towards furfural.86 Temperatures between 180 and 260 °C were employed at initial arabinose concentrations of 14, 67 and 350 mM. The authors recognize the fact that for optimal modeling the kinetic parameters of furfural degradation should be determined separately from the determination of the other kinetic parameters. For this purpose they use the declining furfural concentration in those experiments where after a certain reaction time the sugars had fully disappeared. The authors state that this method is to be preferred over separate kinetic experiments with pure furfural, since in the more complex reaction mixture the furfural degrades faster. However, this statement is not substantiated with any experimental data. Because the estimated Arrhenius parameters for arabinose are of the same order as those reported by Jing et al. for xylose,81 it is propounded that it is justified to use solely xylose as the model compound for biomass hydrolysis. This seems to be a coarse assumption, since, as can be readily deduced from Table 2, xylose reacts (at 200 °C) around 30% faster than arabinose (compare e.g. with the results of Jing81).
Although Kootstra et al. had a diametrically opposite objective of the other studies mentioned here (they tried to minimize the furfural production during acidic hydrolysis of pentosans because furfural is a known inhibitor for yeasts in subsequent sugar-to-ethanol fermentation processes), their study still contains some interesting kinetic results for the degradation of arabinose in acidic solutions.87 The kinetics of arabinose (33 mM) degradation in acidic solutions, with 50 mM fumaric, maleic and sulphuric acid, and in pure water were investigated at 150 and 170 °C. The rate of degradation with sulphuric acid was higher, but, surprisingly, with fumaric or maleic acid the rate was comparable to or even lower than that in pure water. Some tentative explanations are propounded for this difference; however, in these considerations a possible alkaline catalysis in pure water has been disregarded. Their main conclusion from the kinetic study, that arabinose is more stable under these conditions compared to xylose or glucose, does agree with the trends observed in other studies. No furfural yields were reported.
Already in 1932 Hurd and Isenhour performed an extensive study on the kinetics of the formation of furfural from pentoses in acidic solutions.25 A setup with continuous furfural removal by steam distillation was used. The kinetic rate parameters of xylose degradation have been determined for solutions with hydrochloric and sulphuric acid at various (relatively high) concentrations. In Table 2 the two experiments with the highest furfural yields for the two different acids are included. Especially with HCl the yield was exceptionally high (93%), probably due to the continuous extraction of the formed furfural. But it has to be also taken into account that especially the identification methods have been improved significantly during the interlapsed time (which is almost a century).
In 1948 Dunlop published a landmark paper on the formation of furfural from xylose.90 In this paper the disappearance rate of xylose was determined at two different HCl concentrations (50 and 100 mM) at 160 °C. Since in the applied reaction mechanism no direct loss reactions from the pentoses are assumed, only the (total) disappearance rate of xylose was determined. The results show that this rate follows first-order kinetics and that it is proportional to the hydrogen ion concentration.
Schoenemann et al. have presented the kinetic values of xylose dehydration towards furfural in a larger context of designing chemical reactors.82 The proposed reaction mechanism differs from that presented in Fig. 9. It is assumed that xylose dehydrates to furfural via an intermediate and that furfural degrades both individually (‘Verharzung’) and in reaction with this intermediate (‘Kondensation’), see also Fig. 10. However, in the rate expression of this combined intermediate and furfural (‘Kondensation’) reaction the concentration of xylose was included, instead of the intermediate (probably because the latter could not be measured). From calculations based on their experiments this reaction had reaction orders of 1.16 and 0.5 for xylose and furfural, respectively.
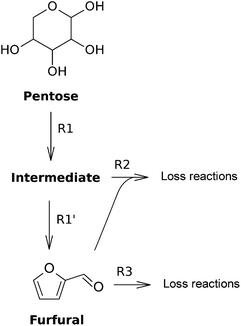 | ||
| Fig. 10 Reaction mechanism for the dehydration of a pentose towards furfural including a combined intermediate and furfural (‘Kondensation’) reaction.82 | ||
The study by Root et al. includes an extensive kinetic evaluation of the dehydration of xylose to furfural.78 Xylose dehydration has been investigated over a wide range of temperatures (160–280 °C) and initial xylose (20.8–1332 mM) and sulphuric acid (50–400 mM) concentrations. They follow a mechanism where furfural both degrades separately and in reaction with an intermediate from xylose, analogous to Schoenemann.82 However, only values for the rate constant k1 have been presented. The assumed mechanism is further verified by experiments starting with both xylose and furfural in the initial reaction solution. Although these results are not presented, it is stated that the value of k1 was not influenced by the addition of any furfural to the initial reaction solution. In the Arrhenius equation for the rate constant k1 additional parameters were added for the temperature dependency of the specific gravity of water, the actual acid–water ratio and the activity coefficient of the hydrogen ions. Also, several correlation terms were added to the differential concentration expressions in order to achieve better predictions over the entire investigated range of conditions.
It is noted here that Zeitsch has presented the kinetic results of the three previously discussed studies in his extensive monograph on furfural production and utilization.12 The kinetic values of Root et al. are used to obtain some indications for the design of a reactor.78
Garrett and Dvorchik have investigated the dehydration of the different aldopentoses towards furfural.30 HCl was used as the catalyst in concentrations ranging from 125 to 1000 mM at reaction temperatures between 60 and 80 °C. Also the initial pentose concentration was varied from 0.1 to 1 mM. It is noted that under these conditions (especially at these relatively low temperatures) the reactions are very slow, and thus maximum furfural yields were obtained after 200 to 800 hours. The most important result of this kinetic study was the comparison of the reactivities of the different aldopentoses. Based on the values of k1 and k2 that were fitted to the experimental data, the order of reactivity of the aldopentoses was determined to be ribose > xylose ∼ lyxose > arabinose. In Table 2 the modeled values of both k1 and k2 are presented, since only for k1 the experimental values have been published. However, the experimental and modeled values for k1 did agree very reasonably. Antal et al. have minutely evaluated the reaction mechanism of xylose dehydration.27 Based on their mechanistic considerations a complex kinetic model was proposed. In this model different reaction pathways are incorporated for the three different isomers of xylose (xylofuranose, xylopyranose and acyclic xylose). The ratio between these isomers was included among the to be estimated parameters of the model. The time-dependent H+ concentration was calculated using the algebraic charge conservation relationship. In the experimental series the initial xylose and sulphuric acid concentrations as well as the reaction time were varied. The highest furfural yield of 64% was obtained with 20 mM of sulphuric acid at 250 °C after 50 seconds. Furthermore, it is noted that under many different conditions also small amounts of pyruvaldehyde were measured. Finally, it was found that pressures between 6.3 and 34.5 MPa did not significantly influence the reaction chemistry.
Oefner et al. have compared xylose degradation in pure water, acidic and alkaline solutions.50 Over a temperature range between 180 and 220 °C this reaction was investigated in pure water, in water with various concentrations of H2SO4 (0.5, 5 or 50 mM) or with 100 mM NaOH. Besides furfural, also other degradation products (pyruvic, formic, glycolic, lactic and acetic acid) have been identified with isotachophoretic analyses. Only the first-order xylose degradation reaction (the sum of R1 and R2 in Fig. 9) has been kinetically modeled. For this reaction the kinetic parameters have been determined using an Arrhenius plot. The value of the activation energy for xylose degradation in an alkaline solution turned out to be significantly different from those of xylose degradation in either pure water or acidic solutions (63.7 versus 119.4 and 120.7 kJ mol−1, respectively). Moreover, it was shown that in the alkaline experiments the yields of the organic acids were significantly higher than those in the other experiments.
Marcotullio et al. have performed an extensive experimental study on the influence of different salts as a secondary catalyst on the dehydration of xylose to furfural. The experimental results are presented as the selectivity and maximum yields based on modeled kinetic rate constants. In 2010 a study was presented using HCl as the primary catalyst and several different chloride-containing salts as the secondary catalyst.39 From these experiments, in which the temperature, acid and chloride concentration were kept constant (see also Table 2), it can be concluded that the cations have a relatively small influence on the maximum furfural yield (for K+, Na+, Ca2+ or Fe3+, the maximum yields are 74.1, 72.8, 72.3 and 62.0, respectively). Only in the case of FeCl3 the yield was significantly lower; however, in this experiment the reaction was much faster. The highest maximum furfural yield (81.3%) is obtained using high concentrations of NaCl (856 mM) as the secondary catalyst. Based on these results, it was postulated that the chloride ion catalyzes the rate-limiting enolization step. In a second study published in 2011, xylose was dehydrated to form furfural using H2SO4 as the primary catalyst.69 In these experiments different potassium-containing salts are added as the secondary catalysts. Both the calculated and measured maximum furfural yields are presented, which agree very reasonably (the latter are presented in Table 2). Again, the differences between the maximum furfural yields of the experiments with different halides (KCl, KBr and KI) are small. See section 2.2.2 for a more detailed discussion on the effects of halide containing salts on the formation of furfural.
Besides the pure furfural degradation experiments, Lamminpää et al. also studied the formation of furfural from xylose with formic acid as the catalyst.79 The experimental results were used to compare three different reaction mechanisms, i.e., a mechanism as presented in Fig. 9, a second mechanism as presented in Fig. 10 and a third mechanism including the loss reactions R2 from both Fig. 9 and 10. It has to be noted that in this study the intermediate concentration has been (numerically) included in the kinetic modeling. In the kinetic expressions the H+ concentration was incorporated using equilibrium equations for the dissociated formic acid. Moreover, the kinetic rate expressions have been divided into an acid-catalyzed and a solvent (water) catalyzed part, resulting in two separate rate constants. It was noted that the solvent-catalyzed rate parameters were not determined in separate experiments. The general conclusion of the comparison of the three different mechanisms with the experimental data is that the loss reaction of xylose alone is prevailing over the loss reaction of an intermediate with furfural. The mechanism presented in Fig. 9 yielded optimal predictions. At 200 °C the H+ concentration was around 50 mM (derived from their Fig. 2).79 It was noted here that the contribution of the acid-catalyzed reaction was about 5 times that of the solvent-catalyzed reaction. The maximum furfural yields have only been presented graphically and were thus extrapolated for the experiment at 200 °C from their Fig. 9.79
Liu et al. have investigated the degradation of xylose and xylotriose in aqueous solutions with various inorganic salts and no acid catalyst present.68 Of the investigated salts FeCl3 resulted in the largest increase in the sugar degradation rate compared to reference experiments in pure water and in a dilute sulphuric acid solution. The order of influence (from small to large) was NaCl, KCl, CaCl2, MgCl2 and FeCl3. It has to be noted that all the salts were added at equal weight percentages (0.8 wt%), thus resulting in different concentrations of the ions (especially the chloride ions). All experiments were performed at 180 °C. The kinetic study focused only on the degradation rate of the sugars, which effectively means that values were calculated for (k1 + k2). The order of this degradation reaction was assumed to be first-order. Not only the rate constants for the degradation of xylose and xylotriose increased significantly with the addition of FeCl3, but also the fraction of unaccounted losses (compared to the amount of furfural formed) increased. The maximum furfural yields (with FeCl3 present) were 23 and 24% for xylose and xylotriose (after 20 and 15 minutes), respectively.
The kinetics of xylose dehydration in a biphasic system was investigated by Weingarten et al.80 In this study a mixture of water and methyl isobutyl ketone (MIBK, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) was heated using a microwave. For comparison purposes, some monophasic (with only an aqueous phase) experiments with both conventional and microwave assisted heating were also performed. It turned out that the microwave heating, under these conditions, did not result in significant differences in the kinetics of xylose degradation and furfural formation compared to conventional heating. In the kinetic model it is assumed that the dehydration and degradation reactions take place only in the aqueous phase; therefore, the same kinetic values are reported for both the monophasic and biphasic experiments. Also, it is assumed (based on rather small differences between the xylose conversion rates in the monophasic and biphasic systems) that xylose is degrading in a reaction with furfural. In the kinetic model for the biphasic system a submodel was included to predict the mass transfer of furfural to the organic phase. At 170 °C, maximum furfural yields of 30 and 80% were measured for monophasic and biphasic systems, respectively. The higher yield in the biphasic system was attributed to the simultaneous furfural production in and extraction from the aqueous phase. However, the kinetic model for the biphasic system was unfortunately not able to predict reliable concentrations of xylose and furfural for the experiments at higher temperatures. This might be due to the fact that no separate degradation reaction of xylose was incorporated into the reaction mechanism.
1) was heated using a microwave. For comparison purposes, some monophasic (with only an aqueous phase) experiments with both conventional and microwave assisted heating were also performed. It turned out that the microwave heating, under these conditions, did not result in significant differences in the kinetics of xylose degradation and furfural formation compared to conventional heating. In the kinetic model it is assumed that the dehydration and degradation reactions take place only in the aqueous phase; therefore, the same kinetic values are reported for both the monophasic and biphasic experiments. Also, it is assumed (based on rather small differences between the xylose conversion rates in the monophasic and biphasic systems) that xylose is degrading in a reaction with furfural. In the kinetic model for the biphasic system a submodel was included to predict the mass transfer of furfural to the organic phase. At 170 °C, maximum furfural yields of 30 and 80% were measured for monophasic and biphasic systems, respectively. The higher yield in the biphasic system was attributed to the simultaneous furfural production in and extraction from the aqueous phase. However, the kinetic model for the biphasic system was unfortunately not able to predict reliable concentrations of xylose and furfural for the experiments at higher temperatures. This might be due to the fact that no separate degradation reaction of xylose was incorporated into the reaction mechanism.
Finally, several papers concerning the dehydration of monosaccharides towards furfural that do not include a kinetic study need to be mentioned here. Firstly, Yang et al. have investigated the dehydration of xylose to furfural with formic acid as the catalyst.37 According to the authors the optimal conditions were 266 mM xylose, 217 mM HCOOH and 180 °C, under which a furfural yield of 74% was achieved. Rong et al. performed a study on the dehydration of xylose to furfural in a biphasic mixture (water and toluene). Both sulphuric acid and either NaCl or FeCl3 were added as the catalysts. A maximum yield of 83% was obtained in a water–toluene mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 (on volume basis), 667 mM xylose, 1019 mM H2SO4 and 2.4 g NaCl. Campos Molina et al. have investigated xylose dehydration in sulphuric acid solutions with NaCl as an additional catalyst and cyclopentyl methyl ester (CPME) as an extracting co-solvent.88 A maximum furfural yield of 59% was obtained for 740 mM xylose and 105 mM H2SO4 at 180 °C. Yemiş et al. studied the production of furfural from xylose in a microwave-assisted process with hydrochloric acid as the catalyst serving as a reference experiment for their investigation of xylan and biomass hydrolysis, see also the next section.89
15 (on volume basis), 667 mM xylose, 1019 mM H2SO4 and 2.4 g NaCl. Campos Molina et al. have investigated xylose dehydration in sulphuric acid solutions with NaCl as an additional catalyst and cyclopentyl methyl ester (CPME) as an extracting co-solvent.88 A maximum furfural yield of 59% was obtained for 740 mM xylose and 105 mM H2SO4 at 180 °C. Yemiş et al. studied the production of furfural from xylose in a microwave-assisted process with hydrochloric acid as the catalyst serving as a reference experiment for their investigation of xylan and biomass hydrolysis, see also the next section.89
It can be concluded that many different kinetic studies have been performed on the dehydration of monomeric pentoses to furfural. However, there are hardly any round robin studies. This hampers a meticulous comparison of the individual results of Table 2 and merely allows for some trend conclusions. Firstly, most authors accept first-order kinetics for all the dehydration reactions of the pentoses, with only some discussions on the order and reactants of the (direct) loss reaction of the pentose. Then, the addition of an acidic catalyst seems to both accelerate the reactions and improve the furfural yields. Also the addition of a secondary (saline) catalyst further improves the rates and yields, although with FeCl3 a kind of optimum seems to have been surpassed, since its addition results in very fast reactions but lower furfural yields, compared to the addition of other salts. Finally, in those studies that employ some kind of furfural extraction from the reacting media, the final yields are significantly higher.
3.3 Furfural formation from biomass
In this section an overview of studies that are concerned with the hydrolysis of biomass resources is included. In order to position the biomass in the reaction network, a simplified reaction mechanism is presented in Fig. 11. In the following, those studies that properly focus on furfural production will be discussed concisely. The majority of these studies do not include a kinetic study, and when they do, the assumed mechanisms and reactions are highly diverse. Therefore, in Table 3 it is merely mentioned whether kinetics are included in these papers. Another useful source of information on this subject can be found in the minireview by Dutta et al.102| Ref. | Biomass resource | Solvent | Catalyst | Temperature (°C) | Max. yield | Kinetics |
|---|---|---|---|---|---|---|
| 91 | Eucalyptus globulus (8.5 g g−1) | H2O–AcOH (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95) 95) |
HCl (0.4 wt%) | 130 | 4.48 g L−1 | Yes |
| 92 | Sorghum straw (0.1 g g−1 H2O) | H2O | H3PO4 (6 wt%) | 134 | 13.7 g L−1 | Yes |
| 93 | Date-palm midribs (50–100 mL g−1) | H2O | H2SO4 (5–15 wt%) | 100–140 | 11–53% of potential | Yes |
| 86 | Wheat straw (0.14 g mL−1) | H2O | None | 230 | 29 mol% | No |
| 86 | Brewery waste (0.28 g mL−1) | H2O | None | 230 | 13 mol% | No |
| 89 | Xylan (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 SLR) 200 SLR) |
H2O | HCl (100 mM) | 180 | 37 wt% of pentose | No |
| 89 | Flax shives (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 SLR) 100 SLR) |
H2O | HCl (100 mM) | 180 | 72 wt% of pentose | No |
| 94 | Wheat straw (150 mL g−1) | H2O | HCl (pH 0.6) | 155 | 51 wt% of pentose | No |
| 88 | Cynara cardunculus (4 wt%) | H2O–CPME (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.33) 2.33) |
H2SO4 (1 wt%) | 170 | 95 mol% | No |
| 88 | Cynara cardunculus (4 wt%) | H2O–CPME (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.33) 2.33) |
H2SO4 (1 wt%) + NaCl (0.4 wt%) | 170 | 99 mol% | No |
| 95 | Olive stones (8.5 wt%) | H2O | H2SO4 (50–250 mM) | 220–240 | 50–65% of potential | No |
| 96 | Rice hulls (25 mL g−1) | H2O | H2SO4 (15%) + ZnO (0.1 g) | 110 | 13.2 wt% | No |
| 97 | Rice husk (4–160 mL g−1) | H2O | H2SO4 (1–7 wt%) | 100–180 | 6–50% of potential | No |
| 98 | Rice straw (0.05 g mL−1) | H2O | H2SO4 (0.5%) | 150 | 59 g kg−1 straw | No |
| 98 | Rice straw (0.05 g mL−1) | H2O–THF (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
H2SO4 (0.5%) + NaCl (30 wt%) | 150 | 118 g kg−1 straw | No |
| 64 | NEH (3.2% wt xylose) | H2O–THF (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.3) 2.3) |
HCl (0.44 M) + NaCl (±20 g) | 210 | 92.2% of potential | No |
| 99 | Corn cob (0.6 LSR) | H2O | FeCl3 (20 mM) + AcOH (3%) | 180 | 68% of potential | No |
| 100 | Corn cob (0.6 LSR) | H2O | FeCl3 (60 mM) + AcOH (2%) | 160–200 | 50–69% of potential | No |
| 100 | Corn cob (0.6 LSR) | Concentrated seawater | FeCl3 (60 mM) + AcOH (2%) | 190 | 73% of potential | No |
| 101 | Corn cob (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 SLR) 8 SLR) |
H2O | H2SO4 (1.75 vol%) | 200 | 13.19 g L−1 | No |
| 101 | Corn cob (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 SLR) 8 SLR) |
H2O | HCl (2 vol%) | 180 | 13.90 g L−1 | No |
The following three studies include reaction kinetics. Abad et al. have investigated the production of furfural from Eucalyptus globulus wood samples in acetic acid–water–HCl solutions.91 Sorghum straw was hydrolyzed using phosphoric acid as the catalyst by Vázquez et al.92 The hydrolysis of midribs of the date-palm tree was studied in sulphuric acid by Bamufleh et al.93
Then, many other studies have been performed on the production of furfural from biomass without a kinetic study. Gairola et al. have presented, in addition to their kinetic study on arabinose dehydration as discussed in the previous section, experimental results of the production of furfural from wheat straw and a brewery waste with supercritical CO2 extraction of the produced furfural.86 Also Yemiş et al. have included, besides a yield study on furfural production from xylose, the results of the microwave assisted hydrolysis of xylan from birchwood, two types of straw and flax shives.89 In another paper by these authors wheat straw was hydrolyzed to furans under similar conditions.94 Campos Molina et al. have investigated Cynara cardunculus (Cardoon) in sulphuric acid solutions with NaCl as an additional catalyst and cyclopentyl methyl ester as a co-solvent.88 Mansilla et al. have performed a study on the hydrolysis of rice hulls in both a one- and a two-stage process and with different metallic oxides as the catalyst, of which the dehydration experiment with the highest furfural yield is reported in Table 3, which is after a pre-hydrolysis step.96 Montané et al. investigated the hydrolysis of olive stones to furfural in dilute sulphuric acid at high temperatures.95 Rice husk has been hydrolysed in a process including furfural extraction by supercritical carbon dioxide by Sangarunlert et al.97 Amiri investigated the hydrolysis of rice straw to both hydroxymethylfurfural and furfural in either single-phase dilute sulphuric acid solutions or in biphasic systems.98 Xing et al. studied the formation of furfural from hydrolysates of Northeastern hardwood in a two-stage (including a prehydrolysis step) and biphasic system, employing both HCl and NaCl as the catalysts.64 Cut corn cob was hydrolyzed by Mao et al. to furfural in an aqueous solution co-catalyzed by FeCl3 and acetic acid, of which the latter is introduced in the reactor by steam injection of an acetic acid solution which simultaneously served as the furfural extractor.99 In a follow-up publication, additional experiments under these conditions, but with (concentrated) seawater as the solvent, were presented.100 Sánchez et al. have investigated liquors obtained from corn cob autohydrolysis with sulphuric and hydrochloric acid as the catalysts, where the autohydrolysis can be regarded as a pre-hydrolysis step.101
A quick review of the results presented in Table 3 yields similar conclusions as have been drawn based on the results of the dehydration of the monosaccharides. Firstly, the employed reaction conditions in the different studies hardly show any overlap between them, making a meticulous comparison very difficult. However, as far as a comparison is possible, it can be concluded that the addition of both a primary (acidic) catalyst and a secondary (saline) catalyst appears to improve the final furfural yield from biomass substrates. Moreover, also the addition of an extracting (organic) phase significantly improves the furfural yields.
Finally, an extensive amount of literature is dedicated to the kinetics of the hydrolysis of biomass with the objective to maximize the yield of monosaccharides. The kinetic models of these studies can be roughly divided into two parts. Firstly, the more complex kinetic models for the hydrolysis of the pentosan or hemicellulosic part of biomass include furfural degradation reactions.103–107 The second (and largest) part of these models regard any further reactions of the monomeric pentoses as a single degradation reaction (and term the product of this reaction either as degradation products or as furfural).108–115
4 Conclusions
Furfural formation in aqueous acidic media has been reviewed from a mechanistic and a kinetic point of view. After carefully reviewing the vast, and sometimes contradictory, experimental evidence published during roughly a century of research, a comprehensive reaction mechanism has been proposed. This mechanism presents more than one route, all starting from acyclic xylose, and involving alternately 1,2-enolization, β-elimination or isomerization via 1,2-hydride shift as key steps. Among recent research trends, those studies that employ combined acid–base catalysts, soluble halide salts and trivalent cations in aqueous solutions appear to be most promising.As far as the kinetics of furfural formation from pentoses and furfural disappearance in aqueous acidic media are concerned, published experimental data span over a relatively wide range of conditions. Analogously, and partly due to the ongoing discussion on the exact reaction mechanism, on the reactants and on the order of the reactions, many different kinetic models have been exploited in these studies, making it hard to compare the results directly or to group the results in one comprehensive model. Therefore, especially for the part on furfural formation, it is recommended to use the data presented here only under the specific conditions as used by each author. However, an attempt has been made to present the published kinetic data in such a manner as to allow a global comparison. Additionally, a very concise overview of research performed on direct furfural production from lignocellulosic materials has also been included.
In conclusion, an intricate set of reactions accompanying furfural formation from pentoses, despite appearing well established in some aspects, is yet to be fully unraveled, especially as regards the complex set of side and loss reactions seemingly involving intermediates of reactions largely unknown. Such uncertainties are reflected in the contradictory kinetic models exploited and kinetic data presented in the literature, which still prevent a common and coherent interpretation.
References
-
B. Kamm, P. Gruber and M. Kamm, Biorefineries Industrial Processes and Products; Status Quo and Future Directions, Wiley-VCH Verlag GmbH & Co, 2006 Search PubMed
.
- V. Menon and M. Rao, Prog. Energy Combust. Sci., 2012, 38, 522–550 CrossRef CAS PubMed
.
-
M. Aresta, A. Dibenedetto and F. Dumeignil, Biorefinery: from biomass to chemicals and fuels, De Gruyter, 2012 Search PubMed
.
- B. Kamm and M. Kamm, Appl. Microbiol. Biotechnol., 2004, 64, 137–145 CAS
.
- H. Ohara, Appl. Microbiol. Biotechnol., 2003, 62, 474–477 CrossRef CAS PubMed
.
- G. Huber, S. Iborra and A. Corma, Chem. Rev., 2006, 106, 4044–4098 CrossRef CAS PubMed
.
- F. Carvalheiro, L. Duarte and F. Girio, J. Sci. Ind. Res., 2008, 67, 849–864 CAS
.
- M. Galbe and G. Zacchi, Appl. Microbiol. Biotechnol., 2002, 59, 618–628 CrossRef CAS PubMed
.
- S. Cheng, I. D'Cruz, Z. Yuan, M. Wang, M. Anderson, M. Leitch and C. Xu, J. Appl. Polym. Sci., 2011, 121, 2743–2751 CrossRef CAS
.
- J. Van Dam, B. De Klerk-Engels, P. Struik and R. Rabbinge, Ind. Crops Prod., 2005, 21, 129–144 CrossRef CAS PubMed
.
-
A. P. Dunlop and F. N. Peters, The Furans, Reinhold Publishing Corporation, New York, 1953 Search PubMed
.
-
K. J. Zeitsch, The chemistry and technology of furfural and its many by-products, Elsevier, 2000, vol. 13 Search PubMed
.
- J. J. Bozell and G. R. Petersen, Green Chem., 2010, 12, 539–554 RSC
.
- G. Dautzenberg, M. Gerhardt and B. Kamm, Holzforschung, 2010, 65, 439–451 Search PubMed
.
- Y. Kar and H. Deveci, Energy Sources, 2006, 28, 909–921 CrossRef CAS
.
- J.-P. De Lange, E. Van der Heide, J. Van Buijtenen and R. Price, ChemSusChem, 2012, 5, 150–166 CrossRef PubMed
.
- A. Corma, S. Iborra and A. Velty, Chem. Rev., 2007, 107, 2411–2502 CrossRef CAS PubMed
.
- A. Mamman, J.-M. Lee, Y.-C. Kim, I. Hwang, N.-J. Park, Y. Hwang, J. S. Chang and J.-S. Hwang, Biofuels Bioprod. Bioref., 2008, 2, 438–454 CrossRef CAS
.
- A. De Lucas, L. Rodríguez, P. Sánchez and A. Carnicer, Sep. Sci. Technol., 1993, 28, 2465–2477 CrossRef CAS
.
- W. de Jong and G. Marcotullio, Int. J. Chem. React. Eng., 2010, 8, A69 Search PubMed
.
- D. Win, Aust. J. Technol., 2005, 8, 185–190 Search PubMed
.
- M. Dashtban, A. Gilbert and P. Fateh, J. Sci. Technol. Forest Prod. Process., 2012, 2, 44–53 Search PubMed
.
- T. Ahmad, L. Kenne, K. Olsson and O. Theander, Carbohydr. Res., 1995, 276, 309–320 CrossRef CAS
.
- M. S. Feather, D. W. Harris and S. B. Nichols, J. Org. Chem., 1972, 37, 1606–1608 CrossRef CAS
.
- C. D. Hurd and L. L. Isenhour, J. Am. Chem. Soc., 1932, 54, 317–330 CrossRef CAS
.
- W. A. Bonner and M. R. Roth, J. Am. Chem. Soc., 1959, 81, 54545456 Search PubMed
.
- M. J. Antal Jr., T. Leesomboon, W. S. Mok and G. N. Richards, Carbohydr. Res., 1991, 217, 71–85 CrossRef
.
- X. Qian, M. Nimlos, M. Davis, D. Johnson and M. Himmel, Carbohydr. Res., 2005, 340, 2319–2327 CrossRef CAS PubMed
.
- M. R. Nimlos, X. Qian, M. Davis, M. E. Himmel and D. K. Johnson, J. Phys. Chem. A, 2006, 110, 11824–11838 CrossRef CAS PubMed
.
- E. Garrett and B. Dvorchik, J. Pharm. Sci., 1969, 58, 813–820 CrossRef CAS
.
- D. W. Harris and M. S. Feather, Carbohydr. Res., 1973, 30, 359–365 CrossRef CAS
.
- J. B. Binder, J. Blank, A. Cefali and R. T. Raines, ChemSusChem, 2010, 3, 1268–1272 CrossRef CAS PubMed
.
- H. S. Isbell, H. L. Frush, W. R. Wade and C. Hunter, Carbohydr. Res., 1969, 9, 163–175 CrossRef CAS
.
- S. J. Eitelman and D. Horton, Carbohydr. Res., 2006, 341, 2658–2668 CrossRef CAS PubMed
.
- V. Choudhary, A. B. Pintar, S. I. Sandler, D. G. Vlachos and R. F. Lobo, ACS Catal., 2011, 1, 1724–1728 CrossRef CAS
.
- V. Choudhary, S. I. Sandler and D. G. Vlachos, ACS Catal., 2012, 2, 2022–2028 CrossRef CAS
.
- W. Yang, P. Li, D. Bo and H. Chang, Carbohydr. Res., 2012, 357, 53–61 CrossRef CAS PubMed
.
- A. Rosatella, S. Simeonov, R. Frade and C. Afonso, Green Chem., 2011, 13, 754–793 RSC
.
- G. Marcotullio and W. de Jong, Green Chem., 2010, 12, 1739–1746 RSC
.
- J. Wu, A. S. Serriani and T. Vuorinen, Carbohydr. Res., 1990, 206, 1–12 CrossRef CAS
.
- K. N. Drew, J. Zajicek, G. Bondo, B. Bose and A. S. Serriani, Carbohydr. Res., 1998, 307, 199–209 CrossRef CAS
.
- A. Wisniewski, J. Szafranek and J. Sokolowski, Carbohydr. Res., 1981, 97, 229–234 CrossRef CAS
.
- A. Wisniewski, J. Sokolowski and J. Szafranek, J. Carbohydr. Chem., 1983, 2, 293–304 CrossRef CAS
.
- M. Kurszewska, E. Skorupowa, J. Madaj and A. Wisniewski, J. Carbohydr. Chem., 2004, 23, 169–177 CrossRef CAS PubMed
.
- F. Fenouillot, A. Rousseau, G. Colomines, R. Saint-Loup and J.-P. Pascault, Prog. Polym. Sci., 2010, 35, 578–622 CrossRef CAS PubMed
.
- G. Flèche and M. Huchette, Starch/Staerke, 1986, 1, 26–30 CrossRef
.
-
G. Marcotullio, PhD thesis, Delft University of Technology, 2011
.
- M. Watanabe, Y. Aizawa, T. Iida, T. M. Aida, C. Levy, K. Sue and H. Inomata, Carbohydr. Res., 2005, 340, 1925–1930 CrossRef CAS PubMed
.
-
H. E. Hoydonckx, W. M. Van Rhijn, W. Van Rhijn, D. E. De Vos and P. A. Jacobs, Ullmann's Encyclopedia of Industrial Chemistry, Wiley VCH Verlag GmbH & Co. KGaA, 2000 Search PubMed
.
- P. Oefner, A. Lanziner, G. Bonn and O. Bobleter, Monatsh. Chem., 1992, 123, 547–556 CrossRef CAS
.
- F. Rice and L. Fishbein, J. Am. Chem. Soc., 1956, 78, 1005–1009 CrossRef CAS
.
- G. Marcotullio, M. A. Tavares Cardoso, W. de Jong and A. H. M. Verkooijen, Int. J Chem. React. Eng., 2009, 7, A67 Search PubMed
.
- D. Williams and A. Dunlop, Ind. Eng. Chem., 1948, 40, 239–241 CrossRef CAS
.
- I. Rose, N. Epstein and A. Watkinson, Ind. Eng. Chem. Res., 2000, 39, 843–845 CrossRef CAS
.
- M. S. Feather, J. Org. Chem., 1969, 34, 1998–1999 CrossRef CAS
.
- B. Danon, L. van der Aa and W. de Jong, Carbohydr. Res., 2013, 375, 145–152 CrossRef CAS PubMed
.
- F. Rice, J. Org. Chem., 1957, 23, 465–468 CrossRef
.
- F. Rice and A. Johnson, J. Org. Chem., 1958, 23, 1966–1969 CrossRef CAS
.
- A. Takagaki, M. Ohara, S. Nishimura and K. Ebitani, Chem. Lett., 2010, 838–840 CrossRef CAS
.
- A. Takagaki, M. Ohara, S. Nishimura and K. Ebitani, Chem. Commun., 2009, 6276–6278 RSC
.
- E. E. Hughes and S. F. Acree, J. Res. Natl. Bur. Stand., 1938, 21, 327–336 CrossRef CAS
.
- E. I. Fulmer, L. M. Christensen, R. M. Hixon and R. L. Foster, J. Phys. Chem., 1936, 40, 133141 Search PubMed
.
- V. Voorhees, Ind. Eng. Chem. Anal. Ed., 1943, 15, 378378 Search PubMed
.
- R. Xing, W. Qi and G. Huber, Energy Environ. Sci., 2011, 4, 2193–2205 CAS
.
- T. vom Stein, P. M. Grande, W. Leitner and P. Domínguez de María, ChemSusChem, 2011, 4, 1592–1594 CrossRef CAS PubMed
.
- E. I. Gürbüz, S. G. Wettstein and J. A. Dumesic, ChemSusChem, 2012, 5, 383–387 CrossRef PubMed
.
- C. Rong, X. Ding, Y. Zhu, Y. Li, L. Wang, Y. Qu, X. Ma and Z. Wang, Carbohydr. Res., 2012, 350, 77–80 CrossRef CAS PubMed
.
- C. Liu and C. Wyman, Carbohydr. Res., 2006, 341, 2550–2556 CrossRef CAS PubMed
.
- G. Marcotullio and W. de Jong, Carbohydr. Res., 2011, 346, 1291–1293 CrossRef CAS PubMed
.
- L. Liu, J. Sun, C. Cai, S. Wang, H. Pei and J. Zhang, Bioresour. Technol., 2009, 100, 5865–5871 CrossRef CAS PubMed
.
- L. Liu, J. Sun, M. Li, S. Wang, H. Pei and J. Zhang, Bioresour. Technol., 2009, 100, 5853–5858 CrossRef CAS PubMed
.
- J. Gravitis, N. Vedernikov, J. Zandersons and A. Kokorevics, ACS Symp. Ser., 2001, 784, 110–122 CrossRef CAS PubMed
.
- H. Zhao, J. E. Holladay, H. Brown and Z. C. Zhang, Science, 2007, 316, 1597–1600 CrossRef CAS PubMed
.
- J. B. Binder and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 1979–1985 CrossRef CAS PubMed
.
-
F. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, Wiley Interscience, 5th edn, 1988 Search PubMed
.
- G. Marcotullio, E. Krisanti, J. Giuntoli and W. de Jong, Bioresour. Technol., 2011, 102, 5917–5923 CrossRef CAS PubMed
.
- B. Voigt and A. Göbler, Cryst. Res. Technol., 1986, 21, 1177–1183 CrossRef CAS
.
- D. Root, J. Seaman, J. Harris and W. Neill, Forest Prod. J., 1959, 9, 158–165 CAS
.
- K. Lamminpää, J. Ahola and J. Tanskanen, Ind. Eng. Chem. Res., 2012, 51, 6297–6303 CrossRef
.
- R. Weingarten, J. Cho, W. Conner and G. Huber, Green Chem., 2010, 12, 1423–1429 RSC
.
- Q. Jing and X. Lu, Chin. J. Chem. Eng., 2007, 15, 666–669 CrossRef CAS
.
- K. Schoenemann and H. Hofmann, Chem. Ing. Technol., 1957, 29, 665–674 CrossRef CAS
.
- R. Curtis and H. Hatt, Aust. J. Sci. Res., 1948, 1, 213–235 CAS
.
- S. Kim, M. Lee, E. Park, S. Lee, H. Lee, K. Park and M.-J. Park, React. Kinet. Mech. Cat., 2011, 103, 267–277 CrossRef CAS PubMed
.
- T. Aida, N. Shiraishi, M. Kubo, M. Watanabe and R. Smith Jr., J. Supercrit. Fluids, 2010, 55, 208–216 CrossRef CAS PubMed
.
- K. Gairola and I. Smirnova, Bioresour. Technol., 2012, 123, 592–598 CrossRef CAS PubMed
.
- A. Kootstra, N. Mosier, E. Scott, H. Beeftink and J. Sanders, Biochem. Eng. J., 2009, 43, 92–97 CrossRef CAS PubMed
.
- M. Campos Molina, R. Mariscal, M. Ojeda and M. López Granados, Bioresour. Technol., 2012, 126, 321–327 CrossRef CAS PubMed
.
- O. Yemiş and G. Mazza, Bioresour. Technol., 2011, 102, 7371–7378 CrossRef PubMed
.
- A. P. Dunlop, Ind. Eng. Chem., 1948, 40, 204–209 CrossRef CAS
.
- S. Abad, J. Alonso, V. Santos and J. Parajó, Bioresour. Technol., 1997, 62, 115–122 CrossRef CAS
.
- M. Vázquez, M. Oliva, S. Téllez-Luis and J. Ramírez, Bioresour. Technol., 2007, 98, 3053–3060 CrossRef PubMed
.
- H. Bamufleh, Y. Alhamed and M. Daous, Ind. Crops Prod., 2013, 42, 421–428 CrossRef CAS PubMed
.
- O. Yemiş and G. Mazza, Bioresour. Technol., 2012, 109, 215–223 CrossRef PubMed
.
- D. Montané, J. Salvadó, C. Torras and X. Farriol, Biomass Bioenergy, 2002, 22, 295–304 CrossRef
.
- H. Mansilla, J. Baeza, S. Urzuá, G. Maturana, J. Villaseñor and N. Durán, Bioresour. Technol., 1998, 66, 189–193 CrossRef CAS
.
- W. Sangarunlert, P. Piumsomboon and S. Ngamprasertsith, Korean J. Chem. Eng., 2007, 24, 936–941 CrossRef CAS
.
- H. Amiri, K. Karimi and S. Roodpeyma, Carbohydr. Res., 2010, 345, 2133–2138 CrossRef CAS PubMed
.
- L. Mao, L. Zhang, N. Gao and A. Li, Bioresour. Technol., 2012, 123, 324–331 CrossRef CAS PubMed
.
- L. Mao, L. Zhang, N. Gao and A. Li, Green Chem., 2013, 15, 727–737 RSC
.
- C. Sánchez, L. Serrano, M. Andres and J. Labidi, Ind. Crops Prod., 2013, 42, 513–519 CrossRef PubMed
.
- S. Dutta, S. De, B. Saha and M. I. Alam, Catal. Sci. Technol., 2012, 2, 2025–2036 CAS
.
- T. Carrasco and C. Roy, Wood Sci. Technol., 1992, 26, 189–208 Search PubMed
.
- G. Garrote, H. Domínguez and J. Parajó, Process Biochem., 2001, 36, 571–578 CrossRef CAS
.
- D. Nabarlatz, X. Farriol and D. Maontané, Ind. Eng. Chem. Res., 2004, 43, 4124–4131 CrossRef CAS
.
- J. Morinelly, J. Jensen, M. Browne, T. Co and D. Shonnard, Ind. Eng. Chem. Res., 2009, 48, 9877–9884 CrossRef CAS
.
- E. Guerra-Rodríguez, O. Portilla-Rivera, L. Jarquín-Enríquez, J. Ramírez and M. Vázquez, Biomass Bioenergy, 2012, 36, 346–355 CrossRef PubMed
.
- N. Eken-Saraçoğlu, S. F. Mutlu, G. Dilmaç and H. Çavuşoğlu, Bioresour. Technol., 1998, 65, 29–33 CrossRef
.
- B. Lavarack, G. Griffin and D. Rodman, Catal. Today, 2000, 63, 257–265 CrossRef CAS
.
- B. Lavarack, G. Griffin and D. Rodman, Biomass Bioenergy, 2002, 23, 367–380 CrossRef CAS
.
- R. Aguilar, J. Ramárez, G. Garrote and M. Vázquez, J. Food Eng., 2002, 55, 309–318 CrossRef
.
- A. Herrera, S. Téllez-Luis, J. Ramírez and M. Vázquez, J. Cereal Sci., 2003, 37, 267–274 CrossRef CAS
.
- E. Canettieri, G. Rocha, J. Carvalho Jr. and J. Silva, Ind. Eng. Chem. Res., 2007, 46, 1938–1944 CrossRef CAS
.
- Y. Lu and N. Mosier, Biotechnol. Prog., 2007, 23, 116–123 CrossRef CAS PubMed
.
- X. Liu, M. Lu, N. Ai, F. Yu and J. Ji, Ind. Crops Prod., 2012, 38, 81–86 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2014 |