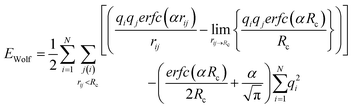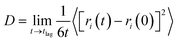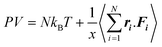Accelerating electrostatic pair methods on graphical processing units to study molecules in supercritical carbon dioxide

Abstract

Traditionally, electrostatic interactions are modelled using Ewald techniques, which provide a good approximation, but are poorly suited to GPU architectures. We use the GPU versions of the LAMMPS MD package to implement and assess the Wolf summation method. We compute transport and structural properties of pure carbon dioxide and mixtures of carbon dioxide with either methane or difluoromethane. The diffusion of pure carbon dioxide is indistinguishable when using the Wolf summation method instead of PPPM on GPUs. The optimum value of the potential damping parameter, α, is 0.075. We observe a decrease in accuracy when the system polarity increases, yet the method is robust for mildly polar systems. We anticipate the method can be used for a number of techniques, and applied to a variety of systems. Substitution of PPPM can yield a two-fold decrease in the wall-clock time.

---

1 Introduction

GPU architectures and their use in molecular dynamics (MD) simulations have attracted much recent attention.^1–4 Maximizing computational throughput on graphical processing units (GPUs)/hybrid architectures is of great interest. Decreasing the wall-clock time for each MD time step allows longer timescales to be sampled, giving greater confidence in the convergence of ensemble averages. GPUs have been widely adopted in various computational disciplines, due to the highly parallel design, low power consumption (FLOPS/Watt) and commodity cost (£/FLOPs). The GPU architecture is optimised for processing massive amounts of parallel calculations, and so has many more cores than a CPU, but at the sacrifice of memory capabilities.

Electrostatic interactions can be divided into first-order effects, which comprise point charge interactions decaying reciprocally with respect to intermolecular distance and higher-order interactions that decay more rapidly. Electrostatic interactions can be modelled explicitly by various methods, including: cut-off truncation,^5–7 switched/shifted cut-off truncation,⁸ Ewald⁹ and its mesh derivatives, particle mesh Ewald (PME),¹⁰ particle–particle particle mesh (PPPM)¹¹ and smoothed particle mesh Ewald (SPME).¹² The Ewald summation provides a good approximation for the electrostatic energy, as the algorithm accounts for periodicity of the simulation domain, but it scales as O(N^3/2). An approximation that is frequently adopted is PPPM, due to its superior scaling, O(NlogN), over the Ewald summation. SPME,¹³ PPPM¹⁴ and multi-level summation¹⁵ have been implemented on the GPU, yet the requirement for fast Fourier transforms (FFTs) intrinsic to Ewald methods, like SPME and PPPM, reduces the parallelism¹⁴ and leads to poor scaling on GPUs. Pair-wise algorithms derived from cut-off techniques show superior scaling O(N) and greater effectiveness on GPUs.

Cut-off techniques can reproduce experimental quantities, for instance, the Madelung constant. Wolf et al.¹⁶ reported that the electrostatic (Coulombic) potential for condensed systems was effectively short-ranged, and the energies are in agreement with Ewald methods when the cut-off sphere reached neutrality. This was observed whilst calculating the Madelung constant for rocksalt (NaCl), where the relationship between truncation distance and electrostatic energy was investigated. When the cut-off sphere was truncated at a distance to achieve charge neutrality, the electrostatic energy was significantly closer to the Madelung energy. The repeating lattice structure of NaCl is well-suited for treatment with the Wolf method, but the supercritical phase of polar solutes can be more difficult to model as the atomic partial charges within the cut-off sphere are dynamic. The resulting shifted Coulomb potential achieves charge neutrality by projecting each atom charge, q_j, from q_i onto the edge of the solvation sphere. Therefore, every jth atom in the solvation sphere of atom i has a charge of equal but opposite sign set at the cut-off (R_c). This results in an artificially neutral solvation sphere for every ith atom, which effectively makes the system charge neutral.

where q_i and q_j are point charges, r_ij is the intermolecular distance between atoms i and j, α is the damping coefficient in Å⁻¹ and R_c is the cut-off distance. To obtain accurate electrostatic contributions, a damping function is applied. The electrostatic energy decay oscillates around a rate of 1/R_c. Introducing the damping function quickly flattens the oscillations as the cut-off increases, effectively determining how fast the complementary error function falls from unity at r_ij = 0, to zero at the cut-off.¹⁶ The damping function adopted is the complementary error function, as it has a close connection to the Ewald sum.¹⁷ The coefficient of the error function, α, denotes the rate at which convergence is achieved. A large α value will converge the energy rapidly using a short cut-off, but the errors can be larger. A smaller α leads to less contamination of the potential, but the sum will fluctuate more rapidly. Assigning a value of 0 to α, results in the truncated shifted-force (SF) potential. This SF calculation is faster than the Wolf method, but the selection of α can enhance the accuracy of electrostatic forces and energies by optimizing agreement to Ewald methods.¹⁸

Simple cut-off based methods are unreliable for computing the forces, as the potential truncates abruptly at the cut-off, which causes forces to be undefined if the molecule lies at the cut-off boundary. The reliance upon Ewald methods instead of efficient cut-off methods has been discussed by Fennel and Gezelter,¹⁷ who compared the accuracy of damped shifted-force (DSF) and shifted potential cut-off methods for water, argon in water, and NaCl. Benchmarking and validation of the DSF potential was applied to polyelectrolyte brushes on GPUs; speedups were achieved of a factor between 1.1 and 3.9, depending on the system and size of the cut-off with respect to PPPM.¹⁹ Group based cut-offs, where the cut-off is dynamically allocated to ensure entire molecules are within the solvation shell, were investigated,¹⁷ but the energies deviated significantly from those obtained using PME.

In this work we assess the applicability of the Wolf method to model electrostatic interactions for various systems in the supercritical region of carbon dioxide. Supercritical carbon dioxide (scCO₂) is an attractive ‘green solvent’ used in many industrial processes, such as caffeine extraction,²⁰ polymer solvation²¹ and synthesis,^22,23 enzyme catalysis^24,25 and stabilization^26,27 and transition metal catalysis.^28,29 Although carbon dioxide does not possess a dipole, it has a significant quadrupole³⁰ (13.4 × 10⁻⁴⁰ Cm²), which means that electrostatic interactions are an important component of interactions involving scCO₂. Su and Maroncelli³¹ observed that neglecting electrostatic interactions, i.e., considering only Lennard-Jones interactions, led to a systematic 14% error in the solvation free energies of polymer-scCO₂ systems. This observation is attributed to quadrupole–dipole and quadrupole–quadrupole interactions,³¹ which are inherently modelled in all point charge models. A nonpolar fluid should be well suited for treatment using the Wolf method, as quadrupolar interactions decay more rapidly than dipolar ones. This bodes well for the efficient electrostatic treatment of systems solvated by carbon dioxide by utilizing the Wolf method on GPU architectures. We also investigate the computational cost of the DSF method, with respect to the Wolf method.

Fluorous polymers are well known to dissolve in scCO₂,^32,33 which has been partially explained by ¹⁹F-NMR experiments, which suggested a number of specific interactions between carbon dioxide and the fluorous solute that increase the solubility.³⁴ Many biomolecular systems are stable in the presence of scCO₂, but this is dependent on the species, the water content, and experimental conditions.²⁴ Protein stability can be observed when scCO₂ solvates the hydrophobic residues, and water solvates the polar/hydrophilic residues.²⁶ Water possesses a strong dipole moment, which will make it less amenable to treatment with the Wolf method. We aim to follow this work with an investigation for protein systems solvated by water and carbon dioxide.

To assess the applicability of the Wolf method to systems containing carbon dioxide, important physical quantities, such as PVT relationships and diffusion coefficients, can be calculated and compared with the values calculated using PPPM. The applicability of the Wolf method to study methane plus carbon dioxide gas hydrates has been reported, and the results show good agreement between lattice sum and reaction field methods.³⁵ Analysis of the convergence behaviour of the Wolf method by Angoshtari and Yavari³⁶ shows the method to be robust, but convergence can be problematic if poor choices are made for the cut-off or α values. In our study, we investigate the effect of increasing the polarity of the fluid by incorporating difluoromethane molecules, which possess a strong dipole. For low polarity systems the Wolf method should be well suited, but as the polarity increases the effect of long-range dipole interactions will become important and we assess the point where Ewald techniques will become necessary.

2. Method

LAMMPS is a multi-purpose MD code,³⁷ which is widely used in the fields of atomistic, coarse-grained and mesoscopic simulations. The code can process massive numbers of particles per simulation, which it achieves using an optimized spatial decomposition technique. The GPU optimized version, written in CUDA C, can run over multiple GPUs, either in conjunction with the CPU or entirely on the GPU. We have implemented the Wolf method into LAMMPS-CUDA the GPU-exclusive version of LAMMPS and LAMMPS-GPU the CPU/GPU implementation, as a new potential incorporating Lennard-Jones and electrostatic interactions. LAMMPS-CUDA was written exclusively for use with CUDA, but LAMMPS-GPU can be compiled and run on AMD GPUs and other applicable accelerators using OpenCL. The new pair style is implemented as a double potential function in LAMMPS as lj/charmm/coul/wolf for CPU, lj/charm/coul/wolf/cuda for LAMMPS-CUDA and lj/charm/coul/wolf/gpu for LAMMPS-GPU. The LAMMPS-CUDA version is solely GPU based, with the exception of file I/O and pre/post simulation setup. The GPU version of LAMMPS utilizes the GPU for the force and/or neighbour list generation, whilst all other operations and I/O are performed on the CPU. The GPU version allows for n CPUs to be used per GPU, whilst the LAMMPS-CUDA version only allows for one CPU per GPU. An important difference between packages is that the GPU version on LAMMPS uses the CPU to calculate FFTs for PPPM, whilst the LAMMPS-CUDA version performs the calculation on the GPU. We have also implemented the DSF implementations, lj/charm/coul/dsf/cuda and lj/charm/coul/dsf/gpu, for benchmarking purposes. We used the CHARMM³⁸ Lennard-Jones potential in the AB form with a switching function in conjunction with the Wolf method. A cut-off of 2.5σ was used for the Lennard-Jones potential, and tapered to zero at 2.65σ, where σ was calculated from A^1/12 in Table 1. We used the rigid EPM2 atomistic force field³⁹ to represent carbon dioxide and parameters derived by Palmer and Anchell⁴⁰ to represent Lennard-Jones and charge interactions for methane and difluoromethane.

Table 1 EPM2 force field parameters for carbon dioxide³⁹ and Palmer and Anchell parameters for methane and difluoromethane.⁴⁰ (A^1/12) and (B^1/6) have units ((kcal mol)^1/12 Å) and ((kcal mol)^1/6 Å) respectively

Atom site	A ^1/12	B ^1/6	q (|e|)
C (CO2)	2.448	2.173	−0.3256
O (CO2)	2.922	2.815	+0.6512
C (CH4)	3.200	3.200	−0.4160
H (CH4)	1.910	1.390	+0.1040
C (CH2F2)	2.900	3.590	+0.0500
H (CH2F2)	1.712	0.000	+0.1550
F (CH2F2)	2.650	2.237	−0.1800

---

We utilized the LAMMPS software to simulate scCO₂ at several densities, comparing the results obtained by using PPPM or the Wolf method. We selected a tolerance setting of 0.0001 for the calculations involving PPPM that enables the root mean square error to be within a factor of 10 000 of the reference force, which is calculated analytically for short-range interactions⁴¹ and in k-space.⁴² The optimum value of α was investigated for binary mixtures of carbon dioxide and methane or difluoromethane. The criterion for selecting α is the level of agreement between the Coulombic energies computed by PPPM and Wolf. To consider the effects of neglecting only the periodic long-range Coulombic effects, we treat the cut-off as being half the length of the simulation box. We also investigate the level of approximation that arises from use of a quarter box cut-off in conjunction with the Wolf method.

2.1 Benchmarking GPU electrostatics

Two boxes of 10 000 and 50 000 carbon dioxide molecules were constructed with a molar density of 0.01 mol cm⁻³ and minimized for 1000 iterations using the conjugate gradient method, to an energy tolerance of 1 × 10⁻⁶ kcal mol⁻¹. Both systems were heated from 0 K to 308.2 K using the Nosè–Hoover thermostat⁴³ with a damping time of 500 fs for 2 ns, followed by 5 ns of equilibration at 308.2 K. We evaluated the performance of the Wolf method on two GPU architectures, Tesla (Tesla C1060) and Kepler (Tesla K10). The K10, released in 2012, is designed for high throughput calculations performed in single precision. The number of giga floating-point operations per second (GFLOPs) is 4577 in single precision, compared to 933 for the C1060. This improvement was achieved in part by increasing the number of cores in the streaming multiprocessor from 8 (Tesla), 32 (Fermi) to 192 (Kepler). Memory bandwidth on the GPU to global memory is 103 GB s⁻¹ for the C1060, but 320 GB s⁻¹ for Kepler K10. We include an eight core Intel Xeon (E5-2609) CPU for benchmarking purposes that has an approximate 77 GFLOPs with 34 GB s⁻¹ bandwidth to RAM. Calculations were performed using single-precision on two separate nodes, both comprise an eight core Xeon CPU and either a Kepler K10 or two Tesla C1060. Multiple GPU tests were only carried out using the C1060, which yielded an almost two-fold increase in performance, which corresponds well to the linear dependency. We use the FFTW 3.3.1 library in single-precision for all k-space calculations of PPPM. We considered two modes for calculations using LAMMPS-GPU, one where all force and neighbour calculations are performed on the GPU, and the other where the force and neighbour calculations are dynamically assigned between CPU and GPU. We used the CUDA 5.0 Tokito (GPU driver v. 304.54), which has produced a noticeable improvement in performance over CUDA 4.0. A new feature, CUDA dynamic parallelism, allows kernels running on the GPU to spawn more grids and to continue to generate work depending on the calculation.⁴⁴ This feature has not been incorporated in our study.

2.2 Pure carbon dioxide

The 10 000 carbon dioxide molecule system was used to generate densities (box lengths) of 0.001 (255.1 Å), 0.002 (202.5 Å), 0.004 (160.72 Å), 0.005 (149.2 Å), 0.01 (118.42 Å) and 0.02 (94.0 Å) mol cm⁻³, all within the supercritical region at 308.2 K. Each box was minimized for 1000 iterations using the conjugate gradient method, with an energy tolerance of 1 × 10⁻⁶ kcal mol⁻¹. The system was heated in the NVT ensemble using the Nosè–Hoover thermostat⁴³ with cubic periodic boundary conditions from 0 K to 308.2 K for 1 ns using a 1 fs time step. This was followed by 1 ns of equilibration. Integration was performed using the time-reversible velocity Verlet algorithm.⁴⁵ The procedure was repeated nine times to generate different equilibrated configurations for the purposes of error analysis, and the resulting standard deviation is noted in the error bars. The mean square displacement (MSD) of the centre of mass of carbon dioxide was obtained by calculating the gradient of the linear portion of the relationship between MSD and lag time over 10 ns production dynamics in the NVT ensemble. The pressures were obtained every 50 fs, and averaged over 10 ns to calculate the PVT relationship.

2.3 Carbon dioxide and solute

To study the effects of polar and non-polar solutes, we considered different quantities of methane and difluoromethane molecules. Five boxes of 10 000 carbon dioxide molecules were constructed with mole fractions χ_(solute) = 0.0001, 0.001, 0.01, 0.09 and 0.5, where the solute was either methane or difluoromethane. These systems correspond to box lengths (Å) of 95.01, 95.99, 97.49, 99.27 and 125.31 for CH₄/CO₂ and 81.64, 81.78, 81.83, 84.44 and 105.16 for CH₂F₂/CO₂. Each system was minimized and heated to 308.2 K using the same procedure as above. The pressure was equilibrated to 80 atmospheres (corresponding to a molar density of ∼0.02 mol cm⁻³), using the Berendsen barostat⁴⁶ with a 1 ps damping time for 20 ns with a 1 fs time step. The procedure was repeated nine times to generate different equilibrated configurations for the purposes of error analysis, and the resulting standard deviation is noted in the error bars. The MSDs of carbon dioxide and solutes were obtained from the linear portion of the relationship over a production run of 10 ns. We compare the errors in Coulombic energy with respect to α for χ_(solute) = 0.09 with PPPM and Wolf, which we performed by decomposing the energy into group contributions. We investigate the relationship between system polarity and diffusion coefficients, and the total Coulombic energy.

One method of quantifying the transport properties of a system is the MSD, and thus the diffusion coefficient using the Einstein relationship.

where D is the macroscopic diffusion coefficient, r_i(t) is the position of the centre of mass at time t, r_i(0) is the initial position of the centre of mass, t_lag is the lag time, and 〈[r_i(t) − r_i(0)]²〉 is the ensemble averaged MSD. The diffusion coefficient is calculated from the slope of the MSD against lag time,⁴⁷ which is a measure of the atomic displacements through time.

The pressure of a system can be calculated using the virial equation (below), and the PVT relationship has an influence on the diffusion coefficients.⁴⁸ The long-range part of PPPM has a different contribution to the pressure.⁴⁹

where P is the pressure of the system, V is the volume, N is the number of particles, x is the dimensionality, K_B is the Boltzmann constant and the term in brackets is the total intermolecular force multiplied by the interaction distances.

3. Results

3.1 Benchmarking

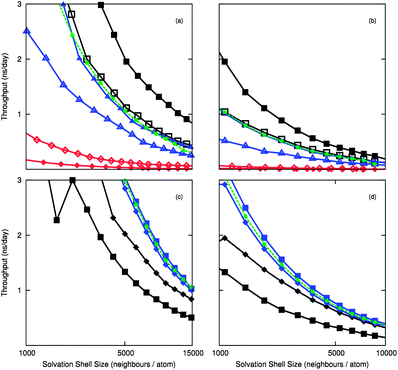
To compare the efficiency of the Wolf method, we measured the computational throughput of the electrostatic routines using the 10 000 and 50 000 molecule systems. The timings of the implementations are calculated with respect to the number of neighbours in the cut-off sphere. Fig. 1(a) and 1(b) compare the throughput for different architectures, and show the acceleration gained when substituting PPPM for Wolf using LAMMPS-CUDA. The computational throughput is almost twice as high with the Wolf treatment than with PPPM. The Wolf method is slower than PPPM on the CPU, which is unexpected, but the CPU is well suited to handle FFTs that feature in PPPM. This is due to faster memory accesses between cache and compute cores, and the less parallel nature of the algorithm. The DSF method is marginally slower than PPPM in LAMMPS-CUDA, but is marginally faster than the Wolf method for the LAMMPS-GPU implementation. The difference between pair styles using LAMMPS-GPU is much less pronounced than LAMMPS-CUDA, where the acceleration gained by using the Wolf or DSF method is approximately 1.5 times faster. The difference between dynamic partitioning and exclusive GPU computation is small for the cut-off methods, and the dynamic mode is marginally quicker. For PPPM the opposite is observed, which could be due to the CPU already being used for the k-space calculations. The Kepler K10 GPU shows the greatest acceleration, which bodes well for future GPU releases.

Fig. 1 Computational throughput as a function of number of neighbours for (a,c) 10 000 CO₂ molecules (B-D) 50 000 CO₂ molecules. Fig. (a) and (B) were calculated using the LAMMPS-CUDA package, and (c) and (d) were calculated using the LAMMPS-GPU package. In (a) and (B), three electrostatic treatments were considered, Wolf (filled shapes), PPPM (unfilled shapes) and DSF (green circles) for different architectures. (Triangles = Tesla C1060, squares = Kepler K10, diamonds = eight core Intel Xeon). In figures (c) and (d) the force/neighbour implementation is shown where the GPU is used exclusively (diamonds) and dynamically assigned between CPU/GPU (squares). PPPM is shown in black, the Wolf method is shown in blue, and the DSF force/neigh exclusively GPU is shown in green.

3.2 Optimum alpha and cut-off parameters

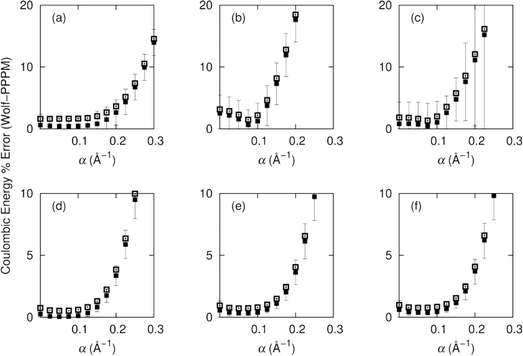
We consider first the accuracy of the electrostatic energy and its convergence as a function of α and cut-off distance. We then turn to the properties computed from the simulation, considering structural, dynamic and thermodynamic aspects. The simulations have all been executed in the supercritical region of carbon dioxide, and therefore each molecule has a large number of neighbours in the solvation sphere. We compare the effects of selecting α values between zero and 0.3 in intervals of 0.025. We decompose the energy interactions into pairwise group contributions to the total Coulombic energy for CH₄ in carbon dioxide, and CH₂F₂ in carbon dioxide. The relationship between α and the accuracy of the Wolf summation method is shown in Fig. 2.

Fig. 2 Percentage error in Coulombic energy between PPPM and Wolf with respect to α for CH₄/CO₂ and CH₂F₂/CO₂ binary mixtures for χ(solute) = 0.1 at 308.2 K, 80 atmospheres. The results are decomposed into (a) (CH₂F₂) CO₂–CO₂ pair errors (B) (CH₂F₂) CH₂F₂–CH₂F₂ pair errors, (c) (CH₂F₂) CO₂–CH₂F₂ pair errors, (d) (CH₄) CO₂–CO₂ pair errors, (e) (CH₄) CH₄–CH₄ pair errors and (f) (CH₄) CO₂–CH₄ pair errors. The black squares and error bars indicate the average error and uncertainty for a half box cut-off, whilst the empty squares show the average error for a quarter box cut-off.

We observe for half box cut-offs the best agreement for Wolf is at low values of α, where for both the polar and non-polar systems the optimum value for α is 0.075. For non-polar systems increasing α beyond 0.2 results in an ∼2–3% error (with respect to the PPPM Coulombic energy), whilst for the polar system the average error is ∼20%. The non-polar CH₄/CO₂ system resulted in the lowest average errors of 0.05% for CO₂–CO₂ interactions, 0.39% for CO₂–CH₄ and 0.34% for CH₄–CH₄. We observe a similar trend for the polar system of CO₂/CH₂F₂ with increased average errors of 0.44% for CO₂–CO₂, 0.47% for CO₂–CH₂F₂ and 0.67% for CH₂F₂–CH₂F₂. At α = 0.075 the greatest variance in the non-polar system is σ² = 0.2 for CH₄–CH₄, and for the polar system the maximum variance is σ² = 2.94 for CH₂F₂–CH₂F₂.

A quarter box cut-off gives greater errors in the Coulombic energies, but follows the same trends as the half box cut-off. For the non-polar system the optimum value for α is 0.05, which is seen for all pair interactions of methane and carbon dioxide.

The average error increases to 0.5% for CO₂–CO₂ and to ∼0.75% for energies involving interactions with methane. The errors vary more when used with the polar system over a wide range of α, but at α = 0.075 the error for all interactions is below 2%. The error increases sharply for the polar system with varying α. For interactions between CH₂F₂–CH₂F₂ the variance is higher than for methane, which can be attributed to the high polarity of both substituents.

3.2 Pure carbon dioxide

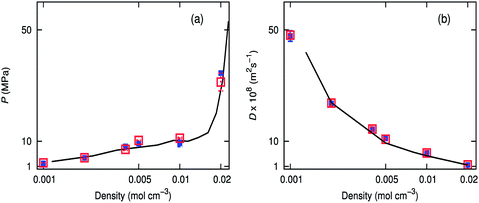
Diffusion coefficients of scCO₂ calculated from MD simulations using the Ewald sum⁵⁰ have been previously compared with experimental results.⁵¹ Our simulations show that the Wolf method gives diffusion coefficients comparable to that of PPPM (Fig. 3b). Calculations were concurrently run on the CPU using the Wolf method, and the energies were within three decimal places. Simulations were also performed at 323.2 K, which show good agreement between PPPM and the Wolf method.† Low density boxes using the Wolf method show the best agreement, but all the densities investigated are within the bounds of error of PPPM. Pressures obtained over a range of densities coincide well with an equation of state,⁵² for both the Wolf and PPPM implementations (Fig. 3a). Both electrostatic methods capture the PVT relationship properties at high and low densities, for both temperatures studied.

Fig. 3 (a) Diffusion coefficients for pure carbon dioxide obtained for PPPM (empty red squares) and Wolf (filled blue squares), compared with experimental (black line) at 308.2 K. b) PVT relationship of pure carbon dioxide simulated using PPPM (empty red squares) or the Wolf method (filled blue squares) compared with experimental (black line) at 308.2 K.

3.3 Binary mixture of carbon dioxide with difluoromethane or methane

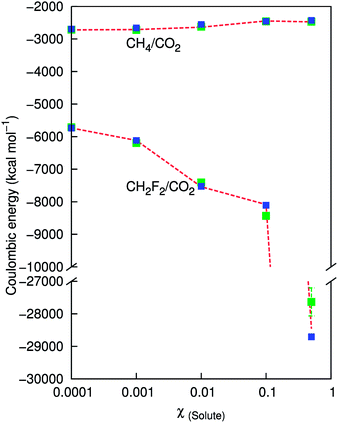
The Coulombic energy for the polar systems is compared for different mole fractions of difluoromethane using the Wolf method and PPPM. As the system becomes more polar, the error of the Wolf method with respect to the PPPM value becomes greater. Fig. 4 shows the total PPPM Coulombic energy, and results for α = 0.2 and α = 0.075. For the system containing 100 difluoromethane molecules, the error is within 0.2% and 1.8% for α = 0.075 and α = 0.2 respectively. As the composition tends towards a 1 : 1 ratio, the errors increase, which indicates, as anticipated, that the Wolf approach is not suitable when the system becomes highly polar. The errors for α = 0.075 are reasonable (0.9%) but for α = 0.2 the errors are 3%. We observe better agreement for methane. For the 1 : 1 binary mixture, the error in α = 0.2 is 1.8% and α = 0.075 is 0.15%. The total Coulombic energy for difluoromethane is more negative than for methane, which can be explained by NPT dynamics resulting in a lower volume box and therefore closer contacts.

Fig. 4 Total Coulombic energy for methane and difluoromethane in carbon dioxide at 308.2 K, 80 atmospheres. The dashed red line indicates the total PPPM energy, whilst the green squares indicate α = 0.2 and the blue squares indicate α = 0.075.

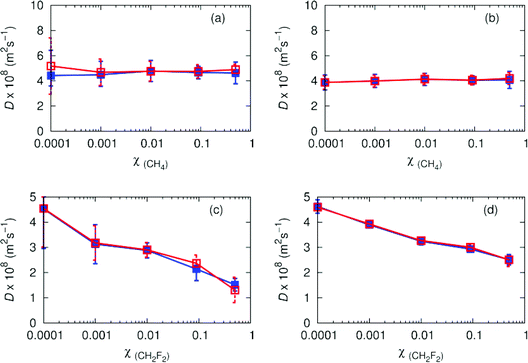
Experimental results from O'Hern and Martin⁵¹ indicate pure carbon dioxide has a diffusion coefficient of 5 (× 10⁸ m² s⁻¹) at 308.2 K, 80 atmospheres. The non-polar binary mixture of CH₄/CO₂ has a diffusion coefficient of ∼5 (× 10⁸ m² s⁻¹) for the inclusion of one methane molecule in 10 000 molecules of carbon dioxide (Fig. 5). As the number of methane molecules increases, the overall diffusion coefficients remain relatively constant. Diffusion coefficients for CH₄ and carbon dioxide are similar, with an average increase of ∼0.6 (× 10⁸ m² s⁻¹) between carbon dioxide and CH₄. As χ_(solute) increases, the accuracy of the solute diffusion coefficients increase, due to better averaging from more solute molecules. With the exception of χ_(solute) = 0.0001 where averaging is poor, the agreement between Wolf and PPPM is good. We observe a reduction in diffusion coefficients for difluoromethane as the polarity increases. The values decay from 4.5 (× 10⁸ m² s⁻¹), to 1.3 (× 10⁸ m² s⁻¹), which can be attributed to favourable interactions between solute and solvent. Agreement between Wolf and PPPM is good, although there is an observable increase in the error in the diffusion coefficients for difluoromethane when the fraction of solute reaches 10%. This indicates the difluoromethane interacts strongly with carbon dioxide, thus limiting diffusion.

Fig. 5 Diffusion coefficients for (a) CH₄ in CO₂/CH₄ (B) CO₂ in CO₂/CH₄ (c) CH₂F₂ in CO₂/CH₂F₂ and (d) CO₂ in CO₂/CH₂F₂ at 308.2 K, 80 atmospheres. Filled blue squares and error bars indicate diffusion coefficients obtained using PPPM, and empty red squares and error bars indicate diffusion coefficients obtained using the Wolf summation method.

To characterise the interactions between difluoromethane and carbon dioxide, we calculate the radial distribution (RDF) between the centre of mass for CH₄/CO₂ and CH₂F₂/CO₂ (Fig. 6) and the associated residence times and coordination numbers are shown in Table 2.

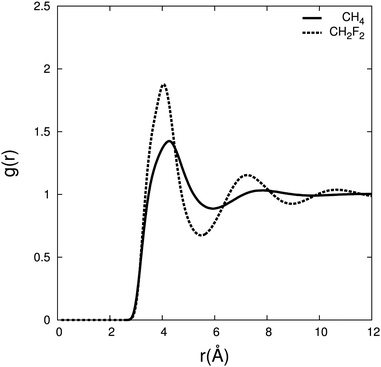Fig. 6 Radial distribution function between the centre of mass of carbon dioxide and CH₄ (solid line), and CH₂F₂ (dashed line) for χ_(solute) = 0.1 at 308.2 K, 80 atmospheres.

Table 2 Residence times and coordination for the centre of mass of carbon dioxide in CH₄ and CH₂F₂ for χ_(solute) = 0.1 at 308.2 K, 80 atmospheres

Shell	Distance limit (Å)	Residence time – Wolf (ps)	Residence time – PPPM (ps)	Coordination number - Wolf	Coordination number - PPPM
Methane
1^st	0.00–5.95	1.2	1.2	8.6	8.6
1^st + 2^nd	0.00–9.60	2.6	2.5	37.2	37.1
2^nd	5.95–9.60	1.3	1.3	28.6	28.5
Difluoromethane
1^st	0.00–5.65	4.6	4.6	12.1	12.1
1^st + 2^nd	0.00–9.24	10.5	10.3	55.6	55.6
2^nd	5.65–9.24	5.9	5.7	45.5	45.5

---

The RDF shows a larger density of carbon dioxide molecules in the difluoromethane mixture in the first and second solvation shell compared to methane. The same trend was noticed in the RDF by Do et al.,⁵³ where the first solvation shell has a higher density for difluoromethane than for methane. The number of carbon dioxide molecules present in the first and second solvation shells is ∼30% higher for difluoromethane, and carbon dioxide resides about four times longer compared to methane. This indicates that carbon dioxide has a higher affinity for difluoromethane.

4. Conclusions and discussion

The Wolf method shows good agreement with PPPM when modelling the electrostatic interactions of scCO₂ on GPUs for non-polar systems, whilst being approximately twice as fast. The choice of α is important, and may need to be investigated on a case by case basis to enable satisfactory agreement. For modelling carbon dioxide in the supercritical region it is advisable to use a half-box cut-off and a low value for α. In this investigation, all values of α less than 0.15 produced errors less than 2% for non-polar interactions, whilst polar interactions require α to be less than 0.1. Upon increasing the polarity of the system, the potential begins to degrade. Errors of the Wolf method with respect to PPPM are approximately 0.2% when considering a 100 : 1 mixture of carbon dioxide and difluoromethane with α = 0.075. We observe a strong affinity of carbon dioxide to difluoromethane compared to methane, which can be seen by a decline in diffusion coefficients with increasing mole fraction of solute. Carbon dioxide resides about four times longer in the solvation sphere of difluoromethane compared to methane.

We can conclude that the significance of using the Wolf method on GPUs allows simulations to reach timescales twice as long as those run with PPPM, without significant loss in accuracy for a carefully chosen value of α for non-polar and mildly polar systems. We aim to follow up the investigation with further analysis of solvent–solute interactions and the study of fluorinated polymers, which have high solubilities in scCO₂. We will be investigating the free energy changes of fluorinated polymers, with an aim of further understanding the high affinity of fluorous polymers for carbon dioxide. Many free energy methods require long timescales in order to reach convergence; utilizing the Wolf method for this purpose will help achieve this goal.

Acknowledgements

This work was supported by the EPSRC, grants EP/I006559/1 and EP/K000128/1. We are grateful for access to the University of Nottingham High Performance Computing facility and MidPlus High Performance Computing facility. We appreciate useful discussions with Professor Paul Kelly and his co-workers (Imperial College) and Dr Chris Skylaris (University of Southampton). We thank Drs Richard Wheatley and Hainam Do for their critical reading of the manuscript.

References

1. J. E. Stone, J. C. Phillips, P. L. Freddolino, D. J. Hardy, L. G. Trabuco and K. Schulten, J. Comput. Chem., 2007, 28, 2618.
2. I. Buch, M. J. Harvey, T. Giorgino, D. P. Anderson and G. De Fabritiis, J. Chem. Inf. Model., 2010, 50, 397.
3. J. A. Baker and J. D. Hirst, Mol. Inf., 2011, 30, 498.
4. M. J. Harvey and G. De Fabritiis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 734.
5. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989.
6. W. F. van Gunsteren and H. J. C. Berendsen, Angew. Chem., Int. Ed. Engl., 1990, 29, 992.
7. M. Bergdorf, C. Peter and P. H. Hünenberger, J. Chem. Phys., 2003, 119, 9129.
8. B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187.
9. P. P. Ewald, Ann. Phys., 1921, 369, 253–287.
10. R. Hockney and J. Eastwood, Computer Simulation Using Particles, CRC Press, 1981.
11. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089.
12. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577.
13. M. J. Harvey and G. De Fabritiis, J. Chem. Theory Comput., 2009, 5, 2371.
14. W. M. Brown, A. Kohlmeyer, S. J. Plimpton and A. N. Tharrington, Comput. Phys. Commun., 2012, 183, 449.
15. D. J. Hardy, J. E. Stone and K. Schulten, Parallel Comput., 2009, 35, 164.
16. D. Wolf, P. Keblinski, S. R. Phillpot and J. Eggebrecht, J. Chem. Phys., 1999, 110, 8254.
17. C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104.
18. J. S. Hansen, T. B. Schrøder and J. C. Dyre, J. Phys. Chem. B, 2012, 116, 5738.
19. T. D. Nguyen, J.-M. Y. Carrillo, A. V. Dobrynin and W. M. Brown, J. Chem. Theory Comput., 2013, 9, 73.
20. H. Peker, M. P. Srinivasan, J. M. Smith and B. J. McCoy, AIChE J., 1992, 38, 761.
21. Z. Li and C. K. Hall, Langmuir, 2005, 21, 7579.
22. J. Jennings, M. Beija, A. P. Richez, S. D. Cooper, P. E. Mignot, K. J. Thurecht, K. S. Jack and S. M. Howdle, J. Am. Chem. Soc., 2012, 134, 4772.
23. H. Lee, E. Terry, M. Zong, N. Arrowsmith, S. Perrier, K. J. Thurecht and S. M. Howdle, J. Am. Chem. Soc., 2008, 130, 12242.
24. Z. Wimmer and M. Zarevúcka, Int. J. Mol. Sci., 2010, 11, 233.
25. A. Gießauf and T. Gamse, J. Mol. Catal. B: Enzym., 2000, 9, 57.
26. R. L. Silveira, J. Martínez, M. S. Skaf and L. Martínez, J. Phys. Chem. B, 2012, 116, 5671.
27. H.-L. Liu, W.-C. Hsieh and H.-S. Liu, Biotechnol. Prog., 2004, 20, 930.
28. W. Leitner, Acc. Chem. Res., 2002, 35, 746.
29. D. J. Heldebrant and P. G. Jessop, J. Am. Chem. Soc., 2003, 125, 5600.
30. D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058.
31. Z. Su and M. Maroncelli, J. Chem. Phys., 2006, 124, 164506.
32. J. M. Desimone, Z. Guan and C. S. Elsbernd, Science, 1992, 257, 945.
33. S. P. Nalawade, F. Picchioni and L. P. B. M. Janssen, Prog. Polym. Sci., 2006, 31, 19.
34. A. Dardin, J. M. DeSimone and E. T. Samulski, J. Phys. Chem. B, 1998, 102, 1775.
35. A. Sadeghifar, M. Dadvar, S. Karimi and A. F. Ghobadi, J. Mol. Graphics Modell., 2012, 38, 455.
36. A. Angoshtari and A. Yavari, Phys. Lett. A, 2011, 375, 1281.
37. S. Plimpton, J. Comput. Phys., 1995, 117, 1.
38. A. D. MacKerell, D. Bashford, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586.
39. J. G. Harris and K. H. Yung, J. Phys. Chem., 1995, 99, 12021.
40. B. J. Palmer and J. L. Anchell, J. Phys. Chem., 1995, 99, 12239.
41. J. Kolafa and J. W. Perram, Mol. Simul., 1992, 9, 351.
42. M. Deserno and C. Holm, J. Chem. Phys., 1998, 109, 7694.
43. W. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
44. NVIDIA, CUDA Dynamic Parallelism Programming Guide, 2012.
45. W. C. Swope, J. Chem. Phys., 1982, 76, 637.
46. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684.
47. X. Michalet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041914.
48. Y. Iwai, H. Higashi, H. Uchida and Y. Arai, Fluid Phase Equilib., 1997, 127, 251.
49. S. Nosé and M. L. Klein, Mol. Phys., 1983, 50, 1055.
50. H. Higashi and K. Tamura, Mol. Simul., 2010, 36, 772.
51. H. A. O'Hern and J. J. Martin, Ind. Eng. Chem., 1955, 47, 2081.
52. R. Span and W. Wagner, J. Phys. Chem. Ref. Data, 1996, 25, 1509.
53. H. Do, R. J. Wheatley and J. D. Hirst, J. Phys. Chem. B, 2010, 114, 3879.

---

Footnote

† Electronic Supplementary Information (ESI) available: See DOI: 10.1039/c4fd00012a

---