A multi-constituent site blocking model for nanoparticle and stabilizing agent transport in porous media†
Matthew D.
Becker
,
Yonggang
Wang
,
Kurt D.
Pennell
and
Linda M.
Abriola
*
Department of Civil and Environmental Engineering, Tufts University, 200 College Avenue, Medford, Massachusetts 02155, USA. E-mail: Linda.Abriola@tufts.edu; Fax: +1 (617) 627 3819; Tel: +1 (617) 627 3237
First published on 16th December 2014
Abstract
A quantitative understanding of the potential influence of engineered and natural stabilizing agents on the transport behavior of engineered nanomaterials will be crucial to assessing their environmental fate. Column transport experiments conducted with CdSe/ZnS quantum dot nanocrystals (QD) stabilized with poly-(acrylic-acid)–octylamine (PAA–OA) yielded retention profiles that exhibited increased retention with distance from the inlet, a trend which could not be reproduced by existing nanoparticle transport models. To address this shortcoming, a new Multi-Constituent Site-Blocking (MCB) model was developed and implemented to simulate coupled transport and retention of nanoparticles and stabilizing agents. Mass balance equations for solution constituents are linked through a Langmuir-type blocking term that accounts for the surface area occupied by each constituent. The model successfully reproduced experimental observations of delayed QD breakthrough and retention profiles. These results support the hypothesis that stabilizing agents present in the nanoparticle suspension inhibit deposition, facilitating enhanced nanoparticle mobility in the columns. Inter-model comparisons and model sensitivity analyses examine the dependence of nanoparticle mobility on the relative concentration and adsorption properties of the stabilizing agents. Modeling results indicate that both synergistic and competitive interactions between nanomaterials and stabilizing agents should be accounted for in order to accurately predict nanoparticle transport behavior in subsurface environments.
Nano impactTo improve stability, nanoparticle suspensions are often amended with surfactants or polymers, compounds that could significantly influence nanoparticle mobility in the subsurface. In the present work, a mathematical model is developed to describe a competitive attachment/adsorption process between quantum dot (QD) nanoparticles and residual polymer coating molecules which were left over from the QD synthesis process. The developed model successfully captured column transport and deposition results that were not describable by traditional nanoparticle transport models. These results offer a new conceptual framework to quantitatively describe the influence of stabilizing agents on nanoparticle transport in porous media and provide insights into the potential for these and other aqueous co-constituents to influence nanoparticle fate in the environment. |
1. Introduction
Many nanotechnology applications employ surfactants or polymers to promote the stability of nanoparticles in aqueous suspensions.1–6 These stabilizing agents have been shown to enhance nanoparticle transport in porous media.7–15 While the general influence of such stabilizing agents has been well-documented, prediction of nanoparticle suspension behavior in porous media remains challenging due to the complex interactions between nanoparticles, co-constituents, and solid surfaces. For example, in a series of packed sand column transport experiments employing polyacrylic acid–octylamine copolymer (PAA–OA)-stabilized CdSe/ZnS quantum dot nanocrystals (QD),6,16–18 lower QD retention was observed in the vicinity of the column inlet.19 This behavior was inconsistent with expectations based upon traditional nanoparticle transport theory.19 After ruling out alternative hypotheses, including the presence of particle detachment or preferential flow paths, the authors attributed this anomalous attachment behavior to the blocking of QD attachment sites by residual PAA–OA molecules in solution. An additional QD–PAA–OA transport experiment, conducted in a sand column pretreated with PAA–OA, yielded complete elution of the nanoparticles, further supporting this hypothesis.Despite experimental observations of co-constituent-enhanced nanoparticle transport in porous media, traditional nanoparticle transport modeling approaches have neglected the potential influence of co-constituents on particle deposition. In the chemical and environmental engineering literatures, nanoparticle transport in porous media is typically modeled using approaches based upon clean-bed filtration theory (CFT).20 CFT conceptualizes particle deposition to the solid phase as a two-step process involving 1) particle transport to the vicinity of the solid medium or “collector” surface and 2) particle attachment governed by attractive and repulsive forces between particles and solid surfaces. The former, quantified as a collector efficiency, is controlled by physical properties such as flow velocity, grain size, nanoparticle size, and porosity,21 while the latter is largely determined by surface chemistry and is typically quantified with a system collision efficiency factor.22 An enhancement of the CFT, termed the modified filtration theory (MFT), assumes that particles attach to the solid phase by a similar two-step deposition process, but also incorporates a solid phase retention capacity. This single-constituent kinetic model has been demonstrated capable of simulating nanoparticle transport in a wide variety of systems.23–26 However, neither the CFT nor MFT model accounts for the influence of secondary constituents on nanoparticle deposition. In addition, neither model is capable of simulating non-monotonic retention behavior, which has been observed in a variety of colloid-porous media systems.27,28
A few recent modeling studies have attempted to incorporate the influence of nanoparticle coatings on deposition behavior by expressing nanoparticle–surface interaction energies and system collision efficiencies in the CFT model as functions of coating molecules.7,29,30 Although these studies provide valuable information regarding the influence of adsorbed nanoparticle coatings on nanoparticle deposition trends in porous media, this modeling approach fails to capture observed departures from CFT,7,19,23 namely late and asymmetrical breakthrough curves. In addition, by considering only nanoparticle-adsorbed molecules, these studies neglect the potential influence of free aqueous co-constituents that adsorb onto the porous medium. Single-constituent kinetic models, although traditionally invoked to simulate nanoparticle transport and deposition, are inherently unable to capture the competitive attachment and adsorption behavior that may be encountered in multi-component aqueous systems. To date, only one modeling study has explored the influence of free aqueous co-constituent molecules on nanoparticle transport.14 In that work, the influence of free aqueous Tween 80 surfactant on nC60 fullerene transport was modeled by coupling two mass balance equations, one for each constituent. However, the model only considered the inhibition of nC60 attachment by steric repulsion arising from adsorbed Tween 80 on sand surfaces and did not incorporate direct competition between suspended nanoparticles and surfactant molecules for available attachment sites.
Motivated by the need for more comprehensive mathematical models and an improved understanding of the influence of stabilizing agents on nanoparticle transport behavior, the present work builds on the experimental observations of Wang et al.19 to develop a mathematical model capable of reproducing QD–PAA–OA transport behavior for a range of flow conditions and porous media. Based upon traditional approaches for simulating macro-scale nanoparticle transport in porous media, a modified first-order kinetic model is developed to simulate co-transport of QDs and the stabilizing PAA–OA additives. Additional column experiments are undertaken for the QD–PAA–OA system to support model refinement and validation. A model sensitivity analysis is then used to examine the influence of PAA–OA concentration and adsorption properties on QD transport and retention behavior.
2. Experimental methods
2.1. QD–PAA–OA column experiments
Experimental procedures followed in this work are similar to those described in Wang et al.19 Briefly, for QD–PAA–OA transport experiments, borosilicate glass columns (2.5 cm i.d. × 10 cm length) were dry packed with either 40–50 mesh (CS) or 80–100 mesh (MS) Ottawa sand (U.S. Silica, Berkeley Springs, WV). The dry-packed columns were purged with CO2 gas and flushed with at least 10 pore volumes (PVs) of degassed 3 mM NaCl solution at pH 7. A non-reactive tracer (3 mM NaBr) test was then conducted to access the hydrodynamic dispersion and flow conditions of each column. Prior to column transport experiments, QD hydrodynamic diameter and zeta potential were measured using a ZetaSizer Nano ZS analyzer (Malvern Instruments Ltd., Southborough, MA, USA) operated in noninvasive back scattering mode at an angle of 173°. The concentration of residual aqueous PAA–OA in QD–PAA–OA stock suspensions was determined using a total organic carbon analyzer (TOC-500A, Shimadzu Scientific Instruments, Columbia, MD, USA) following separation by centrifugation at 5000 rpm for 30 min. A pulse (2–3 PVs) of aqueous QD suspension (ca. 6 × 1015 particles L−1, 10 nM) was introduced into the water-saturated column (ionic strength of 3 mM NaCl and pH of 7), followed by 3 PV of background electrolyte solution to elute QDs remaining in suspension within the porous media. The QD transport experiments (CS-L and MS-L) were performed in an up-flow mode at a flow rate of 0.1 mL min−1 (L), which corresponds to a Darcy velocity of ca. 0.28 m d−1. Effluent samples were collected to produce breakthrough curves, and the columns were sectioned into eight increments to produce solid phase QD deposition profiles.19,242.2. PAA–OA only column experiments
To characterize the transport of PAA–OA in sand, two replicate column experiments were conducted in the coarser sand (PAA-CS-HA and PAA-CS-HB). Following column preparation, a pulse (3 PV) of PAA–OA solution (50 mg PAA–OA/L, 3 mM NaCl, pH 7, free of QDs) was introduced into a column packed with 40–50 mesh Ottawa sand at a flow rate of 1.0 mL min−1 (H). PAA–OA effluent concentrations were measured using an organic carbon analyzer (TOC-VCPH, Shimadzu, Marlborough, MA). To enhance the measurement accuracy, two 4-point calibration curves with concentrations ranging from 0 to 3.125 and from 0 to 50 mg PAA–OA/L were prepared. The method detection limit was 0.6 mg PAA–OA/L based on the method of Hubaux and Vos.312.3. PAA–OA pretreated column experiment
Finally, to explore the influence of PAA–OA pre-treatment on QD–PAA–OA transport, an additional column experiment (PRE-MS-H) was conducted in 80–100 mesh Ottawa sand at a flow rate of 1.0 mL min−1. The general experimental procedures described above were followed, with the exception that the column was preflushed with approximately 3 PVs of PAA–OA solution (430 mg PAA–OA/L, 3 mM NaCl, and pH 7), followed by 10 PVs of background electrolyte to remove any remaining aqueous PAA–OA prior to introducing the QD–PAA–OA suspension.A total of five column experiments were performed in this work, as summarized in Table 1. Data from three additional QD–PAA–OA transport experiments (CS-H, MS-H and FS-H), which were conducted at a flow rate of 1.0 mL min−1, were obtained from Wang et al.19 and are included in Table 1.
| Columna | Experimental parameters | ||||||
|---|---|---|---|---|---|---|---|
| d c (mm) | θ w (−) | v p (m d−1) | α L (mm) | PWf(−) | Retg(%) | MBh(%) | |
| a MS – medium sand (80–100 mesh), FS – fine sand (100–140 mesh), CS – coarse sand (40–50 mesh), H – high flow rate (1.0 mL min−1), L – low flow rate (0.1 mL min−1), PRE – PAA–OA pre-conditioning, PAA – PAA–OA only, A and B indicate duplication. b Mean sand grain diameter. c Volumetric water content. d Pore water velocity. e Longitudinal dispersivity. f QD pulse width. g Retention. h Mass balance. *Experiment presented in Wang et al.19 | |||||||
| CS-L | 0.354 | 0.37 | 0.8 | 0.57 | 3.0 | 30.5 | 94.1 |
| MS-L | 0.163 | 0.38 | 0.8 | 0.67 | 3.1 | 77.2 | 104.0 |
| PRE-MS-H | 0.163 | 0.38 | 7.4 | 0.63 | 3.0 | 0.3 | 98.2 |
| PAA-CS-HA | 0.354 | 0.36 | 7.3 | 0.68 | 3.1 | NA | 99.5 |
| PAA-CS-HB | 0.354 | 0.36 | 7.3 | 0.68 | 3.2 | NA | 95.4 |
| CS-H* | 0.354 | 0.37 | 7.7 | 0.68 | 2.0 | 24.7 | 102.8 |
| MS-H* | 0.163 | 0.39 | 7.3 | 0.63 | 3.0 | 38.3 | 105.6 |
| FS-H* | 0.125 | 0.39 | 7.3 | 0.65 | 3.0 | 99.1 | 100.7 |
3. Mathematical model
3.1. Constituent balance equations
Following the approach of Li et al.,23,24 a coupled system of one-dimensional aqueous phase transport and solid phase-associated mass balance equations, which represents deposition as a modified first order process, was used to describe constituent (nanoparticle or copolymer) transport: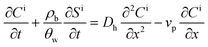 | (1) |
 | (2) |
Here Ci is the concentration of constituent i, QD or PAA–OA, in the aqueous suspension (M/L3); Si is the solid-phase concentration of constituent i (M/M); t is time (t), x is distance from the column inlet (L); vp is the average pore-water velocity (L/t), assumed constant under the homogeneous packing conditions of the experiments; Dh is the hydrodynamic dispersion coefficient for the column (L2/t), ρb is the bulk density of the porous medium (M/L3); and θw is the porosity. In this formulation, transport of each constituent (nanoparticle and copolymer) is modeled by a separate equation pair, an approach that has often been used to simulate the interdependent behavior of a multi-component mixture.10,14,32–34 Two types of solid phase interaction terms are represented by the terms on the right hand side of eqn (2), attachment/detachment of nanoparticles (QDs) and sorption/desorption of copolymer (PAA–OA), each represented by first-order rate expressions;24,35,36 thus, kia is a first-order removal rate for constituent i due to physical attachment or preferential adsorption (1/t) and kid is a first-order detachment or desorption rate. Equation pairs (eqn (1) and (2)) for each constituent are coupled through Ψ, a site blocking function (M/M), assumed to depend upon the solid phase-associated mass of both constituents. In previous (single species) nanoparticle deposition modeling studies, Ψ has been represented as:24
 | (3) |
3.2. Model implementation
The mathematical model, represented by the coupled system of eqn (1) and (2) for each constituent and an expression for Ψ, was implemented using a central-in-space and fully implicit-in-time finite difference scheme in MATLAB R2010a (The MathWorks, Natick, MA).23 Third-type boundary conditions were applied for each constituent at the column inlet, consistent with experimental conditions, and a zero-dispersive-flux condition was implemented at the column outlet. In this scheme, the transport and solid-phase interaction equations for each constituent are solved sequentially; within a given time step k, PAA–OA transport and deposition equations are solved first, followed by solution of QD transport and deposition equations. At time level k, the blocking function Ψ for each constituent is evaluated using information from the previous time level k-1, and the time step size is chosen to be small enough to minimize the error cause by the time-lagged evaluation of Ψ.3.3. Model parameter estimation and fitting
Results of non-reactive tracer tests were used to confirm uniform flow conditions and to estimate the hydrodynamic dispersion coefficient (Dh) for each column experiment by fitting measured breakthrough data to a one dimensional form of the advection–dispersion transport equation using the model CXTFIT.37 The free PAA–OA concentration in the injected QD solutions (C0,PAA) was estimated based upon dilution ratios of the stock solution used in all experiments.Attachment/sorption rate and capacity parameters were estimated by fitting model predictions to experimental breakthrough curves and corresponding retention profiles using a least-squares optimization procedure. Here, the MATLAB R2010a (The MathWorks, Natick, MA) function lsqnonlin was implemented with the following objective function:
 | (4) |
Eqn (4) allows the user to fit breakthrough (ExpBTC) and retention (ExpRET) data independently or simultaneously, depending upon the selection of the two weighting factors, β and γ. In this study, these two factors were fixed for each experiment at values equal to the fraction of the total constituent mass observed in the effluent and retained by the porous medium, respectively (i.e. β + γ = 1). Optimization was performed for three fitting parameters, QD attachment rate (kQDa), QD retention capacity (SQDmax), and PAA–OA adsorption rate (kPAAa). Confidence intervals (95%) for each fitted parameter were calculated using the MATLAB R2010a function nlparci, which assumes an asymptotic normal distribution about each estimated parameter.
4. Results and discussion
4.1. QD transport and retention
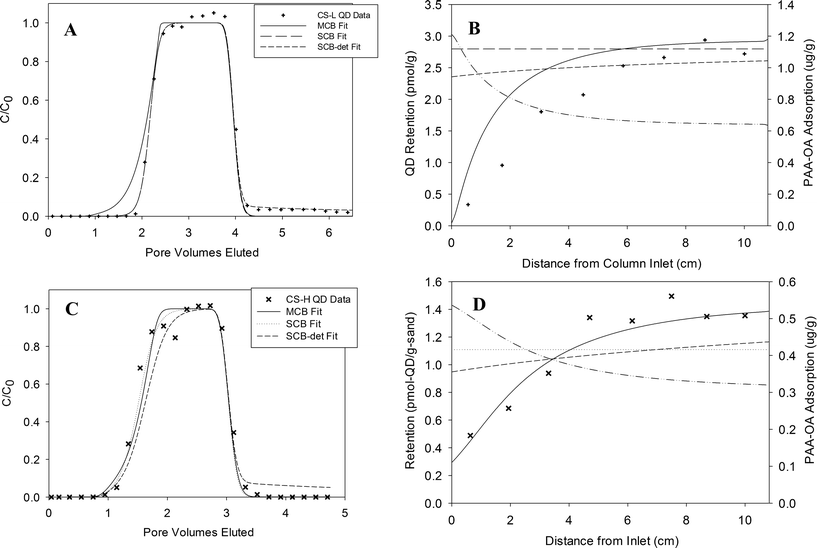
Measured effluent concentrations of PAA–OA coated QDs following pulse injections of ca. 4 PVs of a 10 nM QD–PAA–OA suspension (3 mM NaCl, pH 7) through columns packed with either 40–50 mesh or 80–100 mesh Ottawa sand at a flow rate of 0.1 mL min−1 (pore-water velocity = 0.8 m d−1) are shown in Fig. 1A (symbols). Effluent concentration data are plotted as breakthrough curves (BTCs), where the y-axis represents the normalized effluent concentration (C/C0, where C0 is the applied influent concentration and C is the measured effluent concentration) and the x-axis represents dimensionless time expressed as pore volumes, equivalent to the volume of fluid injected divided by the total pore volume of the column. The measured BTCs (Fig. 1A, symbols) exhibited delayed breakthrough (ca. 2 PV), an asymmetrical shape, and no observable tailing after the injected QD pulse had eluted from the column (ca. 4–4.5 PVs). The corresponding QD retention profiles obtained for 40–50 and 80–100 mesh Ottawa at a flow rate of 0.1 mL min−1, plotted as solid-phase concentration versus distance from the column inlet, are shown in Fig. 1B (symbols). Both retention profiles exhibited the lowest solid phase QD concentrations near the column inlet, and increasing QD concentrations with travel distance. These trends are consistent with QD breakthrough and retention data obtained by Wang et al.19 for column experiments conducted at a higher flow rate (1 mL min−1) in the same sands, as depicted in Fig. 1C and D (symbols). The conditions for each column experiment, as well as the percent of applied QD mass retained within the column and overall mass balance (i.e., sum of eluted and retained mass relative to the total applied mass), are summarized in Table 1. The QD mass balance of all transport experiments was between 94.1% and 105.6%, indicating nearly complete mass recovery in all cases. At ionic strength of 3 mM as NaCl and pH 7, QD zeta potential and hydrodynamic diameter were measured to be −45.8 ± 1.8 mV and 30.8 ± 2.6 nm, respectively.19 | ||
| Fig. 1 MCB model fits (lines) to effluent breakthrough (A and C) and retention profiles (B and D) for QD transport experiments in saturated columns packed with sands of various grain sizes under low (~0.8 m d−1; A and B) and high (~8 m d−1; C and D) flow conditions. Symbols represent experimental data from each QD–PAA–OA column experiment (Table 1). | ||
Inspection of the nanoparticle breakthrough curves reveals a gradual rise to a plateau, followed by a sharp decline in relative concentration after elution of the injected pulse. In addition, the fraction of mass eluted from the column decreases with decreasing flow rate and sand grain size. This behavior has been demonstrated to be the result of a limited attachment capacity, and is consistent with retention capacity modified kinetic models of nanoparticle transport through water-saturated porous media.11,23–25 However, the measured retention data are not consistent with these models, which predict retention profiles characterized by the largest solid-phase concentrations near the column inlet and a decrease in particle retention with distance from the injection point. A more detailed description of the discrepancies between these experimental trends and traditional single species, first-order kinetic modeling approaches is provided in Wang et al.19 These experimental deposition trends, however, are consistent with the presence of surface area blocking by a co-constituent in the nanoparticle suspension that outcompetes nanoparticles for attachment sites. By design, the PAA–OA copolymers preferentially adsorb to the hydrophobic QD shell that protects the water-soluble core from aqueous dissolution.6,16–18 However, because it is virtually impossible to completely remove all free copolymer from the solution following the synthesis process, some residual aqueous PAA–OA will remain in solution with the suspended QDs.19 Here, we hypothesize that residual PAA present in the aqueous QD suspension rapidly adsorbs onto the sand, effectively competing with QD nanoparticles for sites that would otherwise be available for deposition. Since the residual PAA–OA concentration in the injected suspension was relatively low (ca. 2 mg L−1, Table S2†), this effect would be most apparent near the column inlet, as is supported by the data shown in Fig. 1 and 2. Additional evidence of this blocking effect is provided by Wang et al.,19 who found that when 40–50 mesh Ottawa sand was preflushed with a 3 PV pulse of PAA–OA solution (400 mg L−1), minimal QD retention was subsequently observed, confirming the “blocking” effect of adsorbed PAA–OA.
4.2. Mathematical development of multi-constituent blocking function, Ψ
The Ψ term in eqn (2) couples the two systems of balance equations and represents the influence of existing attached or sorbed mass on the availability of sites for additional aqueous–solid phase interaction. Based on the experimental results described above, an appropriate expression for the blocking function, Ψ, was sought to account for the competition of residual PAA–OA for attachment sites.The simplest approach to develop an expression for the competitive blocking function is to assume that all sites are equivalent (a “one-site” model), that is, all of the solid surface area available for QD attachment is also available for PAA–OA adsorption and neither constituent can adsorb to occupied surface area. Because the QD nanoparticles are coated with adsorbed copolymer, it is reasonable to assume that coated QDs and free PAA–OA copolymer molecules have affinity for similar locations on the solid surface. Thus, the one-site model was employed herein.
The total surface area available for attachment/sorption can be expressed as:
| Atotal = AQD + APAA–OA + Aopen | (5) |

| (6) |
 | (7) |
Here, it is assumed that Ψ is a continuous function of fractional surface area in space and time. For the “one-site” model, the areas represented by the particle retention capacity and the polymer adsorption capacity are equivalent and equal to Atotal.
Area scaling factors for QDs (τ) and PAA–OA copolymer (ζ) were developed, based upon molecular size considerations, to relate solid phase concentration to sand surface area occupied by the QDs and PAA–OA molecules. A derivation of these parameters is provided in the ESI.† Using τ and ζ, Ψ can be written in terms of a single maximum retention capacity SQDmax as:
 | (8) |
Similar to the blocking function shown in eqn (3),24 the value of Ψ ranges from 0 to 1, where Ψ = 1 indicates unlimited area available for QD attachment or PAA–OA adsorption and Ψ = 0 indicates that all available area is blocked by solid-phase QDs or PAA–OA molecules. As the available area for deposition is depleted by attachment/sorption of either constituent, Ψ will decrease, thereby scaling each component's first order deposition rate constant, kia. The mathematical model represented by eqn (1), (2), and (8) is referred to as the multi-constituent site-blocking (MCB) model below.
4.3 Mathematical modeling
Application of the MCB model to the QD–PAA–OA column data requires specification of a number of parameters that quantify system flow and transport properties. For each column experiment, velocity, porosity, pulse width, hydrodynamic dispersivity, and mean grain size were determined by direct measurement or estimated by fitting to independent non-reactive tracer tests (Table 1). Parameters that account for solid phase-constituent interactions, however, could not be estimated a priori and must be determined by inverse modeling. These parameters include QD and PAA attachment/adsorption and detachment/desorption rate parameters and the maximum retention capacity: kQDa, kQDd, kPAAa, kPAAd, and SQDmax. Based on the absence of tailing in the QD effluent breakthrough curves (Fig. 1A), kQDd was assumed to be zero for the model fitting effort. Since complete QD breakthrough was observed following PAA–OA pre-conditioning,19 it was further assumed that PAA–OA desorption from the sand was negligible under these experimental conditions. Thus, three parameters, kQDa, kPAAa, and SQDmax, were fit to the column breakthrough and retention data using the nonlinear least squares regression procedure and objective function (eqn (4)) described above.Fits of the MCB model to the measured QD–PAA–OA transport and retention in 40–50 and 80–100 mesh Ottawa sand are presented in Fig. 1A and B, respectively. The MCB model was able to capture both the asymmetry of the QD effluent breakthrough curves and the suppression in QD retention near the column inlet. To further evaluate the ability of the MCB model to capture residual PAA adsorption and competitive blocking of attachment sites, a second set of QD transport experiments conducted by Wang et al.19 was fit with the model (CS-H, MS-H, and FS-H; Fig. 1C and D). These experiments were conducted at a higher flow rate (1.0 ml min−1) and included a finer size fraction of Ottawa sand (100–140 mesh). Inspection of the figures reveals that the MCB model was able to capture the minimal elution of QDs (99.1% retention) and rapid rise in retention near the column inlet for the FS-H experiment. Here, the increased surface area of the finer sand results in a greater capacity to adsorb PAA–OA near the column inlet, leading to the very steep retention profile. In addition, the MCB model was able to capture the observed decrease in solid phase QD concentrations near the column outlet in FS-H. This behavior indicates that the limiting retention capacity (Smax) was not reached throughout the column, and demonstrates that additional QD mass (i.e., longer pulse width or higher concentration) would be required to completely saturate all of the attachment sites. When QD–PAA–OA was introduced into 80–100 mesh Ottawa sand at the higher flow rate (1.0 mL min−1; MS-H), the MCB model did not fit the effluent BTCs as well as in the other three experiments, but the model accurately captured the shape of the QD retention profile (Fig. 2). The more gradual increase in QD retention with travel distance and the lower overall magnitude of attachment (i.e., smaller Smax) reflects the reduced capacity of 80–100 mesh Ottawa sand to adsorb PAA and QDs, respectively, relative to 100–140 mesh Ottawa sand (see further theoretical calculations regarding the surface areas of the sand, QDs, and PAA–OA in the ESI†). The inability of the model to reproduce the observed breakthrough plateau (at a value below 1.0) in MS-H suggests that a second type of surface site could be contributing slightly to QD deposition in that case. However, because this result was only observed for one experiment and to constrain model fitting, the presence of a secondary interaction site type was not considered further.
Fitted parameter values and goodness of fit information for all MCB model simulations are provided in Table 2. Both the fitted QD attachment rates (kQDa) and retention capacity values (SQDmax) increased with decreasing sand grain diameter, consistent with results obtained for other nanoparticle-porous media systems.23 Based on traditional colloid filtration theory (CFT), the first order attachment rate, kQDa (tt−1), is represented as:20
 | (9) |
| Exp | η 0 | MCB modela | SCB – BTC onlyb | SCB – bothc | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k QDa (h−1) | α (−) | S QDmax (pmol g−1) | k PAAa (h−1) | R 2 | k QDa (h−1) | α (−) | S QDmax (pmol g−1) | R 2 | k QDa (h−1) | α (−) | S QDmax (pmol g−1) | R 2 | ||
| a Multi-constituent site blocking model fit to breakthrough and retention simultaneously. b Single constituent site blocking model fit only to breakthrough curve data, retention profiles predicted. c Single constituent site blocking model fit to breakthrough and retention simultaneously. d Single collector efficiency calculated from Tufenkji and Elimelech21 e α values were calculated using eqn (8), by inputting the fitted kQDa values for each case and the corresponding η0. *Experimental data presented in Wang et al.19 | ||||||||||||||
| CS-L | 0.505 | 1.41 | 0.03 | 6.16 | 1058.3 | 0.92 | 3.86 | 0.08 | 2.80 | 0.63 | 3.87 | 0.08 | 2.80 | 0.63 |
| MS-L | 0.774 | 4.29 | 0.03 | 12.76 | 2.50 | 0.98 | 2.02 | 0.01 | 5.75 | 0.97 | 2.05 | 0.01 | 5.76 | 0.98 |
| CS-H* | 0.098 | 8.83 | 0.10 | 3.00 | 77.77 | 0.98 | 11.37 | 0.13 | 0.98 | 0.87 | 10.99 | 0.13 | 1.11 | 0.89 |
| MS-H* | 0.146 | 5.50 | 0.03 | 7.13 | 65.16 | 0.95 | 12.45 | 0.05 | 2.49 | 0.75 | 12.29 | 0.05 | 2.87 | 0.73 |
| FS-H* | 0.174 | 29.48 | 0.07 | 21.16 | 7328.3 | 0.99 | 56.36 | 0.15 | 9.46 | 0.39 | 60.94 | 0.15 | 9.41 | 0.81 |
Fitted parameter 95% confidence intervals were calculated for the parameters used in the MCB model optimization, kQDa, kPAAa, and SQDmax (Table S2†). Confidence intervals for both nanoparticle attachment parameters, kQDa and SQDmax, were smaller than the fitted parameter values, indicating a high degree of confidence. Since the SPAAmax parameter is calculated directly from the SQDmax parameter (eqn (6), ESI†), these small confidence intervals also give increased confidence that the “one-site” model accurately captured the observed attachment behavior. Confidence intervals associated with the PAA–OA adsorption rate parameter (kPAAa), however, yielded intervals that were much larger in magnitude than the parameter values themselves. This result was attributed to a lack of sensitivity of the optimization function (eqn (4)) to variations in kPAAa due to difficulties associated with obtaining low concentration sorption data for PAA–OA. This issue is further addressed in the model sensitivity analysis discussion below.
To further evaluate the ability of the model to reproduce the coupled transport and deposition/sorption of quantum dots and PAA–OA, simulations of two representative QD transport experiments (CS-L and CS-H) are shown in Fig. 2. Here MCB model parameters that were fit to the QD data were used to reproduce PAA–OA solid phase concentration (dash–dot–dot lines, Fig. 2B and D). In the CS-L experiment (Fig. 2A and B), the fitted maximum QD retention capacity (SQDmax) was 6.16 pmol-QD per g-sand (SPAAmax of 1.22 μg-PAA per g-sand). Near the column inlet, the predicted sorbed-phase concentration was 1.21 μg g−1, which represents 99.1% of the surface area available for sorption/attachment. Thus, in this region, only 0.9% of the available capacity remained available for QD attachment, limiting the retained concentration to a low value (0.044 pmol g−1) at the column inlet. In this system, PAA–OA out-competed QD for sites due to its much larger sorption rate (1058.3 h−1vs. 1.41 h−1). Thus, the PAA–OA mass was exhausted first, resulting in the upward-sloping QD retention profile. Similar results were observed in the MCB simulation of CS-H (Fig. 2C and D). However, the QD retention profile in that experiment was flatter than CS-L, which indicated a much lower ratio of PAA–OA sorption rate to QD attachment rate (77.77 h−1vs. 8.83 h−1).
Also shown in Fig. 2 are best fits for two single-constituent kinetic models with site blocking, with and without the detachment term activated (eqn (2)), to the CS-L and CS-H experimental datasets. Consistent with results presented in Wang et al.,19 these simulations demonstrate the inability of these more traditional models to capture the anomalous QD retention trends and further demonstrate the superiority of the MCB model fits. Fig. 2 also suggests that the minimal detachment (i.e. tailing) observed in the CS-L breakthrough data could contribute in only a minor way to the increasing retention trend along the column. This observation supports our decision to neglect detachment in the fitted MCB model. Additionally, Wang et al.19 demonstrated that addition of the detachment term to the mathematical model did not change the values of katt and Smax significantly for the high flow rate data sets (~8 m d−1; CS-H, MS-H, FS-H; Table 2), indicating that the assumption to neglect that term would not alter the kinetic interpretation of the competitive attachment process. Similar comparisons between single- and multi-constituent model predictions were obtained for all column experiments (data not shown). To further compare the performance of the single- and multi-constituent models, Table 2 presents fitted QD transport parameters (kQDa and SQDmax) and corresponding R-squared values. Here, the second column presents parameters derived by fitting the traditional single constituent site blocking model24 model to effluent breakthrough data only, while the third column parameters were derived by fitting that model to the breakthrough and retention data simultaneously. A comparison of single-constituent model R2 – values with those for the MCB model in the first column reveals that the MCB model provides a better fit to the column data for all cases. Note that, in all cases, fitted values for kQDa are similar between single- and multi-constituent models, while fitted values of SQDmax using the single-constituent model are, in general, significantly larger (two or more times) than those obtained by fitting the MCB model. This observation suggests that the presence of the co-constituent (PAA–OA) influences the area available for quantum dot deposition (i.e. SQDmax) and not the rate of deposition (i.e. kQDa) under these experimental conditions. This behavior is consistent with the underlying “one-site” assumption of the model, in that the presence of the stabilizing additive only affects the availability of QD deposition sites, and not the rate of QD deposition.
Particle retention capacity has been shown in the literature to be influenced by both electrostatic and hydrodynamic effects.23,38,39 Since similar nanoparticles and porous media were used for all column experiments in this study, the electrostatic influence on the particle retention capacity was assumed to be similar in all experiments. Following the approach of Li et al.,23 the influence of hydrodynamic effects (e.g., velocity, grain size, grain geometry) on SQDmax was explored for the column experiments presented in this study. Here, fitted SQDmax. values were correlated to the normalized average QD diffusional mass flux across the boundary layer at the sand grain surface, Λ. The results of this analysis are presented in Fig. 3, where the best fit trend line is given as:
 | (10) |
 | ||
| Fig. 3 Relationship between the MCB-fitted maximum QD–PAA–OA retention capacity of the sand surface (Smax) and the normalized mass flux through the diffusion boundary layer (Λ) (eqn (9)). Symbols indicate the fitted Smax values (see Table 1) for individual experiments, and the line is the best fit power law relationship to the data. | ||
Here 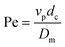 is the particle Peclet number, where Dm is the free liquid molecular diffusion coefficient of the QD nanoparticles (L2/T), calculated using the Stokes–Einstein correlation, and dM is a mean grain size of a medium sand (0.5 mm). The observed decrease of SQDmax with increasing velocity and grain size is consistent with previous findings for nC60 transport in Ottawa sands that were explained by the existence of a “shadow zone”.23,39 The shadow zone is visualized as a down-gradient area on the grain surface where particle deposition is limited due to the influence of approach velocity and grain size on attachment. Higher pore-water velocity and larger sand grain size tend to produce a larger shadow zone, corresponding to a reduced attachment capacity. A possible alternative explanation for this result relates to the influence of nano-scale heterogeneous surface charge on deposition, as mechanistic simulations of colloid retention on heterogeneous surfaces also predict an inverse relationship between velocity and retention capacity.40 This analysis suggests that, although competitive adsorption and attachment strongly influenced the macroscale retention, the hydrodynamic influences on retention capacity for QDs and PAA–OA were similar to those observed in single-constituent systems, behavior that can be predicted by existing mechanistic models for colloid deposition. The correlation in eqn (10) also provides a means to predict retention capacity from hydrodynamic parameters for similar systems.
is the particle Peclet number, where Dm is the free liquid molecular diffusion coefficient of the QD nanoparticles (L2/T), calculated using the Stokes–Einstein correlation, and dM is a mean grain size of a medium sand (0.5 mm). The observed decrease of SQDmax with increasing velocity and grain size is consistent with previous findings for nC60 transport in Ottawa sands that were explained by the existence of a “shadow zone”.23,39 The shadow zone is visualized as a down-gradient area on the grain surface where particle deposition is limited due to the influence of approach velocity and grain size on attachment. Higher pore-water velocity and larger sand grain size tend to produce a larger shadow zone, corresponding to a reduced attachment capacity. A possible alternative explanation for this result relates to the influence of nano-scale heterogeneous surface charge on deposition, as mechanistic simulations of colloid retention on heterogeneous surfaces also predict an inverse relationship between velocity and retention capacity.40 This analysis suggests that, although competitive adsorption and attachment strongly influenced the macroscale retention, the hydrodynamic influences on retention capacity for QDs and PAA–OA were similar to those observed in single-constituent systems, behavior that can be predicted by existing mechanistic models for colloid deposition. The correlation in eqn (10) also provides a means to predict retention capacity from hydrodynamic parameters for similar systems.
4.4. PAA–OA column results and modeling
PAA–OA breakthrough data could not be obtained in the QD–PAA–OA experiments because it was not possible to distinguish between free residual PAA–OA and QD–adsorbed PAA–OA in the effluent, since the residual PAA–OA concentrations were near the detection limit (ca. 0.6 mg L−1). However, separate column experiments were performed to measure PAA–OA transport and to confirm the validity of the fitted PAA–OA sorption parameters (PAA-CS-HA and B). In Fig. 4, MCB model simulations are compared with measured PAA–OA effluent concentration data. Here, the fitted value for kPAAa (77.8 h−1) obtained from the QD–PAA–OA transport experiments conducted in 40–50 mesh sand at a flow rate of 1.0 mL min−1 (CS-H, Table 2) was employed to predict PAA–OA transport. Due to the relatively high influent concentration (50 mg L−1 of PAA–OA) used in these experiments, the breakthrough curve exhibited a steep rise to a maximum concentration plateau. The close agreement of model predictions and observations provides some independent validation of the fitted PAA–OA sorption rate parameters. | ||
| Fig. 4 A – Prediction of PAA–OA breakthrough in 40–50 mesh Ottawa sand using fitted parameters (kPAAa and SQDmax) from the QD–PAA–OA experiment at the corresponding flow rate and grain size, CS-H.19 B – Prediction of QD elution from the column following a PAA–OA pre-conditioning pulse in 80–100 mesh sand at 8 m d−1. C – Prediction of QD Retention and PAA–OA sorption following PAA–OA pre-flood in 80–100 mesh sand. For model predictions in B and C, parameters were taken from the corresponding MCB model fit to MS-H. | ||
In addition to the PAA–OA copolymer-only column experiments, another experiment was performed in which the column was pre-flushed with PAA–OA prior to a pulse injection of QDs (PRE-MS-H; Fig. 4B and C). Here, the adsorption of PAA–OA prior to QD injection blocked attachment sites, which resulted in almost complete QD elution from the column (i.e., 95.5 and 99.4% of the applied mass). Using the fitted parameters from the corresponding QD–PAA–OA experiment (MS-H), the model was able to predict the measured breakthrough and retention curves (Fig. 4C) following the PAA–OA pre-conditioning. This result further supports the hypothesis that PAA–OA copolymer molecules and QDs compete for the same sites on the sand surface, and serves to validate the assumption that all adsorption/attachment sites are accessible to both QDs and PAA–OA molecules (i.e., “one-site” model).
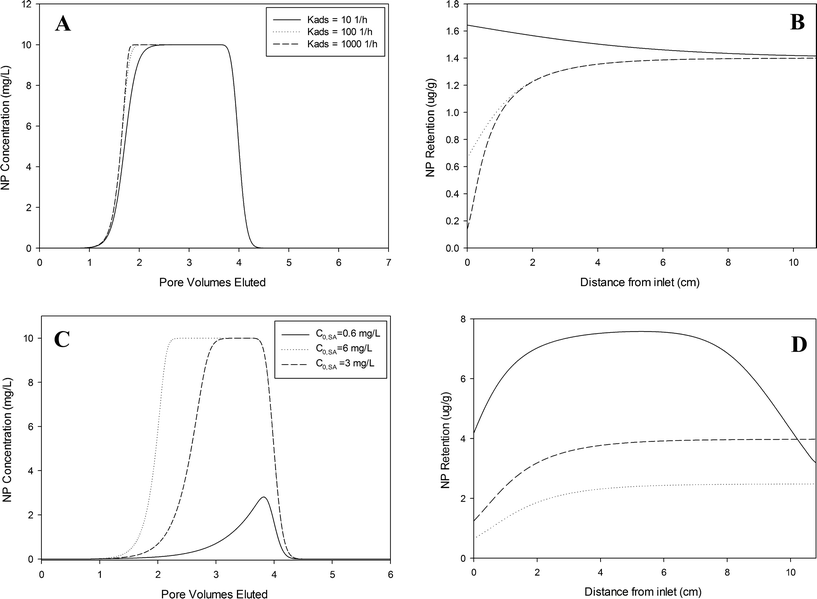
4.5. Model sensitivity analysis
A model sensitivity analysis was performed to explore the potential influence of co-constituents on nanoparticle transport and deposition under a wider range of conditions, including the sorption rate and influent concentration of PAA–OA. The base case conditions were: kQDa = 20 h−1, SQDmax = 2 pmol g−1 (SPAAmax = 0.396 μg g−1), kPAAa = 100 h−1, and C0,PAA = 3 mg L−1. These parameters were chosen to represent the mid-range of fitted values in all experiments presented previously.It is important to note that an increase in the residual PAA–OA concentration would result in less QD retention and more QD elution from the column. Therefore, interpretation of column data using a more traditional single-constituent kinetic model would tend to yield a lower fitted SQDmax value than was actually representative of the system. Application of this fitted retention capacity to predict transport at larger scales could, in turn, yield poor estimates of overall QD retention (see a demonstration in Fig. S4† in the ESI†). More generally, this observation highlights the importance of accurate model conceptualization for nanoparticle fate and transport in the environment, as the routine use of more traditional models, such as a single constituent kinetic model, could result in vast differences in field-scale predictions in comparison with those from more conceptually accurate models.
5. Conclusions
This study provides a mathematical framework, based upon a conceptual modeling approach derived from the competitive solute transport literature that describes the competitive transport and deposition of nanoparticles and co-constituents. Mathematical model parameterization and subsequent sensitivity analyses herein demonstrate that the presence of reactive constituents, including both synthetic stabilizing agents and naturally occurring macromolecules, have the potential to strongly influence the transport and deposition of nanoparticles. Upon release into the environment, nanoparticle suspensions will encounter many naturally occurring co-constituents that could occupy deposition sites in a similar manner as PAA–OA molecules in the present system. In addition to adsorbing molecules associated with nanoparticle synthesis or stabilization (e.g. PAA–OA), environmental relevant concentrations of natural organic matter or naturally occurring colloidal particles could also contribute to competitive attachment/adsorption processes. Furthermore, stabilizing agents (e.g. surfactants) are often added to nanoparticle suspensions and may not only be present as a byproduct of synthesis. Increased concentrations of such constituents would tend to greatly enhance the transport of nanoparticles. In such cases, a multi-constituent site-blocking model could provide a more accurate representation of nanoparticle transport and deposition processes in natural soils. As demonstrated by Fig. 5(C and D), nanoparticle mobility is extremely sensitive to relative concentrations of each constituent, demonstrating the necessity for complete characterization of constituents in a system to ensure accurate predictions of nanoparticle fate and transport in a lab- or field-scale scenario. Mathematical models that account for the effects of co-constituents on particle attachment, such as the MCB model, will be necessary to accurately describe and predict nanoparticle mobility in natural and engineered systems containing multiple constituents.Acknowledgements
The authors wish to acknowledge Drs. Huiguang Zhu and Vicki L. Colvin at Rice University for providing the water soluble quantum dots. This work was supported by the Advanced Energy Consortium: http://www.beg.utexas.edu/aec/ under projects BEG08-11 and BEG13-01. Member companies include BP America Inc., BG Group, Petrobras, Repsol, Schlumberger, Statoil, Shell, and Total. Additional support was provided by the U.S. Environmental Protection Agency STAR Fellowship Program (FP-917312). It has not been formally reviewed by EPA. The views expressed in this publication are solely those of the authors, and EPA does not endorse any products or commercial services mentioned in this publication.References
- A. Sehgal, Y. Lalatonne, J.-F. Berret and M. Morvan, Langmuir, 2005, 21, 9359–9364 CrossRef CAS PubMed.
- H. Takeuchi, H. Yamamoto and Y. Kawashima, Adv. Drug Delivery Rev., 2001, 47, 39–54 CrossRef CAS.
- K. L. Chen and M. Elimelech, J. Colloid Interface Sci., 2007, 309, 126–134 CrossRef CAS PubMed.
- R. C. Doty, T. R. Tshikhudo, M. Brust and D. G. Fernig, Chem. Mater., 2005, 17, 4630–4635 CrossRef CAS.
- S. J. Klaine, P. J. J. Alvarez, G. E. Batley, T. F. Fernandes, R. D. Handy, D. Y. Lyon, S. Mahendra, M. J. McLaughlin and J. R. Lead, Environ. Toxicol. Chem., 2008, 27, 1 CrossRef.
- W. W. Yu, E. Chang, J. C. Falkner, J. Zhang, A. M. Al-Somali, C. M. Sayes, J. Johns, R. Drezek and V. L. Colvin, J. Am. Chem. Soc., 2007, 129, 2871–2879 CrossRef CAS PubMed.
- R. L. Johnson, G. O. B. Johnson, J. T. Nurmi and P. G. Tratnyek, Environ. Sci. Technol., 2009, 43, 5455–5460 CrossRef CAS.
- S. H. Joo, S. R. Al-Abed and T. Luxton, Environ. Sci. Technol., 2009, 43, 4954–4959 CrossRef CAS.
- D. A. Navarro, S. Banerjee, D. F. Watson and D. S. Aga, Environ. Sci. Technol., 2011, 45, 6343–6349 CrossRef CAS PubMed.
- T. Tosco, A. Tiraferri and R. Sethi, Environ. Sci. Technol., 2009, 43, 4425–4431 CrossRef CAS.
- Y. Wang, H. Zhu, M. D. Becker, J. Englehart, L. M. Abriola, V. L. Colvin and K. D. Pennell, J. Nanopart. Res., 2013, 15, 1805 CrossRef.
- Y. Liang, S. A. Bradford, J. Simunek, H. Vereecken and E. Klumpp, Water Res., 2013, 47, 2572–2582 CrossRef CAS PubMed.
- S. Lin, Y. Cheng, J. Liu and M. R. Wiesner, Langmuir, 2012, 28, 4178–4186 CrossRef CAS PubMed.
- Y. G. Wang, Y. S. Li, J. Costanza, L. M. Abriola and K. D. Pennell, Environ. Sci. Technol., 2012, 46, 11761–11769 CrossRef CAS PubMed.
- S. Laumann, V. Micić and T. Hofmann, Water Res., 2014, 50, 70–79 CrossRef CAS PubMed.
- N. A. Lewinski, H. Zhu, H.-J. Jo, D. Pham, R. R. Kamath, C. R. Ouyang, C. D. Vulpe, V. L. Colvin and R. A. Drezek, Environ. Sci. Technol., 2010, 44, 1841–1846 CrossRef CAS PubMed.
- X. Wu, H. Liu, J. Liu, K. N. Haley, J. A. Treadway, J. P. Larson, N. Ge, F. Peale and M. P. Bruchez, Nat. Biotechnol., 2003, 21, 41–46 CrossRef CAS PubMed.
- W. W. Yu, E. Chang, R. Drezek and V. L. Colvin, Biochem. Biophys. Res. Commun., 2006, 348, 781–786 CrossRef CAS PubMed.
- Y. Wang, M. D. Becker, V. L. Colvin, K. D. Pennell and L. M. Abriola, Environ. Sci. Technol., 2014, 48, 10664–10671 CrossRef CAS PubMed.
- K.-M. Yao, M. T. Habibian and C. R. O'Melia, Environ. Sci. Technol., 1971, 5, 1105–1112 CrossRef CAS.
- N. Tufenkji and M. Elimelech, Environ. Sci. Technol., 2004, 38, 529–536 CrossRef CAS.
- M. Elimelech and C. R. O'Melia, Environ. Sci. Technol., 1990, 24, 1528–1536 CrossRef CAS.
- Y. Li, Y. Wang, K. D. Pennell and L. M. Abriola, Environ. Sci. Technol., 2008, 42, 7174–7180 CrossRef CAS.
- Y. Wang, Y. Li, J. D. Fortner, J. B. Hughes, L. M. Abriola and K. D. Pennell, Environ. Sci. Technol., 2008, 42, 3588–3594 CrossRef CAS.
- S. Torkzaban, Y. Kim, M. Mulvihill, J. Wan and T. K. Tokunaga, J. Contam. Hydrol., 2010, 118, 208–217 CrossRef CAS PubMed.
- Y. Wang, Y. Li and K. D. Pennell, Environ. Toxicol. Chem., 2008, 27, 1860 CrossRef CAS.
- D. Wang, L. Ge, J. He, W. Zhang, D. P. Jaisi and D. Zhou, J. Contam. Hydrol., 2014, 164, 35–48 CrossRef CAS PubMed.
- X. Li and W. P. Johnson, Environ. Sci. Technol., 2005, 39, 1658–1665 CrossRef CAS.
- T. Phenrat, J. E. Song, C. M. Cisneros, D. P. Schoenfelder, R. D. Tilton and G. V. Lowry, Environ. Sci. Technol., 2010, 44, 4531–4538 CrossRef CAS PubMed.
- N. Saleh, H.-J. Kim, T. Phenrat, K. Matyjaszewski, R. D. Tilton and G. V. Lowry, Environ. Sci. Technol., 2008, 42, 3349–3355 CrossRef CAS.
- A. Hubaux and G. Vos, Anal. Chem., 1970, 42, 849–855 CrossRef CAS.
- H. van de Weerd, Water Resour. Res., 2002, 38, 1–19 CrossRef.
- S. A. Bradford, S. Torkzaban, H. Kim and J. Simunek, Water Resour. Res., 2012, 48, W09509 CrossRef.
- J. Nowak, K. Gedicke, D. Antos, W. Piątkowski and A. Seidel-Morgenstern, J. Chromatogr. A, 2007, 1164, 224–234 CrossRef CAS PubMed.
- A. W. Adamson and A. P. Gast, Physical Chemistry of Surfaces, Wiley-Interscience, New York, NY, 6th edn, 1997 Search PubMed.
- S. H. Chen and C. W. Frank, Langmuir, 1989, 5, 978–987 CrossRef CAS.
- N. Toride, F. J. Leij and M. T. Van Genuchten, The CXTFIT code for estimating transport parameters from laboratory or field tracer experiments, U.S. Salinity Laboratory; Agricultural Research Service; U.S. Department of Agriculture, Riverside, CA, 1999 Search PubMed.
- P. R. Johnson and M. Elimelech, Langmuir, 1995, 11, 801–812 CrossRef CAS.
- C.-H. Ko and M. Elimelech, Environ. Sci. Technol., 2000, 34, 3681–3689 CrossRef CAS.
- E. Pazmino, J. Trauscht, B. Dame and W. P. Johnson, Langmuir, 2014, 30, 5412–5421 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details on the development of the model mathematical model; further details of experimental methods and conditions; fitted MCB model parameters and corresponding confidence intervals; sensitivity of the optimization function (eqn (4)) to kQDa and kPAAa; MCB model sensitivity to changes in available retention capacity; and illustration of large scale (10 m) transport with a single-component kinetic model and MCB. See DOI: 10.1039/c4en00176a |
| This journal is © The Royal Society of Chemistry 2015 |