 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining experimental and theoretical methods to learn about the reactivity of gas-processing metalloenzymes
Claudio
Greco
c,
Vincent
Fourmond
a,
Carole
Baffert
a,
Po-hung
Wang†
d,
Sébastien
Dementin
a,
Patrick
Bertrand
a,
Maurizio
Bruschi
c,
Jochen
Blumberger
*d,
Luca
de Gioia
*b and
Christophe
Léger
*a
aAix Marseille Université, CNRS, BIP UMR 7281, 13402, Marseille, France. E-mail: christophe.leger@imm.cnrs.fr; Tel: +33 4 91 16 45 29
bUniversità di Milano Bicocca, Department of Biotechnology and Biosciences, Piazza della Scienza 2, 2016, Milan, Italy. E-mail: luca.degioia@unimib.it
cUniversità di Milano Bicocca, Department of Earth and Environmental Sciences, Piazza della Scienza 1, 2016, Milan, Italy
dUniversity College London, Department of Physics and Astronomy, London WC1E 6BT, UK. E-mail: j.blumberger@ucl.ac.uk
First published on 11th September 2014
Abstract
After enzymes were first discovered in the late XIX century, and for the first seventy years of enzymology, kinetic experiments were the only source of information about enzyme mechanisms. Over the following fifty years, these studies were taken over by approaches that give information at the molecular level, such as crystallography, spectroscopy and theoretical chemistry (as emphasized by the Nobel Prize in Chemistry awarded last year to M. Karplus, M. Levitt and A. Warshel). In this review, we thoroughly discuss the interplay between the information obtained from theoretical and experimental methods, by focussing on enzymes that process small molecules such as H2 or CO2 (hydrogenases, CO-dehydrogenase and carbonic anhydrase), and that are therefore relevant in the context of energy and environment. We argue that combining theoretical chemistry (DFT, MD, QM/MM) and detailed investigations that make use of modern kinetic methods, such as protein film voltammetry, is an innovative way of learning about individual steps and/or complex reactions that are part of the catalytic cycles. We illustrate this with recent results from our labs and others, including studies of gas transport along substrate channels, long range proton transfer, and mechanisms of catalysis, inhibition or inactivation.
Broader contextSome reactions which are very important in the context of energy and environment, such as the conversion between CO and CO2, or H+ and H2, are catalyzed in living organisms by large and complex enzymes that use inorganic active sites to transform substrates, chains of redox centers to transfer electrons, ionizable amino acids to transfer protons, and networks of hydrophobic cavities to guide the diffusion of substrates and products within the protein. This highly sophisticated biological plumbing and wiring makes turnover frequencies of thousands of substrate molecules per second possible. Understanding the molecular details of catalysis is still a challenge. We explain in this review how a great deal of information can be obtained using an interdisciplinary approach that combines state-of-the art kinetics and computational chemistry. This differs from—and complements—the more traditional strategies that consist in trying to see the catalytic intermediates using methods that rely on the interaction between light and matter, such as X-ray diffraction and spectroscopic techniques. |
1 Introduction
Chemists are fascinated by the catalytic power of enzymes, which accelerate reactions by many orders of magnitude. Since they were discovered, more than a century ago, the amount of information that has been acquired about their working principles has been phenomenal. Thanks to the contributions of many physical chemists, great progress has been made regarding the use of both classical and quantum mechanics to describe the mechanism at a molecular level. However, depending on the intrinsic complexity of the catalytic system, the level of understanding that theoretical chemists can achieve varies greatly.Regarding enzymes that have either no cofactors or organic cofactors, and where the chemical transformation of the substrate occurs at the protein surface, substrate binding is essentially a matter of docking (rather than a complicated, intramolecular, multi-step diffusive process) and the main features of the mechanism can be inferred from X-ray data and site-directed mutagenesis experiments that identify the crucial amino acids. In these cases, theoretical chemists can focus on detailed yet important aspects of function, such as the role of protein motions in determining the turnover rate. Complications may arise in the case of “floppy” enzymes where a large conformational change on the micro-second time scale might partly determine the turnover rate.
The situation is very different in the case of many other enzymes (including some of those discussed here) that use an inorganic cofactor to transform a small substrate. This is for several reasons: (1) X-ray investigations often give an ambiguous picture of the structure of the active site, and/or, as occurs with hydrogenases, cannot detect the substrate because it is not sufficiently electron-dense; (2) the reactivity of complex inorganic active sites is sometimes difficult to predict, in part because it is largely tuned by the surrounding protein matrix, so that the catalytic mechanism is far from being straightforward (the exact mode of substrate binding, the sequence of events that take place at the active site during catalysis are often unknown); (3) theoretical methods have not yet been tuned to achieve the same accuracy as with organic cofactors, so that the results of calculations must be considered with caution; (4) these enzymes often house several cofactors and the catalytic mechanism involves a number of steps which are very different in nature (long range intramolecular substrate and product diffusion, long range proton and electron transfers and active-site chemistry per se) which occur on sites of the protein that are very far apart from one another. Any of these steps may, under certain conditions, limit the overall rate of the reaction and may therefore determine the enzyme's global catalytic properties. Often it cannot even be ascertained that active site chemistry limits the rate of turnover and regarding three out of the four enzymes discussed here, the calculation of turnover rates using theoretical methods still appears to be out of reach. A combination of theoretical chemistry and experimental methods can nonetheless be very useful to understand many different aspects of the mechanism, as discussed herein.
Fig. 1 summarizes the different approaches, both experimental and theoretical, that can be used independently or in combination to find out how such complex catalysts work. The outcome of experiments and calculations are the observables listed in the central column of Fig. 1 and organized in three groups: thermodynamic, structural and kinetic properties. The mechanism itself is not an observable, which is the main reason why theoretical calculations are essential. Of course, experimental observables derive from the structure and reactivity of the enzyme, but in such a complex way that it is generally not possible to deduce the mechanism from the values of the observables. In that respect, confronting theoretical results to experimental observations can help uncover the molecular details of the catalytic mechanism of an enzyme. This process is sketched in Fig. 1 and illustrated in the last section of this paper.
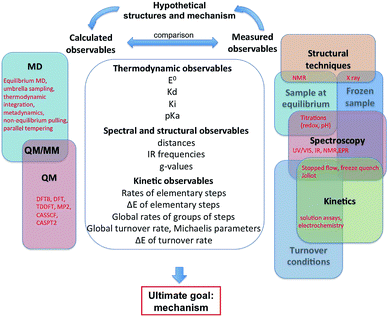 | ||
| Fig. 1 This figure shows a list of the observables that can be calculated or experimentally measured, and the feedback process that can lead to understanding a catalytic mechanism. | ||
The feedback process shown on top of Fig. 1, which is the key to understand the mechanism, is necessarily bootstrapped by experimental observations. We have classified the latter into three main approaches (structural, spectroscopic, kinetic), which can be used to probe three kinds of enzyme samples (at equilibrium, frozen, or turning over under catalytic conditions). Our goal here was not to list all existing techniques, but to show how they relate to each other. Any experiment, indicated in red in the right part of Fig. 1, is at the intersection between two or several domains: for example a redox titration consists in using a spectroscopic technique to monitor the redox state of a sample under equilibrium conditions. Experimental observables are very complex functions of the structures and kinetic properties of intermediates of the catalytic cycle. They can be interpreted to give structural or mechanistic information (e.g. “this IR spectrum shows that there are probably 3 CO ligands”, or “the pH dependence of this rate constant shows that the corresponding reaction involves a protonation”), but they do not usually give a complete description of the catalytic mechanism.
As illustrated in Section 4, direct electrochemistry has proved important in kinetic investigations of metalloenzymes,1 and we briefly introduce the technique here. Enzyme molecules are adsorbed or covalently attached2,3 as a submonolayer onto an electrode; the electrode potential is set to a value that forces the oxidation or the reduction of the enzyme, and the continuous catalytic transformation of substrate results in a flow of electrons across the electrode. This catalytic current is proportional to the turnover frequency times the electroactive coverage of enzyme participating in the reaction. If the electroactive coverage is constant, the current is proportional to turnover rate. That the current can be sampled at sub-second intervals is a strong advantage compared to traditional solution assays. Most significantly, using an electrode adds a control parameter (the electrode potential) to traditional enzyme kinetic measurements performed in solution. By changing the electrode potential, using steps or sweeps, it is possible to observe how the enzyme responds to changes in electrochemical driving force. Provided that kinetic models are used to quantitatively interpret the data, information can be gained about the properties of the enzyme's redox centers and the kinetics of intramolecular electron transfer,4,5 or the (in)activation of the enzyme that often occurs under conditions of extreme potential.6–8 The concentrations of substrate, product or inhibitors can also be changed while the activity is being recorded, making it easy to determine Michaelis and inhibition constants but also, and most importantly, rates of the reaction with inhibitors.9,10 The technique has obvious limitations: not all enzymes can be directly wired to electrodes and some artefacts sometimes arise from the protein/electrode interaction. We have discussed in a previous review some of the artifacts that may occur in PFV experiments.1 Apart from that, the main pitfalls of the technique are the same as those described in all enzyme kinetics textbooks: observing an agreement between a kinetic model and experimental data does not imply that the model is correct (or unique), and ingenious approaches have to be used to learn about the rates of individual steps in the catalytic cycle, or the molecular mechanisms of the chemical transformations that are at stake, based on a global measurement of turnover rate.
Regarding mechanistic investigations, it is important to realize that key intermediates are intrinsically short-lived, and consequently difficult to accumulate, detect and characterize experimentally. This implies that experimental results often need to be complemented by theoretical studies. The growing role of quantum chemical methods in the investigation of metalloenzymes is well testified by the 2013 Nobel Prize in Chemistry, which was awarded to Martin Karplus, Michael Levitt and Arieh Warshel for the development of multiscale computational models of complex chemical systems, i.e. the development of methods, based on classical and quantum mechanical theory, which can be used to study large chemical systems and their reactivity.
The computational methods used to study the molecular properties of metalloenzymes can be classified into two families (left part of Fig. 1). The first includes methods grounded in classical physics, such as Molecular Mechanics (MM) and Molecular Dynamics (MD). MM methods are used to calculate potential energies, whereas the goal of MD calculations is to describe the evolution of the structure of the protein, using Newton equations, based on the known energies of interaction between different atoms. MM and MD calculations allow to investigate the “physical” properties of the system, such as the dynamics of proteins in solution, as well as the diffusion of substrates and inhibitors into enzymes, but such approaches cannot be used to investigate properties that explicitly depend on electrons, such as reaction pathways and most spectroscopic features. The second family of computational tools includes Quantum Mechanical (QM) methods, which allow to calculate reaction energies and spectroscopic properties. QM methods are now routinely used to investigate large molecular systems, such as the active site of enzymes. Among all available QM methods, those based on the Density Functional Theory (DFT) are extremely popular due to their favorable trade-off between accuracy and computational costs.
In the context of bioinorganic chemistry, theoretical methods are useful for learning about active site geometries, for interpreting spectroscopic properties, and for elucidating reaction mechanisms (based on the energies of minima and saddle points along putative reaction pathways). The calculated observables are the same as those determined from experiments, but the approach usually takes a different route. In most theoretical calculations, especially QM, one needs to first postulate a structure or mechanism and then compute the observables. That the calculated observables match the measured ones suggests that the postulated structures are correct. Or the fact that calculated observables do not match experimental ones demonstrates that the mechanistic hypotheses can be ruled out. The comparison with experimental results is also fundamental to ensure that the system is described with sufficient accuracy with the approximations used (for instance, in quantum chemical calculations one has to choose the level of theory, the basis set, the cluster size, etc.). Comparison between theory and experiments can be made on different levels, from a qualitative point of view (“this intermediate is much too high in energy, so it is very unlikely that catalysis proceeds this way”) to semi-quantitative (“theory predicts that this species should be easier to oxidize than this one, in agreement with the experiments”) or quantitative (comparing the calculated and measured values for IR frequencies or rate constants).
Recently, advances in both experimental and theoretical methods have favored the dialogue between the “wet lab” and in silico approaches, and this interaction can now provide answers to open issues in the field of enzyme-catalyzed fuel production. In the present paper, we aim at showing how the combination of computational and experimental methodologies in enzymological studies can be fundamental for favoring the cross-fertilization of ideas, which is a prerequisite for any future change of paradigm in energy production and supply.
In fact, since most technological processes currently rely directly or indirectly on fossil fuels, which are non-renewable (in non-geological time scales) and consumed at an ever-increasing rate, one challenge facing current world economy is related to the availability and cost of energy. In addition, the burning of fossil fuels is continuously increasing CO2 concentration in the atmosphere, causing environmental problems. Therefore, the development and exploitation of alternative and renewable fuel sources and energy carriers, as well as advances in CO2 processing technologies, have very high priority.
The production of solar fuels is one of the best answers to such energy and environmental crisis and certainly one of the grand challenges of this century. Storing sunlight in the form of energy-rich chemical bonds offers the prospect of using existing or only slightly modified technologies that currently run on fossil fuels, such as e.g. car engines. Biology provides much inspiration for the development of such catalysts. Over millions of years, Nature has evolved highly efficient metal-clusters bound to proteins, for the purpose of converting small, inert molecules such as CO2, N2 and even water, with the help of sunlight, into highly energetic molecules (fuels) such as CO, methanol, ammonia or H2. We believe that a deep understanding of these fundamental biological reactions will provide the key for a successful translation into artificial processes. For this to happen, it will be vital to take advantage of the synergistic strengths of combined experimental and computational approaches.
Here is the structure of the paper and the scope of each section. In the second section, we introduce and describe the structures of the four enzymes that we shall discuss throughout the paper. In the third section we discuss how observables can be either measured in experiments or calculated, and at which accuracy; we shall also illustrate the drawbacks and pitfalls of several approaches. In the last section, we critically discuss selected literature in this field. We identify certain discrepancies between experimental and theoretical results, and gaps in the existing knowledge that will clearly be of interest in the future. We emphasize cases where combining experiments and theory provided much more insights than using the two approaches independently. Theoreticians should be able to start from educated guesses based on the experimentalists' results, while experimentalists should be able to perform the experiments that help discriminate between different hypotheses. This synergy is illustrated with several examples taken from our work and the work of others, focussing on four different metalloenzymes, three oxidoreductases ([NiFe] and [FeFe]-hydrogenases, carbon monoxide dehydrogenase) and one non-redox enzyme (carbonic anhydrase), all of which catalyse reactions of importance in the context of renewable energy and environmental-friendly processes.
2 Background information about the four enzymes discussed in this paper
2.1 Hydrogenases
Hydrogenases11,12 are enzymes that catalyse the reversible oxidation of H2 into protons and electrons according to:| H2 ⇌ 2H+ + 2e− | (1) |
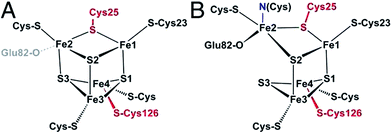
They are divided into two classes based on the metal content of their active site. The so-called “[NiFe]-hydrogenases” house a dinuclear [NiFe] active site, in which the Ni is coordinated by 4 cysteines (two of which bridge the metal ions), and the Fe is coordinated by two CO and one CN− ligand (Fig. 2A). MD and DFT calculations suggest that H2 binds to the Ni ion.13,14 The active site is buried inside the protein matrix, and connected to the solvent via a hydrophobic tunnel that guides the transport of substrate, a network of protonatable amino acids that transfer protons to/from the active site, and a chain of three iron–sulfur clusters to mediate electron transfer to/from the redox partner. These clusters are referred to as “proximal”, “medial” and “distal” according to their distance from the active site.
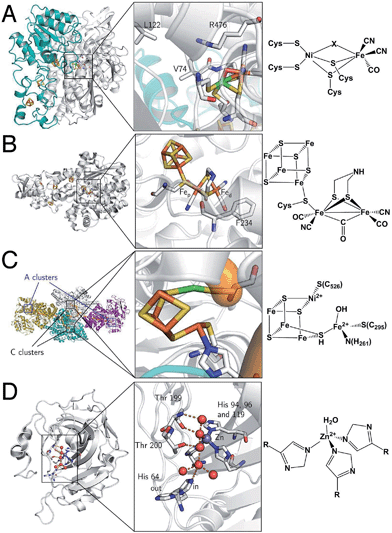 | ||
| Fig. 2 Protein structures and active site structures of the four enzymes discussed in the last section of this paper: [NiFe]-hydrogenase (A), [FeFe]-hydrogenase (B), acetyl-CoA synthase/CO-dehydrogenase (C) and carbonic anhydrase (D). The structures were drawn respectively from PDB 1YQW, 3C8Y, 2Z8Y and 3KS3. | ||
[FeFe]-hydrogenases oxidize or produce H2 at an active site, the so-called H cluster, that is composed of a standard [4Fe4S] cluster covalently attached by a cysteine residue to a [Fe2(CO)3 (CN)2(dtma)] subsite (dtma = dithiomethylamine)15,16 (Fig. 2B). The iron atoms of this [FeFe] subsite are named proximal (Fep) or distal (Fed) according to the distance to the [4Fe4S] cluster. In the catalytic mechanism, the [FeFe] subsite cycles between at least two redox states, referred to as Hox and Hred, which can be formally described as Fe(II)Fe(I) and Fe(I)Fe(I), respectively. Dihydrogen or protons (depending on the direction of the reaction) bind on the distal Fe. The enzyme from Chlamydomonas reinhardtii (Cr) has no cofactor other than the H cluster. The enzymes from Clostridium pasterianum (Cp) and Clostridium acetobutylicum (Ca) bind 4 additional FeS clusters, which act as electron relays. The enzyme from Desulfovibrio desulfuricans (Dd) houses the H cluster and two [4Fe4S] clusters.
2.2 ACS/CODH
Acetyl-CoA synthase/CO-dehydrogenase (ACS/CODH) is a bifunctional enzyme that plays a crucial role in anaerobic bacteria such as acetogenic organisms, which rely on the Wood–Ljungdahl pathway of carbon fixation.17 It is estimated that ≈1011 tons of acetate per year are produced globally from CO2 through this pathway.18 ACS/CODH catalyses the synthesis of acetyl-CoA from CO2, CoA, and a methyl group donated from the corrinoid–iron–sulfur protein (CoFeSP). This complex reaction occurs in two steps, that take place in different subunits: the two-electron reduction of CO2 to CO according to reaction (2) is catalysed in the β subunit, at the C cluster, a [NiFe4S4] active site (Fig. 2C).| CO2 + 2e− + 2H+ ⇌ CO + H2O | (2) |
It is proposed that CO2 binds the C cluster in the so-called Cred2 redox state, with the C atom of CO2 bound to Ni(0), and one O atom to a Fe(II) atom of the cluster. CO and water release leaves the cluster in the Cred1 state (Ni(II)Fe(II)). Electrons are transferred via the B and D clusters to the external electron acceptor. Some aspects of this mechanism are still under debate. For instance, a revised mechanism has been recently suggested where CO2 is inserted into a Ni(II)–hydride bond.19 A second active site, a [Ni2Fe4S4] cluster in the α subunit (the A cluster), catalyses the incorporation of the CO in a methyl group to give acetyl-CoA.
| CH3 − CoIIIFeSP + CO + CoA − SH ⇌ CH3COS − CoA + CoIFeSP + H+ | (3) |
The ACS (α) and CODH (β) subunits of the bifunctional enzyme are associated in a dimer of dimers (α2β2). The C and A clusters are 70 Å apart from one another and a 138 Å long cavity runs along the entire length of the enzyme, connecting all A clusters and C clusters, from the sites where CO is produced to the sites where it is consumed.
2.3 Carbonic anhydrase II (CA II)
This enzyme is a small protein (29 kDa) which catalyses CO2 hydration and HCO−3 dehydration:20,21| CO2 + H2O ⇌ HCO−3 + H+ | (4) |
It is involved in many biological processes, such as maintaining the correct acidity of blood in mammals. It is also important in photosynthesis since the substrate of RubisCO, the enzyme involved in the first major step of carbon fixation, is CO2 rather than its hydrated forms. The active site of CA II is a Zn2+ centre coordinated by three His nitrogens and one water molecule (Fig. 2D).
3 Methods
3.1 A general introduction to computational methods: calculations of structures and spectroscopic properties
Two strategies can be followed for the definition of QM models of metalloproteins. In the cluster approach, only the active site and some neighbouring atoms are taken into account, and the rest of the protein environment is only implicitly modelled. In the QM/MM approach, the active site is described using quantum chemistry, whereas all other atoms of the protein are modelled using a molecular mechanics formalism. Both approaches have advantages and disadvantages, which have been extensively discussed in recent reviews.22–26 The cluster approach is generally well suited for modelling metalloenzymes, since the chemical steps of the catalytic mechanism usually involve only the metal ions and nearby residues.27–30 However, the selection of the atoms included in the model is often far from trivial. In addition, the modelling of the peripheral atoms (i.e. those at the boundary of the QM model) can be problematic.When a cluster model is used, the presence of the protein matrix that surrounds the active site is generally modelled by soaking the QM portion in a continuum dielectric. This is particularly important for metal-containing active sites, which often are not electrically neutral. In fact, an unbalanced charge distribution in the active site can result in unrealistic electron transfers within the model cluster. As a continuum dielectric, several solvation models like the conductor-like screening model (COSMO)31–34 and the polarizable continuum model (PCM) have been developed.35–40
When the architecture and stereoelectronic features of the protein matrix are expected to affect the structural properties of the active site, as well as the regiochemistry of substrates or inhibitors binding, modelling the protein environment in an explicit manner can be very important. The development of QM/MM models, which has allowed the investigation of whole proteins, was pioneered by Warshel and Levitt.41 These methods have become increasingly popular in the last twenty years.
The structures of organic molecules calculated with DFT, which is the only affordable level of theory when dealing with large systems, can be very reliable, with errors on bond distances and angles that are generally lower than 2 pm and a few degrees. Regarding coordination compounds, strong metal ligand bonds (such as those involving CO and CN− ligands) are generally predicted with excellent accuracy, whereas the prediction of weaker metal–ligand bonds can be more problematic. Very weak interactions like hydrogen bonds can also be challenging.
DFT calculations have been useful also for the elucidation of structural properties of proteins. The so-called quantum refinement approach is a crystallographic refinement procedure in which a molecular mechanics force field, which is generally used to supplement the X-ray diffraction data, is replaced with more accurate DFT calculations;42 it has been used to clarify the chemical structure of cofactors or the protonation state of aminoacids. As an example, the nature of the dithiolate ligand in the active site of [FeFe]-hydrogenases (Fig. 2B) was initially controversial, since it was suggested that it may contain C, N, or O as the bridgehead atom. To shed light on this issue, Ryde and collaborators43 carried out quantum refinement calculations taking into account different models of the dithiolate ligand, finding that structures with a N bridgehead atom provide the best fit to the raw crystallographic data, in agreement with previous proposals.44–46 These results were confirmed recently when it became possible to change the nature of the bridging dithiolate ligand:16 the enzyme is active only if the bridging ligand bears a nitrogen atom.
It is also important to keep in mind that metalloproteins often contain metal ions with unpaired electrons, which must be described using spin polarized methods, where electrons with different spin are treated with a different potential. In addition, in some enzymes, such as those containing [4Fe4S] clusters, the metal atoms can interact, generating antiferromagnetic coupling between electrons localized on different atoms. Spin-coupled systems are intrinsically difficult to describe using DFT because their ground state wavefunctions generally correspond to linear combinations of multiple determinants. However, approximate methods have been shown to produce reliable results: in the broken symmetry (BS) approach developed by Noodleman and coworkers47,48 the opposite spins are localized to give a mono-determinant representation of the spin exchange interactions within the molecule.
The prediction of vibrational frequencies, and consequently of IR spectra, is closely related to the accuracy in the calculation of equilibrium geometries. In general, harmonic frequencies computed using DFT, when scaled using ad hoc empirical correction factors, agree very well with experimental data and can allow to distinguish among different plausible chemical structures that might correspond to the species under investigation. As an example, the combination of data obtained from infrared (IR) spectroscopy with the corresponding computed spectra has been one of the most effective approaches used to characterize hydrogenases. In fact, the peculiar presence of CO and CN− ligands in the active site of these enzymes has allowed to monitor the shifts of their vibrational modes and to correlate them with the molecular structure of different redox and protonation states of the enzyme.49–51
The calculation of other spectroscopic properties, such as UV-Vis, CD and EPR, is more challenging and high-level ab initio methods, such as CCSD(T) and CASSCF, are often required to obtain reliable results. However, as these methods are computationally very expensive, theoretical chemists make extensive use of DFT to compute spectroscopic properties of bioinorganic systems24,52,53 and the performance and reliability of this method has recently been discussed.54 In general, computed spectroscopic properties obtained using DFT are not always accurate, and sometimes even qualitative results can be incorrect. For this reason, DFT derived properties must be carefully checked and tuned using experimental data as reference. DFT calculations of Mössbauer isomer shifts for the 57Fe nucleus have generally produced encouraging results.55 In contrast, the computation of EPR parameters is more problematic. Indeed, g-shift values are often underestimated when using standard functionals, and some metal ions, such as Cu(II), can be particularly challenging. The accurate prediction of hyperfine coupling constants can also be difficult, with results that can be strongly dependent on the nature and oxidation state of the metal ion under investigation. Nevertheless, DFT calculations of g values and hyperfine coupling constants have often well complemented data obtained from EPR spectroscopy, as documented by their role in the characterization of structural features of paramagnetic [NiFe]-hydrogenase forms.12
Since only electronic ground states can be rigorously computed using DFT calculations, the investigation of excited states and their properties can be carried out only indirectly. In this context, DFT has benefited from the development of time-dependent linear response theory within the ab initio methods. Time-dependent density functional theory (TDDFT) is now routinely applied to compute the electronic spectra of bioinorganic systems, even though the quality of the results is very dependent on the molecular system under investigation and on the choice of the exchange-correlation functional. Multi-configurational approaches, such as CASPT2 and MRCI, can give more accurate results, but these methods are still computationally very expensive.
3.2 Calculating and measuring thermodynamic parameters
Standard reaction energies of organic molecules, such as additions and substitutions, when computed with DFT methods, are generally within 2–3 kcal mol−1 of the corresponding experimental values. The level of accuracy slightly decreases when considering bioinorganic systems containing transition metals, but the trade-off between accuracy and computational costs remains extremely good, allowing to cautiously discuss and compare computed reaction energies. As an example, an average accuracy of about ±5 kcal mol−1 can be expected in the computation of metal–ligand dissociation energies.52 However, it is important to remark that an error of 1.4 kcal mol−1 in binding energies corresponds to an order of magnitude difference in dissociation constant (Kd) at room temperature; the same problem arises in attempts to deduce rates from activation energies. Also due to the approximations necessarily introduced to model large biological molecules, the discrimination among alternative reaction pathways only on the basis of energy differences between intermediates and transition states can be problematic. In fact, for some difficult cases, such as Cu2O2 or Fe(IV)-oxo containing systems, even a qualitative analysis might lead to wrong conclusions.24 In addition, to describe the energy profile of a reaction, standard free energy differences (ΔG0) should be computed, whereas QM calculations provide directly only the electronic energy differences (ΔE0). The comparison of ΔE0 values is sufficient to discriminate among different reaction pathways when the energy corrections that should be computed and added to ΔE0 to obtain the corresponding ΔG0 values can be assumed to be similar for the different reaction pathways under investigation. Experimental observables are free energies, but their computation is often affected by large errors. First, computed energies should be corrected with the vibrational zero-point energy (ZPE) contribution, which is crucial if the aim is to compute deprotonation energies56 or to evaluate proton-transfer energies and barriers, proton tunneling and kinetic isotope effects.57,58 Second, entropic contributions should be taken into account, and calculated from the roto-translation partition function of the system, at a given T and P. However, only approximated partition functions can be computed for molecules containing a large number of atoms. Of course, entropic corrections are crucial for the description of associative and/or dissociative elementary reaction steps; their values are in the range of +10 kcal mol−1 for an associative reaction step, when considering standard state concentrations.
Regarding experiments, among the various quantities which are directly related to free energy variations, only association/dissociation constants and reduction potentials can be easily measured (if we exclude equilibrium constants between substrate and product and reaction energies, which give no information about the catalyst). This is described hereafter.
| E + L ⇌ EL | (5) |
The main issues in interpreting these results are that not all parameters in units of concentration are true dissociation constants (related to a free energy of binding), and that the different parts of the system that contribute to the apparent affinity of the enzyme for a ligand are difficult to resolve.
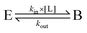
If one is interested in the catalytic transformation of a substrate S into a product P, the change in steady state turnover rate against substrate concentration can often be understood from a very simple scheme:
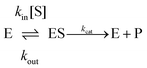 | (6) |
An experimental parameter that is easily measured is the Michaelis constant, Km, defined from the change in turnover frequency (v) against substrate concentration:
 | (7a) |
 | (7b) |
The Michaelis constant is greater than the true dissociation constant Kd = kout/kin unless the transformation of the enzyme–substrate complex is slow compared to substrate release59 and Km = Kd.
True dissociation constants are more easily obtained from inhibition experiments. If the inhibition by a certain ligand is reversible, then the turnover rate reaches a non-zero, steady-state value in the presence of substrate and inhibitor, and the inhibitor binding constant is deduced by looking at how the steady-state turnover rate v changes with inhibitor concentration [I]:
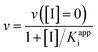 | (8) |
The apparent dissociation constants Kappi can also be deduced from the ratio of experimentally determined binding/dissociation rate constants. It may depend on substrate concentration. For example, if the substrate and the inhibitor compete for binding to the same active site,60 then the apparent Ki measured by changing [I] at a constant [S] is
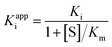 | (9) |
If the inhibitor reversibly binds to form a dead-end complex, as occurs with CO binding to hydrogenase for example, then inhibitor binding is at equilibrium in the steady-state,59 and the measured Ki is a true thermodynamic parameter. H2 inhibits proton reduction in both [NiFe]- and [FeFe]-hydrogenases (the former more strongly than the latter). However, the enzyme–H2 complex is not a dead-end (it is a catalytic intermediate of H2 evolution) and therefore the inhibition constant is not a true dissociation constant; it is actually greater than Kd (ref. 61).
If the inhibitor binds irreversibly on the experimental time scale, then inhibition is complete (provided the concentration of inhibitor is greater than the concentration of enzyme) and the rate of inhibition can be measured,9 but the rate constant of dissociation and the dissociation constant (Ki) cannot.
Reduction potentials can be determined in experiments termed redox titrations, where the system is poised under equilibrium conditions, stepwise reduced or oxidized; the “solution” potential is measured using a platinum electrode and the redox state is monitored using a spectroscopic technique. This is conceptually very simple if the system has a single redox center. If the protein or enzyme houses several redox centers that interact (meaning that the reduction potential of one center is affected by the redox state of the nearby centers), it is important to distinguish between microscopic reduction potentials (that can only be measured if the centers have distinct spectral properties) and macroscopic potentials (that are measured if the centers are indistinguishable in a particular experiment).1,64
Depending on the spectroscopic method used to monitor the redox state of the sample and the spectral properties of the redox cofactors, a large amount of biological material may be required to carry out a complete redox titration. The implementation of the measurement is often tricky. (1) A cocktail of redox mediators has to be present in solution to increase the rate at which the equilibrium is reached; its composition and concentration must be chosen carefully. (2) An artifact may arise from the fact that the redox equilibrium may unexpectedly shift when the sample is frozen to be examined by e.g. EPR (for an effect of temperature on the thermodynamics of intramolecular ET, see e.g.ref. 65). Changes in apparent pH can also occur on freezing aqueous buffer solutions.66 (3) Enzymes like hydrogenases cannot be equilibrated at low potential because they turnover protons, which cannot be removed from the solution. (4) Last, and maybe most importantly, it is rarely checked that the redox process is fully reversible (for an example where it is unexpectedly irreversible, see ref. 67). Overall, the error on E0 is most often larger than ±10 mV, and there are many sources of artifacts that can result in the value being uncertain.
Dynamic electrochemical methods, where the system is not at equilibrium, can also be used to measure reduction potentials.68 The information can sometimes be simply obtained from the result of a voltammetric experiment, where the electrode potential is repeatedly swept up and down to trigger the oxidation and reduction of the center, which is detected as an oxidation or reduction current. If the system has several redox centers, voltammetry measures macroscopic reduction potentials. If the redox reaction is a pure electron transfer or if it is coupled to fast reversible reactions (such as (de)protonation or ligand binding and release), then the thermodynamic information is easily obtained from experiments carried out in the low scan rate limit, where the system remains close to equilibrium. The rate of interfacial electron transfer and/or the rates of the coupled reactions can be deduced from experiments carried out at fast scan rates.69 If the coupled reaction is irreversible, then the reduction potential can only be measured if the electrode potential is swept so quickly as to outrun the coupled reaction,70 but there is no guarantee that this regime can be reached in experiments.
If the coupled reaction is the reversible or irreversible catalytic transformation of a molecule in solution, then the electrochemical response we are considering is a catalytic current, which is proportional to turnover frequency. If we consider the situation where electron transfer between the electrode and the enzyme is direct, the mid-point potential of the catalytic wave is somehow related to the reduction potential of the enzyme's active site, but it is equal to the reduction potential of the active site only in very rare situations. In most cases, the wave potential (the “catalytic potential”) is a global parameter that is affected by the thermodynamics71 and kinetics72 of substrate binding, the kinetics and thermodynamics of intramolecular electron transfer along the redox chain that wires the active site to the electrode,4,5 the kinetics of electrode/enzyme electron transfer73etc. It is now clear that catalytic potentials are parameters that may strongly depart from the reduction potential of the active site. An analogy in this respect is the Michaelis constant, which has the unit of a dissociation constant, but is not a thermodynamic parameter (cf.eqn (7b)).59
The comparison of experimental and calculated reduction potentials may help understand how the environment tunes the redox properties of a metal center. Calculating potentials may also discriminate between several plausible mechanisms. The reduction potential is directly proportional to the free energy change associated to the redox process:
ΔG = ΔEel + ΔGsolv + Ezpe − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(q) ln(q) | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(q) are the enthalpic and entropic contributions for the optimized structure, calculated within the harmonic oscillator/rigid rotor approximation. Due to the difference in charge between reactants and products, reduction potentials are generally strongly affected by the environment. Regarding coordination compounds, the differences in the solvation free energies of the reduced and oxidized species are usually computed using implicit solvation models, such as PCM, COSMO and COSMO-RS,24,74 and their reduction potentials can often be accurately computed using DFT methods (although complications arise in some class of compounds, see as an example some Cu complexes). Such calculations are more problematic in the case of metalloenzymes, because the environment of the redox centre cannot be satisfactorily described using an implicit solvation model. Therefore, the intermolecular interactions between the active site and the environment must be described with QM/MM methods where the effect of the inhomogeneous dielectric environment is treated at an atomistic level. In addition, an adequate sampling of the configurations associated with the environmental degrees of freedom can be crucial, in particular when the active site is flexible or the surrounding residues adopt different conformations. In such case the harmonic approximation, which is usually assumed for calculation of vibrational entropy, is no longer justified. Adequate sampling can be achieved, for instance, with QM- and QM/MM-based molecular dynamics simulations by sampling the vertical electron affinity ΔEvel,75–79
ln(q) are the enthalpic and entropic contributions for the optimized structure, calculated within the harmonic oscillator/rigid rotor approximation. Due to the difference in charge between reactants and products, reduction potentials are generally strongly affected by the environment. Regarding coordination compounds, the differences in the solvation free energies of the reduced and oxidized species are usually computed using implicit solvation models, such as PCM, COSMO and COSMO-RS,24,74 and their reduction potentials can often be accurately computed using DFT methods (although complications arise in some class of compounds, see as an example some Cu complexes). Such calculations are more problematic in the case of metalloenzymes, because the environment of the redox centre cannot be satisfactorily described using an implicit solvation model. Therefore, the intermolecular interactions between the active site and the environment must be described with QM/MM methods where the effect of the inhomogeneous dielectric environment is treated at an atomistic level. In addition, an adequate sampling of the configurations associated with the environmental degrees of freedom can be crucial, in particular when the active site is flexible or the surrounding residues adopt different conformations. In such case the harmonic approximation, which is usually assumed for calculation of vibrational entropy, is no longer justified. Adequate sampling can be achieved, for instance, with QM- and QM/MM-based molecular dynamics simulations by sampling the vertical electron affinity ΔEvel,75–79ΔG = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp(ΔEvel/kBT)〉O ln〈exp(ΔEvel/kBT)〉O | (11) |
| ΔG = (〈ΔEvel〉O + 〈ΔEvel〉R)/2 | (12) |
Even when QM- and QM/MM-based molecular dynamics approaches are used, the results are often affected by large errors. An error of 100 mV may not be acceptable considering that the biological redox scale is very narrow (most relevant reduction potentials range from −400 mV to +500 mV), and yet error of 100 mV corresponds to about 2.3 kcal mol−1, which is well within the present accuracy of DFT methods. Therefore, results obtained from computing electron affinities, ionization energies and reduction potentials are often more useful in a relative or qualitative manner, to distinguish among different species or reaction paths, than for the prediction of absolute values. In other words, such calculations are most useful if one aims at understanding changes in the reduction potential of a cofactor in response to point mutations or other modifications of the environment, or differences in the reduction potential of the same cofactor in different proteins.81,82 In these cases, since the QM system containing the redox active co-factor is the same and changes in reduction potential are due to different interactions with the environment only, the DFT errors are expected to cancel. Indeed, one can assume that the reduction potential differences are mostly due to the protein so that a QM calculation is no longer necessary and the reduction potential can, to first approximation, be calculated entirely with classical force fields81,82 or continuum electrostatics methods.83 A recent example is the calculation of the relative reduction potentials of ten identical c-type heme cofactors bound to the deca-heme protein MtrF,82 as reviewed elsewhere.84 In this study classical MD simulation was employed to compute the reduction potential using thermodynamic integration. The range of potentials computed was in relatively good agreement with experiment, even though the computed potentials were microscopic reduction potentials (all other hemes remaining oxidized), whereas in experiments (protein film voltammetry) macroscopic reduction potentials are measured (the system goes from being fully oxidized to fully reduced as the electrode potential is swept down). The effect of the oxidation state of a neighbouring cofactor on the reduction potential can be significant, in the order of 10 to 95 meV,85–87 but it remains typically below the statistical error caused by the finite length of the MD trajectories.
Several experimental methods, such as equilibrium denaturation measurements at different pH and potentiometric titrations have been applied to evaluate pKas of ionisable residues in proteins. Accurate values of pKas can be measured using multidimensional and multinuclear NMR spectroscopy, by monitoring the pH dependence of 13C, 1H and 15N chemical shifts and corresponding coupling constants of relevant atoms (Cγ for Asp; Cδ for Glu; Cδ, Cδ2, Nε2 and Nδ for His, etc.) previously assigned to specific residues.92–95
Theoretical predictions of pKas are very useful even when experimental values are available, since they can provide a better understanding of the molecular determinants of ionization. Many different methods and levels of theory have been proposed for the calculations of pKas.96 However, in spite of the significant progress since the first work of Tanford and Kirkwood based on the Poisson–Boltzmann equation,97 calculation of pKas remains challenging because of the difficulties in capturing quantitatively the effects of the strong and position dependent short-range electrostatic interactions, and the nonspecific long range interactions between charged sites and with the solvent.98–100
The heterogeneous response of the protein to a change in charge, which depends on the dielectric environment and the local flexibility, is another difficult issue.101–103 As recently reviewed, among the various methods proposed for pKa calculations, none performs significantly better than others.96
The most fundamental approach for describing electrostatics, as well as all other physical interactions, are quantum mechanical (QM) methods which solve the Schrödinger equation at some level of approximation. This approach can be successfully applied to small molecular systems such as single amino acids or small peptides.104–108 In this case full QM geometry optimizations and vibrational frequencies calculations are carried out for the species included in a thermodynamic cycle such as that in Fig. 3.
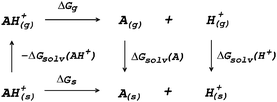 | ||
| Fig. 3 Thermodynamic cycle for the calculation of deprotonation Gibbs free energy in solution (ΔGs). | ||
The Gibbs free energy of reaction in solution (ΔGs) is obtained as the sum of the Gibbs free energy of reaction in vacuum (ΔGg) and the difference in solvation free energies (ΔΔGsolv)
| ΔGs = ΔGg + ΔΔGsolv | (13) |
| ΔΔGsolv = ΔGsolv(A) + ΔGsolv(H+) − ΔGsolv(AH+) | (14) |
| ΔGg = Gg(A) + Gg(H+) − Gg(AH+) | (15) |
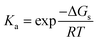 | (16) |
The main source of errors in this approach seems to arise from modelling solvation. In particular, widely used dielectric continuum models (DCM) are frequently the worse approximation for systems where short range solute–solvent interactions are important. The explicit inclusion of a few solvent molecules in close proximity to the solute in addition of using a DCM can be a way to overcome this issue, without making the calculations computationally too expensive.109 In this respect we note that more elaborate DFT based molecular dynamics schemes have been developed for calculations of pKa values, where both the solute and a large number of solvent molecules are treated at the DFT level.108 In addition, the accuracy of the calculated pKas is also significantly improved by using thermodynamic cycles that maximize systematic error cancellations.110 The QM level of theory used in the pKa calculations is also important, as it should be feasible at reasonable computational costs for relatively large-sized systems.
For macromolecular systems like proteins, using a QM method for the entire system is clearly prohibitive due to the computational cost. Most importantly, the use of QM methods is undesirable since electrostatic interactions dominate at large distances, and must be included in the calculation. An approach to overcome these issues is the QM/MM method introduced in Section 3. In this context, ad hoc computational methods for the calculation of pKas have been recently proposed by Li and Jensen and coworkers:111,112 one method is based on a QM representation of the ionisable residues and their immediate environment combined with a continuum description of bulk solvation with the linear Poisson–Boltzmann equation; alternatively, the QM region is surrounded by fragments described by static potentials predetermined using ab initio QM.
Several methods utilizing Molecular Dynamics (MD) and Monte Carlo (MC) simulations have recently been proposed at various levels of approximation. We recall that MD simulations are used to sample all possible conformations of a protein by calculating a long trajectory based on deterministic rules (Newton mechanics) whereas MC simulations consist in randomly generating a large number of conformations, which are accepted or rejected according to their Boltzmann probability. Recent promising models combine (i) atomistic simulations of the protein, performed using MC or MD with a fixed or flexible protein backbone, (ii) an implicit description of the solvent using a Poisson–Boltzmann model (PB), and (iii) a MC sampling of conformations and ionization states of the protein. In these PB based approaches, the protein is defined as a region with a low dielectric constant embedded in a solvent with a high dielectric constant. The value of the dielectric constant of the protein is crucial for the correct prediction of pKas. In this respect, different values have been used, from 4 to 80,113–116 as the appropriate value depends on the distribution of polar and charged residues within the protein and on local protein flexibility.117–119
One of the most commonly used methods for incorporating conformational flexibility into pKa calculations is the so-called Multi-Conformation Continuum Electrostatics (MCCE) method developed by Alexov and Gunner.114,119 In the MCCE the protein side chain flexibility is considered by generating several conformations for each residues which are relaxed using a force field with Lennard-Jones and torsion energies. The resulting conformers, which represent all degrees of freedom including appropriate acid/base ionization states and side chain positions, are then subjected to Monte Carlo sampling to generate the Boltzmann distribution of conformers. A state featuring one conformer for each residue is a microstate. The energy expression to determine the acceptance for a microstate x (ΔGx) is given by:
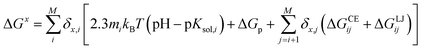 | (17) |
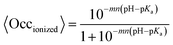 | (18) |
Equilibrium ionization states in proteins have also been investigated by the protein dipole Langevin technique,103,120 and by MD based approaches using either constant-pH MD or free energy perturbation techniques.121–124
3.3 Kinetic parameters
In contrast, regarding complex metalloenzymes, the calculations of rates necessarily focus on one particular step, not the entire cycle. Since reaction rates are macroscopic averages over a very large number of reactive events from the reactant basin to the product basin (and vice versa), following different trajectories, it is necessary to compute a large number of trajectories (dynamics approach) or to use statistical theories based on ensemble distributions. In particular, using MD, the reaction rates can be computed by averaging a statistically representative number of trajectories, obtained using different initial conditions, that take reactants to products. Many approaches exist to carry out such averaging procedure in practice at a reasonable computational cost: “umbrella sampling” is one such method, where the potential energy surface is biased to force the trajectories computed by molecular dynamics simulations to reach the transition state region. The most used statistical approach is grounded in the transition state theory (TST) of Eyring, according to which
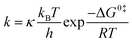 | (19) |
In general, the enzyme kinetics is the result of a large number of elementary steps, most of them reversible, each occurring with a given rate constant. This includes not only the chemical reaction steps at the active site but also the transport processes of substrates/products. For instance, proton transfer from the solvent to buried active sites occurs via a chain of proton exchanges between water and/or protonatable amino acid residues (see Section 3.3.2). Similarly, binding of small ligands to buried active sites can be described as a series of diffusive jumps between protein cavities connecting the solvent with the protein active site (see Section 3.3.3). The time evolution of these kinetic chains can be obtained by solving master equations (a set of differential equations governing the time evolution of all possible states of the system) or by using kinetic Monte Carlo methods. The latter use as input the elementary rate constants obtained for each step, for instance, from TST.
The rate of elementary proton transfer steps taking place in enzymes is generally calculated with the expression given by transition state theory (eqn (19)).
To evaluate the activation free-energy ΔG0‡, a suitable reaction coordinate is chosen so as to follow the reaction progress, like the difference between the donor–proton and acceptor–proton bond distances. Classical MD simulations with extensive umbrella sampling are then carried out to obtain the free-energy profile along the reaction coordinate (called PMF, potential of mean force). ΔG0‡ can be obtained from the difference of the PMF at the maximum (transition state) and minimum (reactant state), see e.g.ref. 129 for details. The PMF also provides the standard free-energy change ΔG0, which is proportional to the ΔpKa of the reaction. The parameters used in semiempirical methods must be determined through a careful calibration based on a set of experimental data. Nuclear quantum mechanical effects due to tunnelling and zero-point energies may be significant in biological proton transfers. Various methods have been proposed to evaluate their contributions, especially in studies devoted to the interpretation of the KIE.130
In enzymes, proton exchanges between the active site and the solvent take place through proton transfer chains made of protonatable groups, like water molecules and/or ionisable residues. The time evolution of these chains can be simulated by using various methods like the center of excess charge, the Langevin equation, or kinetic models leading to a master equation, as described in Section 3.3.3.
In attempts to distinguish between the partition of the ligand between the solvent and the protein and the actual binding on the active site, it is useful to consider a two-step binding model, with the diffusion of the substrate towards a “geminate” (G) position near the active site (with a forward bimolecular constant k1 and a first order rate of release k−1, dissociation constant K1 = k−1/k1) and the chemical binding/release on the active site (with first order rate constants k2 and k−2, equilibrium constant, K2 = k−2/k2).10
 | (20) |
The observed bimolecular rate of ligand binding and first order rate of ligand release are related to the four rate constants above by
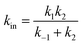 | (21a) |
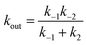 | (21b) |
These equations are obtained by assuming (i) the steady state for G, d[G]/dt = 0 and (ii) that K2 is small (k−2 ≪ k2).
In metalloenzymes that transform small molecules like CO, CO2, and H2, putative substrate tunnels are most easily identified as hydrophobic cavities in (static) X-ray structures. Xenon can be used as a probe in crystallographic studies, because it is supposed to prefer hydrophobic environments, like H2 or O2; it is of a similar size to O2 but it is more electron-rich, thereby facilitating its detection with X-rays. We note that Xe-binding cavities may not reveal CO2 diffusion paths because they may be too small to be used for CO2 transport. Testing the diffusion pathways predicted from crystallographic studies usually consists in using site-directed mutagenesis to try to alter the main routes (most commonly, by increasing the bulk of the side chains that point in the channels) and examine the effect on the rates of ligand binding (see e.g.ref. 132 for a review).
One method for probing the rate of intramolecular diffusion in enzymes may consist in measuring the rate of substrate or ligand binding in experiments where the enzyme–ligand complex has a clear UV-vis signature: the five-coordinate hemes of cytochrome c oxidase and myoglobin lend themselves to this sort of investigations.133,134
Regarding hydrogenases, a particular method for looking at H2 diffusion rates is based on analysing the progress of the isotope exchange reaction, whereby D2 is irreversibly transformed into H2 using protons from the solvent, in two steps that are catalyzed at the [NiFe] active site:
| D2 + H+ → HD + D+ | (22a) |
| HD + H+ → H2 + D+ | (22b) |
Both steps are irreversible, because the solvent H2O provides a very large excess of H+ over D+. The reaction can be monitored by using mass spectrometry to follow the change in concentration of D2, HD and H2, see e.g.Fig. 4. HD is an intermediate along the reaction pathway from D2 to H2, and because the egress of HD competes with its transformation into H2, the slower intramolecular transport, the less HD dissociates from the enzyme's active site and the less it can be detected in the solvent. Modelling the change in HD concentration against time returns the ratio of rate of HD dissociation over H+/D+ exchange at the active site.135 Under certain conditions,63 the data can also be used to directly measure the rate of dissociation, 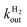 .
.
 | ||
| Fig. 4 Isotope-exchange assay (eqn (22)) of the WT form (A) and L122F-V74I mutant (B) of Desulfovibrio fructosovorans [NiFe]-hydrogenase. The changes in concentrations are used to determine the rate of H2 exit from the enzyme.63,135e0 is the concentration of enzyme. That the mutant produces less HD than the WT enzyme indicates that the mutation slows diffusion along the gas channel. Figure reproduced from ref. 63 (copyright 2012 American Chemical Society). | ||
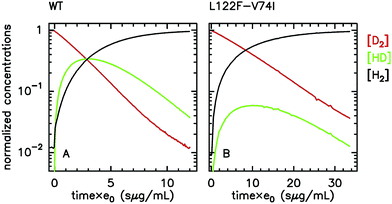
Alternatively, the information about the kinetics of ligand binding may be deduced from turnover-rate measurements: it is indeed possible to determine the rate of binding or release of a competitive inhibitor (“competitive” means that it targets the active site) by monitoring the change in turnover rate upon exposure to the inhibitor. The electrochemical measurement of the rate of binding and release of CO in hydrogenase is illustrated in Fig. 5: the H2-oxidation activity is measured as a current, with the enzyme adsorbed onto an electrode immersed and rotated in a solution continuously flushed with H2, and small aliquots of a solution saturated with CO are repeatedly injected in the cell.9,135 The concentration of CO instantly increases after each injection (the mixing time is about 0.1 s) and then decreases exponentially as CO is flushed away by the stream of H2. The activity decreases after the addition of CO, and it is eventually fully recovered.
 | ||
| Fig. 5 Electrochemical monitoring of the inhibition by CO of H2 oxidation by the L122M-V74M mutant of D. fructosovorans [NiFe]-hydrogenase where the double mutation slows diffusion along the gas channel. An aliquot of solution saturated with CO was injected at t = 0 and the change in current against time reveals CO binding and release. Panel A: CO concentration against time. Panel B: eqn (2) in ref. 60 is fit to the change in current against time (gray) to measure kCO,appin and kout. Figure reproduced from ref. 1 (copyright 2008 American Chemical Society). | ||
We derived in ref. 60 the analytical equation that can be used to fit the electrochemical data recorded after a single injection of CO (as in Fig. 5) to measure kout and the apparent value of kin. The value of kCOout is independent of substrate concentration, but since H2 competes with CO, the “true” value of kin is obtained from its apparent value using:
 | (23) |
An alternative strategy for characterizing the kinetics of inhibition by CO (or O2) consists in fitting the exponential relaxation of the catalytic current that follows a step in inhibitor concentration136 (rather than a burst, as in Fig. 5A). This can be achieved by injecting an aliquot of solution saturated with CO and simultaneously changing the composition of the gas phase above the cell solution. In that case however, it is important to realize that the time constant τ of the relaxation is not 1/kCOin,app[CO], but it is:
| τ = 1/(kCOin,app × [CO] + kCOout) | (24) |
Unless the experiment consists in monitoring the spectroscopic signature of the active site, the rates of diffusion in either direction (kCO1, kCO−1) and the rates of ligand binding and dissociation at the active site (kCO2, kCO−2) cannot be measured independently, and the meaning of the binding/release rate constants must be discussed in relation to eqn (21).
The rate of binding (kCOin) equates the rate of diffusion towards the active site only on condition that the binding at the active site is fast
| kCOin = kCO1 if kCO2 ≫ kCO−1 | (25) |
In this case, the measured rate of ligand released (kout) is the rate of diffusion out multiplied by the dissociation constant,
| kCOout = kCO−1 × KCO2 | (26) |
In other words, the dissociation from the active site acts as a pre-equilibrium for the release of the ligand, as discussed in ESI of ref. 10.
Atomistic simulations, in particular MD, have most often been used in this context independently of experimental investigations. They can give important qualitative information on intramolecular transport, such as the most likely diffusion paths within the protein and the location of key residues that guide, block or gate ligand diffusion. The simulations that have been carried out were either based on long equilibrium molecular dynamics137–140 or on the use of enhanced sampling methods.141–148 With computational capabilities steadily increasing in recent years, it has become possible to compute not only qualitative diffusion paths, but also energetic properties such as activation barriers146,147 and estimates of global free energy surfaces.144,145,148
Nevertheless, rate constants for the diffusion of gas molecules have only rarely been computed. Free energy surfaces could in principle be used to obtain approximate diffusion rates using e.g. TST for each single transition. However, as pointed out in ref. 131, there are two issues. First, the transition of small ligands between protein cavities may be strongly affected by dynamical effects leading e.g. to frequent barrier recrossings. This effect is neglected in standard TST and calculation of respective correction factors for each transition would be cumbersome. Second, for the construction of free energy surfaces collective variables need to be chosen, typically the cartesian position of the gas molecule. While this is an intuitive and suitable choice for fast transitions, it may be a poor choice for slow transitions through narrow passages where gas diffusion is coupled to (“gated by”) side chain motions of amino acid residues. In this case the reaction coordinate for the diffusive transition is likely to be more complicated, involving in addition to the cartesian position of the gas molecule some suitable coordinates describing the motion of the side chain(s) in question.
Considering the above issues, it is preferable to compute diffusion rates directly without prior calculation of equilibrium free energy profiles. Indeed, for relatively small proteins like myoglobin, it has been possible to obtain estimates for diffusion rates by brute force MD simulations. In the work of ref. 138, a relatively large number of trajectories of length 90 ns were generated and the rate constants estimated by counting the number of successful transitions between solvent and active site. Similarly, in ref. 140, rates for CO migration between Xe-binding sites in myoglobin were estimated from equilibrium MD simulations. The results obtained for diffusion were combined with QM calculations for CO binding, to propose a detailed kinetic model that was in reasonable agreement with available experimental data.
Brute force MD simulations are sometimes insufficient to obtain a statistically significant number of successful transitions of gas molecules from the solvent to the enzyme active site. This can be the case for large gas-processing enzymes with active sites buried deep inside the protein, far away from the solvent. The large number of possible but unproductive pathways reduces the probability for successful entry in the active site. Other difficult cases are enzymes with very narrow passages for gas diffusion such as the [NiFe]-hydrogenase mutants studied in ref. 10. Some of us have recently developed a master equation approach with rate constants estimated from equilibrium and non-equilibrium MD simulation, that addresses the sampling problem in these systems.149–152 The method allows us to compute diffusion rates of small ligands, even when these are very slow. Most importantly, the approach yields phenomenological diffusion rate constants, that can be directly compared to experimental rate constants. In the following we describe this computational method in more detail.
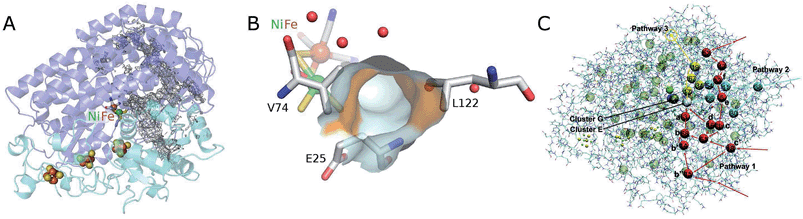
In a first step, one runs one or several long equilibrium MD trajectories of the protein and the surrounding aqueous solution containing 10–100 gas molecules, in the following referred to as ligand (“L”). Small diatomic or triatomic molecules penetrate the protein typically on the pico- to nanosecond time scale and quickly explore the accessible cavities and tunnels inside the protein. In a second step, the equilibrium probability distribution of the gas molecules inside the protein is obtained by defining a grid and counting the number of times a molecule visits a given elementary volume. The probability distribution is then clustered (“coarse grained”) in a way such that the cluster positions coincide as closely as possible with the maxima of the probability distribution (see e.g. the spheres in Fig. 7C). These clusters are then identified as coarse “states” in a kinetic model that describes ligand diffusion as a sequence of hops between these states with rate constants kij, where j is the initial state or cluster and i the final state. The surrounding solvent is considered as a single cluster with rate constants for transitions to protein clusters defined similarly. In a third step the transition rates kij are calculated simply by counting the number of transitions observed in the long equilibrium MD runs. For important transitions that are insufficiently sampled, enhanced sampling methods (such as e.g. non-equilibrium pulling) are used to obtain kij. In the fourth step the transition rates kij are inserted in a master equation, which is a set of coupled first order differential equations for the population of each cluster as a function of time, pi(t), with solution
 | (27) |
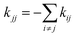 . The master equation (eqn (27)) is solved for given initial conditions (e.g. by setting the gas population inside the protein to zero at time equal zero as is the case in experimental measurements) to obtain the time dependent population of the states as a function of time. For calculating the rate of diffusion to the active site, the quantity of interest is the ligand population in the geminate state, pG(t). In the fifth and last step pG(t) is fit to the phenomenological rate law for reversible diffusion of L to the enzyme active site
. The master equation (eqn (27)) is solved for given initial conditions (e.g. by setting the gas population inside the protein to zero at time equal zero as is the case in experimental measurements) to obtain the time dependent population of the states as a function of time. For calculating the rate of diffusion to the active site, the quantity of interest is the ligand population in the geminate state, pG(t). In the fifth and last step pG(t) is fit to the phenomenological rate law for reversible diffusion of L to the enzyme active site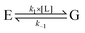 | (28) |
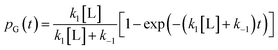 | (29) |
Eqn (29) relates the populations obtained with atomistic MD simulation techniques to the phenomenological rate constants for pure diffusion from the solvent to the active site and vice versa, k1 and k−1, respectively. Within the coarse master equation scheme described above it is straightforward to include the chemical binding step,152
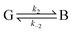 | (30) |
For this, we define an additional “bound” state B, in which the substrate is chemically attached to the enzyme (denoted as EL in eqn (5) above) and the corresponding population pB. The rate constant for transition from state G to B, k2, and for the reverse transition, k−2, is estimated, for instance, using quantum chemical methods as described above. The dimension of the rate matrix in eqn (27) is then increased by one to include the entries for k2 and k−2 and eqn (27) is solved for pB. A fit of pB to the phenomenological rate law for reversible ligand attachment,
 | (31) |
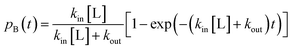 | (32) |
In Section 4 we will discuss applications of this methodology to substrate and inhibitor diffusion in hydrogenase and ACS/CODH, and compare the rate constants computed this way with experimental measurements.
4 Case studies
In this section we present selected examples taken from the literature, to illustrate how the synergy between experimental kinetic studies and computational investigations can inform about the reactivity of complex metalloenzymes such as [FeFe] and [NiFe]-hydrogenases, ACS/CODH and carbonic anhydrase.4.1 [NiFe]-hydrogenase
 | ||
| Fig. 6 Structure of the proximal [4Fe3S] cluster of the O2 resistant [NiFe]-hydrogenase from H. marinus, in the reduced (3+) state (A) and in the superoxidized (5+) state (B). The two “supernumerary” cysteines, Cys25 and Cys126, are indicated in red, Glu82 in gray (A) or black (B). The cysteine closest to the [NiFe] site (Cys23), and the bond to the backbone nitrogen in the superoxidized state (blue), are also indicated. From ref. 155, copyright 2013 by National Academy of Sciences. | ||
To put the results below into context, it is important to remember that [NiFe]-hydrogenases are converted under oxidative (aerobic or anaerobic) conditions into a mixture of inactive states, two of which are referred to by the name or their EPR signatures: NiA and NiB.156 The enzymes recover H2-oxidation activity upon reduction, NiB more quickly than NiA.157 According to X-ray investigations, an oxygenic ligand bridges the Ni and the Fe in the inactive states.45 The fact that the formation of NiA is favored when the enzyme is inactivated by O2 under more oxidizing conditions (higher electrode potential, absence of H2) has been taken as an indication that the oxygenic ligand in NiA is a peroxo produced upon incomplete reduction of the attacking O2;158 however, this hypothesis was ruled out when control experiments showed that the amount of NiA is the same irrespective of whether the enzyme has been inactivated under aerobic or anaerobic conditions.12,63 Certain oxygen tolerant enzymes, which can oxidize H2 in the presence of O2, are inhibited by O2 to form only a NiB state that is similar to that in O2-sensitive hydrogenases except that it reactivates much more quickly.159–161 These enzymes house three high potential FeS clusters,162 including the very flexible, proximal [4Fe3S] cluster, which has been suggested to play a crucial role in the protection of the active site against oxidative inactivation. The [4Fe3S] cluster is linked to the protein by an unusual six-cysteine binding motif. Four of the six cysteine residues bind the cluster in the classical way, whereas one of the supernumerary cysteine residues replaces an inorganic sulfide in the cubane core, and the other is terminally coordinated to one of the Fe atoms. While classical [4Fe4S] clusters are involved in one-electron transfer reactions, the proximal [4Fe3S] cluster found in some O2-tolerant [NiFe]-hydrogenases can attain three redox states within a redox potential span of only 150 mV (and therefore be involved in two-electron transfer reactions), although it is unclear if it is a condition for O2 tolerance.163 The superoxidized state is stabilized by a structural reorganization arising from deprotonation of a backbone-nitrogen atom and concomitant nitrogen coordination to one of the iron atoms. X-ray diffraction results also suggest that in the enzyme from E. coli a Glu residue is coordinated to Fe2 in the superoxidized species (Fig. 6), whereas in the membrane-bound hydrogenase from R. eutropha a dioxygen-derived oxo or hydroxo ligand replaces the Glu sidechain.164
Different spectroscopic techniques (X-ray, EPR, Resonance Raman and Mössbauer) have been complemented by quantum-chemical calculations, with the aim of disclosing structural and electronic properties of the unusual [4Fe3S] cluster. As an example, broken-symmetry DFT calculations complemented Mössbauer measurements, indicating that the superoxidized [4Fe3S]5+ cluster can be described as a mixed-valence Fe2.5+/Fe2.5+ and a diferric pair. The reduced [4Fe3S]3+ has an electronic pattern consistent with a mixed-valence and a diferrous pair, while the [4Fe3S]4+ state can be described as formed by two mixed-valence pairs. Even though these studies agree about the ferric character of the “special” Fe ion (Fe2 in Fig. 6), the spin coupling scheme of the four Fe atoms remains debated. DFT calculations have also been used to study some aspects of the energetics of the interconversion between the three accessible redox states of the [4Fe3S] cluster.155,165
Many mutations of amino acids near the proximal or medial cluster increase the O2-sensitivity of otherwise O2-tolerant [NiFe]-hydrogenases,163,164,166 and it is still unknown how the properties of the electron transfer chain make O2-resistant [NiFe]-hydrogenases form, upon oxidation, only a NiB state that reactivates very quickly. Certain single point mutations in D. fructosovorans [NiFe]-hydrogenase also strongly affect the rates of anaerobic formation and reactivation of the NiB state, for reasons that still need to be clarified. Fourty years after the NiA and NiB inactive states were discovered, we still need to elucidate their structures and mechanisms of formation, not forgetting that different mechanisms may operate under oxidizing aerobic and anaerobic conditions, and lead to the same inactive states.63 In this respect, it is remarkable that the actual reaction of [NiFe]-hydrogenases with O2 has not yet been studied computationally; this is certainly a subject for further studies.
 | ||
| Fig. 7 Structure of D. fructosovorans [NiFe]-hydrogenase depicting the “dry” hydrophobic cavities. (A) The large and small subunits are shown as dark and light blue ribbons, respectively. Also shown are the active site, the chain of FeS clusters that wires the active site to the redox partners, and a grid delineating internal regions accessible to a probe of 1 Å radius. (B) Close up showing the access to the active site as the surface of the atoms that tile the end of the dry tunnel. Smaller, red spheres indicate the position of ordered water molecules in nearby “wet” cavities. Spheres in the background depict the Ni and Fe ions. Their ligands and residues Leu122, Val74 and Glu25 are shown as sticks. The side chains of Val74 and Leu122 define the surface of the tunnel that is shown in orange. (C) Coarse-graining of hydrogen trajectories inside the enzyme. From the diffusive hopping of H2 molecules between cavities in the protein, we define clusters centered at the regions of high gas density inside the protein. The clusters are depicted as spheres together with three typical “pathways” to the active site observed by following the trajectories (pathways 1, 2, and 3, colored in red, blue, and yellow, respectively). Cluster E in white is the cluster that gas molecules temporarily occupy before binding; cluster G in gray is the state in which a gas molecule occupies the active site cavity but is not yet chemically bound to Ni. The labels a, b, etc., denote the approximate positions of the Xe-peaks reported in ref. 13. Figure adapted from ref. 149 (copyright 2011 American Chemical Society) and 10. | ||
The suggestion that bulky side chains at these positions may render certain [NiFe]-hydrogenases O2-resistant by preventing O2 access, which eventually proved wrong,10 was the initial motivation for a series of studies aimed at determining the effects of amino-acid substitutions in the channel on the functional properties of the enzyme: rates of CO binding, CO release and O2 binding, Michaelis constant for H2, and catalytic “bias” (defined as the ratio of the maximal rates of H2 oxidation and production63). Some results are shown in Fig. 8, each data point corresponding to one particular mutant of the [NiFe]-hydrogenase from D. fructosovorans. The mutations of amino acids in the channel change the rates of CO binding by up to a factor of 1000, but most mutations have no significant effect on the dissociation constant for CO (Fig. 8A shows that kout is proportional to kin in this series of mutants, except for the V74Q, E and N substitutions). The comparison of the rates of reaction with CO and O2 in this series of mutants (Fig. 8B) shows that CO inhibits the WT enzyme and most mutants much more quickly than does O2, but in mutants where the diffusion is the slowest, the values of kin for O2 and CO are equal (line “y = x” in panel B). This led to the conclusion that CO and O2 diffuse within the enzyme at the same rate, but O2 reacts slowly at the active site, suggesting that the rate of inhibition by CO is mainly determined by diffusion towards the active site:
| kCOin = kCO1 | (33) |
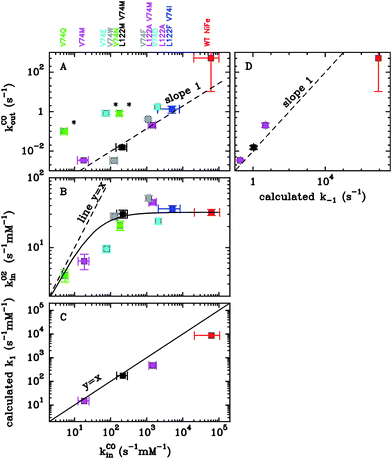 | ||
Fig. 8 Summary of the measured and calculated rates of CO binding and release in a series of [NiFe]-hydrogenase mutants where the conserved Val and Leu residues that shape the gas channel have been substituted (Fig. 7B). Each data point corresponds to one mutant. The panels show the relations between the experimental values of Km, kCOin; kCOout, 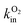 , and calculated kCO1 and kCO−1. Data from ref. 10, 150 and 151. , and calculated kCO1 and kCO−1. Data from ref. 10, 150 and 151. | ||
Molecular dynamics simulations of gas diffusion in [NiFe]-hydrogenases gave important clues about the molecular mechanism of inhibitor transport in some of the wild type and mutant enzymes studied experimentally.149–151 Before we describe the main findings of the MD simulations, we would like to comment first on the accuracy that one can expect from the molecular models that were used in these simulations.
A good test to assess the force field used to describe the interactions between ligands and proteins is the calculation of diffusion constants in various solvents. The force field models used typically reproduce the lowest non-vanishing multipole moment of the ligands in the gas phase and contain Lennard-Jones interactions sites.149,150,152 The solvent is described with the same force field as that used for the protein. Diffusion constants computed for H2, O2, CO and CO2 are summarized in Fig. 9 (data taken from ref. 149, 150 and 152). The experimental values are very well reproduced, albeit not perfectly, with a mean relative unsigned error (MRUE) of 15% for water and 21% for hydrocarbons, where the average was taken over the four gases. For O2, additional calculations were carried out for aprotic dipolar solvents (DMSO, acetone, acetonitrile) resulting in a MRUE of 16%. While there is certainly room for further improvements, the results show that the performance of these simple and computationally efficient force field models is fair.
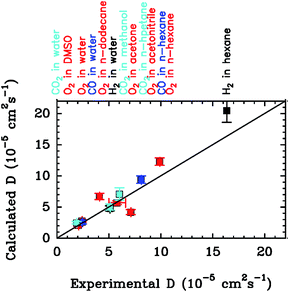 | ||
| Fig. 9 Computed versus experimental diffusion coefficients for diffusion of H2, O2, CO and CO2 in solvents of different polarity. Calculated values were obtained from MD simulation and taken from ref. 149–152. Experimental data were taken from ref. 171–176. | ||
Regarding intramolecular transport in hydrogenase, the advantage of studying CO over e.g. O2 is that CO chemical attachment to the [NiFe] active site is fast (kCO2 ≫ kCO−1). Therefore, the bimolecular CO binding rate is a good proxy of the diffusion rate (eqn (33)), which allows for a direct comparison between simulated rates for gas diffusion and experimentally determined rates. The diffusion rates of CO in [NiFe]-hydrogenase and three mutant enzymes have been computed using the methodology described in Section 2. The results are summarized in Fig. 8C and D (data taken from ref. 150 and 151). The simulated rate constants for diffusion in the active site, k1, are very close to the experimental binding rate constants kin. They range from ≈104 s−1 mM−1 for the WT enzyme down to ≈10 s−1 mM−1 for the V74M mutant (Fig. 8D). The very good agreement obtained in this specific case, with deviations of no more than a factor of 3 in the diffusion rates, can be considered somewhat fortuitous given the imperfections of the force field and the statistical errors due to limited sampling. However, a good order of magnitude estimate for the diffusion rate can be generally expected by such simulations. Panel D shows the experimental value of kCOout against the calculated value of k−1, which can be interpreted using eqn (26). The observation that the data points fall reasonably well on a line of slope 1 in a log–log plot shows that the measured value of kout is indeed proportional to the calculated value of kCO−1. We deduce KCO2 ≈ 10−2, consistent with the approximation made to derive eqn (25). Overall, regarding the kinetics of CO binding and release, the agreement between the model and the data can be taken as an indication that the assumptions underlying the model for gas diffusion developed in Section 2 are sound.
We now discuss the measurements and values of dissociation constants.149,150 According to both experimental results and computations, CO and O2 diffuse about equally fast to the active site of [NiFe]-hydrogenase. Every 100 microseconds a CO or O2 molecule reaches the active site at a gas concentration of the surrounding solution of 1 mM (corresponding to a gas pressure of about 1 atm.). Conversely, it takes only about 100 ns for a gas molecule to diffuse from the active site to the solution. Interestingly, the same time scales have been reported for CO diffusion in myoglobin and for CO2 diffusion in ACS/CODH. To first approximation K1 can be estimated by the ratio of volume per gas molecule in the active site cavity and in solution (since, as explained in ref. 150, the values of K1 are mainly a consequence of the loss of translational entropy as the ligand moves from the solution to the active site cavity). For more quantitative estimates and to understand differences between ligands, MD simulations must be used to account for specific interactions with the solvent/protein. The calculated equilibrium constant for pure ligand diffusion in [NiFe]-hydrogenase obtained from MD simulations is K1 = k−1/k1 ≈ 103 mM, and this value is very similar for H2, CO and O2.
All experimental mutations studies have focused on the V74 L122 motif and indeed it was unequivocally shown that this motif is one of the bottlenecks for gas transport.10,151 However, some of the observed effects were difficult to rationalize. For instance, there was an absence of correlation between the diffusion rate and the “width” of bottleneck shaped by the 74-122 motif. For example, diffusion in the V74M L122A mutant is slowed by a factor of 42 relative to the WT enzyme, even though the gas channel diameter is not significantly reduced.135 Another puzzling observation is that the L122M V74M double mutation is less effective than the V74M single mutation even though the gas channel diameter is similar to the one for the single mutant according to the crystal structure. Simulations have shown that diffusion is in fact controlled by two rather than one motif, one between residues 74 and 476 and the other between residues 74 and 122.151 The existence of two control points in different locations explains why the reduction in the experimental diffusion rate does not simply correlate with the width of the main gas channel measured between L122 and V74. The simulations also helped us understand how inhibitors can access the active site in certain mutants, despite the fact that the access route is blocked according to the crystal structure.151 Considering one of the most effective mutants (V74M), we found that CO molecules reach the active site due to strong thermal fluctuations of the width of the gas channel defined by M74 and L122 and through transitions that are gated by the microsecond dihedral motions of the side chain of a strictly conserved arginine (R476). These findings suggest that attempts to further decrease inhibitor diffusion could focus on making the main gas channel, in particular the two above mentioned motifs, more rigid.
4.2 Substrate transport in ACS/CODH
Gas diffusion is also a key aspect of the reactivity of bifunctional ACS/CODH (Fig. 2C), where structural features allow for the effective transport of substrate and product molecules. In this enzyme, CO2 diffuses from the solvent to the C cluster located deep inside the protein interior, approximately 30 Å from the protein surface. The reaction product CO is then transported from the C cluster to the catalytic A cluster of ACS, that is about 70 Å away. Early experimental studies demonstrated that this transport occurs without CO being released to the solvent.177,178 More recent xenon-binding studies and calculations of cavities in the static structure179–181 showed that the clusters are interconnected by a channel which extends throughout the entire length of the enzyme complex (138 Å). Mutations of putative channel residues resulted in decreased acetyl-CoA production rates, providing convincing evidence that CO molecules use this tunnel.182On a first view, it is puzzling that directional transport of this ligand is possible considering the thermal fluctuations of the protein and the high mobility of the small CO ligand. Why doesn't CO merely take the same route out of the protein as the one CO2 takes to reach the C cluster from the solvent? Afterall, CO is smaller than CO2 and the path that CO2 takes to diffuse from the solvent to the C cluster should also be accessible for diffusion of CO from the C cluster to the solvent. Molecular dynamics simulations answered this question.152 It was shown that the hydrogen bonding network in the active site pocket accommodating the C cluster changes drastically with oxidation state. After formation of CO from CO2, the hydrogen bond network becomes stronger, preventing CO from taking the CO2 access pathway. Hence, the change in the hydrogen bond network leads to obstruction of the CO2 channel and enables the directional flow of CO from the C cluster, where it is produced, to the A cluster of ACS/CODH, where it is utilized.
Another puzzling question is how CO2 diffuses from the solvent to the C cluster of ACS/CODH. Neither Xe-binding studies nor cavity calculations have given indications for a pathway connecting the C cluster and the protein surface.181 Volbeda et al. hypothesized that CO2 could enter the enzyme via the A cluster and travel “backward” through the long CO channel.183 However, the mutations of channel residues do not affect CODH enzymatic activity,182 and CO2 transport against CO flux in the channel would require an elaborate mechanism in order to avoid unproductive molecular collisions.183 Tan et al. suggested that CO2 might enter the C cluster through a channel connecting the two C clusters, as shown in cavity calculation, or via a hydrophobic channel near the CODH dimer interface.184 Finally, Doukov et al. proposed that the CO2 diffusion path is dynamically formed by the thermal motion of the protein.181 Recent MD simulations confirmed that CO2 diffusion into the C cluster is facilitated by a dynamical gas channel that extends orthogonal to the static channel where Xe binds.152 The cavities of this dynamic tunnel that are close to the active site are temporarily created by protein fluctuations, and as such not apparent in available crystal structures.
With regard to binding kinetics, the experimental information is scarce. Kumar et al. determined a rate constant of 2.6 × 104 s−1 mM−1 for the CO driven conversion of Cred1 into Cred2 at 300 K (calculated from the data measured at 5 °C),185 which provides a lower limit for the rate of diffusion of CO to the active site. One can expect that the rate is lower for CO2 due to its larger size. The MD simulations that revealed the dynamic access channel (see above) predicted rates of k1 = 4800 s−1 mM(CO2)−1 for the diffusion of CO2 from the solvent to the C cluster and k−1 = 1.5 107 s−1 for escape from the C cluster to the solvent.152 Interestingly, these rates are on the same order of magnitude as those reported for CO and O2 diffusion in [NiFe]-hydrogenase (see above). Combining the MD simulations with the DFT calculations for CO2 binding to the Cred2 state of ACS/CODH, binding rates of kin = 4.4 s−1 mM−1 have been estimated, similar in magnitude to the experimental turnover rate of the enzyme, kcat = 1.3 s−1.152 It is interesting to note that the rates for diffusion (k1) and for chemical attachment (k2) are very similar, but kin is 3–4 orders of magnitude smaller than both k1 and k2. This can be easily understood when considering the steady-state expression, eqn (21). Since diffusion out of the protein is much faster than chemical attachment (k−1 ≫ k2), kin is given by k2 divided by the equilibrium constant K1 = 103–104 mM.
4.3 Transformations of the H cluster of [FeFe]-hydrogenase
Several combined electrochemical and DFT studies have been carried out with the aim of characterizing the reactivity of [FeFe]-hydrogenases (Fig. 10), even if the quantitative comparison of rate and binding constants obtained using PFV and chronoamperometry experiments with the corresponding computed data can be problematic, due to the limited accuracy of present DFT methods (see Sections 1 and 2).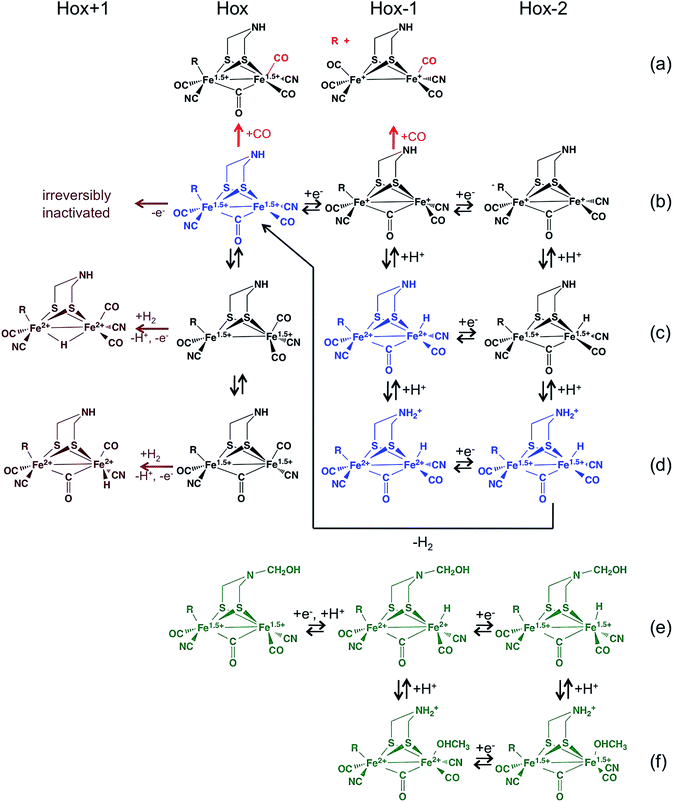 | ||
| Fig. 10 Proposed chemical transformations of the H cluster of hydrogenase, which occur when the enzyme reacts with CO (red),186 formaldehyde (in green)187 and under oxidizing conditions in the presence of H2 (ref. 8). The structures in blue are believed to be part of the catalytic cycle. “R” represents the [4Fe4S] subcluster. The catalytic relevance of the “super-red” species “Hox−2(b)”, where the [4Fe4S] subsite of the H cluster is reduced, is unclear.7,188 | ||
This investigation illustrated how the combined used of PFE and DFT allowed to evaluate plausible reaction pathways for the reactivity of [FeFe]-hydrogenases with HCOH, but also highlighted intrinsic limitations in these approaches. In particular, even if both the formation of a strongly bound methanol molecule and a Schiff base modification of the H cluster are consistent with the enzyme inhibition observed when H2 production is monitored at very negative potentials, these scenarios are necessarily incomplete since they do not account for the observed reversibility of the inhibition process, leading the authors to conclude that the protein environment around the H cluster may play an important role in destabilizing or hindering the formation of the predicted products.
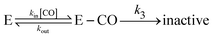 | (34) |
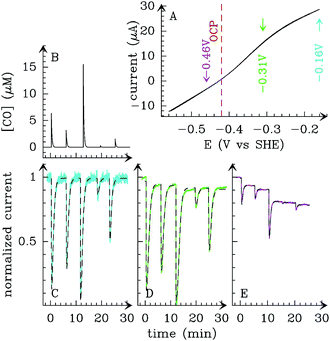 | ||
| Fig. 11 (A) Steady-state voltammogram for Ca [FeFe] hydrogenase. The open circuit potential (OCP) is indicated by a dashed red line. (B) CO concentration against time. (C–E) Normalized current traces showing the activity changes that result from the sequence of injections shown in panel B, recorded at E = −0.16 (C), −0.36 (D), and −0.47V (E). The dashed lines are the best fit to the model based on eqn (34). From ref. 186, copyright 2011 American Chemical Society. | ||
The rate of CO binding depends on electrode potential in a sigmoidal manner, with a mid-point potential that appears to match the value expected for the Hox/Hred transition. The change in rate of irreversible transformation of the enzyme–CO complex and the change in kin occur at the same potential, which suggested that the Hred state is irreversibly degraded after it binds CO. DFT was used to carry out geometry optimization of the partially oxidized and one-electron reduced forms of the H cluster bound to exogenous CO (such enzyme forms are termed Hox-CO and Hred-CO in the following). The experimental free energy of formation of Hox-CO, deduced from the ratio of kout over kin, is reasonably reproduced by calculation (see also ref. 189), although it must be noted that the ±2 kcal mol−1 uncertainty in the calculated value corresponds to a large difference in terms of Kd, a factor of 800. The calculations showed that in Hox-CO, the H cluster is stable, while in the case of Hred-CO, the Fep-S(Cys) bond that covalently attaches the diiron cluster to the enzyme is cleaved (leading to Hox−1(a) in Fig. 10). This behaviour can be qualitatively rationalized simply by using electron count rules: in Hred, the iron atoms already have 18 valence electrons, a configuration which is particularly stable; upon coordination of an additional CO ligand, the weakest bond (the Fep-S(Cys) bond according to DFT) has to be cleaved if the 18-electron rule is still to be fulfilled. The resulting [Fe2(μ-SR)2(CO)4(CN)2]2− complex is a stable species, which explains why the reaction of Hred with CO is partly irreversible. Following bond rupture, the fate of the diiron subcluster should depend on the surrounding protein matrix, and Baffert and coworkers considered as unlikely that the diiron site is released from the protein because the H cluster is deeply buried and shielded from the solvent.186
The reverse reaction, that is, transfer of [Fe2(μ-SR)2(CO)4(CN)2]2− (a 2Fe(I) precursor of the diiron subsite) from the solvent to the active site pocket of an apo form of [FeFe]-hydrogenase, has recently been observed by Happe and collaborators.16,190 This implies that the organometallic complex is able to autonomously integrate into the protein core, and to covalently bind the [4Fe4S] subsite with concomitant release of one carbonyl ligand. However, it is believed that insertion of the 2Fe subcluster occurs through a cationically charged channel that collapses following incorporation.191
This is consistent with the theoretical investigation by Stiebritz and Reiher, who used DFT to examine the regioselectivity of O2 binding.195,196 A subsequent study by Hong and Pachter, based on both MD simulations and DFT calculations, corroborated such picture.197 Blumberger and coworkers investigated the kinetics of the initial O2 binding step using DFT calculations:198 by parametrizing a range-separated density functional using high-level ab initio data as a benchmark, they could compute an activation free energy barrier of 13 kcal mol−1 for O2 attachment to Fed, and a binding free energy of −5 to −7 kcal mol−1. The rate of O2 binding could then be calculated from eqn (21) above. Converting the computed free energies into k2 using TST and adopting values for k1 and k−1 from MD simulations for [NiFe]-hydrogenase, they obtained values for kin of 3.6 s−1 mM−1 and 1.2 s−1 mM−1 for Cp and Dd enzymes, respectively, in fair agreement with the experimental values (2.5 s−1 mM−1 and 40 s−1 mM−1, respectively10). The reason the kinetics of O2 binding and release is different in the three homologous [FeFe]-hydrogenases for which such data have been published10,136,192 remains to be clarified.
In contrast with the above experimental and theoretical evidence that O2 targets the distal Fe on the 2Fe subcluster, X-ray absorption measurements indicated that the main structural consequence of the exposure to O2 is oxidative damage of the [4Fe4S] subcluster.194 Armstrong and coworkers concluded that the destruction of the 4Fe subcluster follows up O2 binding at the catalytic site of [FeFe]-hydrogenase and proposed two mechanistic scenarios: (i) the formation of a reactive oxygen species (ROS) that diffuses towards the [4Fe4S] subcluster and destroys it, or (ii) long-range damaging effects on the same iron–sulfur site exerted by an O2-derived superoxide ligand stably bound to Fed. Happe and collaborators199 ruled out the latter hypothesis by monitoring the time evolution of the X-ray absorption spectra of Cr [FeFe]-hydrogenase exposed to O2. Three kinetic phases could be distinguished. A fast oxygenation phase (faster than 4 s) is characterized by the formation of an increased number of Fe–CO bonds, elongation of the Fe–Fe distance in the binuclear subcluster, and oxidation of one iron ion; the subsequent inactivation phase (≈15 s) causes a 50% decrease of the number of 2.7 Å Fe–Fe distances in the [4Fe4S] subcluster and the oxidation of one more iron ion. The final degradation phase (<1000 s) leads to the disappearance of most Fe–Fe and Fe–S interactions and further iron oxidation. A DFT study again by Reiher and coworkers200 evidenced that the O2-derived species most likely involved in the degradation of the [4Fe4S] subcluster are the OOH radical and H2O2: the direct coordination of the former on the Fe atoms of the cubane is favored, whereas H2O2 reacts more easily with the cysteinyl sulfur ligands of the H cluster model.
In any case, all studies agree about the initial step of O2 attack, and this is relevant to the engineering of [FeFe]-hydrogenase that are more resistant to O2. In particular, based on the observation that electron transfer from the di-iron subsite to O2 makes oxygen attachment thermodynamically favorable, Blumberger and coworkers proposed that mutations that counteract this electron transfer may help to increase oxygen resistance.198 This working hypothesis should now be tested by characterizing the kinetics of inhibition of these mutants.
Taken as a whole, the above results raise hopes that the dialogue between theory and experiments in this challenging case of protein engineering will provide even more fruitful outcomes in the near future.
The key issue in this study was to rationalize the occurrence of different intermediates formed when [FeFe]-hydrogenase are oxidized in the presence of H2. Spectroscopy is difficult to use in this context, since turnover prevents equilibrium from being reached under these conditions, but a redox titration of the enzyme from C. reinhardtii followed by FTIR showed that full oxidation in the absence of H2 destroys the H cluster,44 and PFV experiments demonstrated that if H2 is present, the enzyme inactivates reversibly (at least partly reversibly) at high potential.202
Previous experiments on bio-inspired model complexes203 suggested that oxidation of Hox prior to H2 binding could trigger coordination of the pendant amine in the H cluster to the distal iron atom (Fed); formation of such bond would inactivate the enzyme by preventing H2 binding to Fed. We considered an intramolecular reaction of this kind as a first hypothesis for the mechanism of reversible oxidative inactivation, but we had to rule it out based on the results of DFT calculations. Indeed, a small model of the H cluster in overoxidized state did show barrierless formation of Fed–N bond along geometry optimization, but no such bond is formed when relevant portions of the protein are also included in the model.204
Chronoamperometry experiments can be analysed in a qualitative manner, to observe that the enzyme activates or inactivates, but we have also developed methods for precisely measuring the rates of the transformations in experiments where the electrode potential is repeatedly stepped up and down to trigger (in)activation.6,205,206 Analysing experiments such as those in Fig. 12C, we demonstrated that [FeFe]-hydrogenase undergoes both reversible and irreversible inactivation at high potential. The activity loss, evidenced by a decrease in H2 oxidation current, is clearly bi-exponential, which we interpret as an evidence that the active species (Hox) reversibly converts into two inactive species. Moreover, the dependence on pH of the two rate constants of reactivation of the inactive states indicates that the formation of each inactive species corresponds to a one-electron oxidation of the active site that is coupled to the loss of one proton. This is remarkable because the H cluster has only one acidic proton, on the pendant amine, which should be tightly bound (indeed, DFT calculations suggest that deprotonation leads to the cleavage of one of the C–S bonds within DTMA). Our observation is therefore inconsistent with the former hypothesis that inactivation results from the intramolecular binding of the nitrogen atom of dtma.
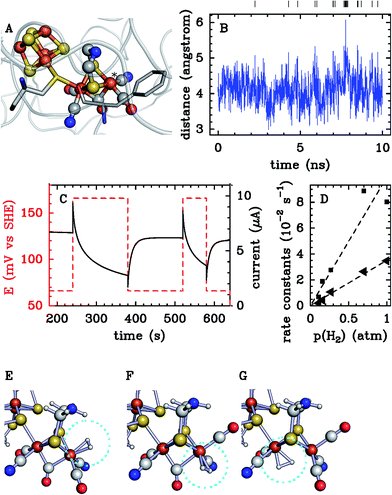 | ||
| Fig. 12 Investigation of the mechanism of oxidative inactivation of [FeFe]-hydrogenase. (A) The active site H cluster of [FeFe] hydrogenases, and its surroundings (adapted from PDB 3C8Y).201 The vacant coordination position on the distal iron is marked by an asterisk. The phenylalanine residue is discussed in the text. (B) Results from MD calculations: thermal fluctuations of the distance between the distal Fe atom of the H cluster (Fed) and the δ2C atom of Phe as a function of simulation time. The vertical lines show the moments when the distance is greater than 5 Å. (C) Electrochemical study. Sequence of potential steps applied to the electrode (red) and the resulting catalytic current (black). (D) Dependence of inactivation rate constants (measured from data such as those in panel C) on H2 partial pressure. (E–G) Results of DFT calculations. (E) Structures of the “normal” H2 adduct. (F) and (G) Structures of the two inactive adducts. Adapted from ref. 8. | ||
In search of the origin of the two protons released upon oxidation, we were tempted to consider that inactivation could result from the binding of a water molecule; indeed, Fed–OH2 bond formation would make water significantly acid. An oxygen atom bound to Fed is present in the models of the crystal structure of Clostridium pasteurianum [FeFe]-hydrogenase,201,207 but it was difficult to imagine that there could be two isomers of this water complex, whereas the electrochemical data clearly reveal the formation of two distinct, inactive species.
Another ligand whose acidity increases upon metal binding is H2. With this idea in mind, we examined the dependence of the reversible inactivation rate constants on H2 partial pressure; the experimental results in Fig. 12D showed that the two rate constants of inactivation are proportional to H2 concentration, meaning that regarding each of the two inactive species, H2 binding is actually the first step of the inactivation reaction. This led us to look for three distinct modes of H2 binding to the H cluster, two of which would be non-productive. Since the only vacant coordination site is on Fed, we hypothesized that alternative coordination sites may be created after the movement of the intrinsic CO ligand that is bound to Fed to an axial position, and/or the movement of the bridging CO to a terminal position on Fed (Fig. 10, Hox(b), (c) and (d) isomers); we considered as unlikely that the CN− ligand on Fed would move, because it is bound to a conserved lysine residue by a hydrogen bond.208 Inspection of the protein crystal structure indicates that the interconversion among the three possible conformers of the H cluster may be impeded by the presence of the bulky side chain of a conserved phenylalanine residue (F234 in Cr hydrogenase) shown in Fig. 12A. However, molecular dynamics calculations showed that thermal fluctuations of the structure are sufficiently large to allow the movements of iron-bound carbonyl ligands and the isomerisation of the active site (Fig. 12B). We used DFT to describe the intermediates involved in the inactivation process. DFT confirmed (through the comparison of reaction energies) that H2 binding can occur not only on the “normal” binding site (Fig. 12E), but also on two minor (i.e. higher in energy) vacant coordination sites (Fig. 12F & G). The calculations suggest that the H–H bond is cleaved in all cases (Fig. 10), but binding on the abnormal sites leads to species that are essentially inactive, because no base is sufficiently close to the coordinated H2 molecule to quickly accept the proton that is produced upon heterolytic cleavage.
This mechanism is supported by other experimental findings, such as the effect of replacing phenylalanine with tyrosine (which prevents isomerisation and slows down reversible inactivation), and the fact that the two inactive states are protected against O2 attack (the coordination sphere of Fed is complete when H2 binds to abnormal positions). The electrochemical data also show that the two H2-bound oxidized forms are not destroyed at high potential, unlike the fully oxidized H2-free H cluster (Hox+1(b) in Fig. 10); this is consistent with the previous observation of Lubitz and coworkers;44 we therefore hypothesised that the oxidative, irreversible inactivation arises from the attack of the distal Fed by a nucleophilic molecule (e.g. water) which competes with H2 binding.
Overall, this is a case where all experiments and calculations converge on the conclusion that the H cluster is more flexible, and its chemistry more versatile, than had been anticipated based on the crystal structure. This may be relevant in the case of other inorganic active sites.
4.4 Long range proton transfer (PT)
The catalytic cycles of the redox enzymes that we discuss here involve transfers of protons and electrons over long distances, between the active site and the solvent or the redox partner. The crystal structures of hydrogenases and CODH immediately give the information about the electron transfer pathways, which is a chain of FeS clusters. However, experimental information about the kinetics of elementary ET steps along this chain is scarce,127,212 and calculations of ET rates virtually non-existent (this contrasts with the situation where hemes mediate long range electron transfer84,213–218).In contrast, the path taken by protons cannot always be deduced from the X-ray structure in a straightforward manner, and calculations by different authors sometimes give different results (in the case of [NiFe]-hydrogenase, the PT pathway is still elusive). Measuring the rate of PT in an enzyme is straightforward only if PT is the rate limiting step, as occurs with carbonic anhydrase. Using site-directed mutagenesis to identify a PT pathway may prove particularly challenging, as illustrated below.
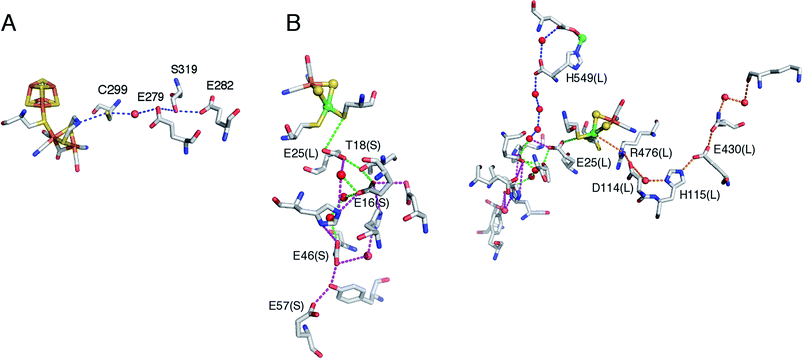 | ||
| Fig. 13 Putative proton transfer pathways in [FeFe] (panel A) and [NiFe]-(panel B) hydrogenases. In A, we number the amino acids according to the sequence of C. Pasteurianum [FeFe]-hydrogenase (pdb 3C8Y). The equivalent pathway in D. desulfuricans [FeFe]-hydrogenase is C178/E156/S198/E159. In B, the letters S and L between brackets are used to indicate that the amino acid is in the small or the large subunit of the dimer, respectively. We show in green and blue the pathways identified by Volbeda and coworkers in ref. 209, in purple the pathway proposed by Teixeira et al. in ref. 210, in orange the pathway proposed by Carrondo et al. in ref. 211. | ||
Hong and collaborators219 used a combination of DFT and QM/MM molecular dynamics simulations to study plausible PT pathways from the enzyme surface to the H cluster. Although free energies were not computed and therefore this study provided only qualitative information, the results are consistent with experimental evidences, and suggest a mechanism in which protons move from E282 to E279 via S319 and from E279 to C299 via water612. Ginovska-Pangovska et al.220 carried out a series of classical MD simulations in the wild type enzyme, as well as in a series of mutants, starting from the assumption that a well-defined and stable hydrogen bonding network is fundamental for efficient PT. Their results also support the pathway shown in Fig. 13A and suggest the existence of a persistent hydrogen bonded core (residues C299 to S319), with less persistent hydrogen bonds at the ends of the pathway for both H2 release and H2 uptake. Long et al.221 combined classical MD simulations, free energy perturbation and QM/MM calculations to quantitatively investigate the kinetics and thermodynamics of the PT pathway described by Hong and collaborators.219 It turned out that the side chains of E279 and E282 could adopt two different conformations, depending on their protonation state, and are well suited to play the role of proton shuttles. In particular, a proton from bulk water can enter the protein through E282, and then be transferred to C299 via pathways that involve E279 and S319.
The importance of S319 and C299 was supported by running calculations with in silico mutants: according to the analysis of the QM/MM MD simulation trajectories, the S319A and C299S mutations prevent PT during the simulation time.219 The effect of single substitutions (C299S, E279D and E282D) has also been assessed in silico by examining the disruption in the hydrogen bonding network.220
The C299S mutant is indeed inactive in H2 evolution according to three independent investigations.223–225 The enzyme retains activity only when C299 is replaced by aspartic acid.225 It has been observed that the C299A, C299S, E279D, E279L and S319A mutants have no H2 evolution activity, but 5 to 30% residual H2 oxidation activity, whereas the E282D and E282L mutants have 5–30% residual activity in both directions.223 The authors rule out the relevance of a second putative PT pathway starting from C299, passing through several modelled water molecules and S298, and ending at the non-conserved K571 residue at the enzyme surface by showing that S298 is not critical for activity (the S298A mutation has no effect).
On the basis of calculations, and assuming E25(L) as the starting point, complete pathways have been proposed (Fig. 13B), using structures of enzymes from D. fructosovorans,209D. gigas210 and D. vulgaris.228 In particular, Baptista and collaborators210 used a combination of Poisson–Boltzmann and Monte Carlo simulations, as well as a distance-based network analysis, to investigate possible proton pathways in D. gigas [NiFe]-hydrogenase, considering different pH values. Poisson–Boltzmann and Monte Carlo techniques were used to compute the pKa values of protonatable groups within the protein, whereas the distance-based network analysis was used to find likely pathways for the proton transport. A PT pathway was proposed between the active site and the surface that mainly involves glutamate and histidine residues: E18(L), H20(L), H13(S), E16(S), Y44(S), E46(S), E57(S), E73(S), and some water molecules (purple in Fig. 13). Fdez Galván et al.209 carried out a QM/MM study of the [NiFe]-hydrogenase from D. fructosovorans, computing reaction and activation energies for plausible pathways. In this case, the calculations were carried out not only on the crystallographic structure, but also considering several structures of the protein obtained from MD simulations. Higher level quantum chemical (DFT) corrections were also made to some of the calculated energy profiles. The pathway characterized by the most favorable energy profile involves PT via E25(L), E16(S), and E46(S) (green in Fig. 13), and corresponds approximatively to the pathway proposed by Teixeira et al. A second pathway (blue in Fig. 13), which involves E25(L), H549(L), and E53(L), was characterized by a less favorable reaction energy profile. Notably, Fdez Galván et al. underlined that the results obtained in their work, as well as in the study by Teixeira et al.,210 could not be considered conclusive because only a limited set of possible pathways was examined. In addition, only “static” pathways were considered, not considering possible alternatives forms produced by medium- or large-scale movements of the protein. In a later work, Summer and Voth228 studied PT in D. vulgaris Miyazaki F [NiFe]-hydrogenase using multi-state empirical valence bond (MS-EVB) reactive MD simulations, coupled to an enhanced path sampling methodology. MS-EVB, which is a molecular-mechanics approach that dynamically allows chemical bonds to break and form during MD simulations, was coupled with metadynamics, which can be used to find complex, nonlinear minimum free-energy pathways. In contrast with the previous computational studies, this methodology allowed to find unbiased PT pathways, i.e. without making a priori assumptions. Each simulation was initialized with a hydronium near residue E34(L), which is the assumed initial site in the PT chain, and three PT pathways were found. The preferred pathway, as deduced considering the frequency with which this pathway was found in all active site geometries and oxidation states under consideration, is in agreement with previous proposals, and involves H13(S), E16(S), T18(S), H36(L), E46(S), E57(S), and E75(S). Notably, the residues E16(S), T18(S) and E75(S) (E16(S), T18(S), and E73(S) in D. gigas) are conserved in the [NiFe]-hydrogenases from all Desulfovibrio species.
A completely different pathway starting with R476 of the large subunit has been proposed on the basis of the examination of the structure of D. desulfuricans hydrogenase211 and recently supported using calculations with the structure of the [NiFe]-enzyme from D. vulgaris.229 The observation that the sequences of the large subunits of almost all membrane-bound [NiFe]-hydrogenases show a highly conserved histidine-rich region, prompted Kovács and collaborators229 to carry out a computational and experimental study on the [NiFe]-hydrogenase from T. roseopersicina. Only two of these conserved histidines are present in the cytoplasmic hydrogenase (H104 and H110, in T. roseopersicina, H124 and H130 in D. vulgaris). Since the structure of the enzyme from T. roseopersicina has not yet been determined, and considering that a homology model could not be used to propose possible proton-hopping mechanisms due to the fact that the positions of structural water molecules could not be predicted, the authors analyzed the X-ray structure of the [NiFe]-hydrogenase from D. vulgaris Miyazaki F. The protonation state of the aminoacids at pH 7.4 and the preferred orientation of the structural water molecules were predicted minimizing the total free energy of the system. Based on the analysis of networks of hydrogen bonds, it was concluded that, among the conserved His residues, only H104 plays an important role in the enzyme function, suggesting that this residue could be part of an alternative PT route involving R487, H104 and D103.
The above results obtained in the computational investigations highlight peculiar problems connected to the prediction of PT pathways. First of all, it should be noted that to properly model PT in proteins one should not only take into account proton migration between different sites (which is a reactive event), but also consider the dynamics of the protein, and the possible involvement of solvent molecules in the PT chain. The most rigorous approach to study such process in an unbiased way would imply to use QM methods to model both the reactive and dynamical behavior of the system, which is clearly prohibitive. Therefore, in a more realistic way, PT pathways have to be studied using complex ad hoc computational schemes, either by postulating a priori possible pathways, or without any bias but using a more qualitative level, which necessarily includes some empirical parameters. In this context, the different computational approaches discussed above have been very helpful for the suggestion and evaluation of plausible PT pathways, even if the comparison of results obtained from different methods is challenging.
It is not easier to discriminate between the three main putative pathways in [NiFe]-hydrogenase using site-directed mutagenesis.
The hypothesis that the first PT relay is E25(L) was supported by site-directed studies, showing that replacing E25 with a non-protonatable glutamine abolishes PT in the enzyme from D. fructosovorans230 and the hydrogen-sensor hydrogenase from Ralstonia eutropha.231 That the active site is functional in the two E25(L)Q mutants was confirmed by the observation that they retain the ability to convert ortho and para dihydrogen.232
In contrast, the relevance of the rightmost pathway in Fig. 13B is supported by the characterization of site-directed mutants of the enzyme from T. roseopersicina: the replacement of E14 (E25(L) in D. fructosovorans) with a glutamine results in only a two-fold decrease of the H2 oxidation/production rates,229 whereas the D103L, H104A and H104F have little activity (D. fructosovorans numbering R476(L), D123(L), H115(L)). The function of the arginine shown in Fig. 13B cannot be tested by site-directed mutagenesis: the attempts to produce the R476K and R476L mutants of D. fructosovorans [NiFe]-hydrogenase and R487I of T. roseopersicina hydrogenase failed, the bacteria did not produce a mature form of the enzyme (unpublished results of ours and ref. 229). Since the amino acids involved in the two pathways are present in both hydrogenases (T. roseopersicina and D. fructosovorans) it is unclear how a single pathway can be functional in each enzyme.
Overall, testing the putative PT pathways in hydrogenases and other complex metalloenzymes appears to be very difficult for a number of reasons.
(1) In contrast to the case of carbonic anhydrase discussed below, there is no indication that PT limits the rate of H2 oxidation, H2 production or isotope exchange in WT [NiFe]-hydrogenase. This implies that a mutation that decreases slightly or increases the rate of PT may have no apparent effect. There is no experimental method that measures the rate of single PT events in hydrogenases. Any quantitative comparison between the results of computational and experimental characterization of site-directed mutants is therefore impossible.
(2) Unlike electron transfer pathways, the putative PT pathways may be highly ramified. Even the E25(L)-E57(S) pathway depicted in Fig. 13B involves many parallel routes. If they were functional, this would imply that several branches of a ramified pathway have to be blocked in a single mutant in order to observe an effect.
(3) Another problem is very general regarding studies based on site-directed mutagenesis: it is not always possible to make sure that substituting an amino acid has no side effects. There are examples in the literature where a mutation intended to interrupt a PT pathway does not have the expected effect because a water molecule is stabilized in the mutant and substitutes for the missing side chain.233
It may also be that structural rearrangements remote from the site of the mutation disrupt the hydrogen bond network or create new PT pathways. Regarding the works cited in this section, none of the mutants have been crystallized to make sure that such effects are not the cause of the observed phenotypes. The (unpublished) observation of ours that the E46(S)Q mutant of D. fructosovorans [NiFe]-hydrogenase has approximatively 50% of the WT H2 oxidation/production rates may suggest that E46(S) is not essential, but only if we can rule out the above mentioned artifacts. In contrast, we have observed that the E16(S)Q and E16(S)V mutations in D. fructosovorans [NiFe]-hydrogenase severely affected both H2 production/oxidation and isotope-exchange activity (unpublished), but it is not unambiguous evidence that PT is impaired in these mutants.
Worse, a mutation design to assess a PT pathway may also affect steps others than proton transfer. The T18(S) amino acid shown in Fig. 13B is next to a cysteine ligand of an electron transfer cluster (C19(S)) and its backbone shapes the substrate gas channel. Replacing T18(S) may affect the activity in a way that is mistakenly interpreted as revealing the disruption of a PT pathway.
(4) Last, the mutation of a side chain putatively involved in PT sometimes prevents protein folding. We have not been able to replace H549(L), which is a direct ligand of a putative Mg ion (turquoise in Fig. 13B) and appears to have a structural role. We also failed to discriminate between the two pathways starting with E25(L) by examining the effect of replacing the E57(S) and H549(L) residues, because the mutants we constructed could not be produced (E57Q, H549R, H549Q, H549V in D. fructosovorans [NiFe]-hydrogenase; unpublished results).
Overall, regarding PT in hydrogenases, we must acknowledge that rather limited results have been achieved since it became possible (in the late 1990's) to use site directed mutagenesis to test the numerous putative pathways detected in the crystal structures. This is because there is no direct measurement of the rate of PT in hydrogenase, and no strong conclusion about the effect of a mutation can be reached if the mutant of interest is not fully characterized using crystallography, spectroscopy, kinetic methods, etc.
The mammalian enzyme carbonic anhydrase II (CAII) catalyses CO2 hydration into HCO−3 and the reverse reaction, which are involved in various physiological processes:
| CO2 + H2O ⇌ HCO−3 + H+ | (35) |
The active site is a Zn centre coordinated by three His nitrogen atoms and one OH− ligand. The catalytic cycle includes a chemical step:
| CO2 + ZnOH− + H2O ⇌ ZnH2O + HCO−3 | (36) |
| ZnH2O + His64 ⇌ ZnOH− + His64, H+ | (37a) |
| His64, H+ + B ⇌ His64 + BH+ | (37b) |
The maximum turnover rate of CAII is 106 s−1 for the hydration reaction and 5 × 105 s−1 for the inverse reaction, which makes this reaction one of the fastest catalyzed reactions. Both rate constants were shown to decrease four-fold when the reactions took place in D2O and it was soon demonstrated that intramolecular PT (reaction (37a)) is rate limiting. The activation free energy deduced from the temperature dependence of the catalytic constant of the hydration reaction is ΔG‡ = 9.0 kcal mol−1 at 25 °C. Carbonic anhydrase is one of the rare enzymes in which the chemical step of catalysis is so fast that intramolecular PT is rate limiting, which allows this transfer to be studied in detail. Several mutated forms of the enzyme were prepared to elucidate the various factors which determine the PT rate. Replacing His64 by alanine decreased the rates 20-fold, but they were restored when proton donors like imidazole and pyridine were added to the solution. In another series of mutants, the variation of the PT rate as a function of ΔpKa = pKa(ZnH2O) − pKa(His64) could be studied. Similar studies were carried out on an isoenzyme, CAIII, were residue 64 is a lysine and proton transfers are two orders of magnitude slower. The crystal structure of CAII revealed that Zn and His64 are 7 Å apart and that they are connected by a network of hydrogen-bonded water molecules. Moreover, the orientation of His64 with respect to the active site can easily change from inward to outward, Fig. 2D. This rich set of data has motivated a number of theoretical studies. To specify the role of His64, the PMF was first calculated with and without His64.234 The calculated values of pKa(ZnH2O), pKa(His64) and ΔG‡ were in good agreement with the data only when His64 was present in the inward orientation. The effect of the His64 to Ala mutation and the rescue by imidazole were also studied. Warshel's group was able to reproduce the variation of the PT rate as a function of ΔpKa in CAIII by using a simplified PT chain made of His64, a water molecule and ZnOH− (ref. 235). These studies underscore the importance of thermodynamic factors like the pKas of His64, of water molecules and more importantly of ZnH2O, which must be close to 7 to ensure catalysis in both directions.
5 Conclusion
In this review we have shown how experimental and computational information can be combined to obtain mechanistic insight into enzyme catalysis that would not be possible to achieve by experimental or computational work alone. We have illustrated this point by discussing a few selected examples, focussing on enzymes that are relevant in the context of renewable fuel production: hydrogenases and carbon-monoxide dehydrogenase.For reasons that we have discussed in the introduction, the catalytic mechanisms of enzymes that use inorganic active sites, such as those discussed in this review, is often very difficult to study. Theoretical methods have been invaluable for predicting and understanding the molecular structure of intermediates by calculating their spectroscopic signatures, but the interplay between experiments and theory should also be useful for learning about the reactivity of these intermediates, and, about the kinetics of their chemical transformations. In particular, with regard to enzyme kinetics, the synergy arises because experimental methods typically report phenomenological rate constants characterising the overall process, whereas computational methods can help disentangle them to a set of rate constants of well defined elementary reaction steps. The ability to devise well defined model system, with infinite spatial resolution, is probably the greatest advantage of computational methods. Finding ways to connect computations on molecular models to actual experimental observations is arguably the greatest challenge.
Regarding the relative contributions of experimentalists and theoreticians in the elucidation of enzyme mechanisms, the question of which of the two plays the most important role is flawed, because the question assumes a two-step strategy where an initial proposal is simply followed by confirmation or refutation. In this review, we have attempted to describe another strategy where experimentalist and theoreticians work hand in hand and combine their expertise to obtain an answer more quickly and, hopefully, spread it over fewer papers.
Acknowledgements
This paper was partly written during a two-week residency in Marseille funded by IMéRA, Institut d'études avancées de l'Université d'Aix-Marseille (http://imera.univ-amu.fr/). P.-H.W. acknowledges the Ministry of Education, Republic of China (Taiwan), for a Ph.D. scholarship. J. B. acknowledges the Royal Society for a University Research Fellowship and the Engineering and Physical Sciences Research Council (EPSRC research grant EP/J015571/1) for financial support. L. D. G. acknowledges support from Ministero dell'Istruzione, dell'Universita e della Ricerca (Prin 2010M2JARJ). The Marseille team acknowledges CNRS, Aix Marseille University, Région PACA, ANR (ANR12BS080014) for funding, and support from FrenchBIC (http://frenchbic.cnrs.fr).References
- C. Léger and P. Bertrand, Chem. Rev., 2008, 108, 2379–2438 CrossRef PubMed.
- O. Rudiger, J. M. Abad, E. C. Hatchikian, V. M. Fernandez and A. L. de Lacey, J. Am. Chem. Soc., 2005, 127, 16008–16009 CrossRef PubMed.
- C. Baffert, K. Sybirna, P. Ezanno, T. Lautier, V. Hajj, I. Meynial-Salles, P. Soucaille, H. Bottin and C. Léger, Anal. Chem., 2012, 84, 7999–8005 CrossRef CAS PubMed.
- C. Léger, F. Lederer, B. Guigliarelli and P. Bertrand, J. Am. Chem. Soc., 2006, 128, 180–187 CrossRef PubMed.
- V. Fourmond, C. Baffert, K. Sybirna, T. Lautier, A. Abou Hamdan, S. Dementin, P. Soucaille, I. Meynial-Salles, H. Bottin and C. Léger, J. Am. Chem. Soc., 2013, 135, 3926–3938 CrossRef CAS PubMed.
- A. A. Hamdan, P.-P. Liebgott, V. Fourmond, O. Gutiérrez-Sanz, A. L. De Lacey, P. Infossi, M. Rousset, S. Dementin and C. Léger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19916–19921 CrossRef PubMed.
- V. Hajj, C. Baffert, K. Sybirna, I. Meynial-Salles, P. Soucaille, H. Bottin, V. Fourmond and C. Léger, Energy Environ. Sci., 2014, 7, 715–719 CAS.
- V. Fourmond, C. Greco, K. Sybirna, C. Baffert, P.-H. H. Wang, P. Ezanno, M. Montefiori, M. Bruschi, I. Meynial-Salles, P. Soucaille, J. Blumberger, H. Bottin, L. De Gioia and C. Léger, Nat. Chem., 2014, 6, 336–342 CrossRef CAS PubMed.
- C. Léger, S. Dementin, P. Bertrand, M. Rousset and B. Guigliarelli, J. Am. Chem. Soc., 2004, 126, 12162–12172 CrossRef PubMed.
- P.-P. Liebgott, F. Leroux, B. Burlat, S. Dementin, C. Baffert, T. Lautier, V. Fourmond, P. Ceccaldi, C. Cavazza, I. Meynial-Salles, P. Soucaille, J. C. C. Fontecilla-Camps, B. Guigliarelli, P. Bertrand, M. Rousset and C. Léger, Nat. Chem. Biol., 2010, 6, 63–70 CrossRef CAS PubMed.
- J. C. Fontecilla-Camps, A. Volbeda, C. Cavazza and Y. Nicolet, Chem. Rev., 2007, 107, 4273–4303 CrossRef CAS PubMed.
- W. Lubitz, H. Ogata, O. Rüdiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148 CrossRef CAS PubMed.
- Y. Montet, P. Amara, A. Volbeda, X. Vernede, E. C. Hatchikian, M. J. Field, M. Frey and J. C. Fontecilla-Camps, Nat. Struct. Mol. Biol., 1997, 4, 523–526 CAS.
- M. Bruschi, M. Tiberti, A. Guerra and L. De Gioia, J. Am. Chem. Soc., 2014, 136, 1803–1814 CrossRef CAS PubMed.
- A. Silakov, B. Wenk, E. Reijerse and W. Lubitz, Phys. Chem. Chem. Phys., 2009, 11, 6592–6599 RSC.
- G. Berggren, A. Adamska, C. Lambertz, T. R. Simmons, J. Esselborn, M. Atta, S. Gambarelli, J.-M. M. Mouesca, E. Reijerse, W. Lubitz, T. Happe, V. Artero and M. Fontecave, Nature, 2013, 499, 66–69 CrossRef CAS PubMed.
- M. Can, F. A. Armstrong and S. W. Ragsdale, Chem. Rev., 2014, 114, 4149–4174 CrossRef CAS PubMed.
- Acetogenesis (Chapman & Hall Microbiology Series), ed. H. L. Drake, Springer, 1994 Search PubMed.
- P. Amara, J.-M. Mouesca, A. Volbeda and J. C. Fontecilla-Camps, Inorg. Chem., 2011, 50, 1868 CrossRef CAS PubMed.
- A. Warshel, J. K. Hwang and J. Aqvist, Faraday Discuss., 1992, 93, 225–238 RSC.
- D. N. Silverman and S. Lindskog, Acc. Chem. Res., 1988, 21, 30–36 CrossRef CAS.
- P. E. M. Siegbahn and F. Himo, J. Biol. Inorg. Chem., 2009, 14, 643–651 CrossRef CAS PubMed.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, Phys. Chem. Chem. Phys., 2012, 14, 12431–12441 RSC.
- T. A. A. Rokob, M. Srnec and L. Rulíšek, Dalton Trans., 2012, 41, 5754–5768 RSC.
- A. V. Nemukhin, B. L. Grigorenko, S. V. Lushchekina and S. D. Varfolomeev, Russ. Chem. Rev., 2012, 81, 1011–1025 CrossRef.
- P. E. Siegbahn and F. Himo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 323–336 CrossRef CAS.
- M. Leopoldini, T. Marino, M. d. C. Michelini, I. Rivalta, N. Russo, E. Sicilia and M. Toscano, Theor. Chem. Acc., 2007, 117, 765–779 CrossRef CAS.
- T. Marino, N. Russo and M. Toscano, J. Am. Chem. Soc., 2005, 127, 4242–4253 CrossRef CAS PubMed.
- O. Amata, T. Marino, N. Russo and M. Toscano, J. Am. Chem. Soc., 2011, 133, 17824–17831 CrossRef CAS PubMed.
- M. E. Alberto, T. Marino, N. Russo, E. Sicilia and M. Toscano, Phys. Chem. Chem. Phys., 2012, 14, 14943–14953 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1996, 100, 3349–3353 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- J. Andzelm, C. Kolmel and A. Klamt, J. Chem. Phys., 1995, 103, 9312 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- N. Rega, M. Cossi, V. Barone, C. Pomelli and J. Tomasi, Int. J. Quantum Chem., 1999, 73, 219–227 CrossRef CAS.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- U. Ryde, Dalton Trans., 2007, 607–625 RSC.
- U. Ryde, C. Greco and L. De Gioia, J. Am. Chem. Soc., 2010, 132, 4512–4513 CrossRef CAS PubMed.
- A. Silakov, C. Kamp, E. Reijerse, T. Happe and W. Lubitz, Biochemistry, 2009, 48, 7780–7786 CrossRef CAS PubMed.
- A. Volbeda, M. H. Charon, C. Piras, E. C. Hatchikian, M. Frey and J. C. Fontecilla-Camps, Nature, 1995, 373, 580–587 CrossRef CAS PubMed.
- H.-J. Fan and M. B. Hall, J. Am. Chem. Soc., 2001, 123, 3828–3829 CrossRef CAS PubMed.
- J. G. Norman, P. B. Ryan and L. Noodleman, J. Am. Chem. Soc., 1980, 102, 4279–4282 CrossRef CAS.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- L. Yu, C. Greco, M. Bruschi, U. Ryde, L. De Gioia and M. Reiher, Inorg. Chem., 2011, 50, 3888–3900 CrossRef CAS PubMed.
- J. W. Tye, M. Y. Darensbourg and M. B. Hall, J. Comput. Chem., 2006, 27, 1454–1462 CrossRef CAS PubMed.
- J. W. Tye, M. Y. Darensbourg and M. B. Hall, Inorg. Chem., 2008, 47, 2380–2388 CrossRef CAS PubMed.
- T. Ziegler and J. Autschbach, Chem. Rev., 2005, 105, 2695–2722 CrossRef CAS PubMed.
- S. P. de Visser, M. G. Quesne, B. Martin, P. Comba and U. Ryde, Chem. Commun., 2014, 50, 262–282 RSC.
- C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- F. Neese, J. Biol. Inorg. Chem., 2006, 11, 702–711 CrossRef CAS PubMed.
- J. L. Chen, L. Noodleman, D. A. Case and D. Bashford, J. Phys. Chem., 1994, 98, 11059–11068 CrossRef CAS.
- W. Pritzkow, J. Prakt. Chem., 1998, 340, 586–587 CrossRef CAS.
- J. Bigeleisen and M. G. Mayer, J. Chem. Phys., 1947, 15, 261 CrossRef CAS.
- A. Cornish-Bowden, Fundamental of Enzyme Kinetics, Portland Press., 2004 Search PubMed.
- M. G. Almeida, B. Guigliarelli, P. Bertrand, J. J. G. Moura, I. Moura and C. Léger, FEBS Lett., 2007, 581, 284–288 CrossRef CAS PubMed.
- V. Fourmond, C. Baffert, K. Sybirna, S. Dementin, A. Abou-Hamdan, I. Meynial-Salles, P. Soucaille, H. Bottin and C. Léger, Chem. Commun., 2013, 49, 6840–6842 RSC.
- M. Y. Okamura, R. A. Isaacson and G. Feher, Biochim. Biophys. Acta, Bioenerg., 1979, 546, 394–417 CrossRef CAS.
- A. Abou Hamdan, S. Dementin, P.-P. Liebgott, O. Gutierrez-Sanz, P. Richaud, A. L. De Lacey, M. Roussett, P. Bertrand, L. Cournac and C. Léger, J. Am. Chem. Soc., 2012, 134, 8368–8371 CrossRef CAS PubMed.
- R. O. Louro, T. Catarino, C. M. Paquete and D. L. Turnera, FEBS Lett., 2004, 576, 77–80 CrossRef CAS PubMed.
- M. Tegoni, M. C. Silvestrini, B. Guigliarelli, M. Asso, M. Brunori and P. Bertrand, Biochemistry, 1998, 37, 12761–12771 CrossRef CAS PubMed.
- D. L. Williams-Smith, R. C. Bray, M. J. Barber, A. D. Tsopanakis and S. P. Vincent, Biochem. J., 1977, 167, 593–600 CrossRef CAS PubMed.
- V. Fourmond, B. Burlat, S. Dementin, P. Arnoux, M. Sabaty, S. Boiry, B. Guigliarelli, P. Bertrand, D. Pignol and C. Léger, J. Phys. Chem. B, 2008, 112, 15478–15486 CrossRef CAS PubMed.
- J. M. Savéant, Elements of molecular and biomolecular electrochemistry, John Willey & sons, Inc., 2006 Search PubMed.
- K. Chen, J. Hirst, R. Camba, C. A. Bonagura, C. D. Stout, B. K. Burgess and F. A. Armstrong, Nature, 2000, 405, 814–817 CrossRef CAS PubMed.
- A. K. Jones, R. Camba, G. A. Reid, S. K. Chapman and F. A. Armstrong, J. Am. Chem. Soc., 2000, 122, 6494–6495 CrossRef CAS.
- C. Léger, A. K. Jones, W. Roseboom, S. P. J. Albracht and F. A. Armstrong, Biochemistry, 2002, 41, 15736–15746 CrossRef.
- P. Bertrand, B. Frangioni, S. Dementin, M. Sabaty, P. Arnoux, B. Guigliarelli, D. Pignol and C. Léger, J. Phys. Chem. B, 2007, 111, 10300–10311 CrossRef CAS PubMed.
- C. Léger, A. K. Jones, S. P. J. Albracht and F. A. Armstrong, J. Phys. Chem. B, 2002, 106, 13058–13063 CrossRef.
- D. Yepes, R. Seidel, B. Winter, J. Blumberger and P. Jaque, J. Phys. Chem. B, 2014, 6850–6863 CrossRef CAS PubMed.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218 CrossRef CAS.
- J. Blumberger and M. L. Klein, J. Am. Chem. Soc., 2006, 128, 13854 CrossRef CAS PubMed.
- J. Blumberger, Phys. Chem. Chem. Phys., 2008, 10, 5651 RSC.
- J. Moens, R. Seidel, P. Geerlings, M. Faubel, B. Winter and J. Blumberger, J. Phys. Chem. B, 2010, 114, 9173–9182 CrossRef CAS PubMed.
- Y. Tateyama, J. Blumberger, T. Ohno and M. Sprik, J. Chem. Phys., 2007, 126, 204506 CrossRef PubMed.
- H. Oberhofer and J. Blumberger, Angew. Chem., Int. Ed., 2010, 49, 3631 CrossRef CAS PubMed.
- M. H. M. Olsson, G. Hong and A. Warshel, J. Am. Chem. Soc., 2003, 125, 5025 CrossRef CAS PubMed.
- M. Breuer, P. Zarzycki, J. Blumberger and K. M. Rosso, J. Am. Chem. Soc., 2012, 134, 9868–9871 CrossRef CAS PubMed.
- A. P. Gamiz-Hernandez, G. Kieseritzki, H. Ishikita and E. W. Knapp, J. Chem. Theory Comput., 2011, 7, 742 CrossRef CAS.
- M. Breuer, K. M. Rosso, J. Blumberger and J. N. Butt, Multi-heme Cytochromes: Structures, Functions and Opportunities, J. R. Soc., Interface, 2014 Search PubMed , under review.
- B. M. Fonseca, C. M. Paquete, C. A. Salgueiro and R. O. Louro, FEBS Lett., 2012, 586, 504–509 CrossRef CAS PubMed.
- M. Pessanha, E. L. Rothery, C. S. Miles, G. A. Reid, S. K. Chapman, R. O. Louro, D. L. Turner, C. A. Salgueiro and A. V. Xavier, Biochim. Biophys. Acta, Bioenerg., 2009, 1787, 113–120 CrossRef CAS PubMed.
- J. Alric, J. Lavergne, F. Rappaport, A. Vermeglio, K. Matsuura, K. Shimada and K. V. P. Nagashima, J. Am. Chem. Soc., 2006, 128, 4136–4145 CrossRef CAS PubMed.
- M. R. Gunner, M. A. Saleh, E. Cross, A. ud Doula and M. Wise, Biophys. J., 2000, 78, 1126 CrossRef CAS PubMed.
- D. S. Spencer, D. Weiss, W. E. Stites, B. Garcia-Moreno, J. J. Dwyer, A. G. Gittis and E. E. Lattman, Biophys. J., 1998, 74, A170 Search PubMed.
- J. J. Dwyer, A. G. Gittis, D. A. Karp, E. E. Lattman, D. S. Spencer, W. E. Stites and B. Garcia-Moreno, Biophys. J., 2000, 79, 1610–1620 CrossRef CAS PubMed.
- C. A. Fitch, D. A. Karp, K. K. Lee, W. E. Stites, E. E. Lattman and B. Garcia-Moreno, Biophys. J., 2002, 82, 3289–3304 CrossRef CAS PubMed.
- Y. Takayama, C. A. Castaneda, M. Chimenti, B. Garcia-Moreno and J. Iwahara, J. Am. Chem. Soc., 2008, 130, 6714–6715 CrossRef CAS PubMed.
- A. L. Hansen and L. E. Key, Proc. Natl. Acad. Sci. U. S. A., 2014, E1705–E1712 CrossRef CAS PubMed , ASAP.
- S. Farrjones, W. Wong, W. Gutheil and W. Bachovchin, J. Am. Chem. Soc., 1993, 115, 6813–6819 CrossRef CAS.
- P. Kukic, D. Farrell, L. P. McIntosh, B. Garcia-Moreno, K. S. Jensen, Z. Toleikis, K. Teilum and J. J. Nielsen, J. Am. Chem. Soc., 2013, 135, 16978–16976 CrossRef PubMed.
- E. Alexov, E. L. Mehler, N. Baker, A. M. Baptista, Y. Huang, F. Milletti, J. E. Nielsen, D. Farrell, T. Carstensen, M. H. M. Olsson, J. K. Shen, J. Warwicker, S. Williams and J. M. Word, Proteins: Struct., Funct., Bioinf., 2011, 79, 3260–3275 CrossRef CAS PubMed.
- C. Tanford and J. G. Kirkwood, J. Am. Chem. Soc., 1957, 79, 5333–5339 CrossRef CAS.
- Y. F. Song, J. J. Mao and M. R. Gunner, Biochemistry, 2003, 42, 9875–9888 CrossRef CAS PubMed.
- M. J. Ondrechen, J. G. Clifton and D. Ringe, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 12473–12478 CrossRef CAS PubMed.
- H. Ishikita, G. Morra and E. W. Knapp, Biochemistry, 2003, 42, 3882–3892 CrossRef CAS PubMed.
- T. Simonson and D. Perahia, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 1082–1086 CrossRef CAS.
- M. R. Gunner and E. Alexov, Biochim. Biophys. Acta, Bioenerg., 2000, 1458, 63–87 CrossRef CAS.
- C. N. Schutz and A. Warshel, Proteins: Struct., Funct., Genet., 2001, 44, 400–417 CrossRef CAS PubMed.
- J. Ho and M. L. Coote, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 649–660 CrossRef CAS.
- J. Ho and M. L. Coote, Theor. Chem. Acc., 2010, 125, 3–21 CrossRef CAS.
- J. Ho, C. J. Easton and M. L. Coote, J. Am. Chem. Soc., 2010, 132, 5515–5521 CrossRef CAS PubMed.
- A. M. Rebollar-Zepeda and A. Galano, Int. J. Quantum Chem., 2012, 112, 3449–3460 CrossRef CAS.
- M. Mangold, L. Rolland, F. Costanzo, M. Sprik, M. Sulpizi and J. Blumberger, J. Chem. Theory Comput., 2011, 7, 1951–1961 CrossRef CAS.
- J. R. Pliego and J. M. Riveros, J. Phys. Chem. A, 2001, 105, 7241–7247 CrossRef CAS.
- A. M. Rebollar-Zepeda, T. Campos-Hernandez, M. T. Ramirez-Silva, A. Rojas-Hernandez and A. Galano, J. Chem. Theory Comput., 2011, 7, 2528–2538 CrossRef CAS.
- H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2004, 55, 689–704 CrossRef CAS PubMed.
- J. H. Jensen, H. Li, A. D. Robertson and P. A. Molina, J. Phys. Chem. A, 2005, 109, 6634–6643 CrossRef CAS PubMed.
- Z. Y. Zhu and M. R. Gunner, Biochemistry, 2005, 44, 82–96 CrossRef CAS PubMed.
- R. E. Georgescu, E. G. Alexov and M. R. Gunner, Biophys. J., 2002, 83, 1731–1748 CrossRef CAS PubMed.
- J. Antosiewicz, J. A. McCammon and M. K. Gilson, Biochemistry, 1996, 35, 7819–7833 CrossRef CAS PubMed.
- L. Sandberg and O. Edholm, Proteins: Struct., Funct., Genet., 1999, 36, 474–483 CrossRef CAS.
- I. Muegge, P. X. Qi, A. J. Wand, Z. T. Chu and A. Warshel, J. Phys. Chem. A, 1997, 101, 825–836 CrossRef CAS.
- T. Simonson, J. Carlsson and D. A. Case, J. Am. Chem. Soc., 2004, 126, 4167–4180 CrossRef CAS PubMed.
- Y. Song, J. Mao and M. R. Gunner, J. Comput. Chem., 2009, 30, 2231–2247 CAS.
- Y. Y. Sham, Z. T. Chu, H. H. Tao and A. Warshel, Proteins: Struct., Funct., Genet., 2000, 39, 393–407 CrossRef CAS.
- J. A. Wallace and J. K. Shen, J. Chem. Theory Comput., 2011, 7, 2617–2629 CrossRef CAS.
- S. L. Williams, C. A. F. de Oliveira and A. J. McCammon, J. Chem. Theory Comput., 2010, 6, 560–568 CrossRef CAS PubMed.
- A. M. Baptista, P. J. Martel and S. B. Petersen, Proteins: Struct., Funct., Genet., 1997, 27, 523–544 CrossRef CAS.
- A. M. Baptista, V. H. Teixeira and C. M. Soares, J. Chem. Phys., 2002, 117, 4184–4200 CrossRef CAS.
- W. J. Ray, Biochemistry, 1983, 22, 4625–4637 CrossRef CAS PubMed.
- K. J. Laidler, J. Chem. Educ., 1988, 65, 250 CrossRef CAS.
- S. Dementin, B. Burlat, V. Fourmond, F. Leroux, P.-P. P. Liebgott, A. Abou Hamdan, C. Léger, M. Rousset, B. Guigliarelli and P. Bertrand, J. Am. Chem. Soc., 2011, 133, 10211–10221 CrossRef CAS PubMed.
- J. Gao, Molecular Dynamics Simulation of Kinetic Isotope Effects in Enzyme-Catalyzed Reactions, in Reaction Rate Constant Computations: Theories and Applications, ed. T. C. Keli Han, RSC, 2013 Search PubMed.
- J. Blumberger and M. L. Klein, Chem. Phys. Lett., 2006, 422, 210 CrossRef CAS.
- P. Bertrand, Molecular Modelling of Proton Transfer Kinetics in Biological Systems, in Reaction Rate Constant Computations: Theories and Applications, ed. T. C. Keli Han, RSC, 2013 Search PubMed.
- R. Elber, Curr. Opin. Struct. Biol., 2010, 20, 162–167 CrossRef CAS PubMed.
- T. Lautier, P. Ezanno, C. Baffert, V. Fourmond, L. Cournac, J. C. Fontecilla-Camps, P. Soucaille, P. Bertrand, I. Meynial-Salles and C. Léger, Faraday Discuss., 2011, 148, 385–407 RSC.
- S. Riistama, A. Puustinen, M. I. Verkhovsky, J. E. Morgan and M. Wikstrom, Biochemistry, 2000, 39, 6365–6372 CrossRef CAS PubMed.
- L. Salomonsson, A. Lee, R. B. Gennis and P. Brzezinski, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 11617–11621 CrossRef CAS PubMed.
- F. Leroux, S. Dementin, B. Burlat, L. Cournac, A. Volbeda, S. Champ, L. Martin, B. Guigliarelli, P. Bertrand, J. Fontecilla-Camps, M. Rousset and C. Léger, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 11188–11193 CrossRef CAS PubMed.
- G. Goldet, C. Brandmayr, S. T. Stripp, T. Happe, C. Cavazza, J. C. Fontecilla-Camps and F. A. Armstrong, J. Am. Chem. Soc., 2009, 131, 14979–14989 CrossRef CAS PubMed.
- V. H. Teixeira, A. M. Baptista and C. M. Soares, Biophys. J., 2006, 91, 2035 CrossRef CAS PubMed.
- J. Z. Ruscio, D. Kumar, M. Shukla, M. G. Prisant, T. M. Murali and A. V. Onufriev, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9204 CrossRef CAS PubMed.
- R. Baron, C. Riley, P. Chenprakhon, K. Thotsaporn, R. T. Winter, A. Alfieri, F. Forneris, W. J. H. van Berkel, P. Chaiyen, M. W. Fraaije, A. Mattevi and J. A. McCammon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10603 CrossRef CAS PubMed.
- M. D′Abramo, A. Di Nola and A. Amadei, J. Phys. Chem. B, 2009, 113, 16346 CrossRef PubMed.
- R. Elber and M. Karplus, J. Am. Chem. Soc., 1990, 112, 9161 CrossRef CAS.
- J. Cohen, K. Kim, M. Posewitz, M. L. Ghirardi, K. Schulten, M. Seibert and P. King, Biochem. Soc. Trans., 2005, 33, 80 CrossRef CAS PubMed.
- J. Cohen, K. Kim, P. King, M. Seibert and K. Schulten, Structure, 2005, 13, 1321 CrossRef CAS PubMed.
- J. Cohen, A. Arkhipov, R. Braun and K. Schulten, Biophys. J., 2006, 91, 1844 CrossRef CAS PubMed.
- J. Cohen and K. Schulten, Biophys. J., 2007, 93, 3591 CrossRef CAS PubMed.
- Y. Nishihara, S. Hayashi and S. Kato, Chem. Phys. Lett., 2008, 464, 220 CrossRef CAS.
- M. Ceccarelli, R. Anedda, M. Casu and P. Ruggerone, Proteins, 2008, 71, 1231 CrossRef CAS PubMed.
- L. Maragliano, G. Cottone, G. Ciccotti and E. Vanden-Eijnden, J. Am. Chem. Soc., 2009, 132, 1010 CrossRef PubMed.
- P. Wang, R. B. Best and J. Blumberger, J. Am. Chem. Soc., 2011, 133, 3548 CrossRef CAS PubMed.
- P. Wang, R. B. Best and J. Blumberger, Phys. Chem. Chem. Phys., 2011, 13, 7708 RSC.
- P. Wang and J. Blumberger, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6399 CrossRef CAS PubMed.
- P. Wang, M. Bruschi, L. De Gioia and J. Blumberger, J. Am. Chem. Soc., 2013, 135, 9493 CrossRef CAS PubMed.
- Y. Shomura, K.-S. Yoon, H. Nishihara and Y. Higuchi, Nature, 2011, 479, 253–256 CrossRef CAS PubMed.
- J. Fritsch, P. Scheerer, S. Frielingsdorf, S. Kroschinsky, B. Friedrich, O. Lenz and C. M. Spahn, Nature, 2011, 479, 249–252 CrossRef CAS PubMed.
- M.-E. E. Pandelia, D. Bykov, R. Izsak, P. Infossi, M.-T. T. Giudici-Orticoni, E. Bill, F. Neese and W. Lubitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 483–488 CrossRef CAS PubMed.
- R. Cammack, D. Patil, R. Aguirre and E. Hatchikian, FEBS Lett., 1982, 142, 289–292 CrossRef CAS.
- V. M. Fernandez, E. C. Hatchikian, D. S. Patil and R. Cammack, Biochim. Biophys. Acta, 1986, 883, 145–154 CrossRef CAS.
- S. L. Lamle, S. P. J. Albracht and F. A. Armstrong, J. Am. Chem. Soc., 2004, 126, 14899–14909 CrossRef CAS PubMed.
- J. A. Cracknell, A. F. Wait, O. Lenz, B. Friedrich and F. A. Armstrong, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20681–20686 CrossRef PubMed.
- M.-E. Pandelia, V. Fourmond, P. Tron-Infossi, E. Lojou, P. Bertrand, C. Léger, M.-T. Giudici-Orticoni and W. Lubitz, J. Am. Chem. Soc., 2010, 132, 6991–7004 CrossRef CAS PubMed.
- V. Fourmond, P. Infossi, M.-T. Giudici-Orticoni, P. Bertrand and C. Léger, J. Am. Chem. Soc., 2010, 132, 4848–4857 CrossRef CAS PubMed.
- M.-E. Pandelia, W. Nitschke, P. Infossi, M.-T. Giudici-Orticoni, E. Bill and W. Lubitz, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6097–6102 CrossRef CAS PubMed.
- M. J. Lukey, M. M. Roessler, A. Parkin, R. M. Evans, R. A. Davies, O. Lenz, B. Friedrich, F. Sargent and F. A. Armstrong, J. Am. Chem. Soc., 2011, 133, 16881–16892 CrossRef CAS PubMed.
- S. Frielingsdorf, J. Fritsch, A. Schmidt, M. Hammer, J. Lwenstein, E. Siebert, V. Pelmenschikov, T. Jaenicke, J. Kalms, Y. Rippers, F. Lendzian, I. Zebger, C. Teutloff, M. Kaupp, R. Bittl, P. Hildebrandt, B. Friedrich, O. Lenz and P. Scheerer, Nat. Chem. Biol., 2014, 10, 378–385 CrossRef CAS PubMed.
- A. Volbeda, P. Amara, C. Darnault, J.-M. Mouesca, A. Parkin, M. M. Roessler, F. A. Armstrong and J. C. Fontecilla-Camps, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5305–5310 CrossRef CAS PubMed.
- R. M. Evans, A. Parkin, M. M. Roessler, B. J. Murphy, H. Adamson, M. J. Lukey, F. Sargent, A. Volbeda, J. C. Fontecilla-Camps and F. A. Armstrong, J. Am. Chem. Soc., 2013, 135, 2694–2707 CrossRef CAS PubMed.
- A. Volbeda, Y. Montet, X. Vernède, E. Hatchikian and J. C. Fontecilla-Camps, Int. J. Hydrogen Energy, 2002, 27, 1449–1461 CrossRef CAS.
- T. Buhrke, O. Lenz, N. Krauss and B. Friedrich, J. Biol. Chem., 2005, 280, 23791–23796 CrossRef CAS PubMed.
- O. Duché, S. Elsen, L. Cournac and A. Colbeau, FEBS J., 2005, 272, 3899–3908 CrossRef PubMed.
- V. H. Teixeira, A. M. Baptista and C. M. Soares, Biophys. J., 2006, 91, 2035–2045 CrossRef CAS PubMed.
- B. Jähne, G. Heinz and W. Dietrich, J. Geophys. Res., 1987, 92, 10767 CrossRef.
- A. Akgerman and J. Gainer, Ind. Eng. Chem. Fundam., 1972, 11, 373 CAS.
- A. Akgerman and J. Gainer, J. Chem. Eng. Data, 1972, 17, 372 CrossRef CAS.
- D. R. Lide, CRC Handbook of Chemistry and Physics, CRC Press, 1995 Search PubMed.
- B. Kowert and N. Dang, J. Phys. Chem. A, 1999, 103, 779 CrossRef CAS.
- M. J. W. Frank, J. A. M. Kuipers and W. P. M. van Swaaij, J. Chem. Eng. Data, 1996, 41, 297 CrossRef CAS.
- E. L. Maynard and P. A. Lindahl, J. Am. Chem. Soc., 1999, 121, 9221 CrossRef CAS.
- J. Seravalli and S. W. Ragsdale, Biochemistry, 2000, 39, 1274 CrossRef CAS PubMed.
- C. Darnault, A. Volbeda, E. J. Kim, P. Legrand, X. Vernede, P. A. Lindahl and J. C. Fontecilla-Camps, Nat. Struct. Mol. Biol., 2003, 10, 271 CAS.
- T. I. Doukov, T. M. Iverson, J. Seravalli, S. W. Ragsdale and C. L. Drennan, Science, 2002, 298, 567 CrossRef CAS PubMed.
- T. I. Doukov, L. C. Blasiak, J. Seravalli, S. W. Ragsdale and C. L. Drennan, Biochemistry, 2008, 47, 3474 CrossRef CAS PubMed.
- X. Tan, H. Loke, S. Fitch and P. Lindahl, J. Am. Chem. Soc., 2005, 127, 5833 CrossRef CAS PubMed.
- A. Volbeda and J. Fontecilla-Camps, J. Biol. Inorg. Chem., 2004, 9, 525 CrossRef CAS PubMed.
- X. Tan, A. Volbeda, J. Fontecilla-Camps and P. Lindahl, J. Biol. Inorg. Chem., 2006, 11, 371 CrossRef CAS PubMed.
- M. Kumar, W. P. Lu, L. Liu and S. W. Ragsdale, J. Am. Chem. Soc., 1993, 115, 11646 CrossRef CAS.
- C. Baffert, L. Bertini, T. Lautier, C. Greco, K. Sybirna, P. Ezanno, E. Etienne, P. Soucaille, P. Bertrand, H. Bottin, I. Meynial-Salles, L. De Gioia and C. Léger, J. Am. Chem. Soc., 2011, 133, 2096–2099 CrossRef CAS PubMed.
- C. E. Foster, T. Krmer, A. F. Wait, A. Parkin, D. P. Jennings, T. Happe, J. E. McGrady and F. A. Armstrong, J. Am. Chem. Soc., 2012, 134, 7553–7557 CrossRef CAS PubMed.
- A. Adamska, A. Silakov, C. Lambertz, O. Rüdiger, T. Happe, E. Reijerse and W. Lubitz, Angew. Chem., Int. Ed., 2012, 51, 11458–11462 CrossRef CAS PubMed.
- L. Bertini, C. Greco, M. Bruschi, P. Fantucci and L. De Gioia, Organometallics, 2010, 29, 2013–2025 CrossRef CAS.
- J. Esselborn, C. Lambertz, A. Adamska-Venkatesh, T. Simmons, G. Berggren, J. Noth, J. Siebel, A. Hemschemeier, V. Artero, E. Reijerse, M. Fontecave, W. Lubitz and T. Happe, Nat. Chem. Biol., 2013, 9, 607–609 CrossRef CAS PubMed.
- D. W. Mulder, E. S. Boyd, R. Sarma, R. K. Lange, J. A. Endrizzi, J. B. Broderick and J. W. Peters, Nature, 2010, 465, 248–251 CrossRef CAS PubMed.
- C. Baffert, M. Demuez, L. Cournac, B. Burlat, B. Guigliarelli, P. Soucaille, P. Bertrand, L. Girbal and C. Léger, Angew. Chem., Int. Ed., 2008, 47, 2052–2055 CrossRef CAS PubMed.
- B. Bennett, B. J. Lemon and J. W. Peters, Biochemistry, 2000, 39, 7455–7460 CrossRef CAS PubMed.
- S. T. Stripp, G. Goldet, C. Brandmayr, O. Sanganas, K. A. Vincent, M. Haumann, F. A. Armstrong and T. Happe, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17331–17336 CrossRef CAS PubMed.
- M. T. Stiebritz and M. Reiher, Inorg. Chem., 2009, 48, 7127–7140 CrossRef CAS PubMed.
- M. T. Stiebritz and M. Reiher, Inorg. Chem., 2010, 49, 8645 CrossRef CAS.
- G. Hong and R. Pachter, ACS Chem. Biol., 2012, 7, 1268–1275 CrossRef CAS PubMed.
- A. Kubas, D. De Sancho, R. B. Best and J. Blumberger, Angew. Chem., Int. Ed., 2014, 53, 4081–4084 CrossRef CAS PubMed.
- C. Lambertz, N. Leidel, K. G. V. Havelius, J. Noth, P. Chernev, M. Winkler, T. Happe and M. Haumann, J. Biol. Chem., 2011, 286, 40614–40623 CrossRef CAS PubMed.
- M. K. Bruska, M. T. Stiebritz and M. Reiher, J. Am. Chem. Soc., 2011, 133, 20588–20603 CrossRef CAS PubMed.
- A. S. Pandey, T. V. Harris, L. J. Giles, J. W. Peters and R. K. Szilagyi, J. Am. Chem. Soc., 2008, 130, 4533–4540 CrossRef CAS PubMed.
- A. Parkin, C. Cavazza, J. Fontecilla-Camps and F. Armstrong, J. Am. Chem. Soc., 2006, 128, 16808–16815 CrossRef CAS PubMed.
- M. T. Olsen, T. B. Rauchfuss and S. R. Wilson, J. Am. Chem. Soc., 2010, 132, 17733–17740 CrossRef CAS PubMed.
- T. Miyake, M. Bruschi, U. Cosentino, C. Baffert, V. Fourmond, C. Léger, G. Moro, L. Gioia and C. Greco, J. Biol. Inorg. Chem., 2013, 18, 693–700 CrossRef CAS PubMed.
- V. Fourmond, P. Infossi, M.-T. Giudici-Orticoni, P. Bertrand and C. Léger, J. Am. Chem. Soc., 2010, 132, 4848–4857 CrossRef CAS PubMed.
- J. G. J. Jacques, B. Burlat, P. Arnoux, M. Sabaty, B. Guigliarelli, C. Léger, D. Pignol and V. Fourmond, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1801–1809 CrossRef CAS PubMed.
- J. W. Peters, W. N. Lanzilotta, B. J. Lemon and L. C. Seefeldt, Science, 1998, 282, 1853–1858 CrossRef CAS PubMed.
- C. Greco, M. Bruschi, P. Fantucci, U. Ryde and L. De Gioia, Chem.–Eur. J., 2011, 17, 1954–1965 CrossRef CAS PubMed.
- I. Fdez Galván, A. Volbeda, J. C. Fontecilla-Camps and M. J. Field, Proteins, 2008, 73, 195–203 CrossRef PubMed.
- V. H. Teixeira, C. M. Soares and A. M. Baptista, Proteins, 2008, 70, 1010–1022 CrossRef CAS PubMed.
- P. M. Matias, C. M. Soares, L. M. Saraiva, R. Coelho, J. Morais, J. Le Gall and M. A. Carrondo, J. Biol. Inorg. Chem., 2001, 6, 63–81 CrossRef CAS PubMed.
- S. Dementin, V. Belle, P. Bertrand, B. Guigliarelli, G. Adryanczyk-Perrier, A. Delacey, V. M. Fernandez, M. Rousset and C. Léger, J. Am. Chem. Soc., 2006, 128, 5209–5218 CrossRef CAS PubMed.
- D. N. Beratan, J. N. Betts and J. N. Onuchic, Science, 1991, 252, 1285–1288 CAS.
- M.-L. L. Tan, I. Balabin and J. N. N. Onuchic, Biophys. J., 2004, 86, 1813–1819 CrossRef CAS PubMed.
- T. R. Prytkova, I. V. Kurnikov and D. N. Beratan, J. Phys. Chem. B, 2005, 109, 1618–1625 CrossRef CAS PubMed.
- A. A. Stuchebrukhov, Theor. Chem. Acc., 2003, 110, 291–306 CrossRef CAS.
- D. M. Smith, K. M. Rosso, M. Dupuis, M. Valiev and T. P. Straatsma, J. Phys. Chem. B, 2006, 110, 15582–15588 CrossRef CAS PubMed.
- M. Breuer, K. M. Rosso and J. Blumberger, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 611–616 CrossRef CAS PubMed.
- G. Hong, A. J. Cornish, E. L. Hegg and R. Pachter, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 510–517 CrossRef CAS PubMed.
- B. Ginovska-Pangovska, M.-H. H. Ho, J. C. Linehan, Y. Cheng, M. Dupuis, S. Raugei and W. J. Shaw, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 131–138 CrossRef CAS PubMed.
- H. Long, P. W. King and C. H. Chang, J. Phys. Chem. B, 2014, 118, 890–900 CrossRef CAS PubMed.
- M. McCullagh and G. A. Voth, J. Phys. Chem. B, 2013, 117, 4062–4071 CrossRef CAS PubMed.
- A. J. Cornish, K. Gärtner, H. Yang, J. W. Peters and E. L. Hegg, J. Biol. Chem., 2011, 286, 38341–38347 CrossRef CAS PubMed.
- P. Knörzer, A. Silakov, C. E. Foster, F. A. Armstrong, W. Lubitz and T. Happe, J. Biol. Chem., 2012, 287, 1489–1499 CrossRef PubMed.
- S. Morra, A. Giraudo, G. Di Nardo, P. W. King, G. Gilardi and F. Valetti, PLoS One, 2012, 7, e48400 CAS.
- E. Garcin, X. Vernede, E. C. Hatchikian, A. Volbeda, M. Frey and J. C. Fontecilla-Camps, Structure, 1999, 7, 557–566 CrossRef CAS PubMed.
- A. Volbeda, P. Amara, C. Darnault, J.-M. M. Mouesca, A. Parkin, M. M. Roessler, F. A. Armstrong and J. C. Fontecilla-Camps, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5305–5310 CrossRef CAS PubMed.
- I. Sumner and G. A. Voth, J. Phys. Chem. B, 2012, 116, 2917–2926 CrossRef CAS PubMed.
- E. Szőri-Dorogházi, G. Maróti, M. Szőri, A. Nyilasi, G. Rákhely and K. L. Kovács, PLoS One, 2012, 7, e34666 Search PubMed.
- S. Dementin, B. Burlat, A. L. De Lacey, A. Pardo, G. Adryanczyk-Perrier, B. Guigliarelli, V. M. Fernandez and M. Rousset, J. Biol. Chem., 2004, 279, 10508–10513 CrossRef CAS PubMed.
- A. Gebler, T. Burgdorf, A. L. De Lacey, O. Rüdiger, A. Martinez-Arias, O. Lenz and B. Friedrich, FEBS J., 2007, 274, 74–85 CrossRef CAS PubMed.
- Hydrogen as a Fuel, Learning from Nature, ed. R. Cammack, M. Frey and R. Robson, Taylor and Francis, London and New York, 2001 Search PubMed.
- K. L. Pankhurst, C. G. Mowat, E. L. Rothery, J. M. Hudson, A. K. Jones, C. S. Miles, M. D. Walkinshaw, F. A. Armstrong, G. A. Reid and S. K. Chapman, J. Biol. Chem., 2006, 281, 20589–20597 CrossRef CAS PubMed.
- C. M. Maupin, R. McKenna, D. N. Silverman and G. A. Voth, J. Am. Chem. Soc., 2009, 131, 7598–7608 CrossRef CAS PubMed.
- C. N. Schutz and A. Warshel, J. Phys. Chem. B, 2004, 108, 2066–2075 CrossRef CAS.
Footnote |
| † Present address: Theoretical Molecular Science Laboratory, RIKEN 2-1 Hirosawa, Wako-shi, Saitama, 351-0198, Japan. |
| This journal is © The Royal Society of Chemistry 2014 |
