Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Towards a better understanding of magnetic exchange mediated by hydrogen bonds in Mn(III)/Fe(III) salen-type supramolecular dimers†
Ivan
Nemec
 ,
Radovan
Herchel
,
Radovan
Herchel
 ,
Tomáš
Šilha
and
Zdeněk
Trávníček
*
,
Tomáš
Šilha
and
Zdeněk
Trávníček
*
Regional Centre of Advanced Technologies and Materials & Department of Inorganic Chemistry, Faculty of Science, Palacký University, 17. listopadu 12, 771 46, Olomouc, Czech Republic. E-mail: zdenek.travnicek@upol.cz; Fax: +420585 634 954
First published on 14th August 2014
Abstract
A thorough study of structural and magnetic properties was performed on a series of trinuclear and dinuclear Mn(III)/Fe(III) complexes consisting of [M(L4)(Solv)]+ and [Fe(CN)5(NO)]2− moieties (M = Fe(III) or Mn(III), Solv = H2O or CH3OH, L4 = tetradentate salen-type ligands), in which dominant magnetic exchange is mediated by OS–H⋯OPh hydrogen bonds in [M(L4)(Solv)]+⋯[M(L4)(Solv)]+ supramolecular dimers. As deduced from magnetic analysis involving the determination of zero-field splitting (ZFS) parameters for Mn(III) and Fe(III) ions, as well as from comprehensive DFT calculations and modelling, it may be concluded that the strength of the magnetic exchange is correlated with the number of hydrogen bonds and with the OPh⋯OS distance between the phenolic oxygen atom of the salen-type ligand (OPh) and the oxygen atom of the solvent molecule coordinated to the adjacent metal atom (OS).
Introduction
In recent years, a significant amount of research has been devoted to the study of molecular magnetic materials due to their potential applications as molecular switches or high-density memory materials.1 There is a continuous effort to correlate the magnetic properties of such materials with their structures, in order to establish rational design methods for the preparation of molecule based magnetic materials. Most of the correlations reported thus far dealt with either the strength of the isotropic magnetic interactions, mediated through the covalent bonds between two paramagnetic metal atoms,2 or with the magnetic anisotropy defined by the zero-field splitting (ZFS) parameters – the prerequisite for observation of slow-relaxation of magnetisation. However, magnetic exchange mediated by non-covalent interactions such as hydrogen bonding or π–π stacking of aromatic rings is emerging as another magnetic exchange coupling phenomenon, especially in the study of organic-based molecular magnets. This kind of exchange might also play an important role in coordination compounds with interesting magnetic properties, e.g. in mediating intrachain exchange interactions, thus giving rise to single-chain magnets,3 in magnetic sponges,4 in the occurrence of slow-magnetic relaxation in polynuclear compounds5 or in simple paramagnetic compounds.6Of particular importance amongst the magnetically interesting coordination compounds are the cyanido-bridged complexes (Prussian blue analogues and related compounds),7,8 which are of interest due to their structural and magnetic properties9 and their potential use as optical devices and catalysts.10 A wide variety of cyanido complexes can be used as bridging units and these can be generally divided into two subgroups: (a) homoleptic cyanido complexes with the general formula [M(CN)x](x−m)− (M = transition metal, x = number of cyanido ligands, m = charge of M) and (b) heteroleptic cyanido complexes [M(L)(CN)x](x+l−m)− (L = organic ligand different from CN, l = charge of L). Such cyanidometallates can react with coordinatively unsaturated complexes (or labile complexes from a kinetic point of view) to form compounds which vary widely in their structures and magnetic properties.
The objective of the work reported herein was to prepare and characterize a series of trinuclear nitroprusside-bridged Mn(III)/Fe(III) complexes containing Schiff base ligands,11 or more specifically, salen-type ligands (L42− = salen2− = N,N′-ethane-bis(salicylideneiminate) dianion; other abbreviations of the ligands used or mentioned in this work can be found in ref. 12), and therefore, such polynuclear salen-type compounds bridged by metallocyanates are briefly discussed below.
The cationic part in the presented complexes consists of the tetradentate salen-like dianionic ligand (L42−) coordinated to the transition metal, thus creating the [M(L4)](m−2)− moiety, where the L4 ligand occupies the equatorial plane of the complex. Two axial positions are potentially available for coordination and therefore the [M(L4)](m−2)− moiety can be considered as a perfect building block for the preparation of low dimensional coordination compounds, and coordination polymers of various dimensions (1D, 2D or 3D) can also be prepared. In general, three basic structural types can be distinguished, where the [M(L4)](m−2)− moiety is coordinated by:
(A) One N-cyanido ligand from the cyanidometallate, and a solvent molecule (most usually water or methanol) in the second axial position. The structure of the resulting complex is low-dimensional and polynuclear due to the terminal function of the solvent ligand (further abbreviated as Solv). However, the Solv molecules often extend the dimensionality of the crystal structure (usually to 1D arrays) by forming hydrogen bonding interactions with suitable acceptor atoms from neighbouring molecules (Scheme 1A, vide infra).
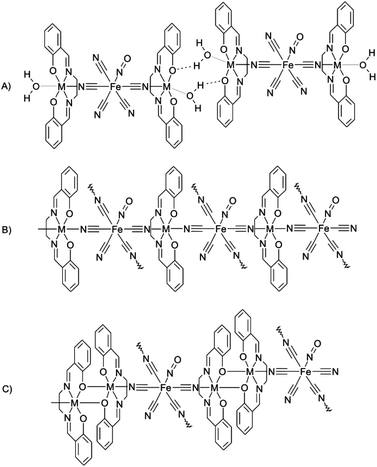 | ||
| Scheme 1 Schematic representations of three structural types which result from reaction of the [M(L4)](m−2)− complexes with cyanidometallates. | ||
(B) Two N-cyanido ligands, each from different adjacent cyanidometallate molecules, and therefore the structure of the resulting complex is polymeric in most cases (Scheme 1B, vide infra).
(C) One N-cyanido ligand from the cyanidometallate, and a phenolic oxygen atom from the adjacent [M(L4)](m−2)− molecule in the second axial position, thus forming a dimeric unit. It must be stressed that this kind of dimer is not unique for MnIII complexes and can also be found in other transition metal complexes (CoII/III,13 FeIII,14 RuIII,15 TiIII,16 ZnII,17 CuII (ref. 18) and NiII,19Scheme 1C).
In our previous work we have reported coordination compounds built from various [MnIII(L4)]+ moieties bridged by [Pt(SCN)4]2− or [Pt(SCN)6]2− complex anions.20,21 Almost all of the prepared compounds were trinuclear with the general formula [{Mn(L4)(Solv)}2{μ-Pt(SCN)x}], where x = 4 or 6, and they thus belong to group (A). For those compounds it was shown that the exchange interactions mediated by the diamagnetic bridging anion are negligible and it was proven that the dominant magnetic exchange pathway occurs via non-covalent interactions, i.e. hydrogen bonding within the supramolecular dimer [Mn(L4)(Solv)]+⋯[Mn(L4)(Solv)]+. Therefore, this kind of supramolecular system represents an ideal object of study for investigation of the magnetic exchange mediation through hydrogen bonding. Furthermore, it was observed that there is a significant difference in the strength of the magnetic exchange, depending on the type of Solv molecule bonded to the MnIII atom. In order to explore this phenomenon thoroughly we have studied another system with a diamagnetic bridging cyanidometallate, i.e. nitroprusside [Fe(CN)5(NO)]2−, and furthermore, we have focused our attention not only on its MnIII complexes, but also on its FeIII ones.
From a literature survey on the above mentioned compounds it is apparent that the nitroprusside–[MIII(L4)]+ compounds (MIII = FeIII, MnIII) which belong to group (A) (Scheme 1A) only include MnIII complexes (explanations of the following ligand abbreviations can be found in Scheme 2): [{Mn(L4i)(H2O)}2{μ-Fe(CN)5(NO)}] (7a),22 [{Mn(L4b)(H2O)}2{μ-Fe(CN)5(NO)}]·2CH3OH (7b), [{Mn(L4m)(CH3OH)}2{μ-Fe(CN)5(NO)}] (7c),23a [{Mn(L4k)(H2O)}2{μ-Fe(CN)5(NO)}]·2H2O (7d)24 and [{Mn(L4l)(H2O)}2{μ-Fe(CN)5(NO)}] (7e).25
 | ||
| Scheme 2 Schematic representations of H2L4 tetradentate Schiff base ligands referred to in this work and their abbreviations. | ||
The compounds which belong to group (B) are polymeric with two-dimensional crystal structures (Scheme 1B). In all reported cases the nitroprusside anion acts as a moiety which bridges four [MIII(L4)]+ entities, and thus creates grid-like sheets built from [{M(L4)}2{μ4-Fe(CN)5NO}]n units. This group contains six coordination polymers: [{Mn(L4j)}2{μ4-Fe(CN)5(NO)}] (7f),26 [{Mn(L4f)}2{μ4-Fe(CN)5(NO)}] (7g),24 [{Fe(L4f)}2{μ4-Fe(CN)5(NO)}]n (7h),27 [{Fe(L4g)}2{μ4-Fe(CN)5(NO)}] (7i),28 [{Mn(L4f)}2{μ4-Fe(CN)5(NO)}]·2H2O (7j)23b and [{Mn(L4f)}2{μ4-Fe(CN)5(NO)}]·2H2O (7k).23a
Group (C), depicted in Scheme 1C, is represented by only one example: [{Mn(L4h)}2{μ4-Fe(CN)5(NO)}] (7l).24 This compound is polymeric with four [{Mn(L4h)}2]2+ dimers bridged by one nitroprusside anion, thus creating a two-dimensional network.
In this article a great deal of attention is devoted to the study of seven novel trinuclear nitroprusside complexes with salen-type Schiff base ligands and the general formula [{MIII(L4)(H2O)}2{μ-Fe(CN)5(NO)}]·xCH3OH, x = 0 or 1 and M = Fe or Mn.
The crystal structures of complexes [{Fe(L4b)(H2O)}2{μ-Fe(CN)5(NO)}]·2CH3OH (3a), [{Fe(L4c)(H2O)}2{μ-Fe(CN)5(NO)}] (4a), [{Mn(L4c)(H2O)}2{μ-Fe(CN)5(NO)}] (4b) and [{Fe(L4d)(H2O)}2{μ-Fe(CN)5(NO)}] (5a) have been determined by single crystal X-ray diffraction. Magnetic measurements were performed on all of the prepared compounds including two additional compounds for which crystal structures were not determined: [{Fe(L4a)(H2O)}2{μ-Fe(CN)5(NO)}]·CH3OH (2a), [{Mn(L4a)(H2O)}2{μ-Fe(CN)5(NO)}]·CH3OH (2b). Furthermore, we report a novel type of nitroprusside complex with an ionic structure, where the [{Mn(L4e)(H2O)}{μ-Fe(CN)5(NO)}]− anion is charge balanced by the [{Mn(L4e)(H2O)(CH3OH)]+ cation (6b).
With the aim to elucidate the magnetic exchange and magnetic anisotropy in each herein reported compound, temperature and field dependent magnetic data were simultaneously fitted to provide trustworthy values of isotropic exchange constants (J) and single-ion zero-field splitting parameters (D). Furthermore, a thorough DFT study was undertaken to determine dominant super-exchange pathways and the roles of minor changes in the crystal structures on the overall magnetic exchanges. The ultimate goal of our investigations is to build up a magneto-structural correlation between the isotropic magnetic exchange constant J and the structural parameters for the group of compounds containing [M(L4)(Solv)]+⋯[M(L4)(Solv)]+ supramolecular dimers. So far several studies devoted to magnetic exchange mediated by O–H⋯O hydrogen bonds have been published,29 but mainly on copper(II) complexes, in which only isotropic exchange is present. In our study, the situation is complicated by zero-field splitting of Fe(III) and Mn(III) atoms, and thus, advanced magnetic analysis had to be employed.
Results and discussion
Crystal structures of trinuclear complexes 3a, 4a, 4b and 5a
The selected bond lengths for herein and previously reported salen-type complexes are summarized in Table 1. The crystal data and structure refinements for compounds reported in this article are given in Table 2.M–Nim![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
M–OPh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
M–NCN | M–OS |
Σ/°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
|
|---|---|---|---|---|---|
| a Average values calculated from two bond length values. b Distortion parameter defined as sum of deviations from 90° of the twelve cis angles in the coordination sphere.30 | |||||
| 3a | 2.109 | 1.896 | 2.151(2) | 2.0548(16) | 37.7 |
| 4a | 2.085 | 1.897 | 2.1512(14) | 2.1309(12) | 56.4 |
| 4b | 1.973 | 1.878 | 2.343(3) | 2.256(2) | 44.4 |
| 5a | 2.084 | 1.889 | 2.163(2) | 2.143(2) | 53.9 |
| 6b mol1 | 1.962 | 1.882 | 2.245(3) | 2.292(2) | 22.4 |
| 6b mol2 | 1.953 | 1.868 | — | 2.309(2) | 29.5 |
| 2.256(2) | |||||
| 7a | 1.970 | 1.863 | 2.355(6) | 2.271(5) | 49.6 |
| 7b | 1.986 | 1.872 | 2.304(6) | 2.223(5) | 27.2 |
| 7c | 1.962 | 1.881 | 2.288(4) | 2.358(3) | 53.8 |
| 7d | 2.036 | 1.900 | 2.263(6) | 2.224(5) | 35.4 |
| 7e | 1.981 | 1.880 | 2.394(2) | 2.258(2) | 46.3 |
| 7f | 1.989 | 1.863 | 2.378(2) | — | 54.1 |
| 7g | 1.985 | 1.888 | 2.305(3) | — | 34.1 |
| 7h | 2.109 | 1.898 | 2.173(6) | — | 57.0 |
| 7i | 2.111 | 1.898 | 2.175(5) | — | 55.3 |
| 7j | 1.987 | 1.888 | 2.304(4) | — | 33.8 |
| 7k | 1.969 | 1.881 | 2.326(3) | — | 35.9 |
| 7l | 1.978 | 1.885 | 2.246(4) | — | 57.7 |
| 3a·2CH3OH | 4a | 4b | 5a | 6b·H2O·CH3OH | |
|---|---|---|---|---|---|
| Formula | C47H40N10O9Fe3 | C45H48N10O11Fe3 | C45H48N10O11Fe1Mn2 | C47H52N10O11Fe3 | C62.5H50N10O10.5Fe1Mn2 |
| M r | 1056.44 | 1072.48 | 1070.66 | 1100.54 | 1274.85 |
| T/K | 150(2) | 150(2) | 150(2) | 150(2) | 150(2) |
| Crystal system | Triclinic, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
Monoclinic, C2/c | Monoclinic, P21/c | Monoclinic, P21/c | Triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
| a/Å | 10.8773(4) | 23.0051(7) | 13.2000(11) | 13.651(5) | 10.6373(3) |
| b/Å | 11.0243(4) | 13.7936(4) | 13.1797(8) | 13.387(5) | 15.3822(4) |
| c/Å | 11.6197(4) | 14.7860(4) | 14.860(2) | 15.434(4) | 18.2505(5) |
| α /° | 99.960(3) | 90.00 | 90.00 | 90.00 | 78.980(2) |
| β /° | 116.960(4) | 96.407(3) | 116.958(8) | 120.29(2) | 79.305(2) |
| γ /° | 105.062(3) | 90.00 | 90.00 | 90.00 | 73.460(2) |
| V/Å3 | 1128.77(10) | 4662.6(2) | 2304.3(4) | 2435.5(14) | 2782.45(13) |
| Z | 1 | 4 | 2 | 2 | 2 |
| D c/g cm−3 | 1.554 | 1.528 | 1.543 | 1.501 | 1.520 |
| μ/mm−1 | 1.021 | 0.993 | 0.923 | 0.952 | 0.778 |
| F (000) | 542 | 2216 | 1104 | 1140 | 1310 |
| Reflections collected/unique | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 554/3948 554/3948 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257/4091 257/4091 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 371/4058 371/4058 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415/4240 415/4240 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 066/9726 066/9726 |
| Data/restraints/parameters | 3948/3/320 | 4091/3/322 | 4058/0/315 | 4240/5/364 | 9726/13/815 |
| Goodness-of-fit (GOF) on F2 | 1.110 | 1.043 | 0.875 | 1.052 | 1.009 |
| R 1, wR2 (I > 2σ(I)) | 0.0350/0.0912 | 0.0238/0.0625 | 0.0469/0.0890 | 0.0303/0.0837 | 0.0426/0.0946 |
| R 1, wR2 (all data) | 0.0415/0.0928 | 0.0295/0.0638 | 0.0972/0.0965 | 0.0417/0.0861 | 0.0735/0.1000 |
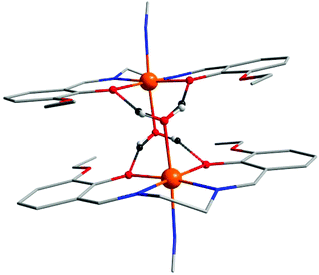
The molecular structures of these complexes are very similar, consisting of trinuclear [{MIII(L4)(H2O)}2{μ-Fe(CN)5(NO)}] moieties (MIII = FeIII or MnIII, Fig. S1–S4 in ESI†) which have slightly bent {H2O–MIII–NC–Fe–CN–MIII–H2O} arrangements (Fig. 1–3). The MIII⋯MIII separations within the trinuclear complexes are very similar (in Å): 10.1621(6) in 3a, 10.1532(5) in 4a, 10.225(2) in 4b and 10.173(4) in 5a. The coordination polyhedra of the [M(L4)(H2O)]+ subunits can be described as axially elongated octahedrons, and the distortion is more obvious for the Mn(III) derivatives due to the Jahn–Teller effect. In general, based on herein and previously reported salen-type complexes, it can be concluded that the Mn(III) compounds show significantly longer axial (usually M–NCN and M–OS bonds; NCN stands for the nitrogen atom of the nitroprusside cyanido group, OS stands for the oxygen atom from the coordinated solvent molecule) bond lengths in comparison with the Fe(III) compounds (ca. d(Mn–NCN) = 2.30 Å, d(Fe–NCN) = 2.17 Å, d(Mn–OS) = 2.27 Å, d(Fe–OS) = 2.10 Å, Table 1). On the contrary, the M–Nim bond lengths are longer in the case of the Fe(III) complexes (ca. d(Mn–Nim) = 1.99 Å, d(Fe–Nim) = 2.11 Å; Nim stands for the nitrogen atom from the imino group of L4). The length of the M–OPh bonds is roughly the same for both central ions (Table 1; OPh stands for the phenolate oxygen atoms). The angular distortions from the ideal octahedron Σ30 are obviously smaller for the Mn(III) compounds (Table 1).
 | ||
| Fig. 1 Fragments of the crystal structures of complexes 4a (up) and 4b (down). The hydrogen atoms are omitted for clarity, except for the atoms responsible for the formation of a “supramolecular dimer” in 4a and 4b due to hydrogen bonds (dashed lines). Selected bond lengths and angles are shown in Fig. S2 and S3 in ESI.† | ||
 | ||
| Fig. 2 Left: Fragments of the crystal structures of complexes 3a (up) and 5a (down). The hydrogen atoms and methanol molecules (3a) are omitted for clarity, except for the atoms responsible for the formation of a “supramolecular dimer” in 3a and 5a due to hydrogen bonds (dashed lines). Selected bond lengths and angles are shown in Fig. S1 and S4 in ESI†. Right: A view of the 2D supramolecular structure in 3a. | ||
 | ||
| Fig. 3 Fragment of the crystal structure of complex 6b. The hydrogen atoms are omitted for clarity, except for the atoms responsible for the formation of a “supramolecular dimer” in 6b due to hydrogen bonds (dashed lines). Numerous π–π stacking interactions within the complex are also highlighted. Selected bond lengths (Å) and angles (°) are shown in Fig. S5 in ESI.† | ||
As mentioned in the introduction, these trinuclear complexes belong to group (A), in which non-covalent connections between polynuclear species are provided by hydrogen bonding between coordinated Solv molecules and phenolate oxygen atoms and thus, roughly linear arrays of centrosymmetric and supramolecular [Mn(L4)(Solv)]+⋯[Mn(L4)(Solv)]+ dimers connected by nitroprusside anions are formed. In the crystal structures of compounds 3a, 4a, 4b and 5a, the Solv molecules (Solv = H2O) form two basic types of interactions: (i) a simple OS–H⋯OS hydrogen bond (in 3a) and (ii) a bifurcated hydrogen bond where two H-atoms from the water molecule interact with four oxygen atom acceptors (two alkoxy (OA) and two phenolate oxygen atoms, in 4a, 4b and 5a). The bifurcated hydrogen bonding prolongs the donor⋯acceptor lengths; in the case of OS⋯OPh contacts (in Å): d(OS⋯OPh) = 2.690(3) in 3avs. 2.792(2) and 2.927(2) in 4a, 2.851(3) and 2.934(3) in 4b, and 2.814(2) and 2.866(2) in 5a. The OS⋯OA hydrogen bonds are longer in general, however, in the crystal structure of 4b we observe one relatively short contact (in Å): d(OS⋯OA) = 3.024(2) and 3.248(2) in 4a, 2.866(3) and 3.115(4) in 4b, and 3.064(2) and 3.279(2) in 5a.
The MIII⋯MIII separations in the supramolecular dimers are within a relatively narrow range (in Å): 4.8728(5) in 3a, 4.5608(4) in 4a, 4.7132(9) in 4b and 4.594(2) in 5a. The crystal structure of 3a differs significantly from the structures of 4a, 4b and 5a due to the presence of a co-crystallized molecule of methanol. This extends the structural dimensionality of the compound to 2D by linking supramolecular chains [{Fe(L4b)(H2O)}2{μ-Fe(CN)5(NO)}]n together through hydrogen bonding between a coordinated water molecule and a methanol molecule which in turn is hydrogen bonded to a non-coordinated nitrogen atom from the nitroprusside bridge of a neighbouring complex (Fig. 2).
Crystal structure of complex 6b
The crystal structure of 6b is depicted in Fig. 3. It consists of the dimeric [{Mn(L4e)(H2O)}{μ-Fe(CN)5NO}] (6b mol1) and [{Mn(L4e)(H2O)(CH3OH)] (6b mol2) moieties, in which both manganese atoms are hexacoordinated with four donor atoms (N2O2) coming from the L4e2− ligand. In 6b mol1 the remaining coordination sites (axial positions) are occupied by two oxygen atoms, coming from the coordinated water and methanol molecules. On the other hand, the axial positions in 6b mol2 are occupied by the oxygen atom from the water molecule and by the nitrogen atom from the bridging cyanido group of the nitroprusside. The average bond lengths are (mol1, mol2; in Å): d(Mn–Nim) = 1.961, 1.953; d(Mn–OPh) = 1.882, 1.868. The axial bond lengths differ due to the different solvent molecules coordinated to the Mn(III) atoms (in Å): d(Mn–OS) = 2.292(3) (H2O) in mol1 and 2.256(3) (CH3OH) and 2.309(3) (H2O) in mol2. It must be noted that the crystal structure of 6b exhibits substitutional disorder on mol2, where the methanol molecule (the main part, with occupation factor of 0.68) is partially substituted by a water molecule which is further hydrogen bonded to another disordered water molecule (Fig. S5 in ESI†).Both complexes create 2D networks of hydrogen bonds owing to the co-crystallized water and methanol molecules (Fig. 3). The [{Mn(L4e)(H2O)}{μ-Fe(CN)5NO}][{Mn(L4e)(H2O)(CH3OH)] assembly (mol1⋯mol2), in which the interconnection between mol1 and mol2 is provided by hydrogen bonding between coordinated water molecules and complementary phenolate oxygen atoms, similarly to in compounds 3a–5a, can be considered as the main building block of the crystal structure. The mol1⋯mol2 assembly is further propagated to a linear 1D chain by a series of hydrogen bonds; the coordinated methanol molecule from mol2 forms a hydrogen bond with a co-crystallized water molecule, which in turn hydrogen bonds to a co-crystallized methanol molecule which is in close contact with the adjacent cyanido group (the trans position with respect to the cyanido group coordinating the Mn atom) from the neighbouring mol1⋯mol2 assembly. Linear supramolecular chains are interconnected via hydrogen bonding between the coordinated water molecule from mol1 and the neighbouring cyanido group (the cis position with respect to the cyanido group coordinating the Mn atom), and between the co-crystallized water molecule and the cyanido group from the neighbouring mol1 moiety.
Infrared spectroscopy
The presence of the Schiff base in each of the complexes was indicated by FT-IR spectra measured in the range 400–4000 cm−1. The spectra of each of the compounds exhibit two weak intensity bands at 3115–3132 and 3025–3037 cm−1 corresponding to asymmetric and symmetric stretching vibrations of the aromatic C–H groups. The characteristic bands assignable to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and (C–C)ar vibrations were observed in the 1613–1625 cm−1 and 1437–1595 cm−1 regions, respectively, for all complexes. Formation of the cyanido-bridges in all the nitroprusside complexes are evidenced by the C
N and (C–C)ar vibrations were observed in the 1613–1625 cm−1 and 1437–1595 cm−1 regions, respectively, for all complexes. Formation of the cyanido-bridges in all the nitroprusside complexes are evidenced by the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N stretching vibration bands in the 2000–2200 cm−1 region. The maximum at 2143 cm−1 in sodium nitroprusside dihydrate may be assigned to the vibration of the cyanido group, while the maxima associated with the same vibration in complexes 2a–6b were observed in the range 2138–2163 cm−1.31 The strong peaks in the region 1906–1922 cm−1 are assignable to the N
N stretching vibration bands in the 2000–2200 cm−1 region. The maximum at 2143 cm−1 in sodium nitroprusside dihydrate may be assigned to the vibration of the cyanido group, while the maxima associated with the same vibration in complexes 2a–6b were observed in the range 2138–2163 cm−1.31 The strong peaks in the region 1906–1922 cm−1 are assignable to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations, which are at lower wavenumbers than that found for the same vibration in the complex Na2[Fe(CN)5NO]·2H2O (1936 cm−1).
O stretching vibrations, which are at lower wavenumbers than that found for the same vibration in the complex Na2[Fe(CN)5NO]·2H2O (1936 cm−1).
Magnetic properties
In all the presented compounds, we can observe the formation of quasi-dimers amongst [{MnIII(L4)(H2O)}]+ or [{FeIII(L4)(H2O)}]+ subunits, held together by hydrogen bonds between coordinated solvent molecules and phenolic oxygen atoms. Within these quasi-dimers, the Mn⋯Mn and Fe⋯Fe separations vary between 4.71–5.06 Å, and 4.59–4.87 Å, respectively, in contrast to their large interatomic separations (more than 10 Å) through covalent bonds formed by diamagnetic nitroprusside bridges.These structural aspects strongly suggest that the super-exchange mechanism is mainly active through hydrogen bonds. The nature of the magnetic exchange can be estimated by inspecting the temperature dependence of susceptibility and the effective magnetic moment of these compounds. The presence of the maximum of the susceptibility (T < 10 K) is a fingerprint of the antiferromagnetically coupled homospin dimer. This results in a decrease in μeff/μB on cooling. Moreover, the interplay of the zero-field splitting on the magnetic properties cannot be neglected, especially for Mn(III) atoms.
Therefore the following spin Hamiltonian was postulated
 | (1) |
where the first term stands for the isotropic exchange (J), the second part is due to the zero-field splitting (D – an axial single-ion ZFS parameter), the third part is the Zeeman term and the last expression represented with the zj variable is the common molecular-field correction parameter, which is due to small intra/inter-chain molecular interactions. The <Sa> is a thermal average of the molecular spin projection in the a direction of the magnetic field defined as Ba = B(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) with the help of polar coordinates. Then, the molar magnetization in the a direction of the magnetic field can be numerically calculated as
θ) with the help of polar coordinates. Then, the molar magnetization in the a direction of the magnetic field can be numerically calculated as
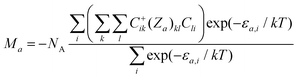 | (2) |
 | (3) |
With the aim to bring more insight into the general properties of the antiferromagnetically coupled dimer with ZFS, the shift in temperature of the maximum of the susceptibility (Tmax) was inspected for varying ratios of D/J, for either S1 = S2 = 2 or S1 = S2 = 5/2 (Fig. 4). There is a simple formula which interconnects the strength of the antiferromagnetic exchange with Tmax, but it is available only for the isotropic case: |J|/kTmax = 0.462 for S1 = S2 = 2 and |J|/kTmax = 0.347 for S1 = S2 = 5/2. In both cases, introducing the non-zero zero-field splitting results in an increase in Tmax, and this change is more emphasized for D < 0 (Fig. 4).
As both antiferromagnetic exchange and ZFS have similar effects on magnetic properties, the decrease in μeff/μB, both the temperature and field dependent magnetization data were experimentally acquired and concurrently used in finding the best-fit parameters of the above introduced spin Hamiltonian (eqn (1)). Furthermore, the standard deviations of the varied parameters were calculated with 95% probability confidence limits.32
Dinuclear complex 6b
The unique molecular and crystal structure of 6b results in the formation of quasi linear and discrete trimers of type MnIII⋯MnIII⋯FeII in which paramagnetic manganese atoms are connected through hydrogen bonds (d(Mn⋯Mn) = 5.0575(7) Å) and the diamagnetic nitroprusside anion serves as a terminal entity. This gives us an opportunity to study the magnetic exchange of the MnIII–MnIII type mediated by water-hydrogen bonds, unaffected by bridging through nitroprusside as found in the remaining reported complexes. The experimental magnetic data are presented in Fig. 5. The room temperature effective magnetic moment of 6b is 7.1 μB, which is very close to the theoretical value of 6.93 μB for two paramagnetic non-interacting centres with S = 2 (g = 2.0). The susceptibility is increasing on cooling and is reaching its maximum at 6.5 K, which is also accompanied by a decrease in μeff below 50 K down to 2.1 μB at 1.9 K. The isothermal magnetization at 2 K is not saturated even at B = 7 T and has a value of Mmol/NAμB = 6.2, which is below the saturation limit of Mmol/NAμB = 8 (2 × S = 2 and g = 2.0). By applying eqn (1)–(3) to both temperature and field dependent magnetic data, we obtained J = −0.72(1) cm−1, g = 2.048(1), D = −3.65(9) cm−1 and zj = −0.06(1) cm−1 (Fig. 5). The negative and large value of the D-parameter is in agreement with the elongated octahedrons of the Mn(III) centres due to the Jahn–Teller effect. However, the coordination chromophores of the respective Mn(III) centres differ in one apical position – {MnO3N3} for Mn1 and {MnO4N2} for Mn2 (Fig. 3), and therefore the calculated D-value serves as an average value of both distinct Mn(III) centers. The most important outcome is that considerably large magnetic exchange is mediated by hydrogen bonds between Mn(III) centers.Trinuclear [{Mn(L4)(H2O)}2{μ-Fe(CN)5(NO)}]·xCH3OH complexes 4b and 2b
Compound 4b shows very similar magnetic properties to compound 6b (Fig. 5), which justifies the presumption that dominant magnetic exchange is mediated through hydrogen bonds (d(Mn⋯Mn) = 4.7132(9) Å) and not through the diamagnetic nitroprusside anion (d(Mn⋯Mn) = 10.225(2) Å). Thus, the magnetic data of 4b were treated using the same procedure as for 6b under the condition that D1 = D2, because there is only one Mn atom in the asymmetric unit. The resulting parameters are J = −0.79(1) cm−1, g = 1.981(2), D = −3.7(1) cm−1 and zj = +0.12(2) cm−1 (Fig. 5). The last reported Mn(III) compound is complex 2b, which exhibits comparable properties to compounds 4b and 6b (Fig. 5). Thus, we used the same model despite the absence of its X-ray crystal structure. The best fit was obtained with the following parameters: J = −0.55(1) cm−1, g = 1.987(2), D = −3.5(2) cm−1 and zj = −0.10(2) cm−1 (Fig. 5).Trinuclear [{Fe(L4)(H2O)}2{μ-Fe(CN)5(NO)}]·xCH3OH complexes 2a, 3a, 4a and 5a
The magnetic behaviours of the trinuclear Fe(III)-nitroprusside complexes 2a, 3a, 4a and 5a were found to be very similar to one another (Fig. 6). The room temperature values of the effective magnetic moment are in the range 8.42–8.57 μB, which is very close to the theoretical value of 8.37 μB for two paramagnetic non-interacting centres with S = 5/2 (g = 2.0). Upon cooling, the μeff/μB dependencies are almost constant down to 50 K and then they start to decrease to values of 3.33, 3.46, 2.68 and 2.73 at T = 1.9 K for 2a, 3a, 4a, and 5a, respectively.Furthermore, the maxima of the molar magnetization (or mean molar susceptibility) ranged from 3.5 to 6.5 K. This fact indicates the presence of antiferromagnetic exchange between Fe(III) centres, mediated by hydrogen bonds and/or the zero-field splitting of the Fe(III) centers. Moreover, the isothermal magnetization measurements at liquid helium temperatures (2.0 and 4.6 K) support this presumption, because the experimental values of Mmol/NAμB are below the theoretical saturation value Mmol/NAμB = g·S·2 = 10 (g = 2.0, S = 5/2) (Fig. 6). Therefore, the same spin Hamiltonian was used as in eqn (1), but in this case S1 = S2 = 5/2 holds. It must be stressed that including the ZFS term has been essential to reliably fit all experimental data together. We have found that slightly better fits could be obtained for positive rather than negative D-parameter values and both sets of values are tabulated for each of the presented compounds in Table 3 (see also Fig. 6 and Fig. S9–12, ESI†). Evidently, weak antiferromagnetic exchange was found in the range −0.52 to −1.05 cm−1. In the case of positive D-parameters, the |D/J| ratios vary between 1.70 and 2.45, but in the case of negative D-parameters, the |D/J| ratios vary between 0.50 and 1.15. To summarize, the values of the antiferromagnetic exchange in Mn(III) and Fe(III) compounds 2a–6b were found to vary in a narrow range between −0.52 cm−1 and −1.05 cm−1, but the ZFS is much larger for the Mn(III) complexes. This is an expected feature for Mn(III) atoms due to the Jahn–Teller effect and larger distortion of the coordination polyhedra.33
| Selected structural dataa | Magnetic analysis datab | DFT calculated data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Compound | M⋯M* (Å) | M⋯M (Å) | OPh⋯OPh* (Å) | OPh⋯OS* (Å) | J (cm−1) | g | D (cm−1) | zj (cm−1) | <S2>HS/<S2>BS | J Ruiz/JYam (cm−1) |
| a M⋯M* is the shortest distance between metal atoms bridged through water mediated hydrogen bonds; M⋯M is the shortest distance between metal atoms bridged by nitroprusside or polythiocyanidoplatinate; OPh⋯OPh* and OPh⋯OS* are distances between the oxygen atoms of two phenol groups, or the oxygen atom of a phenol group and the oxygen atom of a water/methanol molecule, attached to different metal atoms M and M*. b J-values reported in the literature were scaled according to the spin Hamiltonian in eqn (1). c Ref. 22. d Ref. 23. e Ref. 24, comment: J-value is most probably overestimated due to omitting the ZFS term. f Results based on DFT calculations performed on molecular fragments, in which hydrogen atoms were optimized with BP86/def2-TZVP(-f). | ||||||||||
| 2a | — | — | — | — | −0.64(2) | 2.031(2) | +1.1(2) | −0.09(2) | ||
| −0.67(5) | 2.033(3) | −0.48(7) | −0.13(5) | |||||||
| 3a | 4.8728(5) | 10.1621(6) | 3.682(2) | 3.459(2) | −0.53(2) | 2.042(3) | +1.3(2) | −0.24(3) | 30.02/5.02 | −0.45/−0.54 |
| 2.690(3) | −0.52(6) | 2.044(3) | −0.6(1) | –0.29(5) | 30.02/5.02 | |||||
| 4a | 4.5608(4) | 10.1532(5) | 3.263(2) | 2.927(2) | −1.01(4) | 2.064(3) | +1.9(3) | +0.03(3) | 30.02/5.02 | −0.48/−0.57 |
| 2.792(2) | −1.00(5) | 2.070(3) | −0.69(7) | −0.12(6) | 30.02/5.02 | −0.81/−0.98f | ||||
| 5a | 4.593(2) | 10.173(4) | 3.338(2) | 2.865(2) | −0.94(2) | 2.033(1) | +1.6(2) | −0.026(4) | 30.02/5.02 | −0.50/−0.60 |
| 2.814(2) | −1.05(4) | 2.036(2) | −0.53(5) | −0.02(4) | 30.02/5.02 | −0.86/−1.04f | ||||
| 2b | −0.55(1) | 1.987(2) | −3.5(2) | −0.10(2) | ||||||
| 4b | 4.7132(9) | 10.225(2) | 3.296(3) | 2.934(3) | −0.79(1) | 1.981(2) | −3.7(1) | +0.12(2) | 20.07/4.07 | −0.59/−0.74 |
| 2.851(3) | 20.07/4.07 | −0.94/−1.16f | ||||||||
| 6b | 5.0575(7) | — | 3.534(3) | 3.243(3) | −0.72(1) | 2.048(1) | −3.65(9) | −0.06(1) | 20.07/4.07 | −0.55/−0.68 |
| 3.579(3) | 3.022(3) | |||||||||
| 7a | 4.690(2) | 10.358(3) | 3.339(5) | 2.907(6) | −0.88c | 2.05 | −2.62 | — | 20.06/4.06 | −0.98/−1.24f |
| 2.830(7) | ||||||||||
| 7b | 5.152(3) | 10.288(3) | 3.803(5) | 3.338(4) | −0.90d | 2.02 | −2.46 | — | 20.07/4.07 | −0.71/−0.89 |
| 2.790(6) | ||||||||||
| 7d | 5.067(2) | 10.400(2) | 3.496(6) | 3.089(6) | −1.90e | 2.0 | — | — | 20.08/4.08 | −0.61/−0.76 |
| 3.748(6) | 2.910(6) | |||||||||
| 7e | 4.694(1) | 10.388(3) | 3.303(2) | 2.913(2) | — | — | — | — | 20.07/4.07 | −0.50/−0.62 |
| 2.858(2) | 20.07/4.07 | −0.82/−1.04f | ||||||||
| 8 | 4.7007(9) | 12.5840(8) | 3.242(4) | 2.882(4) | −0.88 | 2.09 | −3.06 | +0.21 | 20.09/4.09 | −0.45/−0.56 |
| 2.930(5) | 20.08/4.08 | −0.82/−1.02f | ||||||||
| 9 | 4.858(2) | 12.017(2) | 3.365(8) | 2.707(8), 2.806(8) | −1.31(6) | 1.848(2) | −2.2(1) | −0.41(5) | 20.07/4.07 | −0.76/−0.94 |
| 3.550(8) | 2.779(8), 2.834(8) | 20.07/4.07 | −1.40/−1.74f | |||||||
| 10 | 5.004(2) | 12.044(2) | 3.469(3) | 2.728(3) | −0.53(1) | 1.879(2) | −4.6(2) | +0.23(2) | 20.08/4.08 | −0.54/−0.68 |
| 11 | 5.0682(2) | 11.749(3) | 3.764(2) | 2.777(2) | −0.47(1) | 1.889(2) | −3.6(1) | +0.03(1) | 20.08/4.08 | −0.33/−0.42 |
Furthermore, we strived to find clear magneto-structural correlations either for isotropic exchange (J) or magnetic anisotropy (D) in the reported series of compounds by taking into account various structural parameters. However, the D-parameter does not simply correlate with geometric deformation of the coordination chromophore (Σ), which can be explained by the complexity and variedness of the donor atoms. Conversely, there are some remarks concerning the isotropic exchange which must be taken into account: our previous results20 predicted weaker exchange interactions within the supramolecular dimer [M(L4)(Solv)]+⋯[M(L4)(Solv)]+ when Solv = CH3OH and stronger ones when Solv = H2O. As can be seen from Table 3, this prediction holds true; the compounds containing [M(L4)(CH3OH)]+ fragments possess weaker exchange interactions with J values ranging from −0.3 to −0.6 cm−1, while the compounds containing [M(L4)(H2O)]+ fragments have lower J values ranging from −0.7 to −1.3 cm−1 (when not including most probably overestimated J values, due to the ZFS term being omitted in the magnetic data analysis, for details see Table 3). From the collected data it seems to be apparent that the difference in the quality of the exchange interactions mediated between coordinated methanol and water molecules is not caused by the intrinsic difference between these two solvents, but is most probably due to the different number of hydrogen bonds formed by each particular solvent molecule: CH3OH (2 hydrogen bonds within the dimer), H2O (usually 4 hydrogen bonds). This can be supported by two examples from the present series of nitroprusside bridged compounds.
Compound 3a represents a novel structural type of the [M(L4)(H2O)]+⋯[M(L4)(H2O)]+ supramolecular dimer; it is held by two hydrogen bonds whereas two other remaining hydrogen atoms point to solvent molecules within the lattice (Fig. 2 and 7). Noticeably, the value of the coupling constant (J = −0.52 cm−1) is very similar to those observed for the compounds with Solv = CH3OH (Table 3). Furthermore, compound 6b has another unique asymmetric dimeric synthon with three supportive hydrogen bonds (Fig. 3 and 7); the strength of the exchange interaction (J = −0.72 cm−1) is in between the values typical for CH3OH and H2O.
DFT calculations
In order to support our conclusions from magnetochemical analyses of the experimental data, we performed isotropic exchange parameter calculations using the DFT method for H-bond bridged dinuclear molecular fragments [{MIII(L4)(H2O)(NC)}2] (M = Fe, Mn) for compounds reported herein, 3a–6b, and also for similar compounds reported in literature, 7a–7e. Moreover, we also investigated the role of the diamagnetic nitroprusside anion in mediation of magnetic exchange for compound 4a using the [{FeIII(L4c)(H2O)}2{μ-FeII(CN)5(NO)}] molecular fragment.All the calculations were based on experimental X-ray geometries except for 7a, where some hydrogen atoms were missing in the CSD deposited data (CCDC IGAKEG) and their atomic positions were optimized with the BP86 functional and a def2-TZVP(-f) basis set.
As this work extends from our research on magnetic exchange in transition metal complexes containing diamagnetic bridging polythiocyanidoplatinate,14,15 the same hybrid functional B3LYP together with a def2-TZVP basis set and the scalar relativistic second-order Douglas–Kroll–Hess Hamiltonian were used.
Therefore, the results of relevant hydrogen bond bridged compounds, [{Mn(L4o)(H2O)}2{μ-Pt(SCN)6}] (8), [{Mn(L4n)(H2O)}2{μ-Pt(SCN)4}] (9), [{Mn(L4b)(CH3OH)}2{μ-Pt(SCN)4}] (10) and [{Mn(L4p)(CH3OH)}2{μ-Pt(SCN)4}] (11), where L4n2− = N,N′-benzene-bis(4-aminodiethylenesalicylideneiminate) dianion, L4o2− = N,N′-3-methylbenzene-bis(3-ethoxysalicylideneiminate) dianion and L4p2− = N,N′-ethylene-bis(naphthylidenebenzeneiminate) dianion, were also included in Table 3.
The isotropic exchange analysis was based on the following Heisenberg spin Hamiltonian
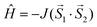 | (4) |
| JRuiz = Δ/(2S1S2 + S1) | (5) |
| JYam = 2Δ/(〈S2〉HS + 〈S2〉BS) | (6) |
First, the DFT calculation for the [{FeIII(L3)(H2O)}2{μ-FeII(CN)5(NO)}] molecular fragment of 4a resulted in insignificant magnetic exchange, JYam = +0.031 cm−1 (JRuiz = +0.026 cm−1), thus supporting our presumption that this superexchange path is very inefficient in promoting magnetic exchange.
Next, the calculation performed for H-bonded dimers [{MIII(L4)(H2O)(NC)}2] (M = Fe, Mn) resulted in the J-values tabulated in Table 3. The JYam-values were found to be in the range from −0.54 to −0.60 cm−1 for [{FeIII(L4)(H2O)(NC)}2] (3a, 4a and 5a), and in the range from −0.56 to −0.94 cm−1 for [{MnIII(L4)(H2O)(NC)}2] and [{MnIII(L4)(H2O)(NCS)}2] (2b–6b and 7b–11). Good agreement between J-values derived from magnetochemical analysis of the experimental data and DFT calculations was obtained for compounds 3a, 4b, 6b and 7b, when taking into account the JYam values. However, larger discrepancies were observed for the remaining compounds, e.g. in the case of 4a, magnetic analyses resulted in Jmag ≈ −1.0 cm−1, which is in contrast to the values of JRuiz = −0.48 cm−1 or JYam = −0.57 cm−1 (Table 3). The question then arises: why does the same DFT method result in such unequal results upon comparison with the magnetic analysis? We can speculate that these discrepancies are due to small changes in the crystal structures, which may occur at a lower temperature than that used for X-ray analysis. To test this possibility, we performed a constrained geometry optimization for the [{FeIII(L4c)(H2O)(NC)}2] molecular fragment of 4a, where the Fe⋯Fe distance was varied between 4.4 and 4.9 Å. The geometry was optimized using the BP86 functional with a def2-TZVP(-f) basis set together with a conductor-like screening model (COSMO), van der Waals corrections (VDW10) and the relativistic effects with the scalar relativistic second-order Douglas–Kroll–Hess Hamiltonian (DKH2). Afterwards, the J-values were calculated at the B3LYP + DKH2/def2-TZVP level of theory for each of the optimized molecular structures to ensure the same condition as that used for the molecular fragments of 3a–11 based on their X-ray structures.
This resulted in the magneto-structural correlation depicted in Fig. 8, from which we can conclude that the antiferromagnetic exchange is increasing with decreasing Fe⋯Fe separation. However, the change of Δ(JDFT)/Δ(dFe–Fe) ≈ 0.5–1.0 cm−1/Å cannot explain the large discrepancies between JDFT and Jmag in terms of possible small changes in the crystal structures induced by cooling to a very low temperature.
Thus, we also tested another hypothesis relating to the positions of the hydrogen atoms in the molecular/crystal structure. It is well known that determination of the hydrogen atom positions from X-ray analysis can be potentially inaccurate, especially when the hydrogen atoms are bonded to atoms with high electronegativities such as oxygen or nitrogen atoms. This was also pointed out in several DFT studies devoted to magnetic exchange mediated by hydrogen bonds in other transition metal complexes.29 Due to these reasons we have to find out how the positions of hydrogen atoms influence the magnetic exchange interactions. Therefore, the positions of hydrogen atoms involved in magnetic exchange pathways (in H-bond bridged dinuclear molecular fragments [{MIII(L4)(H2O)(NC)}2] (M = Fe, Mn) (4a, 5a, 4b, 7a, and 7e) and also for [{Mn(L4)(H2O)(NCS)}2] (8 and 9), while keeping all other atoms in the same positions as determined from their X-ray structures) were optimized using BP86/def-TZVP(-f). The situation for other complexes, namely 3a, 6b, 7b and 7d, is more complex because water molecules are not only involved in hydrogen bonds between closest metal atoms, but they also form hydrogen bonds to methanol molecules (3a and 7b) or to cyanido ligands of the nitroprusside anions from other supramolecular chains (6b and 7d), and so they were excluded.
The H-atom geometry optimization procedure for molecular fragments of 4a, 5a, 4b, 7a, 7e and 8–11 generally resulted in an increase in the O–H bond lengths, which can be demonstrated using O–H distances of water molecules in 4a: d(O–H)X-ray = 0.831 and 0.837 Å and d(O–H)DFT = 0.989 and 0.994 Å (Fig. 9). In next step, the J-values were calculated using B3LYP + DKH2/def2-TZVP and resulted in much larger antiferromagnetic exchange constants (Table 3), which can be exemplified again for 4a: JRuiz = −0.81 cm−1 or JYam = −0.98 cm−1 and especially the latter value is almost identical to Jmag ≈ −1.0 cm−1 determined from magnetic analysis.
These results demonstrate much larger sensitivity of the magnetic exchange towards the position of the hydrogen atom within the O–H⋯O hydrogen bond than towards the M⋯M distance, which can explain some discrepancies observed between J-values derived from magnetic analyses and DFT calculations based on X-ray molecular structures. Furthermore, there is clear evidence that the J-values correlate with average OPh⋯OS distances both in Fe(III) and Mn(III) complexes, as demonstrated in Fig. 8 and 10, respectively.
Experimental section
Materials
All the starting chemicals were of analytical reagent grade and were used as received. FeCl3·6H2O, MnCl2·4H2O, Na2[Fe(CN)5NO]·2H2O, solvents and the organic compounds 1,2-diaminocyclohexane, 1,2-diamino-benzene, ethane-1,2-diamine, propane-1,2-diamine, 2-hydroxy-benzaldehyde, 4-hydroxy-1-naphthaldehyde, 3-ethoxy-2-hydroxybenzaldehyde and triethylamine (Et3N) were obtained from commercial sources (Sigma-Aldrich Co., Acros Organics Co., Lachema Co. and Fluka Co.).Synthesis of the tetradentate Schiff bases H2L4a–H2L4e
These organic compounds were prepared by Schiff base condensations between the following derivatives, i.e. 2-hydroxybenzaldehyde (H2L4a or H2L4c), 2-hydroxy-1-naphthaldehyde (H2L4e) or 3-ethoxy-2-hydroxybenzaldehyde (H2L4b or H2L4d) and the corresponding diamines, i.e. 1,2-diaminocyclohexane (H2L4a), 1,2-diaminobenzene (H2L4b or H2L4e), ethane-1,2-diamine (H2L4c) or propane-1,2-diamine (H2L4d). Methanol solutions of benzaldehyde derivatives (5 mmol in 20 mL) and respective diamines (2.5 mmol in 10 mL) were stirred under reflux at 40 °C for 2 hours, resulting in yellow powder materials after evaporation of the solvent. The solid powdered substances were washed with diethyl ether and dried in a vacuum; yields were higher than 97%.Synthesis of the precursors [Fe(L4a)Cl] (1a) [Mn(L4a)Cl] (1b), [Fe(L4b)Cl] (1c), [Fe(L4c)Cl] (1d), [Mn(L4c)Cl] (1e), [Fe(L4d)Cl] (1f) and [Mn(L4e)Cl] (1g)
A solution of 10 mmol of FeCl3·6H2O or MnCl2·4H2O in 10 mL of methanol was added to a solution of 10 mmol of H2L4a–H2L4e in 20 mL of ethanol. The mixture was stirred for 10 min, and then 20 mmol of triethylamine in ethanol (10 mL) was added. The resulting solution was refluxed for 2 h, then after cooling, diethyl ether was added, which resulted in precipitation of a black or a brown powder. The solid was filtered off, washed with diethyl ether and dried in a vacuum; yields were higher than 90%.Synthesis of the complexes 2a–6b
The dark-brown crystals or dark powders of complexes 2a–6b were obtained from a methanol solution (40 mL) of complexes 1a–1g (0.2 mmol) combined with a methanol–water mixture (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of Na2[Fe(CN)5(NO)]·2H2O (0.1 mmol). The solutions were stirred at room temperature for 4 h. Slow evaporation of the resulting solutions at room temperature afforded the complexes as black single crystals suitable for X-ray diffraction after a week. Black crystals were filtered off, washed twice with water and diethyl ether and dried in a vacuum.
1) of Na2[Fe(CN)5(NO)]·2H2O (0.1 mmol). The solutions were stirred at room temperature for 4 h. Slow evaporation of the resulting solutions at room temperature afforded the complexes as black single crystals suitable for X-ray diffraction after a week. Black crystals were filtered off, washed twice with water and diethyl ether and dried in a vacuum.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1917m ν(N
N); 1917m ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1625vs ν(C
O); 1625vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1595m; 1541m; 1472m ν(C
N)ar; 1595m; 1541m; 1472m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1452vs ν(C
C)ar; 1452vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1357w; 1274w; 1222w; 1193w; 1157w; 1114w; 1110w; 1039w; 1018w; 945w; 858w; 752m.
C)ar; 1357w; 1274w; 1222w; 1193w; 1157w; 1114w; 1110w; 1039w; 1018w; 945w; 858w; 752m.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1922m ν(N
N); 1922m ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1618vs ν(C
O); 1618vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1596m; 1544m; 1468m ν(C
N)ar; 1596m; 1544m; 1468m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1443m ν(C
C)ar; 1443m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1395w; 1307w; 1286w; 1268w; 1233w; 1196w; 1148w; 1052w; 1006w; 995w; 907w; 851w; 753m; 677w.
C)ar; 1395w; 1307w; 1286w; 1268w; 1233w; 1196w; 1148w; 1052w; 1006w; 995w; 907w; 851w; 753m; 677w.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1906m ν(N
N); 1906m ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1613vs ν(C
O); 1613vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar; 1539m; 1467m ν(C
N)ar; 1539m; 1467m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1446m ν(C
C)ar; 1446m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1398w; 1314m; 1268w; 1230w; 1023w; 997w; 904w; 809w; 753m; 661w.
C)ar; 1398w; 1314m; 1268w; 1230w; 1023w; 997w; 904w; 809w; 753m; 661w.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1882vs ν(N
N); 1882vs ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1616vs ν(C
O); 1616vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1581m; 1552m; 1468m ν(C
N); 1581m; 1552m; 1468m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1437m ν(C
C)ar; 1437m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1395w; 1347w; 1295m; 1250m; 1211w; 1174w; 1141w; 1112w; 1074m; 1055w; 1021w; 947w; 857w; 841w; 774w; 732w; 692w.
C)ar; 1395w; 1347w; 1295m; 1250m; 1211w; 1174w; 1141w; 1112w; 1074m; 1055w; 1021w; 947w; 857w; 841w; 774w; 732w; 692w.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1874vs ν(N
N); 1874vs ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1614vs ν(C
O); 1614vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1579m; 1550m; 1465m ν(C
N); 1579m; 1550m; 1465m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1438m ν(C
C)ar; 1438m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1393w; 1346w; 1298m; 1254m; 1216w; 1178w; 1153w; 1108w; 1083m; 1050w; 1018w; 953w; 894w; 843w; 779w; 763w; 732m; 690w; 603m.
C)ar; 1393w; 1346w; 1298m; 1254m; 1216w; 1178w; 1153w; 1108w; 1083m; 1050w; 1018w; 953w; 894w; 843w; 779w; 763w; 732m; 690w; 603m.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1882vs ν(N
N); 1882vs ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1616vs ν(C
O); 1616vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1594s; 1552m; 1463m ν(C
N); 1594s; 1552m; 1463m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1443vs ν(C
C)ar; 1443vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1391m; 1345w; 1322w; 1295m; 1250m; 1218m; 1180w; 1110w; 1076w; 1037w; 1014w; 895w; 850w; 762w; 731m; 605w.
C)ar; 1391m; 1345w; 1322w; 1295m; 1250m; 1218m; 1180w; 1110w; 1076w; 1037w; 1014w; 895w; 850w; 762w; 731m; 605w.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1886vs ν(N
N); 1886vs ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1614vs ν(C
O); 1614vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1587s; 1549m; 1474m ν(C
N); 1587s; 1549m; 1474m ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1454vs ν(C
C)ar; 1454vs ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar; 1387m; 1332w; 1319w; 1287m; 1245m; 1217m; 1184w; 1122w; 1097w; 1017w; 889w; 867w; 787w; 745 m; 645w.
C)ar; 1387m; 1332w; 1319w; 1287m; 1245m; 1217m; 1184w; 1122w; 1097w; 1017w; 889w; 867w; 787w; 745 m; 645w.
General methods
Elemental analysis (CHNS) was performed on a FLASH 2000 CHNS Analyzer (ThermoFisher Scientific). Infrared spectra of the complexes were recorded on a ThermoNicolet NEXUS 670 FT-IR spectrometer using the KBr technique on a diamond plate in the range 400–4000 cm−1 and Nujol techniques in the range 150–600 cm−1. Thermogravimetric (TG) and differential thermal analyses (DTA) were measured on an Exstar TG/DTA 6200 thermal analyzer (Seiko Instruments Inc.). TG/DTA studies were performed in ceramic pans from room temperature to 850 °C with a 2.5 °C min−1 temperature gradient in a dynamic air atmosphere (100 mL min−1).Single-crystal X-ray analysis details
X-ray measurements on the selected crystals of 3a–6b were performed on an Oxford Diffraction XcaliburTM2 equipped with a Sapphire2 CCD detector using Mo-Kα radiation at 100 K. The CrysAlis program package (version 1.171.33.52, Oxford Diffraction) was used for data collection and reduction.34 The molecular structures were solved by direct methods SHELX-97 and all non-hydrogen atoms were refined anisotropically on F2 using full-matrix least-squares procedure SHELXS-97.35 All the hydrogen atoms were found in differential Fourier maps and their parameters were refined using a riding model with Uiso(H) = 1.2 (CH, CH2, OH) or 1.5 (CH3) Ueq. Non-routine aspects of the structure refinements are as follows: in compounds 3a, 4a, 5a and 6b the Fe atom of the nitroprusside lies at the inversion center with disorder of the nitrosyl and cyanido groups in two trans positions. Occupation factors for both disordered parts were set to 0.5.DFT calculations
The theoretical calculations were done with the ORCA 2.9.1 computational package.36a The magnetic exchange (J) was calculated using the hybrid B3LYP functional.36b–e The broken-symmetry (BS) spin state was generated by the “Flip-Spin” feature of the ORCA program and the isotropic exchange constants J were calculated both by Ruiz's formula37 and the Yamaguchi approach.38 The polarized triple-ζ quality basis set (def2-TZVP) proposed by Ahlrichs and co-workers were used for all atoms.39 The relativistic effects were dealt with using the scalar relativistic second-order Douglas–Kroll–Hess Hamiltonian (DKH2) together with a relativistically recontracted version of the def2-TZVP basis set.40 The calculations utilized the RI approximation with the decontracted auxiliary def2-TZVP/J Coulomb fitting basis set and the chain-of-spheres (RIJCOSX) approximation to exact exchange41 as implemented in ORCA. Increased integration grids (Grid5 and Gridx5 in ORCA convention) and tight SCF convergence criteria were used in all calculations. The geometry optimization of molecular fragment [{Fe(L3)(H2O)(NC)}2] (4a) was done using the BP86 functional42 with the def2-TZVP(-f) basis set together with the conductor-like screening model (COSMO),43 van der Waals corrections (VDW10)44 and DKH2. The positions of hydrogen atoms in H-bond bridged dinuclear molecular fragments [{MIII(L4)(H2O)(NC)}2] (M = Fe, Mn) (4a, 5a, 4b, 7a and 7e) and also for [{Mn(L4)(H2O)(NCS)}2] (8 and 9) were calculated again with BP86/de2-TZVP(-f).Conclusions
We have reported the synthesis of trinuclear iron(III) and manganese(III) (2a–5a) and dinuclear manganese(III) (6b) Schiff base complexes utilizing the nitroprusside anion, [FeII(CN)5NO]2−, as a building block. The compounds were characterized by various physical methods (elemental analysis, FT-IR, TG/DTA, single-crystal X-ray analysis), which clearly confirmed their compositions and molecular/crystal structures. It was observed that coordinated water molecules are responsible for the formation of supramolecular 1D chains (3a–5a) or supramolecular dimers (6b) through O–H⋯O type hydrogen bonds. Thorough magnetic analysis, which consisted of the concurrent fitting of temperature and field dependent powder magnetic data, played an important role in properly identifying values of the isotropic exchange J-parameters and zero-field splitting D-parameters.This enabled us, in harmony with DFT calculations of J-parameters, to confirm weak antiferromagnetic exchange (J ≈ −0.5 to −1.3 cm−1) between metal atoms mediated by O–H⋯O hydrogen bonds, while the super-exchange path through the diamagnetic nitroprusside anion was found to be negligible. Moreover, a detailed DFT study was performed to explain some discrepancies between J-values derived from magnetic analysis and DFT calculations themselves. We demonstrated that such DFT calculations are very sensitive to the position of the hydrogen atoms within the O–H⋯O hydrogen bond forming a super-exchange pathway. To summarize, the strength of the magnetic exchange in this class of complexes is controlled by the number of OS–H⋯OPh hydrogen bonds between metal atoms and by the OS⋯OPh distance between the phenolic oxygen atom of the salen-type ligand (OPh) and the oxygen atom of solvent (water, methanol) molecules coordinated to the neighbouring metal atom (OS). These results help to understand magnetic exchange interactions through hydrogen bonding within supramolecular [MIII(L4)(Solv)]+⋯[MIII(L4)(Solv)]+ dimers and they might be useful for estimating the strength of such interactions in more magnetically complicated systems (e.g. systems with paramagnetic bridging complexes or systems possessing magnetic ordering or slow-relaxation of magnetization).
Acknowledgements
We acknowledge the financial support from the Czech Science Foundation (GAČR P207/11/0841), the Operational Program Research and Development for Innovations – European Regional Development Fund (CZ.1.05/2.1.00/03.0058) of the Ministry of Education, Youth and Sports of the Czech Republic, and Palacký University (PrF_2013_015 a 2014009). The authors would like to thank Dr Radka Křikavová for infrared spectroscopy measurements.Notes and references
- (a) C. Chappert, A. Fert and F. N. Van Dau, Nat. Mater., 2007, 6, 813 CrossRef CAS PubMed; (b) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed; (c) C. Felser, G. H. Fecher and B. Balke, Angew. Chem., Int. Ed., 2007, 46, 668 CrossRef CAS PubMed; (d) W. Wernsdorfer, Nat. Nanotechnol., 2009, 4, 145 CrossRef CAS PubMed.
- (a) V. H. Crawford, H. W. Richardson, J. R. Wasson, D. J. Hodgson and W. E. Hatfield, Inorg. Chem., 1976, 15, 2107 CrossRef CAS; (b) J. Glerup, D. J. Hodgson and E. Pedersen, Acta Chem. Scand., 1983, 37, 161 CrossRef; (c) S. M. Gorun and S. J. Lippard, Inorg. Chem., 1991, 30, 1625 CrossRef CAS; (d) N. A. Law, J. W. Kampf and V. L. Pecoraro, Inorg. Chim. Acta, 2000, 297, 252 CrossRef CAS.
- M. Ding, B. Wang, Z. Wang, J. Zhang, O. Fuhr, D. Fenske and S. Gao, Chem. – Eur. J., 2012, 18, 915 CrossRef CAS PubMed.
- (a) J. Larionova, S. A. Chavan, J. V. Yakhmi, A. G. Frøystein, J. Sletten, C. Sourisseau and O. Kahn, Inorg. Chem., 1997, 36, 6374 CrossRef CAS; (b) O. Kahn, J. Larionova and J. V. Yakhmi, Chem. – Eur. J., 1999, 5, 3443 CrossRef CAS; (c) R. Herchel, J. Tuček, Z. Trávníček, D. Petridis and R. Zbořil, Inorg. Chem., 2011, 50, 9153 CrossRef CAS PubMed.
- I. Nemec, M. Machata, R. Herchel, R. Boča and Z. Trávníček, Dalton Trans., 2012, 41, 14603 RSC.
- (a) E. Pardo, M. Verdaguer, P. Herson, H. Rousseliere, J. Cano, M. Julve, F. Lloret and R. Lescouezec, Inorg. Chem., 2011, 50, 6250 CrossRef CAS PubMed; (b) I. Nemec, R. Herchel, I. Šalitroš, Z. Trávníček, J. Moncoľ, H. Fuess, M. Ruben and W. Linert, CrystEngComm, 2012, 14, 7015 RSC; (c) M. Korabik, Z. Repická, L. Martiška, J. Moncol, J. Švorec, Z. Padělková, T. Lis, M. Mazúr and D. Valigura, Z. Anorg. Allg. Chem., 2011, 637, 224 CAS; (d) D. Valigura, J. Moncol, M. Korabik, Z. Pučekova, T. Lis, J. Mrozinski and M. Melnik, Eur. J. Inorg. Chem., 2006, 3813 CrossRef CAS; (e) Z. Vasková, J. Moncoľ, M. Korábik, D. Valigura, J. Švorec, T. Lis, M. Valko and M. Melník, Polyhedron, 2010, 29, 154–163 CrossRef; (f) B. Kozlevčar, N. Kitanovski, Z. Jagličić, N. A. G. Bandeira, V. Robert, B. Le Guennic and P. Gamez, Inorg. Chem., 2012, 51(5), 3094–3102 CrossRef PubMed; (g) J. S. Costa, N. A. G. Bandeira, B. Le Guennic, V. Robert, P. Gamez, G. Chastanet, L. Ortiz-Frade and L. Gasque, Inorg. Chem., 2011, 50(12), 5696–5705 CrossRef CAS PubMed; (h) J. Tang, J. S. Costa, A. Golobič, B. Kozlevčar, A. Robertazzi, A. V. Vargiu, P. Gamez and J. Reedijk, Inorg. Chem., 2009, 48(12), 5473–5479 CrossRef CAS PubMed.
- H. J. Buser, D. Schwarzenbach, W. Petter and A. Ludi, Inorg. Chem., 1977, 16, 2704 CrossRef CAS.
- R. Lescouëzec, L. M. Toma, J. Vaissermann, M. Verdaguer, F. S. Delgado, C. Ruiz-Pérez, F. Lloret and M. Julve, Coord. Chem. Rev., 2005, 249, 2691 CrossRef.
- (a) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52(15), 8300–8302 CrossRef CAS PubMed; (b) H. Kara, A. Azizoglu, A. Karaoglu, Y. Yahsi, E. Gungor, A. Caneschi and L. Sorace, CrystEngComm, 2012, 14, 7320–7329 RSC; (c) H. Miyasaka, T. Madanbashi, A. Saitoh, N. Motokawa, R. Ishikawa, M. Yamashita, S. Bahr, W. Wernsdorfer and R. Clerac, Chem. – Eur. J., 2012, 18, 3942–3954 CrossRef CAS PubMed; (d) X. Shen, Q. Zhang, H. Zhou, H. Zhou and A. Yuan, New J. Chem., 2012, 36, 1180–1186 RSC; (e) E. Colacio, M. Ghazi, H. Stoeckli-Evans, F. Lloret, J. M. Moreno and C. Perez, Inorg. Chem., 2001, 40, 4876 CrossRef CAS PubMed; (f) H. Z. Kou, J. K. Tang, D. Z. Liao, S. Gao, P. Cheng, Z. H. Jiang, S. P. Yan, G. L. Wang, B. Chansou and J. P. Tuchagues, Inorg. Chem., 2001, 40, 4839 CrossRef CAS PubMed; (g) J. Larionova, M. Gross, M. Pilkington, H. Andres, H. Stoeckli-Evans, H. U. Gudel and S. Decurtins, Angew. Chem., Int. Ed., 2000, 39, 1605 CrossRef CAS; (h) M. Ohba, N. Usuki, N. Fukita and H. Okawa, Angew. Chem., Int. Ed., 1999, 38, 1795 CrossRef CAS; (i) Z. J. Zhong, H. Seino, Y. Mizobe, M. Hidai, A. Fujishima, S. Ohkoshi and K. Hashimoto, J. Am. Chem. Soc., 2000, 122, 2952 CrossRef CAS; (j) A. Marvilliers, S. Parsons, E. Riviere, J. P. Audiere, M. Kurmoo and T. Mallah, Eur. J. Inorg. Chem., 2001, 1287 CrossRef CAS.
- (a) M. Ohba and H. Okawa, Coord. Chem. Rev., 2000, 198, 313 CrossRef; (b) M. Verdaguer, A. Bleuzen, V. Marvaud, J. Vaissermann, M. Seuleiman, C. Desplanches, A. Scuiller, C. Train, R. Garde, G. Gelly, C. Lomenech, I. Rosenman, P. Veillet, C. Cartier and F. Villain, Coord. Chem. Rev., 1999, 190, 1023 CrossRef; (c) W. P. Fehlhammer and M. Fritz, Chem. Rev., 1993, 93, 1243 CrossRef CAS; (d) K. R. Dunbar and R. A. Heintz, Prog. Inorg. Chem., 1997, 45, 283 CrossRef CAS; (e) S. M. Holmes and G. S. Girolami, J. Am. Chem. Soc., 1999, 121, 5593 CrossRef CAS; (f) L. G. Beauvais and J. R. Long, J. Am. Chem. Soc., 2002, 124, 12096 CrossRef CAS PubMed; (g) O. Sato, T. Iyoda, A. Fujishima and K. Hashimoto, Science, 1996, 272, 704 CAS; (h) T. D. Harris, H. S. Soo, C. J. Chang and J. R. Long, Inorg. Chim. Acta, 2011, 369, 91 CrossRef CAS.
- (a) H. J. Choi, J. J. Sokol and J. R. Long, Inorg. Chem., 2004, 43, 1606 CrossRef CAS PubMed; (b) P. Przychodze, M. Rams, C. Guyard-Duhayon and B. Sieklucka, Inorg. Chem. Commun., 2005, 8, 350 CrossRef; (c) M. Ferbinteanu, H. Miyasaka, W. Wernsdorfer, K. Nakata, K. Sugiura, M. Yamashita, C. Coulon and R. Clerac, J. Am. Chem. Soc., 2005, 127, 3090 CrossRef CAS PubMed; (d) H. S. Yoo, H. H. Ko, D. W. Ryu, J. W. Lee, J. H. Yoon, W. R. Lee, H. C. Kim, E. K. Koh and C. S. Hong, Inorg. Chem., 2009, 48, 5617 CrossRef CAS PubMed; (e) H. Y. Kou, Y. N. Ni, B. C. Zhou and R. J. Wang, Inorg. Chem. Commun., 2004, 7, 1150 CrossRef CAS; (f) F. Tuyčras, A. Schiller, C. Duhayon, M. Hernandez-Molina, F. F. de Biani, M. Verdaguer, T. Mallah, W. Wernsdorfer and V. Marvaud, Inorg. Chim. Acta, 2008, 361, 3505 CrossRef; (g) M. Atanasov, C. Busche, P. Comba, F. E. Hallak, B. Martin, G. Rajaraman, J. van Slageren and H. Wadepohl, Inorg. Chem., 2008, 47, 8112 CrossRef CAS PubMed.
- H2L4a = N,N′-cyclohexane-bis(salicylideneiminate), H2L4b = N,N′-benzene-bis(salicylideneiminate), H2L4c = N,N′-ethylene-bis(3-ethoxysalicylideneiminate), H2L4d = N,N′-1-methylethylene-bis(3-ethoxysalicylideneiminate), H2L4e = N,N′-benzene-bis(naphthylideneiminate), H2L4f = N,N′-ethylene-bis(salicylideneiminate), H2L4g = N,N′-1-methylethylene-bis(salicylideneiminate), H2L4h = N,N′-1,1,2,2-tetramethyl ethylene-bis(salicylideneiminate), H2L4i = N,N′-ethylene-bis(3-methoxysalicylideneiminate), H2L4j = N,N′-ethylene-bis(5-bromosalicylideneiminate), H2L4k = N,N′-1,3-propylene-bis(5-bromosalicylideneiminate), H2L4l = N,N′-1,3-propylene-bis(3-methoxysalicylideneiminate), H2L4m = N,N′-1,1,2,2-tetramethylethylene-bis(naphthylideneiminate), H2L4n = N,N′-benzene-bis(4-aminodiethylenesalicylideneiminate), H2L4o = N,N′-3-methylbenzene-bis(3-ethoxysalicylideneiminate) and H2L4p = N,N′-ethylene-bis(salicylidenebenzeneiminate).
- (a) R. Dreos, G. Nardin, L. Randaccio, P. Siega, G. Tauzher and V. Vrdoljak, Inorg. Chim. Acta, 2003, 349, 239 CrossRef CAS; (b) R. Blaauw, J. L. van der Baan, S. Balt, M. W. G. de Bolster, G. W. Klumpp, H. Kooijman and A. L. Spek, Chem. Commun., 1998, 1295 RSC; (c) B. C. Wang, B. T. Huie and W. P. Schaefer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 1232 CrossRef; (d) R. Dreos, G. Nardin, L. Randaccio, P. Siega, G. Tauzher and V. Vrdoljak, Inorg. Chem., 2003, 42, 6805 CrossRef CAS PubMed; (e) R. Blaauw, I. E. Kingma, J. H. Laan, J. L. van der Baan, S. Balt, M. W. G. de Bolster, G. W. Klumpp, W. J. J. Smeets and A. L. Spek, J. Chem. Soc., Perkin Trans. 1, 2000, 1199 RSC; (f) J. Welby, L. N. Rusere, J. M. Tanski and L. A. Tyler, Inorg. Chim. Acta, 2009, 362, 1405 CrossRef CAS; (g) S. Bruckner, M. Calligaris, G. Nardin and L. Randaccio, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1671 CrossRef.
- (a) A. Geiss and H. Vahrenkamp, Eur. J. Inorg. Chem., 1999, 1793 CrossRef CAS; (b) C. H. Yang, J. A. Ladd and V. L. Goedken, J. Coord. Chem., 1988, 19, 235 CrossRef CAS; (c) M. Gerloch and F. E. Mabbs, J. Chem. Soc. A, 1967, 1900 RSC; (d) J. L. Resce, J. C. Fanning, C. S. Day, S. J. Uhm, A. F. Croisy and L. K. Keefer, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 2100 CrossRef; (e) E. Evangelio, N. P. Rath and L. M. Mirica, Dalton Trans., 2000, 41, 8010 RSC.
- C. Y. Wong, W. L. Man, C. Wang, H. L. Kwong, W. Y. Wong and T. C. Lau, Organometallics, 2008, 27, 324 CrossRef CAS.
- J. M. McInnes, D. Swallow, A. J. Blake and P. Mountford, Inorg. Chem., 1998, 37, 5970 CrossRef CAS PubMed.
- (a) M. Odoko, N. Tsuchida and N. Okabe, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m708 CAS; (b) N. Meyer and P. W. Roesky, Z. Anorg. Allg. Chem., 2007, 633, 2292 CrossRef CAS; (c) H. Kooijman, A. L. Spek, M. Kuil and P. W. N. M. van Leeuwen, private communication, 2011.
- (a) R. J. Tao, C. Z. Mei, B. T. Liu and J. Y. Niu, Chin. J. Chem., 2006, 24, 1559 CrossRef CAS; (b) M. M. Bhadbhade and D. Srinivas, Inorg. Chem., 1993, 32, 6122 CrossRef CAS.
- Y. Ding, Z. Ku, L. Wang, Y. Hu and Y. Zhou, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, m173 CAS.
- I. Nemec, T. Šilha, R. Herchel and Z. Trávníček, Eur. J. Inorg. Chem., 2013, 5781 CrossRef.
- T. Šilha, I. Nemec, R. Herchel and Z. Trávníček, CrystEngComm, 2013, 15, 5351 RSC.
- M. Clemente-León, E. Coronado, J. R. Galán-Mascarós, C. J. Gómez-García, T. Woike and J. M. Clemente-Juan, Inorg. Chem., 2001, 40, 87 CrossRef.
- (a) C. Yang, Q. Wang, Y. Ma, G. Tang, D. Liao, S. Yan, G. Yang and P. Cheby, Inorg. Chem., 2010, 49, 2047 CrossRef CAS PubMed; (b) H. Shu, Y. Xu and X. Shen, J. Chem. Crystallogr., 2011, 41, 1218 CrossRef CAS.
- R. Ababei, Y. Li, O. Roubeau, M. Kalisz, N. Bréfuel, C. Coulon, E. Harté, X. Liu, C. Mathoniére and R. Clérac, New J. Chem., 2009, 33, 1237 RSC.
- T. Wang, J. Xie, C. Xia, Y. Wu, J. Jing and J. Huaxue, Chin. J. Struct. Chem., 2010, 29, 1265 CAS.
- M. Clemente-León, E. Coronado, J. R. Galán-Mascarós, C. J. Gómez-García, Th. Woike and J. M. Clemente-Juan, Inorg. Chem., 2001, 40, 87 CrossRef.
- A. Yuan, L. Lu, X. Shen and K. Yu, Transition Met. Chem., 2003, 28, 163 CrossRef CAS.
- X. Shen, Z. Xu, A. Juan and Z. Huang, Transition Met. Chem., 2004, 29, 100 CrossRef CAS.
- (a) N. A. G. Bandeira and B. Le Guennic, J. Phys. Chem. A, 2012, 116, 3465 CrossRef CAS PubMed; (b) C. Desplanches, E. Ruiz, A. Rodriguez-Fortea and S. Alvarez, J. Am. Chem. Soc., 2002, 124, 5197 CrossRef CAS PubMed; (c) B. Le Guennic, N. Ben Amor, D. Maynau and V. Robert, J. Chem. Theory Comput., 2009, 5, 1506 CrossRef CAS.
- R. Pritchard, S. A. Barrett, C. A. Kilner and M. A. Halcrow, Dalton Trans., 2008, 3159 RSC.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B: Applications in Coordination, Organometalic and Bioinorganic Chemistry, Wiley, New York, 5th edn, 1997 Search PubMed.
- The standard deviations were calculated as σi = (Pii−1·S/(N − k))−1/2, where Pij = ∑(δμn/δai·δμn/δaj) and S = ∑(μn − μnexp)2 with n = 1 to N; ai and aj are fitted parameters, N is number of experimental points (sum of temperature and field dependent data), μn and μnexp are the calculated and experimental effective magnetic moments for a given temperature and magnetic field. The σi was then multiplied by Student's t95% to provide confidence limits with 95% probabilities listed in text.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757 CrossRef.
- CrysAlis CCD and CrysAlis RED, Version 1.171.33.52, Oxford Diffraction Ltd, England, 2009 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- (a) F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS; (d) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef; (e) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- (a) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391 CrossRef CAS; (b) E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982 CrossRef CAS PubMed.
- (a) K. Yamaguchi, Y. Takahara and T. Fueno, in Applied Quantum Chemistry, ed. V. H. Smith, Reidel, Dordrecht, 1986, p. 155 Search PubMed; (b) T. Soda, Y. Kitagawa, T. Onishi, Y. Takano, Y. Shigeta, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223 CrossRef CAS.
- (a) A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef CAS; (b) A. Schafer, C. Huber and R. J. Ahlrichs, Chem. Phys., 1994, 100, 5829 Search PubMed; (c) F. Weigend and R. Ahlrichs, Chem. Phys., 2005, 7, 3297 CAS.
- A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908 CrossRef.
- (a) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98 CrossRef CAS; (b) R. Izsak and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822 CrossRef; (c) J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 34, 7406 CrossRef.
- S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235 CrossRef CAS PubMed.
- (a) S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed; (c) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 998967–998971. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4dt02025a |
| This journal is © The Royal Society of Chemistry 2014 |