Open Access Article
Open Access ArticleThe bonding situation in triethylchalcogenostiboranes – polarized single bonds vs. double bonds†
Stefan
Heimann
,
Dieter
Bläser
,
Christoph
Wölper
,
Rebekka
Haack
,
Georg
Jansen
and
Stephan
Schulz
*
Institute of Inorganic Chemistry, University of Duisburg-Essen, 45117 Essen, Germany. E-mail: stephan.schulz@uni-due.de; Fax: +49 201 1833830; Tel: +49 201 1834635
First published on 13th August 2014
Abstract
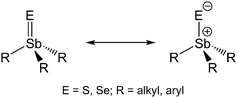
Triethylchalcogenostiboranes Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E (E = S 1, Se 2) were synthesized and their solid state structures were determined. The Sb–Se bond length is the shortest ever reported. Short Sb⋯E contacts were not observed. According to quantum chemical calculations, the bonding situation in 1 and 2 is best described as a polarized Sb–E single bond.
E (E = S 1, Se 2) were synthesized and their solid state structures were determined. The Sb–Se bond length is the shortest ever reported. Short Sb⋯E contacts were not observed. According to quantum chemical calculations, the bonding situation in 1 and 2 is best described as a polarized Sb–E single bond.
Introduction
The preparation and characterization of compounds containing double bonds between heavier main group 15 elements (Sb, Bi) and chalcogens (S, Se, or Te) have attracted much attention in the last few decades.1 The stabilization of such compounds typically requires sterically overcrowded ligands (kinetic stabilization) to prevent self-condensation and/or polymerization (ring formation) of these compounds. Moreover, Dostál et al. recently demonstrated the promising effect of N,C,N-pincer-type ligands for the stabilization of monomeric antimony(III) chalcogenides of the general type LSbE (E = S, Se).2 These complexes contain terminal Sb–E bonds, which show a high polar bonding character, Sbδ+–Eδ− (E = Se, Te), due to the donation of electron density from the N atoms to the Sb atoms. However, theoretical studies proved that the terminal Sb–E bonds in hypothetical PhSb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E molecules are less polar and exhibit more double bond character due to the lack of extra donor atoms. In addition, Breunig et al. suggested the presence of a terminal antimony−selenium double bond in the tungsten complex (CO)5W(CH(SiMe3)2)Sb
E molecules are less polar and exhibit more double bond character due to the lack of extra donor atoms. In addition, Breunig et al. suggested the presence of a terminal antimony−selenium double bond in the tungsten complex (CO)5W(CH(SiMe3)2)Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se in benzene solution, but this compound was shown to be dimeric with a central Sb2Se2 core in the solid state by X-ray studies.3 In remarkable contrast, solid state structures of organoantimony(V) chalcogenides R3SbE bearing an unsupported terminal Sb
Se in benzene solution, but this compound was shown to be dimeric with a central Sb2Se2 core in the solid state by X-ray studies.3 In remarkable contrast, solid state structures of organoantimony(V) chalcogenides R3SbE bearing an unsupported terminal Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E double bond are almost unknown, to date, even though chalcogenostiboranes of the general type R3SbE (E = O, S, Se; R = alkyl, aryl) were initially prepared more than 150 years ago. Carl Jakob Löwig and Eduard Schweizer reported in 1850 on the redox reaction of Et3Sb with elemental sulfur and selenium,4 in which the Sb atom is oxidized from the formal oxidation state +III to +V. Even though the analogous Me-substituted thiostiborane Me3SbS and other trialkylthio- and -selenostiboranes have been synthesized since then,5 triphenylthiostiborane Ph3SbS, initially reported by Kaufmann by reaction of Ph3SbCl2 with H2S,6 represents the only structurally characterized triorganylthiostiborane R3Sb
E double bond are almost unknown, to date, even though chalcogenostiboranes of the general type R3SbE (E = O, S, Se; R = alkyl, aryl) were initially prepared more than 150 years ago. Carl Jakob Löwig and Eduard Schweizer reported in 1850 on the redox reaction of Et3Sb with elemental sulfur and selenium,4 in which the Sb atom is oxidized from the formal oxidation state +III to +V. Even though the analogous Me-substituted thiostiborane Me3SbS and other trialkylthio- and -selenostiboranes have been synthesized since then,5 triphenylthiostiborane Ph3SbS, initially reported by Kaufmann by reaction of Ph3SbCl2 with H2S,6 represents the only structurally characterized triorganylthiostiborane R3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S.7 Pebler et al. described the short Sb–S bond in Ph3SbS (2.244(1) Å) as a partial double bond, resulting from a dπ–pπ interaction.7 In contrast, Otera et al. investigated the bonding situation in Me3SbS and calculated a positive charge of +0.6 at the Sb atom, indicating the Sb–S bond to be best described as a polar single bond with some ionic stabilization.8 In contrast, selenostiboranes R3Sb
S.7 Pebler et al. described the short Sb–S bond in Ph3SbS (2.244(1) Å) as a partial double bond, resulting from a dπ–pπ interaction.7 In contrast, Otera et al. investigated the bonding situation in Me3SbS and calculated a positive charge of +0.6 at the Sb atom, indicating the Sb–S bond to be best described as a polar single bond with some ionic stabilization.8 In contrast, selenostiboranes R3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se, which were also introduced as ligands in coordination chemistry,9 have not been characterized by single crystal X-ray diffraction, to date. Therefore, it is still unclear whether the Sb–E bond in Sb(V)chalcogenides should be described as a polar single bond or as a real double bond (Scheme 1).
Se, which were also introduced as ligands in coordination chemistry,9 have not been characterized by single crystal X-ray diffraction, to date. Therefore, it is still unclear whether the Sb–E bond in Sb(V)chalcogenides should be described as a polar single bond or as a real double bond (Scheme 1).
Vibrational spectroscopy was used to clarify the bonding situation. The Sb–E stretching vibration frequencies for a Sb–E single bond (Sb–S 338 cm−1; Sb–Se 234 cm−1) and Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E double bond (Sb
E double bond (Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S 485 cm−1; Sb
S 485 cm−1; Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se 333 cm−1) were calculated using Gordy's rules10 and compared with the experimental values of Et3Sb
Se 333 cm−1) were calculated using Gordy's rules10 and compared with the experimental values of Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S (439 cm−1, CCl4 solution; 422 cm−1, KBr pellet) and Et3Sb
S (439 cm−1, CCl4 solution; 422 cm−1, KBr pellet) and Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se (272 cm−1, KBr pellet)11 as well as Me3Sb
Se (272 cm−1, KBr pellet)11 as well as Me3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S (431 cm−1, KBr pellet), respectively.12 However, since the experimental values fall in between the calculated values, a clear distinction between both bonding situations was not possible.
S (431 cm−1, KBr pellet), respectively.12 However, since the experimental values fall in between the calculated values, a clear distinction between both bonding situations was not possible.
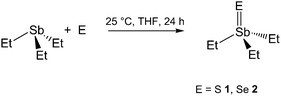
Due to our long-term interest in closed-shell compounds of heavy group 15 and group 16 elements, we recently started to investigate the solid state structures of trialkylbismuthanes R3Bi,13 tetraalkyldistibanes and dibismuthanes R4E2 (E = Sb, Bi)14 as well as chalcogen-bridged compounds of the general type (R2Sb)2E15. We herein report on the synthesis and solid state structures of Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S 1, Et3Sb
S 1, Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se 2 and Et3SbBr23, respectively.
Se 2 and Et3SbBr23, respectively.
Results and discussion
Et3SbS (1) and Et3SbSe (2) were synthesized by reaction of Et3Sb with elemental sulfur and selenium, respectively, according to a slightly modified literature method (Scheme 2).5c In contrast, any attempts to synthesize the corresponding triethyltellurostiborane Et3SbTe by reaction of Et3Sb with elemental Te or n-Bu3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Te as well as by reaction of Et3SbBr23 with TeLi2 failed.
Te as well as by reaction of Et3SbBr23 with TeLi2 failed.
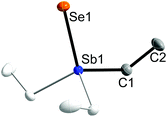
Single crystals of 1 and 2 were grown upon storage of freshly prepared solutions in THF at −30 °C. Fig. 1 and 2 show the solid state structures of 1 and 2, which crystallize as colorless needles in the trigonal space group P31c (1) and in the hexagonal space group P63mc (2). The C1 atom in 2 is disordered over two positions related via mirror-symmetry. The central structural parameters of 1 and 2 are summarized in Table 1. In addition, colorless crystals of Et3SbBr23 were obtained upon storage of a solution in ether at −30 °C (ESI†).
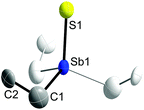 | ||
| Fig. 1 Solid state structure of 1 (thermal ellipsoids are shown at 50% probability levels); H atoms are omitted for clarity. Symmetry generated part in pale colours (3-fold axis). | ||
| 1 | 2 | 3 | |
|---|---|---|---|
| Sb–E [Å] | 2.381(7) | 2.4062(8) | 2.6469(3), 2.6513(3) |
| Sb–C [Å] | 2.130(13) | 2.142(4) | 2.127(3), 2.131(3), 2.134(3) |
| ∡C–Sb–C [°] | 107.8(5) | 106.58(14) | 115.10(10), 120.78(11), 124.10(10) |
| ∡C–Sb–E [°] | 111.1(5) | 112.23(13) | 88.25(8), 89.58(8), 89.77(8), 90.72(8), 90.77(8), 90.95(8) |
| ∡Br–Sb–Br | — | — | 177.655(12) |
| Sb⋯E [Å] | 3.956(9) | 4.1227(11) | — |
| ∡E–Sb⋯E [°] | 180 | 180 | — |
The Sb atoms in 1 and 2 adopt slightly distorted tetrahedral coordination spheres and the C–Sb–C bond angles (107.8(5)° 1; 106.58(14)° 2) are smaller compared to the C–Sb–E bond angles (111.1(5)° 1; 112.23(13)° 2). The Sb–C bond lengths in 1 (2.130(13) Å), 2 (2.142(4) Å) and 3 (av. 2.131(1) Å) are very similar and comparable to those observed for trialkylstibines SbR3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and trialkyldihalostiboranes R3SbX2
16 and trialkyldihalostiboranes R3SbX2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 such as i-Bu3SbBr2 (av. 2.130 Å),18 [(Me3Si)2CH]3SbBr2 (av. 2.149 Å),19 and (PhCH2)3SbBr2 (av. 2.185 Å).20 Only Me3SbBr2 showed significantly shorter Sb–C bond distances (av. 2.043 Å,21 2.047 Å22). In addition, simple Lewis-acid–base adducts of trialkylstibines with group 13 metal complexes, in which the Sb atom is also fourfold-coordinated,23 also showed comparable Sb–C bond lengths except for Me3Sb–GaCl3, containing the strong Lewis acid GaCl3 (av. 2.106(3) Å).24
17 such as i-Bu3SbBr2 (av. 2.130 Å),18 [(Me3Si)2CH]3SbBr2 (av. 2.149 Å),19 and (PhCH2)3SbBr2 (av. 2.185 Å).20 Only Me3SbBr2 showed significantly shorter Sb–C bond distances (av. 2.043 Å,21 2.047 Å22). In addition, simple Lewis-acid–base adducts of trialkylstibines with group 13 metal complexes, in which the Sb atom is also fourfold-coordinated,23 also showed comparable Sb–C bond lengths except for Me3Sb–GaCl3, containing the strong Lewis acid GaCl3 (av. 2.106(3) Å).24
The most interesting bonding parameters are the Sb–chalcogen bond lengths. The Sb–S bond length of 1 (2.381(7) Å) is in between the calculated values for the Sb–S single bond (Sb–S 2.43 Å)25 and the Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S double bond (2.27 Å).26 In addition, the Sb–S bond lengths as observed in Ph3Sb
S double bond (2.27 Å).26 In addition, the Sb–S bond lengths as observed in Ph3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S (2.244(1) Å),7a,b the only triorganothiostiborane yet investigated by X-ray diffraction, (Me3SbS)2Me2SnCl2 (2.305(1) Å),27 and in the monomeric Sb(III)sulfide LSbS (2.2929(17) Å)2a are significantly shorter, whereas those observed in the corresponding dimeric, sulfur-bridged compounds [LSbS]2 are elongated by almost 10 pm (2.4875(10), 2.4790(11) Å).28 In contrast, the Sb–S bond lengths observed in Sb(III) sulfides such as S(SbEt2)2 (2.429(5), 2.462(7) Å)15a and Sb(2,4,6-i-Pr3-SC6H2) (Sb–S 2.418(2), 2.420(2), 2.438(2) Å) are significantly elongated.29
S (2.244(1) Å),7a,b the only triorganothiostiborane yet investigated by X-ray diffraction, (Me3SbS)2Me2SnCl2 (2.305(1) Å),27 and in the monomeric Sb(III)sulfide LSbS (2.2929(17) Å)2a are significantly shorter, whereas those observed in the corresponding dimeric, sulfur-bridged compounds [LSbS]2 are elongated by almost 10 pm (2.4875(10), 2.4790(11) Å).28 In contrast, the Sb–S bond lengths observed in Sb(III) sulfides such as S(SbEt2)2 (2.429(5), 2.462(7) Å)15a and Sb(2,4,6-i-Pr3-SC6H2) (Sb–S 2.418(2), 2.420(2), 2.438(2) Å) are significantly elongated.29
2 is the first structurally characterized trialkylselenostiborane and shows the shortest Sb–Se bond reported to date. The Sb–Se bond length (2.4062(8) Å) is significantly shorter than the corresponding calculated value for the respective Sb–Se single bond (Sb–Se 2.56 Å)25 and is in perfect agreement with the calculated Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se double bond value (Sb–Se 2.40 Å).26 In addition, the Sb–Se bond lengths as observed in the N,C,N pincer-type complexes LSb
Se double bond value (Sb–Se 2.40 Å).26 In addition, the Sb–Se bond lengths as observed in the N,C,N pincer-type complexes LSb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se (2.4329(5), 2.4396(7) Å),2 in Sb(III)–Se compounds such as [(CHSiMe3)2SbSe]2[W(CO)5] (2.5574(6), 2.5586(6) Å)3 and (MeSe)3Sb (2.568(1)–2.588(1) Å)30 as well as those reported for polyanions [Sb4Se9]4− (2.4232(9)–2.5154(9) Å)31 are also elongated. Neither 1 nor 2 show short intermolecular Sb⋯E contacts, which is in remarkable contrast to those observed in chalcogen-bridged complexes of the general type (R2Sb)2E (E = S, Se, Te).15a Even though the Et3Sb
Se (2.4329(5), 2.4396(7) Å),2 in Sb(III)–Se compounds such as [(CHSiMe3)2SbSe]2[W(CO)5] (2.5574(6), 2.5586(6) Å)3 and (MeSe)3Sb (2.568(1)–2.588(1) Å)30 as well as those reported for polyanions [Sb4Se9]4− (2.4232(9)–2.5154(9) Å)31 are also elongated. Neither 1 nor 2 show short intermolecular Sb⋯E contacts, which is in remarkable contrast to those observed in chalcogen-bridged complexes of the general type (R2Sb)2E (E = S, Se, Te).15a Even though the Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S as well as Et3Sb
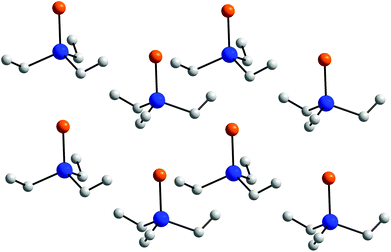
S as well as Et3Sb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Se molecules are perfectly linearly packed in the crystal as can be seen from Fig. 3, the intermolecular Sb⋯S (3.955(6) Å) and Sb⋯Se bond distances (4.1227(10) Å) clearly exceed the sum of the van der Waals radii (Sb–S 3.86; Sb–Se 3.96 Å).32
Se molecules are perfectly linearly packed in the crystal as can be seen from Fig. 3, the intermolecular Sb⋯S (3.955(6) Å) and Sb⋯Se bond distances (4.1227(10) Å) clearly exceed the sum of the van der Waals radii (Sb–S 3.86; Sb–Se 3.96 Å).32
Quantum chemical calculations
The structures of trialkylchalcogenostiboranes can be generally described in terms of a ylid–ylen mesomery (see Scheme 1) as is typically used for methylene phosphoranes, the so-called Wittig reagents.33 In order to clarify the bonding situation in 1 and 2, quantum chemical calculations were performed with density functional theory employing the B-P86 exchange correlation functional34 and a third generation dispersion correction.35 Geometry optimizations of the monomeric species 1a and 2a were carried out in the def2-QZVP basis set36 of the TURBOMOLE program package37 making use of the resolution of the identity approximation38 and a relativistic effective core potential for Sb.39 The calculated Sb–C bond lengths for the resulting C3 symmetrical gas phase structures 1a and 2a were obtained as 2.175 Å and 2.176 Å, respectively, slightly longer (0.04 Å) than the crystal structure values. The C–Sb–C bond angles for 1a (104.9°) and 2a (104.2°) were also found to be virtually identical. They are roughly 2–3° smaller than the corresponding crystal structure parameters, indicating weak intermolecular interactions with the neighboring molecule in the solid state structure (vide infra). While the calculated Sb–S bond length of 2.257 Å is notably smaller (by 0.12 Å) than the corresponding crystal structure parameter, the calculated Sb–Se bond length of 2.393 Å is in agreement within 0.02 Å with the experimental value.In order to get an idea of the packing effects within the linear chains we performed geometry optimizations of linear aggregates 1b and 2b of three monomers of 1 and 2, respectively, within C3 symmetry constraints. We verified that symmetry-unrestricted geometry optimizations destroy the linear chain arrangement, thus proving that it is not a minimum of the potential energy surface of the trimeric aggregate. The bond lengths of the central monomer (1b: C–Sb 2.169 Å, Sb–S 2.270 Å; 2b: C–Sb 2.170 Å, Sb–Se 2.406 Å) change only slightly with respect to the gas phase monomers. Yet, the C–Sb–C bond angles (1b: 106.5°; 2b: 105.8°) enlarge by more than 1°, improving agreement with the crystal structure data. The Sb⋯S intermolecular distance involving the Sb atom of the central monomer was calculated as 4.051 Å, the other one involving the S atom of the central monomer was obtained as 4.093 Å. They deviate by less than 0.14 Å from the crystal structure value of 1. The corresponding Sb⋯Se intermolecular distances were determined as 4.219 and 4.255 Å, respectively, also deviating by less than 0.14 Å from the crystal structure value of 2.
Dissociation of the linear trimeric aggregate 1b into its monomers 1a requires 57.7 kJ mol−1, a bit more than twice the calculated dissociation energy of a C3 symmetry-constrained linear dimeric aggregate of 1 (26.3 kJ mol−1). It should be noted that the dissociation energy of the water dimer is about 20% lower (all dissociation energies without zero point vibration energy correction).40 Dissociation of linear dimeric and trimeric aggregates of 2 requires 25.4 and 55.2 kJ mol−1, respectively. According to a natural population analysis (NPA)41 of the monomeric structure 1a, the sulfur atom bears a considerable charge of −0.73 e, and the Sb atom bears a charge of +1.53 e. The magnitudes of these partial charges increase even for the central monomer of the trimeric aggregate 1b (S: −0.83 e, Sb: 1.57 e; similar yet smaller changes for the remaining monomers – see ESI†). This suggests a noticeable electrostatic contribution to the aforementioned dissociation energies. Yet, taking the empirical dispersion correction contained in the B-P86+D3 results as an indicator for the importance of dispersion interactions between the monomers, they also turn out to be highly important: the dispersion contribution to the dissociation energy of the linear dimer of 1 amounts to 18.4 kJ mol−1 and for the trimer it amounts to 37.3 kJ mol−1, i.e. about 2/3 of the total interaction energy. The magnitudes of the dispersion contribution to the dissociation energies of the linear dimeric (19.1 kJ mol−1) and trimeric (38.6 kJ mol−1) aggregates of 2 are even slightly larger. On the other hand the partial charges on Se (2a: −0.64 e, central monomer of 2b: −0.74 e) and Sb (2a: +1.43 e, 2b: +1.48 e) are slightly smaller than in 1a/1b, thus explaining the slight decrease in the total dissociation energies. According to these findings, one can conclude that the bond polarity decreases with an increasing chalcogen atomic number as was reported earlier.2a,42 Moreover, dispersion interactions play a major role in the stabilization of the crystal structure.
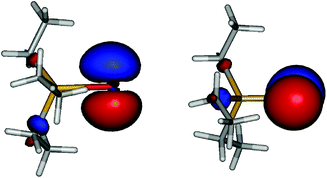
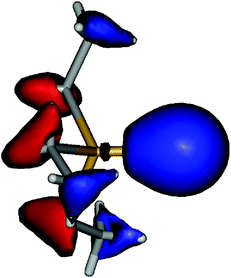
Coming back to the question of the bonding situation in the monomers, natural bond orbital (NBO)41 analysis suggests the presence of three lone pair orbitals on the sulfur atom in 1, and similarly three lone pair orbitals on the selenium atom in 2. One of the lone pair orbitals consists of the valence shell s orbital (1: 89%; 2: 92%), the remaining two are pure valence shell p orbitals orthogonal to the Sb–E bond, thus precluding the existence of a Sb–E double bond in both cases. The remaining p orbital is involved in a single covalent bond between Sb and E. A glance at the canonical molecular orbitals confirms this picture: the degenerate HOMO/HOMO−1 (Fig. 4, ESI Fig. S1†) pair is strongly localized on the E atom, while HOMO−20 (Fig. 5, ESI Fig. S2†) mainly consists of a deformed s orbital on E.
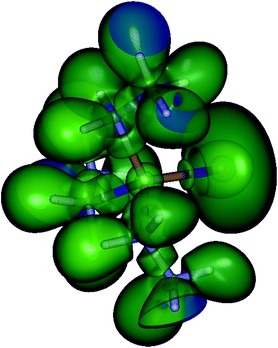
Finally, a plot of the electron localization function (ELF)43 also does not indicate a double bond character between Sb and E (Fig. 6 and ESI Fig. S3†). This and the large negative NPA partial charge on S in 1 and also on Se in 2 led us to conclude that the ylide form with one covalent and one ionic bond (cf.Scheme 1) is the dominant mesomeric structure in both cases. The relatively short Sb–Se bond thus must therefore be attributed to the strong ionic contribution to the overall bond.
Conclusions
Two trialkylchalcogenostiboranes of the type Et3SbE (E = S 1, Se 2) were structurally characterized. Even though the Sb–Se bond in 2 represents the shortest one ever reported, the shortening of the Sb–E bonds in 1 and 2 results from a strong electrostatic interaction between the central Sb atom and the chalcogen bonding partner as both bonds are strongly polarized, Sb(δ+)–E(δ−). Computational calculations gave no hint on the presence of a Sb–E double bond due to π-interactions. Dispersion interactions play a major role in the stabilization of the crystal structure.Experimental
All manipulations were performed in a glovebox under an Ar atmosphere or using standard Schlenk techniques. Solvents were carefully dried over Na/K and degassed prior to use. 1H and 13C{1H} NMR spectra were referenced to internal deuterobenzene (C6D5H, 1H: δ = 7.154; 13C: δ = 128.0).General synthesis of 1 and 2
Et3SbS 1 and Et3SbSe 2 were prepared according to a slightly modified literature method.5c 10 g (47.86 mmol) SbEt3 was added dropwise at ambient temperature to a stirred suspension of 50 mmol E (E = S, 1.60 g; Se, 3.95 g) in 150 mL of THF and stirred for 24 h. Filtration through a P4 glass frit and removal of the solvent at reduced pressure gave 1 and 2 as colorless crystalline solids. Single crystals of 1 and 2 were obtained upon storage of a concentrated solution of 1 and 2 in THF at −30 °C for 48 h.Et3SbS 1. Yield: 11.30 g (98%). 1H-NMR (300 MHz, C6D6, 25 °C): δ/ppm = 1.01 (t (br), 9H, CH3), 1.23 (q, 3JHH = 7.4 Hz, 6H, CH2). 13C-NMR (75 MHz, C6D6, 25 °C): δ/ppm = 8.6 (CH2), 13.4 (CH3).
Et3SbSe 2. Yield: 13.50 g (98%). 1H-NMR (300 MHz, C6D6, 25 °C): δ/ppm = 0.98 (t (br), 9H, CH3), 1.28 (q, 3JHH = 7.8 Hz, 6H, CH2). 13C-NMR (75 MHz, C6D6, 25 °C): δ/ppm = 9.9 (CH2), 12.7 (CH3).
Et3SbBr23. Yield: 6.71 g (95%). 1H-NMR (300 MHz, C6D6, 25 °C): δ/ppm = 1.21 (t, 3JHH = 7.8 Hz, 9H, CH3), 2.44 (q, 3JHH = 7.8 Hz, 6H, CH2).
Single crystal X-ray diffraction
Crystallographic data of 1–3,‡ which were collected on a Bruker AXS SMART diffractometer (MoKα radiation, λ = 0.71073 Å) at 150(1) K (1), 100(1) K (2) and 100(1) K (3), are summarized in Table S1 (ESI†). The solid-state structures of 1–3 are shown in Fig. 1–3. The structures were solved by direct methods (SHELXS-97) and refined anisotropically by full-matrix least-squares on F2 (SHELXL-97).45,463 was refined as non-merohedral twin based on HKL4 data. Absorption corrections were performed semi-empirically from equivalent reflections on the basis of multi-scans (Bruker AXS APEX2). Hydrogen atoms were refined using a riding model or rigid methyl groups.Acknowledgements
St. S. and G. J. like to thank the University of Duisburg-Essen for financial support. St.S. is also grateful to the Mercator Research Center Ruhr (MERCUR) for financial support.Notes and references
- R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877 CrossRef CAS PubMed; P. P. Power, Chem. Rev., 1999, 99, 3463 CrossRef PubMed.
- (a) P. Šimon, R. Jambor, A. Růžička, A. Lyčka, F. De Proft and L. Dostál, Dalton Trans., 2012, 41, 5140 RSC; (b) L. Dostál, R. Jambor, A. Růžička, A. Lyčka, J. Brus and F. de Proft, Organometallics, 2008, 27, 6059 CrossRef.
- H. J. Breunig, I. Ghesner and E. Lork, J. Organomet. Chem., 2002, 664, 130 CrossRef CAS.
- C. Löwig and E. Schweizer, Liebigs Ann. Chem., 1850, 75, 315 CrossRef PubMed.
- (a) A. Hantzsch and H. Hibbert, Ber. Dtsch. Chem. Ges., 1907, 40, 1508 CrossRef CAS PubMed; (b) W. J. C. Dyke and W. J. Jones, J. Chem. Soc., 1930, 1921 RSC; (c) R. A. Zingaro and A. Merijanian, J. Organomet. Chem., 1964, 1, 369 CrossRef CAS; (d) G. N. Chremos and R. A. Zingaro, J. Organomet. Chem., 1970, 22, 637 CrossRef CAS.
- L. Kaufmann, Chem. Ber., 1908, 41, 2762 CrossRef CAS PubMed; W. J. Lile and R. C. Menzies, J. Chem. Soc., 1950, 617 RSC.
- (a) J. Pebler, F. Weller and K. Dehnicke, Z. Anorg. Allg. Chem., 1982, 492, 139 CrossRef CAS PubMed; (b) F. Weller and K. Dehnicke, Naturwissenschaften, 1981, 68, 523 CrossRef CAS; (c) G. S. Zhdanov, V. A. Pospelov, M. M. Umanski and V. P. Glushkova, Dokl. Akad. Nauk SSSR (Russ.) (Proc. Nat. Acad. Sci. USSR), 1953, 92, 983 CAS.
- J. Otera and R. Okawara, Inorg. Nucl. Chem. Lett., 1970, 6, 855 CrossRef CAS.
- N. Kuhn and H. Schumann, J. Organomet. Chem., 1985, 288, c51 CrossRef CAS.
- W. Gordy, J. Chem. Phys., 1946, 14, 305 CrossRef CAS PubMed.
- G. N. Chremos and R. A. Zingaro, J. Organomet. Chem., 1964, 1, 369 CrossRef.
- M. Shindo, Y. Matsumura and R. Okawara, J. Organomet. Chem., 1968, 11, 299 CrossRef CAS.
- S. Schulz, A. Kuczkowski, D. Bläser, C. Wölper, G. Jansen and R. Haack, Organometallics, 2013, 32, 5445 CrossRef CAS.
- (a) S. Schulz, S. Heimann, A. Kuczkowski, C. Wölper and D. Bläser, Organometallics, 2013, 32, 3391 CrossRef CAS; (b) A. Kuczkowski, S. Heimann, A. Weber, S. Schulz, D. Bläser and C. Wölper, Organometallics, 2011, 30, 4730 CrossRef CAS.
- (a) S. Heimann, S. Schulz, D. Bläser and C. Wölper, Eur. J. Inorg. Chem., 2013, 4909 CAS; (b) S. Heimann, D. Bläser, C. Wölper and S. Schulz, Organometallics, 2014, 33, 2295 CrossRef CAS.
- A CCDC database search gave 4 hits. The average Sb–C bond lengths were found to range from 2.148 to 2.183 Å; mean value: 2.132(7) Å.
- A CCDC database search for trialkylbishalogenostiborane R3SbX2 (R = alkyl, X = halogen) gave 13 hits (2.043–2.185 Å; mean value: 2.126(8) Å).
- L. Balazs, G. Balazs, H. J. Breunig, I. Ghesner and E. Lork, Polyhedron, 2003, 22, 1719 CrossRef CAS.
- L. Balazs, H. J. Breunig, I. Ghesner and E. Lork, J. Organomet. Chem., 2002, 648, 33 CrossRef CAS.
- G. Becker, O. Mundt, M. Sachs, H. J. Breunig, E. Lork, J. Probst and A. Silvestru, Z. Anorg. Allg. Chem., 2001, 672, 699 CrossRef.
- J. Werner, W. Schwarz and A. Schmidt, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 1981, 36, 556 Search PubMed.
- H. C. Wang, E. J. Gaffney, C. R. Dybowski and A. L. Rheingold, J. Organomet. Chem., 1996, 512, 21 CrossRef CAS.
- A CCDC database analysis gave 11 hits. The Sb–C bond lengths ranged from 2.104 to 2.205 Å; mean value: 2.160(9) Å. For a review on this type of complex see also: S. Schulz, Adv. Organomet. Chem, 2003, 49, 225 Search PubMed.
- C. Hering, M. Lehmann, A. Schulz and A. Villinger, Inorg. Chem., 2012, 51, 8212 CrossRef CAS PubMed.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186 CrossRef PubMed.
- P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 12770 CrossRef PubMed.
- J. Beckmann, D. Dakternieks, A. Duthie and R. C. Foitzik, Z. Anorg. Allg. Chem., 2003, 629, 1508 CrossRef CAS PubMed.
- (a) L. Dostál, R. Jambor, A. Růžička, R. Jirásko, V. Lochař, L. Beneš and F. de Proft, Inorg. Chem., 2009, 48, 10495 CrossRef PubMed; (b) L. Dostál, R. Jambor, A. Růžička, R. Jirásko, E. Černošková, L. Beneš and F. de Proft, Organometallics, 2010, 29, 4486 CrossRef.
- M. Bochmann, X. Song, M. B. Hursthouse and A. Karaulov, Dalton Trans., 1995, 1649 RSC.
- H. J. Breunig, S. Gülec, B. Krebs and M. Dartmann, Z. Naturforsch., B: Chem. Sci., 1989, 44, 1351 CAS.
- D. Jia, Y. Zhang, Q. Zhao and J. Deng, Inorg. Chem., 2006, 45, 9812 CrossRef CAS PubMed.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806 CrossRef CAS PubMed.
- G. Wittig and U. Schöllkopf, Chem. Ber., 1954, 87, 1318 CrossRef PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- (a) F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753 CrossRef CAS PubMed; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- (a) TURBOMOLE V6.3 2011, a development of the University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com; (b) R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS; (c) M. Häser and R. Ahlrichs, J. Comput. Chem., 1989, 10, 104 CrossRef PubMed; (d) O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346 CrossRef CAS PubMed; (e) M. v. Arnim and R. Ahlrichs, J. Chem. Phys., 1999, 111, 9183 CrossRef PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057 RSC.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563 CrossRef CAS PubMed.
- M. Torheyden and G. Jansen, Mol. Phys., 2006, 104, 2101 CrossRef CAS.
- (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735 CrossRef CAS PubMed; (b) A. E. Reed, L. A. Curtis and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- U. Herzog and G. Rheinwald, Organometallics, 2001, 20, 5369 CrossRef CAS.
- (a) A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS PubMed; (b) A. Savin and B. Silvi, Nature, 1994, 371, 683 CrossRef.
- H. J. Breunig, M. Ates, S. Gülec and K. H. Ebert, in Synthetic Methods of Organometallic and Inorganic Chemistry, ed. W. H. Herrmann, 1996, vol. 3, p. 205 Search PubMed.
- SHELXS-97: G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 467 CrossRef.
- G. M. Sheldrick, SHELXL-97, Program for Crystal Structure Refinement, Universität Göttingen, 1997 CrossRef CAS PubMed See also: G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Crystallographic data of 1, 2, and 3 and computational results. CCDC 1001644–1001646. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4dt01940g |
| ‡ The crystallographic data of 1, 2, and 3 (excluding structure factors) are deposited with the Cambridge Crystallographic Data Centre as supplementary publication nos. CCDC-1001646 (1), CCDC-1001644 (2) and CCDC-1001645 (3). |
| This journal is © The Royal Society of Chemistry 2014 |