Unveiling the mechanism of selective gate-driven diffusion of CO₂ over N₂ in MFU-4 metal–organic framework

Abstract

The metal–organic framework MFU-4 shows preferential adsorption of CO₂ over N₂. This cannot be explained in terms of pore size only. Computational modelling suggests that the unique structure and flexibility of its small 8Cl-cube pore shows a unique gate-diffusion behaviour with different responses to CO₂ and N₂.

---

Introduction

Gate-driven adsorption phenomena have recently attracted much interest due to the possibility of tuning which adsorbates trigger the physical or chemical interactions responsible for the gate opening or closure in a structure. Three conditions must be present in materials presenting gate-driven adsorption: a microporous structure, at least a part of the structure is particularly soft (flexible), and this flexibility should relate to the pore size. A number of metal–organic frameworks (MOFs) have recently been reported to show this behaviour.^1–3

Breathing MOFs are an extreme case where the entire structure responds to the adsorbate by changing space group and unit cell volume. This has been found in layered MOFs,⁴ DUT-8² and notably in MIL-53.^3,5 Less flexible MOFs can also show gate-driven adsorption such as ZIF-7,^6,7 where the gate opening (closure) is triggered by a benzene ring rotation activated at different pressures depending on the adsorbate.

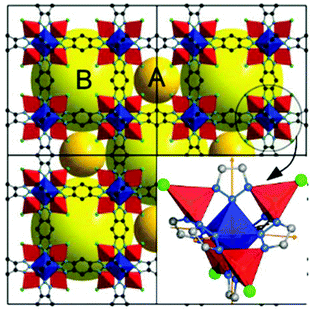
Here we focus on MFU-4⁸ (Fig. 1), which belongs to this latter category of less flexible MOFs, as it contains a robust framework, thermally stable up to 350 °C, and resistant to air and water, owing to its strong Zn–N bonds. The structure comprises ‘Kuratowski units’ with Zn found in octahedral (1 atom) and tetrahedral coordination (4 atoms), as can be seen in Fig. 1. The linker is benzo(1,2-d:4,5-d)-bistriazolate, bonded to the octahedral Zn through the central nitrogen of the N–N–N moiety within the triazolate ring, and to the tetrahedral Zn through the other nitrogens. Each Kuratowski unit contains 1 central octahedral Zn and 4 peripheral tetrahedral Zn ions. Each tetrahedral Zn is bonded to 3 N donors and one chloride ligand. Upon cross-linking of these secondary building units (Fig. 1) in a linear fashion, the metal–organic framework MFU-4, in the space group Fm3̄m, is formed.

Fig. 1 Pore system of MFU-4 containing small (A) and large (B) pores. Inset: coordination unit of MFU-4: Zn₅Cl₄[triazolate]₆. C gray, N blue, Cl green, tetrahedral Zn red, octahedral Zn dark blue. Zn atoms (1 octahedral and 4 tetrahedral) locate at the centre of each polyhedra.

In this study we report selective adsorption of CO₂ over N₂ in MFU-4 and we unveil the mechanism for this selectivity. There is an industrial interest in this separation process for CO₂ sequestration or removal from flue gas.^9,10 CO₂ and N₂ have a fairly similar size, 3.30 and 3.64 Å respectively, using the kinetic spherical diameters or, with elliptical shapes, 5.40 × 3.30 and 4.2 × 3.64 Å respectively, according to Ma and Balbuena.¹¹ Based on rigid cylinder-like pores, Ma and Balbuena predict the CO₂/N₂ selectivity as a function of the cylinder cross sectional area. CO₂ selectivity is found for pores <4.75 Å, while a slight N₂ selectivity (1.0–1.2) appears at larger pores. MFU-4 does not contain a cylindrical pore, but still these results indicate a threshold window size (<4.75 Å) for selectivity of CO₂ over N₂. The size of the small pore of MFU-4 (ca. 4.1 Å) suggests that MFU-4 could be, in principle, a good material to test in CO₂|N₂ separations.

Experimental

MFU-4 pore system

MFU-4 contains an alternate system of equal number of large and small pores (forming a 8Cl-cube) in the three crystallographic directions with a 6 : 6 connectivity, with each 8Cl-cube providing entrances to six large voids (Fig. 2).

Fig. 2 Small pore of MFU-4 formed by 8 Cl atoms (highlighted) in a cubic-like geometry. Each of the 6 faces (formed by a square of 4 Cl atoms) of this cube, called ‘8Cl-cube’, connects this small pore (‘A’ in Fig. 1) with a large pore (‘B’ in Fig. 1). Atom colors: C gray, N blue, Cl green, tetrahedral Zn red, octahedral Zn dark blue, H white.

Diffusion across MFU-4 requires to cross the small pores which act as bottlenecks. Small pores are made of 8 chloride anions in a cubic arrangement with adjacent chloride anions approaching each other at van der Waals distances of 4.1 Å, within the range for preferential diffusion of CO₂ over N₂. Chloride ligands are linked to tetrahedrally coordinated Zn, and the considerable flexibility of the N–Zn–Cl angle leads to a large variability of the Cl positions and hence a very flexible small pore.

Adsorption experiments

The fairly linear adsorption isotherms of CO₂ and N₂ at 298 K (Fig. 3) show a clear preference for the uptake of CO₂ with an ideal adsorption selectivity ∼13.

Fig. 3 Adsorption isotherms of CO₂ and N₂ in MFU-4 at 298 K.

This linearity is attractive for pressure swing adsorption (PSA) applications, and indicates that CO₂ adsorption is still far from saturation. No hysteresis was observed in the desorption, demonstrating that equilibrium was obtained. The N₂ uptake at 298 K is quite low, pointing to strong diffusion hindrance in MFU-4. This is illustrated by transient uptake profiles of CO₂ and N₂ at 195 and 298 K upon exposure to a pressure step (Fig. 4). The data shows that a small amount of N₂ adsorbs quite fast (∼1 min) and then saturation is reached. Lower uptakes of N₂ with respect to CO₂ can be related to diffusion limitations.

Fig. 4 Transient uptake profiles of CO₂ and N₂ at 195 and 298 K upon exposure to a pressure step.

Taking into account that a model using a single particle size does not explain the experimental uptakes, contributions of different particle sizes were included in the model using SEM data which revealed particles sizes between 0.6 and 20 μm. This analysis was used to calculate the apparent diffusivities for the two gases at 195 and 298 K. From these results, apparent activation energies were calculated with values 6.9 kJ mol⁻¹ (for CO₂) and 18.5 kJ mol⁻¹ (for N₂).

MFU-4 and MFU-4l,¹² having similar structure but larger pores, have been used as a model substrate for the determination of isosteric heats of adsorption. The heats of CO₂ and N₂ adsorption are 24.4 and 14.7 kJ mol⁻¹ at zero coverage, and its variation with coverage was also obtained (Fig. 5). More details can be found as ESI† (sections §4 and §5).

Fig. 5 Dependences of the isosteric heats of adsorption on loading for CO₂ and N₂ in MFU-4.

Computational details

Computational strategy

In order to understand the mechanism of selective adsorption in MFU-4, a twofold computational strategy has been followed.

First, quantum chemistry DFT energy minimisation methods have been used in order to calculate the energetic, including transition states, of the diffusion of CO₂ and N₂ through the small pore of MFU-4. Second, using a new set of DFT calculations, a new force field has been parameterised using the DFT energetics for fitting. This includes the energetics of the small cage at different conformations of the 8Cl-cube, as well as the interactions of the two adsorbates (N₂ and CO₂) with this small cage. With the new force field, molecular dynamics (MD) have been performed in order to reproduce loading and thermochemical behaviour of the real system considering explicitly full flexibility for all the atoms of the system.¹³ Full details are included in the ESI† (sections §1–§3).

Activation energies for CO₂ and N₂ in MFU-4

Within the first strategy, using first-principles calculations, a large cluster of MFU-4 has been selected in order to mimic properly the flexibility of the material, and also to model the intersection between the large and small pores as well as a number of surrounding atoms.

A cluster of MFU-4 (Fig. 6) was considered in order to calculate the energies of CO₂ and N₂ in specific locations near the small pore.

Fig. 6 (Top) Cluster of MFU-4 employed to calculate the energetics of the diffusion paths (paths calculated in dotted lines) of CO₂ and N₂ using DFT/CAM-B3LYP. N₂ follows a path equivalent to 1–2–3–2′–1′. Whilst CO₂ follows a path equivalent to 1–2–4–2′–1′. All dotted lines lie in a plane whose point ‘3’ locates at the centre of the small pore (8 Cl-cube). Atom colors: C gray, N blue, Cl green, Zn gray, H white. (Bottom) Energetic profiles of CO₂ and N₂.

Gaussian09¹⁴ software and DFT methods have been used throughout. Functional CAM-B3LYP was chosen due to its capability to account for long-range corrections introduced in the functional through the Coulomb-attenuating method. Along the same lines, large basis sets are required in order to capture the physics of the long range interactions. Due to the large size of the system, we opted by using the Def2-QZVP basis set only for the diffusing molecule (either N₂ or CO₂) and also the atoms located in the neighbourhood of the diffusing molecule, which means the 8 Cl atoms as well as those Zn and H atoms located nearby. All the other atoms were kept fixed and were described with 3-21G basis set. The few degrees of freedom imply that the energies of the diffusion paths (Fig. 6) can only be taken qualitatively. Including the diffusing molecule, this gives 1873 basis functions (cluster-MFU-4 + N₂) and 1894 basis functions (cluster-MFU-4 + CO₂).

The diffusion pathways have been calculated, and they give a different behaviour for each molecule. For CO₂ and N₂, crossing the 8Cl-cube following the path 1–2–3–2′–1′ (see Fig. 6) is possible, with the respective barriers calculated at CAM-B3LYP/Def2-QZVP level being ca. 24 and 34 kJ mol⁻¹ for CO₂ and N₂ (Fig. S1–S3 in ESI†). Importantly, a second mechanism for diffusion occurs only for CO₂, where hopping is observed between two contiguous 4Cl-faces (path 1–2–4–2′–1′ in Fig. 6), with an activation energy of 8.8 kJ mol⁻¹. With each face of the 8Cl-cube (small pore) connected to a different large cavity, this is a large→small→large hopping. The calculated activation energies, 8.8 and 33.6 kJ mol⁻¹, compare qualitatively with the experimentally obtained 6.9 and 18.5 kJ mol⁻¹ for CO₂ and N₂ respectively.

Parameterisation of a force field for MFU-4|CO₂|N₂

From the force fields available in the literature, only Universal Force Field¹⁵ (UFF) can be considered here, as it is the only one initially containing the required bonds for the simulation of the MFU-4 metal–organic framework with Zn–N, N–C, C–C, C–H and Zn–Cl covalent bonds (where C and N are an aromatic and a pyrazole, carbon and nitrogen respectively). Likewise, UFF contains also all the three-body and four-body terms arising in the MFU-4 structure. Using UFF it is possible to minimise the structure of MFU-4 obtaining cell parameters within 1% and bond distances within 8% of the reported from powder XRD data.⁸

However, the relative energies of the different conformations of Cl atoms in MFU-4, were not well reproduced by this force field according to first-principles results based on cluster calculations using TZVP¹⁶ basis set and different DFT functionals containing dispersion corrections¹⁷ (ωB97XD,¹⁸ B97-D3,¹⁹ M06X-D3,²⁰ CAM-B3LYP-D3²¹ and B2PLYP-D²²). Equally, UFF could not reproduce either of the adsorbate-MFU-4 interactions for CO₂ and N₂, as compared to the first-principles results. Attempts to use other force fields also failed. Hence, using first-principles data, some of the energetic terms of the UFF were reparameterised.

Regarding the relative energies of the different conformations of Cl atoms in MFU-4, they are not well reproduced by UFF. This has been found by comparing the relative energies of different geometries as calculated with UFF and with several DFT-D (where -D stands for dispersion-corrected) functionals using TZVP basis set. In order to try to stick as much as possible to previously existing force fields, we have made a thorough literature review of epsilon and sigma parameters for Cl and H, with the results shown in Fig. S6 and S7,† implying the use of the following force fields: Kamath et al.,²³ UFF,¹⁵ Dietz and Heinzinger,²⁴ Kovacs et al.,²⁵ Lopes et al.,²⁶ Harnes et al.,²⁷ reaxFF,²⁸ Liu et al.,²⁹ Bureekaew et al.,³⁰ and Torres et al.³¹

Being the energetics of the flexibility of the small pore a central point which is directly related to the diffusivity of any adsorbate through MFU-4, a modification of UFF is mandatory to describe more correctly the flexibility of MFU-4, and this has been done in the present study. Using cluster-based quantum-chemistry DFT-D data, two steps have been followed in the parameterisation:

Step-1. First, without considering the adsorbate molecules, five parameters were found crucial to mimic the flexibility of the MFU-4 structure: the Lennard-Jones terms for Cl and H atoms (epsilon, sigma for H and Cl, eqn (1)), and the three-body term regarding the floppiness of the Cl–Zn–N angle in MFU-4 (k_ClZnN, eqn (2)).

For this task, a smaller cluster of MFU-4 has been fully optimised to its minimum energy conformation using ωB97XD functional and TZVP basis set. Apart from the minimum energy, five additional conformations of the cluster were considered, with the positions of the Cl ligands randomly moved ±0.75 Å from their equilibrium position, keeping the Zn–Cl bond distance fixed. All the other atoms were kept fixed. The corresponding ωB97XD/TZVP energies were calculated and tabulated with respect to the minimum energy conformation. These energies were used as target in order to fit the following parameters of the new forcefield (Table 1).

Table 1 Parameters that have been changed from UFF to simulate MFU-4 (eqn (1) and (2)). ε and k in kcal mol⁻¹; σ in Å

	ε Cl	σ Cl	ε H	σ H	k Cl–Zn–N
new-FF	0.200	3.828	0.023	1.482	18.5
UFF	0.227	3.947	0.044	2.886	141.4

---

With this procedure, for the calculation of the new-FF energies, only the Lennard-Jones, bond bending (Cl–Zn–N), dihedral (Cl–Zn–N–N and Cl–Zn–N–C), and electrostatic terms were needed. The atomic charges were obtained from the same DFT calculations using the Mulliken analysis.

Step-2. The previous step concerns internal parameters of the MFU-4. In this step, parameters concerning the interactions MFU-4-adsorbate were obtained.

For this purpose, several configurations corresponding to CO₂ and N₂ diffusion paths, similar to those previously described in Fig. S1–S4,† have been considered. With each configuration, the interaction energy was calculated as:

E_ads=E_{(MFU-4 adsorbate)} − E_(MFU-4) − E_(adsorbate) (3)

where ‘adsorbate’ is either CO₂ or N₂. The resulting energies have been taken as interaction energies between the adsorbate and MFU-4.

Then, the same single point calculations were considered using the new-FF, and in this case, new Lennard-Jones parameters for the adsorbate atoms, C, O, N were found with the condition that the new-FF energy should be as close as possible to the DFT value. Tables 2 and 3 show the improvement with respect to UFF. The atomic charges in the new-FF were obtained from the Mulliken analysis of the DFT results.

Table 2 Interaction energies (kJ mol⁻¹), as calculated from eqn (3) for five configurations of CO₂ inside the pores of the MFU-4 cluster. Highlighted in bold is the adsorption energy considered as the isosteric heat of adsorption

	ωB97XD/TZVP	new-FF	UFF
MFU-4⋯CO2	−22.3	−18.0	−17.4
	−24.9	−16.2	−11.9
	−5.8	−8.2	−11.6
	2.2	1.3	−4.3
	11.2	13.0	4.7

---

Table 3 Interaction energies (kJ mol⁻¹), as calculated from eqn (3) for five configurations of N₂ inside the pores of the MFU-4 cluster. Highlighted in bold is the adsorption energy considered as the isosteric heat of adsorption

	ωB97XD/TZVP	new-FF	UFF
MFU-4⋯N2	−13.2	−9.6	−9.7
	7.6	4.8	0.2
	8.5	7.6	2.6
	19.3	19.5	11.8
	32.0	35.5	24.1

---

These DFT calculations (ωB97XD/TZVP) have allowed to obtain the adsorption energies of CO₂ and N₂. Using all the adsorbate/MFU-4 geometries employed above and searching the minimum energy using the first-principles methods and geometry optimisation algorithms, the adsorption energies 24.9 and 13.2 kJ mol⁻¹ have been found (Tables 2 and 3), which compare well with the experimental observations for MFU-4 (24.4 and 14.7 kJ mol⁻¹ for CO₂ and N₂ respectively, Fig. 5).

Hence, the interaction between the adsorbates and the MFU-4 cluster were taken into account in order to reparameterise the Lennard-Jones of the C, O and N atoms in CO₂ and N₂. The new Lennard-Jones parameters are shown in Table 4.

Table 4 Parameters that have been changed from UFF to simulate the interaction between MFU-4 and the adsorbates CO₂ and N₂. C1 is carbon in CO₂, O1 is oxygen in CO₂, N1 is nitrogen in N₂. This new force field should only be applied to the MFU-4|CO₂|N₂ system

	UFF		New ff
	ε (kcal mol^−1)	σ (Å)	ε (kcal mol^−1)	σ (Å)
C1	0.105	3.851	0.161	3.420
O1	0.060	3.500	0.055	3.897
N1	0.069	3.660	0.059	3.860

---

Molecular dynamics of CO₂ and N₂ in MFU-4

In order to further explain the diffusional features of CO₂ and N₂, we performed a molecular dynamics study using the new force field.

With the new force field, molecular dynamics have been performed within the NVT ensemble for 2 ns with the explicit relaxation of all the atoms of the system using LAMMPS.³² The results give more information than that obtained from the static DFT results. At low (10 molecules per unit cell³³) CO₂ loading and 298 K (movie 1, see ESI†) no diffusion is observed, and the same is observed for N₂, and this is in part due to the presence of minimum energy positions inside the large pore. At higher loading³³ and 298 K, a completely different picture appears for CO₂ with many large–small–large pore crossings observed (movie 2, see ESI,† and Fig. 7) due to the larger mobility of the molecules, more widespreadly distributed across the pore, spending more time close to the 8Cl-cube (small pore).

Fig. 7 (Top) Intercage diffusional path of CO₂ in MFU-4 corresponding to the dynamics at 298 K and high loading. The small pore (8Cl-cube) is in the centre of the figure. A large–small–large pore crossing is observed for a CO₂ molecule. The other CO₂ molecules are hidden for clarity. The arrows indicate subsequent snapshots. (Bottom) An equivalent, close-up view of the CO₂ crossing including time count.

Fig. 7 (top) shows a CO₂ molecule initially outside the central 8Cl-cube (1^st snapshot). Then, the CO₂ molecule enters the central 8Cl-cube (2^nd and 3^rd snapshots) through a large→small pore crossing. Then, the CO₂ molecule exits the central 8Cl-cube (4^th and 5^th snapshots) through a small→large pore crossing, and stays in the large pore (6^th snapshot).

CO₂, due to its long shape, keeps the gate open while it is inside the deformed 8Cl-cube and this facilitates the way out, which happens in a short period of time, resulting in a fast (43 ps) large→small→large hopping (Fig. 7, bottom).

The specific feature, only present for CO₂ adsorbed within MFU-4, which contributes largely to explain the enhanced CO₂ mobility, is the fact that increasing loadings result in a larger interaction of CO₂ with the tetrahedral Zn atoms, causing a displacement of the Cl from its equilibrium position and opening the gate of the small pore (Fig. 8, left).

Fig. 8 Diffusion features of CO₂ (left) and N₂ (right) in MFU-4. The larger size (or: greater length) of CO₂ keeps the 8Cl-gate open (see arrow in the displaced chloride), increasing the probability of jumping out, while N₂ cannot, and stays longer, resulting in lower diffusivity. Atom colors: C gray, N blue, Cl green, Zn gray, H white.

For N₂ at high loading and 298 K a different picture is observed (movie 3, see ESI†). Very few pore crossings are observed, in agreement with the previous result of a larger activation energy, but most importantly, the molecular dynamics shows that when the N₂ molecule enters the small pore, it remains inside (Fig. 8, right) for longer periods of time than the CO₂ molecule.

When N₂ is inside the 8Cl-cube, all the Cl-gates tend to remain closed because of the shorter length of the molecule (Fig. 9). In fact the position of the N₂ molecule inside the small pore is an energy minimum (position ‘3’ in Fig. S1 and S2†), whilst for CO₂ it is a maximum (position ‘3’ in Fig. S3 and S4†). This explains the longer time of residence of N₂ which contributes to the lower diffusivity with respect to CO₂. A schematic picture (Fig. 10) shows how the relative lengths of the adsorbates (CO₂ and N₂) contribute to leave the gate of the small pore either open (Fig. 10, left; CO₂) or closed (Fig. 10, right; N₂).

Fig. 9 Intercage diffusional path of N₂ in MFU-4. Entering the small pore (8Cl-cube) also requires a displacement of a Cl ligand, but once N₂ is inside (bottom right snapshot), the 8Cl-cube remains in a ‘closed-gate’ conformation. In fact, an energetic stabilisation is observed for the bottom-right conformation, in clear difference with the mechanism for CO₂.

Fig. 10 Snapshot views of the large (larger balls highlighted) and small pores of MFU-4 showing the different mechanisms for CO₂ and N₂ diffusion. N₂ (right) stabilised inside the small pore with the chloride ligands (smaller balls highlighted) in cubic shape. CO₂ (left), ‘pushing’ a Cl-gate while inside the small pore, leaving more space to diffuse out.

A full analysis of the molecular dynamics trajectories shows that crossing events were only found at the higher loadings sampled, corresponding to 20 molecules (either CO₂ or N₂) per unit cell (a = 21.697 Å) of MFU-4. In the case of CO₂, 11 crossing events were observed, whilst in the case of N₂ only 2 occurred. This is also in support of all the previous findings and the smaller diffusivity experimentally observed for N₂ (Fig. 3 and 4).

Conclusions

Summarising, CO₂ and N₂ interact differently with the small pore of the MFU-4 structure. Such small pore is made of 8 chloride ligands which interact through van der Waals and coulombic forces, and are each coordinatively bonded to a tetrahedral Zn atom containing a soft Cl–Zn–N bending angle, all of this giving a very flexible pore.

Starting from a CO₂ molecule in the external surface of MFU-4, the strong interaction of CO₂ with the chlorine ligands leads to frequent events where CO₂ ‘pushes’ a Cl-gate and penetrates inside the 8Cl-cube. Due to the comparatively large length of the CO₂ molecule with respect to the Cl⋯Cl distance, the Cl-gate remains ‘open’ (Fig. 8, left) while CO₂ is inside the 8Cl-cube. This favours a fast migration-out, and hence the CO₂ remains comparatively short times inside the 8Cl-cube. On the other hand, when N₂ enters the 8Cl-cube, remains inside longer time due to its shorter size. This is because the shorter length of N₂ (with respect to CO₂) allows the Cl-gate to remain ‘close’ while N₂ is inside the 8Cl-cube (Fig. 8, right). This contributes to a stabilisation and ‘gate closure’ while N₂ is inside the 8Cl-cube, hence leading to lower diffusivity.

The mechanism for selective adsorption of CO₂ over N₂ in MFU-4 has been unveiled with the help of computational methods. The consistency of the computational results is provided by the agreement with adsorption experiments, which indicate a clearly preferred adsorption of CO₂ over N₂. The respective activation energies (from calculations 8.8 and 33.6 kJ mol⁻¹, and from measurements 6.9 and 18.5 kJ mol⁻¹ for CO₂ and N₂ respectively) indicate a reasonable agreement, although for N₂ a certain discrepancy is observed. The adsorption energies (from calculations 24.9 and 13.2 kJ mol⁻¹, and from experiments 24.4 and 14.7 kJ mol⁻¹ for CO₂ and N₂ respectively) show a remarkable agreement in spite of the approximations made in the computational part. The limitations of the force field and the models employed, as well as the intrinsic difficulty of reproducing the framework-adsorbate and adsorbate–adsorbate dispersion interactions with high accuracy is responsible of a certain discrepancy of the computational results with respect to the experiments, such as the activation energy for the N₂ diffusion (calculated as 33.6 and measured as 18.5 kJ mol⁻¹). However, in spite of some discrepancy in the numerical values, we believe the relative features have been well captured and they are sufficient to unveil the mechanisms of diffusion of CO₂ and N₂ in MFU-4.

From the commercial viewpoint, the current results show that MFU-4 should not be a competitive material for CO₂|N₂ separations mainly due to the fact that the diffusion is too slow for CO₂. Although initially the pore size (ca. 4.1 Å) seems within an optimum range for this separation process and the diffusion of N₂ is sufficiently constrained, an appropriate material should show a faster diffusion for CO₂. The problem in MFU-4 is that crossing events for CO₂ tend to be less frequent than what should be required. Most of the time, CO₂ molecules diffuse inside the large pore where a large region of low energy is found, this meaning that jump motions towards the small pore of the appropriate direction and velocity are probabilistically unfavoured. In any case, unveiling the mechanism of selective diffusion can be of help to design similar strategies with other adsorbates and related materials. Further research on this topic will address these issues.

Acknowledgements

G. S. thanks the Spanish government for the provision of Severo Ochoa project (SEV 2012-0267) and SGAI-CSIC for computing time. Financial support by the DFG (Priority Program SPP 1362 “Porous Metal–organic Frameworks”) is gratefully acknowledged (D. V. and D. D.).

Notes and references

1. T. K. Maji, R. Matsuda and S. Kitagawa, A flexible interpenetrating coordination framework with a bimodal porous functionality, Nat. Mater., 2007, 6, 142.
2. H. C. Hoffmann, B. Assfour, F. Epperlein, N. Klein, S. Paasch, I. Senkovska, S. Kaskel, G. Seifert and E. Brunner, High-Pressure in Situ ¹²⁹Xe NMR Spectroscopy and Computer Simulations of Breathing Transitions in the Metal–Organic Framework DUT-8(Ni), J. Am. Chem. Soc., 2011, 133, 8681.
3. A. Boutin, M. A. Springuel-Huet, A. Nossov, A. Gedeon, T. Loiseau, C. Volkringer, G. Ferey, F.-X. Coudert and A. H. Fuchs, Breathing Transitions in MIL-53(Al) Metal–Organic Framework Upon Xenon Adsorption, Angew. Chem., Int. Ed., 2009, 48, 8314.
4. A. Kondo, H. Noguchi, S. Ohnishi, H. Kajiro, A. Tohdoh, Y. Hattori, W. C. Xu, H. Tanaka, H. Kanoh and K. Kaneko, Novel Expansion/Shrinkage Modulation of 2D Layered MOF Triggered by Clathrate Formation with CO₂ Molecules, Nano Lett., 2006, 6, 2581.
5. P. Serra-Crespo, E. Gobechiya, E. V. Ramos-Fernández, J. Juan-Alcañiz, A. Martinez-Joaristi, E. Stavitski, C. E. A. Kirschhock, J. A. Martens, F. Kapteijn and J. Gascon, Interplay of metal node and amine functionality in NH₂-MIL-53: modulating breathing behavior through intra-framework interactions, Langmuir, 2012, 28, 12916.
6. C. Gücüyener, J. van den Bergh, J. Gascon and F. Kapteijn, Ethane/Ethene Separation Turned on Its Head: Selective Ethane Adsorption on the Metal–Organic Framework ZIF-7 through a Gate-Opening Mechanism, J. Am. Chem. Soc., 2010, 132, 17704.
7. J. van den Bergh, C. Gücüyener, E. Pidko, E. J. M. Hensen, J. Gascon and F. Kapteijn, Understanding the anomalous paraffin selectivity of ZIF-7 in the separation of light alkane/alkene mixtures, Chem. – Eur. J., 2011, 17, 8832.
8. S. Biswas, M. Grzywa, H. P. Nayek, S. Dehnen, I. Senkovska, S. Kaskel and D. Volkmer, A cubic coordination framework constructed from benzo-bistriazolate ligands and zinc ions having selective gas sorption properties, Dalton Trans., 2009, 6487.
9. A. L. Dzubak, L.-C. Lin, J. Kim, J. A. Swisher, R. Poloni, S. N. Maximoff, B. Smit and L. Gagliardi, Ab initio carbon capture in open-site metal–organic frameworks, Nat. Chem., 2012, 4, 810.
10. D. Wu, Q. Yang, C. Zhong, D. Liu, H. Huang, W. Zhang and G. Maurin, Revealing the Structure-Property Relationships of Metal–Organic Frameworks for CO₂ Capture from Flue Gas, Langmuir, 2012, 28, 12094.
11. Y. Ma and P. B. Balbuena, Window effect on CO₂/N₂ selectivity in metal organic framework materials, Chem. Phys. Lett., 2012, 552, 136.
12. D. Denysenko, M. Grzywa, M. Tonigold, B. Streppel, I. Krkljus, M. Hirscher, E. Mugnaioli, U. Kolb, J. Hanss and D. Volkmer, Elucidating gating effects for hydrogen sorption in MFU-4-type triazolate-based metal–organic frameworks featuring different pore sizes, Chem. – Eur. J., 2011, 17, 1837.
13. D. Dubbeldam, R. Krishna and R. Q. Snurr, Method for Analyzing Structural Changes of Flexible Metal–Organic Frameworks Induced by Adsorbates, J. Phys. Chem. C, 2009, 113, 19317.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision D.01), Gaussian, Inc., Wallingford, CT, 2009.
15. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, UFF: a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114, 10593.
16. A. Schaefer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian-basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835.
17. (a) S. Grimme, Density functional theory with London dispersion corrections, Comput. Mol. Sci., 2011, 1, 211; (b) L. Goerigk and S. Grimme, A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions, Phys. Chem. Chem. Phys., 2011, 13, 6670.
18. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
19. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465.
20. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functional, Theor. Chem. Acc., 2008, 120, 215–241.
21. T. Yanai, D. Tew and N. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
22. L. Goerigk and S. Grimme, Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals: Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2011, 7, 291–309.
23. G. Kamath, G. Georgiev and J. J. Potoff, Molecular Modeling of Phase Behavior and Microstructure of Acetone-Chloroform-Methanol Binary Mixtures, J. Phys. Chem. B, 2005, 109, 19463–19473.
24. (a) W. Dietz and K. Heinzinger, Ber. Bunsen-Ges. Phys. Chem., 1984, 8, 543; (b) Dietz and Heinzinger force field cited in: I. G. Tironi and W. F. van Gunsteren, A molecular dynamics simulation study of chloroform, Mol. Phys., 1994, 83, 381–403.
25. H. Kovacs, J. Kowalewski and A. Laaksonen, Molecular dynamics simulation of liquid mixtures of acetonitrile and chloroform, J. Phys. Chem., 1990, 94, 7378.
26. J. N. Canongia-Lopes, J. Deschamps and A. A. H. Padua, Modeling Ionic Liquids Using a Systematic All-Atom Force Field, J. Phys. Chem. B, 2004, 108, 2038–2047.
27. J. Harnes, M. Abu-samha, H. Bergersen, M. Winkler, A. Lindblad, L. J. Sæthre, O. Björneholm and K. J. Børve, The structure of mixed methanol/chloroform clusters from core-level photoelectron spectroscopy and modeling, New J. Chem., 2011, 35, 2564–2572.
28. O. Rahaman, A. C. T. van Duin, S. Vyacheslav, S. Bryantsev, J. E. Mueller, S. D. Solares, W. A. Goddard III and J. Douglas, Development of a ReaxFF Reactive Force Field for Aqueous Chloride and Copper Chloride, J. Phys. Chem. A, 2010, 114, 3556–3568.
29. Z. Liu, T. Chen, A. Bell and B. Smit, Improved United-Atom Force Field for 1-Alkyl-3-methyl-imidazolium Chloride, J. Phys. Chem. B, 2010, 114, 4572–4582.
30. S. Bureekaew, S. Amirjalayer, M. Tafipolsky, C. Spickermann, T. K. Roy and R. Schmid, MOF-FF A flexible first-principles derived force field for metal–organic frameworks, Phys. Status Solidi B, 2013, 1.
31. E. Torres and G. A. DiLabio, Density-Functional Theory with Dispersion-Correcting Potentials for Methane: Bridging the Efficiency and Accuracy Gap between High-Level Wave Function and Classical Molecular Mechanics Methods, J. Chem. Theory Comput., 2013, 9, 3342–3349.
32. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1.
33. The ‘low’ loading corresponds to 10 molecules per (cubic) unit cell of MFU-4, with a = 21.697 Å and a cell volume of 10 214.08 ų. The ‘high’ loading is twice.

---

Footnote

† Electronic supplementary information (ESI) available: Includes movies and full details of the computational models and further experimental results. See DOI: 10.1039/c4dt00365a

---