Towards a quantitative understanding of palladium metal scavenger performance: an electronic structure calculation approach

Abstract

Dispersion corrected density functional theory (DFT-D) has been applied to understand the performance of several palladium metal scavengers. Nine different sulfur-based ligands and three different palladium metal sets have been investigated in detail. Based on a thorough analysis of the thermodynamic binding parameters ΔH, ΔG and ΔS, we have identified the best binding modes for all scavenger ligands. Bis-monodentate coordination is favoured over chelation in ΔH and ΔG values for most of the scavenger ligands. Special attention has been paid to the ligand strain energies, which account for the structural changes of the ligands upon complexation indicating that small (5-membered) chelates are considerably less favourable than expected. Some ligands can use their longest chain (>7-atoms) to yield trans chelates, which ligands with shorter chains (≤6-atoms) are unable to form. A secondary amino nitrogen (RR′NH) is found to be the best donor with highest binding enthalpy for Pd(II) metal systems. In terms of the strength of the initial binding interactions, –SMe > –SH; capping thiols (–SH) as thioethers (–SMe) is therefore suggested to be an effective strategy in scavenger design. These observations mark the beginning of a knowledge base of the full range of possible interactions, leading to the construction of a sulfur ligand database for the design of scavenger systems.

---

Introduction

Metal-catalysed reactions have served as powerful tools in organic synthetic chemistry. Typical metal catalysed or metal mediated reactions, which include couplings, rearrangements, metathesis and redox transformations are all now used for the discovery¹ and manufacture² of pharmaceutical and other high value products. Palladium catalysed reactions have become ubiquitous in syntheses of new active pharmaceutical ingredients (APIs) in recent years.³ The main disadvantage associated with these reactions is the presence of residual metal in APIs which creates toxicity and regulatory issues.⁴ Metal residues can also cause problems in discovery phase through false positives in assay and toxicity testing. Rigorous metal removal is therefore an imperative.

A number of processes have been developed for the removal of metal impurities from pharmaceutical intermediates and products.^4,5 Standard methods of metal removal, such as distillation, use of ion exchange resins, precipitation, extraction, and crystallisation usually have significant disadvantages and residues can persist even beyond rigorous purification steps of this type.⁶ Functionalised materials which can scavenge residual metals from APIs or waste streams represent a strategic solution to these problems. One of the key advantages of using these materials is that the functionality can be designed to have a very high affinity towards specific metal residues. The molecular backbones of APIs often bear a number of functional groups and stereogenic centres situated in close proximity; these functional arrays are created to ensure binding to molecular targets. However, strong binding of precious metal atoms can be an unwanted outcome; the design of an effective metal scavenger therefore requires the incorporation of combinations of ligands or functional groups that have an overall higher affinity for the metal than that of the API.

A wide range of multifunctional and complex metal scavengers are required when the APIs and related intermediates are structurally diverse. PhosphonicS has developed and applied a range of successful multifunctionalised materials based on mesoporous silica, which possess siloxane (Si–O–Si) bonds linking organic functionality to the silica framework, for the removal of palladium residues from product streams;⁷ some of these have been deployed at scale.⁸ Materials based on polystyrene matrices are also available commercially. Sulfur-based organic functional groups which offer potential strong metal–ligand interactions, and which can be exploited in metal sequestration are privileged in the design of these materials.

The final product of a palladium metal-catalysed reaction may be contaminated by impurities in which the metal is present in different oxidation states.⁹ For our study, Pd(0) and Pd(II) have been selected as the initial metal centres for investigation because of their ubiquity in catalysis, and the availability of detailed knowledge about their catalytic mechanisms.¹⁰

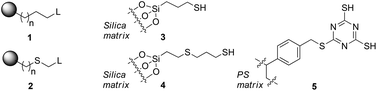
Scavenger materials are represented by generic structures 1 and 2. Linkers may be purely hydrocarbon, or contain a thioether linkage, depending on the method of synthesis.¹¹ Species 3 (Silicycle SiliaMetS Thiol), 4 (PhosphonicS SPM32) and 5 (Biotage MP-TMT) represent the types of materials available commercially and in current use.

In this contribution, we have studied detailed thermodynamic aspects of the basic chemistry exploited by scavenger materials during the scavenging process. This approach provides a quantitative understanding of the performance of several scavengers containing sulfur-based functionality based on electronic structure calculations of binding parameters for metal–scavenger binding. We have used three different metal sets that represent palladium species ubiquitous in coupling reaction chemistry. We have replaced the linkage to the silica matrix (Fig. 1) for each scavenger material with a methyl group to simplify the calculations. This represents an approximation but it is unlikely that a longer tether will significantly affect the Lewis basicity of the sulfide. A key goal of the study is the exposure of the effectiveness of the internal thioether ligand, a key design feature of the materials.

Fig. 1 Representative mono- and multidentate sulfur-based silica scavenger materials.

The binding between the metal sets and the ligands was investigated using the reactions shown in Scheme 1. Reaction (1) is used for the calculation of binding parameters (ΔH, ΔG and ΔS) for bis-monodentate coordination of the functional groups to the metal centres, and reaction (2) is used for chelation between the metal centres and bidentate ligands.

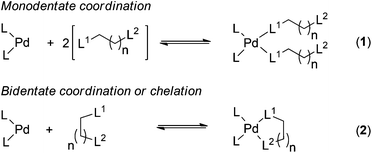Scheme 1 Model metal–ligand binding reactions; L is the arbitrary ligand associated with the metal sets, L¹ and L² represent donor sites of a multidentate ligand.

The aim of this work is to model a range of established palladium scavengers which contain a thioether sulfur as part of a linkage to a solid support, to study the conformational preferences of the ligand arrays they present, and to assess the importance of the thioether moiety as a participating centre in a chelate array. Based on these observations, important initial principles and findings are presented which begin the construction of a sulfur ligand knowledge base for the design of the next generation of metal scavenger systems.¹²

Computational methods

Dispersion-corrected density functionals have recently been applied to the study of transition metal complexes relevant to organometallic catalysis, with promising results.^13,14 We have therefore selected the M06-L,¹⁵ B97-D¹⁶ and B2PLYP¹⁷ functionals for our current study. The three functionals are each combined with three different basis set combinations. For Pd, the Stuttgart relativistic ECPs are used to describe the core (46 electrons), together with the associated triple-ζ basis as implemented in the Gaussian program.¹⁸ This ECP has been reported to perform well for Pd.¹⁹ All other atoms (including halogen Cl) are treated with three different basis sets (6-311++G(d,p),²⁰ 6-311G(d,p)²⁰ and 6-31G(d,p)²¹). The following naming convention is used to denote these basis sets in the text below: BS1: [Stuttgart RECP + associated triple-ζ basis] on Pd and 6-31G(d,p) on all other atoms; BS2: [Stuttgart RECP + associated triple-ζ basis] on Pd and 6-311G(d,p) on all other atoms; BS3: [Stuttgart RECP + associated triple-ζ basis] on Pd and 6-311++G(d,p) on all other atoms.

In the absence of fortuitous error cancellation, the larger the basis set, the more accurate it is. In this case, the largest basis set BS3 can therefore be taken as the benchmark among the three. However, the computational time associated with BS3 will be significantly higher than BS2 and BS1; the use of BS3 is therefore not practical for the investigation of the full range of ligands and binding motifs described in Fig. 4. We therefore investigated the use of the smaller basis sets for this task. The methods were compared based on consistency of structural parameters with the X-ray crystal structure, consistency in relative enthalpies with the highest level of theory tested, and computational cost (CPU time). In this study the benchmark level of theory is the B2PLYP functional in conjunction with the BS3 basis set.

The polarising effect of solvent on the binding energy of the systems is expected to be minimal given the neutral nature of the ligands. Nonetheless, we have carried out exploratory calculations to confirm this for ligands 10 and 12, which indicate the effect to be a slight reduction in the binding energy by ∼2 kcal mol⁻¹. The implicit solvent effect of methanol (selected because it is the simplest alcohol solvent, and alcohol solvents are often present in reactions and streams for scavenging) has been calculated using the polarizable continuum model (PCM) as implemented in Gaussian 09.²² Some aspects of the electronic structures have been analysed using Natural Bond Orbital (NBO) calculations at the same level of theory using NBO 3.1 program²³ which is implemented in Gaussian 09. All computations are performed with the Gaussian 09 program.²⁴

Results and discussion

1. Method calibration

We have calculated the binding enthalpies and energies between metal sets 6–8 and ligand 9 (Fig. 2). These metal sets represent Pd(II) in different ligand environments (6 and 7) and Pd(0) in a model chelated bis-phosphine environment (8). Ligand 9 is the simplest thiol ligand relevant to the fuller ligand set (vide infra).

Fig. 2 Metal sets for the investigation of the scavenging process.

The results are presented fully in Tables S1 and S2 respectively in the ESI.† Based on the binding enthalpy/energy values obtained, the B97-D functional in conjunction with basis BS2 provides a reliable level of theory for current systems at an acceptable balance between accuracy and computational cost.

There were no significant structural differences between the complex geometries obtained with the three different functionals.

The accuracy of the structures generated was confirmed with the help of known crystal structures (complex S1, S2 and S3 in the ESI†); we found that both M06-L and B97-D functionals in conjunction with BS2 could reproduce bond lengths to within 0.05 Å of values from crystallographic data. The small deviations may be due to the fact that the model approach is not capable of accounting for crystal-packing effects in this case. Because the B97-D functional in conjunction with BS2 was able to reproduce binding enthalpies (ΔH) relative to the benchmark data, and structural features relative to the crystallographic data accurately, it was selected for further investigation of a wider range of complexes. A complete discussion of the method evaluation is presented in the ESI.†

2. Geometry

Complex geometries depend on the metal centre present; 6 and 7 form square planar complexes. For 6, we optimized both cis and trans square planar complexes; the trans complex with ligand 9 is 9.21 kcal mol⁻¹ more stable than the cis complex at the B97-D/BS2 level of theory. Cationic 9 formed from palladium acetate 7, can only bind the oxygens of the acetate ligand cis-to each other; optimized geometries for the cis square planar complexes of 7 with geometrical parameters are presented in Fig. S2 and Table S5 in the ESI.† Complexes containing 8 and two monodentate ligands 9 are tetrahedral. Optimized geometrical parameters for the 8/9 complexes using three different functionals in conjunction with BS2 are presented fully in Fig. S3 and Table S6 in the ESI.†

The adoption of the tetrahedral geometry for the complexes of 8 is due to the metal's occupancy of its zero oxidation state, instead of the +2 oxidation state in 6 and 7. These two different geometrical arrangements can be explained with standard ligand field theory as shown in Fig. 3. The Pd(II) system has d⁸ electronic configuration which favours a square planar geometry with an empty d orbital. This empty d orbital (conventionally designated the d_x²−y²) offers a path (along x and y axes) for each of four ligands to approach the metal and avoid electron–electron repulsions. In contrast, Pd(0) prefers to adopt a tetrahedral geometry to limit electron–electron repulsion between the ligand and the 10 d electrons of the Pd as far as possible. The tetrahedral geometry has the smallest difference between the highest and lowest energy orbitals; with 10 electrons, all orbitals are filled and the tetrahedral geometry offers the lowest energy arrangement possible. Tetrakis(triphenylphosphino)-palladium(0) is one of the best examples in the literature of a tetrahedrally coordinated Pd(0) metal centre.²⁵

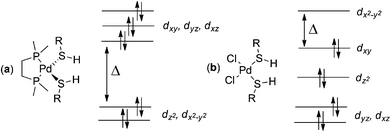Fig. 3 Electronic distribution for Pd(0)/tetrahedral complexes (a) and Pd(II)/square planar complexes (b) formed from 8 and 6 respectively, with ligand 9.

3. Binding of the scavenger ligands to Pd(II) metal centres

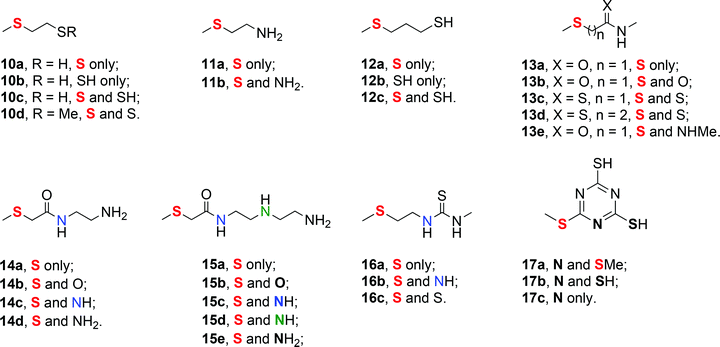
We have investigated the full scavenger ligand set presented in Fig. 4. The ligand set tests the monodentate binding strengths of –SH, –SMe, –NH₂, –NHMe, C=O and C=S ligand components in various contexts, and in combination in chelates of various compositions and ring sizes, representing the range of interactions present in the most popular commercial scavenger materials. The full set was bound to 6 and 7; the Pd(0) system 8 was only investigated with a limited ligand set which represents the most widely used commercial products.

Fig. 4 Full set of ligands with codings for their binding site(s).

3a. cis–trans Isomerisation on monodentate coordination with 6. In the methodological evaluation for 6, monodentate coordination of ligand 9 afforded cis and trans complexes, with the trans species being more stable. This observation was also tested with the rest of the ligands (10–16) and the relative enthalpies of the trans and cis complexes are shown in Table 1. Evaluating enthalpic cis–trans differences at this stage is important because it will inform our interpretation of chelate binding energies (vide infra).

Table 1 Relative enthalpies (H_rel = H_cis − H_trans, kcal mol⁻¹) for the trans complexes of 6 with each monodentate ligand, relative to the analogous cis complex, calculated at B97-D/BS2 level of theory

Monodentate ligand	H rel
9	−9.2
10a	−8.7
11a	−8.3
12a	−7.2
13a	−2.0
14a	−2.2
15a	−2.1
16a	−7.9

---

Table 1 shows that all of the ligands prefer to form a trans complex with 6. The preference for the trans arrangement is much greater for ligands 9, 10a to 12a, and 16a (about 7–9 kcal mol⁻¹), but still significant for 13a to 15a (about 2 kcal mol⁻¹). The values presented in Table 1 effectively separate all species into two groups, which could reflect the presence of the amide moiety in ligands 13a to 15a. In the cis arrangements, the ligands that contain an amide moiety are able to form two hydrogen bonds between the amide N–H and the Cl ligands attached to the metal centre. In contrast, occupancy of the trans orientation allows only one of these hydrogen bonds to form and is therefore destabilised relative to the cis complexes.

3b. Comparative energetics of mono- and multidentate ligand binding. Table 2 compares and contrasts the energetics of monocoordination and chelate formation for selected ligands with 6. The table focuses on the ligand set represented in commercial scavengers; a more complete table (Table S10†) containing the binding parameters for 6 with a fuller ligand set (10–17) is presented in the ESI.† Multidentate scavenger ligands are clearly designed to favour chelation; intuitively, 5- and 6-membered chelates would be expected, and these would require the use of cis binding sites on the metal. Because we have shown the clear advantage of trans monocoordination, we have also explicitly investigated trans chelate complexes for the more flexible longer chain ligands.

Table 2 Binding enthalpies (ΔH, kcal mol⁻¹), free energies (ΔG, kcal mol⁻¹) and entropies at 298 K (TΔS, kcal mol⁻¹) for selected ligands with different binding modes to metal system 6, calculated at the B97-D/BS2 level

Complexes	ΔH	ΔG	TΔS
6a/9	−73.9	−50.8	−23.1
Type 10
6/10a	−82.7	−59.4	−23.3
6/10b	−71.7	−51.5	−20.3
6/10c	−60.1	−46.1	−13.9
6/10d	−65.8	−51.5	−14.3
Type 12
6/12a	−82.6	−56.8	−25.8
6/12b	−74.6	−50.9	−23.7
6/12c	−60.2	−44.4	−15.8
Type 15
6/15a	−78.7	−54.1	−24.6
6/15b	−44.9	−32.9	−12.0
6/15c	−53.8	−39.3	−14.5
6/15d-cis	−72.2	−54.9	−17.3
6/15d-trans	−77.8	−60.1	−17.7
6/15e-cis	−67.9	−49.9	−18.1
6/15e-trans	−87.8	−69.5	−18.2
Type 17
6/17a	−40.8	−28.1	−12.6
6/17b	−36.6	−23.9	−12.6

---

We have computed the binding parameters (enthalpies (ΔH), free energies (ΔG) and entropies (ΔS)) for all of the ligands in their different binding modes with metal system 6. The mono coordinated complexes were all trans, while cis and trans chelated complexes were investigated where accessible.

A number of interesting features were revealed by the study of the first ligand type 10; trans-monodentate coordination (10a, 10b) via thiol (–SH) or thioether (–SMe) is enthalpically favoured over chelation. Thioether coordination is over 10 kcal mol⁻¹ stronger than thiol coordination enthalpically, a significant and unexpected difference; the same behaviour was observed for ligand type 12. The 10c/10d comparison shows that the advantage of thioethers is also realised within chelates. This finding supports the design of commercial scavenger materials which privilege the internal thioether linkage.

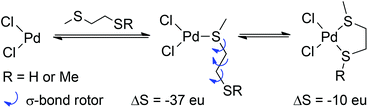
Both ligand types form 5-membered chelates; the most favourable chelate (with 10d) is still less stable than the trans-10a complex by 8 kcal mol⁻¹. It would appear that 5-membered chelates are not favourable for these simple bis-thiol or bis-sulfide ligands. The correct evaluation of the free energy of ligand binding requires that entropy changes are accounted for correctly. Taking the average value of −21.8 kcal mol⁻¹ for TΔS for the formation of trans-10a and trans-10b yields a value of 73 eu for ΔS (at 298 K). This corresponds to a ΔS of ca. 37 eu per ligand, very close to typical values for bimolecular reactions.²⁶ The corresponding value of TΔS for chelate formation is 14 kcal mol⁻¹, or ΔS ≈ 47 eu. The difference of 10 eu represents the cost of immobilising rotors in the ligand following initial monocoordination; as the cost of immobilising one σ-bond rotor is ca. 4 eu, the quantitative treatment of binding entropy would appear to be accurate, because three rotors must be frozen when a 5-membered chelate forms (Scheme 2).

Scheme 2 Entropy loss through ligand binding and chelate formation.

The difference in binding entropies between chelates from 10c/10d, and 12c, is consistent with the presence of one additional C–C bond around which free rotation can occur in 12 (at 298 K, a difference of ∼1 kcal mol⁻¹ corresponds to ca. 4 eu associated with the internal rotation).

While monocoordination appears strongly competitive in these model studies, the local concentration of thiol on the scavenger materials is likely to be quite low because they are based on rigid matrices which are loaded relatively lightly with ligands, and this relatively high local dilution of ligands will erode any advantage of monocoordination significantly. Materials which bear chelating ligands which offer multiple coordination sites avoid this problem of very low local ligand concentration.²⁷

The binding enthalpy (ΔH) order runs parallel to the binding free energy (ΔG) as displayed in Fig. S7 (ESI†) where the variation of binding parameters (ΔH and ΔG) are plotted for all metal–ligand complexes. Subsequent discussion is therefore restricted to the relative enthalpies in most cases. The effects of the presence of different types of chalcogenide donor centres were tested with ligand type 13 (see Table S10 in the ESI†). No particularly favourable modes of binding were discovered but sulfur centres displayed a distinct advantage. For example, a thioether/thiocarbonyl donor pair (13c) was 17 kcal mol⁻¹ more effective than the thioether/carbonyl sites in 13b. Increasing the chain length from n = 1 (13c) to n = 2 (13d) had an effect of about 2 kcal mol⁻¹ on chelation.

Ligand 15 presents a rich array of potential complexes of different types and geometries. trans Bis-monocoordination of the thioether (15a) was significantly more favourable than the formation of the 5-membered chelate from either 15b or 15c. The latter, which features amide NH as the second donor centre, was unexpectedly 9 kcal mol⁻¹ more stable than the complex between 6 and 15b which involves a C=O⋯Pd interaction. Ligand 15d forms an 8-membered chelate which can be cis- or trans configured; to our surprise, the trans-chelate was 6 kcal mol⁻¹ more favourable than the cis-stereoisomer and only 1 kcal mol⁻¹ less favourable than trans bis-monocoordination of the thioether in 15a, so for the first time, a chelated mode is directly competitive with monodentate binding. The formation of the trans 11-membered chelate in which ligand 15e was complexed to 6 was very strongly favoured, by 20 kcal mol⁻¹ over the cis-stereoisomer, and 9 kcal mol⁻¹ over trans bis-monocoordination. The more flexible longer chain ligand therefore shows for the first time, a decisive and unambiguous advantage over the binding of two separate ligands. Despite the relatively high cost of the loss of internal rotational modes, the advantage over trans bis-monocoordination is preserved in a free energy difference of 15 kcal mol⁻¹ over 6/15a. Fig. 5 displays the chelate complexes of 14d and 15e with 6, along with the relative enthalpies for cis and trans isomers in kcal mol⁻¹; the behaviour of 14d also represents (at lower conformational complexity) the complexes available from 15d in cis- and trans-8-membered chelates.

Fig. 5 cis and trans Chelates of 6 with 14 and 15: (a) cis-6/14d; (b) trans-6/14d; (c) cis6/15e; (d) trans-6/15e. The relative enthalpies (H_rel in kcal mol⁻¹) are shown in bold.

A similar set of calculations was carried out for metal set 7; Table 3 presents the results. A complete table (Table S11†) containing the binding parameters for 7 with the full set of ligands is presented in the ESI.† Species 7 represents a catalytically active monocationic palladium complex obtained when an acetate ligand dissociates from palladium acetate. The binding enthalpies and free energies shown in Table 3 reflect the considerably increased Lewis acidity of the palladium centre in 7 relative to that in 6. The values obtained for TΔS are very similar for 6 and 7, which is to be expected as the entropy of binding is a function of molecularity and ligand flexibility, and not the metal centre. As discussed previously, cis binding is forced in the complexes of 7 because of the nature of the acetoxy ligand so all the chelates represented in Table 3 are the cis-stereoisomers. Nevertheless, the 8-membered cis-chelate from 15d is competitive with monocoordination, and the 11-membered cis-chelate from 15e is strongly favoured over monocoordination, showing the presence of the internal thioether linkage to advantage.

Table 3 Binding enthalpies (ΔH, kcal mol⁻¹), free energies (ΔG, kcal mol⁻¹) and entropies at 298 K (TΔS, kcal mol⁻¹) for selective ligands with different binding modes to 7, calculated at the B97-D/BS2 level of theory

Complexes	ΔH	ΔG	TΔS
Type 10
7/10a	−121.9	−98.9	−22.9
7/10b	−110.5	−88.7	−21.8
7/10c	−102.7	−88.4	−14.3
Type 12
7/12a	−121.7	−97.3	−24.3
7/12b	−111.7	−87.8	−23.8
7/12c	−104.3	−88.9	−15.3
Type 15
7/15a	−127.3	−103.0	−24.3
7/15b	−97.3	−84.2	−13.2
7/15c	−94.8	−80.3	−14.5
7/15d	−121.3	−103.9	−17.5
7/15e	−128.5	−110.9	−17.6
Type 17
7/17a	−85.5	−72.1	−13.4
7/17b	−81.8	−68.6	−13.2

---

4. Decomposition of complexation energies

The total complexation energy (ΔE_complex) corresponds to the reactions presented in Scheme 1. This quantity measures the difference in electronic energy between the components and the complexes. The complexation energy implicitly contains the strain energy required to deform the ligands from their equilibrium geometry. In order to determine whether the benefit of having larger ring systems for the chelating ligands is correlated to the strain energy of the ligands (ΔE^L_strain), the total complexation energy was decomposed to show the contribution of the ligand strain. Table 4 contains the decomposed energies for chelating ligand 15 in its chelating binding modes. A complete table containing all the chelating ligands with their strain energies for several binding modes is presented in Table S12 in the ESI.†

Table 4 Ligand strain energies (ΔE^L_strain, kcal mol⁻¹) and complexation energies (ΔE_complex, kcal mol⁻¹) for ligands 15 binding with 6

Complexes	ΔE^Lstrain	ΔEcomplex
6/15b	11.5	−46.3
6/15c	11.3	−55.5
6/15d-cis	6.3	−75.2
6/15d-trans	5.6	−80.3
6/15e-cis	8.8	−70.7
6/15e-trans	4.6	−90.5

---

From Table 4, it is clear that the longest chain species 15e favours trans complex formation with the lowest contribution from the strain energy of the ligand (4.6 kcal mol⁻¹). This effect is also observed in the 8-membered chelate complexes with 15d, although the difference between the strain energy in the cis and trans configurations is reduced. The highest strain energies for 15 results when the 5-membered ring chelates of 6/15b and 6/15c are formed (∼11 kcal mol⁻¹, Table 4).

Table S12† shows that strain energy from the ligand can contribute 2–12 kcal mol⁻¹ to the complexation energy depending upon the type of binding. With a constant chain length (S/O or S/N coordination), the strain energies are about 10 kcal mol⁻¹ for 13 to 15 irrespective of binding modes. For 16, S–S chelation incurs almost double the strain energy which arises from S–N chelation. Strain energies for ligands 10 to 12 are in the range of 2–5 kcal mol⁻¹ with 3 kcal mol⁻¹ variation due to the difference in chain length between 10 and 12.

5. Binding of the scavenger ligands to a model bis(trialkylphosphino)Pd(0) centre

The ligand binding properties of 8 were explored with four different ligands 10, 12, 15 and 17. A number of possible monocoordinate and chelating modes were considered, analogous to those examined for 6 and 7. Table 5 shows the energetic parameters for all possible binding modes of the ligands (see Fig. 4 for naming). As 8 forms tetrahedral complexes, the cis/trans stereoisomerism which complicated the behaviour of the square planar complexes of 6 and 7 does not arise.

Table 5 Binding enthalpies (ΔH, kcal mol⁻¹), free energies (ΔG, kcal mol⁻¹) and entropies (ΔS, kcal mol⁻¹) for selected ligands with different binding modes calculated at B97-D/BS2 level with metal system 8

Complexes	ΔH	ΔG	TΔS
Type 10
8/10a	−28.4	−7.1	−21.2
8/10b	−22.0	−3.6	−18.4
8/10c	−19.0	−7.1	−11.9
8/10d	−21.2	−8.8	−12.3
Type 12
8/12a	−26.0	−2.4	−23.5
8/12b	−21.1	0.2	−21.3
Type 15
8/15a	−26.5	−3.3	−23.2
8/15e	−26.2	−10.5	−15.7
Type 17
8/17	−20.4	−9.6	−10.8

---

For complexes 8/15, monocoordination of two molecules through –SMe has the highest binding enthalpy (−26.5 kcal mol⁻¹), which is comparable to the strength of the 11-membered chelate from 15e (−26.2 kcal mol⁻¹). Structures for the alternative metal–ligand chelates S/O, S/N and S/N_mid were investigated but none of the attempts yielded a tetrahedral Pd(0) chelate complex. At every attempt, the tetrahedral chelate complex minimised to a tricoordinate complex in which the ligand is bound to the metal centre via thioether-S, indicating a more favourable interaction for the thioether-S binding relative to the alternative coordination through either the carbonyl O or secondary amine. Similar observations were also made with tetrahedral chelation of 12c through a 6-membered ring. For 10a, the monocoordination through thioether sulfur is about 7 kcal mol⁻¹ stronger than chelation through two thioether sulfurs in 10d and the monocoordination through thiol in 10b is about 3 kcal mol⁻¹ better than chelation through thiol and thioether sulfur in 10c. For both 10 and 12, thioether sulfur coordination to the metal centre is more favourable than thiol coordination. This observation is consistent with the trends observed for square planar Pd(II) metal complexes.

Both attempts to find a tetrahedral complex between 8 and 17via chelation involving nitrogen and sulfur (17a or 17b) resulted in a tricoordinate complex, in which the ligand is coordinated through the nitrogen alone (17c). Fig. S8 in the ESI† shows two different chelated starting geometries that minimise to a structure in which only N-coordination is observed.

All the binding enthalpies for the Pd(0) complexes from 8 are lower than those for Pd(II) species 6 and 7 suggesting very strongly that palladium removal with scavenger materials should be considerably easier when the material is present in the higher oxidation state.²⁸

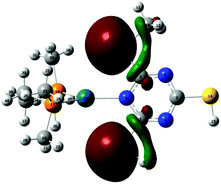
A natural bond orbital (NBO) analysis²³ has been performed on the 8/17c complex to explore the extent of coordination of the different atom centres to the metal and to rationalise the observation of the N-coordinated complex alone.

Second order perturbation energies from NBO analysis measure the strengths of the interactions between two different moieties. This analysis shows that the dominant interaction is between N(6) of the ligand and Pd(16) centre. In addition, two of the S-atoms (S(7) and S(8)) from the ligand are also interacting with the metal centre which further stabilises the tricoordinate complex (Fig. 6).

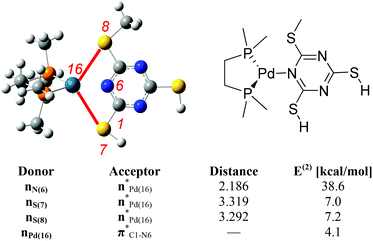Fig. 6 Selected second order perturbation energies E⁽²⁾ (kcal mol⁻¹) and selected interatomic distances (Å) from NBO analysis for 8/17c complex. Atom numbers are shown in red.

Interacting lone pair orbitals of S(7) and S(8) from the ligand are presented together in Fig. 7. These lone pairs are predominantly (67%) 3s in character, with a small contribution from the hybrid sp²-orbital which forms the C–S bond.

Fig. 7 The interaction between Pd(16) and one lone pair (LP) orbital on S(7) and S(8).

6. Investigation of ligand 15 in the absence of thioether binding; other modes of monocoordination and chelation

We have assumed that thioether binding is privileged but it may be that entirely different combinations of Lewis basic centres are more favourable. To investigate the binding capability of other binding sites in 15, we have chosen to examine complexes with metal set 6. Table 6 represents the binding parameters for a range of possible complexes without thioether binding. The data obtained binding via modes 15a–15e which involve thioether binding are also presented again to facilitate comparison (Fig. 8).

Fig. 8 Alternative binding mode labelling for 15.

Table 6 Binding enthalpies (ΔH, kcal mol⁻¹), free energies (ΔG, kcal mol⁻¹) and entropies at 298 K (TΔS, kcal mol⁻¹) for L1 with different binding modes including binding without thioether-S with 6

Complexes	ΔH	ΔG	TΔS
Type 15 using thioether-S
6/15a	−78.7	−54.1	−24.6
6/15b	−44.9	−32.9	−12.0
6/15c	−53.8	−39.3	−14.5
6/15d-cis	−72.2	−54.9	−17.3
6/15d-trans	−77.8	−60.1	−17.7
6/15e-cis	−68.0	−49.9	−18.1
6/15e-trans	−87.8	−69.5	−18.2
Type 15 not using thioether-S
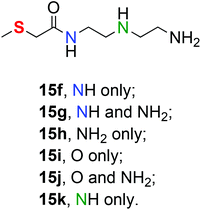
6/15f	−66.4	−40.8	−25.6
6/15g	—	—	—
6/15h	−95.1	−70.3	−24.8
6/15i	−69.4	−37.2	−32.2
6/15j	−76.4	−59.1	−17.3
6/15k	−103.4	−76.6	−26.8

---

Of the six different possible ways of binding to the metal centre which do not involve thioether-S which we explored, monocoordination through the secondary amino group in 15k results in the highest binding enthalpy at −103.4 kcal mol⁻¹. Binding through the primary amino group in 15h results in a comparable binding enthalpy at −95.1 kcal mol⁻¹. These two nitrogen sites offer the strongest binding of all the ligand atoms investigated. The most stable trans chelate from 15e lies 16 kcal mol⁻¹ above mono coordinated complex 15k.

We could not locate the 8-membered chelate complex which involves the amide nitrogen and the terminal primary amino group (15g). Every attempt led to the formation of the most stable trans chelate 15e, which is presented in Fig. S9 in the ESI.† However, the inability to form the 8-membered chelate is a reflection of the preference for these systems to form large (≥10) ring chelates (vide supra) rather than the binding ability of the amino groups.

Finally, our treatment of potentially acidic binders (RSH, RNH₂, RR′NH) requires comment. We have treated these species exclusively as neutral ligands; we have not evaluated the strengths of the interactions of their conjugate bases (RS⁻, RNH⁻, RR′N⁻) with metal centres. Mechanistic models of thioether formation proposed by Hartwig²⁹ and explored experimentally by Jutand³⁰ involve initial coordination of the neutral thiol to the metal, followed by deprotonation; in the absence of amine bases, the deprotonation is slow. Jutand and co-workers could not rule out a classical mechanism involving proton transfer between thiol and amine to afford a thiolate/ammonium ion pair entirely, but presented strong evidence for metalation/deprotonation. The strength of the initial binding of the metal to scavenger materials is therefore evaluated most accurately by considering neutral species, rather than their conjugate bases.

Conclusions

The binding of nine different sulfur-based ligands derived from metal scavenger materials, to three different palladium metal sets has been modelled. Dispersion corrected density functional theory (DFT-D) reveals that monocoordination is the most favoured binding mode for most ligands with different metal sets. Studies with longer chain ligands show that chelation through large chains (>7-atoms) are more favourable than small chains (≤6-atoms). In addition, trans complexes form more easily than cis complexes through chelation. Larger (8-membered) chelates were competitive with bis monocoordinate complexes. Unexpectedly, the formation of a trans 11-membered chelate was the most favoured binding mode.

Thioether (–SMe) ligand sites were generally more effective than the corresponding thiols while a secondary amino nitrogen (RR′NH) is the best donor type, with the highest binding enthalpy for Pd(II) metal systems (6 and 7). While bis monocoordination appears strongly competitive in these model studies, the local concentration of any supported ligand on the scavenger materials is likely to be quite low, and this relatively high local dilution of ligands will erode any advantage of bis monocoordination significantly. The design of materials which bear chelating ligands based on multiple coordination sites therefore represents an astute and effective solution to this problem, with the internal thioether providing a significant contribution to a strong interaction.

Acknowledgements

This material is based upon work supported by PhosphonicS Ltd. and the Glasgow Centre for Physical Organic Chemistry (funded by the Engineering and Physical Science Research Council (UK), EP/E036244/1). We would also like to acknowledge the help of Dr Samit Majumder, University of Calcutta, for his help in finding relevant crystal structures.

Notes and references

1. For recent reviews of transition metal-catalysed reactions in synthesis, see: (a) P. B. Arockiam, C. Bruneau and P. H. Dixneuf, Chem. Rev., 2012, 112, 5879; (b) I. P. Beletskaya and A. V. Cheprakov, Organometallics, 2012, 31, 7753; (c) A. N. Campbell and S. S. Stahl, Acc. Chem. Res., 2012, 45, 851; (d) D. Y. K. Chen and S. W. Youn, Chem.–Eur. J., 2012, 18, 9452; (e) J. F. Hartwig, Acc. Chem. Res., 2012, 45, 864; (f) J. A. Palmes and A. Aponick, Synthesis, 2012, 3699; (g) L. D. Wang, W. He and Z. K. Yu, Chem. Soc. Rev., 2013, 42, 599; (h) A. Suzuki, Angew. Chem., Int. Ed., 2011, 50, 6722; (i) C. E. I. Knappke and A. Jacobi von Wangelin, Chem. Soc. Rev., 2011, 40, 4948.
2. For large scale and manufacturing applications, see: (a) J. Magano and J. R. Dunetz, Chem. Rev., 2011, 111, 2177; (b) V. F. Slagt, A. H. M. de Vries, J. G. de Vries and R. M. Kellogg, Org. Process Res. Dev., 2010, 14, 30; (c) J. G. de Vries, in Organometallics as Catalysts in the Fine Chemical Industry, ed. M. Beller and H. U. Blaser, 2012, vol. 42, p. 1; (d) I. N. Houpis, , in Organometallics as Catalysts in the Fine Chemical Industry, ed. M. Beller and H. U. Blaser, 2012, vol. 42, p. 103; (e) P. Ryberg, in Organometallics as Catalysts in the Fine Chemical Industry, ed. M. Beller and H. U. Blaser, 2012, vol. 42, p. 125.
3. J. S. Carey, D. Laffan, C. Thomson and M. T. Williams, Org. Biomol. Chem., 2006, 4, 2337.
4. C. Y. Chen, P. Dagneau, E. J. J. Grabowski, R. Oballa, P. O'Shea, P. Prasit, J. Robichaud, R. Tillyer and X. Wang, J. Org. Chem., 2003, 68, 2633.
5. (a) C. E. Garrett and K. Prasad, Adv. Synth. Catal., 2004, 346, 889; (b) C. J. Welch, J. Albaneze-Walker, W. R. Leonard, M. Biba, J. DaSilva, D. Henderson, B. Laing, D. J. Mathre, S. Spencer, X. Bu and T. Wang, Org. Process Res. Dev., 2005, 9, 198; (c) J. T. Bien, G. C. Lane and M. R. Oberholzer, Top. Organomet. Chem., 2004, 6, 263; (d) J. P. Huang, X. X. Chen, S. X. Gu, L. Zhao, W. X. Chen and F. E. Chen, Org. Process Res. Dev., 2010, 14, 939; (e) L. J. Wang, L. Green, Z. Li, J. M. Dunn, X. D. Bu, C. J. Welch, C. Y. Li, T. B. Wang, Q. Tu, E. Bekos, D. Richardson, J. Eckert and J. Cui, Org. Process Res. Dev., 2011, 15, 1371.
6. (a) For detection of very low levels of Pd in “Pd-free” couplings, see K. Inamoto, L. D. Campbell, T. Doi and K. Koide, Tetrahedron Lett., 2012, 53, 3147 ; for misleading mechanistic results caused by trace amounts of Pd, see (b) R. B. Bedford, M. Nakamura, N. J. Gower, M. F. Haddow, M. A. Hall, M. Huwe, T. Hashimoto and R. A. Okopie, Tetrahedron Lett., 2009, 50, 6110.
7. N. Galaffu, S. P. Man, R. D. Wilkes and J. R. H. Wilson, Org. Process Res. Dev., 2007, 11, 406.
8. G. Reginato, P. Sadler and R. D. Wilkes, Org. Process Res. Dev., 2011, 15, 1396.
9. There is considerable ambiguity about the speciation of palladium in many catalyst systems; for a study of ligandless Pd(II) systems, see: L. A. Adrio, B. N. Nguyen, G. Guilera, A. G. Livingston and K. K. Hii, Catal. Sci. Technol., 2012, 2, 316.
10. (a) J. Jover, N. Fey, M. Purdie, G. C. Lloyd-Jones and J. N. Harvey, J. Mol. Catal. A: Chem., 2010, 324, 39; (b) S. Kozuch and J. M. L. Martin, ACS Catal., 2011, 1, 246; (c) R. Meir, S. Kozuch, A. Uhe and S. Shaik, Chem.–Eur. J., 2011, 17, 7623; (d) J. F. Hartwig, Inorg. Chem., 2007, 46, 1936.
11. J. R. H. Wilson, A. C. Sullivan and S. Man, Substituted organopolysiloxanes and use thereof, WO2006013060, 2006.
12. For leading references to the phosphorus knowledge base (P-K-B), see: (a) J. Jover, N. Fey, J. N. Harvey, G. C. Lloyd-Jones, A. G. Orpen, G. J. J. Owen-Smith, P. Murray, D. R. J. Hose, R. Osborne and M. Purdie, Organometallics, 2010, 29, 6245; (b) N. Fey, B. M. Ridgway, J. Jover, C. L. McMullin and J. N. Harvey, Dalton Trans., 2011, 40, 11184.
13. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 and references therein.
14. (a) S. Grimme, J. Comput. Chem., 2004, 25, 1463; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787; (c) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
15. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
16. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
17. (a) S. Grimme, J. Chem. Phys., 2006, 124, 034108; (b) T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397.
18. D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123.
19. S. Rousseaux, M. Davi, J. Sofack-Kreutzer, C. Pierre, C. E. Kefalidis, E. Clot, K. Fagnou and O. Baudoin, J. Am. Chem. Soc., 2010, 132, 10706.
20. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650; A. D. Pople and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639.
21. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257; M. M. Francl, W. J. Petro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654.
22. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
23. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO 3.0 Program.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision A.1), Gaussian, Inc., Wallingford, CT, 2009.
25. D. R. Coulson, L. C. Satek and S. O. Grim, Inorg. Synth., 1972, 13, 121.
26. (a) M. I. Page and W. P. Jencks, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 1678; (b) C. Galli and L. Mandolini, Eur. J. Org. Chem., 2000, 3117.
27. For discussions of site isolation and site–site interactions, and the relevance of matrix structure, see: (a) A. Basso and M. Bradley, Tetrahedron Lett., 2003, 44, 2699; (b) R. R. Shi, F. Wang and B. Yan, Int. J. Pept. Res. Ther., 2007, 13, 213; (c) A. A. Poeylaut-Palena and E. G. Mata, Org. Biomol. Chem., 2010, 8, 3947.
28. For a physicochemical study of scavenging and scavenged Pd leaching, see: L. Huang, T. P. Ang, Z. Wang, J. Tan, J. Chen and P. K. Wong, Inorg. Chem., 2011, 50, 2094.
29. (a) G. Mann, D. Baranano, J. F. Hartwig, A. L. Rheingold and I. A. Guzei, J. Am. Chem. Soc., 1998, 120, 9205; (b) E. Alvaro and J. F. Hartwig, J. Am. Chem. Soc., 2009, 131, 7858.
30. X. Moreau, J. M. Campagne, G. Meyer and A. Jutand, Eur. J. Org. Chem., 2005, 3749.

---

Footnote

† Electronic supplementary information (ESI) available: Details of computational method evaluation, binding parameters (ΔH, ΔG and TΔS) for the full set of ligands, decomposition of complexation energies, structural changes during optimisation, optimised Cartesian coordinates at B97-D/BS2 level of theory. See DOI: 10.1039/c3dt52282b

---