Chemical applications carried out by local pair natural orbital based coupled-cluster methods

Abstract

The scope of this review is to provide a brief overview of the chemical applications carried out by local pair natural orbital coupled-electron pair and coupled-cluster methods. Benchmark tests reveal that these methods reproduce, with excellent accuracy, their canonical counterparts. At the same time, the speed up achieved by exploiting the locality of the electron correlation permits us to tackle chemical systems that, due to their size, would normally only be addressable with density functional theory. This review covers a broad variety of the chemical applications e.g. simulation of transition metal catalyzed reactions, estimation of weak interactions, and calculation of lattice properties in molecular crystals. This demonstrates that modern implementations of wavefunction-based correlated methods are playing an increasingly important role in applied computational chemistry.

---

Manuel Sparta

Manuel Sparta (Belluno, 1979) received his Master Degree in Chemistry from the University of Ferrara and his PhD working with Profs V. R. Jensen and K. Boerve from the University of Bergen in 2007. After postdoctoral appointments at University of Aarhus (2007–2010) and UCLA (2010–2012), he joined the group of Prof. F. Neese at the Max Planck Institute for Chemical Energy Conversion where he works on the application of local pair natural orbital correlated methods to the study of the reactivity of transition metal complexes and metalloenzyme active sites.

Frank Neese

Frank Neese (Wiesbaden, 1967) received his PhD working with Prof. P. Kroneck (1997, University of Konstanz). After a postdoctoral work at Stanford University with Prof. E. I. Solomon, he returned to Konstanz for his habilitation. He was a group leader at the Max Planck Institute (MPI) for Bioinorganic Chemistry before becoming full professor at the University of Bonn (2006). Since 2011, he has been the Director of the MPI for Chemical Energy Conversion. His work focuses on magnetic spectroscopies, local pair natural orbital theories, spectroscopy oriented configuration interaction, structure and reactivity of transition metal complexes and metalloenzymes. He is the lead author of the ORCA program.

---

Introduction

Electronic structure methods are playing an increasingly important role in the understanding of organometallic and bioinorganic systems. However, a researcher that embarks on the computational study of these complex systems is bound to the use of approximate electronic structure methods with an inherent level of accuracy while accounting for the associated computational expenses. As a result, the method of choice for the vast majority of organometallic and bioinorganic applications is density functional theory (DFT) as it combines computational efficiency and excellent accuracy in a black-box manner.^1–4 Nevertheless, each application of DFT needs to be carefully pondered as the level of accuracy is not homogeneous among different systems and it depends on the specific exchange–correlation functional adopted. In fact, performing preliminary benchmarks to determine the optimal functional for the problem at hand is often unavoidable. Furthermore, there are no systematic ways for improving or estimating the confidence level of a given result.

On the other hand, wavefunction-based ab initio methods can be systematically improved and converged toward the exact solution of the Schrödinger equation. Among the ab initio quantum mechanical methods the coupled-cluster model with single and double excitations corrected by perturbative triples (CCSD(T)) has become the “gold standard” of computational chemistry.^5–8 However, the very high computational expense and the high order scaling (O(N⁷)) of the canonical procedure render CCSD(T) unsuitable for routine applications. Hence its use is usually restricted to benchmark studies on very small systems.

One of the challenges in modern theoretical chemistry method developments has been to devise and implement approximations that expedite correlated ab initio methods without loss of accuracy. The strategies adopted involve the partition of the system of interest into fragments^9–21 or the construction of correlation domains while the whole system is treated at once.^22–41 In recent years, our group has been active in the field of local correlation methods and developed a way to take advantage of the locality of the electron correlation by means of Pair Natural Orbitals (PNOs, see Theoretical background). The framework for the development of the correlated method was named the Local Pair Natural Orbital (LPNO) where the term “Local” alludes to the fact that the internal space is spanned by localized internal orbitals.^42,43 Further improvements gave rise to the Domain-based Local Pair Natural Orbital (DLPNO).^44,45 Several correlated methods have been implemented in the (D)LPNO foundations and, acknowledging the efficiency and accuracy demonstrated, the use of PNOs in local correlation calculations has rapidly regained popularity. Tew, Helmich and Hättig have used pair natural orbitals in the implementation of explicitly correlated Møller–Plesset perturbation theory (MP2, MP3).^38,39 Helmich and Hättig, focusing on excitation energies, explored how to reduce the number of double excitation amplitudes in response calculations with PNOs and localized occupied orbitals⁴⁶ and subsequently implemented the iterative coupled-cluster method CC2.⁴⁰ Krause and Werner systematically compared the use of projected atomic orbitals, pair natural orbitals and orbital specific virtual orbitals (OSVs) concluding that, for a given accuracy, the PNO correlation domains are, in average, four time smaller than the one obtained with PAOs or OSVs.⁴⁷ Kallay and coworkers presented a local coupled-cluster method that combines the cluster-in-molecule approach with virtual orbitals constructed including approximate MP2 natural orbitals.^48,49

In this review, in spite of the early age of the (D)LPNO-based methods, we provide an overview of chemical applications where their robustness, accuracy and affordability were exploited, in the hope that this motivates more researchers to apply ab initio correlated methods to their work. Furthermore, the wide-ranging scope of the studies covered in this survey demonstrates how modern implementations of highly accurate wavefunction-based correlated methods have a broad range of applicability and are becoming more common in many branches of computational chemistry.

Theoretical background

In 1955 Löwdin reported that natural orbitals ordered with respect to their occupation number guarantee the most rapid convergence of the Configuration–Interaction (CI) expansion.⁵⁰ Elaborating on this observation, Edmiston and Krauss introduced the concept of PNOs,^51,52 where the basic idea consists of using a specific set of NOs to correlate each electron pair. This initiated the development of correlation methods based on PNOs, with the pioneering contributions of Kutzelnigg, Ahlrichs, Meyer, Staemmler and coworkers.^53–63 Although it was demonstrated that the application of PNOs in correlated calculations drastically reduced the computational expenses of the methods with only small errors in the correlation energy, this approach was abandoned as the laborious integral transformations and disk storage associated with the PNOs were considered to be insurmountable bottlenecks for large applications.

Recently, our group attempted to revive the use of PNOs in correlated calculations by applying density-fitting approximations and by taking advantage of modern computational architectures.^42,43 The first method implemented in the LPNO foundations was the coupled-electron pair approximation (CEPA)⁴² initially developed by Meyer.^60–62 CEPA has shown to provide results that are of intermediate quality between CCSD and CCSD(T).^64,65 The coupled-cluster with single and double excitations model (CCSD)⁴³ as well as the parameterized coupled-cluster singles and doubles model (pCCSD)⁶⁶ were made available within the LPNO framework. Subsequently, the LPNO-CCSD method was completely redesigned to address its inherent fifth order scaling. The new implementation combines the concepts of PNOs and Projected Atomic Orbitals (PAOs).⁴⁴ PAOs were introduced by Pulay and Saebo,^22–26 and extensively used in the development of various correlation methods by Werner and Schütz.^27–33 The resulting DLPNO-CCSD was found to be near linear scaling.⁴⁴ Finally, the addition of perturbative treatment of the triple excitations led to the DLPNO-CCSD(T) model.⁴⁵

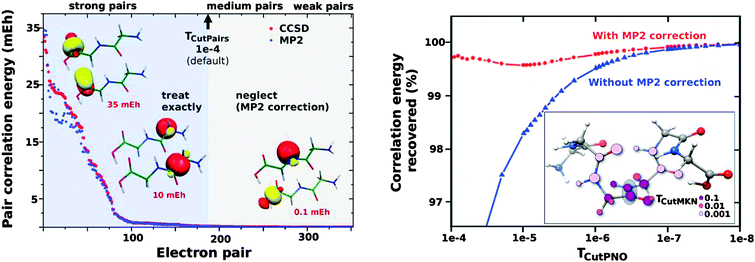
The key aspects of the DLPNO coupled-cluster methods can be briefly summarized. The initial step consists of the localization of the occupied orbitals obtained from a single determinant reference wavefunction calculation. The electron correlation for the whole system is given by the sum of over electron pair correlation energies ε_ij (i and j refer to localized occupied orbitals). Using a local MP2 estimate of the pair correlation energy, the electron pairs are partitioned into “strong” (pair correlation larger than the T_CutPairs threshold) and “weak” (see the left panel in Fig. 1). Only strong pairs are explicitly treated in the coupled-cluster procedure, whereas the MP2 estimates for the weak pairs are added a posteriori to the total correlation energy. For each strong pair, the virtual space for the correlation consists of PNOs constructed from the MP2 pair densities. PNOs with occupation numbers larger than the T_CutPNO threshold (default value: 3.33 × 10⁻⁷) are kept and a MP2 correction, accounting for the truncation of the virtual space, is computed (see the right panel in Fig. 1). PNOs and integrals needed are expanded in terms of PAO domains, whose size is controlled by the T_CutMKN threshold (molecular structure inserted in the right panel of Fig. 1). For a more comprehensive description of the LPNO and DLPNO methods, we refer to the original literature.^42–45

Fig. 1 Left panel: the strong pair approximations. Pairs of localized orbitals are partitioned into “strong” and “weak” based on MP2 pair correlation estimates. Strong pairs enter the coupled-cluster procedure whereas MP2 additive corrections to the total correlation energy are computed for the weak pairs. Right panel: PNO truncation of the virtual space. Percentage of the correlation energy recovered for a given electron pair as a function of the T_CutPNO threshold. Inset: representation of the PAOs domains as a function of the T_CutMKN threshold (the gray shadow highlights the position of the correlated orbitals).

All the (D)LPNO methods were implemented and distributed free of charge to the quantum chemistry community via the ORCA⁶⁷ suite of programs.

Applications of the LPNO-based methods

In the following sections, a series of recent applications of the (D)LPNO coupled-cluster methods will be discussed. These contributions are scattered in the field of computational chemistry, ranging from the ab initio study of transition metal catalyzed reactions to the computation of lattice properties in molecular crystals. In the first part, examples that deal with reactivity (reaction mechanisms, activation energies, selectivity) in transition metal-based catalysts, enzymatic active sites and organic systems will be addressed. The second part will focus on noncovalent interactions and conformational spaces of isolated molecules and extended systems. The common thread between these diverse applications is that ab initio local correlated methods, capable of matching the accuracy of their canonical counterparts, can be now used to investigate chemical problems that were previously only addressable with density functional methods.

Transition metal chemistry

Chirality is a very important and widespread concept in biology: building blocks in biological systems such as amino acids and sugars are chiral. Many enzyme active sites and drug receptors are asymmetric meaning that only the correct enantiomer will interact with the target. This means that there is a great need for procedures capable of producing enantiomerically pure compounds. The enantioselective hydrogenation is a powerful tool that enables us to obtain chiral compounds from prochiral precursors.⁶⁸

In this respect, the asymmetric hydrogenation of prochiral olefins using Rh catalysts is the prototype of an enantioselective transition metal-catalyzed reaction. The reaction mechanism in the presence of the ligand [(R,R)-MeDuPHOS] was studied for two substrates: α-formamidoacrylonitrile and N(1-tertbutylvinyl)formamide by Anoop et al.⁶⁹ (see Scheme 1).

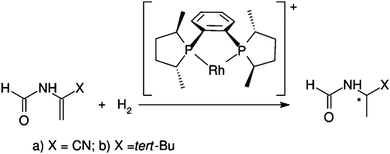Scheme 1 Asymmetric hydrogenation of enamides. Reprinted with permission from A. Anoop, W. Thiel and F. Neese, J. Chem. Theory Comput., 2010, 6, 3137–3144. Copyright 2010 American Chemical Society.

The method adopted in this work is the local pair natural orbital coupled-cluster theory with single and double excitations (LPNO-CCSD). The method was carefully calibrated with respect to canonical CCSD and CCSD(T) results on a truncated model system. For this specific system, it was observed that the lack of the perturbative triple correction and the errors due to basis set incompleteness do not affect substantially the reaction energy profiles calculated with LPNO-CCSD/def2-TZVP. In conclusion, the energies computed for the full system are believed to be within 1–2 kcal mol⁻¹ of the CCSD(T)/CBS limit.⁶⁹

Several pathways for the hydrogenation process were investigated for both substrates, and it was concluded, in agreement with previous theoretical studies, that the enantioselectivity of the process is rooted in the different reactivity of the catalyst-substrate adduct. In practice, the presence of the polar amide group enables bidentate coordination of the substrate to the metal center. Subsequently, the substituents (cyano vs. tert-butyl) at the C=C influence the reactivity of the adduct determining the less energetically demanding site for the attack of H₂. In turn, this leads to an excess of the (S) enantiomeric product for the butyl system whereas the R-product is obtained for the cyano system. For both substrates, the computational prediction regarding the stereochemistry of the major product was found to be in agreement with the experiment.⁶⁹

As shown, the applicability of the Rh based catalyst is restricted by the requirements of a polar functionalization of the substrates. To overcome this limitation Pfaltz and coworkers⁷⁰ developed iridium complexes capable of promoting the enantioselective hydrogenation of unfunctionalized alkenes. The key feature of these complexes is the presence of a chiral chelating ligand that couples a heterocycle containing a sp² hybridized nitrogen atom with a trisubstituted phosphorus (or N-heterocyclic carbene) as shown in the PHOX ligand.⁷¹ Recently, the catalytic cycle for the hydrogenation of ethylene and five trisubstituted prochiral olefin substrates promoted by the Ir–PHOX complex was investigated in our group⁷² by employing the DLPNO-CCSD(T) method. In this case, ab initio electronic energies were combined with solvation and thermochemical corrections computed with DFT to access Gibbs free energies of the species in solution. For this system, it was shown that the fine balance between steric repulsion and Van der Waals interaction between the substituted oxazoline terminus of the ligand and the substituents on the olefin substrates determines whether the Si-face or Re-face coordination of the prochiral substrate is more reactive. For all the substrates, the predicted enantiomeric excesses were found in good agreement with the available experimental data.⁷²

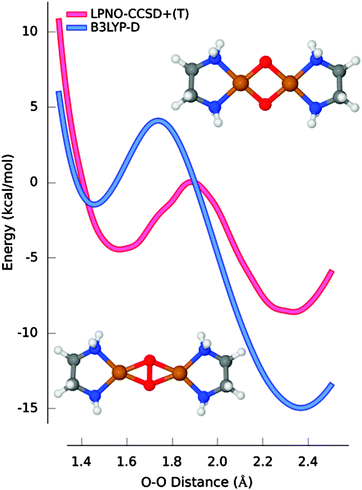
The possibility of obtaining high quality ab initio data for systems containing more than one metal atom was explored in a detailed study on the equilibrium between the peroxo and bis-(μ-oxo) isomers of [Cu₂(en)₂(O)₂]²⁺. In this case, the scan of the potential energy surface (PES) connecting the two structures was conducted using LPNO-CCSD energies in the complete basis set limit complemented with canonical perturbative triple corrections obtained with a small basis set. In all calculations, relativistic effects as well as solvation correction were accounted for.⁷³ The systematic survey determined that the bis-(μ-oxo) isomer is more stable than the peroxo counterpart, in agreement with experimental results. Furthermore, it was concluded that the inclusion of relativistic corrections is important for a proper estimation of the relative stabilities. Relativistic corrections computed with three different approaches (second-order Douglas–Kroll–Hess (DKH) transformation, zeroth-order approximation for relativistic effects (ZORA) or effective core potentials (ECPs)) concur that the net effect of relativity is the stabilization of the bis-(μ-oxo) isomer. Solvation effects (accounted for with a dielectric continuum model) were found to give a similar contribution.

In Fig. 2, the best ab initio estimate (scalar-relativistic LPNO-CCSD/CBS supplemented with solvent and triple excitation corrections) is taken as reference and compared with the most accurate of the DFT functionals (B3LYP-D). Although B3LYP-D correctly predicts that the bis-(μ-oxo) isomer is the most stable, the energy difference is overestimated by 9.3 kcal mol⁻¹ and the position of the minimum for peroxo species is calculated to be 0.1 Å too short. Interestingly, although this system is often regarded as a prototypical multireference case, the analysis of the wavefunction across the PES suggested that the multireference character in this system is very limited.⁷³

Fig. 2 The most accurately calculated PES and the corresponding one calculated with B3LYP-D, ZORA and COSMO corrections using the def2-TZVP basis set. The peroxo and bis-(μ-oxo) structures of [Cu₂(en)₂(O)₂]²⁺. Adapted with permission from D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2011, 7, 1511–1523. Copyright 2011 American Chemical Society.

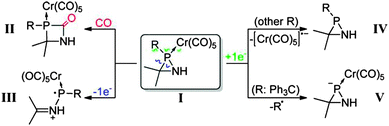
While in the previous examples, coupled-cluster based methods were adopted, there are cases where CEPA types of approaches were preferred. For example, LPNO-CEPA/1 was applied to investigate the stability and reactivity of azaphosphiridine P-pentacarbonylchromium(0) complexes.⁷⁴ The chemistry covered in this contribution is summarized in Scheme 2.⁷⁴

Scheme 2 Reactivity of the azaphosphiridine P-pentacarbonylchromium(0) complex. Reprinted with permission A. Espinosa, C. Gomez and R. Streubel, Inorg. Chem., 2012, 51, 7250–7256. Copyright 2012 American Chemical Society.

This computational study suggested that in the presence of additional carbon monoxide, CO insertion into the P–N bond may occur yielding the 1,3-azaphosphetidin-2-one complex. Furthermore, it was shown that the opening of the ring promoted by the moderate ring strain can be controlled through appropriate tuning of the electronic properties and steric bulk of the P-substituent.⁷⁴

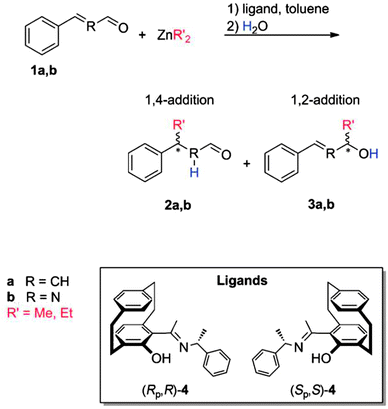
One further example where high level LPNO-CEPA/1 calculations were performed to obtain reliable reaction barriers and binding energies is due to Kubas et al.⁷⁵ In their study, the addition of dialkylzinc to a,b-unsaturated aldehydes (an important class of reactions for C–C bond formation) was investigated. In specific, the asymmetric additions of dimethyl- and diethyl-Zn, catalyzed by [2.2]paracyclophane-based N,O-ligands, was considered (see Scheme 3).⁷⁵

Scheme 3 Asymmetric addition reaction of dialkylzinc to a,b-unsaturated aldehydes: (1) cinnamaldehyde 1a and (2) N-formylbenzylimine 1b catalysed by [2.2]paracyclophane-based ligands 4. 2a,b and 3a,b are 1,4-addition and 1,2-addition products, respectively. Adapted with permission A. Kubas, S. Brase and K. Fink, Chem. – Eur. J., 2012, 18, 8377–8385. Copyright 2012 John Wiley & Sons.

LPNO-CEPA/1 results were used to assess the performances of a set of popular theoretical methods. Based on their benchmark study, the authors concluded that the stereoselectivity of the reaction as well as binding energies were properly addressed by DFT when empirical dispersion corrections were accounted for. However, the use of the highly correlated wavefunction-based method was necessary for a correct prediction of the regioselectivity of the reaction.⁷⁵

Enzymatic reactions

The hydroxylation reaction catalyzed by p-hydroxybenzoate hydroxylase has been studied by a quantum mechanical/molecular mechanical (QM/MM) approach and the use of correlated ab initio methods in QM/MM calculations was thoroughly examined.⁷⁶ Since the height of the activation barrier is dominated by the quantum mechanical energy contribution, the use of high-level correlated methods was found to be essential to obtain a quantitative agreement with the experimental free energy of activation.⁷⁶ The performance of DLPNO-CCSD(T) on the system at hand was investigated (M. Sparta, W. Thiel and F. Neese, unpublished results) and a good agreement with the reference data was obtained (see Fig. 3).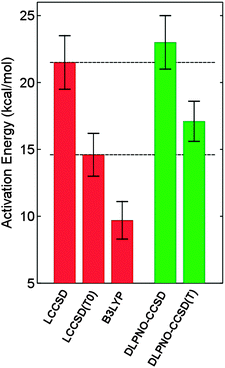

Fig. 3 Hydroxylation of the substrate p-hydroxybenzoate by the cofactor flavin hydroperoxide in the active site of PHBH. Average activation barriers and the associated standard deviation (as error bars) are shown (kcal mol⁻¹) for 10 snapshots representative of the molecular dynamics simulation of the enzyme. LCCSD, LCCSD(T0) and B3LYP (basis set: (aug)-cc-pvTZ) values are taken from ref. 76. Basis set for the DLPNO calculations: def2-TZVP.

Organic chemistry

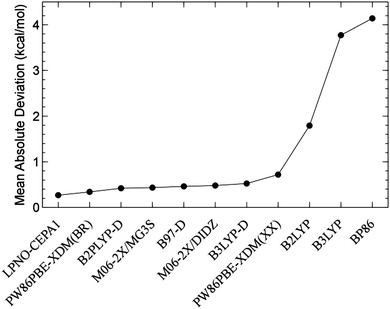
The base-catalyzed reaction of cyclobutane-1,2-dione was recently investigated by Sultana and Fabian with a variety of ab initio and density functional (M06-2×) methods.⁷⁷ The authors examined three reaction pathways, whose products are 1-hydroxycyclopropane-1-carboxylate, α-oxobutanoate and γ-oxobutanoate, respectively. Based on the activation and reaction energies computed with LPNO-CEPA, it was concluded that the formation of 1-hydroxycyclopropane-1-carboxylate via the benzilic acid rearrangement is the only feasible reaction pathway, in agreement with previous experimental observations.⁷⁷

Finally, in the validation of the DLPNO-CCSD(T) method, a benchmark dataset consisting of 51 reaction energies, for which accurate results have been recently published by Friedrich and Hänchen,⁷⁸ was considered. The database covers a large set of chemically interesting processes (e.g. isomerizations, hydrogenations, allylic shifts and oxidations) and it shows a broad spectrum of reaction energies (0.1 to 150 kcal mol⁻¹). With the default setting for the thresholds controlling the DLPNO procedure, all the errors in the energy reaction dataset with respect to semicanonical reference calculations are found to be smaller than 1 kcal mol⁻¹ (Mean Absolute Deviation, MAD = 0.31 kcal mol⁻¹).⁷⁹ A similar result was obtained by Schwabe in his benchmark study of LPNO-CEPA and LPNO-pCCSD, for a database designed to validate electronic structure methods for isomerization reactions of large organic molecules.⁸⁰

Noncovalent interactions

The study of noncovalent interactions represents a very active area of research due to the importance of these effects in many fields of chemistry, biology, and materials science. Since an accurate treatment of electron correlation is crucial to address these interactions, substantial efforts have been devoted to test and validate the (D)LPNO-based methods against highly accurate reference data.

In 2006, Hobza and coworkers developed a widely used benchmark set for studying noncovalent intermolecular interactions (the S22 set).⁸¹ Liakos et al. investigated the accuracy of the LPNO-CEPA/1 method for the S22 dataset.⁸² When compared with the most accurate ab initio results available, LPNO-CEPA/1 was found to deliver a MAD of 0.24 kcal mol⁻¹ and this accuracy exceeds that of most purpose specific density functionals (see Fig. 4).

Fig. 4 Mean absolute deviation for the 22 reactions of the S22 set. Adapted with permission D. G. Liakos, A. Hansen and F. Neese, J. Chem. Theory Comput., 2011, 7, 76–87. Copyright 2011 American Chemical Society.

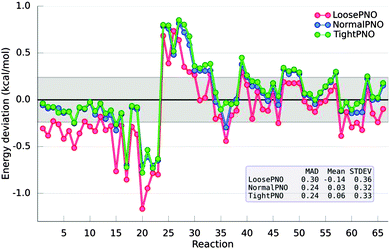
In 2011, the S22 dataset was extended to account for a larger variety of interactions such as hydrogen bonds, aliphatic–aliphatic and π-aliphatic interactions, giving rise to the S66 dataset.⁸³ The accuracy of the DLPNO-CCSD(T) method was recently assessed by probing the S66 interaction energies. Based on this investigation, three different sets of the thresholds that control the DLPNO procedure were selected (namely LoosePNO, NormalPNO and TightPNO) to allow users to optimally balance performance and accuracy. In agreement with the previous results for the S22 dataset, it was found that a MAD of 0.24 kcal mol⁻¹ is obtained with the default settings (see NormalPNO in Fig. 5) for the DLPNO-CCSD(T) calculations when compared to their semicanonical CCSD(T) counterparts.⁷⁹

Fig. 5 Deviations with respect to semicanonical CCSD(T) for the S66 dataset obtained with three variations of the truncation parameters that control the DLPNO-CCSD(T) method (namely LoosePNO, NormalPNO and TightPNO). The gray shadow highlights the region within 1 kJ mol⁻¹. Basis set: cc-pVDZ.

Antony et al. conducted a survey on protein–ligand interaction energies with dispersion corrected DFT and high-level wavefunction-based methods.⁸⁴ The systems investigated are truncated models (from 50 to 300 atoms) of structures deposited in the Protein Data Bank and are considered to be representative of noncovalent interactions occurring in drug-target adducts. For this investigation, LPNO-CEPA/1(CBS) was used as non-empirical reference to evaluate the performances of DFT-D. In agreement with earlier studies, it was concluded that DFT-D generally overestimates the binding energy by ca. 10% (2–4 kcal mol⁻¹ for large interactions).

The S66 dataset was used to investigate basis set extrapolation schemes for total energies as well as for weak intermolecular interactions.⁸⁵ A common approach to handle basis set incompleteness consists of complementing high-level calculations with a basis set limit estimate computed with a lower level of theory, typically second-order Möller–Plesset. Alternative schemes, where the MP2 is replaced by LPNO-CEPA/1, were investigated. It was shown that, owing to the highly systematic nature of the deviations between canonical and LPNO methods, more accurate results can be obtained employing LPNO-CEPA/1 in the extrapolation procedure.⁸⁵

Assessment of conformational spaces

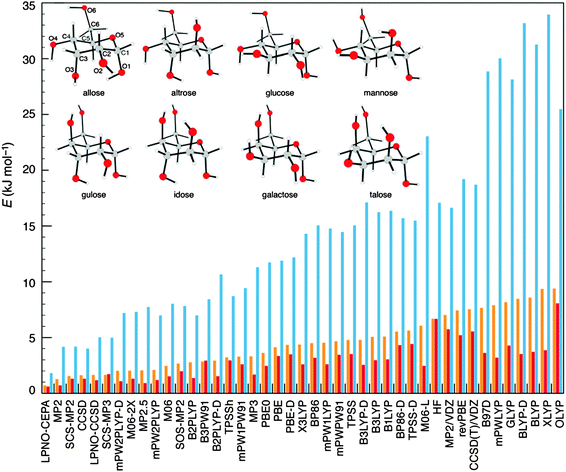
The accuracy shown by the LPNO-based correlated methods in the description of weak interactions^79,82,84,85 (as discussed in the previous section) suggests that these methods are well suited for the study of the conformational space of chemical systems. To test this hypothesis, Sameera and Pantazis investigated the conformational space of monosaccharides by constructing a database of 58 structures representative of all types of isomerism exhibited by eight α-D-aldohexoses.⁸⁶ The isomers included hydroxymethyl rotamers, anomers, ring conformers, furanose, and open-chain forms. An exhaustive survey of the performance of 10 wavefunction-based methods and 31 DFT functionals compared to coupled-cluster calculations extrapolated to the complete basis set limit, CCSD(T)/CBS, was conducted. Among the ab initio methods, LPNO-CEPA was found to be the most accurate choice, interestingly LPNO-CCSD and its canonical counterpart show almost identical errors. Finally, it was shown that none of the DFT functionals investigated delivers the same accuracy of the best wavefunction-based methods (see Fig. 6).⁸⁶

Fig. 6 Graphical summary of the performance of all methods included in the present study in terms of total average error (orange bars), average errors excluding open-chain isomerism (red bars), and maximum absolute errors (blue bars). Inset: The eight α-pyranose aldohexoses investigated. Adapted with permission W. M. C. Sameera and D. A. Pantazis, J. Chem. Theory Comput., 2012, 8, 2630–2645. Copyright 2012 American Chemical Society.

Similarly, two datasets based on the relative energies of the conformers of melatonin and butane-1,4-diol were used in the benchmark of the DLPNO-CCSD(T) method.⁷⁹ When compared to the semicanonical counterpart, the DLPNO-based approach delivered MAD equal to 0.04 and 0.22 kcal mol⁻¹ for butane-1,4-diol and melatonin, respectively.⁷⁹

In addition to the aforementioned benchmark surveys, the accuracy of the LPNO methods has been exploited in application studies. For example, Dhaked and Bharatam investigated, with LPNO-CCSD and LPNO-CEPA/1, the tautomeric (enamine, imine and nitronic acid, see Fig. 7) forms of N-ethyl-N′-methyl-2-nitro-1,1-ethenediamine.⁸⁷ This compound served as a model to address the nitroethenediamine moiety present in several medicinally important molecules such as ranitidine. Data obtained at the MP2 level of theory suggested that the latter was more stable by ca. 1 kcal mol⁻¹ whereas various DFT functionals predicted the former to be more stable by 6–9 kcal mol⁻¹. The LPNO results indicate that the imine tautomers are only about 1–2 kcal mol⁻¹ less stable than the enamine global minimum.⁸⁷

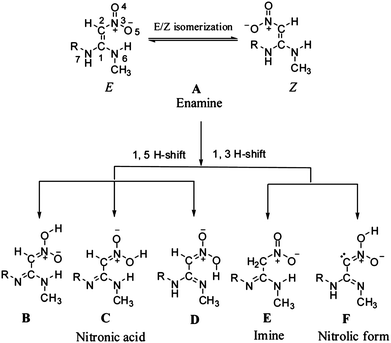Fig. 7 Possible tautomers of ranitidine. Reproduced from ref. 87 with permission from The Royal Society of Chemistry.

Harvey and coworkers reported on the accuracy of interproton distances derived from Nuclear Overhauser Effect data (NOE).^88,89 After observing that, contrary to the common perception, NOE measurements are accurate enough to establish interproton distances for rigid molecules⁸⁸ the authors investigated whether the approach can be extended to molecular systems that exhibit multiple configurations in solutions. To tackle this problem, the relative energies of the different conformers of a flexible molecule (4-propylaniline) were computed with LPNO-CEPA/1 to derive the populations at equilibrium.⁸⁹ The good agreement between the theoretically- and NOE-derived average interproton distances supports the accuracy of NOE based data.⁸⁹

Ashtari and Cann employed LPNO-CCSD to investigate, from a theoretical point of view, poly-proline chains and derivatives for chiral high performance liquid chromatography (HPLC).^90,91 In chiral HPLC, the selective moiety (in this case proline chains) is immobilized on the surface so that its chirality confers selectivity on the stationary phase. In order to characterize the stationary phase based on the selector on the surface, the authors initially investigated the major conformers for each proline chain assessing their relative energy with LPNO-CCSD/6-311G(d,p). Subsequently, force fields were developed and selected based on their ability to reproduce the relative energies of the conformers as predicted by LPNO-CCSD. Molecular dynamics simulations, employing the derived force fields, were carried out to characterize each chiral interface.^90,91

Extended systems

The accuracy shown by the LPNO based method for the computation of weak interactions and its efficiency (compared to canonical ab initio methods) allow for the use of a local method in the prediction of properties of extended systems via a careful application of finite models. For example, Maganas et al. investigated the vanadium oxide (V₂O₅) crystal.⁹² This solid consists of layers of square pyramidal VO₅ units in which the oxygen atoms at the base of the pyramid are shared between two vanadium atoms on the same layer. The apical oxygen gives a short V=O bond pointing toward a vanadium atom of a neighboring layer. A hydrogen-saturated cluster model, namely V₄O₁₈H₁₆, was investigated with DFT (pure, hybrid and double-hybrid) and ab initio methods (MP2 and LPNO-CCSD) concluding that at an equilibrium distance, the interaction energy per V=O⋯V unit is equal to 4–5 kcal mol⁻¹.⁹²

During the development of analytic potential to be used in the study of the interaction between formaldehyde and carbon based nanostructures (graphene sheets and carbon nanotubes), Dodda and Lourderaj used a formaldehyde–pyrene model system.⁹³ Various ab initio and DFT methods were tested against CCSD(T) references and it was concluded that the most accurate results were obtained with LPNO-CEPA/1 in the complete basis set limit. The LPNO-CEPA/1 data were then fitted to an analytical potential energy capable of correctly characterizing minima structures not included in the fitting procedure confirming its global nature.⁹³

Sancho-García and coworkers used reference calculations at the LPNO-pCCSD/1a level of theory to construct a database of anthracene dimer interactions representative of those found within the molecular crystal.^94,95 The dataset was used to assess the accuracy of DFT-D based methods that, in turn, gave fairly accurate estimation of the cohesive energy of the anthracene crystal.⁹⁴ In addition, the LPNO-pCCSD/1a results were compared against the experimental sublimation energy (electronic component), demonstrating that the method accurately reproduces values in the 1–2 kJ mol⁻¹ range from its experimental counterpart.⁹⁵

In a combined experimental and theoretical study, the transport properties of four commercial cationic membranes toward two counterions (namely H⁺ and Na⁺) were investigated.⁹⁶ In their study, the authors attempted to correlate ab initio calculations on membrane models with experimental conductometric measurements to explain the difference in the mobility of the two ions. In this case LPNO-CEPA was the method of choice in the computation of binding energies.

In passing, we note that larger models can now be investigated thanks to the near linear scaling obtained within the DLPNO framework. For example the first calculation at the CCSD(T) level on an entire protein (Crambin, 644 atoms, 6100+ basis functions) was recently reported.⁴⁵

Conclusions

In this review we have provided a brief overview of the chemical applications that have been done to date with the local pair natural orbital coupled-electron pair and coupled-cluster methods. It is evident that these methods reproduce their canonical counterparts with excellent accuracy (a few tenths of a kcal mol⁻¹) while leading to orders of magnitude computational savings. Although it is inevitable that any local correlation method introduces some errors, in a well-constructed local method, there will only be a few truncation parameters and the results should converge towards their canonical counterparts if these truncation parameters are tightened. This is the case for the (D)LPNO methods and the default truncation parameters have been chosen such that errors relative to the canonical calculation with the same basis set are typically below 1 kcal mol⁻¹, which, in our opinion, is sufficient for most computational chemistry applications. Higher accuracy is achievable at rapidly increasing computational cost. Nevertheless, the LPNO methods are robust and user-friendly in the sense that no adjustments of truncation parameters are necessary owing to the fact that the pair natural orbitals adapt themselves to any chemical environment. Furthermore, the average number of PNOs per electron pair is approaching a constant as the one-particle basis set is approaching completeness. Hence, the calculations behave excellently with respect to basis set extension. Thus, the advantage of (D)LPNO calculations over canonical ones will become larger for extended basis sets. Unlike the method based on projected atomic orbitals,⁹⁷ (D)LPNO calculations are not free of the basis set superposition error but rather behave analogous to their canonical counterparts in this respect.

The broad variety of the chemical applications covered in this review demonstrate that there is a rapid increase in the use of the (D)LPNO methods in conjunction with or in favor of DFT. In our view it is likely that these methods will play an increasingly important role in computational chemistry for large molecules or even extended systems. Obviously much further development work is necessary in order to proceed beyond the closed-shell systems described in this review. However, such further developments are now being pursued in a number of research groups and hence there is every reason to be optimistic about the future of these methods.

References

1. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
2. M. E. Alberto, T. Marino, N. Russo, E. Sicilia and M. Toscano, Phys. Chem. Chem. Phys., 2012, 14, 14943–14953.
3. F. Neese, Coord. Chem. Rev., 2009, 253, 526–563.
4. F. Neese, J. Biol. Inorg. Chem., 2006, 11, 702–711.
5. W. Klopper, J. Noga, H. Koch and T. Helgaker, Theor. Chem. Acc., 1997, 97, 164–176.
6. P. Constans, P. Y. Ayala and G. E. Scuseria, J. Chem. Phys., 2000, 113, 10451–10458.
7. M. Pitonak, F. Holka, P. Neogrady and M. Urban, THEOCHEM, 2006, 768, 79–89.
8. R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352.
9. W. Forner, J. Ladik, P. Otto and J. Cizek, Chem. Phys., 1985, 97, 251–262.
10. W. Forner, Chem. Phys., 1987, 114, 21–35.
11. K. Rosciszewski, K. Doll, B. Paulus, P. Fulde and H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 14667–14672.
12. H. Stoll, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6700–6704.
13. D. G. Fedorov and K. Kitaura, J. Chem. Phys., 2005, 123, 134103–134111.
14. W. Li and S. H. Li, J. Chem. Phys., 2004, 121, 6649–6657.
15. K. Kristensen, I. M. Hoyvik, B. Jansik, P. Jorgensen, T. Kjaergaard, S. Reine and J. Jakowski, Phys. Chem. Chem. Phys., 2012, 14, 15706–15714.
16. M. Ziolkowski, B. Jansik, T. Kjaergaard and P. Jorgensen, J. Chem. Phys., 2010, 133, 014107.
17. W. Li, P. Piecuch, J. R. Gour and S. H. Li, J. Chem. Phys., 2009, 131, 114109.
18. W. Li and P. Piecuch, J. Phys. Chem. A, 2010, 114, 8644–8657.
19. J. Friedrich and K. Walczak, J. Chem. Theory Comput., 2013, 9, 408–417.
20. J. Friedrich, D. P. Tew, W. Klopper and M. Dolg, J. Chem. Phys., 2010, 132, 164114.
21. J. Friedrich, M. Hanrath and M. Dolg, J. Chem. Phys., 2007, 126, 154110.
22. S. Saebo, W. Tong and P. Pulay, J. Chem. Phys., 1993, 98, 2170–2175.
23. S. Saebo and P. Pulay, Annu. Rev. Phys. Chem., 1993, 44, 213–236.
24. S. Saebo and P. Pulay, Chem. Phys. Lett., 1985, 113, 13–18.
25. S. Saebo and P. Pulay, J. Chem. Phys., 1988, 88, 1884–1890.
26. S. Saebo and P. Pulay, J. Chem. Phys., 1987, 86, 914–922.
27. M. Schütz, J. Yang, G. K. Chan, F. R. Manby and H. J. Werner, J. Chem. Phys., 2013, 138, 054109.
28. M. Schütz and H. J. Werner, J. Chem. Phys., 2001, 114, 661–681.
29. M. Schütz and H. J. Werner, Chem. Phys. Lett., 2000, 318, 370–378.
30. M. Schütz, G. Rauhut and H. J. Werner, J. Phys. Chem. A, 1998, 102, 5997–6003.
31. M. Schütz, G. Hetzer and H. J. Werner, J. Chem. Phys., 1999, 111, 5691–5705.
32. J. Yang, G. K. Chan, F. R. Manby, M. Schütz and H. J. Werner, J. Chem. Phys., 2012, 136, 144105.
33. H. J. Werner and M. Schütz, J. Chem. Phys., 2011, 135, 144116.
34. G. E. Scuseria and P. Y. Ayala, J. Chem. Phys., 1999, 111, 8330–8343.
35. P. E. Maslen, A. D. Dutoi, M. S. Lee, Y. H. Shao and M. Head-Gordon, Mol. Phys., 2005, 103, 425–437.
36. J. E. Subotnik and M. Head-Gordon, J. Chem. Phys., 2005, 123, 64108.
37. J. E. Subotnik, A. Sodt and M. Head-Gordon, J. Chem. Phys., 2006, 125, 074116.
38. D. P. Tew, B. Helmich and C. Hättig, J. Chem. Phys., 2011, 135, 074107.
39. C. Hättig, D. P. Tew and B. Helmich, J. Chem. Phys., 2012, 136, 204105.
40. B. Helmich and C. Hättig, J. Chem. Phys., 2013, 139, 084114.
41. J. Yang, Y. Kurashige, F. R. Manby and G. K. Chan, J. Chem. Phys., 2011, 134, 044123.
42. F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108.
43. F. Neese, A. Hansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 064103.
44. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
45. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
46. B. Helmich and C. Hättig, J. Chem. Phys., 2011, 135, 214106.
47. C. Krause and H. J. Werner, Phys. Chem. Chem. Phys., 2012, 14, 7591–7604.
48. Z. Rolik, L. Szegedy, I. Ladjanszki, B. Ladoczki and M. Kallay, J. Chem. Phys., 2013, 139, 094105.
49. Z. Rolik and M. Kallay, J. Chem. Phys., 2011, 135, 104111.
50. P. O. Löwdin, Phys. Rev., 1955, 97, 1474–1489.
51. C. Edmiston and M. Krauss, J. Chem. Phys., 1966, 45, 1833.
52. C. Edmiston and M. Krauss, J. Chem. Phys., 1965, 42, 1119.
53. R. Ahlrichs and W. Kutzelnigg, J. Chem. Phys., 1968, 48, 1819.
54. M. Gelus, R. Ahlrichs, V. Staemmler and W. Kutzelnigg, Theor. Chim. Acta, 1971, 21, 63.
55. V. Staemmler and M. Jungen, Chem. Phys. Lett., 1972, 16, 187.
56. V. Staemmler, Theor. Chim. Acta, 1973, 31, 49–61.
57. W. Kutzelnigg, V. Staemmler and C. Hoheisel, Chem. Phys., 1973, 1, 27–44.
58. F. Driessle, R. Ahlrichs, V. Staemmler and W. Kutzelnigg, Theor. Chim. Acta, 1973, 30, 315–326.
59. W. Meyer, J. Chem. Phys., 1973, 58, 1017–1035.
60. W. Meyer, Theor. Chim. Acta, 1974, 35, 277–292.
61. W. Meyer and P. Rosmus, J. Chem. Phys., 1975, 63, 2356–2375.
62. H. J. Werner and W. Meyer, Mol. Phys., 1976, 31, 855–872.
63. C. E. Dykstra, H. F. Schaefer and W. Meyer, J. Chem. Phys., 1976, 65, 5141–5146.
64. F. Wennmohs and F. Neese, Chem. Phys., 2008, 343, 217–230.
65. C. Hampel, K. A. Peterson and H. J. Werner, Chem. Phys. Lett., 1992, 190, 1–12.
66. L. M. Huntington, A. Hansen, F. Neese and M. Nooijen, J. Chem. Phys., 2012, 136, 064101.
67. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
68. R. Noyori, Asymmetric Catalysis In Organic Synthesis, Wiley, New York, 1994.
69. A. Anoop, W. Thiel and F. Neese, J. Chem. Theory Comput., 2010, 6, 3137–3144.
70. A. Lightfoot, P. Schnider and A. Pfaltz, Angew. Chem., Int. Ed., 1998, 37, 2897–2899.
71. D. H. Woodmansee and A. Pfaltz, in Iridium Catalysis, ed. P. G. Andersson, Springer-Verlag, Berlin, 2011, vol. 34, pp. 31–76.
72. M. Sparta, C. Riplinger and F. Neese, J. Chem. Theory Comput., 2014, 10, 1099–1108.
73. D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2011, 7, 1511–1523.
74. A. Espinosa, C. Gomez and R. Streubel, Inorg. Chem., 2012, 51, 7250–7256.
75. A. Kubas, S. Brase and K. Fink, Chem. – Eur. J., 2012, 18, 8377–8385.
76. R. A. Mata, H. J. Werner, S. Thiel and W. Thiel, J. Chem. Phys., 2008, 128, 025104.
77. N. Sultana and W. M. F. Fabian, Beilstein J. Org. Chem., 2013, 9, 594–601.
78. J. Friedrich and J. Hänchen, J. Chem. Theory Comput., 2013, 9, 5381–5394.
79. D. G. Liakos, M. Sparta, J. M. L. Martin and F. Neese, manuscript in preparation, 2014.
80. T. Schwabe, J. Comput. Chem., 2012, 33, 2067–2072.
81. P. Jurecka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985–1993.
82. D. G. Liakos, A. Hansen and F. Neese, J. Chem. Theory Comput., 2011, 7, 76–87.
83. J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427–2438.
84. J. Antony, S. Grimme, D. G. Liakos and F. Neese, J. Phys. Chem. A, 2011, 115, 11210–11220.
85. D. G. Liakos and F. Neese, J. Phys. Chem. A, 2012, 116, 4801–4816.
86. W. M. C. Sameera and D. A. Pantazis, J. Chem. Theory Comput., 2012, 8, 2630–2645.
87. D. K. Dhaked and P. V. Bharatam, RSC Adv., 2013, 3, 25268–25277.
88. C. P. Butts, C. R. Jones and J. N. Harvey, Chem. Commun., 2011, 47, 1193–1195.
89. C. R. Jones, C. P. Butts and J. N. Harvey, Beilstein J. Org. Chem., 2011, 7, 145–150.
90. M. Ashtari and N. M. Cann, J. Chromatogr. A, 2011, 1218, 6331–6347.
91. M. Ashtari and N. M. Cann, J. Chromatogr. A, 2012, 1265, 70–87.
92. D. Maganas, M. Roemelt, M. Havecker, A. Trunschke, A. Knop-Gericke, R. Schlogl and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 7260–7276.
93. L. S. Dodda and U. Lourderaj, Phys. Chem. Chem. Phys., 2013, 15, 17479–17486.
94. J. C. Sancho-García and Y. Olivier, J. Chem. Phys., 2012, 137, 194311.
95. J. C. Sancho-García, J. Arago, E. Orti and Y. Olivier, J. Chem. Phys., 2013, 138, 204304.
96. L. V. Karpenko-Jereb, A. M. Kelterer, N. P. Berezina and A. V. Pimenov, J. Membr. Sci., 2013, 444, 127–138.
97. H.-J. Werner and K. Pflüger, in Ann. Reports in Comput. Chem., ed. C. S. David, Elsevier, 2006, vol. 2, pp. 53–80.

---