Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum-chemical insights into mixed-valence systems: within and beyond the Robin–Day scheme
M.
Parthey
and
M.
Kaupp
*
Technische Universität Berlin, Institut für Chemie, Theoretische Chemie, Sekr. C7, Straße des 17. Juni 135, 10623 Berlin, Germany. E-mail: martin.kaupp@tu-berlin.de
First published on 29th April 2014
Abstract
In mixed-valence (MV) systems essentially identical, more or less electronically coupled, redox centres are brought into formally different oxidation states by removal or addition of an electron. Depending on the strength of electronic coupling, an electron or a hole is either concentrated on one of the redox centres, or it is symmetrically delocalised onto several sites, or the situation is somewhere in between, which leads to the classification system for MV systems introduced by Melvin Robin and Peter Day. These different characteristics are of fundamental importance for the understanding of electron transfer processes. Applications of quantum-chemical methods to aid the classification and to unravel the nature of the electronic structure and spectroscopic data of both organic and transition-metal MV systems, have gained tremendous importance over the last two decades. In this review, we emphasise the prerequisites the quantum-chemical methods need to fulfill to successfully describe MV systems close to the borderline between Robin–Day classes II and III. These are, in particular, a balanced treatment of exchange, dynamical and non-dynamical correlation effects, as well as consideration of the crucial influence of the (solvent or solid-state) environment on the partial localisation of charge. A large variety of applications of quantum-chemical methods to both organic and inorganic MV systems are critically appraised here in view of these prerequisites. Practical protocols based on a combination of suitable density functional methods with continuum or non-continuum solvent models provided good agreement with experimental data for the ground states and the electronic excitations of a large range of MV systems close to the borderline. Recent applications of such methods have highlighted the crucial importance of conformational effects on electronic coupling, all the way to systems where conformational motion may cause a thermal mixing of class II and class III situations in one system.
Martin Kaupp received his PhD in 1992 with P. v. R. Schleyer in Erlangen and his Habilitation 1997 in Stuttgart, after a postdoc in Montréal. He became professor at Universität Würzburg in 1999. Since 2010 he is professor of Theoretical Chemistry at Technische Universität Berlin. Martin Kaupp's wide research interests include development and applications of quantum chemical methods to calculate NMR and EPR parameters, density functional theory, relativistic effects, as well as computational bioinorganic, inorganic, organic and organometallic chemistry. He has authored more than 220 publications. In 2001 he received the Dirac Medal of the World Association of Theoretical and Computational Chemists (WATOC). |
1. Introduction
The importance of electron transfer (ET) in most areas of chemistry, biology, and materials sciences can hardly be overestimated. In this vast field, mixed-valence (MV) compounds have played a prominent role as central models for basic understanding of ET, as well as for various applications, some of which we will mention further below. The amount of synthetic, electrochemical, and spectroscopic work that has gone into the study of MV systems over the past 50 years is dazzling and certainly outside the scope of this review. We will focus here on the recently increased impact that quantum-chemical (QC) methods have had on the unravelling of ET in molecular, both organic and transition-metal, MV systems, especially when considered together with the relevant spectroscopic studies. We will first motivate the need for QC studies by discussing some basic models of ET together with the difficulties in establishing the details by spectroscopy alone. We will then point out the challenges for a quantitative computational treatment of MV systems at or near the localised–delocalised borderline, that have for a long time hampered more accurate studies. This has led our group to design and validate semi-empirically a scheme based on density functional theory (DFT) and suitable modelling of solvent environment. Part of the methodology and initial work on organic MV radical cations has already been reviewed. Here we extend the discussion to a wider range of organic MV systems and to improved solvent models. In particular, however, we will focus on recent work on transition-metal MV complexes, in the wider context of previous attempts of QC modelling in the field. These recent studies have led, among other things, to a new view of the importance of rotational conformers, guiding us beyond the usual two-state or three-state models of ET in MV systems.1.1 Classifications of mixed-valence systems
A wide range of molecular and solid-state systems is embodied in the MV concept, and various models have been devised to classify the ET characteristics. Generally, one views a MV system as a molecule or solid in which a given redox centre appears at least twice, in two different oxidation states, connected by a suitable bridging unit that typically provides for some electronic coupling between the redox centres. The thermal or optically induced ET between the (two or more) redox centres is at the heart of attention, but ET from or to the bridging unit, which is becoming increasingly more widely recognised, also plays a role in the overall ET mechanisms and spectroscopic profiles. The large variety of redox centres and bridge units and the different coupling between them accounts for the multitude of MV systems that can be envisioned or exist, either purposefully or accidentally constructed by synthetic chemists or present in nature. The “classical” MV systems are based on transition-metal redox centres connected by bridging ligands. Examples are Prussian Blue on the “serendipity” branch of the field or the Creutz–Taube ion and its derivatives1,2 that feature prominently in the purposeful study of ET in transition-metal systems. However, many other molecules have been known that were classified as MV only much later. Examples are the radical anions of aryl compounds with two or more nitro substituents. These have been known and studied spectroscopically since the early 1960s, but they were recognised as MV systems only much later, where the nitro-substituted part of the aryl ring features as redox centre, and the remaining aryl part plays the role of bridging unit.3–5 This served to introduce organic redox centres to the field, which have received grown attention due to their involvement in organic molecular electronics. Notable examples are those based on triaryl-amine redox-active units (see below). Organic MV systems are usually also based on organic bridges, but “inverted” MV systems with organic redox centres and transition-metal-based bridges are also known as discussed below.We may even widen the MV concept to such exotic species as the H2+ ion, which may be viewed as the smallest conceivable MV system. We will generally restrict ourselves to MV systems where the formal redox states differ by one unit, which for two redox centres typically leads to open-shell compounds in the ground and excited states.6 Of course, MV systems with larger electron-number differences are conceivable. Their closed-shell variants have been classified as donor–acceptor systems.6 Systems with non-identical redox centres further extend the picture and may call for a looser MV definition.7 In many cases redox-non-innocence of the bridge or of terminal ligands of transition metal complexes additionally complicates the redox-centre assignment.8–11
Here we will focus on organic and transition-metal MV systems, which formally contain only two identical redox centres, but are linked by bridges which may exhibit redox-non-innocent behaviour. Such systems can be analysed within the famous Robin–Day classification scheme (Fig. 1).12 The three primary Robin–Day classes correspond to (I) two completely decoupled diabatic redox states and fully localised redox centres, (II) moderate electronic coupling between the centres leading to a double-well adiabatic ground-state potential-energy curve with partly localised charges and a barrier for thermal ET (the electronic coupling, 2Hab, is smaller than the Marcus reorganisation energy λ), and (III) strong coupling with 2Hab ≥ λ leading to a single ground-state minimum without ET barrier and the charge being delocalised symmetrically over both redox centres. The reorganisation λ is usually divided into the inner reorganisation energy λi arising from structural changes within the molecule during ET, and the outer reorganisation energy λo arising from solvent rearrangements.6,13 An intermediate class II/III introduced by Meyer et al.14 will be mentioned further below. Lear and Chisholm introduced a new class IV, which represents a subclass of class III taking into account vibronic progression.15 This review will focus largely on systems close to the borderline between class II and class III, which is most challenging for both experiment and theory.
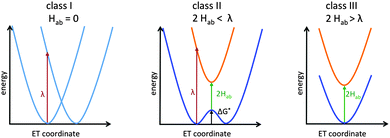 | ||
| Fig. 1 Potential curves for the three primary Robin–Day classes: class I (left), class II (middle) and class III (right). | ||
1.2 Application examples
Here we give a brief glimpse of some application areas of MV systems beyond their role as models to understand ET.The oxygen-evolving complex of the photosystem II, which catalyses the light-driven water oxidation, represents a typical example for an active site with predominant MV active states.18,19 The Mn4Ca(μ-On) core features a tetranuclear transition metal cluster, where different (MV) oxidation states are reached as a consequence of light-induced electron removal (i.e. photo-oxidation).20 Broken-symmetry DFT calculations have clearly demonstrated localised class II character for the relevant states, and standard functionals like B3LYP have been found to provide a reasonable picture of the electronic structure of these MV clusters, which seem to be far from the borderline to class III.
Another type of multinuclear enzyme site is represented by the dinuclear CuA site in various copper enzymes, e.g. cytochrome c oxidase. Here the MV Cu+ICu+II state appears to be a delocalised class III system, but perturbations due to mutation may alter the protein environment sufficiently to cause partial localisation.16,21–23 In contrast, partial delocalisation characterises many of the important biological iron–sulfur clusters, which renders these systems a challenge for both clear-cut experimental and theoretical descriptions. Charge distribution in FeS clusters depends crucially on coordination number of the metals and the extent of magnetic coupling between them (ferromagnetic coupling favours charge delocalisation, whereas antiferromagnetic coupling appears to give rise to charge localisation).16
On the other hand, switching functions or data storage are facilitated by a certain degree of localisation (“trapping”) of charge carriers, pointing to class II situations with appreciable barriers. Here the currently envisioned targets include the controversially discussed “quantum-dot cellular automata” made up of MV complexes. These may be related to coding information in quantum computers32–34 and to molecular transistors.24 Driven by the technological and economic pursuit of “Moore's Law”, the functional area of a transistor has been halving every eighteen to twenty-four months over the last decades, allowing the number of transistors per chip to double in each technology generation, and thus giving rise to smaller and more powerful electronic devices.24,35 Although studies suggest another two decades of potential progress in silicon nanoelectronics,36 a switch from the size-limited traditional materials towards molecular components will be required to continue this process of transistor scaling. Due to their versatile adjustable electronic properties, MV systems represent promising targets towards molecule-based electronics. Both organic and inorganic MV compounds are used in photovoltaic devices, where we may highlight dye-sensitised solar cells. Here MV systems may act as dye, as well as redox shuttle, and remarkable efficiencies have already been achieved.37–39
2. Limits in the experimental classification and the need for a quantum-chemical description
Information on the extent of charge localisation–delocalisation in an MV system can be obtained by various experimental techniques. Most commonly the assignment to a Robin–Day class is based on the analysis of the IVCT band, which typically occurs in the NIR region of the electromagnetic spectrum. The potential for multiple electronic transitions of similar energy but different electronic origin, together with the asymmetric IVCT band-shapes that characterise strongly coupled MV systems, renders derivation of the ET characteristics and electronic structure from NIR spectra alone very difficult in many MV transition-metal complexes, despite the popularity of such analyses. In organic MV systems the IVCT band usually appears as the lowest-energy band in the spectrum, facilitating the assignment.6Other important spectroscopic techniques involve somewhat different energy and time scales, e.g. vibrational spectroscopies (IR, Raman), Stark spectroscopy, Mössbauer spectroscopy, and EPR spectroscopy. At the borderline between class II and III, small activation barriers and fast ET processes may give rise to contradictory findings with different spectroscopic techniques, due to the different time scales of the spectroscopic methods, which can be comparable to the rates of ET, inner-sphere reorganisation processes, and solvent dynamics.
In some early studies the presence of symmetry-broken crystal structures was used as classification criterion, but of course the solid state may differ significantly from the situation in solution. Despite the fact that crystals are normally grown at low temperatures, at which the ET process is slowed down, crystal structures may be distorted due to packing, counter ion, or other crystal effects.40 For example salen type complexes often exhibit symmetry-broken structures in the crystal, but may feature delocalised charge in solution.41–44 Additionally, for complexes with free coordination sites, direct coordination of Lewis basic solvents may occur.
IR and vibrational Raman spectroscopy represent very fast and powerful methods to obtain information on the electronic structure of the ground state of MV systems.45 They are often used in combination with UV-vis-NIR spectroscopy as part of a spectroelectrochemical approach.46 Indications of charge localisation are easily derived from the IR spectra of complexes, which are symmetric in their non-mixed-valence forms. The splitting of IR bands due to the energy difference in modes, which are degenerate in the delocalised case (e.g. ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) vibrations) or the appearance of new IR bands, which do not involve changes of the permanent dipole moment in the case of a symmetrically distributed electron density, point to symmetry-broken structures.47–49 Satellite groups, such as local auxiliary ligands, may allow monitoring of modes, e.g. ν(NO) or ν(CO), which depend strongly on the oxidation state of the metal centre and thus are sensitive to the charge distribution.50 Analogously, information on electronic structure may be derived from Raman spectra.45,51
C) vibrations) or the appearance of new IR bands, which do not involve changes of the permanent dipole moment in the case of a symmetrically distributed electron density, point to symmetry-broken structures.47–49 Satellite groups, such as local auxiliary ligands, may allow monitoring of modes, e.g. ν(NO) or ν(CO), which depend strongly on the oxidation state of the metal centre and thus are sensitive to the charge distribution.50 Analogously, information on electronic structure may be derived from Raman spectra.45,51
Mössbauer spectroscopy is sensitive to oxidation state and charge distribution and corresponds to short time scales. Limitations pertain to the Mössbauer-active nuclei, where 57Fe is the most prominent example.52–54
The paramagnetic nature of most MV systems complicates the use of NMR spectroscopy due to paramagnetic line broadening.
Variable-temperature EPR spectroscopy is widely used to determine ET barriers in organic MV systems.5,55,56 Applications to MV transition-metal complexes are more limited, due to difficulties in extracting hyperfine coupling constants.47 In principle the isotropic hyperfine coupling constant of a MV system corresponds to the value obtained for an analogous monometallic complex, if the charge is localised. For a class III system it is close to half the value of the monometallic analogue. In addition, line broadening effects in the EPR spectrum may reveal ET processes that are slower than or comparable to the EPR time scale (10−9 s).57
The ET characteristics of MV compounds are most typically analysed within the frameworks of the Marcus–Hush and (generalised) Mulliken–Hush equations.58–66 Assuming that we are able to extract the necessary parameters of these models (mainly) from the NIR spectra, a rather detailed view is provided. As this article will focus on the direct computation of the adiabatic potential energy surfaces rather than on their indirect construction from experimentally estimated approximate diabatic potential energy curves, we will not provide a detailed discussion of the Marcus–Hush or Mulliken–Hush approaches. We refer the reader to a recent, very detailed discussion.6
However, problems with the application of these models often arise from the lack of sufficient spectroscopic information to support the requisite data analyses. A common way to analyse NIR spectra is to fit the spectroscopic absorption band profiles with Gaussian functions. In principle, the population of both ground and excited state vibrational levels can, to some extent, be taken into account assuming that these follow a Boltzmann distribution. Unfortunately this assumption is only valid for clear-cut class II or class III complexes in the Robin–Day scheme, as pointed out by Brunschwig et al.13 and Lambert and Heckmann.6 For systems close to the class II/class III borderline, the NIR band gets more and more asymmetric, as there is a cut-off at the smallest energy possible for an electronic transition. Due to this asymmetry of the band envelope, Gaussian functions are no longer a very suitable approximation and caution with Gaussian deconvolutions is advocated, when the investigated system is not a clear-cut class II or class III complex.
In addition to the vibrational progression, an alternative explanation for the band asymmetry of the Creutz–Taube ion was suggested by Meyer et al.:14 the asymmetry of the IVCT band of the Creutz–Taube ion is explained by the coupling of two of the proposed IVCT transitions at 6320 cm−1 and 7360 cm−1. The fact that the band shape does not change in low-temperature experiments was used as an argument to rule out vibronic effects. High-level quantum-chemical studies did not reproduce these transitions.67 Asymmetric band shapes are also observed for organic MV compounds near the class II/class III borderline, ruling out d-orbital contributions as explanation for the asymmetry in the band envelope.
In principle, the problems arising from asymmetric band envelopes can be circumvented by fitting only the high-energy part of the IVCT band with Gaussian functions. For this analysis, the IVCT band must be both clearly assigned and sufficiently well removed from other transitions to give an unobstructed view of the band edge. While this is possible for most organic systems with only two redox centres, for most MV transition metal complexes multiple transitions close in energy are observed. These transitions may lead to overlapping band-envelopes, and render a direct assignment of transition energies and bandwidth impossible.
Based on the semi-empirical model proposed by Meyer et al., experimental spectra of 3d and 4d complexes are normally fitted with three Gaussian functions.14 This localised model assumes two interconfigurational (IC) bands, which arise from excitations from orbitals localised at the hole-carrying (more highly oxidised) metal centre to orbitals at the same centre, and three IVCT bands originating from separate electronic excitations from three dπ-orbitals of the other metal centre. The IC transitions are normally parity forbidden, and only gain intensity if the system exhibits noticeable spin–orbit coupling. As the latter tends to be significant only for 5d systems, 3d and 4d metal complexes are typically expected to exhibit only the three IVCT excitations.
Hence alternatives to analyses of UV-vis-NIR bands to understand ET characteristics of MV systems are needed. This holds also for other parameters inherent in the simplified models, such as electron-transfer distances or the adiabatic dipole moment of the excited states. These tend to be difficult to extract from experiment. It is thus desirable to compute, e.g., excited-state parameters and compare them to the measured spectra. This is only one of the many aspects that call for a full, general, and quantitative quantum-chemical treatment of MV systems.
3. Challenges for a quantum-chemical description of MV systems close to the borderline
3.1 Wave-function-based methods
The proper treatment of Coulomb correlation is one of the main challenges in the accurate description of MV systems. UHF calculations provide a dramatic bias towards a localised situation, usually accompanied by strong spin contamination (in particular for the symmetrical transition state in a class II situation). UMP2 calculations are reported to suffer from the same unphysical exaggerated spin contamination.68 We distinguish dynamical and static (“non-dynamical”) correlation, keeping in mind that the separation between these two contributions is ill-defined.69 From previous experience it is clear that a quantitative description of localisation–delocalisation in MV systems close to the borderline of classes II and III requires a high level of treating both contributions. The static part may in some cases (but probably not too frequently) lead to a break-down of single-reference approaches. Including only the static correlation contributions, e.g. within a complete-active-space self-consistent-field (CASSCF) ansatz, does not cure the over-localisation (sometimes, the symmetrical structure has been enforced by constraints70).Adequate treatment of the dynamical correlation part requires good convergence with respect to the one-particle basis set. Given the steep scaling of typical methods with system size, their application to chemically relevant MV systems is very limited. In fact, examination of the basis sets used in the available ab initio post-HF studies suggests that the appreciable fractions of dynamical correlation required to describe a class III situation reasonably close to the borderline so far do not seem to have been achieved, neither for organic71–73 nor for transition-metal MV67,74,75 systems (see examples below in Section 4).
Most multi-determinantal approaches have thus been applied within a semi-empirical framework, using the AM1 Hamiltonian for organic MV systems68,76–81 or the INDO parameterisation for transition-metal complexes.82,83 In fact, until recently, AM1/CI calculations together with continuum solvent models had been the only methods that allowed at least to some extent a distinction between organic class II and class III MV systems close to the borderline.78 Limitations in the accuracy of the approach necessarily arise from the semi-empirical parameterisation. Different CI schemes have been applied, including either all valence single excitations68 or a full CI in a very small active space81 (typically three electrons in two orbitals) of the full-CI part of the calculation.
3.2 Density functional theory
The approximate inclusion of correlation via the exchange–correlation functional at effectively single-determinant cost makes Kohn–Sham DFT the most popular quantum-chemical method of our days. With standard functionals it is assumed that some of the static left–right correlation in bonds is simulated by the (semi-)local exchange functional. This comes, however, at the price of so-called self-interaction errors. These are also termed, more suitably in the present context, “delocalisation errors”.84–91 Indeed, standard functionals of the generalised-gradient-approximation (GGA) type or even the most popular hybrid functional B3LYP,92–94 where 20% of the semi-local exchange is replaced by exact Hartree–Fock exchange, generally arrive at a far too delocalised electronic structure for MV systems close to the borderline and are thus not suitable for analysis of these compounds.95 That is, a delocalised class III situation is erroneously produced on the class II side when sufficiently close to the border, which is just the opposite of the HF or CASSCF based approaches (see above). We note, however, that excitation energies for class III systems are typically reproduced well by B3LYP calculations. We see thus that we deal with a rather sensitive balance between opposing effects. We will come back to possible solutions for this dilemma further below.Van Voorhis advocated the use of constrained DFT (CDFT) in such situations, where charge localisation is enforced by adding system-dependent constraints to the Hamiltonian.96–98 That is, the information about how many electrons should be placed at a given redox centre is an input parameter of the calculation. The predictive power of such an approach is obviously very limited. It has been used mainly to extract ET parameters needed for the Marcus–Hush and generalised Mulliken–Hush treatments based on (enforced localised) diabatic states.33,96–102
Regarding the excitation energies, another, related problem with standard functionals, e.g. of the GGA type, arises. It is well known that for typical charge-transfer transitions, such functionals underestimate the corresponding excitation energies dramatically, and the reasons have been discussed extensively.103–106 But as nicely pointed out by Peach et al.,107 some types of charge-transfer transitions are less critical in this context. Even more importantly, the problem can be partly remedied by including a suitable amount of exact exchange, (Eexactx) into the functional, in a suitable variant of hybrid functional (see Section 3.4).
As we move to transition-metal systems, we also have to consider the problem of spin contamination. While an increase of Eexactx admixture diminishes delocalisation errors, it also tends to increase spin polarisation. It is well known that for transition-metal complexes, too much exact exchange may cause unphysical exaggerated valence-shell spin polarisation, which in turn leads to spin contamination (i.e. 〈S2〉 > S(S + 1), where S is the nominal total spin of the system).108–112 This effect is well known for hybrid DFT calculations on transition-metal complexes, and it is most pronounced for systems with significantly metal–ligand antibonding character of the singly occupied molecular orbital(s).29 Consequences of spin contamination are discussed vigorously.111–115 The S2 expectation value of the Kohn–Sham determinant strictly pertains to the so-called “non-interacting reference system” and its physical significance is thus being disputed.113,114,116 Definitions more in the spirit of Kohn–Sham DFT have been formulated.117 Empirically, increased spin contamination has been found to notably deteriorate the quality of electronic structure and, e.g., EPR parameters.109–112,114,115 Similar observations pertain to TDDFT calculations of excitation spectra.118 As spin polarisation and spin contamination increase with the amount of Eexactx admixture, caution with orbital assignments is advocated, and the S2 expectation value should always be checked.
3.3 Environmental effects
Most of the relevant MV systems are charged, and experimentally they are typically studied in a polar solvent environment. In fact, experimental gas-phase data are essentially absent in this field. It is thus obvious, that solvent and counter-ion effects are crucial ingredients for a reliable quantum-chemical protocol. Polar solvents will usually stabilise a localised, valence-trapped situation compared to a delocalised charge distribution. Gas-phase calculations, which were the standard approach until about 10 years ago, thus are clearly biased towards a too delocalised description. In fact, there are clear spectroscopic indications (see also further below for computational results) that even a moderate increase of solvent polarity may change a class III to a class II system, provided it is close to the borderline.119–121 While sometimes calculations included continuum solvent models in single-point calculations of, e.g., excitation spectra,122 neglect of solvent effects in the ground-state structure optimisation of a class II system often provided (incorrect) symmetrical structures to start with, thereby invalidating the subsequent spectroscopic calculations.An explicit inclusion of the solvent into the quantum-chemical model, or possibly a QM/MM ansatz, where the solvent is treated classically together with a QM treatment of the solute, can in principle provide a realistic description. However, the dynamical nature of the solute–solvent interactions requires such simulations to include the molecular dynamics on a sufficient time scale. While this type of explicit ab initio MD or QM/MM based MD studies has become an important tool in other areas of research, they have not yet entered the stage in the study of MV systems so far, at least not to a notable extent. This is probably due to the complications described in the previous two sections regarding the electronic-structure treatment itself. Given the recent emergence of practical–pragmatic solutions to the correlation problems (see next section), we expect that over the next years dynamical studies will gain substantial importance in the field of mixed-valency.
Thus, continuum solvent models so far dominate computations on MV systems, and we will provide examples throughout this article. An extension beyond continuum models that allows an adequate treatment also for protic solvents, has involved Klamt's D-COSMO-RS ansatz,123 which will also be described below. A very interesting approach based on force-field Monte-Carlo simulations and an integral equation formalism is the RISM-SCF procedure, which has also recently been applied to MV systems.124,125
There are no suitable continuum models to include counter-ion effects. This is why these have so far been largely neglected. It may be expected that counter ions will receive more scrutiny, as MD studies will enter the field. The importance of counter-ion effects depends of course on the system. Bulky MV systems like the typical triarylamine radical cations are likely affected less than smaller MV systems, e.g. some organic radical anions.
3.4 A reliable DFT-based protocol
The above discussion makes clear that, to reliably describe the properties of MV systems close to the borderline between class II and class III, a suitable quantum-chemical protocol has to account in detail for dynamical and non-dynamical correlation without suffering from extensive self-interaction errors, and it has to cover at the same time the relevant environmental effects. Notably, these features should already be included accurately in the ground-state structure optimisation, in contrast to many studies we find in the literature. Otherwise, computations of excitation energies or other spectroscopic parameters may suffer from the inaccurate structures. For an even more accurate description of excitation spectra, vibronic coupling has to be considered. In the absence of specific solvation effects, such as hydrogen bonding or the dynamic exchange of solvent molecules within the coordination sphere of a metal centre, it is expected that the bulk solvent effects may be covered adequately by dielectric continuum solvent models like COSMO126 or other “polarisable continuum models” (PCM).127,128 As mentioned in Section 3.1, their combination with the AM1/CI method provided the earliest semi-quantitative computational classification of organic MV systems close to the borderline.Within a Kohn–Sham DFT setting, the judicial inclusion of exact exchange into the functional should allow a balance to be reached between the treatment of left–right correlation in bonds (improved by semi-local ingredients of the exchange functional) and a reduction of delocalisation errors due to self-interaction (improved by more exact exchange). This leads naturally into the realm of hybrid functionals, where we may distinguish between constant exact-exchange admixture in global hybrids, an admixture depending on the interelectronic distance in so-called range-separated hybrids,129–140 or a real-space position-dependent admixture in so-called local hybrids.141–149 While detailed validation of the latter for MV systems is still pending, the two former classes have been evaluated in some detail (see below), initially for triarylamine (TAA) radical cations, subsequently for organic MV radical anions, and most recently for transition-metal complexes.
The initial validation of global hybrids for TAA radical cations120,121 (see below) in conjunction with continuum solvent models led to an optimum exact-exchange admixture of 35% in a customised one-parameter hybrid BLYP35, which was constructed analogous to the B1LYP model.150 While this is an ad hoc construction, later studies on smaller and thus computationally more convenient organic MV radical anions151,152 allowed an even larger set of functionals to be screened and showed, e.g., that the well-known BMK meta-GGA global hybrid functional153 also provides a very reasonable compromise. The BMK functional incorporates 42% exact-exchange admixture, somewhat ameliorated by contributions from local kinetic energy density. Global hybrids with appreciably less exact exchange overestimate delocalisation. Functionals with larger exact-exchange admixtures give too localised electronic structure.120,121,151,152,154 Indeed, it turned out that the exact-exchange admixture is the by far most important aspect of a global hybrid that has to be selected to achieve optimum performance for the treatment of MV systems.
Range-separated hybrids with 100% exact exchange in the long range, such as ωB97X,155 and LC-BLYP,136 so far tended to provide a too localised description, whereas CAM-B3LYP137 (which interpolates between 19% at short range and 65% at long range107,137) appeared to be just slightly too localised for organic MV radical anions. The “nonempirical tuning” of the range-separation parameter has been suggested as a means to adjust the delocalisation error, also recently for organic MV systems.156 A disadvantage is that such a tuning provides a different range-separation parameter for different molecules or even for different structures of one molecule, leading to size-consistency problems.157
The currently popular double hybrids exhibit too large exact-exchange admixture to be accurate for MV systems close to the border, and the MP2 contribution to the correlation functional tends to be problematic at the transition state of thermal ET for class II systems.120 These validation studies, which required the adequate inclusion of solvent effects, will be discussed in some more detail in the following sections, as will be the extension to MV transition-metal complexes.158–160 Overall, the BLYP35/COSMO based protocol and its variations using either suitable alternative functionals or alternative solvent models have turned out to provide an unprecedentedly detailed bracketing of localisation vs. delocalisation close to the borderline in a wide variety of MV systems.
4. Validation for and applications to organic MV systems near the borderline
4.1 Bis-triarylamine radical cations
The initial validation studies of the protocol for purely organic TAA systems have already been reviewed recently.121 We therefore only reiterate a few of the major conclusions of that work, which resulted in the first version of the abovementioned computational scheme. These systems had been studied earlier by a wide variety of methods, and some of the problems discussed in Section 3 above were observed by a variety of authors.121 TAA MV radical cations are of interest due to a range of possible applications, and they have been studied by a wide variety of spectroscopic and computational methods.6,79,120,121,154,161–172 Moreover, their character can be tuned very well by the choice of bridge unit, end cap, and even by the solvent, so that a wide variety of data for cases close to the border between class II and class III situations (from both sides) is available. Regarding the challenges for a computational treatment, the TAA-based systems have advantages and disadvantages: the relatively large size of the experimentally studied systems puts appreciable demands on computational efficiency, whereas the bulky aryl substituents at the amine redox centres tend to shield the positive charge well, causing specific solvation effects to be of minor importance in most cases. The latter aspect supports the convenient use of continuum solvent models.The systematic variation of exact-exchange admixture in B1LYP-style global hybrid functionals, and of the dielectric constant of the continuum solvent model appropriate to the condition of the experimental studies available for an appreciable variety of TAA-based MV radical cations led to the abovementioned preference for the BLYP35 functional combined with continuum solvent models as the basis for the initial version of the protocol discussed above (Section 3.4).120,121 Notably, TDDFT calculations using the same functional, solvent, and basis sets (in these initial studies SVP basis sets) provided surprisingly good agreement with the experimental excitation energies for the IVCT band. For class II systems, the excitation energies were underestimated somewhat. This had to be expected, as in this case the IVCT band has distinct charge-transfer character, and DFT tends to underestimate such excitation energies, sometimes dramatically so. However, the maximum deviations were rather tolerable, about 1000–1500 cm−1, suggesting that 35% exact-exchange admixture turns out to be a reasonable compromise. It may be assumed that the deviations are largest for the most weakly coupled systems. Indeed, for strongly coupled delocalised class III cases, where the character of the IVCT band is more that of a delocalised single-chromophor π–π* excitation, the excitation energies were overestimated by up to ca. 1000 cm−1 (blue circles in Fig. 2). Most importantly, the very systematic performance confirmed the accurate description of the underlying optimised ground-state structures, as the excitation energies crucially depend on whether a localised or delocalised structure is used.
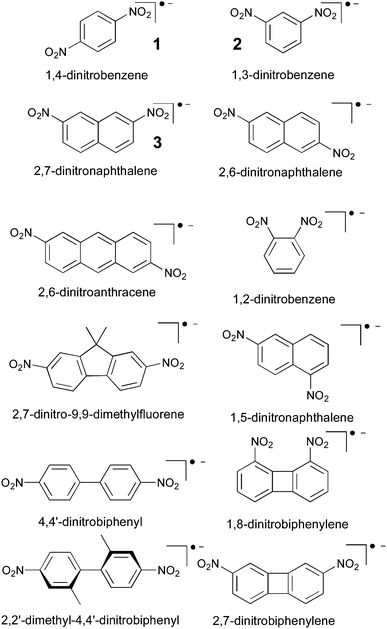 | ||
| Fig. 2 Dinitro radical anions investigated in ref. 3 and 151. | ||
These validation studies showed clearly that (a) standard functionals like B3LYP exhibit too large delocalisation errors to be reliable for class II TAA systems, and (b) the inclusion of solvent effects at least by a continuum solvent model is crucial for class II cases. We note, however, that B3LYP calculations, even without solvent effects, provide good excitation energies for clear-cut class III systems, where delocalisation errors and neglect of solvent effects do not affect the results too much. Somewhat lower exact-exchange admixtures compared to the abovementioned BLYP35 functional tend to lower IVCT excitation energies and thus actually improve agreement with experiment for class III cases, as demonstrated by a recent study173 at PBE0150 level (25% exact exchange; COSMO solvation), or by work on multibranched TAA systems using B3LYP and a PCM model.174 In a TDDFT study of class III triarylamine-substituted arylene bisimides,122 the CAM-B3LYP range-separated hybrid functional (at B3LYP/gas-phase optimised structures) yielded reasonable excitation energies. Use of a PCM model in the TDDFT single-points improved significantly the agreement between computed and experimental ionisation potentials and electron affinities in CH2Cl2.
A very recent DFT study on cross-conjugated TAA MV systems dealt with conformational effects on ET,175 which will be discussed in Section 5.4 below. Notably, PBE0/6-31G(d) calculations with a PCM acetonitrile solvent model correctly reproduced localised ground-state minima for the relatively weakly coupled class II systems involved. Not unexpectedly, the IVCT transition energies were, however, underestimated by a factor of about two, reflecting deficiencies of the TDDFT treatment with a functional containing only 25% Eexactx admixture. Yet good agreement with experimentally determined electronic coupling matrix elements was obtained, and these depended significantly on conformation. Interestingly, an evaluation of the range-separated hybrid functionals CAM-B3LYP and LC-ωPBE indicated a drastic overestimate of the experimental IVCT excitation energies,175 in particular for the latter functional (see also Sections 4.3 and 4.4 below).
4.2 Metal-bridged bis-biarylamines and bis-triarylamines
Bis-biarylamines and bis-triarylamines incorporating a metal in the bridge unit176–180 are also covered in this section, in spite of the metal involved. Their behaviour is very similar to purely organic bis-triarylamine radical cations, as the bridge tends to be involved only marginally/indirectly in the ET process.176,179–181 Yet, the spectroscopy of these systems may become richer in case of transition-metal systems, as in addition to the N → N+ IVCT transition also metal → N+ charge-transfer transitions are usually obtained in the UV-vis-NIR region. So far it appears that mainly class II systems have been reported.176,179–181 Compounds in which thermal ET may proceed via the purely organic 2-2′-bipyridine part of the bridge (coordinating to different transition metals) may be a notable exception.178 Here introduction of iridium leads to a class II/class III borderline complex, whereas Ru or Re bridges give class II behaviour. The BLYP35/C-PCM(CH2Cl2) protocol was applied. It gave good account of the influence of solvent effects, but the authors concluded that the distinction between purely organic and transition-metal bridged systems was not completely faithful.178For a weakly coupled class II Ga-bridged TAA MV system, it was found that M06/def2-SV(P) calculations in an integral equation formalism variant of the PCM model (IEFPCM, e.g. reviewed in ref. 127) solvation model faithfully reproduced the class II behaviour. However, the corresponding TDDFT calculations underestimated the IVCT energy significantly (3764 cm−1 compared to 6390 cm−1).181 This likely reflects the fact that M06 exhibits only 27% exact-exchange admixture, i.e. less than the BLYP35-based protocol delineated above.
Platinum-bridged TAA systems, had already been studied in 2004 by Jones et al.176 Parthey et al. have recently applied the BLYP35/COSMO protocol to such systems and found good agreement with measured ground- and excited-state properties.159 Introduction of the Pt bridge reduces electronic coupling compared to purely organic TAA systems with comparable bridge length, and thus moves the system even more into the class II range. Such calculations aid decisively in the assignment of the optical transitions. We note in passing the conceptual similarities of these metal-bridged TAA systems to other MV compounds where essentially organic radical ligands are coordinated to and thus bridged by a diamagnetic metal centre, such as for example certain salen-type complexes, where both class II and class III examples may be found.41–43,182,183
4.3 Dinitro-aryl radical anions
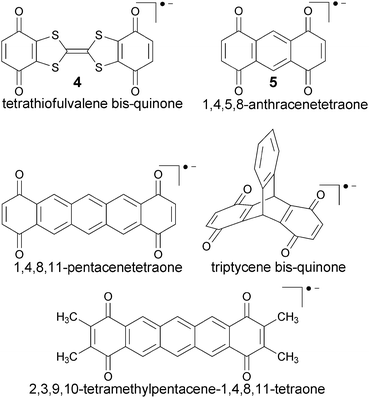
Dinitro aryl radical anions represent one of the earliest examples of organic MV systems, studied widely since the 1960s (in fact before the advent of the concept of mixed-valency), in particular by EPR spectroscopy.184–195 They cover both class II and class III, as well as borderline cases (see below), in spite of being typically much smaller than the bulky TAA systems discussed above. This makes them also particularly suitable to evaluate methodological aspects of electronic-structure methods. Their anionic nature and the small substituents make them furthermore more sensitive to specific solvent effects and possibly counter-ion effects, providing appreciable challenges to computational studies.We may consider the nitro groups as the redox centres, albeit the spin densities extend considerably into the aryl bridge moieties. The extent of electronic coupling depends strongly on whether the system exhibits a Kekulé or non-Kekulé substitution pattern. In general coupling is stronger for an odd bond number (Kekulé) between the redox centres than for even numbers (non-Kekulé). In most systems the charged nitro groups are accessible for solvent coordination. Indeed there are molecules such as 1,4-dinitrobenzene, 1 (cf.Fig. 2), which exhibit delocalised charge distributions and vanishing thermal ET barriers (extracted from EPR experiments) in aprotic solvents,3,5,196 but class II behaviour and appreciable barriers in alcohol solvents (e.g.1 exhibits free-energy ET barriers ΔG* between 22 ± 2 kJ mol−1 in ethanol and 36 ± 3 kJ mol−1 in octan-1-ol4). Non-Kekulé systems like 1,3-dinitrobenzene, 2 (Fig. 2) have sizeable barriers already in polar aprotic solvents, but the barriers still increase significantly in alcohols, obviously due to the effects of hydrogen bonding.68
Due to their relatively small size, dinitro aryl radical anions have been targeted by a number of quantum-chemical studies at various computational levels, and with various degrees of solvent modelling. Gas-phase unrestricted HF and MP2 calculations were found to suffer from exaggerated spin contamination. Nelsen, Clark et al. studied 2 employing single-excitation CI within the framework of the semi-empirical AM1 MO method.68 Gas-phase optimisations give a symmetrical structure, in contradiction with the experimentally observed class II character in polar solvents like acetonitrile. Inclusion of solvent effects by the COSMO model provided charge localisation for appropriate dielectric constants.
An interesting study by Yoshida et al. used state-averaged CASSCF calculations and included solvent effects (for MeCN and MeOH) by the reference interaction site self-consistent-field model (RISM-SCF).124 This is an advanced solvent model based on averaging over classical Monte-Carlo simulations for solvent motion that is expected to account also for hydrogen-bonding effects in alcohols. On the other hand, the neglect of dynamical correlation effects at CASSCF level is expected to bias the calculations towards a too localised picture (see Section 3.1). Indeed, the computed ET barriers at this level appear strongly overestimated (e.g., for 2 in MeCN, a 298 K ΔG* value of 60.63 kJ mol−1 was obtained, which is roughly a factor 3 too large). Other CASSCF calculations on 2 gave gas-phase activation energies on the order of 20 kJ mol−1.197 This would be more in line with the solution ESR data. But as the neglected effects of the polar solvent would increase the barrier (Section 3.3), and dynamical correlation effects would lower it (Section 3.1), this is obviously the right answer for the wrong reason. Other gas-phase CASSCF and MRMP2 calculations on 2 gave very small ET barriers and somewhat non-intuitive energy profiles.99 While CASSCF calculations do not cover dynamical correlation, the treatment of dynamical correlation at MRMP2 level has a strong basis set dependence (Section 3.1). The basis sets used (6-31G*) appear too small in this context. Those authors also applied the CDFT method to force localised structures.
As one might expect, unconstrained standard B3LYP DFT calculations on such systems are inadequate for class II situations, as they are biased towards delocalised structures. This holds true even if solvent modelling is included.198 One trick in such a situation to still extract useful ET parameters may be the use of Koopmans' theorem for the neutral compound at the structure of the radical ion.3,5
The small size of the dinitro aryl radical anions has invited a detailed study of DFT approaches combined with solvent models.151 The protocol described above, based on the BLYP35 functional and continuum solvent models, has been validated for a test set of six dinitroaromatic radical anions, including 1 and 2 (Fig. 2). The results were then compared against those obtained with other functionals, and the novel D-COSMO-RS solvent model has been evaluated for protic solvent effects. The range of functionals tested included meta-GGA global hybrid functionals representing different exact-exchange admixtures (the Minnesota M05,199 M06,200 M05-2X,201 M06-2X,200 and the BMK153 functional), range-separated hybrids (CAM-B3LYP,137 ωB97X,155 and LC-BLYP136), and double-hybrids (B2PLYP202 and B2PLYPD203). A wide range of ground-state properties were considered, and TDDFT calculations were applied to the IVCT excitation (cf.Fig. 3).
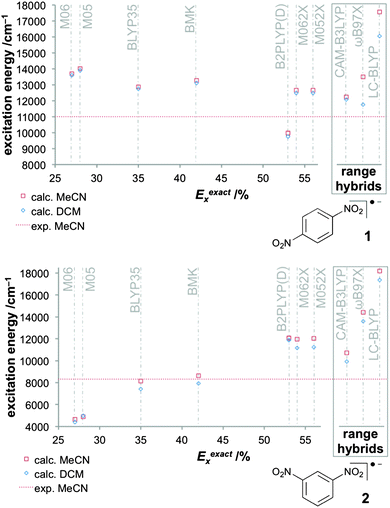 | ||
Fig. 3 Computed excitation energies with different functionals for the class III system 1 (top) and for the class II system 2 (bottom) in two solvents (C-PCM) compared to experimental values in MeCN (11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 for 1 and 8320 cm−1 for 2).151 Reprinted with permission from M. Renz, M. Kess, M. Diedenhofen, A. Klamt and M. Kaupp, J. Chem. Theory Comput., 2012, 8, 4189. Copyright 2012 American Chemical Society. 000 cm−1 for 1 and 8320 cm−1 for 2).151 Reprinted with permission from M. Renz, M. Kess, M. Diedenhofen, A. Klamt and M. Kaupp, J. Chem. Theory Comput., 2012, 8, 4189. Copyright 2012 American Chemical Society. | ||
Performance of BLYP35 and continuum solvent models in aprotic solvents was closely comparable to what had been found previously for TAA-based radical cations (see above). That is, experimental class II/class III distinctions were reproduced very well for a given solvent. IVCT excitation energies for class II systems were under-, those for class III systems overestimated (cf.Fig. 3), typically by up to 1000 cm−1 (in case of 2, the agreement between theory and experiment was closer than expected, 8140 cm−1vs. 8320 cm−1).
Among the other functionals tested, only the BMK meta-GGA hybrid (42% exact-exchange admixture) and the CAM-B3LYP range-separated hybrid (interpolating between 19% at short range and 65% at long range107,137) turned out to be more or less competitive to BLYP35. Both functionals tended to give slightly more pronounced localisation (e.g. larger ET barriers) and somewhat larger excitation energies for class II cases. This renders the BMK functional rather attractive in this context, as it is a thermochemically competitive functional, in contrast to BLYP35. The other global hybrids either overdelocalised (M05, M06) or overlocalised (M05-2X, M06-2X) significantly, and gave rather unrealistic IVCT excitation energies and ET barriers for class II systems, reflecting their rather different exact-exchange admixtures (Fig. 3). The double hybrids also provided a too localised description, consistent with their rather large Eexactx admixture (53%). Interestingly, B2PLYP nevertheless gave excessively low ET barriers, apparently due to an overstabilisation of the symmetrical transition states by the MP2-like correlation contribution, and it was the only functional giving too low IVCT excitation energies for class III systems (Fig. 3). The two range-separated hybrids ωB97X and LC-BLYP, which both feature 100% exact exchange at long range, both gave a significantly too localised description, accompanied by dramatic symmetry-breaking effects at several of the ET transition states for class II systems. This suggested a poor description of non-dynamical left–right correlation effects, as similar but even more pronounced deficiencies were found for HF wave functions.151 Apart from the BMK functional, the MPW1K hybrid functional204 with similar Eexactx admixture (42.8%) provided promising performance in preliminary tests. This is interesting, as the functional has shown promise in the study of transition-metal complexes.205,206
A striking result was obtained regarding modelling of protic solvent effects. While standard continuum solvent models are clearly inadequate to capture the difference between aprotic and protic solvents (e.g. the dielectric constants of MeCN and MeOH are almost the same), the recent D-COSMO-RS model123,207 performed remarkably well.151,152 For example, it gave the experimentally observed switch from class III to class II behaviour for 1 upon going from MeCN to MeOH (see above), as well as the experimentally observed increase of the ET barriers for the more clear-cut class II cases 2 and 2,7-dinitronaphthalene radical anion 3 by roughly a factor 2.151 This is notable in view of the fact that D-COSMO-RS does not explicitly account for the individual solvent molecules, but brings in hydrogen bonding by parameterisation within the relatively sophisticated underlying statistical thermodynamics framework, for the cost of a standard COSMO calculation. The self-consistent D-COSMO-RS model, which so far had not been evaluated much elsewhere, thus appears to provide a very convenient way to include protic solvent effects into standard quantum-chemical calculations.
4.4 Diquinone radical anions
Diquinone radical anions are a related class of MV systems, with similar features regarding size and solvent-accessibility, as the dinitro aryl systems discussed above. Three quantum-chemical studies with quite different methodologies have recently focused on the tetrathiofulvalene bis-quinone radical anion (Q-TTF-Q−) 4 (Fig. 4).97,98,140,152 Interest in 4 has been fuelled by the possible importance of the TTF linker as a strong π-donor bridge for organic molecular electronics.208 Its NIR spectrum in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of ethyl acetate and tert-butanol is dominated by a broad band at around 7700 cm−1, and the thermal ET barrier ΔH* was determined to be about 31 kJ mol−1 by ESR.208 A class II situation was inferred also in other polar solvents, but lack of solubility prevented a more detailed study of the barriers.
1 mixture of ethyl acetate and tert-butanol is dominated by a broad band at around 7700 cm−1, and the thermal ET barrier ΔH* was determined to be about 31 kJ mol−1 by ESR.208 A class II situation was inferred also in other polar solvents, but lack of solubility prevented a more detailed study of the barriers.
Not unexpectedly, gas-phase optimisation at B3LYP level gave a delocalised class III structure.97 Wu and van Voorhis used this system to evaluate the usefulness of their CDFT approach to force the system to localise.97,98 Indeed, a double-well potential is then obtained.97 Subsequent TDDFT calculations at the same CDFT level gave a too low IVCT excitation energy of 4575 cm−1, which was attributed to the lack of solvent reorganisation energy in the simulations.
In an independent DFT and CASSCF/CASPT2 study of 4 in various charge states, Ortí et al.209 also operated under the assumption that the mono-anionic MV form is a class II system in the gas phase. While B3LYP and PBE0 provided a class III situation in the gas phase and clearly too low ET barriers in solution (dimethyl sulfoxide PCM solvent model), symmetry-breaking already in the gas phase was obtained with BHHLYP (50% Eexactx),92 M06-2X (54%), and the range hybrids CAM-B3LYP, ωB97X, and ωB97XD,210 with appreciable barriers for the last two functionals. Consequently, the barriers in solution were drastically overestimated for ωB97X and ωB97XD, and still appreciably too large for BHHLYP, M06-2X, and CAM-B3LYP (somewhat surprisingly in view of the above discussion, the CAM-B3LYP and BHHLYP barriers were even somewhat larger than the M06-2X results).209 As IVCT excitation energies were all computed without consideration of solvent effects, they were inevitably all far too low, except for the CAM-B3LYP data but including the CASSCF(3,3)/CASPT2/6-31+G** results.209
5. Mixed-valence transition metal complexes
In view of the importance of MV transition-metal complexes for the general understanding of ET, based on pioneering experimental/spectroscopic studies since the 1970s, it is not surprising that such systems have also been in the focus of an appreciable amount of computational studies. This section will cover some of the historical development of such quantum-chemical work, without claiming to be comprehensive, followed by more recent, state-of-the-art studies. We will explicitly exclude computational work on mixed-valency in extended solids.5.1 The Creutz–Taube ion and its relatives
As the first synthetic transition-metal MV complex with predominantly delocalised character, and due to its importance in the early understanding of ET processes between two transition-metal centres, the famous Creutz–Taube ion [{Ru(NH3)5}2(μ-pz)]5+, 6, has probably been studied more than any other MV transition-metal complex, both experimentally and computationally. In fact, a new Robin–Day class II/III has been coined specifically for 6 (see e.g.ref. 14 and references therein). We do not intend to cover the extensive literature on the various different aspects of ET in the Creutz–Taube ion (vibronic effects, solvent effects, class II/III), which have been reviewed many times, for example in ref. 14 and 211. In particular, we will not attempt to evaluate the importance of vibronic effects, which have been studied in impressive detail as described in the references cited above. Our focus will be on the electronic-structure methods and on the effects of environment. Also, we will not attempt a comprehensive coverage of quantum-chemical studies, all the way back to the first extended-Hückel MO study.69 The wide range of methods applied and their advantages and disadvantages can probably be illustrated as follows:The earliest studies at Xα and related levels did not attempt to optimise ground states, but focussed generally on electronic structure and electronic transitions. Given the local DFT and gas-phase character of these calculations, a clear bias towards class III behaviour is obvious.212–214 Indeed, the first DFT-based structure optimisations used “pure” (LDA and/or GGA-type) functionals and thus inevitably provided equal Ru–N(pyr) bond lengths and overall symmetric structures.215,216 Depending somewhat on the basis sets and functionals, the optimised Ru–N(pyr) distances were clearly larger than the experimental values, but the computed ΔSCF calculations of excitation energies gave reasonable results.216 Hardesty et al.70 obtained a similar overestimate of the Ru–N(pyr) distance at B3LYP hybrid level but much closer agreement with experiment at MP2 level (these calculations enforced C2v symmetry and thus necessarily equal bond lengths). Subsequent DFT calculations that included solvent effects at the PCM level gave much shorter Ru–N(pyr) bonds and thus closer agreement with experiment.217,218 Yet, these calculations used symmetry, and thus a possible symmetry breaking could not be evaluated. It appears likely that the much shorter bond lengths obtained at MP2 level were a compensation between sizeable basis-set superposition errors due to the too small basis sets used at that time70 and the neglected environmental effects.
Symmetry breaking at the HF level and a tendency towards a more delocalised description upon including electron correlation for the Creutz–Taube ion had been mentioned earlier in a combined semi-empirical CNDO and ab initio CASSCF study.74 Yet, at that time full optimisations at adequate levels could not yet be done. Nevertheless, these studies were the first that incorporated continuum solvent models in the quantum-chemical treatment. The first full optimisations probably pertain to an INDO-based study, used to demonstrate a new set of INDO parameters for Ru.82 A somewhat asymmetric structure was obtained, consistent with the HF-like nature of the single-determinant INDO wavefunction. Consequently, subsequent INDO-CISD single-point calculations gave a more delocalised wave function.82 The computed IVCT excitation energy was nevertheless significantly too low.
The probably most sophisticated ab initio computations on 6 were Bolvin's single-point CASSCF and CASPT2 calculations (done at a slightly idealised structure derived from crystallographic data).67 In accordance with the findings of Broo and Larsson,74 CASSCF yields rather poor agreement with experimental UV-vis-NIR data due to the missing dynamical correlation in the ground-state wavefunction. Subsequent MS-CASPT2 calculations (with PCM solvent) gave excellent agreement with measured excitation bands (e.g. 6400 cm−1 compared to the experimental IVCT band at 6370 cm−1). Interestingly, even transitions accessible only by magnetic circular dichroism spectroscopy were nicely reproduced, and EPR g-tensors in good agreement with experiment were obtained.30
The aforementioned first DFT calculations including solvent effects were part of a multi-step procedure aimed at evaluating the solvent contributions to the reorganisation energy and thus to the IVCT energy.217 While this involved conceptually diabatic localised states, the structure was taken to be delocalised. This relatively complicated procedure, which involved both TDDFT and CASSCF steps (with solvent effects included only in the latter), afforded overall also a good IVCT excitation energy (6170 cm−1).217
Even more sophisticated solvent treatments used classical molecular dynamics (MD) for explicit water molecules, within a model approach.220 MD for the solvent motion was also used at the PBE0 DFT level for the related but more localised cyano-bridged ruthenium complex [(H3N)5Ru-μ-NC-Ru(CN)5]−,221 in the context of simulating the L3-edge X-ray absorption data of this class II system. The comparison of experimental UV-vis-NIR data and TDDFT calculations at PBE0 and B3LYP level with COSMO(H2O) solvent model for this class II system had been performed earlier.222
As part of a study on the importance of rotamers for ET in MV complexes (Section 5.4), the BLYP35/COSMO(MeCN) protocol has recently been applied also to the Creutz–Taube ion.219 Notable spin contamination (〈S2〉 = 0.99) and extensive negative spin density on the pyrazine ligand were found at this level with 35% Eexactx admixture. This is a known feature of such hybrid functionals for open-shell transition-metal complexes in cases when the singly occupied molecular orbital(s) exhibit(s) significantly metal–ligand antibonding character.109–111 This is clearly the case for 6 (cf.Fig. 5, top right). The overall results for ground-state structure and IVCT band of 6 nevertheless matched experimental observations rather well. In particular, the computations confirmed a description as a system exceedingly close to the borderline between class III and class II. That is, two slightly different Ru–N(pyr) bond lengths (2.027 Å vs. 2.017 Å, rather close to experimental values in two different solid-state structures40) indicated the onset of localisation, but the computed spin density remained largely symmetrical and delocalised (Fig. 5, bottom left). The TDDFT results for the IVCT excitation energy at this optimised structure depended somewhat on the treatment of non-equilibrium solvation, with the CPCM model in Gaussian09 providing the lower value (EIVCT = 6250 cm−1) compared to the COSMO implementation in TURBOMOLE 6.4 (EIVCT = 7046 cm−1), and thus somewhat better agreement with experiment. Most notably, a conformational relaxed scan of the relative orientation of redox centres and pyrazine bridge at the same BLYP35/COSMO(MeCN) level gave partial localisation of the spin density onto one of the Ru centres when the ligand was rotated away from the minimum structure by 45°, i.e. when it eclipses the equatorial ammonia ligands.219 This confirms the borderline Robin–Day character of 6 and opens questions about the role of conformational motion, which is addressed further below.
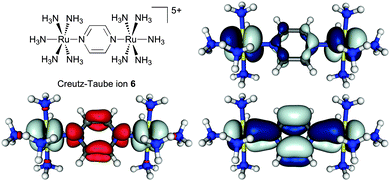 | ||
| Fig. 5 Isosurface plots of spin density (bottom left, ±0.002 a.u.) and β-SOMO (top right)/β-HOMO (bottom right) (±0.03 a.u.) of the Creutz–Taube ion, 6, calculated at the BLYP35/def2-SVP/COSMO(MeCN) level.219 Adapted with permission from M. Parthey, J. B. G. Gluyas, M. A. Fox, P. J. Low and M. Kaupp, Chem. – Eur. J., DOI: 10.1002/chem.201304947. Copyright @ 2014 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
5.2 Polyynediyl-bridged organometallic complexes
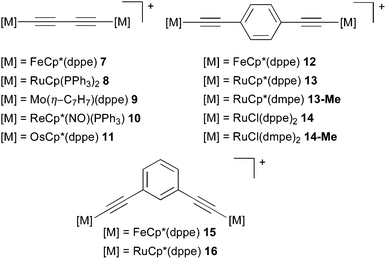
Organometallic MV complexes have recently received increased interest due to their often appreciable thermal and chemical stability, which may make them suitable as building blocks in molecular electronics applications. Here we will focus on the subclass of polyyne-bridged complexes (Fig. 6, left; the diethynylphenyl-bridged complexes on the right will be discussed below in Section 5.3), which have been in the focus of significant computational work and give rise to interesting spectroscopic features and questions. Moreover, these complexes are considered in the context of long-range ET materials (molecular wires),28,50,223,224 and as mimics of linear carbon allotropes.225 A variety of reviews and book sections address these all-carbon bridged MV systems.28,223,224,226–229 We note in passing the importance of bridged oligoferrocene complexes.52,230–233Comparable to the purely organic MV systems covered in Section 4, the entire range from weakly coupled class I or II to strongly coupled class III systems is accessible for these organometallic examples by chemical modification and by changing the solvent environment. For example, change of either the metal centres, in the case of the diynediyl-bridged28,30,47–50,57,224,234–241 and diethynyl-benzene-bridged complexes,28,242,243 and/or modification of the diethynylaromatic bridging ligand (e.g. in iron33,100,224,244–251 and ruthenium complexes206,243), are ways to tune the behaviour. While remarkable chain sizes have been achieved synthetically, e.g. a 28 carbon-atom polyynediyl bridge between two platinum centres,252 we will focus here on the diynediyl-bridged complexes. In these compounds the choice of the terminal metal redox centre is a critical determinant of whether a system exhibits localised (e.g. [{Mo(η-C7H7)(dppe)}2(μ-C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC
CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)]+, 9)57 or delocalised charge distribution (e.g. [{FeCp*(dppe)}2(μ-C
C)]+, 9)57 or delocalised charge distribution (e.g. [{FeCp*(dppe)}2(μ-C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC
CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)]+, 7).28,224,240
C)]+, 7).28,224,240
Two metal atoms coupled by a “carbon wire” made such systems attractive targets for computational studies. The majority of this work dealt with strongly coupled class III systems, where obviously the standard gas-phase DFT treatments with functionals like BP86 or B3LYP correctly reproduced the delocalized, symmetrical ground-state character of the mixed-valence species. Examples are the class III MV iron complexes [{FeCp(CO)2}2(μ-(C)n)]+ (n = 4–8), models for the related Fe–C4–Fe and Re–C4–Re monocationic complexes 7 and 10 and their mixed Fe–Re complex,48 a series of related diiron and dirhenium molecular wires,253 diynediyl-bridged manganese MV systems,30,241,254 the ruthenium complex 8,235 as well as iron/ruthenium and iron/rhenium analogues of this system.237
Interestingly, a relatively early HF calculation on the dirhenium MV complex 10 indicated SCF convergence problems.47 While the DFT calculations were generally consistent with the delocalised class III situations derived experimentally for the homodinuclear complexes, some localisation onto the iron centre was computed (B3LYP, gas phase) on the mixed Fe–Re complex.48 Yet, a too delocalised spin-density distribution compared to the experimentally established class II character49 may be discerned.
Often, the extent of spin density on the carbon bridge vs. the metal centres has been of central interest. For the dirhenium complex 10 and analogues with longer bridges up to 20 carbon atoms, Reiher et al. investigated spin-state energies (also for the neutral and dicationic complexes) and spin densities at BP86 and partly B3LYP* level (15% Eexactx admixture in the latter case).255 In addition to the doublet-quartet splitting of the MV cationic form, the singlet–triplet splitting of the dication was investigated for the full systems. Not unexpectedly, spin-state splittings were found to decrease with increasing chain length. While the doublet ground state of the MV system had some tendency to localise the spin at the Re centres, the quartet exhibited more spin on the bridge, in particular for the longer bridges. The gas-phase nature of the calculations and the functionals used may exaggerate the delocalization onto the bridge somewhat.
Computationally studied counterexamples to the predominantly class III molecular wires discussed above are provided by the weakly coupled class II dimolybdenum complex 9,57 by the diruthenium complex 16,206 and by some carborane-bridged molybdenum256 and ruthenium205 complexes. Neither B3LYP calculations on 9 nor application of the MPW1K hybrid functional (Eexactx admixture 42.8%) in the gas-phase calculations apparently reproduced the class II character of this MV cation.57 For the particularly weakly coupled carborane-bridged dimolybdenum and diruthenium systems, MPW1K calculations gave a localised structure and spin-density distribution, even though solvent effects were not considered.205,256 Together with the clear-cut class III examples discussed above, this shows that, as we move away from the borderline between class II and class III, some of the shortcomings of the computational treatment become less serious.
5.3 Complexes containing diethynylaromatic bridges
Increasing the length of the all-carbon chains was found to deteriorate the chemical stability of the polyynediyl-bridged MV complexes. Introduction of aromatic spacers has therefore become a welcome means to increase the metal–metal distances while maintaining good stability and still appreciable, albeit possibly somewhat weaker, electronic coupling between the metal centres.245,257 Substantial efforts have thus been invested into the study of organometallic complexes containing diethynylaromatic bridges (cf.Fig. 6, right), including computational work.Interestingly, some of these dinuclear iron and polyyne-bridged ruthenium complexes (and some trinuclear iron species) proved to be sufficiently stable to be studied by scanning tunnelling microscopy (STM) on a gold surface, including their mixed-valence states.33,100,258,259 This allowed their single-molecule characterisation in such an adsorbed environment, complementary to the usual spectroscopic studies in solution or in the solid state. These investigations were accompanied by DFT calculations to simulate the STM images. Fig. 7 shows examples of measured and simulated images of two diiron complexes, namely 12 with a 1,4-diethynylbenzene bridge and 15 with a 1,3-diethynylbenzene bridge (cf.Fig. 6). The stronger electronic coupling by the para-substituted linker in 12 makes this a class III – class II borderline case in polar aprotic solution,246,260 and class III on the surface, as indicated by a relatively symmetrical image in the latter case (Fig. 7).33,100
 | ||
| Fig. 7 Comparison of simulated and experimental STM images under opposite biases for 12 (a, left) and 15 (b, right). CDFT (B3LYP) was employed to obtain charge localisation.100 Reprinted with permission from R. C. Quardokus, Y. Lu, N. A. Wasio, C. S. Lent, F. Justaud, C. Lapinte and S. A. Kandel, J. Am. Chem. Soc., 2012, 134, 1710. Copyright 2012 American Chemical Society. | ||
In contrast, the meta-substitution in 15 leads to a class II situation, again both in polar solution249 as well as on the gold surface33,100 (Fig. 7). Standard BP86 or B3LYP gas-phase calculations gave delocalised situations for both complexes33,100,244,249 and thus failed to reproduce symmetry breaking for 15 or for a corresponding trimetallic 1,3,5-triethynylbenzene-bridged iron complex.249 Therefore constrained DFT simulations were subsequently applied. Of course the predictive value is limited, as the same constraints applied to 12 will also give an asymmetric image.33,100
Simplified models of 15 and of closely related diethynylpyridine-bridged complexes were also computed at B3LYP level by Costuas et al.261 Some structural symmetry breaking could be observed in some of the optimisations. However, negligible energy differences (around 1 kJ mol−1) between localised and delocalised structures indicated problems in the descriptions, which is not surprising at the given gas-phase DFT level. Subsequent CASSCF and MR-CI calculations provided localised electronic structures, in spite of missing environmental effects. This is unsurprising given that the CASSCF calculations do not include dynamical electron correlation, and the MR-CI calculations recovered very little of it, due to the very small basis sets used (STO-3G).261
Similarly to its iron analogue, the 1,3-diethynylbenzene-bridged ruthenium complex 16 (Fig. 6) exhibits class II behaviour in solution. Fox et al. modelled this system and a related complex with Ru(dppe)2Cl end caps, at the MPW1K gas-phase level.206 In spite of the neglected solvent effects, partially localised structures were obtained with this enhanced Eexactx admixture, yet substantially more delocalisation of spin density onto the bridge was computed compared to analogous iron complexes.
5.4 Rotamers: the importance of conformational motion
The importance of conformations for ET transfer rates has been acknowledged for a long time in various contexts, way beyond the scope of the present article, but of course including the field of MV systems.117,262–271 One means to restrict conformational freedom is the introduction of steric constraints,270,271e.g. by tethering.272–274 Linkers have been constructed specifically, e.g. to force certain dihedral angles within the bridge. In not too restricted situations, the results of spectroscopic experiments almost always correspond to an average over a sampling of conformational degrees of freedom.Here quantum-chemical calculations may aid in the evaluation of the effects of such conformational motion, and a variety of studies along these lines has been performed.239,261,275–277 With respect to certain optoelectronic properties, it is in fact important to describe correctly not only the ground-state conformational energy surface but also that in crucial excited states. Shortcomings of TDDFT in case of charge-transfer-type excited states have been noted,278,279 and more sophisticated methods280 may have to be applied. In this section, we will focus on conformational effects in the types of organometallic systems discussed in the two preceding sections but note that conformational effects are increasingly also in the focus of quantum-chemical studies on other MV systems. This includes recent work on organic TAA-based systems (cf. Section 4.1 above) with partly saturated bridges, where the predominant pathways for ET depend crucially on conformation.175
Experimental research on conformational effects in organometallic carbon-bridged species of the type discussed above has been reviewed by Low.257 We will focus our attention on the corresponding computational work. As a prerequisite for studies on binuclear MV systems, a number of computational studies focused on spin-density delocalisation as a function of conformation in mononuclear Fe and Ru complexes bearing a diethynylaromatic ligand that becomes the bridge in corresponding dinuclear species.54,243,277,281–283 This provides insight into the coupling between metal d-orbitals and the ligand π-system as a function of rotation angle.
A number of computational studies have evaluated the relative orientation of the two end caps in all-carbon-bridged MV complexes. As for the abovementioned mononuclear complexes, most of these studies used standard functionals and gas-phase conditions (but see below) and thus are expected to provide an overall too delocalised description. BP86/gas-phase calculations on a truncated model of the C2-linked complex [{Ru(dppe)Cp}2(μ-C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)]+
C)]+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 provided a lowest-energy minimum structure with a Cp(midpoint)–Ru–Ru–Cp(midpoint) torsion angle of 55°, likely due to direct steric interactions between the end caps. A transoid minimum (torsion angle 180°) at somewhat higher energy was also found. In addition to a main excitation near 16
239 provided a lowest-energy minimum structure with a Cp(midpoint)–Ru–Ru–Cp(midpoint) torsion angle of 55°, likely due to direct steric interactions between the end caps. A transoid minimum (torsion angle 180°) at somewhat higher energy was also found. In addition to a main excitation near 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1, TDDFT calculations for this latter minimum provide low-intensity peaks at lower energies. However, due to the relatively large barriers the NIR spectra are likely dominated by the lowest-energy minimum in this case. Rotamers were also found in similar BP86/gas-phase computations on trimetallic ruthenium complexes.276
200 cm−1, TDDFT calculations for this latter minimum provide low-intensity peaks at lower energies. However, due to the relatively large barriers the NIR spectra are likely dominated by the lowest-energy minimum in this case. Rotamers were also found in similar BP86/gas-phase computations on trimetallic ruthenium complexes.276
The BLYP35/COSMO computational protocol was applied to the class III complex [{Ru(PPh3)2Cp}2(μ-C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC
CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)]+, 8 (Fig. 6),158 to evaluate the origin of an additional high-energy shoulder found in its NIR spectrum (Fig. 8). The latter could not be explained in the original analysis.235 Full BLYP35/COSMO(CH2Cl2) structure optimisation gave an almost Ci-symmetric trans conformer trans-8. TDDFT calculations at the same level provided a π–π* transition corresponding excellently to the principal component in the NIR spectrum (Fig. 8).
C)]+, 8 (Fig. 6),158 to evaluate the origin of an additional high-energy shoulder found in its NIR spectrum (Fig. 8). The latter could not be explained in the original analysis.235 Full BLYP35/COSMO(CH2Cl2) structure optimisation gave an almost Ci-symmetric trans conformer trans-8. TDDFT calculations at the same level provided a π–π* transition corresponding excellently to the principal component in the NIR spectrum (Fig. 8).
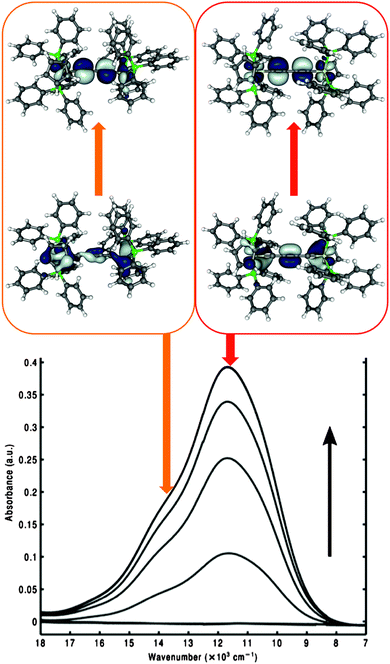 | ||
Fig. 8 Isosurface plots (±0.03 a.u.) of the orbitals involved in the NIR transitions of 8 calculated at the BLYP35/(def2-)SVP/COSMO(CH2Cl2) level and experimental spectrum collected during spectroelectrochemical oxidation in CH2Cl2/0.1 M NBu4PF6.158 The excitation around 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 only gains intensity for rotameric forms, which exhibit approximately orthogonal disposition of the Cp rings around the RuC4Ru axis. Adapted with permission from M. Parthey, J. B. G. Gluyas, P. A. Schauer, D. S. Yufit, J. A. K. Howard, M. Kaupp and P. J. Low, Chem. – Eur. J., 2013, 19, 9780. Copyright @ 2013 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. 000 cm−1 only gains intensity for rotameric forms, which exhibit approximately orthogonal disposition of the Cp rings around the RuC4Ru axis. Adapted with permission from M. Parthey, J. B. G. Gluyas, P. A. Schauer, D. S. Yufit, J. A. K. Howard, M. Kaupp and P. J. Low, Chem. – Eur. J., 2013, 19, 9780. Copyright @ 2013 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
A subsequent relaxed scan of the P–Ru–Ru–P dihedral Ω from 0° to 180° (180° corresponds to trans-8), and structure optimisation of resulting local minima led to two further class III rotamers: a cisoid form cis-8 is almost isoenergetic with trans-8 and provides almost identical transitions. In contrast, the slightly higher-energy conformer perp-8, in which the Cp moieties are nearly perpendicular to each other, exhibits an additional, less intense MLCT excitation at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982 cm−1 (Fig. 8). This provides an explanation for the experimentally observed shoulder in the NIR spectrum and indicates the importance of conformation of the redox centres even for such a simple “all-carbon wire”.
982 cm−1 (Fig. 8). This provides an explanation for the experimentally observed shoulder in the NIR spectrum and indicates the importance of conformation of the redox centres even for such a simple “all-carbon wire”.
In contrast to other examples discussed below, however, all conformations retain a fully delocalised class III character, explaining the absence of new vibrational bands and the relative solvent-independence of the IVCT band. Notably, the assignment of the NIR shoulder to an MLCT transition of the perpendicular conformation in 8 was experimentally confirmed by the synthesis and spectroscopic analysis of the tethered system [{RuCp}2(μ-C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CC
CC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C)(μ-Ph2P(CH2)5PPh2)2]+. This pseudo-macrocyclic complex is conformationally restricted to a limited rotamer subspace around the cisoid form. While it exhibits largely similar spectroscopic properties as cis-8, the shoulder assigned to perpendicular rotamers is absent in the NIR spectrum of the tethered complex.
C)(μ-Ph2P(CH2)5PPh2)2]+. This pseudo-macrocyclic complex is conformationally restricted to a limited rotamer subspace around the cisoid form. While it exhibits largely similar spectroscopic properties as cis-8, the shoulder assigned to perpendicular rotamers is absent in the NIR spectrum of the tethered complex.
In case of diethynylaromatic bridges, both the relative orientation of the redox centres and of the bridge may be important. DFT studies of the 1,4-diethynylbenzene-linked diiron complex 12 and its heterobimetallic analogue containing one Fe(dppe)Cp* and one Mo(η-C7H7)(dppe) end cap indicated an appreciable dependence of the spin-density distribution of the MV cationic form on the relative conformation of the two redox centres.57
The closely related 1,4-diethynylbenzene-bridged MV diruthenium complexes 13 and 14284,285 (cf.Fig. 6) were experimentally identified as class III systems, but several features in their spectra raised puzzling questions: (a) similar to the situation for 8 above, the NIR bands exhibited high-energy shoulders that lacked a convincing explanation; (b) the IR spectrum exhibited not only the features expected for class III systems but extra C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretching modes and aryl breathing modes that should be absent for a centrosymmetric complex.243,285 This motivated a detailed computational study of both the bridge and redox centre rotation at the BLYP35/COSMO level for 13 and 14, as well as for the Creutz–Taube ion 6.219 Two-dimensional relaxed scans on the truncated model complexes 13-Me and 14-Me, (dppe replaced dmpe), full optimisations of ground-state minima for truncated and untruncated complexes, as well as subsequent TDDFT calculations were carried out.
C stretching modes and aryl breathing modes that should be absent for a centrosymmetric complex.243,285 This motivated a detailed computational study of both the bridge and redox centre rotation at the BLYP35/COSMO level for 13 and 14, as well as for the Creutz–Taube ion 6.219 Two-dimensional relaxed scans on the truncated model complexes 13-Me and 14-Me, (dppe replaced dmpe), full optimisations of ground-state minima for truncated and untruncated complexes, as well as subsequent TDDFT calculations were carried out.
The 2D relaxed scan for 13-Me (Fig. 9) indicated that the bridge rotation (angle Θeff) has a greater influence on the spin-density distribution than the redox centre rotation (angle Ω, Fig. 10), but that it is also associated with a larger energy penalty. Yet the entire conformational space covers only an energy range of less than 30 kJ mol−1 (Fig. 9). Minima are obtained for the transoid (Ω = 180°, Θeff = 0°) and cisoid (Ω = 0°, Θeff = 0°) conformations, which exhibit the strongest electronic coupling due to the optimal overlap between the bridging ligand π-system and the metal d-orbitals of similar symmetry. The largest energies are obtained when the bridge is nearly perpendicular to the optimal orientation and thus the spin density is localised on one redox centre and the neighbouring ethynyl unit (Fig. 10). When only the relative conformation of the two redox centres is varied, while the bridge is kept in its optimal position, the diethynylphenyl part of the molecule bears significant amounts of spin density for all rotamers. In contrast the relative contribution of the two redox centres gets more and more shifted towards one metal moiety due to the decreased electronic coupling. The charge-localised local maximum in conformer space is less than 15 kJ mol−1 above the minima (Fig. 9).
 | ||
| Fig. 9 Computed potential energy surface of truncated 13-Me (BLYP35/COSMO(CH2Cl2) level).219Ω represents the dihedral angle for the redox centres and Θeff for the bridge rotation. Adapted with permission from M. Parthey, J. B. G. Gluyas, M. A. Fox, P. J. Low and M. Kaupp, Chem. – Eur. J., DOI: 10.1002/chem.201304947. Copyright @ 2014 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
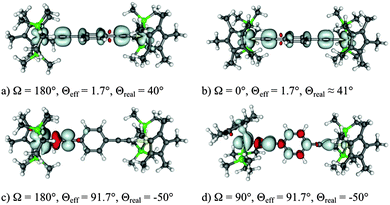 | ||
| Fig. 10 Spin density isosurface plots (±0.002 a.u.) of truncated 13-Me for different points on the potential energy surface (BLYP35/COSMO(CH2Cl2) level; cf.Fig. 9 for the potential energy surface).219 Adapted with permission from M. Parthey, J. B. G. Gluyas, M. A. Fox, P. J. Low and M. Kaupp, Chem. – Eur. J., DOI: 10.1002/chem.201304947. Copyright @ 2014 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
In contrast to 8, 13 exhibits a solvatochromic NIR shoulder, which gains intensity in the more polar acetone/CH2Cl2 (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture. This can be explained by comparing the BLYP35/COSMO(CH2Cl2) TDDFT results for the entire relaxed scan of 13-Me. A Boltzmann-weighted averaging of computed excitation energies and intensities in combination with Gaussian broadening gives good agreement with the measured band envelope. The shoulder arises from structures with partially localised class II character, while the main band gains intensity mainly from class III type conformers. Hence the shoulder exhibits the typical solvent dependence of class II systems, while the main feature stays nearly unchanged in different solvents.
1) mixture. This can be explained by comparing the BLYP35/COSMO(CH2Cl2) TDDFT results for the entire relaxed scan of 13-Me. A Boltzmann-weighted averaging of computed excitation energies and intensities in combination with Gaussian broadening gives good agreement with the measured band envelope. The shoulder arises from structures with partially localised class II character, while the main band gains intensity mainly from class III type conformers. Hence the shoulder exhibits the typical solvent dependence of class II systems, while the main feature stays nearly unchanged in different solvents.
Full optimisation of 13 provided three minima, trans-13, cis-13, and perp-13. Both trans-13 and cis-13 give rise to only one intense π–π* excitation corresponding to the main peak in the NIR spectrum (TDDFT-BLYP35/COSMO(CH2Cl2) level), whereas the partially localised (class II !) perp-13 conformer provides excitations that may be associated with the high-energy shoulder.219 This has been further confirmed by harmonic vibrational frequency analyses of the three conformers. While trans-13 and cis-13 account only for two closely spaced ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) stretching bands, due to its non-symmetrical localised structure perp-13 explains the occurrence of more strongly split ν(C
C) stretching bands, due to its non-symmetrical localised structure perp-13 explains the occurrence of more strongly split ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) bands, as well as of an aryl breathing mode.243
C) bands, as well as of an aryl breathing mode.243
A similar outcome was obtained for the related complex 14. An even shallower conformational potential energy landscape, and somewhat less pronounced charge localisation has been computed. Again the low-energy shoulder in the NIR spectrum arises from partially localised portions of the conformational space, and vibrational analysis of fully optimised structures accounts for the simultaneous observation of features in the IR spectra indicating both class II and class III behaviour.219
A similar relaxed scan for the classical Creutz–Taube ion 8 also revealed structures exhibiting both delocalised and localised spin densities.219 However, in this case only one conformational minimum has been found. Moreover, contributions from the partially localised regions of conformational space to the NIR band were found to be too small to affect a notable modification of the overall band shape.
6. Summary and outlook
Close to the borderline between class II and class III mixed-valence systems, the challenges for both experimental and computational classification are obviously much larger than for more clear-cut delocalised or localised situations. Quantum-chemical methods that allow us to move very close to the borderline and allow essentially quantitative predictions have emerged only very recently, and they clearly will require further refinement. Nevertheless, the examples discussed in this article demonstrate the remarkable potential of quantitative quantum-chemical treatments of MV systems.Due to their favourable scaling with system size, DFT approaches have become the most widely used methods also in this field. Yet, most standard functionals are biased towards a too delocalised description, whereas some other highly advertised functionals overshoot into the overlocalised direction. Judicious inclusion of exact exchange into the functional is mandatory if DFT is to be applied successfully in this field. Global hybrid functionals with about 30–45% exact-exchange admixture so far turned out to provide a reasonable compromise, when augmented by an appropriate treatment of (solvent or solid-state) environmental effects, as the latter often favour a more localised charge and spin distribution (see below). Then both DFT treatment of ground-state structures and properties and subsequent TDDFT calculations of excitation spectra provide valid connections to experimental observation and even predictive quality. Further improved functionals, either of the range-separated hybrid variety, local hybrid functionals with position-dependent exact-exchange admixture, or even more sophisticated constructions, may well provide further enhanced accuracy. Post-Hartree–Fock approaches are an obvious further direction to pursue in this field. However, many of the applications of such methods reviewed here suffered in particular from far too small single-particle basis sets. In view of the steep basis-set dependence of the post-HF methods, these lead to a dramatic underestimation of dynamical correlation effects. As the latter tend to favour more delocalised electronic structure, too small basis sets tend to bias the calculations towards a too localised description. Sometimes compensation with errors arising from neglect of environmental effects (which tends to favour too delocalised charge and spin) might then even provide the qualitatively right answer for the wrong reason. In many MV systems examined so far, the consideration of a multi-configurational character of the ground-state wave function was less important than expected and less important than the influence of the other factors discussed, in particular those due to the environment. It will thus be interesting to evaluate in more detail than done so far the usefulness and performance of predominantly single-reference approaches like coupled-cluster theory for MV systems. A caveat might apply to the symmetrical transition states for thermal electron transfer in class II systems, where symmetry breaking of the underlying UHF wave functions might present a more serious difficulty. Related problems have been identified for double-hybrid functionals or for certain density functionals with too excessive exact-exchange admixture.
The importance of environmental effects for charge localisation can hardly be overemphasised. As most spectroscopic experiments on MV systems tend to be performed in polar solvents, solvent models become central to a reasonable computational description, already during ground-state optimisation. Continuum solvent models appear to provide a straightforward first approximation for most aprotic solvents, provided that specific solvent effects like hydrogen bonding or the exchange of solvent molecules within the coordination sphere of a transition-metal centre are not of overriding importance. In many computational studies, the importance of non-equilibrium solvation effects during TDDFT computations of vertical excitations has been highlighted. We have also emphasised that a change of solvent polarity may change the character of an MV system fundamentally. This is known from spectroscopic experiments with different solvents, and it is supported strongly by the most recent computational studies. In fact, many class II MV systems with reasonably strong electronic coupling are probably localised only due to the solvent influence and might represent class III cases in the gas phase or in a non-polar environment. This should be kept in mind when assessing the suitability of a given electronic-structure method in correctly describing MV systems. In fact, hydrogen-bonding from protic solvents may localise even systems that are still delocalised in polar aprotic solvent environments. Continuum solvent models fail to cover hydrogen-bonding effects adequately and thus are not suitable to distinguish sufficiently between such situations. One may then have to augment the electronic-structure calculations by explicit solvent modelling, which usually involves time-consuming molecular dynamics or Monte-Carlo simulations, e.g. within a QM/MM framework. Very few successful applications of such approaches to MV systems have been reported so far, e.g. within the RISM-SCF framework. Interestingly, the much cheaper Direct-COSMO-RS approach also appears to provide a reasonably faithful description of the influence of protic solvents in this context. An area requiring substantially more efforts in the future is how to appropriately include counter-ion effects into such quantum-chemical treatments of electron transfer in MV systems.
Finally, this article has emphasised the importance of conformational motion for the coupling between the redox centres. While conformational effects on electron transfer have been appreciated for a long time, a quantitative computational procedure to model them had been lacking. Recent computational studies with appropriate methodology showed how different thermally accessible conformations may alter the spectral characteristics of organic or inorganic MV systems. In case of a series of organometallic diruthenium complexes, the computations demonstrated that conformational motion may even average to some extent localised and delocalised electronic and molecular structures, leading us beyond the traditionally more one-dimensional understanding of the Robin–Day classification scheme.
Acknowledgements
Special thanks are due to Manuel Renz, mixed-valence pioneer in the Kaupp group. Paul J. Low and Christoph Lambert are acknowledged for the excellent collaborations and discussions. The authors' own work in this field has been supported by DFG project KA1187/13-1, by the Berlin DFG cluster of excellence on “Unifying Concepts in Catalysis” (UniCat), and initially by DFG graduate research school GRK 1221 in Würzburg. MP is grateful to UniCat, the Berlin International Graduate School of Natural Sciences and Engineering (BIG-NSE), and the German Academic Exchange Service (DAAD) for funding.Notes and references
- C. Creutz and H. Taube, J. Am. Chem. Soc., 1969, 91, 3988 CrossRef CAS.
- C. Creutz and H. Taube, J. Am. Chem. Soc., 1973, 95, 1086 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver, J. I. Zink and J. P. Telo, J. Am. Chem. Soc., 2005, 127, 10611 CrossRef CAS PubMed.
- J. P. Telo, G. Grampp and M. Shohoji, Phys. Chem. Chem. Phys., 1999, 1, 99 RSC.
- J. P. Telo, A. S. Jalilov and S. F. Nelsen, J. Phys. Chem. A, 2011, 115, 3016 CrossRef CAS PubMed.
- A. Heckmann and C. Lambert, Angew. Chem., Int. Ed., 2012, 51, 326 CrossRef CAS PubMed.
- P. Day, N. S. Hush and R. J. H. Clark, Philos. Trans. R. Soc., A, 2008, 366, 5 CrossRef CAS PubMed.
- M. D. Ward and J. A. McCleverty, J. Chem. Soc., Dalton Trans., 2002, 275 RSC.
- W. Kaim, Inorg. Chem., 2011, 50, 9752 CrossRef CAS PubMed.
- O. F. Koentjoro, R. Rousseau and P. J. Low, Organometallics, 2001, 20, 4502 CrossRef CAS.
- P. A. Schauer and P. J. Low, Eur. J. Inorg. Chem., 2012, 390 CrossRef CAS.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 10, 247 CrossRef CAS.
- B. S. Brunschwig, C. Creutz and N. Sutin, Chem. Soc. Rev., 2002, 31, 168 RSC.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655 CrossRef CAS PubMed.
- B. J. Lear and M. H. Chisholm, Inorg. Chem., 2009, 48, 10954 CrossRef CAS PubMed.
- E. I. Solomon, X. Xie and A. Dey, Chem. Soc. Rev., 2008, 37, 613 RSC.
- V. K. K. Praneeth, M. R. Ringenberg and T. R. Ward, Angew. Chem., Int. Ed., 2012, 51, 10228 CrossRef CAS PubMed.
- S. Schinzel, J. Schraut, A. V. Arbuznikov, P. E. M. Siegbahn and M. Kaupp, Chem. – Eur. J., 2010, 16, 10424 CrossRef CAS PubMed.
- P. E. M. Siegbahn, Acc. Chem. Res., 2009, 42, 1871 CrossRef CAS PubMed.
- B. Kok, B. Forbush and M. McGloin, Photochem. Photobiol., 1970, 11, 457 CrossRef CAS.
- W. E. Antholine, D. H. W. Kastrau, G. C. M. Steffens, G. Buse, W. G. Zumft and P. M. H. Kroneck, Eur. J. Biochem., 1992, 209, 875 CrossRef CAS.
- P. M. H. Kroneck, W. E. Antholine, D. H. W. Kastrau, G. Buse, G. C. M. Steffens and W. G. Zumft, FEBS Lett., 1990, 268, 274 CrossRef CAS.
- J. A. Farrar, W. G. Zumft and A. J. Thomson, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 9891 CrossRef CAS.
- P. J. Low, Dalton Trans., 2005, 2821 RSC.
- J.-P. Launay, Chem. Soc. Rev., 2001, 30, 386 RSC.
- J.-P. Launay, Coord. Chem. Rev., 2013, 257, 1544 CrossRef CAS PubMed.
- F. Coat and C. Lapinte, Organometallics, 1996, 15, 477 CrossRef CAS.
- F. Paul and C. Lapinte, Coord. Chem. Rev., 1998, 178, 431 CrossRef.
- S. Ballmann, W. Hieringer, D. Secker, Q. L. Zheng, J. A. Gladysz, A. Gorling and H. B. Weber, ChemPhysChem, 2010, 11, 2256 CrossRef CAS PubMed.
- K. Venkatesan, O. Blacque and H. Berke, Dalton Trans., 2007, 1091 RSC.
- W. B. Davis, W. A. Svec, M. A. Ratner and M. R. Wasielewski, Nature, 1998, 396, 60 CrossRef CAS PubMed.
- M. Lieberman, S. Chellamma, B. Varughese, Y. L. Wang, C. Lent, G. H. Bernstein, G. Snider and F. C. Peiris, in Molecular Electronics Ii, ed. A. Aviram, M. Ratner and V. Mujica, New York Acad Sciences, New York, 2002, vol. 960, p. 225 Search PubMed.
- Y. Lu, R. Quardokus, C. S. Lent, F. Justaud, C. Lapinte and S. A. Kandel, J. Am. Chem. Soc., 2010, 132, 13519 CrossRef CAS PubMed.
- S. B. Braun-Sand and O. Wiest, J. Phys. Chem., 2003, 107, 285 CrossRef CAS.
- M. Lundstrom, Science, 2003, 299, 210 CrossRef CAS PubMed.
- J. D. Meindl, Q. Chen and J. A. Davis, Science, 2001, 293, 2044 CrossRef CAS PubMed.
- C. A. Bignozzi, R. Argazzi, R. Boaretto, E. Busatto, S. Carli, F. Ronconi and S. Caramori, Coord. Chem. Rev., 2013, 257, 1472 CrossRef CAS PubMed.
- A. Orbelli Biroli, F. Tessore, M. Pizzotti, C. Biaggi, R. Ugo, S. Caramori, A. Aliprandi, C. A. Bignozzi, F. De Angelis, G. Giorgi, E. Licandro and E. Longhi, J. Phys. Chem. C, 2011, 115, 23170 CAS.
- A. Yella, H. W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Gratzel, Science, 2011, 334, 629 CrossRef CAS PubMed.
- U. Furholz, S. Joss, H. B. Burgi and A. Ludi, Inorg. Chem., 1985, 24, 943 CrossRef.
- T. Storr, P. Verma, R. C. Pratt, E. C. Wasinger, Y. Shimazaki and T. D. P. Stack, J. Am. Chem. Soc., 2008, 130, 15448 CrossRef CAS PubMed.
- Y. Shimazaki, T. D. P. Stack and T. Storr, Inorg. Chem., 2009, 48, 8383 CrossRef CAS PubMed.
- L. Chiang, A. Kochem, O. Jarjayes, T. J. Dunn, H. Vezin, M. Sakaguchi, T. Ogura, M. Orio, Y. Shimazaki, F. Thomas and T. Storr, Chem. – Eur. J., 2012, 18, 14117 CrossRef CAS PubMed.
- Y. Shimazaki, T. Yajima, F. Tani, S. Karasawa, K. Fukui, Y. Naruta and O. Yamauchi, J. Am. Chem. Soc., 2007, 129, 2559 CrossRef CAS PubMed.
- J. T. Hupp and R. D. Williams, Acc. Chem. Res., 2001, 34, 808 CrossRef CAS PubMed.
- W. Kaim and A. Klein, Spectroelectrochemistry, RSC Publishing, Cambridge, 2008 Search PubMed.
- M. Brady, W. Q. Weng, Y. L. Zhou, J. W. Seyler, A. J. Amoroso, A. M. Arif, M. Bohme, G. Frenking and J. A. Gladysz, J. Am. Chem. Soc., 1997, 119, 775 CrossRef CAS.
- H. J. Jiao, K. Costuas, J. A. Gladysz, J. F. Halet, M. Guillemot, L. Toupet, F. Paul and C. Lapinte, J. Am. Chem. Soc., 2003, 125, 9511 CrossRef CAS PubMed.
- F. Paul, W. E. Meyer, L. Toupet, H. J. Jiao, J. A. Gladysz and C. Lapinte, J. Am. Chem. Soc., 2000, 122, 9405 CrossRef CAS.
- F. Coat, M. A. Guillevic, L. Toupet, F. Paul and C. Lapinte, Organometallics, 1997, 16, 5988 CrossRef CAS.
- V. Petrov, J. T. Hupp, C. Mottley and L. C. Mann, J. Am. Chem. Soc., 1994, 116, 2171 CrossRef CAS.
- T. Y. Dong, X. Q. Lai, Z. W. Lin and K. J. Lin, Angew. Chem., Int. Ed. Engl., 1997, 36, 2002 CrossRef CAS.
- M. E. Pandelia, D. Bykov, R. Izsak, P. Infossi, M. T. Giudici-Orticoni, E. Bill, F. Neese and W. Lubitz, Proc. Natl. Acad. Sci. U. S. A., 2012, 110, 483 CrossRef PubMed.
- F. Paul, F. Malvolti, G. da Costa, S. Le Stang, F. Justaud, G. Argouarch, A. Bondon, S. Sinbandhit, K. Costuas, L. Toupet and C. Lapinte, Organometallics, 2010, 29, 2491 CrossRef CAS.
- S. F. Nelsen, D. A. Trieber, J. J. Wolff, D. R. Powell and S. Rogers-Crowley, J. Am. Chem. Soc., 1997, 119, 6873 CrossRef CAS.
- K. Lancaster, S. A. Odom, S. C. Jones, S. Thayumanavan, S. R. Marder, J.-L. Bredas, V. Coropceanu and S. Barlow, J. Am. Chem. Soc., 2009, 131, 1717 CrossRef CAS PubMed.
- E. C. Fitzgerald, N. J. Brown, R. Edge, M. Helliwell, H. N. Roberts, F. Tuna, A. Beeby, D. Collison, P. J. Low and M. W. Whiteley, Organometallics, 2012, 31, 157 CrossRef CAS.
- N. S. Hush, Electrochim. Acta, 1968, 13, 1005 CrossRef CAS.
- N. S. Hush, Prog. Inorg. Chem., 1967, 8, 391 CrossRef CAS.
- N. S. Hush, Coord. Chem. Rev., 1985, 64, 135 CrossRef CAS.
- J. R. Reimers and N. S. Hush, Chem. Phys., 1989, 134, 323 CrossRef CAS.
- C. Creutz, M. D. Newton and N. Sutin, J. Photochem. Photobiol., A, 1994, 82, 47 CrossRef CAS.
- N. Sutin, Prog. Inorg. Chem., 1983, 30, 441 CrossRef CAS.
- R. J. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15 CrossRef CAS.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213 CrossRef CAS PubMed.
- M. D. Newton, in Electron Transfer-from Isolated Molecules to Biomolecules, Pt 1, ed. J. Jortner and M. Bixon, John Wiley & Sons Inc, New York, 1999, vol. 106, p. 303 Search PubMed.
- H. Bolvin, Inorg. Chem., 2007, 46, 417 CrossRef CAS PubMed.
- S. F. Nelsen, M. N. Weaver, A. E. Konradsson, J. P. Telo and T. Clark, J. Am. Chem. Soc., 2004, 126, 15431 CrossRef CAS PubMed.
- M. J. G. Peach, D. J. Tozer and N. C. Handy, Int. J. Quantum Chem., 2011, 111, 563 CrossRef CAS.
- J. Hardesty, S. K. Goh and D. S. Marynick, THEOCHEM, 2002, 588, 223 CrossRef CAS.
- D. Dehareng, G. Dive and A. Moradpour, Int. J. Quantum Chem., 2000, 76, 552 CrossRef CAS.
- W. Helal, S. Evangelisti, T. Leininger and D. Maynau, J. Comput. Chem., 2009, 30, 83 CrossRef CAS PubMed.
- E. Fernandez, L. Blancafort, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 2000, 122, 7528 CrossRef CAS.
- A. Broo and S. Larsson, Chem. Phys., 1992, 161, 363 CrossRef CAS.
- Y. Carissan, J.-L. Heully, F. Alary and J.-P. Daudey, Inorg. Chem., 2004, 43, 1411 CrossRef CAS PubMed.
- S. F. Nelsen and F. Blomgren, J. Org. Chem., 2001, 66, 6551 CrossRef CAS PubMed.
- S. F. Nelsen and M. D. Newton, J. Phys. Chem. A, 2000, 104, 10023 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver and J. P. Telo, J. Am. Chem. Soc., 2007, 129, 7036 CrossRef CAS PubMed.
- C. Lambert, S. Amthor and J. Schelter, J. Phys. Chem. A, 2004, 108, 6474 CrossRef CAS.
- S. Barlow, C. Risko, S. J. Chung, N. M. Tucker, V. Coropceanu, S. C. Jones, Z. Levi, J. L. Bredas and S. R. Marder, J. Am. Chem. Soc., 2005, 127, 16900 CrossRef CAS PubMed.
- S. Barlow, C. Risko, S. A. Odom, S. Zheng, V. Coropceanu, L. Beverina, J.-L. Brédas and S. R. Marder, J. Am. Chem. Soc., 2012, 134, 10146 CrossRef CAS PubMed.
- A. Broo and P. Lincoln, Inorg. Chem., 1997, 36, 2544 CrossRef CAS.
- O. V. Sizova, A. I. Panin, N. V. Ivanova and V. I. Baranovskii, J. Struct. Chem., 1997, 38, 366 CrossRef CAS.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 194112 CrossRef PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2007, 126, 104102 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Science, 2008, 321, 792 CrossRef CAS PubMed.
- E. R. Johnson, P. Mori-Sanchez, A. J. Cohen and W. T. Yang, J. Chem. Phys., 2008, 129, 204112 CrossRef PubMed.
- P. Mori-Sánchez, A. Cohen and W. Yang, Phys. Rev. Lett., 2009, 102, 066403 CrossRef.
- P. Mori-Sanchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2006, 125, 201102 CrossRef PubMed.
- Y. Zhang and W. Yang, J. Chem. Phys., 1998, 109, 2604 CrossRef CAS PubMed.
- X. Zheng, M. Liu, E. R. Johnson, J. Contreras-Garcia and W. Yang, J. Chem. Phys., 2012, 137, 214106 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- P. J. Stephens, J. F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- M. Lundberg and P. E. M. Siegbahn, J. Chem. Phys., 2005, 122, 224103 CrossRef PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321 CrossRef CAS PubMed.
- Q. Wu and T. Van Voorhis, J. Phys. Chem. A, 2006, 110, 9212 CrossRef CAS PubMed.
- Q. Wu and T. Van Voorhis, J. Chem. Phys., 2006, 125, 164105 CrossRef PubMed.
- T. Ogawa, M. Sumita, Y. Shimodo and K. Morihashi, Chem. Phys. Lett., 2011, 511, 219 CrossRef CAS PubMed.
- R. C. Quardokus, Y. Lu, N. A. Wasio, C. S. Lent, F. Justaud, C. Lapinte and S. A. Kandel, J. Am. Chem. Soc., 2012, 134, 1710 CrossRef CAS PubMed.
- F. Ding, H. Wang, Q. Wu, T. Van Voorhis, S. Chen and J. P. Konopelski, J. Phys. Chem. A, 2010, 114, 6039 CrossRef CAS PubMed.
- A. Kubas, F. Hoffmann, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, J. Chem. Phys., 2014, 140, 104105 CrossRef PubMed.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943 CrossRef CAS PubMed.
- D. J. Tozer, J. Chem. Phys., 2003, 119, 12697 CrossRef CAS PubMed.
- O. Gritsenko and E. J. Baerends, J. Chem. Phys., 2004, 121, 655 CrossRef CAS PubMed.
- N. T. Maitra, J. Chem. Phys., 2005, 122, 234104 CrossRef PubMed.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- J. Baker, A. Scheiner and J. Andzelm, Chem. Phys. Lett., 1993, 216, 380 CrossRef CAS.
- M. Munzarova and M. Kaupp, J. Phys. Chem. A, 1999, 103, 9966 CrossRef CAS.
- M. L. Munzarova, P. Kubacek and M. Kaupp, J. Am. Chem. Soc., 2000, 122, 11900 CrossRef CAS.
- C. Remenyi and M. Kaupp, J. Am. Chem. Soc., 2005, 127, 11399 CrossRef CAS PubMed.
- C. Remenyi, R. Reviakine and M. Kaupp, J. Phys. Chem. B, 2007, 111, 8290 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun and G. b. I. Csonka, J. Chem. Theory Comput., 2009, 5, 902 CrossRef CAS.
- A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 2007, 126, 214104 CrossRef PubMed.
- A. S. Menon and L. Radom, J. Phys. Chem. A, 2008, 112, 13225 CrossRef CAS PubMed.
- C. R. Jacob and M. Reiher, Int. J. Quantum Chem., 2012, 112, 3661 CrossRef CAS.
- J. Wang, A. D. Becke and V. H. Smith, Jr., J. Chem. Phys., 1995, 102, 3477 CrossRef CAS PubMed.
- A. Ipatov, F. Cordova, L. J. Doriol and M. E. Casida, THEOCHEM, 2009, 914, 60 CrossRef CAS PubMed.
- S. Barlow, C. Risko, V. Coropceanu, N. M. Tucker, S. C. Jones, Z. Levi, V. N. Khrustalev, M. Y. Antipin, T. L. Kinnibrugh, T. Timofeeva, S. R. Marder and J.-L. Brédas, Chem. Commun., 2005, 764 RSC.
- M. Renz, K. Theilacker, C. Lambert and M. Kaupp, J. Am. Chem. Soc., 2009, 131, 16292 CrossRef CAS PubMed.
- M. Kaupp, M. Renz, M. Parthey, M. Stolte, F. Würthner and C. Lambert, Phys. Chem. Chem. Phys., 2011, 13, 16973 RSC.
- A. Pron, R. R. Reghu, R. Rybakiewicz, H. Cybulski, D. Djurado, J. V. Grazulevicius, M. Zagorska, I. Kulszewicz-Bajer and J.-M. Verilhac, J. Phys. Chem. C, 2011, 115, 15008 CAS.
- F. Eckert and A. Klamt, AIChE J., 2002, 48, 369 CrossRef CAS.
- N. Yoshida, T. Ishida and F. Hirata, J. Phys. Chem. B, 2008, 112, 433 CrossRef CAS PubMed.
- S. Aono, M. Nakagaki, T. Kurahashi, H. Fujii and S. Sakaki, J. Chem. Theory Comput., 2014, 10, 1062 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- A. Pedone, M. Biczysko and V. Barone, ChemPhysChem, 2010, 11, 1812 CAS.
- H. Stoll and A. Savin, in Density Functional Methods in Physics, ed. R. M. Dreizler and J. da Providencia, Plenum, New York, 1985, p. 177 Search PubMed.
- A. Savin, in Recent Developments and Applications of Modern Density Functional Theory, ed. J. M. Seminario, Elsevier, Amsterdam, 1996 Search PubMed.
- T. Leininger, H. Stoll, H. J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 CrossRef CAS PubMed.
- T. M. Henderson, B. G. Janesko and G. E. Scuseria, J. Phys. Chem. A, 2008, 112, 12530 CrossRef CAS PubMed.
- T. M. Henderson, B. G. Janesko and G. E. Scuseria, J. Chem. Phys., 2008, 128, 194105 CrossRef PubMed.
- T. M. Henderson, A. F. Izmaylov, G. E. Scuseria and A. Savin, J. Chem. Phys., 2007, 127, 221103 CrossRef PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS PubMed.
- I. C. Gerber and J. G. Angyan, Chem. Phys. Lett., 2005, 415, 100 CrossRef CAS PubMed.
- M. J. G. Peach, T. Helgaker, P. Salek, T. W. Keal, O. B. Lutnaes, D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2006, 8, 558 RSC.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- A. V. Arbuznikov and M. Kaupp, Int. J. Quantum Chem., 2011, 111, 2625 CrossRef CAS.
- H. Bahmann, A. Rodenberg, A. V. Arbuznikov and M. Kaupp, J. Chem. Phys., 2007, 126, 011103 CrossRef PubMed.
- M. Kaupp, H. Bahmann and A. V. Arbuznikov, J. Chem. Phys., 2007, 127, 194102 CrossRef PubMed.
- A. V. Arbuznikov, H. Bahmann and M. Kaupp, J. Phys. Chem. A, 2009, 113, 11898 CrossRef CAS PubMed.
- M. Kaupp, A. Arbuznikov and H. Bahmann, Z. Phys. Chem., 2010, 224, 545 CrossRef CAS.
- J. Jaramillo, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 1068 CrossRef CAS PubMed.
- J. Perdew, V. Staroverov, J. Tao and G. Scuseria, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 052513 CrossRef.
- B. G. Janesko and G. E. Scuseria, J. Chem. Phys., 2007, 127, 164117 CrossRef PubMed.
- B. G. Janesko and G. E. Scuseria, J. Chem. Phys., 2008, 128, 084111 CrossRef PubMed.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1997, 274, 242 CrossRef CAS.
- M. Renz, M. Kess, M. Diedenhofen, A. Klamt and M. Kaupp, J. Chem. Theory Comput., 2012, 8, 4189 CrossRef CAS.
- M. Renz and M. Kaupp, J. Phys. Chem. A, 2012, 116, 10629 CrossRef CAS PubMed.
- A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405 CrossRef CAS PubMed.
- S. F. Völker, M. Renz, M. Kaupp and C. Lambert, Chem. – Eur. J., 2011, 17, 14147 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- C. Sutton, T. Körzdörfer, V. Coropceanu and J.-L. Brédas, J. Phys. Chem. C, 2014, 118, 3925 CAS.
- A. Karolewski, L. Kronik and S. Kümmel, J. Chem. Phys., 2013, 138, 204115 CrossRef PubMed.
- M. Parthey, J. B. G. Gluyas, P. A. Schauer, D. S. Yufit, J. A. K. Howard, M. Kaupp and P. J. Low, Chem. – Eur. J., 2013, 19, 9780 CrossRef CAS PubMed.
- M. Parthey, K. B. Vincent, M. Renz, P. A. Schauer, D. S. Yufit, J. A. K. Howard, M. Kaupp and P. J. Low, Inorg. Chem., 2014, 53, 1544 CrossRef CAS PubMed.
- K. B. Vincent, Q. Zeng, M. Parthey, D. S. Yufit, J. A. K. Howard, F. Hartl, M. Kaupp and P. J. Low, Organometallics, 2013, 32, 6022 CrossRef CAS.
- M. Malagoli and J. L. Bredas, Chem. Phys. Lett., 2000, 327, 13 CrossRef CAS.
- J. Bonvoisin, J. P. Launay, W. Verbouwe, M. Van der Auweraer and F. C. De Schryver, J. Phys. Chem., 1996, 100, 17079 CrossRef CAS.
- V. Coropceanu, M. Malagoli, J. M. Andre and J. L. Bredas, J. Chem. Phys., 2001, 115, 10409 CrossRef CAS PubMed.
- V. Coropceanu, M. Malagoli, J. M. Andre and J. L. Bredas, J. Am. Chem. Soc., 2002, 124, 10519 CrossRef CAS PubMed.
- V. Coropceanu, C. Lambert, G. Nöll and J. L. Bredas, Chem. Phys. Lett., 2003, 373, 153 CrossRef CAS.
- V. Coropceanu, N. E. Gruhn, S. Barlow, C. Lambert, J. C. Durivage, T. G. Bill, G. Noll, S. R. Marder and J. L. Bredas, J. Am. Chem. Soc., 2004, 126, 2727 CrossRef CAS PubMed.
- C. Lambert and G. Nöll, J. Am. Chem. Soc., 1999, 121, 8434 CrossRef CAS.
- C. Lambert and G. Nöll, Angew. Chem., Int. Ed., 1998, 37, 2107 CrossRef CAS.
- D. R. Kattnig, B. Mladenova, G. Grampp, C. Kaiser, A. Heckmann and C. Lambert, J. Phys. Chem., 2009, 113, 2983 CAS.
- P. J. Low, M. A. J. Paterson, H. Puschmann, A. E. Goeta, J. A. K. Howard, C. Lambert, J. C. Cherryman, D. R. Tackley, S. Leeming and B. Brown, Chem. – Eur. J., 2004, 10, 83 CrossRef CAS PubMed.
- Y. Hirao, M. Urabe, A. Ito and K. Tanaka, Angew. Chem., Int. Ed., 2007, 46, 3300 CrossRef CAS PubMed.
- N. Utz and T. Koslowski, Chem. Phys., 2002, 282, 389 CrossRef CAS.
- B. C. De Simone, A. D. Quartarolo, S. Cospito, L. Veltri, G. Chidichimo and N. Russo, Theor. Chem. Acc., 2012, 131, 1225 CrossRef PubMed.
- C. Liu, K.-C. Tang, H. Zhang, H.-A. Pan, J. Hua, B. Li and P.-T. Chou, J. Phys. Chem. A, 2012, 116, 12339 CrossRef CAS PubMed.
- E. Göransson, R. Emanuelsson, K. Jorner, T. F. Markle, L. Hammarström and H. Ottosson, Chem. Sci., 2013, 4, 3522 RSC.
- S. C. Jones, V. Coropceanu, S. Barlow, T. Kinnibrugh, T. Timofeeva, J.-L. Bredas and S. R. Marder, J. Am. Chem. Soc., 2004, 126, 11782 CrossRef CAS PubMed.
- R. J. Bushby, C. Kilner, N. Taylor and R. A. Williams, Polyhedron, 2008, 27, 383 CrossRef CAS PubMed.
- H.-J. Nie, X. Chen, C.-J. Yao, Y.-W. Zhong, G. R. Hutchison and J. Yao, Chem. – Eur. J., 2012, 18, 14497 CrossRef CAS PubMed.
- C. J. Yao, J. N. A. Yao and Y. W. Zhong, Inorg. Chem., 2011, 50, 6847 CrossRef CAS PubMed.
- Y.-M. Zhang, S.-H. Wu, C.-J. Yao, H.-J. Nie and Y.-W. Zhong, Inorg. Chem., 2012, 51, 11387 CrossRef CAS PubMed.
- B. J. Liddle, S. Wanniarachchi, J. S. Hewage, S. V. Lindeman, B. Bennett and J. R. Gardinier, Inorg. Chem., 2012, 51, 12720 CrossRef CAS PubMed.
- T. J. Dunn, L. Chiang, C. F. Ramogida, K. Hazin, M. I. Webb, M. J. Katz and T. Storr, Chem. – Eur. J., 2013, 19, 9606 CrossRef CAS PubMed.
- T. Storr, E. C. Wasinger, R. C. Pratt and T. D. P. Stack, Angew. Chem., Int. Ed., 2007, 46, 5198 CrossRef CAS PubMed.
- A. H. Maki and D. H. Geske, J. Chem. Phys., 1960, 33, 825 CrossRef CAS PubMed.
- R. L. Ward, J. Am. Chem. Soc., 1961, 83, 1296 CrossRef CAS.
- R. L. Ward, J. Chem. Phys., 1960, 32, 410 CrossRef CAS PubMed.
- J. H. Freed and G. K. Fraenkel, J. Chem. Phys., 1963, 39, 326 CrossRef CAS PubMed.
- J. H. Freed and G. K. Fraenkel, J. Chem. Phys., 1964, 40, 1815 CrossRef CAS PubMed.
- J. H. Freed and G. K. Fraenkel, J. Chem. Phys., 1964, 41, 699 CrossRef CAS PubMed.
- J. H. Freed, P. H. Rieger and G. K. Fraenkel, J. Chem. Phys., 1962, 37, 1881 CrossRef CAS PubMed.
- J. Gendell, J. H. Freed and G. K. Fraenkel, J. Chem. Phys., 1962, 37, 2832 CrossRef CAS PubMed.
- J. E. Harriman and A. H. Maki, J. Chem. Phys., 1963, 39, 778 CrossRef CAS PubMed.
- W. E. Griffiths, C. J. W. Gutch, G. F. Longster, J. Myatt and P. F. Todd, J. Chem. Soc. B, 1968, 785 RSC.
- C. J. W. Gutch and W. A. Waters, Chem. Commun., 1966, 39 RSC.
- C. J. W. Gutch, W. A. Waters and M. C. R. Symons, J. Chem. Soc. B, 1970, 1261 RSC.
- S. F. Nelsen, A. E. Konradsson, M. N. Weaver and J. P. Telo, J. Am. Chem. Soc., 2003, 125, 12493 CrossRef CAS PubMed.
- M. N. Mikhailov, A. S. Mendkovich, M. B. Kuzminsky and A. I. Rusakov, THEOCHEM, 2007, 847, 103 CrossRef CAS PubMed.
- L. S. Hernandez-Munoz, F. J. Gonzalez, I. Gonzalez, M. O. F. Goulart, F. C. d. Abreu, A. S. Ribeiro, R. T. Ribeiro, R. L. Longo, M. Navarro and C. Frontana, Electrochim. Acta, 2010, 55, 8325 CrossRef CAS PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Phys., 2005, 123, 161103 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364 CrossRef.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397 RSC.
- B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811 CrossRef CAS.
- M. A. Fox, R. L. Roberts, T. E. Baines, B. Le Guennic, J.-F. Halet, F. Hartl, D. S. Yufit, D. Albesa-Jové, J. A. K. Howard and P. J. Low, J. Am. Chem. Soc., 2008, 130, 3566 CrossRef CAS PubMed.
- M. A. Fox, J. D. Farmer, R. L. Roberts, M. G. Humphrey and P. J. Low, Organometallics, 2009, 28, 5266 CrossRef CAS.
- S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235 CrossRef CAS PubMed.
- N. Gautier, F. Dumur, V. Lloveras, J. Vidal-Gancedo, J. Veciana, C. Rovira and P. Hudhomme, Angew. Chem., Int. Ed., 2003, 42, 2765 CrossRef CAS PubMed.
- J. Calbo, J. Arago and E. Ortí, Theor. Chem. Acc., 2013, 132, 1 CrossRef CAS PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- W. Kaim, A. Klein and M. Glockle, Acc. Chem. Res., 2000, 33, 755 CrossRef CAS PubMed.
- M. J. Ondrechen, D. E. Ellis and M. A. Ratner, Chem. Phys. Lett., 1984, 109, 50 CrossRef CAS.
- M. J. Ondrechen, J. Ko and L. T. Zhang, J. Am. Chem. Soc., 1987, 109, 1672 CrossRef CAS.
- L. T. Zhang, J. Ko and M. J. Ondrechen, J. Am. Chem. Soc., 1987, 109, 1666 CrossRef CAS.
- Z. Chen, J. Bian, L. Zhang and S. Li, J. Chem. Phys., 1999, 111, 10926 CrossRef CAS PubMed.
- A. Bencini, I. Ciofini, C. A. Daul and A. Ferretti, J. Am. Chem. Soc., 1999, 121, 11418 CrossRef CAS.
- J. R. Reimers, Z. L. Cai and N. S. Hush, Chem. Phys., 2005, 319, 39 CrossRef CAS PubMed.
- T. Todorova and B. Delley, Inorg. Chem., 2008, 47, 11269 CrossRef CAS PubMed.
- M. Parthey, J. B. G. Gluyas, M. A. Fox, P. J. Low and M. Kaupp, Chem. – Eur. J., 2014 DOI:10.1002/chem.201304947.
- J. R. Reimers, B. B. Wallace and N. S. Hush, Philos. Trans. R. Soc., A, 2008, 366, 15 CrossRef CAS PubMed.
- B. E. Van Kuiken, M. Valiev, S. L. Daifuku, C. Bannan, M. L. Strader, H. N. Cho, N. Huse, R. W. Schoenlein, N. Govind and M. Khalil, J. Phys. Chem. A, 2013, 117, 4444 CrossRef CAS PubMed.
- I. Kondov, V. Vallet, H. B. Wang and M. Thoss, J. Phys. Chem. A, 2008, 112, 5467 CrossRef CAS PubMed.
- M. I. Bruce and P. J. Low, in Advances in Organometallic Chemistry, Vol. 50, ed. R. West and A. F. Hill, Elsevier Academic Press Inc, San Diego, 2004, vol. 50, p. 179 Search PubMed.
- J.-F. Halet and C. Lapinte, Coord. Chem. Rev., 2013, 257, 1584 CrossRef CAS PubMed.
- W. A. Chalifoux and R. R. Tykwinski, Nat. Chem., 2010, 2, 967 CrossRef CAS PubMed.
- P. Aguirre-Etcheverry and D. O'Hare, Chem. Rev., 2010, 110, 4839 CrossRef CAS PubMed.
- K. Costuas and S. Rigaut, Dalton Trans., 2011, 40, 5643 RSC.
- P. J. Low and M. I. Bruce, Adv. Organomet. Chem., Academic Press, 2001, vol. 48, p. 71 Search PubMed.
- A. Ceccon, S. Santi, L. Orian and A. Bisello, Coord. Chem. Rev., 2004, 248, 683 CrossRef CAS PubMed.
- R. C. Quardokus, N. A. Wasio, R. P. Forrest, C. S. Lent, S. A. Corcelli, J. A. Christie, K. W. Henderson and S. A. Kandel, Phys. Chem. Chem. Phys., 2013, 15, 6973 RSC.
- D. Miesel, A. Hildebrandt, M. Korb, P. J. Low and H. Lang, Organometallics, 2013, 32, 2993 CrossRef CAS.
- D. L. Lichtenberger, H.-J. Fan and N. E. Gruhn, J. Organomet. Chem., 2003, 666, 75 CrossRef CAS.
- R. G. Hadt and V. N. Nemykin, Inorg. Chem., 2009, 48, 3982 CrossRef CAS PubMed.
- M. I. Bruce, B. G. Ellis, P. J. Low, B. W. Skelton and A. H. White, Organometallics, 2003, 22, 3184 CrossRef CAS.
- M. I. Bruce, P. J. Low, K. Costuas, J.-F. Halet, S. P. Best and G. A. Heath, J. Am. Chem. Soc., 2000, 122, 1949 CrossRef CAS.
- M. I. Bruce, M. L. Cole, K. Costuas, B. G. Ellis, K. A. Kramarczuk, C. Lapinte, B. K. Nicholson, G. J. Perkins, B. W. Skelton, A. H. White and N. N. Zaitseva, Z. Anorg. Allg. Chem., 2013, 639, 2216 CrossRef CAS.
- M. I. Bruce, K. Costuas, T. Davin, B. G. Ellis, J.-F. Halet, C. Lapinte, P. J. Low, M. E. Smith, B. W. Skelton, L. Toupet and A. H. White, Organometallics, 2005, 24, 3864 CrossRef CAS.
- M. I. Bruce, K. Costuas, T. Davin, J.-F. Halet, K. A. Kramarczuk, P. J. Low, B. K. Nicholson, G. J. Perkins, R. L. Roberts, B. W. Skelton, M. E. Smith and A. H. White, Dalton Trans., 2007, 5387 RSC.
- M. I. Bruce, K. Costuas, B. G. Ellis, J.-F. Halet, P. J. Low, B. Moubaraki, K. S. Murray, N. Ouddai, G. J. Perkins, B. W. Skelton and A. H. White, Organometallics, 2007, 26, 3735 CrossRef CAS.
- N. Le Narvor, L. Toupet and C. Lapinte, J. Am. Chem. Soc., 1995, 117, 7129 CrossRef CAS.
- S. Kheradmandan, K. Heinze, H. W. Schmalle and H. Berke, Angew. Chem., Int. Ed., 1999, 38, 2270 CrossRef CAS.
- E. C. Fitzgerald, A. Ladjarafi, N. J. Brown, D. Collison, K. Costuas, R. Edge, J.-F. o. Halet, F. d. r. Justaud, P. J. Low, H. n. Meghezzi, T. Roisnel, M. W. Whiteley and C. Lapinte, Organometallics, 2011, 30, 4180 CrossRef CAS.
- M. A. Fox, B. Le Guennic, R. L. Roberts, D. A. Brue, D. S. Yufit, J. A. K. Howard, G. Manca, J.-F. Halet, F. Hartl and P. J. Low, J. Am. Chem. Soc., 2011, 133, 18433 CrossRef CAS PubMed.
- F. De Montigny, G. Argouarch, K. Costuas, J.-F. Halet, T. Roisnel, L. Toupet and C. Lapinte, Organometallics, 2005, 24, 4558 CrossRef CAS.
- S. I. Ghazala, F. Paul, L. Toupet, T. Roisnel, P. Hapiot and C. Lapinte, J. Am. Chem. Soc., 2006, 128, 2463 CrossRef CAS PubMed.
- N. Le Narvor and C. Lapinte, Organometallics, 1995, 14, 634 CrossRef CAS.
- Y. Tanaka, J. A. Shaw-Taberlet, F. d. r. Justaud, O. Cador, T. Roisnel, M. Akita, J.-R. Hamon and C. Lapinte, Organometallics, 2009, 28, 4656 CrossRef CAS.
- T. Weyland, K. Costuas, A. Mari, J.-F. Halet and C. Lapinte, Organometallics, 1998, 17, 5569 CrossRef CAS.
- T. Weyland, K. Costuas, L. Toupet, J.-F. Halet and C. Lapinte, Organometallics, 2000, 19, 4228 CrossRef CAS.
- T. Weyland, C. Lapinte, G. Frapper, M. J. Calhorda, J. F. Halet and L. Toupet, Organometallics, 1997, 16, 2024 CrossRef CAS.
- T. Weyland, I. Ledoux, S. Brasselet, J. Zyss and C. Lapinte, Organometallics, 2000, 19, 5235 CrossRef CAS.
- Q. L. Zheng, J. C. Bohling, T. B. Peters, A. C. Frisch, F. Hampel and J. A. Gladysz, Chem. – Eur. J., 2006, 12, 6486 CrossRef CAS PubMed.
- P. Belanzoni, N. Re, A. Sgamellotti and C. Floriani, J. Chem. Soc., Dalton Trans., 1998, 1825 RSC.
- F. J. Fernandez, K. Venkatesan, O. Blacque, M. Alfonso, H. W. Schmalle and H. Berke, Chem. – Eur. J., 2003, 9, 6192 CrossRef CAS PubMed.
- C. Herrmann, J. Neugebauer, J. A. Gladysz and M. Reiher, Inorg. Chem., 2005, 44, 6174 CrossRef CAS PubMed.
- N. J. Brown, H. N. Lancashire, M. A. Fox, D. Collison, R. Edge, D. S. Yufit, J. A. K. Howard, M. W. Whiteley and P. J. Low, Organometallics, 2011, 30, 884 CrossRef CAS.
- P. J. Low, Coord. Chem. Rev., 2013, 257, 1507 CrossRef CAS PubMed.
- N. A. Wasio, R. C. Quardokus, R. P. Forrest, S. A. Corcelli, Y. Lu, C. S. Lent, F. Justaud, C. Lapinte and S. A. Kandel, J. Phys. Chem. C, 2012, 116, 25486 CAS.
- S. Guo and S. A. Kandel, J. Phys. Chem. Lett., 2010, 1, 420 CrossRef CAS.
- S. Ibn Ghazala, F. Paul, L. Toupet, T. Roisnel, P. Hapiot and C. Lapinte, J. Am. Chem. Soc., 2006, 128, 2463 CrossRef PubMed.
- K. Costuas, O. Cador, F. Justaud, S. Le Stang, F. Paul, A. Monari, S. Evangelisti, L. Toupet, C. Lapinte and J.-F. Halet, Inorg. Chem., 2011, 50, 12601 CrossRef CAS PubMed.
- B. S. Brunschwig and N. Sutin, J. Am. Chem. Soc., 1989, 111, 7454 CrossRef CAS.
- R. J. Geue, A. J. Hendry and A. M. Sargeson, J. Chem. Soc., Chem. Commun., 1989, 1646 RSC.
- S. Woitellier, J. P. Launay and C. W. Spangler, Inorg. Chem., 1989, 28, 758 CrossRef CAS.
- J. P. Launay, M. Tourrelpagis, J. F. Lipskier, V. Marvaud and C. Joachim, Inorg. Chem., 1991, 30, 1033 CrossRef CAS.
- A. Harriman, Mol. Cryst. Liq. Cryst., 1991, 194, 103 CrossRef CAS.
- A. C. Benniston, V. Goulle, A. Harriman, J.-M. Lehn and B. Marczinke, J. Phys. Chem., 1994, 98, 7798 CrossRef CAS.
- A. C. Benniston and A. Harriman, Chem. Soc. Rev., 2006, 35, 169 RSC.
- S. V. Rosokha, D. L. Sun and J. K. Kochi, J. Phys. Chem. A, 2002, 106, 2283 CrossRef CAS.
- D. Hanss and O. S. Wenger, Eur. J. Inorg. Chem., 2009, 3778 CrossRef CAS.
- D. Hanss, M. E. Walther and O. S. Wenger, Coord. Chem. Rev., 2010, 254, 2584 CrossRef CAS PubMed.
- D. M. D'Alessandro and F. R. Keene, Chem. Phys., 2006, 324, 8 CrossRef CAS PubMed.
- D. M. D'Alessandro and F. R. Keene, Pure Appl. Chem., 2008, 80, 1 CrossRef CAS.
- D. M. D'Alessandro, F. R. Keene, S. D. Bergman and M. Kol, Dalton Trans., 2005, 332 RSC.
- P. P. Romanczyk, K. Noga, A. J. Wlodarczyk, W. Nitek and E. Broclawik, Inorg. Chem., 2010, 49, 7676 CrossRef CAS PubMed.
- C. Olivier, K. Costuas, S. Choua, V. Maurel, P. Turek, J. Y. Saillard, D. Touchard and S. Rigaut, J. Am. Chem. Soc., 2010, 132, 5638 CrossRef CAS PubMed.
- M. H. Chisholm, F. Feil, C. M. Hadad and N. J. Patmore, J. Am. Chem. Soc., 2005, 127, 18150 CrossRef CAS PubMed.
- P. Wiggins, J. A. G. Williams and D. J. Tozer, J. Chem. Phys., 2009, 131, 091101 CrossRef PubMed.
- D. Rappoport and F. Furche, J. Am. Chem. Soc., 2004, 126, 1277 CrossRef CAS PubMed.
- A. Köhn and C. Hattig, J. Am. Chem. Soc., 2004, 126, 7399 CrossRef PubMed.
- M. A. Fox, R. L. Roberts, W. M. Khairul, F. Hartl and P. J. Low, J. Organomet. Chem., 2007, 692, 3277 CrossRef CAS PubMed.
- F. Gendron, A. Burgun, B. W. Skelton, A. H. White, T. Roisnel, M. I. Bruce, J.-F. Halet, C. Lapinte and K. Costuas, Organometallics, 2012, 31, 6796 CrossRef CAS.
- M. H. Chisholm, Coord. Chem. Rev., 2013, 257, 1576 CrossRef CAS PubMed.
- O. Lavastre, J. Plass, P. Bachmann, S. Guesmi, C. Moinet and P. H. Dixneuf, Organometallics, 1997, 16, 184 CrossRef CAS.
- A. Klein, O. Lavastre and J. Fiedler, Organometallics, 2006, 25, 635 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |