Open Access Article
Open Access ArticleSupramolecular dynamics
Cornelia
Bohne
Department of Chemistry, University of Victoria, PO Box 3065, Victoria, BC, Canada V8W 3V6. E-mail: cornelia.bohne@gmail.com; Fax: +1-250-721-7147; Tel: +1-250-721-7151
First published on 27th November 2013
Abstract
Supramolecular systems are reversible and their dynamics is an inherent and essential property. The conceptual framework for kinetic studies of these systems is presented with a focus on the considerations required for experimental design. Selected examples for guest binding to cyclodextrins, cucurbit[n]urils, DNA, serum albumins and bile salt aggregates are presented that describe the type of information obtained from dynamic studies that are not available from thermodynamic investigations.
Key learning points– Dynamics/reversibility is an inherent property of supramolecular systems– Association and dissociation processes are coupled – Competitive pathways are used to gain kinetic information – Dynamic characterization leads to different and complementary information obtained from thermodynamics – Kinetics can be more sensitive to changes to a system than it's thermodynamics |
Introduction
Supramolecular systems occupy the space between the molecular and the nano to meso-scale worlds. Supramolecular systems are also positioned between molecular and biological systems with respect to size and complexity. Therefore, supramolecular systems provide a bottom up approach to achieve functional materials and mimetic systems for biology.Supermolecules are formed from molecular building blocks held together by interactions that can be specific and directional, such as hydrogen bonds and π-stacking, or non-directional, such as the hydrophobic effect or electrostatic interactions.1,2 Reversibility is a key distinguishing feature between supramolecular systems and molecules. This feature is tied to human perception since most molecules do not change over the time frame of interest to humans, while supramolecular systems do. As a consequence the conceptual framework to characterize and describe molecules and supramolecular systems are different in important aspects.
Molecules are the same with respect to their composition irrespective of the state of matter they are in. An unreactive molecule does not change if found as a solid or when dissolved in a liquid. In contrast, the environment in which building blocks are placed can be determinant on the existence of a supramolecular system. A system formed by hydrogen bonds may exist in non-polar solvents but may not form at all in water when hydrogen bonding of the building blocks with the solvent predominates.
In the case of molecules and supramolecular systems, chemists focus on connectivity, structure and function (Fig. 1). The key difference is that in the case of molecules the focus is on one molecule, while in the case of supramolecular systems the focus is on the system as a whole. The realization of this key conceptual difference has led to the development of the field of systems chemistry.3–5
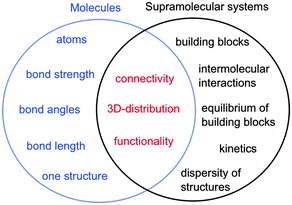 | ||
| Fig. 1 Parameters of molecules (left in blue) and supramolecular systems (right in black) that define core properties (centre in red). | ||
Molecules are described by the connectivity between atoms that lead to three-dimensional structures and reactive moieties, frequently systematized as functional groups. Supramolecular systems have a higher order of organization where the connectivity is established by intermolecular interactions between molecular blocks. These systems frequently have several different structures present simultaneously and the systems are dynamic. Functions achieved by supramolecular systems are an expression of the collective system and these functions are frequently different from the sum of functions achieved by the individual building blocks. Therefore, traditional characterization methods used by chemists, such as the determination of the structure of one supermolecule at a time is not sufficient to characterize supramolecular systems. Thermodynamic studies are required to determine the composition of the system, while kinetic studies are essential because supramolecular systems are dynamic and the dynamics are frequently key to the properties of the systems, such as in the case of catalysis, guest release or transport.
The objective of this article is to address how kinetic experiments are employed to gain mechanistic information that cannot be uncovered from thermodynamic studies when the system is at equilibrium. This article will focus on host–guest systems with defined stoichiometries. The concepts for the kinetic experiments will be presented with examples on how kinetic information addresses specific mechanistic questions. Detailed descriptions on the techniques used and surveys of their applications to specific supramolecular systems can be found in previous reports.6–8
Relationship between thermodynamics and kinetics
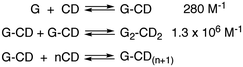
In molecular chemistry the relative stability of reactants and products for a series of reactions is frequently linked to the rate of reactions. This line of arguing has underlying concepts, such as the Hammond postulate, and is based on the assumption that reactions being compared are “similar”. This similarity is related to the pathway of the reaction and the structure of the transition state, which ultimately defines the rate of the reaction. In other words, the mechanism of the reaction has to be the same for the reactions being compared. This type of argument seems to imply that if the thermodynamics of a reaction is known the kinetics can be predicted. These concepts are very useful when discussing molecular systems because of the large body of mechanistic information available. Chemists have a good perception on which bonds in a molecule are the weakest ones or the different types of reactions that functional groups can be involved in. However, the underlying mechanistic understanding of supramolecular systems is not sufficiently complete to permit extrapolating trends on the dynamics of the system from thermodynamic information as shown in the illustrative example that follows.Cyclodextrins are cyclic hosts systems that can include hydrophobic guests, such as 1 and 2 (Scheme 1).9 A 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex is formed by the inclusion of the phenol moiety into α-cyclodextrin. Equilibrium constants (K11) were determined from binding isotherms constructed from changes in the absorption of 1 or 2 when complexed to α-cyclodextrin (Table 1). An increase in the size of the guest, by inclusion of an ethyl group on the phenol, led to a higher equilibrium constant indicating that a larger portion of the hydrophobic volume within the host's cavity was filled. The association and dissociation rate constants were determined from temperature jump experiments (see below for theoretical details). The dynamics for the binding of the ethyl derivative 2 are much slower than for 1 (Table 1). The lower association rate constant for 2 suggests that distortion of the cyclodextrin ring was required to accommodate 2, but once the complex was formed the dissociation process was also slowed down. This trend and its magnitude could not have been predicted from the values of the equilibrium constants because the equilibrium constant is related to the ratio of the rate constants (Scheme 1) and either or both rate constants can change. The equilibrium constant for 2 increased by a factor of 1.7, while the association and dissociation rate constants decreased by factors of 2200 and 2900, respectively. Translating the change in the residence time (1/k−) of 1 and 2 in the cyclodextrin into times scales familiar to humans would mean a residence time of 2 in the host of 8 years compared to a residence time of 1 of only 1 day. Such large changes in dynamics can have profound influences on the function of supramolecular systems. For example, if cyclodextrin were used as delivery systems the cargo would be delivered faster for 1 than for 2.
1 complex is formed by the inclusion of the phenol moiety into α-cyclodextrin. Equilibrium constants (K11) were determined from binding isotherms constructed from changes in the absorption of 1 or 2 when complexed to α-cyclodextrin (Table 1). An increase in the size of the guest, by inclusion of an ethyl group on the phenol, led to a higher equilibrium constant indicating that a larger portion of the hydrophobic volume within the host's cavity was filled. The association and dissociation rate constants were determined from temperature jump experiments (see below for theoretical details). The dynamics for the binding of the ethyl derivative 2 are much slower than for 1 (Table 1). The lower association rate constant for 2 suggests that distortion of the cyclodextrin ring was required to accommodate 2, but once the complex was formed the dissociation process was also slowed down. This trend and its magnitude could not have been predicted from the values of the equilibrium constants because the equilibrium constant is related to the ratio of the rate constants (Scheme 1) and either or both rate constants can change. The equilibrium constant for 2 increased by a factor of 1.7, while the association and dissociation rate constants decreased by factors of 2200 and 2900, respectively. Translating the change in the residence time (1/k−) of 1 and 2 in the cyclodextrin into times scales familiar to humans would mean a residence time of 2 in the host of 8 years compared to a residence time of 1 of only 1 day. Such large changes in dynamics can have profound influences on the function of supramolecular systems. For example, if cyclodextrin were used as delivery systems the cargo would be delivered faster for 1 than for 2.
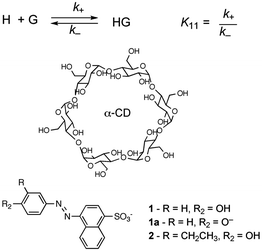 | ||
Scheme 1 Structures for α-cyclodextrin and 3′-alkyl-4′-hydroxyphenylazo-1-naphthalene-4 sulfonates that form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes with the cyclodextrin. 1 complexes with the cyclodextrin. | ||
| K 11 (M−1) | k + (103 M−1 s−1) | k − (s−1) | K 11(calc.) (M−1) | |
|---|---|---|---|---|
| 1 | 270 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
240 |
| 1a | 650 | 170 | 260 | 650 |
| 2 | 460 | 6 | 19 | 320 |
The same work also provides an example on the influence of solvent interactions.9 The equilibrium constant of the phenolate (1a) with α-cyclodextrin is higher than for phenol 1, which seems counter-intuitive because the charged species was expected to be more soluble in the aqueous phase. Kinetic experiments showed that for phenolate 1a the association and dissociation rate constants decreased significantly compared to 1. The larger decrease for k− led to the higher equilibrium constant. Phenolate 1a is better solvated than phenol 1 and for this reason the association rate constant is lower for 1a. However, once the complex is formed the charged phenolate needs to pass through the relatively hydrophobic cavity of the cyclodextrin leading to a larger effect of the charge on the dissociation process.
The example above underscores the importance of kinetic measurements which had been realized early on for studies of small molecule binding to supramolecular hosts9 or biomolecules, such as DNA.10–12 The slower development of kinetic studies compared to the ability to synthesize increasingly complex supramolecular systems is related to the need for real-time kinetic measurements combined with studies at short time scales.
Framework for kinetic studies
Kinetics of reactions can be measured either in real-time, where changes in concentration of reactants or products are followed with respect to time, or the kinetics are measured as relative rates, where the concentrations of final products for the reaction of interest are compared to concentrations of products for a standard reaction for which the mechanism and rate constants are known. Relative methods are not suitable for kinetic studies of supramolecular systems because of the lack of a deep mechanistic understanding of these reactions and the lack of standard reactions to which unknown reactions can be compared.Real-time measurements require the detection of kinetics on the time scale over which the reaction occurs. This requirement posed a challenge because of the small length scale of the objects involved that leads to kinetics over fast time scales. The relationship between length and time can be calculated as the time it takes for a small molecule to diffuse over the length of a host system. For example, the height of cyclodextrins is 0.78 nm and in water at room temperature it takes 2 to 3 ns for a molecule to diffuse over this length. This example shows that the dynamics for complexes with nanometer size can occur in the nano- to microsecond time-domain. Therefore, the characterization of the dynamics of supramolecular systems required the development of suitable techniques and methods for the measurement of kinetics in real-time.
Most techniques used to measure fast kinetics rely on the perturbation of an equilibrium, where the kinetics is measured as a relaxation process to the new equilibrium.7,8 The perturbation occurs over a time shorter than required to reach the system's new equilibrium and for the discussion below the perturbation will be considered to be instantaneous. Mathematical approaches, such as reconvolution of the time profile for the perturbation, are used when the time duration of the perturbation needs to be considered.
The rate for the formation of a host–guest complex with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (Scheme 1) is given by:
1 stoichiometry (Scheme 1) is given by:
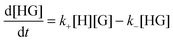 | (1) |
| kobs = k+[H] + k− | (2) |
The value of kobs is the same if changes in concentration of the guest or the host–guest are measured. The kinetics are measured for experimental conditions where an observable is different for the guest and the host–guest complex. Absorption and fluorescence measurements are frequently employed and, in general, the molar absorptivity coefficient or fluorescence quantum yields are different, but are not zero, for either the host or the host–guest complex. As a consequence, the experimental signal is the sum of signals for the guest and the complex (Fig. 2). The amplitude of the experimental trace is related to the difference in concentration of guest and host–guest complex at equilibrium compared to the initial concentrations taking into account the proportionality constants between signal and concentration, i.e. molar absorptivity coefficients or fluorescence quantum yields. It is important to emphasize again that the observed rate constants for the three simulations shown in Fig. 2 are the same, and only the amplitudes vary. Experimental conditions are chosen to maximize the amplitude of the experimental signal to improve the signal-to-noise ratio of the experiment and therefore increase the precision of the parameters measured.
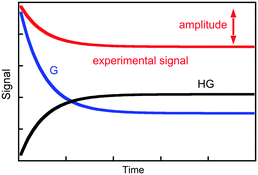 | ||
| Fig. 2 Time dependence for the individual signal of the guest (blue) and host–guest (black), and the composite signal corresponding to the experimental trace (red). | ||
The experimental rate constant (kobs) for relaxation kinetics always includes terms for the association and dissociation processes. In the example for the formation of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 host–guest complex, the association process includes the host concentration. Changing this concentration alters the magnitude of kobs. Slowing down the reaction is normally desired to ensure that the kinetics are slower than the time resolution of the technique employed. The limitation for decreasing the host concentration is an experimental one, and is determined by the signal-to-noise ratio that decreases when the host concentration is lowered.
1 host–guest complex, the association process includes the host concentration. Changing this concentration alters the magnitude of kobs. Slowing down the reaction is normally desired to ensure that the kinetics are slower than the time resolution of the technique employed. The limitation for decreasing the host concentration is an experimental one, and is determined by the signal-to-noise ratio that decreases when the host concentration is lowered.
The upper limit for a bimolecular reaction is set by the rate of diffusion of the reactants in solution. Therefore, the upper limit for the association rate constant (k+) for complex formation corresponds to the diffusion rate constant in a given solvent. This concept is useful when differentiating between possible reaction mechanisms since any mechanism that leads to a bimolecular rate constant with a value above the diffusion controlled limit can be discarded.
The dissociation process frequently corresponds to a unimolecular reaction and varying the concentrations of reactants or products cannot change the magnitude of the dissociation rate constant. Therefore, the value for the dissociation rate constant sets the lower limit for the observed rate constant. This lower limit determines the type of kinetic technique that can be employed since the time resolution of the measurement has to be faster than the time constant (1/kobs) for the dynamics being investigated.
Relaxation kinetics are either measured by increasing the concentration of one or more reactants, where the kinetics for product formation are measured, or a dilution experiment is performed where the product concentration decreases. As stated above, the association and dissociation processes are coupled and the type of experiment, product formation or product dissociation, cannot be employed to individually determine the values for k+ and k−. However, there are limiting situations where only one of the rate constants can be determined experimentally. The association term (k+[H]) can predominate if only high host concentrations can be used. In this case, the precision for the value of k− is poor. In such scenario the dependence of kobs with the host concentration is linear but the intercept of the plot defined by eqn (2) has a large error. The other limiting situation occurs when the bimolecular association process is slow and does not contribute to the observed rate constant for the relaxation process. In this case, the kinetics are measured in a dilution experiment where the kobs value does not vary with the concentration of host and it corresponds to the dissociation rate constant. When only one of the rate constants is measured then the second one is calculated from the equilibrium constant since the latter constant corresponds to the ratio of the association and dissociation rate constants (Scheme 1).
Choice of techniques
The aspects that need to be considered when designing kinetic studies to investigate the dynamics of supramolecular systems are the determination of the identity of the species present, the type of signal to be used for the binding isotherm and kinetic studies, and the time scale for the kinetic studies (Fig. 3).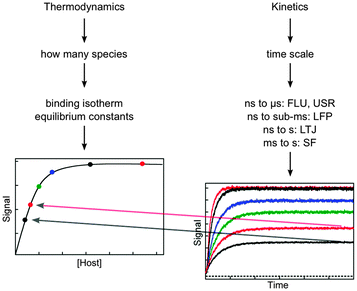 | ||
| Fig. 3 Considerations for the experimental design based on thermodynamic and kinetic studies. The amplitude of the kinetic studies at increasing concentrations of host (from the bottom to top in the right hand graph) has to fall onto the binding isotherm determined in thermodynamic studies (dots in left hand graph). The techniques for kinetic studies are:7,8 time-resolved fluorescence (FLU), ultrasonic relaxation (USR), laser flash photolysis (LFP), laser temperature jump (LTJ) and stopped-flow (SF). | ||
Thermodynamic and kinetic studies require an observable to be identified that is different for the free host or guest and the host–guest complex. Techniques with time resolutions faster than microseconds (μs) require the detection of either fluorescence or absorption (UV-Vis, ultrasonic waves, infrared), with the most common methods being fluorescence or UV-Vis absorption.
The next step before kinetic experiments are performed is to determine the species present at equilibrium. These experiments are frequently based on absorption or fluorescence studies but other complementary techniques, such as NMR and isothermal titration calorimetry are also employed. The advantage of using more than one technique is that complementary information on the system can be obtained. For example, NMR is instrumental in obtaining structural information, while isothermal titration calorimetry experiments are valuable to recover thermodynamic parameters in addition to equilibrium constants and stoichiometries of products, such as enthalpies and entropies of reactions. The requirements for the determination of binding isotherms are beyond the scope of this article and can be found in the literature.13
One important aspect of the thermodynamic experiments is that it provides a measure of the system at equilibrium that can be compared to the kinetic measurements once re-equilibration occurred. The intensity measured for the binding isotherm has to be the same as the final intensity in the kinetic experiment after normalization for the sensitivity of the detectors in both experiments. Therefore, the normalized amplitude values (colored dots in the left graph in Fig. 3) obtained from the kinetic experiments (right graph in Fig. 3) fall onto the binding isotherm. If such a correlation does not occur, then the kinetics was not followed over the proper time scale and some of the kinetic events have not been captured. In other words, the comparison between the intensities of the thermodynamic and kinetic experiments determines if the system reached equilibrium in the kinetic experiment.
The host concentration range over which information is obtained for thermodynamic and kinetic experiments are different. In the case of the thermodynamic experiments, most of the information for the binding isotherm is obtained when between 20% and 80% of the guest is bound,13 although equilibrium constants for lower percentage of binding can be obtained. In contrast, for kinetic experiments the reaction becomes faster even when the binding isotherm is saturated (compare the upper black and red traces in the right graph of Fig. 3). Therefore, kinetic information can be obtained when most of the guest is bound to the host.
Each kinetic technique has a specific time domain for which it can be used.7,8 Fast kinetic techniques have to be employed when the time constant for the experiment is faster than a few seconds, because solutions cannot be mixed manually. UV-Vis absorption is used as an observable where it is related to concentrations of reactants or products in laser flash photolysis (LFP), laser temperature jump (LTJ) and stopped-flow (SF) experiments, while ultrasonic relaxation (USR) is based on the absorption of ultrasonic waves. In all these cases absorption is an analytical tool to follow the kinetics of the reaction. Fluorescence can be used in the same way for LTJ and SF experiments, but in the case of time-resolved fluorescence experiments (FLU) the lifetime of the excited state influences the kinetics. Other time-resolved spectroscopic techniques, such as time-resolved infra-red14 and time-resolved circular dichroism15 have found application in other fields, such as studies of reactive intermediates and dynamics of biopolymers, respectively. These techniques would in future be useful for the study of supramolecular dynamics.
The lower limit of the time domain for each technique is determined by how fast a perturbation can be created. Pulsed excitation with lasers is used to create excited states in Flu and LFP experiments. The perturbation in these experiments is the creation of excited states, which are different molecules from their ground states. Lasers can have femtosecond pulses, but the lower limit of interest for supramolecular dynamics studies is nanoseconds. In addition, lasers are used to heat the solvent in LTJ experiments, which sets the lower time domain to nanoseconds. Temperature jump (TJ) can also be achieved by an electrical discharge and the time resolution for TJ experiments is microseconds. In LTJ and TJ experiments the perturbation is the change in the temperature of the system. SF is a technique where solutions are rapidly mixed when pressure is applied to the mixing syringes and the time-resolution of this technique is milliseconds. Rapid changes in concentration create the perturbation in SF experiments. In USR the perturbation is created by the absorption of sound waves when these are in resonance with the frequency of the relaxation kinetics of the system. The frequency generators used dictate the lower and upper limits for USR studies.
The upper limit for LTJ, TJ and SF experiments is related to the stability of the excitation sources used for the monitoring of the absorption or fluorescence of the system. The upper limit of 1 second was indicated in Fig. 3 because alternate manual mixing techniques can be used when the relaxation kinetics is slower than 1 second. Time-resolved FLU and LFP experiments can only be performed for the duration of time the excited state is present because these techniques rely on the detection of excited states. Fluorescence occurs from singlet excited states, which for organic molecules have lifetimes from nanoseconds to a few microseconds. In LFP studies the absorption of triplet excited states are detected that can have lifetimes as long as hundreds of microseconds.
Fluorescence correlation spectroscopy (FCS) and NMR are techniques used to measure the dynamics of supramolecular systems that do not require the perturbation of an equilibrium. FCS is based on intensity fluctuations for individual molecules in the detection volume and the signal is sensitive to the changes in fluorescence intensities when the host–guest complex is formed and dissociates. The advantage of FCS studies is the wide time range (nanoseconds to seconds) over which the kinetics can be measured. However, differentiation between the various relaxation processes can be challenging making the modelling of the results difficult if several relaxation processes occur, limiting somewhat the application of this technique.7,8 In the case of NMR, kinetic information is obtained when line broadening is observed. The broadening and coalescence into one peak is normally induced by changes in temperature and the association and dissociation rate constants are obtained from the fit of the broadening of the peaks. The major advantage of NMR studies is that structural information for the host–guest complex is obtained. The major disadvantage of NMR is the need to use high concentrations.7,8
Comparison of techniques
Ethidium bromide (3) emits very weakly in water and its fluorescence quantum yield increases significantly when intercalated between the base pairs in DNA, making 3 an ideal probe for kinetic studies. TJ,16 pressure jump,17 SF,16 and FCS,11 were used to study this system. The DNA samples were different for the different studies and comparisons are possible for the magnitude of the rate constants and the mechanisms that are consistent with the kinetic data. A detailed discussion on the technical aspects related to the different techniques used can be found in a previous report.7One relaxation time was observed in the initial studies and the kinetics was analyzed assuming a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding stoichiometry (see equations in Scheme 1 and eqn (2)). Studies for the binding of 3 with calf-thymus DNA (ct-DNA) or poly[d(G–C)] using different techniques showed that the association rate constant of 3 is much lower than the rate constant for diffusion in water (7.4 × 109 M−1 s−1, 25 °C)18 indicating that not every encounter between 3 and DNA or poly[d(G–C)] led to intercalation (Table 2). The dissociation rate constants were also similar for the different techniques employed.
1 binding stoichiometry (see equations in Scheme 1 and eqn (2)). Studies for the binding of 3 with calf-thymus DNA (ct-DNA) or poly[d(G–C)] using different techniques showed that the association rate constant of 3 is much lower than the rate constant for diffusion in water (7.4 × 109 M−1 s−1, 25 °C)18 indicating that not every encounter between 3 and DNA or poly[d(G–C)] led to intercalation (Table 2). The dissociation rate constants were also similar for the different techniques employed.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry determined by FCS,11 TJ,16 SF16 and pressure jump17
1 stoichiometry determined by FCS,11 TJ,16 SF16 and pressure jump17
Studies at higher concentrations of DNA and with better signal-to-noise ratios led to the observation of relaxation kinetics with more than one relaxation process. The rate constants for the two relaxation processes showed a linear dependence with the DNA concentration. Analysis of the data was consistent with a mechanism where 3 binds to two different sites on DNA (site A and B) and migration of 3 between the sites occurs in a bimolecular reaction with another DNA molecule (Scheme 2 and Table 3).16,19
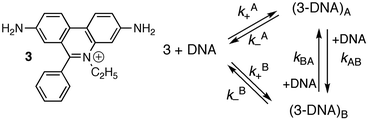 | ||
| Scheme 2 Structure of ethidium bromide (3) and mechanism showing the interchange between two different intercalation sites for 3 with DNA. | ||
| k A+ (106 M−1 s−1) | k A− (s−1) | k B+ (106 M−1 s−1) | k B− (s−1) | k AB (105 M−1 s−1) | k BA (105 M−1 s−1) | |
|---|---|---|---|---|---|---|
| TJ | 1.4 | 170 | 0.26 | 59 | 1.3 | 2.5 |
| SF | 7.3 | 39 | 1.1 | 14 | 6.0 | 15 |
The association and dissociation rate constants for the two sites differ by factors between 3 and 7. The absolute values for the association and dissociation rate constants for the binding of 3 with sites A and B are different for the TJ experiments performed with ct-DNA compared to the SF studies using sonicated ct-DNA, but the ratios between the rate constants for the binding dynamics with sites A and B are similar for both experiments. The equilibrium constants for sites A and B differ by a factor between two and three. The binding of 3 to sites A and B can probably not be differentiated in thermodynamic studies because the equilibrium constants are close and the changes in the emission quantum yield for bound 3 compared to the quantum yield in water are similar for binding of 3 to sites A and B of DNA. These results show that kinetic studies can be instrumental to obtain information for binding sites that are very similar and cannot be differentiated in thermodynamic studies.
The power of competitive pathways
Cucurbit[n]urils (CB[n]s) are macrocyclic host systems that can have much higher binding constants for guests that previously observed for other macrocycles, such as cyclodextrins.20,21 High binding efficiencies are observed for positively charged guests, where the charge interacts with the carbonyl groups at the portals of the host and the hydrophobic moieties of the guests are included in the CB[n] cavity. Initial kinetic studies indicated that the guest binding dynamics with CB[n]s were slow.22–24 A recent kinetic study using stopped-flow measurements for the binding of 2-naphthyl-1-ethylammonium cation (4) showed that the dynamics for this guest with CB[7] was fast.25 The mechanism consistent with the experimental results is shown in Scheme 3 where 4 binds to free CB[7] and in a competitive manner CB[7] binds sequentially to two sodium cations. The key to unravel the mechanism for this reaction was to realize that the competition of the binding of CB[7] with 4 and Na+ led to a shift of the binding kinetics to the millisecond time domain making it possible to measure the kinetics in SF experiments.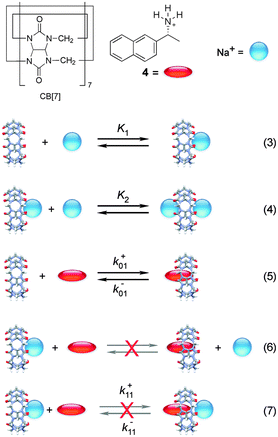 | ||
| Scheme 3 Mechanism for the binding of 2-naphthyl-1-ethylammonium cation (4) with cucurbit[7]uril (CB[7]) in the presence of sodium cations. Reactions (6) and (7) are inconsistent with the results.25 | ||
The fluorescence intensity for 4 increases when bound to CB[7]. CB[n]s are not very soluble in water and readily bind cations at the portals. For this reason, binding isotherms were measured at varying, but low, sodium cation concentrations. At the Na+ concentrations employed the binding of two sodium cations with CB[7] is negligible. The value for K1, the binding of the first sodium with CB[7], is 130 ± 10 M−1, while the equilibrium constant between 4 and CB[7] is (1.06 ± 0.05) × 107 M−1. The binding constant for the second Na+ (K2) of 21 ± 2 M−1 was determined in kinetic experiments (see below).
The binding kinetics of 4 with CB[7] in the absence of sodium cations were shown to be faster than the 1 ms time-resolution of the SF set-up. Addition of sodium traps some of the CB[7] in the form of CB[7]·Na+ and Na+·CB[7]·Na+ complexes, decreasing the concentration of free CB[7] and leading to a slow down of the reaction. The ratio between the concentrations of CB[7], CB[7]·Na+ and Na+·CB[7]·Na+ was constant throughout the kinetics for the binding of 4 with CB[7] because the Na+ concentration was much higher than the concentration of 4 and the equilibration between CB[7] and Na+ cations was much faster than milliseconds. One relaxation process was observed, where the value of kobs and the amplitude increased as the concentration of CB[7] was raised.
The equilibria between Na+ and CB[7] are coupled with the reaction between 4 and CB[7]. Therefore, the fast equilibria between Na+ and CB[7] are included in the expression for kobs (eqn (8)). The same values for k−01 (55 ± 7 s−1) were obtained from the linear relationship between kobs and the CB[7] concentration for kinetic studies in the presence of different Na+ concentrations (0.075–0.20 M). This result eliminates the possibility that the displacement reaction between free 4 and CB[7]·Na+ occurs leading to the formation of 4@CB[7] and free Na+ (eqn (6), Scheme 3). For such a reaction the dissociation rate for the 4@CB[7] complex would increase as the concentration of Na+ was raised leading to different intercepts for the dependence of kobs with the CB[7] concentration.
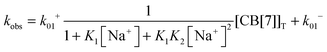 | (8) |
One other mechanistic possibility was that 4 could bind to free CB[7] (eqn (5)) and simultaneously to CB[7]·Na+ (eqn (7)). In this case, the dissociation rate constant from both complexes (k−01 and k−11, Scheme 3) would have to be similar because only one relaxation process was observed. Simulation of the dependence of kobs with the concentration of Na+ led to an upper limit of the association rate constant for 4 with CB[7]·Na+ (k+11) that is at least 40 times lower than the association rate constant for 4 with free CB[7] (k+01). This results suggest that if the 4@CB[7]·Na+ complex is formed its contribution is minor and can be assumed to be negligible.
Previous thermodynamic studies with CB[n]s had suggested that two sodium cations could be complexed to this host.26,27 This conclusion was reached because non-linear relationships were observed with the Na+ concentration for the overall binding constants for host–guest complexes. Kinetic studies for the binding of 4 with CB[7] provided an opportunity to establish the number of Na+ cations that bind to CB[7].25 The overall association rate constant (right term of eqn (9)) is dependent on the sodium ion concentration. This dependence fits well to eqn (9), but does not fit at all when it is assumed that only one Na+ binds to CB[7] (Fig. 4). This result unambiguously shows that two sodium cations bind to CB[7].
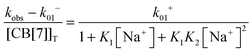 | (9) |
The value for the association rate constant of 4 with CB[7] of (6.3 ± 0.3) × 108 M−1 s−1 was recovered from the fit of the data to eqn (9). The equilibrium constant of 4 with CB[7] calculated from the ratio of k+01 and k−01 ((1.2 ± 0.2) × 107 M−1) is the same as the value determined in the binding isotherm studies ((1.06 ± 0.05) × 107 M−1). This equality indicates that the kinetic studies are consistent with the thermodynamic ones. Such an equivalency shows that all relevant kinetic events have been captured and that the mechanism proposed is self-consistent.
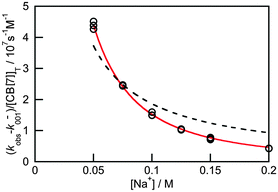 | ||
| Fig. 4 Dependence of the overall association rate constant with the concentration of Na+. The red solid line corresponds to the fit of the data to eqn (9), which assumes that two sodium cations are bound to CB[7]. The dashed line corresponds to the best fit when the binding of only one sodium cation to CB[7] is assumed. (Reprinted with permission from H. Tang, D. Fuentealba, Y. H. Ko, N. Selvapalam, K. Kim and C. Bohne, J. Am. Chem. Soc., 2011, 133, 20623–20633. Copyright 2011 American Chemical Society.) | ||
The association rate constant for 4 with CB[7] is similar to association rate constants measured for guests with cyclodextrins6 and it is one order of magnitude smaller than the rate for diffusion in water. This reduction is probably related to the fact that a guest approaching the sides of CB[n]s or cyclodextrins are not likely to form complexes. Therefore, the reasons for the higher equilibrium constants observed with CB[7] are not due to significant changes in the association rate constant of the guest. Analysis of the binding dynamics of 2-naphthyl-1-ethanol, which is similar to 4, to β-cyclodextrin, which is the cyclodextrin with dimensions similar to CB[7], shows that the difference in equilibrium constants is related to the dissociation rate constants. The dissociation rate constant is 1.8 × 105 s−1 for 2-naphthyl-1-ethanol bound to β-cyclodextrin,28 compared to 55 s−1 for 4 bound to CB[7].25
The detailed description above on the study of the binding of 4 with CB[7] shows the mechanistic detail that can be obtained from kinetic studies. Kinetic studies led to the determination that the guest was bound primarily to free CB[7] and established that guests in CB[7] have longer residence times than in other macrocycles. Fitting of the kinetic data was also more sensitive to the number of Na+ bound to CB[7] than the sensitivity to different models in the binding isotherm studies.
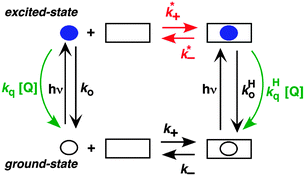
A different approach is to study the binding of excited guests to hosts. Competitive pathways play an important role when the binding kinetics of excited guests to hosts are investigated because the decay of the guest's excited state competes with the dynamics of the host–guest system.6,8 The formation of an excited state introduces a perturbation to the system, because excite states are different molecules from their ground states. The formation of a triplet excited state with higher polarity was exploited to study the binding dynamics of xanthone and thioxanthone with cyclodextrins and their derivatives.29,30 The equilibrium constant for the triplet guest is much lower than for the ground state. For example, a 50 M−1 equilibrium constant was measured for triplet xanthone with β-cyclodextrin, while the ground state equilibrium constant was 1100 M−1. The association rate constants for the guest's ground and excited states were the same, while the dissociation rate constant increased for the triplet state.29 Unfortunately, only a few molecules show shifts in their triplet absorption spectra, which are required to directly measure the dynamics of the guest–host binding by measuring the kinetics using LFP. A broader approach is to use competitive quenching experiments.6,8
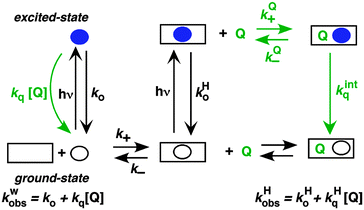
The two inherently competitive pathways when excited states are formed in supramolecular systems are the excited state decay and the dynamics for the host–guest equilibration (Scheme 4). If the lifetime of the excited state is sufficiently long (i.e. k0 is low) then the excited state can move between the solvent and the host as expressed by k*− and k*+. This is the case for triplet excited states, which have lifetimes in the microsecond time domain. In contrast, if the lifetime of the excited state is shorter than the binding dynamics then the “clock stops too early” and the excited state does not have a chance to move between the host and the solvent and no kinetic information on the guest binding with the host can be obtained. In this latter case the excited state is compartmentalized and it is used as a probe for the different environments (see below).
A further competitive pathway is introduced by adding a quencher molecule (Q) that reacts with the excited state.6,8 In the absence of a host system the observed rate constants (kobs, eqn (10)) increase linearly with the quencher concentration. In the presence of a host system the excited guest is quenched in the solvent (kq) or within the host (kHq) and a quencher is chosen for which the quenching in the solvent is more efficient than in the host (kq > kHq). In this case, the lifetime of the guest in the solvent shortens to a greater extent than the lifetime for the excited guest inside the host. As the concentration of quencher is raised the differential between the lifetime for the excited guest in the host and solvent becomes larger. At a high quencher concentration the lifetime for the excited guest in the solvent is so short that the excited state cannot associate again with the host and the rate-limiting step becomes the exit of the excited guest from the host. The quenching plot is curved (eqn (11)) and approaches a linear relationship at high quencher concentrations since the last term of eqn (11) becomes negligible. The association and dissociation rate constants are recovered from the fit of the quenching plot to eqn (11). Qualitatively the slower the host–guest dynamics becomes the farther away the curved quenching plot for guest–hosts system is from the linear quenching plot observed for the excited guest in the solvent.
| kobs = k0 + kq[Q] | (10) |
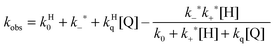 | (11) |
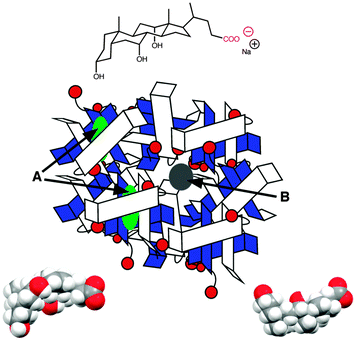
Bile salts, such as sodium cholate (Fig. 5), form aggregates in solution because bile salt molecules have convex hydrophobic faces, while the concave faces containing the hydroxyl groups are fairly hydrophilic. The hydrophobic faces of the bile salts interact forming small aggregates called primary aggregates. As the concentration of bile salts is increased, continuously larger structures are formed from the aggregation of the primary aggregates. These larger structures have secondary binding sites. Bile salts efficiently solubilize hydrophobic guests and their structure in water was initially described as being micelles. However, bile salts form aggregates with much lower aggregation numbers (<10 for primary aggregates) than micelles and the aggregate continues to grow as the monomer concentration is raised. In the case of sodium cholate, primary aggregates are formed at concentrations of 10 mM, while secondary aggregates are present at 40 mM of the bile salt. Experiments with a series of guest molecules showed that guests can be bound to the primary aggregates (A in Fig. 5) or secondary aggregates (B in Fig. 5). The differentiation between these two sites and determination of their properties was only possible with kinetic studies.31,32
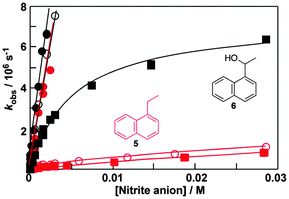
Fluorescence experiments showed that in the presence of sodium cholate the fluorescence intensity of two naphthalene derivatives (5 and 6, Fig. 6) increased and the singlet excited state lifetimes for both compounds were lengthened.32 These results suggested that 5 and 6 were incorporated into the bile salt aggregates. However, the plots for the quenching of triplet 5 and 6 with nitrite anions were markedly different (Fig. 6). In water linear quenching plots were observed for 5 (2.7 × 109 M−1 s−1) and 6 (3.4 × 109 M−1 s−1) with rate constants that were close to the diffusion-controlled limit. In the presence of 10 mM sodium cholate the quenching plot for 6 was the same as in water suggesting that 6 was not incorporated into the bile salt aggregates. In contrast, the quenching plot for triplet 5 with 10 mM bile salt was curved. This result suggests that 5 was bound to sodium cholate aggregates and the excited state was protected from the nitrite anions that mainly reside in the aqueous phase. Indeed, the quenching rate constant for triplet 5 inside the host (kHq, 3.7 × 107 M−1 s−1) was 70 times lower than in water. At the sodium cholate concentration of 10 mM primary aggregates are formed and the quenching experiments showed that 6 does not bind to primary aggregates, while 5 is bound to the aggregates.
At a concentration of 40 mM of sodium cholate, secondary aggregates are present and the quenching plots for 5 and 6 are curved (Fig. 6). However, much less curvature is observed for 6 than for 5, indicating that the binding dynamics is faster for 6 than for 5. The dissociation rate constant recovered was 60 times higher for 6 (8 × 106 s−1) than for 5 (0.14 × 106 s−1). The quenching of the triplet of 6 in the aggregate (1 × 108 M−1 s−1) was more efficient than the quenching of aggregate bound 5 showing that the secondary aggregates are more accessible to anions. These experiments show that 5 and 6 are bound to different sites in the bile salt aggregate. Guest binding to primary aggregates led to better protection from interaction with species in the aqueous phase and also led to a longer residence time than observed for guests bound to the secondary sites. These kinetic results showed that bile salt aggregates have two binding sites with different properties and therefore bile salt aggregates have more structure than conventional micelles formed from linear surfactants.
Determination of association rate constants
Singlet excited states have nanosecond lifetimes and are, in general, too short lived to be able to move from the host system into the solvent and vice versa. The host–guest dynamics is then uncoupled from the lifetime of the excited state and the excited state guests can be viewed as stationary (Scheme 5). Fluorescence from singlet excited states are frequently used to probe the properties of host environments, such as polarity. Fluorescence can also be used to measure the access of a quencher to the host system, leading to information on the quencher–host dynamics (Scheme 5). The excited state in water and in the host lead to different lifetimes and addition of quencher leads to a shortening of each these lifetimes. The increases of the observed rate constants for the excited guest in water (kwobs) and in the host (kHobs) vary linearly with the quencher concentration.The overall quenching rate constant for the excited state in the host is related to the dynamics of the quencher between the solvent and host (kQ+, kQ−) and the intrinsic quenching rate constant (kintq) within the host. When the host system is large, as for example for micelles, the quencher in the host may not encounter the excited guest before it exits again into the solvent. In this case, the dynamics of quencher binding to the host is coupled with the lifetimes of the fluorophores in the host and the solvent and non-exponential decays are observed for the excited state of the guest. This case will not be discussed in detail here since it is not applicable to host–guest systems. The mathematical treatment33 and a theoretical analysis on how to identify the several mechanisms for guest and quencher binding to micelles33,34 can be found in the literature.
Entry of a quencher into a host–guest complex places the quencher in close proximity to the excited guest. The overall quenching rate constant (kHq) is related to the quencher association and dissociation rate constants and the intrinsic quenching rate constant within the host (eqn (12)). A high intrinsic quenching rate constant can be assumed if a quencher is chosen that in homogenous solvent has a diffusion controlled quenching rate constant, which indicates that each encounter leads to quenching. The encounter complex in solution has a higher dissociation rate constant than the exit of the quencher from the host. Therefore, the value of kQ− can be assumed to be negligible compared to kintq and the measured quenching rate constant is equal to the association rate constant for the quencher with the host. In this scenario, the decay of the excited guest corresponds to a one exponential function when all guest molecules are bound to the host or the decay corresponds to a sum of exponentials where the guest is compartimentalized in the host and the solvent. The assumption of guest compartimentalization can be verified experimentally by observing constant pre-exponential factors for each one of the lifetime components of the decay.8
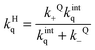 | (12) |
Polyaromatic hydrocarbons (Scheme 6) bind to the primary aggregates of bile salt aggregates. The fluorescence of these compounds is efficiently quenched by iodide anions with quenching rate constants in water (or water/ethanol for 9) that are close to the diffusion-controlled limit (4–6 × 109 M−1 s−1). In the presence of sodium cholate the quenching rate constants are significantly reduced (Scheme 6).31,32,35 These quenching rate constants correspond to the association rate constant of iodide anions with bile salt primary aggregates. Large differences were observed for the quenching rate constants, suggesting that the access of iodide anions to the primary aggregate was dependent on the structure and shape of the guest located inside the aggregate. Similar quenching rate constants are expected for different guests included into the same host where the structure of the host does not change significantly as is the case for macrocycles. The results with bile salts indicate that the packing of the cholate monomers around the guest can change significantly leading to different accessibilities of the iodide anions. This behaviour suggests that bile salt aggregates are adaptable structures. The differences observed for the iodide anion quenching rate constants in the case of naphthalenes 5, 7 and 8 shows that appended alkyl substituents can pack better against the fairly rugged and non-planar hydrophobic surface of cholate (see bottom right space filling model in Fig. 6) leading to more compact host–guest complexes for 5 and 7. In the case of 9, the planar guest is likely too large leading to non-optimal packing. This level of information on the host–guest structure would have been difficult to obtain from other spectroscopic studies because of the low concentrations of guest employed and the inability to obtain X-Ray crystallographic data. Bile salt aggregates have intermediate properties as hosts when compared to those observed for micelles, which provide a hydrophobic pseudo-phase, and rigid macrocycles with defined spaces. The adaptability of bile salts aggregates makes them very suitable for solubilisation processes, while maintaining the solubilised guest functionality, as was shown for photochromic compounds,36 and these systems can be used to develop functional materials.
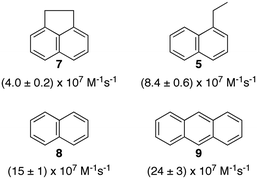 | ||
| Scheme 6 Structure of guests that bind to the primary aggregates of sodium cholate and the quenching rate constants by iodide anions of the aggregate bound singlet excited states of the guests. The quenching rate constants correspond to average values in the presence of 20 and 40 mM sodium cholate.31,32,35 | ||
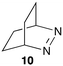
The reactivity of excited guests within the interior of a host can be employed to determine the association rate constant for the host–guest complex. The kinetics become simplified when the excited guest enters the host and reacts without having the ability to exit before being deactivated. The ideal situation is to have a quenching process in which deactivation of the excited state occurs without formation of products. Such a scenario eliminates the possibility of competitive binding of products and the photochemical decomposition of the guest during the experiment. 2,3-Diazabicyclo(2.2.2)oct-2-ene (10) (Scheme 7) fulfils this requirement because its singlet excited state in water is long (420 ns) and its lifetime is shortened through an “aborted” hydrogen transfer process from suitable donors, such as hydrocarbons.37
Compound 10 binds to β-cyclodextrin with an equilibrium constant of 1100 M−1.38 The decay of the singlet excited state had two exponential components. The short-lived component of 95 ns was constant at all β-cyclodextrin concentrations and was assigned to the lifetime of singlet excited 10 inside the host. The lifetime is shortened compared to the one in water because excited 10 reacts with the walls of β-cyclodextrin and is deactivated. The long-lived component of the excited state decay of 10 was shortened when the concentration of β-cyclodextrin was raised indicative of a bimolecular reaction between 10 and β-cyclodextrin. This reaction was assigned to the association of excited 10 with the host with a rate constant of 4.0 × 108 M−1 s−1. A dissociation rate constant of 3.6 × 105 s−1 can be calculated from the equilibrium constant and association rate constant (Scheme 1) with the assumption that the equilibrium constants for the ground and excited states of 10 with β-cyclodextrin are similar. The calculated residence time of 10 in β-cyclodextrin (2.8 μs) is indeed much longer than the lifetime of 10 inside the host (95 ns) and the excited state is deactivated before it can exit the host.
Determination of dissociation rate constants
The dissociation rate constant of guests can be obtained from competitive quenching studies of triplet excited states as described above, where the contribution of the association process to the observed rate constant is decreased as quenching of excited guests in the solvent becomes faster.A different approach, which does not rely on the formation of an excited state, is to use a sequestration method where the guest is competitively bound to a different host than for the host–guest complex of interest.7 SF measurements are used where a solution containing the host–guest system of interest is mixed with a second solution containing the sequestering host. A sufficiently high concentration of the sequestering host is required to ensure that the free concentration of guest is sufficiently low so that the term k+[guest] is negligible compared to k− (eqn (2)) for the host–guest system of interest. The observed rate constant in this case is the dissociation rate constant of the guest from the host–guest complex of interest. An essential control experiment is to study the kinetics in the presence of different concentrations of sequestering host in order to ensure that the sequestering host is not interacting with the host–guest system of interest. A fast association of the guest with the sequestering host is also a requirement to ensure that the rate-limiting step is the dissociation of the guest from the host–guest complex of interest. This method was used to study the binding of actinomycin to DNA, where sodium dodecyl sulfate (SDS) micelles were used to sequester the guest.12 The dissociation rate constant for actinomycin from DNA was much lower than for other analogues that had no biological activity, despite the similarity of their equilibrium constants.
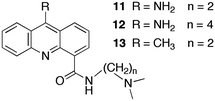
The sequestration technique was employed to measure the dissociation rate constants of 9-aminoacridine carboxamides from DNA.39,40 This class of molecules intercalates into DNA and the presence of a long residence time in the DNA was correlated with the antitumor activity of these compounds. Compounds 11 to 13 (Scheme 8) are a small subset of the compounds studied that shows how structural changes affect the binding dynamics of these guests with DNA. The decay for the kinetics observed in the SF experiments showed up to four relaxation times (Table 4). The comparison between the amplitude measured in the SF experiments with the amplitude obtained from equilibrium studies determined if a kinetic component faster than the SF time resolution occurred.
| DNA | τ 1 (ms) | τ 2 (ms) | τ 3 (ms) | τ 4 (ms) | F (%) | |
|---|---|---|---|---|---|---|
| 11 | poly[d(G–C)] | 3 | 76 | 230 | 106 | |
| poly[d(A–T)] | 4 | 8 | 70 | |||
| ct-DNA | 6 | 28 | 86 | 428 | 90 | |
| 12 | ct-DNA | 4 | 16 | 52 | 85 | |
| 13 | ct-DNA | 7 | 30 | 90 | 530 | 97 |
Binding of 11 to polydeoxynucleotides showed that 11 has faster overall binding dynamics with poly[d(A–T)] than with poly[d(G–C)], since with the former a significant portion of the kinetics occurs during the mixing time of the SF and the two observed relaxation times recovered are faster than the slowest two relaxation times for poly[d(G–C)]. This result is consistent with the preferential intercalation of 11 between G–C pairs. Four relaxation times were observed for the dissociation of 11 from ct-DNA. Intercalation of 11 occurs in the minor groove of DNA and the pendant group is involved in specific hydrogen bonds with the G base in DNA. This mode of interaction is proposed to be responsible for the observation of four relaxation times including the long relaxation time of hundreds of milliseconds, which correlates with biological activity. A longer alkyl chain on the carboxamide (12) disrupts the interaction of the pendant group and the long relaxation time is not present for 12. Compound 13 has a lower equilibrium constant when compared to 11 but the relaxation times for the dissociation process are somewhat slower, especially for the longest time. The slower dynamics of 13 with DNA is likely due to the bulkiness of the methyl group compared to the amino group that may require a larger distortion for the intercalation and dissociation of 13 with DNA when compared to 11.
Effect of complexity on host–guest dynamics
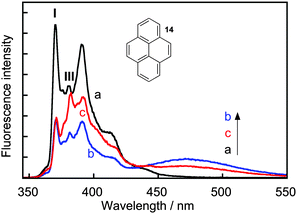
Complexity in supramolecular systems can be expressed in different ways. Two possibilities are host–guest complexes that have simultaneous formation of different complexes or the ability of one host to have more than one binding site for the same guest, where different binding sites have different properties. Two examples where kinetics played a key role in the characterization of such systems are presented.Pyrene (14) forms three types of complexes with γ-cyclodextrin (Scheme 9).41 Two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes form a 2
1 complexes form a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex with the characteristic excimer emission for 14 that is red shifted (maximum at 470 nm) with respect to the monomer emission (Fig. 7). At high concentrations of γ-cyclodextrin the excimer intensity decreases because 14 forms a complex with two or more γ-cyclodextrins where 14 is present in monomeric form. This latter complex was initially assigned to a 1
2 complex with the characteristic excimer emission for 14 that is red shifted (maximum at 470 nm) with respect to the monomer emission (Fig. 7). At high concentrations of γ-cyclodextrin the excimer intensity decreases because 14 forms a complex with two or more γ-cyclodextrins where 14 is present in monomeric form. This latter complex was initially assigned to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex,41 but temperature studies showed that at high concentrations of γ-cyclodextrin aggregates of the host are also present.42 The formation of the 1
2 complex,41 but temperature studies showed that at high concentrations of γ-cyclodextrin aggregates of the host are also present.42 The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n complex was confirmed by analyzing the emission spectra for the monomer of 14 where the ratio of the I and III bands is sensitive to the polarity of the solvent. The very low I/III ratio observed in the presence of 20 mM γ-cyclodextrin (Fig. 7) indicates that 14 is located in a non-polar environment.
n complex was confirmed by analyzing the emission spectra for the monomer of 14 where the ratio of the I and III bands is sensitive to the polarity of the solvent. The very low I/III ratio observed in the presence of 20 mM γ-cyclodextrin (Fig. 7) indicates that 14 is located in a non-polar environment.
 | ||
Scheme 9 Sequential formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2 1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes between pyrene (14, G) and γ-cyclodextrin (CD) and formation of an aggregated species containing monomeric 14. 2 complexes between pyrene (14, G) and γ-cyclodextrin (CD) and formation of an aggregated species containing monomeric 14. | ||
The kinetics for the formation of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex were measured in SF experiments. At low γ-cyclodextrin concentrations (<5 mM) the kinetics were complete within 200 ms and the association rate constant for 2
2 complex were measured in SF experiments. At low γ-cyclodextrin concentrations (<5 mM) the kinetics were complete within 200 ms and the association rate constant for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex formation was (6 ± 1) × 107 M−1 s−1, while the dissociation rate constant was 73 ± 5 s−1. The lower limit for the association and dissociation rate constants for the 1
2 complex formation was (6 ± 1) × 107 M−1 s−1, while the dissociation rate constant was 73 ± 5 s−1. The lower limit for the association and dissociation rate constants for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex were estimated to be 108 M−1 s−1 and 3.6 × 105 s−1.41 This result shows that increasing the complexity from two building blocks of the 1
1 complex were estimated to be 108 M−1 s−1 and 3.6 × 105 s−1.41 This result shows that increasing the complexity from two building blocks of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex to four building blocks of the 2
1 complex to four building blocks of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex led to an increase in the residence time of the guest inside the host by at least a factor of 4900 times; the equivalent from lengthening the time from 1 day to 13 years. This example shows that the dynamics of supramolecular systems can shift to very different time scales with small changes to the system, i.e. different concentration ratios in this case, and these results underscore the need to measure the dynamics of systems over very different time scales.
2 complex led to an increase in the residence time of the guest inside the host by at least a factor of 4900 times; the equivalent from lengthening the time from 1 day to 13 years. This example shows that the dynamics of supramolecular systems can shift to very different time scales with small changes to the system, i.e. different concentration ratios in this case, and these results underscore the need to measure the dynamics of systems over very different time scales.
At higher γ-cyclodextrin concentrations the kinetics became biphasic where the initial formation of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex was followed by a lowering of the 2
2 complex was followed by a lowering of the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 concentration over a longer period of time. The slow relaxation process was assigned to the formation of 1
2 concentration over a longer period of time. The slow relaxation process was assigned to the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n complexes. The presence of 1
n complexes. The presence of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n complexes was clear from the binding isotherm studies, but the much slower formation for this complex was only uncovered from kinetic studies. This system provides one of the first examples where the formation a host–guest complex, the 2
n complexes was clear from the binding isotherm studies, but the much slower formation for this complex was only uncovered from kinetic studies. This system provides one of the first examples where the formation a host–guest complex, the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex, is under kinetic control. The formation of different species at equilibrium and different kinetics depending on the concentration of the components of the system is an example on how systems chemistry is expressed in supramolecular chemistry.
2 complex, is under kinetic control. The formation of different species at equilibrium and different kinetics depending on the concentration of the components of the system is an example on how systems chemistry is expressed in supramolecular chemistry.
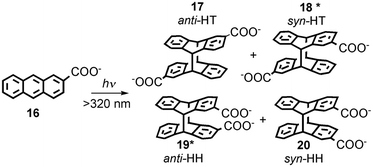
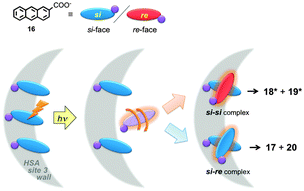
Serum albumins are chiral host systems that can be employed to enhance the chiral selectivity of bimolecular reactions, such as in the photodimerization of 2-anthracenecarboxylate (16, Scheme 10), where two of the products (18* and 19*) are chiral. Photophysical studies were employed to study the mechanism for the enhancement of the chiral selectivity.43–46
Human (HSA) and bovine (BSA) serum albumins have at least four binding sites with decreasing binding affinities for 16. Several guests can be bound to the same binding sites. A much higher enantiomeric excess was observed for the reaction in HSA than in BSA.45 Lifetime measurements for the singlet excited state of 16 and accessibility of aqueous quenchers to excited 16 bound to the proteins showed that the different binding sites had very different properties. The formation of products is dynamic and requires the movement of 16 to form the dimer. This result contrasts with the reactivity of 16 in small host–guest complexes, such as complexes with cyclodextrins,47 where the reaction occurs immediately upon excitation. Quenching studies showed that site 3 of both proteins led to the highest enantiomeric excess. Site 3 has a modest binding affinity for 16. An interplay exists between the efficiency of binding and bimolecular reactivity. Tight binding is unproductive, while a modest binding affinity ensures that the reaction occurs in a chiral environment and makes possible the turnover of the reaction.
The local mobility of 16 in HSA was determined in time-resolved anisotropy studies where the rotational correlation time of 16 was measured.48 The use of specific inhibitors made it possible to determine that the rotational correlation time for molecules of 16 bound to site 3 of HSA is similar to the rotational correlation time of the protein, indicating that molecules of 16 are mostly immobile in site 3. This information together with product distribution studies led to the mechanism where the three molecules of 16 bound to site 3 of HSA have the same pro-chiral face protected by the protein (Fig. 8). The excited molecule then is released from the protein wall and the si–si encounter complex forms one of the enantiomers of products 18* and 19*. This example shows that a combination of techniques, some of them based on kinetic measurements, can be employed to differentiate between guests bound to the different sites of the same host.
Conclusions
A conceptual framework was presented on how to characterize the dynamics of supramolecular systems. One key point is that dynamic information cannot be obtained from thermodynamic characterization. Indeed, examples were described where changes in equilibrium constants where seemingly counter-intuitive in the absence of kinetic information. Moreover, the kinetics of a system can be more sensitive to mechanistic changes than thermodynamic studies. Dynamic studies are instrumental in cases where different species are present when one can “zero in” on a specific species with unique spectroscopic signatures. The efficacy of competitive kinetics was shown in the modulation of concentration of reactants, or for the quenching of excited states involved in host–guest complexes. The examples presented throughout this article showed that kinetic studies will be instrumental as one of the crucial techniques required to tackle the complexity in systems chemistry, where supramolecular chemistry provides a relatively simple subset.Acknowledgements
The author thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) for the financial support of her research in supramolecular dynamics.Notes and references
- J. L. Atwood, J. E. D. Davies, D. D. MacNicol, F. Vögtle and J. M. Lehn, Comprehensive Supramolecular Chemistry, Pergamon, New York, 1996 Search PubMed.
- J. M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160 RSC , and references therein.
- M. Kindermann, I. Stahl, M. Reimold, W. M. Pankau and G. von Kiedrowski, Angew. Chem., Int. Ed., 2005, 44, 6750–6755 CrossRef CAS PubMed.
- R. F. Ludlow and S. Otto, Chem. Soc. Rev., 2008, 37, 101–108 RSC.
- G. von Kiedrowski, S. Otto and P. Herdewijn, J. Syst. Chem., 2010, 1:1, 1–6 CrossRef.
- C. Bohne, Langmuir, 2006, 22, 9100–9111 CrossRef CAS PubMed , and references therein.
- T. C. S. Pace and C. Bohne, Adv. Phys. Org. Chem., 2008, 42, 167–223 CrossRef CAS , and references therein.
- C. Bohne, in Supramolecular Photochemistry: Controlling Photochemical Processes, ed. V. Ramamurthy and Y. Inoue, John Wiley & Sons, Singapore, 2011, pp. 1–51, and references therein Search PubMed.
- F. Cramer, W. Saenger and H. C. Spatz, J. Am. Chem. Soc., 1967, 89, 14–20 CrossRef CAS.
- E. J. Gabbay, D. Grier, R. E. Fingerle, R. Reimer, R. Levy, S. W. Pearce and W. D. Wilson, Biochemistry, 1976, 15, 2062–2070 CrossRef CAS.
- D. Magde, E. S. Elson and W. W. Webb, Phys. Rev. Lett., 1972, 29, 705–708 CrossRef CAS.
- W. Müller and D. M. Crothers, J. Mol. Biol., 1968, 35, 251–290 CrossRef.
- K. A. Connors, Binding Constants - The Measurement of Molecular Complex Stability, John Wiley & Sons, New York, 1987 Search PubMed.
- Y. Wang, T. Yuzawa, H. Hamaguchi and J. P. Toscano, J. Am. Chem. Soc., 1999, 121, 2875–2882 CrossRef CAS.
- J. W. Lewis, R. A. Goldbeck, D. S. Kliger, X. Xie, R. C. Dunn and J. D. Simon, J. Phys. Chem., 1992, 96, 5243–5254 CrossRef CAS.
- F. J. Meyer-Almes and D. Porschke, Biochemistry, 1993, 32, 4246–4253 CrossRef CAS.
- R. B. Macgregor Jr., R. M. Clegg and T. M. Jovin, Biochemistry, 1987, 26, 4008–4016 CrossRef CAS.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press, Boca Raton, 3rd edn, 2006 Search PubMed.
- L. P. G. Wakelin and M. J. Waring, J. Mol. Biol., 1980, 144, 183–214 CrossRef CAS.
- J. Lagona, P. Mukhopadhyay, S. Chakrabarti and L. Isaacs, Angew. Chem., 2005, 44, 4844–4870 CrossRef CAS PubMed.
- M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. Liu, L. Isaacs, W. Chen, S. Moghaddam, M. K. Gilson, K. Kim and Y. Inoue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742 CrossRef CAS PubMed.
- R. Hoffmann, W. Knoche, C. Fenn and H.-J. Buschmann, J. Chem. Soc., Faraday Trans., 1994, 90, 1507–1511 RSC.
- C. Marquez and W. M. Nau, Angew. Chem., Int. Ed., 2001, 40, 3155–3160 CrossRef CAS.
- W. L. Mock and N. Y. Shih, J. Am. Chem. Soc., 1989, 111, 2697–2699 CrossRef CAS.
- H. Tang, D. Fuentealba, Y. H. Ko, N. Selvapalam, K. Kim and C. Bohne, J. Am. Chem. Soc., 2011, 133, 20623–20633 CrossRef CAS PubMed.
- M. Megyesi, L. Biczok and I. Jablonkai, J. Phys. Chem. C, 2008, 112, 3410–3416 CAS.
- M. Shaikh, J. Mohanty, A. C. Bhasikuttan, V. D. Uzunova, W. M. Nau and H. Pal, Chem. Commun., 2008, 3681–3683 RSC.
- T. C. Barros, K. Stefaniak, J. F. Holzwarth and C. Bohne, J. Phys. Chem. A, 1998, 102, 5639–5651 CrossRef CAS.
- Y. Liao, J. Frank, J. F. Holzwarth and C. Bohne, J. Chem. Soc., Chem. Commun., 1995, 199–200 RSC.
- L. T. Okano, T. C. Barros, D. T. H. Chou, A. J. Bennet and C. Bohne, J. Phys. Chem. B, 2001, 105, 2122–2128 CrossRef CAS.
- L. L. Amundson, R. Li and C. Bohne, Langmuir, 2008, 24, 8491–8500 CrossRef CAS PubMed.
- O. Rinco, M.-C. Nolet, R. Ovans and C. Bohne, Photochem. Photobiol. Sci., 2003, 2, 1140–1151 CAS.
- M. H. Gehlen and F. C. De Schryver, Chem. Rev., 1993, 93, 199–221 CrossRef CAS , and references therein.
- N. Boens and M. Van der Auweraer, ChemPhysChem, 2005, 6, 2352–2358 CrossRef CAS PubMed.
- C. Ju and C. Bohne, Photochem. Photobiol., 1996, 63, 60–67 CrossRef CAS.
- R. Li, C. S. Santos, T. B. Norsten, K. Morimitsu and C. Bohne, Chem. Commun., 2010, 46, 1941–1943 RSC.
- W. M. Nau, G. Greiner, H. Rau, J. Wall, M. Olivucci and J. C. Scaiano, J. Phys. Chem. A, 1999, 103, 1579–1584 CrossRef CAS.
- W. M. Nau and X. Zhang, J. Am. Chem. Soc., 1999, 121, 8022–8032 CrossRef CAS.
- L. P. G. Wakelin, A. Adams and W. A. Denny, J. Med. Chem., 2002, 45, 894–901 CrossRef CAS PubMed.
- L. P. G. Wakelin, G. J. Atwell, G. W. Rewcastle and W. A. Denny, J. Med. Chem., 1987, 30, 855–861 CrossRef CAS.
- A. S. M. Dyck, U. Kisiel and C. Bohne, J. Phys. Chem. B, 2003, 107, 11652–11659 CrossRef CAS.
- P. J. Wright and C. Bohne, Can. J. Chem., 2005, 83, 1440–1447 CrossRef CAS.
- T. Wada, M. Nishijima, T. Fujisawa, N. Sugahara, T. Mori, A. Nakamura and Y. Inoue, J. Am. Chem. Soc., 2003, 125, 7492–7493 CrossRef CAS PubMed.
- M. Nishijima, T. C. S. Pace, A. Nakamura, T. Mori, T. Wada, C. Bohne and Y. Inoue, J. Org. Chem., 2007, 72, 2707–2715 CrossRef CAS PubMed.
- M. Nishijima, T. Wada, T. Mori, T. C. S. Pace, C. Bohne and Y. Inoue, J. Am. Chem. Soc., 2007, 129, 3478–3479 CrossRef CAS PubMed.
- T. C. S. Pace, M. Nishijima, T. Wada, Y. Inoue and C. Bohne, J. Phys. Chem. B, 2009, 113, 10445–10453 CrossRef CAS PubMed.
- C. Yang and Y. Inoue, in Supramolecular Photochemistry: Controlling Photochemical Processes, ed. V. Ramamurthy and Y. Inoue, John Wiley & Sons, Singapore, 2011, pp. 115–153, and references therein Search PubMed.
- D. Fuentealba, H. Kato, M. Nishijima, G. Fukuhara, T. Mori, Y. Inoue and C. Bohne, J. Am. Chem. Soc., 2013, 135, 203–209 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |