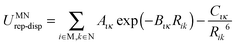Predicting crystal structures of organic compounds

Abstract

Currently, organic crystal structure prediction (CSP) methods are based on searching for the most thermodynamically stable crystal structure, making various approximations in evaluating the crystal energy. The most stable (global minimum) structure provides a prediction of an experimental crystal structure. However, depending on the specific molecule, there may be other structures which are very close in energy. In this case, the other structures on the crystal energy landscape may be polymorphs, components of static or dynamic disorder in observed structures, or there may be no route to nucleating and growing these structures. A major reason for performing CSP studies is as a complement to solid form screening to see which alternative packings to the known polymorphs are thermodynamically feasible.

---

Sarah L. Price

Sally (officially Sarah) Price studied Natural Sciences at University of Cambridge where she did a PhD in Theoretical Chemistry with Anthony Stone, deriving models for the forces between hydrogen molecules using quantum mechanical calculations. She worked at the Universities of Chicago and Cambridge, before becoming a lecturer at University College London, where she is now a Professor specialising in Computational and Physical Chemistry. Her research involves developing programs to model the organic solid state with theoretically based intermolecular potentials and using computational “crystal structure prediction” as part of multi-disciplinary investigations of pharmaceutical and other organic materials.

---

Key learning points

(1) Crystal Structure Prediction (CSP) methods only generate ordered crystal structures and an approximation to their relative energies.

(2) The extent of the search needs to be appropriate for the molecular flexibility and aim of the study, but typically 10³–10⁶ plausible crystal structures are generated.

(3) Lattice energy landscapes are very demanding of the computational method used, which usually involves high-level quantum mechanical calculations on the molecule or crystals. These calculations are for perfect static lattices, neglecting the effects of temperature.

(4) The crystal energy landscape is the set of crystal structures that are sufficiently low in energy to be thermodynamically plausible as polymorphs. The complexity of the crystal energy landscape is determined by the molecule, and can differ markedly between closely related molecules, such as isomers.

(5) The crystal energy landscape usually includes many more structures than experimentally observed polymorphs. Understanding why, in terms of kinetics of crystallisation, is the main challenge to polymorph prediction.

1. Introduction to current computational “Crystal Structure Prediction” methods

Crystal Structure Prediction (CSP) programs¹ were designed to find the crystal structure of an organic molecule, starting from the chemical diagram. They are based on the assumption that the crystal structure will be the thermodynamically most stable of all possible structures. However, polymorphism,^2,3 the observation of different crystal structures containing only the same molecules, immediately shows that some crystal structures are not the thermodynamically most stable. Although some polymorphs are enantiotropically related (i.e. the stability order changes with temperature), there are many monotropically related polymorphs where one or more polymorphs are metastable at all temperatures. Molecules often crystallise first in a metastable polymorph,^3,4 which may appear to be stable because of difficulty in transforming to the more stable form. The phenomena of “late appearing” and “disappearing” polymorphs are probably linked to changes in crystallisation conditions, such as new impurities, triggering the first nucleation of a new solid form and then the effect of seeds of this form on subsequent crystallisations.³ Thus CSP studies are practically useful for determining the range of thermodynamically favoured crystal packings independent of the kinetics of crystallisation which can depend on a wide range of controllable and less easily controlled crystallisation conditions.

Since polymorphs differ in their physical properties, the consistent production of the same polymorph is essential for all molecular crystalline products. This is particularly important for the pharmaceutical industry, as a change in polymorph can change the solubility and dissolution rate. A knowledge of the solid-state structural landscape of a molecule⁵ and the interdependence of the structure, properties, processing and performance of a drug (the pharmaceutical materials science tetrahedron)⁶ is essential for choosing the solid state form with the optimal compromises of physical properties, and to exclude the crystallisation of unwanted forms in industrial manufacture. Considerable expertise has been built up within the pharmaceutical industry in the multi-disciplinary searching and characterising of organic solids,⁷ with CSP studies emerging as a complementary tool.⁸

Research into polymorphism is changing the view of the complexity of the organic solid state. Although there are only crystal structures of polymorphs for about 5% of the molecules in the Cambridge Structural Database (CSD),^9,10 this reflects one of the primary uses of crystallography to confirm molecular structure and the difficulty of growing single crystals suitable for X-ray analysis rather than the incidence of polymorphism. A survey¹¹ from one of the polymorph screening companies of 245 molecules that they had screened, reported that 50% showed polymorphism and 90% had multiple crystalline and non-crystalline solid forms. (The term form is wider than polymorph, as it also includes solvates etc.) Correspondingly, the use of CSP methods has developed into calculating and interpreting the crystal energy landscape of a molecule,¹² the set of crystal structures which are sufficiently low in energy, to be thermodynamically feasible polymorphs.

The crystal energy landscape rarely contains only one crystal structure, i.e. it is relatively rare for a molecule to have one way of packing with itself that is significantly more favourable, than any other. The fields of crystal engineering and self-assembly are dominated by multicomponent systems because of the scarcity of molecules that can close pack with strong intermolecular interactions defining a unique packing in all three dimensions. Hence, the main use of CSP studies is to find the range of different packings that are thermodynamically plausible crystal structures. The most stable should be an observed crystal structure. In the cases when there is one structure that is significantly more stable than any others, for example, isocaffeine which has an unusually large energy gap of about 6 kJ mol⁻¹ (see Fig. 1), then polymorphs are very unlikely. The more common case, such as the isomer caffeine (Fig. 1), where there are structures that are thermodynamically competitive requires qualitative interpretation of the crystal energy landscape. How are these structures related? How does the relationship between the structures limit the possibilities of the structures nucleating and growing under different conditions? Thus, CSP studies aid thinking about what alternative outcomes there may be for crystallisation processes. As such they are a complement to experimental screening aimed at finding all solid forms, where it is clear from the huge developments in this area that it is impossible to cover all the range of experimental conditions that have led to the discovery of new polymorphs.¹⁴

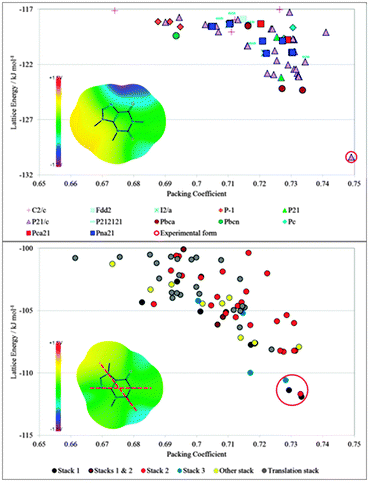Fig. 1 The contrasting distributions of CSP generated crystal structures of (top) isocaffeine and (bottom) caffeine.¹³ Each symbol gives the lattice energy and packing coefficient (proportional to density for isomers) of a mechanically stable crystal structure. The crystal energy landscape of isocaffeine contains only one low energy structure, (which corresponds to the known structure), whereas that for caffeine contains a group of layer structures with different stackings of the molecule. The difference in the crystal energy landscapes can be rationalised by the intermolecular interactions as represented by the electrostatic potential on the van der Waals surface plus 1.2 Å; +1.5 V corresponds to an interaction energy of +1.4 kJ mol⁻¹ with a positive point charge of 0.01e. The low temperature experimental structure of caffeine has disorder components corresponding to rotation by 180° about the two marked axes.¹³

2. CSP methodology – state of validation and key considerations

Crystal structure prediction (CSP) methods have been subjected to the severest form of review by the Blind Tests of Crystal Structure Prediction organised by the Cambridge Crystallographic Data Centre. They organise the collection of unpublished crystal structures, and send out a set of chemical diagrams to those developing CSP methods, with the challenge to submit three predictions of the crystal structure by a given deadline. The account of the fifth and most recent blind test¹⁵ in 2010 is a source of detailed references as to the various approaches used, with the previous tests showing the evolution of methods since 1999.¹Fig. 2 shows the molecular systems considered in the latest test, where most target crystal structures were the first determination of a crystal structure containing just the given molecule(s), allowing the working assumption that participants were seeking to predict the thermodynamically most stable structure, although some molecules in previous tests have been found to be polymorphic. Polymorph prediction was tested by the challenge to predict polymorphs III and IV of gallic acid monohydrate. Its computed crystal energy landscape helped correct the interpretation of the diffraction data of polymorph III and instigated experimental work which produced a further polymorph (V) of the monohydrate, as well as new structures for the anhydrate and over 20 solvates.¹⁶ The 2010 test¹⁵ showed that no method is currently able to reliably predict the crystal structures of this range of organic molecules (Fig. 2). Indeed, an important lesson from the blind tests is that some organic crystal structures are fairly easy to predict, whereas others, such as caffeine (Section 4.2) may never be possible. It depends on the specific molecule and whether it has one good way of packing with itself, or many almost equi-energetic, equally bad compromises – a situation that seems likely to be linked with difficulty in nucleating and growing sufficient quality samples for crystallographic structure determination.

Fig. 2 Summary of the results of the most recent 2010 blind test of crystal structure prediction.¹⁵x/y denotes that x of the y groups entering had the correct structure within their three submissions.

The methodology of CSP studies is evolving fast, and so for details of the range of methods used by the groups that accepted the challenge see references within,¹⁵ and check citations of this paper for new methods. This article will concentrate on the basic considerations for a CSP study, done in conjunction with experimental work, that are in common with the methods that have been most successful in the blind tests. These methods, in principle, can be developed to not rely on the availability of experimental data, which is important for the molecular design of new organic materials such as energetics. However the interpretation of the output of a CSP study in terms of its implications for crystallisation control often needs to build on the increasing experience of using CSP studies as a complement to interdisciplinary experimental work.

2.1 Molecular bonding

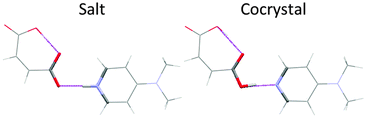
A CSP method will generate crystal structures based on an assumed molecular structure, and for multi-component systems an assumed stoichiometry. It is possible that none of these may actually exist. The molecule may crystallise in a different tautomer: the thermodynamically most stable structure of barbituric acid was only recently discovered¹⁷ in the enol form, whereas the previously known polymorphs contain the keto form. A solvate or cocrystal may not form, or crystallise with a different stoichiometry. It is essential to assume the covalent bonding in the initial stage; a completely free search for a given number of nuclei and electrons would also generate crystal structures of other isomers and decomposition products. Full unconstrained optimisation of the crystal structures at the final stage could allow some changes in covalent bonding, but this cannot be relied upon. Many of the CSP low energy structures of simple pyridine carboxylic acid cocrystals are sufficiently different¹⁸ from those of the corresponding pyridinium carboxylate salts, that computational proton migration in the solids would not occur, although in other cases the structures are so similar that the proton is observed to be disordered in the diffraction experiment (Fig. 3).

Fig. 3 Proton positions are very important in crystal energy calculations but diffraction data does not always position them correctly, and X-ray data produces short covalent bonds to hydrogen. The distinction between salt and cocrystal may only have minor changes in the shape of the dimer, as in the common motif illustrated, but this can have a significant effect on the low energy structures and their relative energies.

With the molecular bonding chosen, we can define our crystal energy as relative to infinitely separated molecules in their lowest energy conformation. By ignoring molecular vibrations (even the zero-point motions) and so considering a perfect infinite static lattice compared with the infinitely separated molecules (all nominally at a temperature of 0 K), we can approximate our crystal energy as the lattice energy E_latt. The effect of pressure can be added, but the differences in density between polymorphs are usually so small that this term is generally neglected unless the experimental work is done with applied pressure.

The lattice energy, E_latt, can be conceptually broken up into two components, the intermolecular interactions between the molecules, U_inter, and the change in the molecular energy between the crystal and gas, ΔE_intra, so that

E_latt = U_inter + ΔE_intra

Many CSP methods are based on making this division, and indeed the development of CSP methods started with molecules whose rigidity meant that the second term could be ignored.

2.2 Molecular structure and conformational flexibility

A molecule generally adopts a low energy conformation within its crystal structures: i.e. ΔE_intra, the conformational energy penalty paid for changing the molecular conformation to improve the hydrogen bonding or close packing is generally quite small. The main exception is when a molecule in isolation has an internal hydrogen bond, but can adopt a more stable crystal structure by changing conformation to make an intermolecular hydrogen bond. An analysis of the range of conformations to be considered and how their relative energies are to be assessed is a critical part of the CSP process for larger, flexible molecules.¹⁹

Small adjustments in conformation, such as changes in torsion angles by a few degrees, rotation of a methyl group or amine pyramidalisation, can change the lattice energy significantly. (Indeed, an investigation of how much lattice energies change if the molecular structure is held rigid at the conformation determined by crystallography at different temperatures, or worse still, if the proton positions are not corrected for the systematic error in X-ray structures that shortens bond lengths to hydrogen, can be very instructive. The use of calculations to confirm or correct the proton positions, which cannot be accurately located from the diffraction data is increasing.) These minor types of conformational change can be taken care of at the final stage of structure optimisation in a CSP study. However, even for a rigid molecule, the use of the molecular structure taken from the crystal can bias the search towards the observed packing, so the input conformation has to have the isolated molecule geometry and symmetry, and is usually derived by an ab initio optimisation of the isolated molecule.

Larger differences in conformation, such that the close packings of the molecular van der Waals surfaces would be qualitatively different, have to be covered in the search. Although the molecular conformations observed in crystal structures are generally low in energy, how close this is to a local or global minimum energy conformer²⁰ for the isolated molecule depends on flatness of the torsional potentials. If each conformation is in a deep energy well, then separate searches may be performed for each conformer. However, if there is a low energy barrier between conformers that give rise to a very different overall shape, then this flexibility needs to be included in the search from the earliest stages.

It is challenging to evaluate a reliable conformational energy surface for larger molecules, even in isolation, as the intramolecular dispersion plays an important role and this is not well captured by ab initio methods. For example, routine self-consistent-field (SCF) calculations give a broad minimum in the conformational profile for phenyl rotation in fenamic acids (2-(phenylamino)-benzoic acids) in the region which corresponds to a low population of experimental structures²¹ and to a local maximum (∼5 kJ mol⁻¹) for higher quality ab initio methods that include electron correlation. Searches where the conformational energy term favours the wrong conformations will generate structures that are too unrealistic to be useful as starting points for refinement with more expensive methods. This can be a problem with many force-fields that are used in biological modelling. Hence the GRACE program uses many periodic dispersion corrected density functional calculations to parameterise a molecule-specific force-field for use in its search,²² and CrystalPredictor uses an interpolated grid of isolated molecule ab initio intramolecular energies.²³

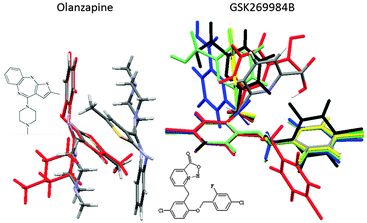
Surveys of the conformations of related molecular fragments within their crystal structures are generally good guides to conformational preferences in other phases, and hence a useful cross-check that the appropriate range of conformations could be generated in the CSP study. Once the crystal energy landscape has been calculated, a comparison of the conformations within the crystal structures will reveal which subset of the range of conformations can pack densely with favourable intermolecular interactions. For example, for olanzapine, there are two low energy conformational wells, but one conformation does not produce plausible crystal structures (Fig. 4).²⁴ In contrast, GSK269984B has very different gross as well as hydrogen bonding conformations on its crystal energy landscape, raising the question as to why the conformation is the same (apart from the hydrogen bonding proton), within all the experimental crystal structures.¹⁹

Fig. 4 Conformations are very important as the range of conformers that may occur for in the gas, liquid and all solutions could also appear in the crystal structures and need to be covered in the search. The dimer of olanzapine found in its 59 crystal structures (atomic colouring) overlaid with an alternative low energy conformation (red) that did not generate any plausible crystal structures. Overlay of the conformations of GSK269984B found in the low energy crystal structures within 3.5 kJ mol⁻¹ of the global minimum (experimental structure, atomic colours) in E_latt, but ΔE_intra varies by 30 kJ mol⁻¹ because of the difference between the two inter- and the intramolecular hydrogen bonding configurations.

2.3 Extent of search

A CSP study also requires decisions on the extent of crystallographic space that needs to be covered for all the conformations. A critical parameter is the number of independent molecules in the asymmetric unit cell (Z′ for one component systems). If this is greater than 1, as it has to be for a cocrystal, salt or solvate, then the search space is increased by the number of variables (usually 6 for 2 independent molecules) needed to define the relative position of the independent molecules within the unit cell. For one-component organic crystals, it is common to restrict the search to Z′ = 1, so the space group symmetry generates the other molecules within the unit cell and reduces the number of search variables to those required by the space group. So for example, for a rigid molecule (no conformational variables) in the most common space-group for organic molecules, P2₁/c, which has 4 molecules in the monoclinic unit cell, the only search variables are the 3 cell lengths, one cell angle β and six parameters defining the orientation and position of the molecule relative to the cell axes. However, the restriction to Z′ = 1 would miss many polymorphs, with the importance of Z′ > 1 structures becoming more appreciated as crystallographers solve more such structures.²⁵ Whilst some Z′ > 1 polymorphs are closely related to simpler Z′ = 1 structures and can be viewed as trapped “crystals on the way” or incomplete crystallisations, or may be lower temperature polymorphs, there are structures that are intrinsically Z′ > 1, for example the most stable polymorph of 7-fluoroisatin²⁶ (Fig. 5). The incidence of high Z′, let alone intrinsically disordered, modulated and incommensurate structures, etc.,²⁵ means that a complete search that would find all observed crystal structures for any organic molecule is a practical impossibility. However, for many purposes a Z′ = 1 search will answer many questions about the possible crystal packings of a molecule, and most, if not all, of a Z′ = 2 search will just produce closely related and duplicate structures to those found in Z′ = 1. However, it is well worth thinking through whether there is a tendency to Z′ > 1 structures within the family of compounds, or the possibility of a particular hydrogen-bonding motif with Z′ > 1.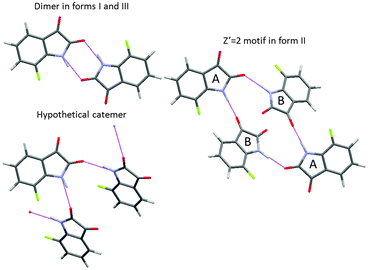

Fig. 5 The number of molecules in the asymmetric unit cell Z′ can be important, as in the case of 7-fluoroisatin, where the expected doubly hydrogen bonded dimer appears in form I and the closely related Z′ = 2 form III, but in the most stable form II the two independent molecules use different hydrogen bond acceptors, a motif that is intrinsically Z′ = 2 which could not have been generated in the Z′ = 1 search. Catemeric structures are found higher in energy on the crystal energy landscape.²⁶

The cost versus benefits of the completeness of the search, which depends on the aim of the study, also applies to the choice of the 230 space groups to be covered. Most organic molecules crystallise in a fairly small range of monoclinic, triclinic and orthorhombic space groups, and it would not be worth the computational expense of including tetragonal, hexagonal or cubic space groups unless there was some experimental evidence, high molecular symmetry or a tendency of your type of molecule to suggest it would be worthwhile. Only a small number of space groups can be adopted by a chiral molecule, and a search in just 5 of these is likely to be adequate. For non-chiral molecules and racemic compounds, you would also need to consider the space groups that contain inversion operators or mirror planes, but with an additional 15 space groups you would cover the most populated.²⁷

The vastness of the search space and the computational cost of accurate methods of evaluating the lattice energy require that all searches are hierarchical, in that some approximate estimate is made of the relative energies in the search, duplicates are removed and then only the more promising are reassessed with more accurate energy evaluations. Since lattice energy minimisation techniques generally only go to the nearest local minimum, there are trade-offs between the completeness of the search method, the accuracy of lattice energy being minimised, and the rate at which structures are discarded. These, like the human and computing resources required, can be very molecule as well as CSP method and computer system dependent; anyone embarking on CSP studies should consult the published papers and documentation of the program suite chosen after reviewing the current alternatives.^1,15 Physical insight into the basis of the calculation can prevent disappointment. For example, the “Prom” search approach²⁷ is based on sequentially building up clusters by adding crystallographic symmetry elements and continuing or discarding structures according to a simple force-field evaluation. In contrast the MOLPAK²⁸ search is based on seeking densely packed structures in common coordination types using a pseudo-hard sphere model. (MOLPAK was designed for energetic materials where density is a key property.) Both programs will very quickly generate a few thousand plausible crystals structures for a rigid molecule, with the Prom procedure more liable to miss structures which do not contain a strongly cohesive centrosymmetric (hydrogen bonded) dimer, and MOLPAK more likely to miss structures which do. Orders of magnitude more plausible crystal structures would be generated by more extensive search methods, such as GRACE,²² or CrystalPredictor,²³ where there are parameters for monitoring the rate of appearance of new structures to converge the search, as evaluated by fairly accurate, molecule specific force-field models. These programs can also handle very flexible molecules, and multi-component systems, where the search may be terminated for practical reasons at over a million plausible structures.

The issue of removing duplicate structures is not straightforward, mirroring the difficulty in defining the distinction between polymorphs and experimental sample and temperature dependent structural variations.⁹ Simulated powder X-ray diffraction patterns are often used, but there are cases where crystal structures that differ when you look at the elements can have very similar powder patterns. Overlaying the molecular coordination sphere, usually a 15 molecule cluster, could exclude polymorphs with longer range packing differences.

Finally, testing that a computer generated crystal structure has no imaginary frequency vibrational modes of the crystal and that it is mechanically stable, can reveal that optimising the crystal structure within a given space group has produced a transition state between lower symmetry structures with more independent molecules in the asymmetric unit. If the energy lowering from removing the symmetry constraint is small, then the molecular motion in the crystal may mean that it is observed in the higher symmetry structure.

Any CSP program that will only automatically and completely search through the vast swathes of possible ordered crystal structures would waste considerable computer and human time. A little knowledge of crystallography of the appropriate family of molecules, and thoughtful choices appropriate to the aim of the study can usually define a practically useful search that can be complemented by other calculations. These should be on the known structures, including those derived by computational desolvation (removing solvate molecules and optimising), or computational substitution (swapping the molecule in crystal structures of related molecules) and could include mini-searches (e.g. just in P2₁/c) using plausible small clusters of molecules or unusual conformations as the search input.

2.4 Model for the lattice energy

The final, and arguably most critical choice, that has to be made is the method of evaluating the crystal energy in the final stage of the search in order to decide which crystal structures are thermodynamically plausible as polymorphs. This choice depends on the molecule: the search is essentially finding the compromises between the close-packing favoured by the van der Waals forces, and the repulsion from the overlap of the molecular charge density, and the functional group dependent forces such as hydrogen-bonding, π⋯π stacking, halogen bonding etc., as allowed by the molecular flexibility. The intermolecular lattice energy has to be quantified using the theory of intermolecular forces²⁹ to give an approximate analytical model for all the contributions, which are then summed up over the crystal lattice to provide U_inter. Crudely, the electrostatic term determines the favourable relative orientations of the molecules, the repulsion is critical in determining the close contact distances and the dispersion gives the universal attractive contribution which favours denser structures. The molecular distortions which may occur to improve the packing density, hydrogen bonding distances etc., are quantified by ΔE_intra. The quality of the results will depend on correctly balancing the terms, which are important for the specific molecule. Alternatively, it is increasingly possible not to subdivide the contributions, and use a quantum mechanical method to refine the crystal structure to find the nearest minimum in the lattice energy. A breakthrough in success in the blind tests came in 2007 with the use of periodic ab initio methods with an empirical dispersion correction that had been specifically developed for organic crystal modelling.³⁰ Alternative dispersion-corrected density functional periodic calculations schemes that are available to academics (with supercomputer powers) are looking promising.³¹ However, as shown in the 2010 blind test,¹⁵ there is currently no method of evaluating the lattice energy of organic molecules, typical of pharmaceuticals, their salts and hydrates, that can be assumed to be accurate enough to rank the structures when the energy differences can be fractions of a kJ mol⁻¹. Indeed, the evaluation of lattice energies of small organic molecules is a very active research area for computational chemistry as the problems in modelling dispersion and polarisation and all other contributions to U_inter with equal accuracy that is well balanced with the intramolecular forces makes modelling even the lattice energy accurately very demanding.^32,33

Hence the computational method should be chosen after being tested for being able to reproduce the crystal structures and give plausible relative lattice energies for the known polymorphs of the molecule, or related molecules. The lattice energy minimum closest to these experimental structures is the closest approximation to these structures that could be found in the CSP study. If the lattice parameters have changed by more than the few % which could be attributed to thermal expansion, or the molecules rotated or translated significantly from their experimental positions, or the molecule changed its conformation (these changes are usually very strongly correlated) then a CSP study with this model for the lattice energy is a waste of time.

When the CSP search has been concluded, if there is a large energy gap between structures as for isocaffeine (Fig. 1), then the ranking will not be sensitive to your approximations in calculating the energy, and a confident prediction can be made. We can estimate whether the theoretical underpinnings of a given type of crystal energy evaluation is suitable for a given molecule, in terms of its size, functional groups, likely conformational flexibility and intermolecular interactions, so that a CSP study is worthwhile. However, it is the molecule itself that determines whether it has one good way of packing with itself, or a range of equally bad compromises giving such small energy differences that the ranking of structures may not be possible with the best affordable methods. If the known structures are not at or near the global minimum, then this could be an artefact of the chosen method of energy evaluation. This needs to be tested by recalculating the relative lattice energies of the low energy structures with a range of alternative programs, based on different assumptions (e.g.ref. 34, but more methods such as Pixel²⁷ are now being used) before too much time is invested in the experimental search for the elusive more stable “predicted” polymorphs.

The blind tests of crystal structure prediction have shown the limitations of the easy to use, PC based modelling methods that rely on traditional force-fields.^15,35 This can be attributed to the limitations of the functional form, particularly in using atomic charges, and in using the same charges to model both inter- and intramolecular interactions. This does not mean that CSP studies using such force-fields will not give useful results for some molecules (where the parameterisation of the force-field is particularly good) and for some purposes.⁵ This could include the generation of ideas about possible structures for helping interpret experimental data, or for testing methods that incorporate non-thermodynamic aspects of crystallisation, such as informatics approaches¹⁵ using the CSD.

A successful intermediate between conventional force-fields and periodic electronic structure calculations is based on the separation of inter- and intramolecular energies and using distributed multipoles rather than point charges to evaluate the intermolecular lattice energy. The specific representation of the electrostatic effects of the non-spherical features such as lone pairs and π electron density makes a considerable difference to the ability to represent the directionality of hydrogen bonding and π⋯π stacking. Using distributed multipoles rather than an atomic charge representation of the same molecular charge density considerably improves the proportion of rigid molecule crystal structures found close to the global minimum.³⁶ The resulting anisotropic atom–atom model intermolecular potential is implemented in the organic solid state modelling code DMACRYS.³⁷ Most CSP studies using a distributed multipole electrostatic model have combined it with an empirical isotropic atom–atom model potential, of the form

where the repulsion and dispersion interactions are between atom i of type ι in molecule M and atom k of type κ in molecule N, which are separated by a distance R_ik. The parameters for different types of atoms have been derived by empirical fits to groups of crystal structures and sublimation energies. Other, less empirical models based on the theory of intermolecular forces, with anisotropic atom–atom repulsion potentials, are being used successfully for CSP and property studies for rigid molecules.²⁹ The empirical fitting of repulsion–dispersion potentials means that errors, including the neglect of the induction energy and other contributions, which are not explicitly modelled, are partially absorbed into parameters. This may not be adequate, particularly for representing the relative energies of different types of hydrogen bonding.³⁴ The induction energy can be explicitly evaluated from the atomic dipolar polarisabilities and permanent atomic multipoles, but the change in charge distribution of a molecule induced by the electrostatic fields from the surrounding (symmetry related) molecules requires iterating to self-consistency.³⁷ A less accurate, but often effective method of representing the intermolecular polarisation within the crystal, and its effect on the relative conformational energies, ΔE_intra, is to perform the molecular wavefunction calculation in a polarisable continuum, where a value of ε = 3 appears appropriate for neutral molecules.³⁸ These are just some of an emerging range of methods that can give more accurate energy evaluations, but are currently too expensive for use in optimising many crystal structures, which can be used in a final energy evaluation.

For flexible molecules, the conformational energy penalty ΔE_intra contributes directly to E_latt, and the redistribution of charge within the molecule as it changes conformation, represented by the distributed multipoles, affects U_inter. Both can be very dependent on the quality of the electronic structure method used (see Section 2.2), which can usually be of a higher quality for a molecule than is affordable for electronic structure calculations on crystals. Hence, the refinement of the molecular conformation within the crystal structure relies on multiple evaluations of the molecular wavefunction, which is made feasible by the database structure in CrystalOptimizer.³⁹ However this approach, unlike periodic electronic structure methods, does require explicit selection of which molecular torsion and bond angles are likely to differ significantly between crystal structures and in the isolated molecule (as approximated by quantum mechanics).

Once all these choices have been made, the CSP study can be performed. There are many compromises in terms of human and computing time, availability of software etc. that have to be matched to the aim of the study. The size of the group of structures that will need further examination will always depend on the molecule (the information you are seeking) but also the extent of your search and the uncertainty in your relative energies (which qualifies your discussion of the results).

2.5 Choice of methods for describing the crystal structures

The most important output is the crystal structures that are thermodynamically plausible. Indeed, the point of doing the CSP study (apart from competing in blind tests!) is to see what types of packing of the molecule are competitive in energy with those that are experimentally known. In some cases, it can be that all the low energy structures contain the same expected strong interactions, such as a doubly hydrogen bonded dimer, and you are generating the different ways of packing this dimer. It can be that CSP has shown an unexpected hydrogen bonding motif, such as the catemer structures being competitive with the expected amide dimers, as found for carbamazepine.⁴⁰ Pondering over the alternative crystal structures generated is the most rewarding, and often human time-consuming part of the study, requiring the art of describing and comparing crystal structures, as traditionally performed by crystallographers in discussing polymorphism. However, as CSP may generate hundreds of crystal structures, which need to be compared with each other and the experimental structures, some degree of automation is required. Diverse methods of comparing dozens of crystal structures are being developed⁴¹ and used to find features, such as dimers, stacks or layers and other supramolecular constructs, or hydrogen bonding motifs, that are in common or differ between the low energy structures.

Thus, performing CSP studies requires a complex interplay of different programs, the choice of which is likely to depend on the type of molecule being studied, as well as many other factors. They can be packaged to automate the workflow for different computer architectures though, as Section 4 shows, the human interpretation of the results in terms of structural differences and similarities still has to evolve.

3. Illustration of a CSP study: naproxen

The range of decisions that need to be made can be illustrated⁴² by the CSP study of the non-steroidal anti-inflammatory drug naproxen (Fig. 6) which is marketed in a chirally pure form whose crystal structure was known. The joint experimental theoretical study wished to establish the structure of racemic naproxen and how well the energy differences between the two forms could be estimated, as this energy difference is central to designing crystallisation processes for separating enantiomers. A MOLPAK²⁸ search with Z′ = 1 in 19 space groups covering 39 common packing types, using each of the 8 low energy conformational minima, confirmed that a racemic structure should be more stable than the homochiral form. No experimental evidence was found for other phases, but considerable efforts to grow a single crystal of the racemic compound were fruitless, so the structure had to be solved from powder X-ray diffraction. Indexing the powder pattern suggested a Pbca space group and so this space group was searched more thoroughly using CrystalPredictor. The observation that there was a small but significant bend between the two aromatic components of the naphthalene fragment in the known chiral crystal structure increased the conformational variables (Fig. 6) that had to be refined within the crystal structures using CrystalOptimizer.³⁹ Analysis of the hydrogen bonding patterns and molecular stacking using XPac showed the expected result that the carboxylic acid dimer only occurs in racemic structures, but also revealed that two different types of hydrogen bonding chains can occur for either homochiral or racemic structures. There is a common layer in the four most stable structures, which may account for the difficulty in growing crystals of the racemate suitable for single crystal diffraction. The global minimum in the search was actually a transition state, and lowering the symmetry stabilised the lattice energy by 1 kJ mol⁻¹ from a minor shifting of layers and differences in conformation. Solid state NMR was used to confirm that the structure was indeed Pbca Z′ = 1, which was consistent with the estimate that even the zero-point motions would average over the Z′ = 2 Pca2₁ lattice energy minima.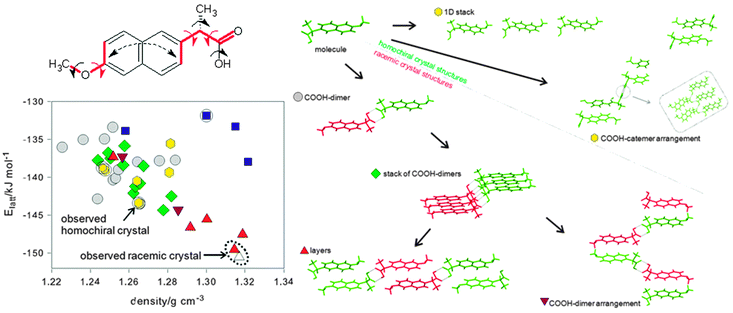

Fig. 6 The crystal energy landscape of naproxen,⁴² with the input conformational analysis and the classification of structures by packing motif. The three torsion angles indicated by red arrows differed significantly in the 8 conformational energy minima that were used as input into the search, and they, plus the additional torsions indicated by black arrows, were refined in each crystal structure in the final stage of structural optimisation. The structures on the energy landscape are classified firstly by chirality; a circle if they only contain the S-enantiomer (green) and so are enantiopure, otherwise the structure is racemic and also contains the R-enantiomer (red); and secondly by the most extensive supramolecular constructs contained in the structure. The blue squares indicate hydrogen bonding of the carboxylic acid to the methoxy groups, which is less thermodynamically plausible. △ is a Z′ = 2 variant of the racemic experimental structure. Reprinted with permission from Cryst. Growth Des., 2011, 11, 5659. Copyright 2011 American Chemical Society.

Whilst the CSP study was successful in assisting the determination of the racemic structure, and both racemic and enantiopure structures were the most stable within the appropriate set of space groups, the lattice energy difference between the two structures varied from 6 to 9 kJ mol⁻¹, depending on the (respectable) molecular wavefunction and plausible dielectric constants used in a polarisable continuum model for ΔE_intra and the distributed multipoles.⁴² The enthalpy difference between the structures derived from the heat of melting at 155.8 ± 0.3 °C and 156.2 ± 0.1 °C respectively was 1.5 ± 0.3 kJ mol⁻¹, and from solubility difference measurements in an ethanol–water mixture between 10 and 40 °C of 2.4 ± 1.0 kJ mol⁻¹. These results formed the basis of discussion of the many approximations used in the comparison of the energies of the chiral and racemic crystals.⁴² There is still some way to go before even the lattice energy contribution can be calculated with the accuracy required for the design of chiral resolution processes.

4. Interpreting the lattice energy landscape for thermodynamic control of crystallisation

If the result of a CSP study is that the most stable structure on the lattice energy landscape is significantly more stable than any other, as in the example of isocaffeine (Fig. 1), then there is a clear prediction this will be the only crystal structure containing just the molecule (i.e. monomorphism). When, as is usually the case, there are more structures within the energy range of plausible polymorphism, the question arises as to which could be possible polymorphs. Our current understanding of the kinetic factors, which lead to two or more polymorphs being able to coexist under the same thermodynamic conditions is very limited. There are examples of concomitant polymorphism,³ where two or more polymorphs crystallise in the same experiment.⁴ Indeed, the challenge of finding conditions to grow phase pure samples of the different polymorphs can frustrate the reliable measurement of the properties of the different crystal forms that are needed to design crystallisation processes or estimate relative stability, such as solubilities and heats of fusion. Hence, we are at the stage of contrasting experimental searches of polymorphs against the calculated crystal energy landscapes, trying to develop our ability to interpret the crystal energy landscape to predict undiscovered polymorphs. A recent review reflecting the authors experience of almost two hundred CSP studies, most of which had been done in collaboration with experimentalists working on the system, entitled “Why don't we find more polymorphs?”⁴³ illustrates some possible answers to this question. Here, it is more appropriate to look first at how far we can push the thermodynamic argument, from calculated lattice energy landscapes to crystal structure prediction, and then look at the kinetic (as well as other scientific and sociological) considerations (Section 5), in which nucleation plays an important role.

The definition of a crystal energy landscape as the set of crystal structures whose energies are sufficiently close to the most stable to be thermodynamically plausible as polymorphs, requires a decision as to what is “sufficiently close”. Polymorphic energy differences are typically less than a few kcal mol⁻¹,³ though it is the barrier to rearranging to the more stable form, rather than absolute energy difference, which is important. For example, desolvating a solvate crystal structure can lead to a high-energy form, which may be kinetically stabilised. Hence, allowing for some error in the relative lattice energy, structures within a cut-off of 7–10 kJ mol⁻¹ of the global minimum for a neutral molecule, or the point at which there is a marked increase in the number of structures which are approximately equi-energetic, are typically taken as the upper boundary of the crystal energy landscape. Whilst there is generally an increase in the number of crystal structures with decreasing stability (and also decreasing density), this can vary significantly, for example the lattice energy landscape of caffeine (Fig. 1), where there are a group of structures at the global minimum. Would it be worth refining the relative lattice energies of these structures, for example by periodic electronic structure (DFT-D) calculations on each, or does the thermodynamic argument require other approaches?

4.1 Calculate free energies instead of lattice energies

The molecular motions within the crystal means that many lattice energy minima will not be free energy minima. The static, perfectly ordered infinite crystal structures produced in a CSP search can be a misleading picture³⁵ though producing realistic computer models of finite organic crystals at normal temperatures with representative defects, and their ability to undergo reconstructive phase transitions, is a challenge for the future. Molecular Dynamics studies of benzene and 5-fluorouracil crystals show the contrast in the proportion of lattice energy minima that can transform to a more stable one: the number of free energy minima for benzene is close to the number of observed polymorphs, whereas only a quarter of the sixty structures comparable in energy to the two known polymorphs of 5-fluorouracil were not free energy minima at 310 K.⁴⁴ This is consistent with the two 5-fluorouracil polymorphs not showing any transformation below the melting point, as is often observed when a pair of polymorphs have different hydrogen bonding motifs, whereas benzene undergoes facile solid state transformations and rotates in its plane even at low temperatures.³⁵ Hence, the number of lattice energy minima that are artefacts of the neglect of the molecular motions within the crystal structure is very dependent on the ease of solid state transformations between the (hypothetical) crystal structures. This is determined by the structural differences.

Many organic solid-state polymorphic phase transformations are difficult, as once the molecule is close packed within a crystal, there is a significant barrier to rearrangement. It has been argued that all organic molecular transitions are first order, with the phase change requiring a nucleation and growth mechanism, rather than a mechanism that goes from single crystal to single crystal, maintaining translational symmetry throughout. The type of polymorphism that can be most readily observed by crystal to crystal transformation on changing the temperature can come from the high temperature, higher symmetry phase being a dynamic average over lower symmetry lattice energy minima. Examples are plastic or dynamically disordered phases. Since the high temperature phase of caffeine (form I) is a dynamically disordered layer structure, it seems likely that a Molecular Dynamics simulation starting from any of the group of low energy caffeine structures would result in form I caffeine.

4.2 Is static disorder plausible?

Another possible contribution to thermodynamic relative stability is configurational entropy arising from disorder. Static disorder is likely when the crystal energy landscape contains two or more structures that are so closely related both in structure and energy that it is hard to imagine molecules being able to assemble into perfect ordered crystals of either structure. This static disorder has been demonstrated in the case of eniluracil (Fig. 7) where there are a plurality of low energy structures, which are effectively the same if you do not distinguish between the C4=O and C6–H groups. These two groups are not involved in forming the hydrogen-bonded ribbons and barely affect the interdigitation of the ethynyl groups. These crystal structures are sufficiently close in energy that configurational entropy stabilises a disordered structure.⁴⁵ This type of calculation for evaluating the configurational entropy from the lattice energies of an ensemble of ordered supercells, generated by a site-occupancy disorder model, can also account for the low temperature structure of caffeine¹³ which has 20 molecules in the unit cell and Z′ = 2.5. The group of low energy structures on the caffeine lattice energy landscape (Fig. 1) represents just some of the ordered structures that contribute to the static disorder in form II caffeine. The small energy gaps on the crystal energy landscape and the intrinsic static and dynamic disorder in caffeine polymorphs correlates with the pseudo symmetry in the intermolecular interactions of caffeine. The difference in the intermolecular interactions explains the differences in the crystal energy landscapes and crystallisation behaviour of caffeine and its isomer isocaffeine (Fig. 1).

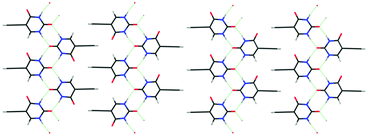Fig. 7 Similarities in CSP generated crystal structures can suggest that crystallising in one ordered structure is unlikely. For eniluracil a range of structures based on this layer, which are almost identical if a C=O and C–H group are not distinguished, are very close in energy and show nearly identical powder X-ray diffraction patterns. Left; non-polar hydrogen-bonded ribbons with the ethynyl groups interdigitated so ribbons are anti-parallel, right; polar ribbons interdigitated in parallel (giving a polar crystal). The possible interdigitation of these two motifs emphasises how the number of possible structures would increase with the extent of the CSP search. The configurational entropy associated with these structures⁴⁵ shows that the most stable structure would be disordered, as found experimentally.

4.3 Is the structure metastable to other molecular compositions and phases?

As Section 2.1 indicates, even the lowest energy structure may not be found because it is not stable relative to other chemical compositions. Solvates or cocrystals may be unstable relative to their components or another stoichiometry. The lattice energy differences are generally small, just as the experimental thermodynamic driving force for cocrystal formation is often small and affected by contributions such as the difference in solvation energy if the other molecule is present. The equilibria between various hydrates and the anhydrate are dependent on temperature and relative humidity. So although there have been successful predictions of the stoichiometry of cocrystals, solvates and hydrates, for example ref. 46 and 47 and references to and therein, the interpretation in terms of the low energy structures can be more convincing than the energy differences. For example, the 1 : 2 stoichiometry of urea : acetic acid structures is the only one in which all the hydrogen bonding can be satisfied⁴⁶ and 2,5-dihydroxybenzoic acid forms no hydrates because it is more stable and denser in the anhydrous phase than its isomer, 2,4-dihydroxybenzoic acid, for which a stable hemihydrate and metastable monohydrate were found in an equivalent experimental screen.⁴⁷

A more subtle issue for thermodynamic prediction is the role of solvent, which can be undetected by routine crystallography if it is mobile within the crystal structure. Investigations prompted by the relatively high lattice energy of carbamazepine form II⁴⁸ found solvent molecules moving quite freely in the channels. The issue of guest molecules changing the thermodynamics as well as the kinetics of crystallisation is beginning to be explored: polymorphs found by desolvating solvates may be highly metastable; the framework structures of organic inclusion compounds can be found as high energy, low density structures on the crystal energy landscape; and indeed CSP has been able to predict the structures of porous organic molecules without explicitly considering the solvent.^43,49 Indeed, analysis of the structures on densely populated crystal energy landscapes are beginning to be used to discuss gel formation, amorphous states and other issues relating to the prevention or apparent inability of molecules to crystallise.⁴³

Thus, calculating accurate relative free energies of all different possible solid phases of a molecule is a challenge that extends far beyond the capabilities of CSP approaches. However, because thermodynamics is rarely the only factor that determines the observed solid forms of organic molecules, a CSP study provides a guide to the potential complexity of the solid state by generating the favoured modes of self-assembly of a molecule. As such CSP studies can form a complement to solid form screening, where considerable effort needs to be expended to try to crystallise without inadvertent seeds of the known forms and to vary the crystallisation conditions to try to either ensure or avoid thermodynamic control of the crystallisation process.^7,8,14,19

5. Interpreting the crystal energy landscape – which metastable structures could be practically important polymorphs?

Whilst there is a strong relationship between the experimental structural landscape⁵ and the computed crystal energy landscape of a molecule,¹² there are usually more thermodynamically feasible crystal structures computed than known polymorphs. This raises the question of which of these structures could be found as polymorphs, given the right crystallisation conditions. There are many factors that determine the relative nucleation and growth rates of polymorphs, and defining the recipe to crystallise a given polymorph reproducibly is sometimes challenging.⁵⁰ Currently, we can perform a CSP study, and from the lattice energy landscape and knowledge of the differences between the structures, estimate which structures seem likely to be free energy minima because of the barrier to solid state transformation. If there are unknown structures that appear to be thermodynamically plausible as metastable polymorphs, this raises some questions.

5.1 Could the structure nucleate and grow as a distinct polymorph?

Unless solid-state transformations are facile, the crystal packing becomes fixed at the temperature and pressure at which it is formed. It is the reorientation and conformational changes of the molecules as they associate during the time allowed for crystallisation from the melt, vapour or solution that determines whether a molecule crystallises in the stable or metastable form.

Qualitative estimates of whether two structures are so closely related that only the more stable would crystallise, or sufficiently different that there would be a barrier to interconversion during nucleation,⁴³ can be based on dominant strong interactions such as hydrogen bonding. However, after the 2001 blind test, the consensus was that two molecules were likely to have polymorphs with different hydrogen bonding motifs. Two new polymorphs of 6-amino-2-phenylsulfonylimino-1,2-dihydropyridine were found, but screening of 3-azabicyclo[3.3.1]nonane-2,4-dione found a high-temperature plastic phase. Further calculations then showed that this spherical molecule could reorientate very readily as the imide hydrogen bonding was very weak. Hence, hydrogen bonds, as defined by software that uses distance criteria, is not a reliable guide to the barriers to changing hydrogen bonding motif during nucleation.

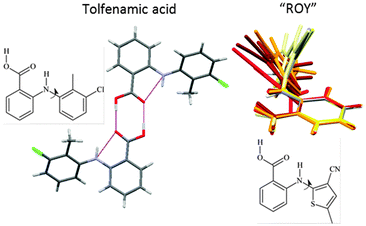
The ability to trap molecules in metastable polymorphs because they cannot rearrange readily can also be associated with larger functional groups and conformational flexibility. The concept of a polymorphophore (Fig. 8) as a molecular fragment that appears to promote polymorphism is exemplified by the fenamates²¹ and ROY (this nickname for 5-methyl-2-[(2-nitrophenyl)amino]-3-thiophenecarbonitrile comes from the distinctive red-orange-yellow colours of its polymorphs which differ in the torsion angle).^4,21 Both systems have an aromatic ring which has a very low barrier to rotation through a wide range of angles in the isolated molecule. Once the aromatic rings interdigitate in forming the nucleus or crystal, the conformational flexibility is drastically reduced, helping different packings with different torsion angles to be trapped as polymorphs. The crystal energy landscapes of both tolfenamic acid²¹ and ROY²³ show that their known polymorphs are competitive in energy with other structures which may yet prove to correspond to other polymorphs, such as the structurally uncharacterised forms of ROY.⁴ In contrast, both a bromo-derivative of ROY and fenamic acid appear to be monomorphic. For fenamic acid the low energy structure generated in a Z′ = 1 CSP study²¹ was so closely related to the observed Z′ = 2 structure, and the next most stable structure, 2 kJ mol⁻¹ higher in energy, that it seems most unlikely that the computer generated structure could be trapped as a distinct polymorph. Thus, the relationship between the low energy structures on the crystal energy landscape shows whether there are low energy structures that are more readily kinetically trapped for polymorphophores.

Fig. 8 The type of conformational flexibility that can lead to kinetic trapping of structures, producing polymorphophores, (left) a fenamate, tolfenamic acid, showing the building block whose phenyl “paddle-wheels” vary in conformation in the five polymorphs and (right) an overlay of the conformations in the 7 structurally characterised polymorphs of ROY, with the most stable (Y) in atomic colours.

5.2 Can we find the right experiment to nucleate this polymorph?

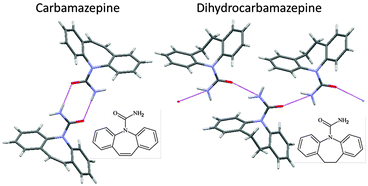
Interest in CSP has been aroused by the discovery of polymorphs corresponding to calculated low energy structures, for example, form II aspirin in a failed cocrystallisation experiment, form II 5-fluorouracil by crystallising from dry nitromethane and form II maleic acid in an attempt to recrystallise a caffeine–maleic acid cocrystal produced by grinding. These crystallisation conditions are unusual, in that either the presence or absence of another molecule appears to be important in producing the first crystal of the new form. The role of other molecules in the serendipitous finding of new polymorphs of substances that have been heavily studied, (which can be calamitous if it leads to disappearing polymorphs), emphasises the impossibility of experimentally covering all types of crystallisation conditions that have led to the discovery of a new polymorph of any molecule.¹⁴ Hence, the computer prediction that an unknown crystal structure appears to be thermodynamically plausible automatically raises the question as to whether an experiment can be designed to find the polymorph.

This has been demonstrated in the case of carbamazepine, a generic anti-epileptic that has been extensively used in polymorphism studies. The crystal energy landscape showed that some packings of catemeric hydrogen bonded amide chains were thermodynamically competitive with structures containing the doubly hydrogen bonded dimer, including the four known polymorphs. A closely related molecule, dihydrocarbamazepine, had a polymorph which was isostructural with a CSP generated catemeric form. Subliming carbamazepine in the presence of a seed crystal of dihydrocarbamazepine form II allowed the nucleation and growth of catemeric carbamazepine form V on the heteromolecular template (Fig. 9).⁴⁰

Fig. 9 The first catemeric polymorph of carbamazepine (form V) was produced by sublimation onto the isostructural dihydrocarbamazepine form II crystal. This showed the ability of a seed template of dihydrocarbamazepine catemers (right) to disrupt the formation of the dimer motif (left) seen in carbamazepine forms I–IV.

Less specific properties of the low energy crystals may be useful in designing crystallisation strategies. Examination of the hydrogen bonding can suggest that experiments in specific solvents may be worthwhile,⁵¹ whereas denser structures could be targeted by crystallisation under pressure. However, the range of polymorphs is clearly limited by the ability to vary the crystallisation conditions sufficiently to change the mode of self-assembly. The difficulty with assessing this is illustrated by the role of impurities in crystallisation: whilst impurities can have a major effect on polymorph screening and characterisation, including inhibiting crystallisation,⁷ there are also cases such as form I sulphathiazole and form II progesterone, where specific, chemically related impurities appear needed to produce a long-lived metastable form.⁴³ Recently a designed hetero-nuclear seed has been found so effective at producing the predicted but previously unobtainable caffeine:benzoic acid cocrystal that four different laboratories collaborated to establish its role.⁵²

5.3 Eliminating the possibility of nucleating other polymorphs

The physical properties of many molecules, particularly thermal instability or limited solubility in all solvents, will severely limit the range of crystallisation experiments that are feasible. It can be very difficult to ensure that the crystallisation experiment is not seeded with nuclei of the known forms, particularly if the input material is not (and perhaps cannot be) amorphous. Since the main value of CSP is to assess the risk of “unexpected” crystallisation outcomes, the challenge is to be sure that a calculated low energy crystal structure could never be found, or at least not within the process conditions for an industrial product.

You can be confident that crystallising a naturally enantiopure molecule can only lead to polymorphs in chiral space groups, unless there is the possibility of racemisation during the crystallisation. Some conformational changes are unlikely; in the last blind test¹⁵ some groups included both cis and trans amide conformations of the model pharmaceutical XX (Fig. 2) in their search, but this stereochemistry is likely to be defined during synthesis and not change during crystallisation. However, when the barriers to gross conformational changes are smaller, the range of conformations and the types of solute association in solution may vary with the solvent molecule. For example, the observation that olanzapine is in a dimer (Fig. 4) in all its crystalline forms, despite the crystal energy landscape having thermodynamically competitive structures which do not contain the dimer but otherwise resemble known polymorphs,²⁴ suggests that the dimer forms early in the crystallisation process. Does the unusually rapid crystallisation of the only anhydrate polymorph found in extensive screening of GSK269984B¹⁹ mean that seeding by nuclei of this form cannot be avoided? In this case, although it seems unlikely that none of the solutions contained some of the conformers seen in the low energy calculated metastable forms (Fig. 4), the anhydrate and solvates all had essentially the same conformation as the isolated molecule apart from the hydrogen bonding proton.

5.4 Could the polymorph exist but not have been detected or structurally characterised?

Establishing whether thermodynamically plausible polymorphs could be found is limited by the degree of screening and characterisation that is practically possible. Unless the powder X-ray diffraction of the bulk sample is compared with that simulated from solved single crystal structures, there may be undetected polymorphs amongst the remaining crystals. The ability to determine crystal structures from powder X-ray diffraction is increasing, with crystal energy landscapes being used to suggest plausible structures, add confidence, and solve ambiguities in proton positions. Indeed CSP is beginning to be used to help solve the crystal structures from high-resolution solid state ¹H NMR or from electron diffraction patterns. The application of transmission electron microscopy to find crystallites with distinct morphologies and use CSP to help determine the crystal structure of theophylline form VI is particularly noteworthy, as the new polymorph occurred in a mixture with form II at a concentration below the limits of detection of analytical methods routinely used for pharmaceutical characterisation.⁵³

6. Conclusion

The increasing computer power in the last two decades has made reasonable CSP searches possible for an increasing range of molecular systems, and there have been many successful predictions of organic crystal structures. However, it has also become apparent that many molecules do not have one crystal structure that is sufficiently more stable than any others for polymorphism to be unlikely. During the same period, the emergence of increasingly sophisticated experimental methods of finding and characterising solid forms has shown that the incidence of polymorphism is much higher than had been expected from the days when crystallographers concentrated on molecular structure and the first adequate crystal that could be grown. Hence, CSP methods are now being used as part of the interdisciplinary range of studies to establish the range of solid forms of a molecule. This is required to ensure that the solid form with the best compromise of physical properties can be manufactured reliably. Calculating the crystal energy landscape should estimate the maximal diversity in the range of polymorphs and hence solid-state properties.

Although crystal energy landscapes have been contrasted with careful experimental work for a few hundred molecular systems, the range of different crystalline behaviours observed, even within families of closely related molecules (as exemplified by caffeine and isocaffeine in Fig. 1), means that the interpretation of the landscapes with small energy gaps between different structures is necessarily tentative. Considerably more experience is needed before we can eliminate thermodynamically plausible structures as unlikely to be observed because they cannot crystallise distinct from slightly more stable related structures, or design an experiment to find the novel polymorph. Observing the complex interplay between nucleation and growth of different polymorphs is challenging, even in the most advantageous cases,⁴ let alone when impurities or heterogeneous surfaces play a role in the first nucleation of a new polymorph. A careful CSP study can either reduce or expand the amount of experimental work needed to determine the full complexity of the solid form landscape of a molecule by either confirming that all practically important polymorphs are known, or suggesting that additional structures that should be targeted. The complexity of crystallisation behaviour is very specific to the molecule.

Acknowledgements

The many people from different disciplines who worked on the CPOSS (Control and Prediction of the Organic Solid State) project www.cposs.org.uk, and the EPSRC for funding some of them under the Basic Technology program GR/S24114 and EP/F03573X/1. This paper has been shaped by discussions with many people at meetings associated with CPOSS, the Cambridge Crystallographic Data Centre blind tests of CSP and the EPSRC Directed Assembly Network (EP/H035052/1 and EP/K014382/1 Nucleation and Crystallisation theme). Drs Louise Price, Doris Braun and Matthew Habgood are particularly thanked for their help with producing this manuscript. This paper is dedicated to the memory of Herman Ammon (1936–2013), one of the pioneers of CSP, whose generous help with the program MOLPAK enabled me to start working in this field.

Notes and references

1. G. M. Day, Crystallogr. Rev., 2011, 17, 3–52.
2. J. Bernstein, Cryst. Growth Des., 2011, 11, 632–650.
3. J. Bernstein, Polymorphism in Molecular Crystals, Clarendon Press, Oxford, 2002.
4. L. Yu, Acc. Chem. Res., 2010, 43, 1257–1266.
5. G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967.
6. C. C. Sun, J. Pharm. Sci., 2009, 98, 1744–1749.
7. R. Hilfiker, Polymorphism in the Pharmaceutical Industry, Wiley-VCH, Weinheim, 2006.
8. R. A. Storey and I. Ymén, Solid state characterization of pharmaceuticals, Wiley, Chichester, 2012.
9. J. van de Streek and S. Motherwell, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 504–510.
10. F. H. Allen and R. Taylor, Chem. Soc. Rev., 2004, 33, 463–475.
11. G. P. Stahly, Cryst. Growth Des., 2007, 7, 1007–1026.
12. S. L. Price, Acc. Chem. Res., 2009, 42, 117–126.
13. M. Habgood, Cryst. Growth Des., 2011, 11, 3600–3608.
14. A. Llinas and J. M. Goodman, Drug Discovery Today, 2008, 13, 198–210.
15. D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. la Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. Hofmann, F. Hofmann, K. Jose, V. P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551.
16. D. E. Braun, R. M. Bhardwaj, A. J. Florence, D. A. Tocher and S. L. Price, Cryst. Growth Des., 2013, 13, 19–23.
17. M. U. Schmidt, J. Bruning, J. Glinnemann, M. W. Hutzler, P. Morschel, S. N. Ivashevskaya, J. van de Streek, D. Braga, L. Maini, M. R. Chierotti and R. Gobetto, Angew. Chem., Int. Ed., 2011, 50, 7924–7926.
18. S. Mohamed, D. A. Tocher and S. L. Price, Int. J. Pharm., 2011, 418, 187–198.
19. S. Z. Ismail, C. L. Anderton, R. C. B. Copley, L. S. Price and S. L. Price, Cryst. Growth Des., 2013, 13, 2396–2406.
20. A. J. Cruz-Cabeza and J. Bernstein, Chem. Rev. DOI:10.1021/cr400249d.
21. O. G. Uzoh, A. J. Cruz-Cabeza and S. L. Price, Cryst. Growth Des., 2012, 12, 4230–4239.
22. M. A. Neumann, J. Phys. Chem. B, 2008, 112, 9810–9829.
23. M. Vasileiadis, A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 677–685.
24. R. M. Bhardwaj, L. S. Price, S. L. Price, S. M. Reutzel-Edens, G. J. Miller, I. D. H. Oswald, B. Johnston and A. J. Florence, Cryst. Growth Des., 2013, 13, 1602–1617.
25. J. W. Steed, CrystEngComm, 2003, 5, 169–179.
26. S. Mohamed, S. A. Barnett, D. A. Tocher, K. Shankland, C. K. Leech and S. L. Price, CrystEngComm, 2008, 10, 399–404.
27. A. Gavezzotti, Molecular Aggregation: Structure Analysis and Molecular Simulation of Crystals and Liquids, Oxford University Press, Oxford, 2007.
28. J. R. Holden, Z. Y. Du and H. L. Ammon, J. Comput. Chem., 1993, 14, 422–437.
29. A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, Oxford, 2nd edn, 2013.
30. M. A. Neumann and M. A. Perrin, J. Phys. Chem. B, 2005, 109, 15531–15541.
31. A. M. Lund, A. M. Orendt, G. I. Pagola, M. B. Ferraro and J. C. Facelli, Cryst. Growth Des., 2013, 13, 2181–2189.
32. J. Kendrick, F. J. Leusen, M. A. Neumann and J. van de Streek, Chem.–Eur. J., 2011, 17, 10735–10743.
33. S. L. Price, Int. Rev. Phys. Chem., 2008, 27, 541–568.
34. P. G. Karamertzanis, G. M. Day, G. W. A. Welch, J. Kendrick, F. J. J. Leusen, M. A. Neumann and S. L. Price, J. Chem. Phys., 2008, 128, 244708–244717.
35. A. Gavezzotti, New J. Chem., 2013, 37, 2110–2119.
36. G. M. Day, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1023–1033.
37. S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490.
38. T. G. Cooper, K. E. Hejczyk, W. Jones and G. M. Day, J. Chem. Theory Comput., 2008, 4, 1795–1805.
39. A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016.
40. J. B. Arlin, L. S. Price, S. L. Price and A. J. Florence, Chem. Commun., 2011, 47, 7074–7076.
41. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.
42. D. E. Braun, M. Ardid-Candel, E. D'Oria, P. G. Karamertzanis, J. B. Arlin, A. J. Florence, A. G. Jones and S. L. Price, Cryst. Growth Des., 2011, 11, 5659–5669.
43. S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 313–328.
44. P. G. Karamertzanis, P. Raiteri, M. Parrinello, M. Leslie and S. L. Price, J. Phys. Chem. B, 2008, 112, 4298–4308.
45. M. Habgood, R. Grau-Crespo and S. L. Price, Phys. Chem. Chem. Phys., 2011, 13, 9590–9600.
46. A. J. Cruz-Cabeza, G. M. Day and W. Jones, Chem.–Eur. J., 2008, 14, 8830–8836.
47. D. E. Braun, P. G. Karamertzanis and S. L. Price, Chem. Commun., 2011, 47, 5443–5445.
48. A. J. Cruz-Cabeza, G. M. Day, W. D. S. Motherwell and W. Jones, Chem. Commun., 2007, 1600–1602.
49. J. T. A. Jones, T. Hasell, X. F. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Nature, 2011, 474, 367–371.
50. T. Threlfall, Org. Process Res. Dev., 2000, 4, 384–390.
51. W. I. Cross, N. Blagden, R. J. Davey, R. G. Pritchard, M. A. Neumann, R. J. Roberts and R. C. Rowe, Cryst. Growth Des., 2003, 3, 151–158.
52. D. K. Bucar, G. M. Day, I. Halasz, G. G. Z. Zhang, J. R. G. Sander, D. G. Reid, L. R. MacGillivray, M. J. Duer and W. Jones, Chem. Sci., 2013, 4, 4417–4425.
53. M. D. Eddleston, K. E. Hejczyk, E. G. Bithell, G. M. Day and W. Jones, Chem.–Eur. J., 2013, 19, 7883–7888.

---