Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A kinetic study of the CH2OO Criegee intermediate self-reaction, reaction with SO2 and unimolecular reaction using cavity ring-down spectroscopy†
Rabi
Chhantyal-Pun
a,
Anthony
Davey
a,
Dudley E.
Shallcross
a,
Carl J.
Percival
b and
Andrew J.
Orr-Ewing
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: a.orr-ewing@bristol.ac.uk
bCentre for Atmospheric Science, School of Earth, Atmospheric and Environmental Sciences, University of Manchester, Simon Building, Oxford Road, Manchester, M13 9PL, UK
First published on 22nd December 2014
Abstract
Criegee intermediates are important species formed during the ozonolysis of alkenes. Reaction of stabilized Criegee intermediates with various species like SO2 and NO2 may contribute significantly to tropospheric chemistry. In the laboratory, self-reaction can be an important loss pathway for Criegee intermediates and thus needs to be characterized to obtain accurate bimolecular reaction rate coefficients. Cavity ring-down spectroscopy was used to perform kinetic measurements for various reactions of CH2OO at 293 K and under low pressure (7 to 30 Torr) conditions. For the reaction CH2OO + CH2OO (8), a rate coefficient k8 = (7.35 ± 0.63) × 10−11 cm3 molecule−1 s−1 was derived from the measured CH2OO decay rates, using an absorption cross section value reported previously. A rate coefficient of k4 = (3.80 ± 0.04) × 10−11 cm3 molecule−1 s−1 was obtained for the CH2OO + SO2 (4) reaction. An upper limit for the unimolecular CH2OO loss rate coefficient of 11.6 ± 8.0 s−1 was deduced from studies of reaction (4). SO2 catalysed CH2OO isomerization or intersystem crossing is proposed to occur with a rate coefficient of (3.53 ± 0.32) × 10−11 cm3 molecule−1 s−1.
Introduction
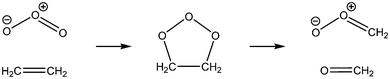
In 1949 Rudolph Criegee1 proposed that an intermediate (later to be called a Criegee intermediate) was formed during the ozonolysis of alkenes. On addition of ozone to an alkene a primary ozonide (POZ) is formed which decomposes to form a carbonyl and a Criegee intermediate (CI).2–4 Taking ethene as an example, the following reaction sequence leads to the formation of the simplest CI, CH2OO.The Criegee intermediate formed can undergo rapid unimolecular decomposition, often to yield OH radicals,5–7 but a second much slower decomposition has been observed and attributed to so called stabilised CI (SCI).6,7 These SCI are formed with internal energies below the threshold to unimolecular decomposition and are sufficiently long lived to undergo reaction with atmospheric trace gases. SCIs were postulated but remained undetected in the gas-phase until the work of Taatjes and co-workers,8–12 who showed that these SCIs could be generated through photolysis of alkyl diiodide species in the presence of oxygen, e.g.
| CH2I2 + hν → CH2I + I | (1) |
| CH2I + O2 → CH2OO + I | (2) |
| CH2I + O2 + M → ICH2O2 + M | (3) |
This breakthrough has led to many recent studies that have investigated the UV/visible,13–19 IR20,21 and microwave22–24 spectra, as well as several kinetic studies of CH2OO and CH3CHOO with SO2, NO, NO2, carbonyls, alkenes and organic acids.8–11,16,25–30 Direct studies, i.e. ones that monitor the decay of SCI or a proxy of the SCI (e.g. HCHO, OH) return rate coefficients that are considerably larger than previous indirect estimates based on end product analysis.2 These new kinetic data suggest a greater role for SCI species in the atmospheric oxidation of SO2 and NO2 in particular.
Field measurements support a role for the SCI assisted production of H2SO4 (ref. 31) and although model studies disagree as to the extent, they do agree that there is a non-negligible impact of CIs on oxidation of SO2.32–34 If the gas-phase oxidation of SO2 to SO3 (and subsequently H2SO4) by SCI competes with, or even dominates in regions of the lower troposphere, over the oxidation by OH, the formation of H2SO4 may be accelerated and aerosol nucleation rates affected.32,33
| CH2OO + SO2 → HCHO + SO3 | (4) |
| OH + SO2 → HOSO2 | (5) |
There is considerable debate concerning the impact of these new data, with models predicting effects ranging from significant through to more modest. Given the differences in chemical scheme used in these various model studies as well as model resolution, current disagreement on SCI impact remains to be resolved. However, models that contain detailed chemistries, e.g. the Master Chemical Mechanism32 and its surrogate the Common Representative Intermediates scheme,33 return a more significant impact than those models with less hydrocarbon chemistry.34 A major issue at the core of these discrepancies concerns the two loss processes that dominate the SCI concentration, unimolecular loss and reaction with water vapour:
| CH2OO → Products | (6) |
| CH2OO + H2O → Products | (7) |
Welz et al., Li et al., and Percival et al. noted that significant SCI levels are predicted if k6 is around 200 s−1 or less and if k7 is less than around 1 × 10−16 cm3 molecule−1 s−1.9,32,33 Further work is required to determine k6 and k7 more accurately.
Recent work has shown that the rate coefficient for the self-reaction of CH2OO (reaction (8)) is very large.35
| CH2OO + CH2OO → 2HCHO + O2 | (8) |
Although this reaction has no atmospheric relevance, it could be important in laboratory studies that probe the kinetics and mechanisms of alkene ozonolysis.36 In this paper we report measurements of k4, k6 and k8 at room temperature over a range of pressure, using near UV cavity ring-down spectroscopy (CRDS) to detect CH2OO. Where appropriate, we compare with previously reported rate coefficients obtained using alternative methods.
Experimental
Cavity ring down spectroscopy was used to probe temporal profiles of CH2OO signals in flowing gas samples using the known![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (1A′) ←
(1A′) ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) (1A′) electronic absorption band in the near ultraviolet (UV) spectral region. UV probe radiation was generated by frequency doubling the visible radiation output of a dye laser (Sirah CobraStretch, with pyridine 1 dye) pumped by the second harmonic of a Nd:YAG laser (Continuum Surelite III-10). A probe wavelength of 355 nm was chosen to maximize CH2OO absorption13,16 and minimize interferences. The ESI† provides detailed discussion of possible interferences and their elimination.
(1A′) electronic absorption band in the near ultraviolet (UV) spectral region. UV probe radiation was generated by frequency doubling the visible radiation output of a dye laser (Sirah CobraStretch, with pyridine 1 dye) pumped by the second harmonic of a Nd:YAG laser (Continuum Surelite III-10). A probe wavelength of 355 nm was chosen to maximize CH2OO absorption13,16 and minimize interferences. The ESI† provides detailed discussion of possible interferences and their elimination.
The third harmonic of a Continuum Surelite I-10 Nd:YAG laser (λ = 355 nm; 100 mJ per pulse; energy density ∼500 mJ cm−2, <10 ns pulse duration) was used to photolyze CH2I2 to start the chemistry leading to production of CH2OO. The unfocussed photolysis beam had a diameter of 5 mm with a top-hat intensity profile, and crossed the probe beam (with beam waist of 0.24 mm) at an angle of 5°, giving an overlap length of 5.7 cm in the centre of the CRDS cavity. The delay between the two laser pulses was controlled by a BNC 555 digital delay generator.
High reflectivity mirrors (R > 99.9% at 355 nm, 100 cm radius of curvature) were mounted 106 cm apart at opposite ends of a glass tube to form the ring-down cavity. Light escaping from one end mirror of the cavity was monitored by a photodiode (New Focus 1801) and digitized by an 8 bit oscilloscope (LeCroy Waverunner 6030; 350 MHz, 2.5 GSamples per s). Typical ring-down times <6 μs were much shorter than the 1–10 ms timescales used for reaction kinetics measurements under our experimental conditions.
The 6 cm diameter glass tube confined the flow of reagent and bath gases along the detection axis of the spectrometer. The flow rates for all gases were regulated by calibrated mass flow controllers (MKS 1479A and 1179A). The precursor molecule, diiodomethane (CH2I2, 99%), and sulphur dioxide (SO2, ≥99.9%) were purchased from Sigma-Aldrich. CH2I2 was purified further by freeze–pump–thaw cycling before use. High purity nitrogen (N2) and oxygen (O2) were obtained from Air Liquide. Pre-mixtures of CH2I2 in N2 (0.7 Torr/750 Torr) and SO2 in N2 (5 or 750 Torr/1500 Torr) were made and allowed to mix for at least a day to obtain a homogenous mixture. Low flows (20 sccm) of nitrogen were passed through purge lines close to the ring down mirrors to prevent mirror contamination. All the other gases were passed into the flow tube through a port close to the centre of the cavity. 1.0 to 2.0 Torr of the precursor premixes, 1.0 Torr of oxygen and various pressures of nitrogen were used for the experiments. Sample pressures were measured by two capacitance manometers (0–10 Torr and 0–1000 Torr) located close to the centre of the flow tube. Total flow rates (excluding the mirror purges) ranged from 50–500 sccm, and we verified that the purge flows did not significantly change the overall column length of the gas mixture used in kinetic studies over the total pressure range 7–30 Torr by measuring absorption by CH2I2 or added NO2. We obtained average gas sample lengths of 37 ± 3 cm that are a factor of 6.5 longer than the overlap region of the photolysis and probe laser beams in which the chemistry of interest occurs. The arrangement of the overlap of the probe and much-larger diameter photolysis laser beams gives a flat concentration profile across the probe region at early times, and diffusion out of the probe volume is expected to be a first order process. We also calculate that mass flow across the probe volume will have negligible effects over the timescales of our kinetic measurements.
Further details of the spectrometer and optimization of experimental conditions are provided in the ESI.†
Results and discussion
(I) CH2OO + CH2OO reaction
Relatively high concentrations of CH2OO need to be produced in laboratory experiments in order to provide enough signal for kinetic measurements. In the present work, typical initial CH2OO concentrations of 2.5–5.0 × 1012 molecule cm−3 were generated. Under such conditions, the self-reaction can contribute significantly to the overall loss of CH2OO. Recently, Su et al. reported a CH2OO self-reaction rate constant of k8 = (4 ± 2) × 10−10 cm3 molecule−1 s−1 by monitoring depletion of infrared bands.35 This value was refined to k8 = (6.0 ± 2.1) × 10−11 cm3 molecule−1 s−1 by Buras et al., by simultaneous monitoring of the near UV band of CH2OO and near IR absorption of iodine atoms.37 Recently, Ting et al. reported a k8 value of (8 ± 4) × 10−11 cm3 molecule−1 s−1 using broadband UV absorption spectroscopy and monitoring CH2OO depletion along with that of CH2I and IO.38 Reaction of CH2I with O2 was used to produce CH2OO in all of these studies. Using photoionization mass spectrometry, this chemical route was shown to produce sufficient CH2OO radical concentration to perform kinetic measurements.9 In this work we used a similar reaction pathway shown by reactions (1) and (2) to produce CH2OO. Other than the self-reaction, we also considered the following removal pathways for CH2OO and I.| CH2OO + I + M → ICH2O2 + M | (9) |
| CH2OO + I → ICH2 + O2 | (10) |
| CH2OO + I → HCHO + IO | (11) |
| CH2OO + ICH2O2 → Products | (12) |
| I + I + M → Products | (13) |
Under our experimental conditions, CH2I is expected to react with O2 within the first time step (200 μs) of the kinetic measurements. The branching ratio of reactions (2) and (3) determines the yield of CH2OO which increases with a decrease in the concentration of the third body (M). Under low pressure conditions and in the absence of other reactant species, the self-reaction (8), and reactions (9)–(11) with iodine atoms, are expected to be the major loss mechanism for CH2OO. At higher pressures, contribution from reaction (12) will increase. Assuming the fast self-reaction to be the dominant loss mechanism, the decay traces of CH2OO were fitted to an integrated second order decay expression. Further justification for this fitting procedure is provided later. For a second order decay mechanism,
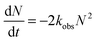 | (14) |
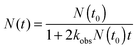 | (15) |
In eqn (15), N(t0) is the initial CH2OO concentration. In our cavity ring-down measurements, probe light intensity decay rate constants, κ, (or ring-down times, τ = 1/κ) are measured with and without the photolysis laser on to give a transient absorption signal. The concentration of the absorbing species is given by
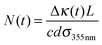 | (16) |
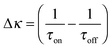 | (17) |
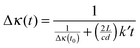 | (18) |
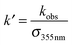 | (19) |
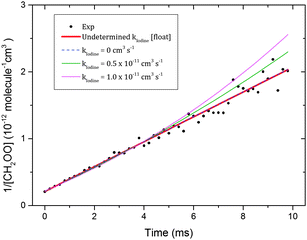
The ESI† summarizes possible sources of interferences at the 355 nm probe wavelength and our procedure for their elimination. The interference-subtracted decay traces were fitted to eqn (18) as exemplified by the data shown in Fig. 1. Data points starting from a 200 μs time delay to around 10 ms were included in the fit. Reaction (2) is calculated to have a half-life of 11.8 μs based on the bimolecular rate coefficient of 1.82 × 10−12 cm3 molecule−1 s−1 (ref. 16) and hence is expected to be complete by 200 μs. Experimental conditions were selected such that the CH2OO signal depletes by greater than 90% by a photolysis-probe delay of 10 ms. Under such conditions, non-second order loss mechanisms like diffusion and mass flow do not contribute significantly to the decay mechanism, as discussed in the Experimental section. Details of the experiments to characterize the non-second order loss mechanisms in the detection region of the flow tube are presented in the ESI.†
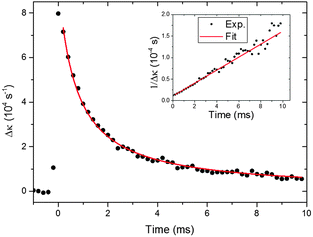 | ||
| Fig. 1 Time-dependent CH2OO intermediates signal under conditions in which the self-reaction (8) dominates. Black circles show the experimental CH2OO signal and the red line is a fit of the experimental signals to eqn (18). The initial CH2OO concentration was ∼5.1 × 1012 molecule cm−3. The inset shows the reciprocal of the experimental and fitted Δκ values as a function of time for clarity. | ||
CH2OO decay traces were obtained for different initial concentrations of the CH2OO (see ESI†) and at different bath gas (N2) pressures. Fig. 2 shows the fitted k′ values obtained from kinetic decay traces as a function of the bath gas concentration. These values are also provided in Table S4 in the ESI.† The quality of the second order fits for the CH2OO decay traces under all the pressure conditions (7 to 30 Torr) is excellent, with adjusted R2 values greater than 0.99. A second order decay form of the type used in the analysis is strictly valid for a bimolecular reaction in which the two reactants are of equal concentrations. Thus, the extracted k′ values should derive primarily from the self-reaction of CH2OO or reaction of CH2OO with similar concentrations of other molecules like ICH2OO, I atom or a mixture of both. The obtained values show a positive dependence on N2 bath gas pressure. The I atom yield is expected to decrease with increasing pressure, whereas the contribution from the reaction between ICH2OO and CH2OO should increase with an increase in pressure. The CH2OO self-reaction rate coefficient has been calculated to be independent of pressure.30,35 The pressure range studied in the current work offers a window in which the concentrations of CH2OO and of co-reactants, either ICH2OO or I atoms, are such that the overall CH2OO decay follows a second order form. The relative contributions of these reactions to the value of k′ are discussed later.
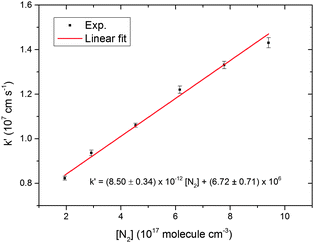 | ||
| Fig. 2 CH2OO overall scaled second order decay rate coefficient, k′, as a function of N2 concentration. The error bars are the 1σ uncertainties from the fits of kinetic decay traces such as that shown in Fig. 1 to eqn (18). | ||
An empirical linear fit was performed for the plot of k′ values as a function of N2 concentration as shown in Fig. 2. The quality of the fit is good, with an adjusted R2 value greater than 0.99, and the intercept was taken as the zero pressure limit value for k′. The rate of reaction (9) should decrease with a decrease in the third body concentration, which lowers the yield of ICH2OO, whereas the rate coefficients for (10) and (11) are calculated to be independent of pressure35 and could contribute significantly to the CH2OO loss along with the dominant self-reaction under low pressure conditions. A quantitative analysis of the pressure dependence evident in Fig. 2 is presented in the ESI,† and our observations can be accounted for if the rate coefficient for reaction of CH2OO with ICH2OO is k12 ≈ 2 × 10−10 cm3 molecule−1 s−1. This value is consistent with the rate coefficient for CH2OO + HO2 of k = 2.23 × 10−10 cm3 molecule−1 s−1 calculated by Long et al.39 and is a factor of ∼4 lower than the limiting capture rate for a barrierless reaction that we predict from estimated dipole moments for CH2OO and ICH2OO.
The zero pressure limit value for k′ can therefore be taken as an upper limit for the CH2OO self-reaction rate coefficient k8 scaled by σ355nm (eqn (19)). Table 1 shows the kobs values obtained by using the zero pressure limit k′ value and the σ355nmvalues reported by various sources. The CH2OO σ355nm value from the work of Ting et al. is expected to be the most accurate as the CH2OO σ375nm value reported in their study is similar to the value obtained by Buras et al. using a different method. Thus, with incorporation of the quoted uncertainty for σ355nm values, k8 ≤ 7.98 × 10−11 cm3 molecule−1 s−1 is the best estimate for the self-reaction rate coefficient of CH2OO from this empirical approach.
| k′ (106 cm s−1) | σ 355nm (10−17 cm2 molecule−1) | σ 355nm source | k obs (10−11 cm3 molecule−1 s−1) |
|---|---|---|---|
| a The value of σ355nm (with uncertainty on the order of a factor of 2) was obtained from a Gaussian fit to the spectrum reported by Beames et al. | |||
| 6.72 ± 0.17 | 1.13 ± 0.05 | Ting et al.18 | 7.59 ± 0.39 |
| 2.5a | Beames et al.13 | 16.8a | |
| 3.6 ± 0.9 | Sheps16 | 24.2 ± 6.1 | |
To estimate the contributions from reactions (10) and (11) to the value of kobs, numerical kinetic fits were performed for the 7 Torr total pressure CH2OO decay trace. This chosen decay trace should have minimum contribution from the pressure dependent reactions. The I atom self-reaction, (13), CH2OO + I reaction and the CH2OO self-reaction, (8), were used in the model for the numerical fit. The CH2OO + I reaction takes into account the combined effects from reactions (10) and (11) and kIodine is taken as its overall rate coefficient. The initial I atom concentration was fixed to twice the CH2OO concentration and a rate coefficient value of 2.83 × 10−15 cm3 molecule−1 s−1 was used for reaction (13), obtained using a kinetic rate coefficient expression (M = N2 = 7 Torr, T = 298 K) reported previously.40Fig. 3 shows the results of the fits obtained by varying the kIodine values while floating the k8 values. No significant contribution from kIodine was found as the fits obtained with the kIodine value floated and with no contribution from the CH2OO + I reaction (i.e. kIodine = 0 cm3 molecule−1 s−1) were identical. The kIodine value could not be determined from these fits because the dominant removal process for CH2OO is self-reaction (k8 ≫ kIodine) under our conditions. The fits obtained by using kIodine values of 0.5 and 1.0 × 10−11 cm3 molecule−1 s−1 are of significantly lower quality, consistent with the observations of Buras et al. The k8 values obtained from these different fits are listed in Table 2. Taking 1.0 × 10−11 cm3 molecule−1 s−1 as a conservative upper limit estimate for kIodine, the fitted k8 value (6.85 ± 0.13) × 10−11 cm3 molecule−1 s−1 is taken as a lower limit. Combining this lower limit estimate with the upper limit estimate from the empirical analysis and propagating the uncertainties, a value of (7.35 ± 0.63) × 10−11 cm3 molecule−1 s−1 is obtained as the best estimate for k8 in the current work.
The k8 value obtained from the current work is compared with ones reported previously in Table 3. Our k8 value is well within the bounds of uncertainty of the value reported by Buras et al.37 Both of these values are significantly lower than the one reported by Su et al.35 Although the k8 values from this work and the work of Buras et al. agree well, the analyses performed are quite different. Their kinetic study was performed by monitoring absorbance of CH2OO and I atoms. A kinetic model was used to obtain the upper limit for the CH2OO + I rate coefficient that simultaneously fitted I atom and CH2OO decay traces, taking into account self-reactions, unimolecular losses, and cross-reactions. However, a simpler model showed that the CH2OO + I reaction is in the pseudo first order limit, and the overall loss of CH2OO signal results from contributions from the CH2OO self-reaction and this pseudo first order reaction of CH2OO and I. Both of these approaches led Buras et al. to suggest a maximum rate coefficient value of 1 × 10−11 cm3 molecule−1 s−1 for the overall reaction of I atom with CH2OO, so the self-reaction dominates. The yields for both I atom and CH2OO increase with a decrease in pressure, and thus the pseudo first order contribution of the CH2OO + I reaction to the overall CH2OO decay is expected to be either similar, or perhaps larger, in the pressure range used in the current work. However, the CH2OO decay profiles obtained in the current study are predominantly second order. Contrary to the observations of Buras et al., we see a definite increase in the effective second order rate coefficient value with pressure, most likely because of contributions from reactions (9) and (12) (see above, and ESI†). These contributions, instead of the CH2OO + I reaction, might cause the decay of CH2OO to assume first-order behaviour with further increase in pressure, and could explain the observations of purely second order CH2OO decay in the current work and the combined first and second order decays of Buras et al. Nevertheless, both approaches should be equivalent in principle to separate the contributions from the self-reaction and other reactions of CH2OO.
Inclusion of the CH2OO self-reaction could be important in the kinetic models for analysis of the end-products of alkene-ozonolysis reactions used to determine the consequences of Criegee intermediate chemistry in the atmosphere. However, the scope of the current work is to obtain bimolecular reaction rate coefficients for the reaction of CH2OO with atmospherically relevant species and inclusion of the overall second order loss of CH2OO in kinetic analysis schemes should suffice. Further detailed discussion of the contribution of the second order loss of CH2OO in the presence of other reagents is presented in the ESI.† Inclusion of the second order loss mechanism will be especially important to characterize accurately the small, but atmospherically relevant, rate coefficients for reactions of CI with species like H2O. Also, in the CH2I2 + O2 synthesis method, the CH2OO second order loss contribution increases with pressure as shown in Fig. 2, and thus should be included in the analysis of experimental results obtained at higher pressures.
(II) CH2OO + SO2 reaction
CH2OO oxidizes SO2 to SO3 (reaction (4)) and hence may contribute to atmospheric sulphuric acid production. The bimolecular reaction rate of CH2OO + SO2 has been characterized extensively under low pressure and ambient temperature conditions via direct and indirect studies. These reaction rate coefficients have been used to verify the presence of CH2OO and to obtain its near-UV absorption spectrum.16 However, direct studies at atmospherically relevant pressures and temperatures are still lacking. This section presents some preliminary work on the effect of extending the pressure range and the inclusion of the self-reaction in the analysis to obtain the reaction rate coefficient of CH2OO with SO2 using the direct method. It also explores a possible catalytic isomerization or intersystem crossing (ISC) of CH2OO in the presence of low concentrations of SO2 that is proposed to account for some of our experimental observations.CH2OO decay traces obtained in the presence of SO2 are expected to have contributions from both first and second order loss mechanisms
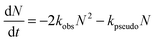 | (20) |
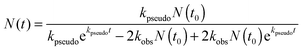 | (21) |
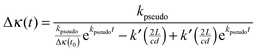 | (22) |
The k′ values were fixed to the values obtained from the previous section, whereas Δκ(t0) and kpseudo values were floated in the fits. This analysis requires no assumption to be made about the correct value of σ355nm. Fig. 4 shows the decays of CH2OO signal in the presence of different concentrations of SO2. The SO2 concentration range used and the robustness of the pseudo first order approximation are justified in detail in the ESI.† These decay traces were fitted to eqn (22) to obtain kpseudo values for each SO2 concentration. Fig. 5 shows the kpseudo values as a function of SO2 concentration. The gradient of a linear fit gives the CH2OO + SO2 bimolecular reaction rate coefficient.
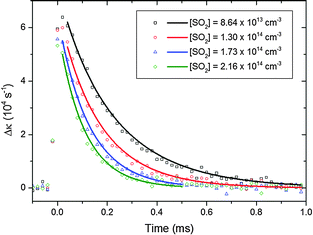 | ||
| Fig. 4 CH2OO decay traces in the presence of various concentrations of SO2. The initial CH2OO concentration was ∼3.3 × 1012 molecule cm−3. All the decay traces were taken at 10 Torr total pressure. Each individual trace was background subtracted using the method described in the ESI.† The solid lines show the fits performed using eqn (22). | ||
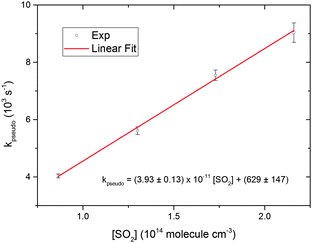 | ||
| Fig. 5 Linear fit to pseudo first order rate coefficients plotted as a function of SO2 concentration. The rate coefficients were taken from the fits shown in Fig. 4. The error bars are 1σ value of the individual fits. The uncertainties in the linear fit expression are 1σ values from the fit. | ||
CH2OO decay traces in the presence of SO2 were measured for different total pressures in the flow tube. The N2 pressure was varied while keeping the O2 (1 Torr) and CH2I2–N2 premix (1 Torr) pressures constant to alter the total pressure. Experiments were conducted for several [SO2] values to allow pseudo first-order analysis under all total-pressure conditions. Fig. 6 shows the CH2OO + SO2 bimolecular reaction rate coefficients, k4, as a function of total pressure obtained from this work and from previous studies. These values are also provided in Table S4 in the ESI.† The k4 values obtained at different pressures agree within the error of the fits and a pressure independent k4 value, (3.80 ± 0.04) × 10−11 cm3 molecule−1 s−1, is obtained by taking an error weighted average. This value is in excellent agreement with the previously reported values9,16 also obtained via direct measurement of CH2OO.
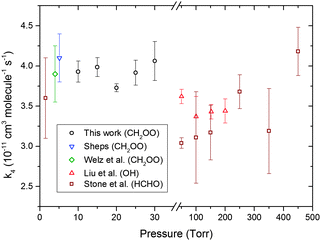 | ||
| Fig. 6 CH2OO + SO2 bimolecular reaction rate coefficient as a function of pressure from various sources including the current work. Error bars are 1σ values. The inset key identifies the species monitored in other studies of reaction (4). | ||
The k4 values obtained previously at higher pressures via methods monitoring HCHO28 or OH26 fluorescence show no dependence on pressure, in agreement with the results obtained in this work for pressures from 10–30 Torr. However, the pressure independent k4 values obtained in this work and from other CH2OO loss studies are larger than the ones obtained from the more indirect measurements of HCHO or OH production. In the case of the OH fluorescence experiment, OH radicals can form via unimolecular dissociation of CH2OO, and the k4 value ((3.53 ± 0.29) × 10−11 cm3 molecule−1 s−1) was obtained from the linear fit of relatively small pseudo first order rate coefficient values (150 to 250 s−1). Under such conditions, contributions from the second order reaction of CH2OO are significant, and correction for this competing pathway for CH2OO removal should increase the derived k4 value.
(III) CH2OO unimolecular reaction
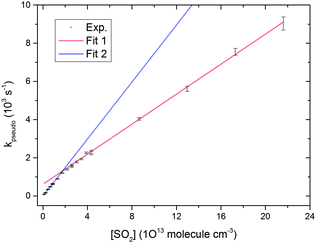
The unimolecular reaction (6) may be an important loss mechanism for CH2OO under atmospheric conditions, along with bimolecular reactions with H2O.33 No rigorous direct experimental study has been performed so far to obtain a CH2OO unimolecular decay rate coefficient. Fig. 4 and 5 illustrate the pseudo first order analysis performed to obtain bimolecular rate coefficient for the CH2OO + SO2 reaction. The intercept value of the linear fit in Fig. 5 should be related to the first order loss of CH2OO. Unimolecular decay, diffusion and mass flow across the detection axis of the spectrometer could all contribute to the observed first order loss of CH2OO, but we present evidence in ESI† that the latter two effects are small on the ≤1 ms measurement times of these experiments. There should not be significant contribution from wall loss as the radicals are synthesized and probed at the same region in the middle of the 6 cm diameter flow tube. Second order fits of the CH2OO decay traces in the absence of SO2 do not show significant first order contributions, as exemplified in Fig. 1, because of a small first order contribution relative to the dominant second order CH2OO loss process. However, non-zero intercept values (>500 s−1) were obtained in the pseudo first order analysis at different total pressures, which appear inconsistent with the fits to second order (self-reaction) decays. To resolve this issue, experiments were performed to obtain CH2OO decay traces in the presence of lower concentrations of SO2, more comparable with the CH2OO concentration.Fig. 7 shows the CH2OO decay trace obtained at the lowest SO2 concentration used in the current work, and the fit using eqn (22) to obtain the first order contribution. Although the pseudo first-order approximation might be expected to break down at the lower end of our SO2 concentration range, numerical modelling shows that a pseudo first-order treatment remains valid because of the rapidity of the CH2OO self-reaction. The overall kinetics are still well-described by simultaneous second and first order fits (adjusted R2 > 0.99). The inset in Fig. 7 shows the non-linear behaviour of the plot of the reciprocal of Δκ as a function of time caused by a first order contribution to the dominant second order decay (CH2OO self-reaction). Fig. 8 shows the pseudo first order rate coefficients obtained from analysis of the CH2OO decay traces taken over our whole range of low to high SO2 concentrations. We see the onset of curvature in the plot for [SO2] values that are still in more than four-fold excess over the initial concentration of CH2OO. Separate linear fits were performed for the four highest (8.64 × 1013 to 2.16 × 1014 molecule cm−3) and four lowest (1.08 × 1012 to 6.48 × 1012 molecule cm−3) SO2 concentrations. The linear fit expressions obtained are (3.93 ± 0.13) × 10−11 × [SO2] + 629 ± 147 and (7.46 ± 0.29) × 10−11 × [SO2] + 11.6 ± 8.0 for the high and low SO2 concentration regimes, respectively. Linear Fit 1 gives the CH2OO + SO2 reaction contribution, whereas linear Fit 2 suggests a different mechanism also contributes at low SO2 concentrations.
 | ||
| Fig. 7 CH2OO decay trace obtained in the presence of low [SO2] (1.1 × 1012 molecule cm−3). The initial concentration of CH2OO was ∼4.9 × 1012 molecule cm−3. The solid lines show the fits performed using eqn (22). The inset shows the reciprocal of the experimental and fitted Δκ values as a function of time for clarity. A first order contribution of 92 ± 6 s−1 was obtained from this fit. | ||
We hypothesize an SO2-catalysed but reversible isomerization or ISC mechanism, in competition with reaction to HCHO + SO3, to explain what we see. A generalized kinetic analysis incorporating the idea is presented in the ESI† and accounts for the observed dependence of kpseudo on [SO2]. Previous theoretical work by Vereecken et al. suggests 17% of the CH2OO + SO2 reaction leads to singlet bisoxy radical + SO2via a pathway with a submerged energy barrier,30 and this isomerization mechanism is one candidate for our experimental observations. However, we note that the reversibility of our proposed mechanism conflicts with the calculations of Vereecken et al. which place the ground states of isomers of CH2OO more than 60 kJ mol−1 lower in energy than the Criegee intermediate. An alternative candidate is formation of a triplet state species via intersystem crossing and the calculations of Vereecken et al. lend some support to this suggestion. These authors identified that, in the vicinity of the OCH2OS(O)O biradical adduct of CH2OO and SO2, the singlet and triplet states are split by less than 0.4 kJ mol−1; at near degeneracy here or elsewhere in the CH2OO – SO2 configuration space, singlet–triplet mixing may be significant and lead to reversible ISC.
In the absence of an alternative explanation for our experimental observations, we are forced to propose an as-yet unidentified intermediate species such as a triplet biradical, or question the accuracy of the existing calculations, which use single reference methods to describe biradical intermediates that (as the authors themselves argue) would be better treated with multi-reference techniques. Our suggested mechanism remains tentative and clearly is subject to testing if multi-reference electronic structure calculations are performed, or the triplet state reaction pathways are mapped. We therefore do not place undue emphasis on this mechanism here, and further details of our model and analysis instead appear in the ESI.†
The analysis based on our proposed mechanism shows that the pseudo first order rate coefficient at high SO2 concentration can be attributed to bimolecular reaction of CH2OO and SO2 but the intercept of fit 1 depends on both the rate coefficient for unimolecular dissociation of CH2OO in the absence of SO2 and that for the intermediate isomer, as well as the ratio of forward and backward isomerization rate coefficients. This analysis is supported by numerical fitting, which is also discussed in the ESI.† The intercept value for Fit 1 does not have significant dependence on total pressure (intercept values at pressures, 10 to 30 Torr, are provided in Table S4 in the ESI†) and a pressure independent value of 704 ± 47 s−1 was obtained. In the low SO2 pressure regime, our model indicates that the pseudo first order rate coefficient should be the sum of contributions from bimolecular reaction and catalysed isomerization/ISC by SO2, justification for which is provided in the ESI.† A value of (3.53 ± 0.32) × 10−11 cm3 molecule−1 s−1 was obtained for the catalysed isomerization/ISC rate coefficient by subtraction and propagation of errors of the slope values obtained from Fit 1 and Fit 2.
The intercept of the low SO2 concentration fit (Fit 2), 11.6 ± 8.0 s−1, is taken as an upper limit for the unimolecular loss of CH2OO in the absence of SO2-induced isomerization/ISC, because it may also contain diffusion and mass flow contributions. Unimolecular rate coefficient values from 100 to 200 s−1 have been used previously for atmospheric chemistry modelling of stabilized CH2OO.33 These values were taken as an estimated upper limit from laboratory based studies of CH2OO.9 Several recent studies have also reported upper limit estimates for the unimolecular loss rate coefficient around 200 s−1.16,26,37 Significant contribution from wall reactions prevented accurate determination of the CH2OO unimolecular loss rate coefficient. Olzmann et al. estimated the CH2OO unimolecular loss rate to be 0.33 s−1 based on electronic structure calculations, which is much lower than the estimates from previous kinetic studies using direct sources of CH2OO.42 The CH2OO unimolecular rate coefficient upper limit value obtained in the current study is more in keeping with the theoretical study. The present study therefore shows that a pathway for CH2OO losses by catalysed isomerization or ISC could bridge the discrepancies between the prior experimental and theoretical estimates.
(IV) Atmospheric implications
SO2 concentrations of 1010 to 1011 molecule cm−3 have been reported in rural and urban environments, respectively.30 Thus, the CH2OO + SO2 reaction should be in the low pressure limit (for SO2 collisions) in these environments and both the proposed isomerization (or ISC) and bimolecular reaction should be important CH2OO loss pathways. Both of these reactions should also compete with the unimolecular decomposition of CH2OO. Maximum pseudo first order reaction rate coefficients of 12, 1.3 and 1.4 s−1 are calculated for the CH2OO unimolecular reaction, the hypothesized SO2-catalysed CH2OO isomerization reaction and CH2OO + SO2 bimolecular reaction using the rate coefficient obtained in this work and a typical atmospheric SO2 concentration of 3.8 × 1010 molecule cm−3.30 The lower limiting value for the unimolecular reaction rate coefficient of CH2OO compared with the one used in a previous modelling study33 should yield a prediction of higher concentration of stabilized CH2OO in the atmosphere.The CH2OO + H2O and CH2OO + (H2O)2 reactions are expected to be the most important atmospheric CH2OO loss mechanisms. Pseudo first order reaction rate coefficients for the CH2OO + H2O and CH2OO + (H2O)2 reactions could be as high as 36 and 81 s−1 based on maximum rate coefficient estimates of 9 × 10−17 and 3 × 10−13 cm3 molecule−1 s−1 and typical atmospheric concentration of 4 × 1017 and 2.7 × 1014 molecule cm−3 for H2O and (H2O)2 respectively.12,28,30 Precise measurements of the CH2OO + H2O and CH2OO + (H2O)2 reaction rate coefficients are needed for more accurate estimates. The work of Leather et al. derived a ratio for k6/k7 = 3.3 × 1017 molecule cm−3, and using the upper limit value for k6 obtained in this work leads to an estimate for k7 = 3.5 × 10−17 cm3 molecule−1 s−1 (with a range of 1–6 × 10−17 cm3 molecule−1 s−1 based on the uncertainty in k6 obtained here).43 These estimates for k7 are smaller but consistent with the work of Stone et al.,28 and larger than the values used in various studies to estimate urban, regional and global CI levels.3,9,11,12,33 Hence, CI levels in these studies may be underestimated, but caution is needed as the rate coefficient for reaction of CI species with water dimers has come under some scrutiny recently and may be sufficiently large to offset this change. Nevertheless, the possibility of significant levels of CI in the boundary layer in particular are supported by this work.
Conclusions
Rate coefficient values for CH2OO self-reaction, reaction with SO2 and unimolecular reaction were obtained at 293 K and under low pressure (7 to 30 Torr) conditions using cavity ring-down spectroscopy. Rate coefficient values for the CH2OO self-reaction and reaction with SO2 obtained in the current study are in agreement with previously reported values obtained by different methods. The rate coefficient value for CH2OO unimolecular reaction was found to be significantly lower compared to the estimates from previous experimental studies, but in line with a theoretical estimate. Reversible isomerization or intersystem crossing of CH2OO that is catalysed by SO2 is proposed to explain the discrepancy between previous experimental estimates and the theoretical calculations.Acknowledgements
This work was funded by Natural Environment Research Council (NERC) grant NE/K004905/1. We are grateful to Leonid Sheps and Craig Taatjes (Sandia National Laboratory) for valuable discussions.References
- R. Criegee and G. Wenner, Liebigs Ann. Chem., 1949, 564, 9–15 CrossRef CAS.
- D. Johnson and G. Martson, Chem. Soc. Rev., 2008, 37, 699–716 RSC.
- C. A. Taatjes, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2014, 16, 1704–1718 RSC.
- J. G. Calvert, R. Atkinson, J. A. Kerr, S. Madronich, G. K. Moortgat, T. J. Wallington and G. Yarwood, The mechanims of atmospheric oxidation of the alkenes, Oxford University Press, 2000 Search PubMed.
- J. H. Kroll, J. S. Clarke, N. M. Donahue, J. G. Anderson and K. L. Demerjian, J. Phys. Chem. A, 2001, 105, 1554–1560 CrossRef CAS.
- J. H. Kroll, S. R. Sahay, J. G. Anderson, K. L. Demerjian and N. M. Donahue, J. Phys. Chem. A, 2001, 105, 4446–4457 CrossRef CAS.
- L. Lu, J. M. Beames and M. I. Lester, Chem. Phys. Lett., 2014, 598, 23–27 CrossRef CAS PubMed.
- C. A. Taatjes, G. Meloni, T. M. Selby, A. J. Trevitt, D. L. Osborn, C. J. Percival and D. E. Shallcross, J. Am. Chem. Soc., 2008, 130, 11883–11885 CrossRef CAS PubMed.
- O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207 CrossRef CAS PubMed.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, E. P. F. Lee, J. M. Dyke, D. W. K. Mok, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2012, 14, 10391–10400 RSC.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. F. Lee, J. M. Dyke, D. L. Osborn, D. M. K. Mok and C. J. Percival, Science, 2013, 340, 177–180 CrossRef CAS PubMed.
- O. Welz, A. J. Eskola, L. Sheps, B. Rotavera, J. D. Savee, A. M. Scheer, D. L. Osborn, D. Lowe, A. M. Booth, P. Xiao, M. A. H. Khan, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Angew. Chem., Int. Ed., 2014, 53, 4547–4550 CrossRef CAS PubMed.
- J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Am. Chem. Soc., 2012, 134, 20045–20048 CrossRef CAS PubMed.
- J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Chem. Phys., 2013, 138, 244307 CrossRef PubMed.
- J. H. Lehman, H. Li, J. M. Beames and M. I. Lester, J. Chem. Phys., 2013, 139, 141103 CrossRef PubMed.
- L. Sheps, J. Phys. Chem. Lett., 2013, 4, 4201–4205 CrossRef CAS.
- E. P. F. Lee, D. K. W. Mok, D. E. Shallcross, C. J. Percival, D. L. Osborn, C. A. Taatjes and J. M. Dyke, Chem. – Eur. J., 2012, 18, 12411–12423 CrossRef CAS PubMed.
- W. L. Ting, Y. H. Chen, W. Chao, M. C. Smith and J. J. M. Lin, Phys. Chem. Chem. Phys., 2014, 16, 4039–4049 RSC.
- F. Liu, J. M. Beames, A. M. Green and M. I. Lester, J. Phys. Chem. A, 2014, 118, 2298–2306 CrossRef CAS PubMed.
- Y. T. Su, Y. H. Huang, H. A. Witek and Y. P. Lee, Science, 2013, 340, 174–176 CrossRef CAS PubMed.
- J. Ahrens, P. T. M. Carlsson, N. Hertl, M. Olzmann, M. Pfeifle, J. L. Wolf and T. Zeuch, Angew. Chem., Int. Ed., 2014, 53, 715–719 CrossRef CAS PubMed.
- M. Nakajima and Y. Endo, J. Chem. Phys., 2013, 139, 101103 CrossRef PubMed.
- M. C. McCarthy, L. Cheng, K. N. Crabtree, O. Martinez, T. L. Nguyen, C. C. Womack and J. F. Stanton, J. Phys. Chem. Lett., 2013, 4, 4133–4139 CrossRef CAS.
- M. Nakajima and Y. Endo, J. Chem. Phys., 2014, 140, 134302 CrossRef PubMed.
- Z. J. Buras, R. M. I. Elsamra, A. Jalan, J. E. Middaugh and W. H. Green, J. Phys. Chem. A, 2014, 118, 1997–2006 CrossRef CAS PubMed.
- Y. Liu, K. D. Bayes and S. P. Sander, J. Phys. Chem. A, 2014, 118, 741–747 CrossRef CAS PubMed.
- L. Vereecken, H. Hardera and A. Novellia, Phys. Chem. Chem. Phys., 2014, 16, 4039–4049 RSC.
- D. Stone, M. Blitz, L. Daubney, N. U. M. Howes and P. Seakins, Phys. Chem. Chem. Phys., 2014, 16, 1139–1149 RSC.
- B. Ouyang, M. W. McLeod, R. L. Jones and W. J. Bloss, Phys. Chem. Chem. Phys., 2013, 15, 17070–17075 RSC.
- L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2012, 14, 14682–14695 RSC.
- R. L. Mauldin-III, T. Berndt, M. Sipila, P. Paasonen, T. Petaja, S. Kim, T. Kurten, F. Stratmann, V. M. Kerminen and M. Kulmala, Nature, 2012, 488, 193–196 CrossRef PubMed.
- J. Li, Y. Qi, B. Q. Yi and P. Yang, Atmos. Environ., 2013, 79, 442–447 CrossRef CAS PubMed.
- C. J. Percival, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, D. O. Topping, D. Lowe, S. R. Utembe, A. Bacak, G. McFiggans, M. C. Cooke, P. Xiao, A. T. Archibald, M. E. Jenkin, R. G. Derwent, I. Riipinen, D. W. K. Mok, E. P. F. Lee, J. M. Dyke, C. A. Taatjes and D. E. Shallcross, Faraday Discuss., 2013, 165, 45–73 RSC.
- J. R. Pierce, M. J. Evans, C. E. Scott, S. D. D'Andrea, D. K. Farmer, E. Swietlicki and D. V. Spracklen, Atmos. Chem. Phys., 2013, 13, 3163–3176 CrossRef.
- Y. T. Su, H. Y. Lin, R. Putikam, H. Matsui, M. C. Lin and Y.-P. Lee, Nat. Chem., 2014, 6, 477–483 CrossRef CAS PubMed.
- C. A. Taatjes, D. E. Shallcross and C. J. Percival, Nat. Chem., 2014, 6, 461–462 CrossRef CAS PubMed.
- Z. J. Buras, R. M. I. Elsamra and W. H. Green, J. Phys. Chem. Lett., 2014, 5, 2224–2228 CrossRef CAS.
- W.-L. Ting, C.-H. Chang, Y.-F. Lee, H. Matsui, Y.-P. Lee and J. J.-M. Lin, J. Chem. Phys., 2014, 141, 104308 CrossRef PubMed.
- B. Long, X.-F. Tan, Z.-W. Long, Y.-B. Wang, D. S. Ren and W.-J. Zhang, J. Phys. Chem. A, 2011, 115, 6559–6567 CrossRef CAS PubMed.
- D. L. Baulch, J. Duxbury, S. J. Grant and D. C. Montague, J. Phys. Chem. Ref. Data, 1981, 10, 1–721 CrossRef PubMed.
- J. H. Espenson, Chemical Kinetics and Reaction Mechanisms, The McGraw-Hill Companies, Inc, USA, 1995 Search PubMed.
- M. Olzmann, E. Kraka, D. Kremer, R. Gutbrod and S. Andersson, J. Phys. Chem. A, 1997, 101, 9421–9429 CrossRef CAS.
- K. E. Leather, M. R. McGillen, A. T. Archibald, S. R. Utembe, M. E. Jenkin, R. G. Derwent, M. C. Cooke, D. E. Shallcross and C. J. Percival, Atmos. Chem. Phys., 2012, 12, 469–479 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp04198d |
| This journal is © the Owner Societies 2015 |