 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Highly efficient green-light ionization of an aryl radical anion: key step in a catalytic cycle of electron formation†
Christoph
Kerzig
and
Martin
Goez
*
Martin-Luther-Universität Halle-Wittenberg, Institut für Chemie, Kurt-Mothes-Str. 2, D-06120 Halle (Saale), Germany. E-mail: martin.goez@chemie.uni-halle.de
First published on 16th October 2014
Abstract
A sustainable generation of hydrated electrons with green light would allow solar-driven applications of this potent reductant, such as the detoxification of halogenated organic waste. Using two-color laser flash photolysis, we have studied the photoionizations of the 1,5-naphthalene disulfonate radical anion and triplet with 532 nm as well as 355 nm. The radical anion is prepared by reducing the triplet with the bioavailable ascorbate monoanion under physiological conditions; its photoionization recovers the starting substrate, so turns the reaction sequence into a catalytic cycle. A comparison of the four ionizations suggests that their efficiency is strongly influenced by the electronic configuration of the state ejecting the electron. The quantum yield for ionizing the radical anion with 532 nm (0.27) is at least four times higher than for the very few known examples of such green-light ionizations and comparable to the most efficient UV ionizations known to date, so this system might represent a breakthrough towards the “green” production of hydrated electrons.
1 Introduction
Aqueous photoionizations hold great promise because they permit a controlled release under natural or even physiological conditions of the hydrated electron eaq˙−, a species that is as strong and reactive a reductant as activated alkali metals and has a natural life long enough for bimolecular attacks on additives.1 These unique properties of eaq˙− have already been put to use under laboratory conditions for the efficient degradation of chlorinated2,3 and even fluorinated4 organics, which characteristically are toxic, yet extremely persistent, so accumulate in the environment. Hence, the optimization of photoionizations with respect to the quantum yields and operating wavelengths could eventually result in applications of eaq˙− on a larger scale, for instance, for the reductive detoxification of organic pollutants.With that ultimate aim in mind, solar-driven photoionizations appear most desirable. Thermodynamically, however, electron detachment from a stable compound by a single photon demands wavelengths in the UV region, where the intensity of the terrestrial solar spectrum sharply drops. In direct consequence of that energetic aspect, a highly excited state of the substrate is involved, and as long as that state is still a bound or resonance state,5 electron ejection thus has to compete with extremely fast radiationless deactivation. That argument can rationalize why even at 266 nm, which supplies ample photon energy but is completely absorbed by the ozone layer, the quantum yields of reported monophotonic ionizations never exceed 30% and are often more than an order of magnitude lower.6–9
Simultaneously meeting the energetic requirement and avoiding a highly excited state with its associated short life seems only possible by using two photons of lower energy in succession and storing the energy of the first photon in an intermediate that is not an excited state. This concept is substantiated by our repeated observation that radical anions of ketones and quinones exhibit five- to ten-fold higher photoionization quantum yields than the corresponding triplets.10–14 A further advantage of these chemical intermediates is the absence of photophysical deactivation, tantamount to an intrinsically longer life, which maximizes the probability of absorbing the ionizing photon even at low photon fluxes. What finally singles out radical anions as special is the fact that their ionization regenerates their parent compounds, which turns the whole reaction sequence, absorption – reductive quenching by a sacrificial donor – absorption, into a catalytic cycle, so in principle allows the production of unlimited amounts of eaq˙− without consumption of the photoactive substrate.
The following considerations apply to the optimization of such a cycle: because the quantum yield of excitation is always unity, the first photon may lie in the UV range, but the color of the ionizing photon should be optimally matched to the solar spectrum,15 that is, should ideally be green. The latter in turn calls for an energy-rich radical anion, as the energy of a green photon (2.33 eV at 532 nm) falls slightly short of the formation energy of eaq˙− (2.77 V vs. NHE).1 To maximize the radical anion yield, the excited substrate should undergo efficient intersystem crossing to the triplet state, because that state can be quenched with much lower donor concentrations owing to its longer life and produces a triplet radical-ion pair, for which reverse electron transfer is spin-forbidden.16 The donor, being the only species consumed in the cycle, should be inexpensive and preferentially bioavailable; ideally, it should quench under physiological conditions. Lastly, the ionization step itself should be monophotonic because otherwise two photons would have to impinge on the radical anion within nanoseconds, which can only be achieved by pulsed laser illumination.
All these criteria are fulfilled by the system that we have investigated in this work, using two-color laser flash photolysis. The substrate chosen is the water-soluble 1,5-naphthalene disulfonate (NDS2−), which efficiently forms a high-energy triplet state 3NDS2− (quantum yield, 0.88; triplet energy, 2.58 eV)17 upon excitation with 308 nm. As we have found, the triplet is quenched by the ascorbate monoanion (HAsc−) at neutral pH to give the radical anion NDS˙3−. Because that aryl radical anion is more energy-rich by at least 60 kJ mol−1 than the carbonyl radical anions reported on earlier by us,10,11,18 which required near-UV light for their ionization, it appears as an ideal candidate for an ionization with green light.
2 Results and discussion
2.1 Reaction mechanism
Fig. 1a displays the concentration traces of the reaction products NDS˙3− and eaq˙− in a representative two-color laser flash photolysis experiment on our substrate NDS2− in the presence of the quencher HAsc−. The protocol for obtaining these concentrations is described in Section S2.5 of the ESI.† | ||
| Fig. 1 Green-light photoionization of NDS˙3−. (a) Concentrations of NDS˙3− (red) and eaq˙− (blue) during a two-pulse laser flash photolysis experiment on a deoxygenated aqueous solution of 1.4 × 10−4 M NDS2− and 2 mM HAsc− at pH 7.6 with the pulse scheme shown as the inset. The small amount of eaq˙− produced by the first flash is due to a side reaction (UV photoionization of the excited substrate); the eaq˙− yield through green-light ionization of the radical anion by the second flash is higher by one order of magnitude. (b) Cyclic photoionization mechanism for NDS2− in the presence of HAsc− acting as electron donor. For further details, see text and ESI.† | ||
The function of the first laser pulse (308 nm) is to convert the substrate into its triplet state 3NDS2−; at the pulse intensity selected by us that conversion is maximized (15%) while the undesired UV ionization of the excited naphthalene19 during that pulse is minimized (0.3%). The ensuing interpulse delay serves to accumulate the radical anion NDS˙3− through the quenching of 3NDS2− by HAsc−; we chose that waiting period and the quencher concentration for optimum concentrations of NDS˙3− at the moments the two lasers fire (as high as possible at the start of the second pulse, to enhance the sensitivity; as low as possible during the first pulse, to suppress a photoionization of the radical anion already by that pulse). The second laser pulse (532 nm) finally brings about a green-light ionization of the radical anion on a large scale, as is evidenced in Fig. 1a by the bleaching of more than 50% of NDS˙3− accompanied by the formation of the same amount of eaq˙−.
No electrons are produced in control experiments without radical anions, that is, when the quencher or the first laser pulse are absent. The radical anions are also the only species converted by the second flash: besides them, only the triplet would absorb at 532 nm (for all spectra, see Section S2 of the ESI†) but features a significantly lower molar absorption coefficient and has largely vanished at the end of the interpulse delay. All these findings are in perfect accordance with the catalytic cycle of photoionization of Fig. 1b.
2.2 Radical anion formation and decay
As has emerged, the photoionizable radical anion NDS˙3− is the key species in the catalytic cycle of Fig. 1b. To prepare NDS˙3−, we used reductive quenching of the triplet 3NDS2− by the ascorbate monoanion HAsc− (eqn (1)) | (1) |
Our attempts to follow that reaction by monitoring the concentrations of its products were obstructed by the subsequent protonation of NDS˙3−, which removes its absorptions in the visible region and changes the UV absorptions in the range suitable for observing HAsc˙. That protonation is mechanistically complex, fast enough to modify the buildup of NDS˙3− in Fig. 1a, and not suppressible by a faster quenching and a shorter interpulse delay because we already used the maximum concentration of HAsc− compatible with homogeneous absorption of the initial 308 nm laser pulse.
In contrast, the triplet provides a reliable observable for investigating the quenching. At the maximum of its visible band, 440 nm, the only other absorbing species is NDS˙3−, and the latter in turn has a band centered at 725 nm, where all other species are transparent (compare, the spectra in Section S2 of the ESI†). Hence, the triplet decay is accessible from traces recorded at 440 nm and 725 nm with all other experimental parameters unchanged: the contribution of NDS˙3− to the 440 nm trace is obtained by multiplying the 725 nm trace with the ratio of molar absorption coefficients (ε440/ε725 = 1.36), and subtracting it from the 440 nm trace extracts the pure triplet signal with optimum sensitivity and regardless of how the concentration of NDS˙3− is affected by its protonation. Fig. 2a illustrates that separation, which we found to isolate a first-order decay in accordance with eqn (1).
To determine the quenching rate constant kq, we repeated that procedure with different quencher concentrations and analyzed the concentration dependence of the triplet lifetime (Fig. 2b, main plot and inset). The Stern–Volmer plot is linear, indicating purely dynamic quenching, with a Stern–Volmer constant of 2.70 × 103 M−1; with the unquenched lifetime of 57.5 μs under our experimental conditions, a quenching rate constant of 4.7 × 107 M−1 s−1 thus results.
The reduction of 3NDS2− by HAsc− is rather slow, considering that photoinduced electron transfer reactions are frequently diffusion-controlled. An explanation is provided by its Gibbs energy ΔG°,20 in eV (eqn (2)),
| ΔG° = E°(HAsc˙/HAsc−) − E°(NDS2−/NDS˙3−) – ΔE0,0 + wP − wR | (2) |
Despite the moderate value of kq, the triplet is still quenched efficiently by fairly low donor concentrations because its natural life is so long. The half-quenching concentration of HAsc− is as small as 370 μM, and the degree of quenching rises to 85% under the conditions of Fig. 1a. However, a significant fraction of quenching events does not yield free radical anions of our substrate. As Fig. 3a shows, the concentration trace for NDS˙3− is describable by a formation with the same rate as the triplet decay but an efficiency η of only 0.56, and by a subsequent slow decrease with a half life of 25 μs.
 | ||
Fig. 3 Radical anion formation and decay in the quenching of 3NDS2− by HAsc− under the conditions of Fig. 1a but with 2.65 mM of HAsc−. (a) Measured and simulated concentration traces for species X, normalized to the initial triplet concentration. Black and red dots, experimental data points for the triplet and the radical anion; black solid line, fit of exp[−k1t] to the triplet decay, best-fit parameter k1 = 1.42 × 105 s−1; red solid line, fit of R(t), 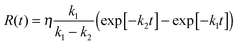 to the radical-anion curve with k1 fixed at the previous value, best-fit parameters η = 0.56 and k2 = 2.8 × 104 s−1; purple dashed line, calculated concentration S(t) of unprotonated plus protonated radical anion, i.e., S(t) = η(1 − exp[−k1t]); dark green dashed line, calculated concentration trace for the protonated radical anion, i.e., difference between the two preceding curves. At 10 μs, the concentration ratio S(t)/R(t), i.e., of the substrate-derived radicals in all their forms and in the form of the radical anion only, is 1.2 with the best-fit parameters given above. (b) Kinetic spectrum at 10 μs after the 308 nm pulse (orange solid line and filled dots); contributions of 3NDS2− (black dash-dotted line), NDS˙3− (red dashed line), and Asc˙− (purple dotted line); residuals of the decomposition (light green solid line and open dots). Further explanation, see text. to the radical-anion curve with k1 fixed at the previous value, best-fit parameters η = 0.56 and k2 = 2.8 × 104 s−1; purple dashed line, calculated concentration S(t) of unprotonated plus protonated radical anion, i.e., S(t) = η(1 − exp[−k1t]); dark green dashed line, calculated concentration trace for the protonated radical anion, i.e., difference between the two preceding curves. At 10 μs, the concentration ratio S(t)/R(t), i.e., of the substrate-derived radicals in all their forms and in the form of the radical anion only, is 1.2 with the best-fit parameters given above. (b) Kinetic spectrum at 10 μs after the 308 nm pulse (orange solid line and filled dots); contributions of 3NDS2− (black dash-dotted line), NDS˙3− (red dashed line), and Asc˙− (purple dotted line); residuals of the decomposition (light green solid line and open dots). Further explanation, see text. | ||
The unexpectedly low η might be caused by two different reactions of the spin-correlated radical pair 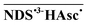 (eqn (3)), which is the initial product of electron-transfer quenching of the triplet. The pair is born with the multiplicity of its precursors, so in a triplet state. Escape from the cage affords the desired free radicals NDS˙3− but has to compete with two geminate processes: reverse electron transfer leads back to the starting materials but is only possible after intersystem crossing, whereas in-cage proton transfer transforms the primary pair into a secondary one that is no longer capable of releasing NDS˙3−; in ketone–amine systems we have already studied such transformations,25 which are not subject to any spin restrictions and occur within the spin-correlated life of the pairs, that is, on a subnanosecond timescale.
(eqn (3)), which is the initial product of electron-transfer quenching of the triplet. The pair is born with the multiplicity of its precursors, so in a triplet state. Escape from the cage affords the desired free radicals NDS˙3− but has to compete with two geminate processes: reverse electron transfer leads back to the starting materials but is only possible after intersystem crossing, whereas in-cage proton transfer transforms the primary pair into a secondary one that is no longer capable of releasing NDS˙3−; in ketone–amine systems we have already studied such transformations,25 which are not subject to any spin restrictions and occur within the spin-correlated life of the pairs, that is, on a subnanosecond timescale.
 | (3) |
The decomposition into components of the transient spectrum displayed in Fig. 3b rules out the proton-transfer pathway and sustains the electron-transfer route. First, a sharp peak centered at about 340 nm, which has been observed for the protonated radical anions of naphthalene and naphthalene-2-sulfonate,26,27 would be expected for HNDS˙2− but is not yet noticeable at the post-flash delay used in Fig. 3b; because the in-cage proton transfer would have to yield that transient in approximately the same amount as NDS˙3− to be consistent with the observed η, that signal should have been quite prominent. Second, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 concentration ratio between Asc˙− (which is the only observable form of the free ascorbate-derived radicals; see Section S2.4 of the ESI†) and NDS˙3− imposed by the primary quenching remains unchanged by back electron transfer, whereas in-cage proton transfer as well as protonation of free NDS˙3− increase that ratio by removing NDS˙3− without influencing the concentration of Asc˙−. Under the experimental conditions of Fig. 3b, the protonation of free NDS˙3− alone accounts for a ratio [Asc˙−]
1 concentration ratio between Asc˙− (which is the only observable form of the free ascorbate-derived radicals; see Section S2.4 of the ESI†) and NDS˙3− imposed by the primary quenching remains unchanged by back electron transfer, whereas in-cage proton transfer as well as protonation of free NDS˙3− increase that ratio by removing NDS˙3− without influencing the concentration of Asc˙−. Under the experimental conditions of Fig. 3b, the protonation of free NDS˙3− alone accounts for a ratio [Asc˙−]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NDS˙3−] of 1.2 (see, figure caption). That value would not alter if the observed η were due to electron return, but would have to rise to 2.1 if in-cage proton transfer were responsible. By decomposing the spectrum as shown in Fig. 3b, we determined a ratio of 1.2, which unambiguously identifies the back electron transfer as the reason for the low η.
[NDS˙3−] of 1.2 (see, figure caption). That value would not alter if the observed η were due to electron return, but would have to rise to 2.1 if in-cage proton transfer were responsible. By decomposing the spectrum as shown in Fig. 3b, we determined a ratio of 1.2, which unambiguously identifies the back electron transfer as the reason for the low η.
As a corollary, intersystem crossing of  by the radical-pair mechanism28 must be unusually fast, which might reflect a substantial increase of the g value by the sulfonation. On the other hand, in view of the thermodynamic instability of aryl radical anions in water (the pKa values of the corresponding acids are significantly larger than 14),29,30 the protonation of NDS˙3− is surprisingly slow. Both processes are certainly undesirable because they reduce the overall quantum yield but they do not necessarily compromise the stability of the system: the former quantitatively regenerates the substrate, while the latter is slow enough to be rendered unimportant at our light intensities, where NDS˙3− is photoionized much faster than it can be protonated.
by the radical-pair mechanism28 must be unusually fast, which might reflect a substantial increase of the g value by the sulfonation. On the other hand, in view of the thermodynamic instability of aryl radical anions in water (the pKa values of the corresponding acids are significantly larger than 14),29,30 the protonation of NDS˙3− is surprisingly slow. Both processes are certainly undesirable because they reduce the overall quantum yield but they do not necessarily compromise the stability of the system: the former quantitatively regenerates the substrate, while the latter is slow enough to be rendered unimportant at our light intensities, where NDS˙3− is photoionized much faster than it can be protonated.
2.3 Green-light photoionization
To check whether the photoionization of NDS˙3− is accompanied by side reactions, we recorded kinetic spectra as in Fig. 3b also after the second laser pulse, which gave no indication whatsoever for the presence of any other species besides those included in the mechanism of Fig. 1b. We take this as evidence that ionization is the only chemical reaction pathway of excited NDS˙3−. Based on these findings, we determined the molar absorption coefficient of NDS˙3− relative to that of eaq˙−, that is, by comparing bleaching and electron formation (see, Section S2.3 of the ESI†). That calibration eliminates all errors due to uncertainties of the optical path length and imperfections of the excitation homogeneity. With the molar absorption coefficient so obtained the equality of one radical anion being consumed per one electron produced holds at any laser intensity, as the mechanism of Fig. 1b demands; this is established by the plot of Fig. 4a. | ||
| Fig. 4 Intensity dependent measurements of the green-light ionization of NDS˙3−. (a) eaq˙− formation as a function of NDS˙3− bleaching at different intensities of the ionizing laser pulse; other experimental parameters as in Fig. 1a. [NDS˙3−]pre is the prepulse concentration of the radical anion. (b) Relative actinometry with [Ru(bpy)3]2+ as standard. Filled circles, intensity dependences of eaq˙− formation from NDS˙3− (blue) and MLCT formation from [Ru(bpy)3]2+ (gray). Initial absorbance of both solutions at 532 nm, 4.0 × 10−3 cm−1. The dashed lines are the best-fit functions [X]max (1 − exp[−aI532]) with the maximum concentration [X]max and the fit parameter a. Solid lines, initial slopes a[X]max, with the photoionization quantum yield given by their ratio, 0.27. Further details, see text. | ||
The dependence of the electron yield on the intensity of the green laser flash can be seen in Fig. 4b. It evidently features a linear low-intensity regime with a straight-line extrapolation to the origin,31 so identifies the green-light ionization of the radical anion as monophotonic. This is also very plausible because for that reaction, eqn (4), the sum of the photon energy (2.33 eV at 532 nm) and the energy gain by the recovery of the substrate from the radical anion (1.97 eV)22 greatly surpasses the formation energy of eaq˙− (2.77 eV),1
 | (4) |
The same considerations help rationalize why the triplet is not ionized with green light according to eqn (5) despite a weak absorption at 532 nm: triplet energy (2.58 eV)17 plus photon energy barely outweigh the energetic requirements for the oxidation of the substrate (E°(NDS˙−/NDS2−) = 2.03 eV vs. NHE)32 and the formation of eaq˙−,
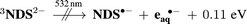 | (5) |
We measured the photoionization quantum yield of NDS˙3− by relative actinometry with ruthenium(tris)bipyridine as the reference. Upon green-light excitation, [Ru(bpy)3]2+ quantitatively produces a luminescent metal-to-ligand charge-transfer excited state MLCT,33 which does not decompose even at the highest laser intensities accessible with our setup;34 obtaining the MLCT concentration from the luminescence is straightforward because the system is easily driven so near to complete conversion to MLCT that a reliable calibration curve can be recorded. To this end, Fig. 4b also includes the results of variable-intensity laser flash photolysis on a solution of [Ru(bpy)3]2+ at the same optical density at 532 nm as NDS˙3−.
The ratio of initial slopes of the two intensity dependences, for eaq˙− formation from NDS˙3− and for MLCT formation from [Ru(bpy)3]2+, directly gives the quantum yield for green-light ionization of NDS˙3−; saturation effects are absent in this low-intensity range, and as with the above determination of the molar absorption coefficient of NDS˙3−, the comparison method cancels excitation imperfections. The obtained quantum yield φ532 of 0.27 outperforms the highest ever reported for a monophotonic ionization in the green (the doubly deprotonated terephthalate radical anion, 0.07)35 by as much as a factor of four.
2.4 UV photoionization
By using 355 nm instead of 532 nm we add 1.17 eV to the photon energy, making the photoionization of the triplet in the UV nearly as exergonic as that of the radical anion in the green (1.28 eV vs. 1.53 eV, compare eqn (4) and (5)), and likewise raising the exergonicity of the radical anion photoionization to as much as 2.70 eV. Yet, the absence of thermodynamic restrictions does not remove the disparity of the ionization efficiencies, as is evidenced by Fig. 5.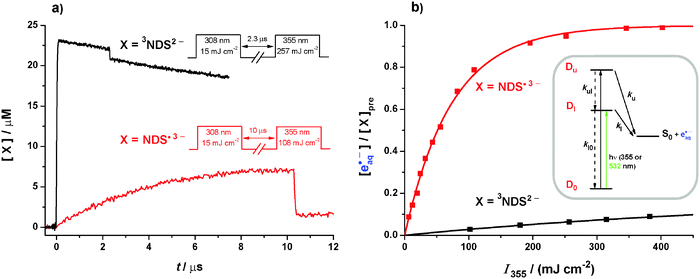 | ||
| Fig. 5 355 nm photoionization of 3NDS2− (black) and NDS˙3− (red). In the experiments on 3NDS2−, the pH was 12.3; in the experiments on NDS˙3−, the donor concentration was 2.1 mM; all other parameters were as in Fig. 1a except for the pulse sequences given in subfigure 5a. (a) Experimental concentration traces and pulse sequences. (b) Main plot, electron concentrations normalized to the prepulse concentration of the respective electron precursor X as functions of the intensity I355 of the ionizing pulse. Inset, kinetic scheme for radical-anion photoionization through two adjacent autoionizing states Du and Dl. Further explanation, see text. | ||
Fig. 5a compares kinetic traces recorded during 355 nm photoionization of the triplet and of the radical anion, where we applied the photoionizing pulses with intensities compensating for the different absorptions of 3NDS2− and NDS˙3−. Although the same absolute amount of each intermediate is thus excited, the bleaching is seen to be about five times larger in the case of the radical anion. To ensure that this effect is not caused by the formation of an absorbing product in the triplet photoionization, we performed that experiment in strongly basic solution (at pH 12.3), where the formal radical cation NDS˙− of the substrate is rapidly scavenged by hydroxide ions to give a species that is transparent in the visible range.19 Kinetic spectra recorded before and after the bleaching were identical, and their decay characteristics were also unchanged. Further control experiments showed that the donor-derived radical anion Asc˙− is inert at 355 nm. Hence, the observed bleaching difference reflects a difference in the quantum yields.
Bleaching of 3NDS2− and NDS˙3− is accompanied by electron formation; in both cases, the amount of eaq˙− produced equalled the amount of the precursor destroyed within 1%. The intensity dependences are displayed in Fig. 5b. In the experiments on the radical anion, a small correction (≤5%) had to be applied to take into account the triplet still present at the moment of the ionizing pulse (compare Fig. 3a). For the determination of the photoionization quantum yields, we again used relative actinometry with [Ru(bpy)3]2+ as the standard. The MLCT state of [Ru(bpy)3]2+ is itself photoionized at 355 nm but that process becomes only noticeable at higher pulse energies;34 by restricting the actinometry to the low-energy regime, we obtained photoionization quantum yields φ355 at 355 nm of 0.08 for the triplet and 0.42 for the radical anion.
Whereas φ355 for the triplet and φ532 for the radical anion are the true quantum yields φl for electron detachment from the lowest autoionizing state of the respective intermediate, φ355 for the radical anion is a compound quantity comprising direct electron ejection from the upper state Du with the true quantum yield φu and indirect ejection from the lower state Dl reached by radiationless deactivation (see the spectra in Section S2 of the ESI†). That situation can be analyzed with the kinetic scheme given as the inset of Fig. 5b. Setting up the photokinetic equations in the usual way and rearranging leads to eqn (6) for φu,
 | (6) |
Inserting the experimental quantities gives 0.20 for φu. In view of the necessary approximations involved, in particular the neglect of individual rate constants for the vibrationally excited states of Du and Dl, the absolute number is not very meaningful but we take this result to indicate that direct electron ejection is slightly more likely for the lower state than for the higher despite the considerable energy difference.
The electronic configuration of the state reached by the second photon might provide an explanation. The following reasoning is based on a Koopmans' picture of photoionization, an approximation that has proved very successful for interpreting the photoelectron spectra of organic hydrocarbons with conjugated π-systems.36 Only in the case of a type-I excitation, meaning the promotion of an electron from the SOMO (singly occupied molecular orbital) to a virtual orbital, does the ionization of a radical anion recover the parent compound in its electronic ground state; type-II or type-III excitations, that is, from a doubly occupied orbital to the SOMO or to a virtual orbital, are correlated with an excited state of the substrate as the by-product of eaq˙−.5 Because the singlet energy of NDS2− is at least 3.8 eV, as calculated from the red edge of the absorption band (compare the spectrum in the ESI†), type-II and type-III excitations should not lead to ionization of NDS˙3− at our laser wavelengths. By the same token, ionization of 3NDS2− is unlikely to be feasible by a transition other than from the higher SOMO to a virtual orbital.
The absorption spectra of the triplet and the radical anion of naphthalene have been thoroughly investigated and characterized.5,37–39 Because the substitution with the two sulfonate groups does not exert a significant influence on these spectra (compare, Sections S2.1–S2.3 of the ESI†), we take the unsubstituted hydrocarbon as a model for NDS2−, and use the Mullikan symbols in D2h for identification of the orbitals. Adopting the coordinate system of ref. 39, the lower SOMO of the triplet (SOMOl) is 1au, and the upper SOMO of the triplet (SOMOu) as well as the SOMO of the radical anion are 2b1g.
Owing to interactions with σ* orbitals, the transition SOMO → SOMO + 2 (2b1g → 3b3u) is responsible for both absorption bands of the radical anion in the visible; although the B3g states so reached lie above the ionization threshold, discrete absorption bands are still observed because of shape resonances.5 With 532 nm, which corresponds to the minimum between the bands, both transitions are excited, but because they are both type-I transitions it should not make much of a difference whether the vibrational ground state of the higher-energy electronic state or a vibrationally excited state of the lower-energy electronic state is reached. The situation is different for 355 nm excitation. Although that wavelength practically coincides with the maximum of the near-UV band, this simplicity is deceptive: the band is a superposition of the type-II transition SOMO − 1 → SOMO (1au → 2b1g) in addition to two—with the splitting again due to interactions with σ* orbitals—type-I transitions from the SOMO to the SOMO + 3 (2b1g →2au).5 The fact that the absorption at 355 nm partly involves a nonionizing transition is consistent with the slightly smaller true quantum yield for ionization of NDS˙3− with 355 nm compared to 532 nm.
The type-I transition SOMOu → SOMOu + 2 (2b1g → 3b3u) contributes to the visible absorption band of the triplet but there is a dominant admixture of type-II transitions, the most important being SOMOl − 3 → SOMOu + 2, i.e., 1b1g → 3b3u.38 The next band at higher energy is too far in the UV-C for its wings to be noticeably excited with 355 nm and furthermore contains only 50% of a type-I transition.37 The low quantum yield of 355 nm photoionization of 3NDS2− can thus be rationalized with the same arguments as above, in addition to the shorter life of the higher excited state.
3 Experimental section
Our investigation method was two-color laser flash photolysis with optical detection of the intermediates. The setup is described in detail in Section S1 of the ESI.†The chemicals were obtained commercially in the highest available purity and used as received (disodium 1,5-naphthalene disulfonate hydrate, >98%, TCI; sodium ascorbate, >99%, Alfa Aesar; ruthenium(tris)bipyridine dichloride hexahydrate, 99%, abcr; sodium chloride, >99.5%, Fluka). Ultrapure Millipor MilliQ water (specific resistance, 18.2 MΩ cm) was the solvent. All solutions were purged with argon (5.0, Air Liquide) or N2O (4.5, Linde) for 30 minutes before and for the whole duration of the experiments. To avoid the well-known oxidation of sodium ascorbate,40 we added the required amount in solid form to the already degassed solutions immediately before starting the experiments. We employed the substrate NDS2− as its disodium salt Na2NDS because that does not affect the natural pH of our aqueous solutions, in contrast to the disulfonic acid. As Na2NDS is hygroscopic, we determined its water content (7.02%) by a thermogravimetric analysis (TA Instruments TGA2950) to obtain the exact substrate concentration.
All steady-state absorption spectra were recorded with a Shimadzu UV-2102 spectrophotometer.
4 Conclusions
Of the very few known monophotonic green-light ionizations in polar solvents,35,41–44 that of the doubly deprotonated terephthalate radical anion has the highest quantum yield (φion = 0.07)35 reported so far. The system studied in the present work constitutes a very significant advance because φion is four times as high for it, which compares favourably with the quantum yields of the most efficient UV photoionizations known to date,6 although the energy of the ionizing photon is lower by almost 200 kJ mol−1. As our investigation of the wavelength dependence has shown, however, the energy balance only provides a criterion of whether a photoionization is basically feasible or not but has little predictive power for the quantum yield; our results suggest that the electronic configuration of the excited electron precursor is a far more important factor.Similar substrates with more highly conjugated aromatic systems appear very promising candidates for optimizing the cyclic photoionization mechanism of Fig. 1b. First, the photochemical generation of their radical anions is possible with light of longer wavelengths, even in the visible range, thus making more effective use of the solar spectrum. Second, aryl radical anions in general are sufficiently energy-rich45 for their green-light photoionization to be feasible, but also comparatively long-lived,27,46 thus increasing the probability of absorbing the ionizing photon at much lower light levels than those of a pulsed laser.
Acknowledgements
Financial support provided by the Chemical Industry Funds to C.K. is gratefully acknowledged. We thank Till Walther for performing the TGA measurement.References
- J. W. T. Spinks and R. J. Woods, An Introduction to Radiation Chemistry, Wiley, New York, 2nd edn, 1976 Search PubMed.
- X. Li, J. Ma, G. Liu, J. Fang, S. Yue, Y. Guan, L. Chen and X. Liu, Environ. Sci. Technol., 2012, 46, 7342–7349 CrossRef CAS PubMed.
- Y. Peng, S. He, J. Wang and W. Gong, Radiat. Phys. Chem., 2012, 81, 1629–1633 CrossRef CAS PubMed.
- Z. Song, H. Tang, N. Wang and L. Zhu, J. Hazard. Mater., 2013, 262, 332–338 CrossRef CAS PubMed.
- Y. Honda, T. Shida and H. Nakatsuji, J. Phys. Chem. A, 2012, 116, 11833–11845 CrossRef CAS PubMed.
- F. Saito, S. Tobita and H. Shizuka, J. Photochem. Photobiol., A, 1997, 106, 119–126 CrossRef CAS.
- M. Wang, L.-L. Cheng, H. Zhu, K. Li, Q.-S. Wu, S.-D. Yao and S.-L. Wang, J. Photochem. Photobiol., A, 2009, 208, 104–109 CrossRef CAS PubMed.
- M. P. Yurkova, I. P. Pozdnyakov, V. F. Plyusnin, V. P. Grivin, N. M. Bazhin, A. I. Kruppa and T. A. Maksimova, Photochem. Photobiol. Sci., 2013, 12, 684–689 CAS.
- L.-L. Cheng, M. Wang, H. Zhu, K. Li, R.-R. Zhu, X.-Y. Sun, S.-D. Yao, Q.-S. Wu and S.-L. Wang, Spectrochim. Acta, Part A, 2009, 73, 955–959 CrossRef PubMed.
- M. Goez and B. H. M. Hussein, Phys. Chem. Chem. Phys., 2004, 6, 5490–5497 RSC.
- M. Goez and V. Zubarev, Chem. Phys., 2004, 307, 15–26 CrossRef CAS PubMed.
- M. Goez and V. Zubarev, J. Phys. Chem. A, 1999, 103, 9605–9613 CrossRef CAS.
- M. Goez, V. Zubarev and G. Eckert, J. Am. Chem. Soc., 1998, 120, 5347–5348 CrossRef CAS.
- M. Goez and V. Zubarev, Angew. Chem., Int. Ed., 2006, 45, 2135–2138 CrossRef CAS PubMed.
- http://rredc.nrel.gov/solar/spectra/am1.5/ASTMG173/ASTMG173.html, retrieved 15.09.2014.
- G. J. Kavarnos and N. J. Turro, Chem. Rev., 1986, 86, 401–449 CrossRef CAS.
- M. Nemoto, H. Kokubun and M. Koizumi, Bull. Chem. Soc. Jpn., 1969, 42, 2464–2470 CrossRef CAS.
- M. Goez and C. Kerzig, Angew. Chem., Int. Ed., 2012, 51, 12606–12608 CrossRef CAS PubMed.
- S. Steenken, C. J. Warren and B. C. Gilbert, J. Chem. Soc., Perkin Trans. 2, 1990, 335–342 RSC.
- S. E. Braslavsky, Pure Appl. Chem., 2007, 79, 293–465 CrossRef CAS.
- P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755 CrossRef CAS PubMed.
- A. P. Shestov and N. A. Osipova, Sb. Statei, Nauchno-Issled. Inst. Org. Poluprod. Krasitelei, 1961, 2, 13–45 Search PubMed.
- K. Kasama, A. Takematsu and S. Arai, J. Phys. Chem., 1982, 86, 2420–2427 CrossRef CAS.
- A. A. Frost and R. G. Pearson, Kinetics and Mechanism, John Wiley and Sons, New York, 2nd edn, 1961 Search PubMed.
- M. Goez and I. Sartorius, J. Phys. Chem. A, 2003, 107, 8539–8546 CrossRef CAS.
- J. H. Fendler, H. A. Gillis and N. V. Klassen, J. Chem. Soc., Faraday Trans. 1, 1974, 70, 145–153 RSC.
- A. Treinin and E. Hayon, J. Am. Chem. Soc., 1976, 98, 3884–3891 CrossRef CAS.
- R. Kaptein and L. J. Oosterhoff, Chem. Phys. Lett., 1969, 4, 195–197 CrossRef CAS.
- V. D. Parker, M. Tilset and O. Hammerich, J. Am. Chem. Soc., 1987, 7905–7906 CrossRef CAS.
- Z. V. Todres, Ion-Radical Organic Chemistry: Principles and Applications, CRC Press, Boca Raton, 2nd edn, 2008 Search PubMed.
- U. Lachish, A. Shafferman and G. Stein, J. Chem. Phys., 1976, 64, 4205–4211 CrossRef CAS PubMed.
- S. M. Hubig, J. Lumin., 1991, 47, 137–145 CrossRef.
- S. Campagna, F. Puntoriero, F. Nastasi, G. Bergamini and V. Balzani, Top. Curr. Chem., 2007, 280, 117–214 CrossRef CAS.
- M. Goez, D. von Ramin-Marro, M. H. O. Musa and M. Schiewek, J. Phys. Chem. A, 2004, 108, 1090–1100 CrossRef CAS.
- P. Natarajan and R. W. Fessenden, J. Phys. Chem., 1989, 93, 6095–6100 CrossRef CAS.
- S. F. Nelsen, M. N. Weaver, D. Yamazaki, K. Komatsu, R. Rathore and T. Bally, J. Phys. Chem. A, 2007, 111, 1667–1676 CrossRef CAS PubMed.
- T.-K. Ha and U. P. Wild, J. Comput. Chem., 1982, 3, 1–5 CrossRef CAS.
- H. Chakraborty and A. Shukla, ArXiv e-prints, 2014, arXiv:1406.6954.
- T. Bally, C. Carra, M. P. Fülscher and Z. Zhu, J. Chem. Soc., Perkin Trans. 2, 1998, 1759–1765 RSC.
- M. B. Davies, J. Austin and D. A. Partridge, Vitamin C: Its Chemistry and Biochemistry, The Royal Society of Chemistry, Cambridge, 1st edn, 1991 Search PubMed.
- M. Hara, S. Samori, X. Cai, M. Fujitsuka and T. Majima, J. Phys. Chem. A, 2005, 109, 9831–9835 CrossRef CAS PubMed.
- J. K. Thomas and P. L. Piciulo, J. Am. Chem. Soc., 1979, 101, 2502–2503 CrossRef CAS.
- L. J. Johnston and R. W. Redmond, J. Phys. Chem. A, 1997, 101, 4660–4665 CrossRef CAS.
- R. W. Redmond, J. C. Scaiano and L. J. Johnston, J. Am. Chem. Soc., 1990, 112, 398–402 CrossRef CAS.
- M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, Taylor and Francis, Boca Raton, 3rd edn, 2006 Search PubMed.
- Y. Yamamoto, S. Shiraki and Y. Kawamura, J. Chem. Soc., Perkin Trans. 2, 1992, 2241–2245 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, absorption spectra and properties of the relevant chemical species. See DOI: 10.1039/c4cp04156a |
| This journal is © the Owner Societies 2014 |

