Open Access Article
Open Access ArticleEffect of the electropositive elements A = Sc, La, and Ce on the microscopic dynamics of AV2Al20
Michael Marek
Koza
*a,
Andreas
Leithe-Jasper
b,
Erik
Sischka
b,
Walter
Schnelle
b,
Horst
Borrmann
b,
Hannu
Mutka
a and
Yuri
Grin
b
aInstitut Laue Langevin, 6 Rue Jules Horowitz, B.P. 156, 38042 Grenoble, Cedex 9, France. E-mail: koza@ill.eu
bMax–Planck–Institut für Chemische Physik fester Stoffe, Nöthnitzer Straße 40, 01187 Dresden, Germany
First published on 22nd October 2014
Abstract
We report on the inelastic response of AV2Al20 (with A = Sc, La and Ce) probed by high-resolution inelastic neutron scattering experiments. Intense signals associated with the dynamics of Sc, La and Ce are identified in the low-energy range at 6–14 meV in ScV2Al20 and at 8–16 meV in LaV2Al20 and CeV2Al20. Their response to temperature changes between 2 and 300 K reveals a very weak softening of the modes upon heating in LaV2Al20 and CeV2Al20 and a distinguished blue shift by about 2 meV in ScV2Al20. By means of density functional theory (DFT) and lattice dynamics calculations (LDC) we show that the unusual anharmonicity of the Sc-dominated modes is due to the local potential of Sc featured by a strong quartic term. The vibrational dynamics of ScV2Al20 as well as of LaV2Al20 and CeV2Al20 is reproduced by a set of eigenmodes. To screen the validity of the DFT and LDC results they are confronted with data from X-ray diffraction measurements. The effect of the strong phonon renormalization in ScV2Al20 on thermodynamic observables is computed on grounds of the LDC derived inelastic response. To set the data in a general context of AV2Al20 compounds and their physical properties we report in addition computer and experimental results of the binary V2Al20 compound.
I. Introduction
Crystalline compounds such as skutterudites (AT4X12 with A = alkali, alkaline-earth, rare-earth, actinide metals or thallium, T = Fe, Ru, or Os; X = P, As, or Sb), silicon- and germanium-based clathrates, β-pyrochlore oxides (AOs2O6 with A = K, Rb, and Cs) and AV2Al20 (with A = Al, Sc, Ga, Y, Lu, La, and Ce), to name a few only, are formed by a network of interconnected polyhedra which features open voids and allows different electropositive elements A to be embedded into them.1–3 In many of these compounds experiments established the presence of apparently localized vibrational modes at energies as low as a few millielectronvolts only, i.e. within the range of acoustic phonons.4–17 Often, results of diffraction and bulk experiments conducted on these compounds can be satisfactorily approximated by implying the existence of a low-energy Einstein mode. For this reason these compounds are often referred to as Einstein solids, a term applied originally to AlxV2Al20.18 A few of these Einstein solids show an unusual response to temperature changes. Thereby, the low-energy modes exhibit a blue-shift upon heating and inspired to be dubbed ‘rattling’ modes.4,14,19–23Numerous experimental studies on the electronic and heat transport properties of Einstein solids indicate a distinguished interaction of the localized low-energy modes with electrons and phonons of the compounds. Low-energy modes facilitate Cooper-pairing and, thus, superconductivity in metals.13,14,21,22,24–26 They form an obstruction to thermal transport accomplished by long wavelength phonons.27–29 The last feature is being paid great attention to for its potential exploitation in thermoelectric devices whose materials require very low lattice thermal conductivities κl(T) for excellent performance.
Over the past few years, microscopic experiments such as inelastic neutron scattering (INS) and dedicated simulation and modelling techniques have refined the perception of the localized low-energy vibrations. It is found that collective modes, i.e. phonons, can account for the properties of the low-energy inelastic response with high quality.15,16,20,30–40 Weaker bonding of the electropositive elements with the polyhydral matrices results in rather low energies of their collective, hybrid modes. The formation of low-energy vibrational eigenmodes is as well facilitated by high masses of the electropositive elements often used for the alloying. In any case the low-energy modes are characterized by distinguished dispersion ω(Q), i.e. the energy ℏω(Q) of eigenstates varies strongly with their momentum ℏQ and gives rise to a number of van Hove singularities ∂ω(Q)/∂Q = 0 at different Q.41–44 The van Hove singularities manifest themselves as multiple maxima in Q-averaged inelastic responses such as the vibrational density of states Z(ω). Whereas in experiments probing momentum- and energy-averaged signals, such as heat capacity measurements and thermal displacement studies, they are settled as an apparent single Einstein frequency.45–47
The importance of the low-energy phonons for the lattice thermal conductivity is not completely clear since κl(T) is modified strongly by other properties of the compounds. For example, topological and chemical disorder and partial filling of the voids are some dominant effects reducing κl(T) significantly.48–50 They are indeed common to and vary appreciably in most of the Einstein solids listed above. To draw conclusions of general validity upon the effect of the low-energy ‘rattling’ modes on the thermal conductivity a compound has to be studied whose low-energy dynamics is known to have a primary impact on κl(T) and can be tuned in a wide range of energies by the inclusion of distinct electropositive elements.
In this paper we discuss that AV2Al20 accepting a variety of electropositive elements A such as Al, Sc, Ga, Y, Lu, La, Ce, and Yb is a promising compound for such studies. The AV2Al20 compounds adopting the cubic CeCr2Al20 structure type which is sketched in Fig. 1 are built-up by slightly distorted icosahedra formed by Al(48f) and Al(96g) (Wyckoff positions are given in parentheses) atoms surrounding the V atoms. These icosahedra are linked together by the Al(48f) atoms along the [110] direction. Such inter-connected icosahedra form a tetrahedral framework with the Al(16c) atoms being in the center of hexagonal prisms. These prisms share common triangular faces with the icosahedra and are thus composed of Al(96g) atoms. In this architecture the A atoms reside in spacious voids occupying the (8a) position (see Fig. 1). They are coordinated by 12 Al(96g) atoms forming a truncated tetrahedron. Another 4 Al(16c) atoms cap the hexagonal faces of the truncated tetrahedron. This kind of coordination polyhedron with 16 vertices is called the Friauf polyhedron and is frequently encountered in complex topologically close-packed intermetallic crystal structures.
The distinct dependence of κl(T) on different filler atoms is highlighted in Fig. 2 which depicts experimental data on Sc and La containing V2Al20. The results demonstrate a strong suppression of κl(T) in ScV2Al20 and indicate a peculiar temperature (T) dependence. Thereby κl(T) is steadily increasing upon heating with no indication of a maximum as it is expected from a crystalline compound with a well-defined Debye temperature (ΘD).41,42 To shed light on this peculiar property we probe the microscopic dynamics of ScV2Al20, LaV2Al20 and CeV2Al20 by T-dependent INS experiments and identify their low-energy vibrational eigenmodes. We demonstrate that the T response of these eigenmodes is tuned from a rather classical anharmonic behaviour in LaV2Al20 and CeV2Al20, i.e. red-shifting upon heating, to a ‘rattling’ like anharmonicity in ScV2Al20, i.e. blue-shifting upon heating.
The INS experiments are accompanied by X-ray diffraction studies on a series of Al, Sc, La and Ce containing AV2Al20 and backed up by density functional theory (DFT), lattice dynamics calculations (LDC) and powder averaged lattice dynamics calculations (PALD) of AV2Al20 with A = □, Sc, La, and Ce. With A = □ we refer throughout this paper to the computer generated binary compound with voids left unoccupied. To allow a close-up view of the inelastic signal specific to the elecropositive elements their scattering power in INS requires to be sufficiently high. For this reason the focus is set on the Sc and La containing compounds. The scattering power of Ce is small thus the signal in INS from CeV2Al20 reflects the dynamics of the poly-anionic matrix, however, modified by the coupling with Ce.
II. Experiments and density functional calculations
A. Sample preparation and characterization
AV2Al20 (A = Sc, La, and Ce) samples of the ternary compounds were prepared by a multi-step synthetic approach. First, binary precursor compounds VAl3, ScAl3, LaAl4, and CeAl4 were synthesized by arc melting of the elemental metals (Sc ingots, Chempur 99.9 wt%, La rods, Ames 99.9 wt%, Ce rods, and Ames 99.9 wt%). The binary compounds were placed in corundum crucibles, sealed in evacuated quartz ampoules and heat treated at 900 °C for 5 days. After that they were ground in a hard-metal mortar to a fine powder (particle size <100 μm) which was then blended with Al powder in stoichiometric ratios following equation: AAlx + 2VAl3 + (14 − x)Al → AV2Al20.Sample batches of 3g each were cold compacted in press forms without the use of lubricants. The resulting tablets were placed in corundum crucibles, sealed in quartz tubes under an atmosphere of about 400 mbar Ar gas. After slow heating to 600 °C the samples were kept at this temperature for 1 week for an initial heat treatment. Then they were reground and re-compacted and annealed at temperatures of 700 to 750 °C for one week. These steps were repeated until reactions were completed.
The ternary compounds were obtained as dense sintered sample specimens. A minor impurity of free Al metal was detected by X-ray diffraction and microprobe analysis. Tiny crystals of ScV2Al20 could be isolated from a sample with ScV2Al20 composition prepared by arc melting of the elements, annealed at 660 °C for one month, followed by heat treatment at 800 °C for 1 week in a corundum crucible which was sealed in a quartz tube under an atmosphere of 400 mbar Ar gas.
Metallographic microstructure analyses on polished surfaces were performed by optical microscopy and electron probe microanalysis. The latter investigations were carried out by energy dispersive analysis (EDX) on a Philips XL 30 scanning electron microscope. The chemical composition deduced by EDX analysis is: Sc0.9(1)V2Al20, La0.9(1)V2Al20, and Ce0.9(2)V2Al20. Note that for clarity we set aside the notion of the filling ratios throughout this paper.
B. X-Ray diffraction and thermal conductivity
Powder X-ray diffraction (XRD) measurements were made using CoKα radiation (λ = 1.789007 Å) applying the Guinier-Huber technique. Single crystal data for ScV2Al20 and AlxV2Al20 were collected on a Rigaku R-axis RAPID diffractometer (Mo Kα, λ = 0.71073 Å). Crystallographic structure refinements and calculations were made using the WINCSD51 and SHELXL-97 (ref. 52) program packages. Achieved reliability factors52 of the single crystal structure refinements are: ScV2Al20 (R1 = 0.029 for 246 Fo > 4(Fo); wR2 = 0.051). For the full profile powder refinements:51 LaV2Al20 (R intensity: 0.0517, 0.094) and CeV2Al20 (R intensity: 0.056, 0.099).The thermal conductivity κ(T) (see Fig. 2) was determined simultaneously with electrical resistivity ρ(T) and the Seebeck coefficient S(T) using a commercial setup (option TTO, PPMS, Quantum Design). The lattice contribution to thermal conductivity, κl(T), was estimated by subtracting the conduction electron contribution κe from the total κ(T). κe was estimated by the Wiedemann–Franz law with L0 = 3(πkB/3e)2 ≈ 2.45 × 10−8 J s−1 Ω K−1.
C. Inelastic neutron scattering experiments
INS experiments were carried out with compounds ScV2Al20, LaV2Al20, and CeV2Al20 on the time-of-flight spectrometers IN4@ILL and IN6@ILL located at the European neutron source Institut Laue Langevin in Grenoble, France. The cold-neutron spectrometer IN6@ILL was utilized in the time-focusing mode with the best energy resolution set to 7.5 meV at the anti-Stokes line and the incident neutron wavelength λi = 4.14 Å. The thermal-neutron spectrometer IN4@ILL was utilized in the elastic focusing mode, i.e. with best energy resolution set to 0 meV and two different wavelengths λi. Both λi were chosen for best resolution of the low-energy modes in the studied compounds resulting in λi = 2.2 Å for ScV2Al20 and λi = 1.8 Å for LaV2Al20 and CeV2Al20.Powdered specimen of the compounds of about 20 g each was measured at temperatures T between 2 and 300 K. We applied T ≈ 100 and 300 K for all samples on IN6@ILL. On IN4@ILL ScV2Al20 and LaV2Al20 were measured at T ≈ 2, 50, 100, 200 and 300 K whereas CeV2Al20 was studied at 2, 70, 230 and 300 K. Precise T values are reported with the data hereafter. Standard procedures for data correction and conversion were utilized. Data are corrected for empty can scattering, for absorption, self-attenuation and frame overlap effects, for different detector efficiencies of the multidetector units, and for the energy dependent efficiency of the Helium-3 counters. Scattering lengths and absorption cross sections tabulated in the literature were exploited.53 Their values are listed in Table 1.
| Element | σ coh | σ inc | σ tot | a.m.u. | σ tot/a.m.u. [×102] |
|---|---|---|---|---|---|
| Al | 1.495 | 0.008 | 1.503 | 26.982 | 5.570 |
| V | 0.018 | 5.08 | 5.1 | 50.942 | 10.011 |
| Sc | 19 | 4.5 | 23.5 | 44.956 | 52.273 |
| La | 8.53 | 1.13 | 9.66 | 138.91 | 6.954 |
| Ce | 2.94 | 0.00 | 2.94 | 140.12 | 2.098 |
The dynamic structure factors S(ω,T) were calculated as a scattering-angle averaged signal. To highlight the effect of the Debye–Waller factor (DWF) on the dynamic response functions the S(ω,T) are corrected for the Bose–Einstein thermal occupation number. The generalized density of states G(ω) was derived taking full account of the incoherent approximation formalism.40,43,44,54,55
D. Ab initio lattice dynamics calculation
First principles calculations were performed using the projector-augmented wave formalism of the Kohn–Sham DFT at the generalized gradient approximation (GGA) level, implemented in the Vienna ab initio simulation package (VASP).56–60 The GGA was formulated by the Perdew–Burke–Ernzerhof density functional.61,62 The Gaussian broadening technique was adopted. All calculations presented in this study were performed with one unit cell comprising 176 and 184 atoms for □V2Al20 and AV2Al20, respectively. A k-mesh of 7 × 7 × 7 points in the Monkhorst–Pack scheme and the energy cut-off of 375 eV were applied.A series of energy minimization runs for a variation of the cell volume up to ±5% were carried out to compute the equation of state (EoS) of the compounds. Bulk moduli Bo, their pressure derivatives B′ and equilibrium volumes Vo were derived from a match of the Birch–Murnaghan equation
 | (1) |
The vibrational dynamics of the compounds were calculated by the direct method implemented in the program PHONON based on Hellmann–Feynman forces derived from a series of single point energy calculations.64,65 A Q-mesh of 2 × 105 points was utilized for the calculation of the total Z(ω) and partial Zn(ω) vibrational densities of states with n denoting the constituents of the compounds. The corresponding response functions such as thermal displacement parameters Uniso(T),
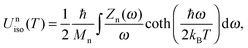 | (2) |
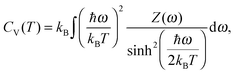 | (3) |
Anharmonicity effects were examined from Hellmann–Feynman forces computed with structures whose lattice parameters were varied by ±1 ‰ from the equilibrium values. Mode Grüneisen parameters
 | (4) |
 | (5) |
 | (6) |
 | (7) |
To allow a direct comparison of the computer generated response with experimental data we applied the PALD technique to compute the Q-resolved and orientationally averaged phonon form-factors of the compounds.33,36,39,40 A total of 105Q-points in the wave vector range 0–10 Å−1 was exploited for the PALD response. Extracting the phase-space region monitored using the IN6@ILL and IN4@ILL instruments, accounting for the scattering lengths and cross sections of the compounds' constituents, and approximating the energy resolution of the spectrometers allow computing PALD-generated Q-averaged generalized density of states G′(ω) in analogy to the measured G(ω). To highlight the strong differences in the scattering properties of the compounds' constituents we report in Table 1 their scattering power. Note for example that the probability of scattering neutrons from scandium is almost one order of magnitude higher than the scattering probability from aluminum, hence, leading to an enhanced departure of the measured spectral density G(ω) from the phonon density of states Z(ω).
III. Results
A. Equation of state and structural properties
Fig. 3 depicts the EoS data and the resulting lattice parameters in comparison to the X-ray powder and single-crystal diffraction results and to literature data. Parameters obtained from the fits with eqn (1) are listed in Table 2. Table 3 offers a comparison of the fractional coordinates x, y, z obtained for the DFT optimized structures and derived from the X-ray diffraction experiments.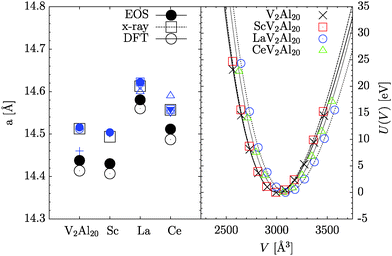 | ||
| Fig. 3 Left, lattice parameters a of AV2Al20 compounds derived from EoS data (large ●), X-ray scattering results (large □), and DFT optimized structures (large ○) The ternary compounds are characterized by the occupants of the 8a site. Literature data are reported as small symbols. They are extracted from ref. 24 and 25 (small ●), ref. 22 (small ○), ref. 77 (+), ref. 70 (□), ref. 76 (△), ref. 78 (▽), ref. 71 (▼). Right, energy difference dependent on the cell volume. Lines correspond to fit results of the Birch–Murnaghan equation of state indicated as eqn (1). | ||
| □ | Sc | La | Ce | |
|---|---|---|---|---|
| a′ [Å] | 14.5121(3) | 14.4936(8) | 14.6126(6) | 14.5570(7) |
| a* [Å] | 14.5125(7) | 14.5057(7) | — | — |
| a o [Å] | 14.4378(3) | 14.4303(3) | 14.5805(3) | 14.512(2) |
| B o [GPa] | 86.02(6) | 91.470(3) | 88.77(5) | 91.9(2) |
| B′ [GPa] | 4.34(2) | 4.32(1) | 4.35(2) | 4.45(8) |
| a [Å] | 14.4135 | 14.4068 | 14.5601 | 14.4870 |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (227), origin choice 2) obtained for the DFT optimized structures and derived from X-ray experiments on polycrystalline and single-crystal specimens. Listed are fractional coordinates xyz of the cation sites. The fractional coordinates of Al(16c), A(8a), and V(16d) correspond to (0 0 0), (1/8 1/8 1/8), and (1/2 1/2 1/2) respectively. The compounds are characterized by the occupants of the 8a site
m (227), origin choice 2) obtained for the DFT optimized structures and derived from X-ray experiments on polycrystalline and single-crystal specimens. Listed are fractional coordinates xyz of the cation sites. The fractional coordinates of Al(16c), A(8a), and V(16d) correspond to (0 0 0), (1/8 1/8 1/8), and (1/2 1/2 1/2) respectively. The compounds are characterized by the occupants of the 8a site
| DFT calculation | Powder X-ray | Single crystal X-ray | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | ||
| □ | Al(48f) | 0.4849 | 1/8 | 1/8 | 0.4857(2) | 1/8 | 1/8 | 0.48506(5) | 1/8 | 1/8 |
| Al(96g) | 0.0599 | x | 0.3227 | 0.0613(1) | x | 0.3221(8) | 0.05982(2) | 0.05982(2) | 0.32304(4) | |
| Sc | Al(48f) | 0.4858 | 1/8 | 1/8 | 0.4854(3) | 1/8 | 1/8 | 0.4858(1) | 1/8 | 1/8 |
| Al(96g) | 0.0595 | x | 0.3239 | 0.0596(4) | x | 0.3267(3) | 0.0596(1) | x | 0.3236(1) | |
| La | Al(48f) | 0.4872 | 1/8 | 1/8 | 0.4864(3) | 1/8 | 1/8 | |||
| Al(96g) | 0.0585 | x | 0.3263 | 0.0596(4) | x | 0.3267(3) | ||||
| Ce | Al(48f) | 0.4875 | 1/8 | 1/8 | 0.4866(3) | 1/8 | 1/8 | |||
| Al(96g) | 0.0590 | x | 0.3252 | 0.0589(4) | x | 0.3254(3) | ||||
We note a good match of the DFT results with the experimental data. In particular, the changes in the lattice parameter a upon the variation of the cation A are reproduced successfully. Note that for the comparison of the DFT derived □V2Al20 with literature data results of weakly doped ternary compounds have been chosen, such as Ga0.05V2Al20 with 14.51179(1) Å from ref. 22 and Al0.3V2Al20 with 14.5157(8) Å from ref. 24.
There is a small, however, clear deviation of the DFT data towards smaller values when compared with measured a. Its extent can be attributed to the thermal expansion of the compounds, as all experimental results referred to here have been obtained at room temperature in contrast to the zero-point ground-state DFT calculations. Kontio et al. established in ref. 66 an increase of a by about 0.03 Å between 100 and 295 K for Al0.85V2Al20. For Al0.2V2Al20 we estimate an increase by about 0.05 Å between 0 and 200 K from linear expansion data of Safarik et al. in ref. 23.
A close match is observed for DFT results of Jahnátek et al. reporting a = 14.460 Å in ref. 67 and Wang et al. reporting a = 14.449 Å in ref. 68. An equally good match is found for the bulk moduli with B = 85 GPa and B0 = 86.1 GPa determined by Jahnátek et al. and Wang et al., respectively. Safarik et al. established BT,S(T = 0) ≈ 87.7 GPa for Al0.2V2Al20 in experiments.23
B. Lattice dynamics calculations
The computed Γ-point frequencies are listed in Table 4. They correspond to ωoi exploited in eqn (7). Phonon dispersions ℏω(Q) along high-symmetry directions are reported in Fig. 4. For clarity we restrict the presentation of the phonon eigenmodes to the low-energy region only. At higher energies the density of eigenmodes is too high to allow significant conclusions upon differences in ℏω(Q) between the different compounds. A more apprehensible information is hence offered by the total Z(ω) and partial vibrational densities of states Zn(ω). They are reported in Fig. 5.| □V2Al20 | ScV2Al20 | LaV2Al20 | CeV2Al20 | |
|---|---|---|---|---|
| T 1u(I) | 0.0 | 0.0 | 0.0 | 0.0 |
| T 1u(I) | 3.727 | 1.894 | 3.023 | 3.234 |
| T 1u(I) | 4.133 | 4.108 | 3.288 | 3.824 |
| T 1u(I) | 4.830 | 4.903 | 5.082 | 5.165 |
| T 1u(I) | 5.991 | 5.913 | 6.018 | 6.103 |
| T 1u(I) | 6.642 | 6.297 | 6.752 | 6.676 |
| T 1u(I) | 7.583 | 6.861 | 7.239 | 7.045 |
| T 1u(I) | 7.844 | 7.432 | 7.359 | 7.325 |
| T 1u(I) | 8.529 | 7.683 | 7.514 | 7.505 |
| T 1u(I) | 9.626 | 8.604 | 8.254 | 8.311 |
| T 1u(I) | 11.392 | 9.599 | 9.392 | 9.420 |
| T 1u(I) | 12.681 | 10.952 | 10.263 | 10.463 |
| T 1u(I) | 12.896 | 12.438 | 12.629 | |
| T 2g(R) | 4.313 | 2.001 | 3.186 | 3.157 |
| T 2g(R) | 5.309 | 4.723 | 4.905 | 4.927 |
| T 2g(R) | 6.270 | 5.487 | 5.613 | 5.563 |
| T 2g(R) | 7.042 | 6.533 | 6.507 | 6.508 |
| T 2g(R) | 9.014 | 7.399 | 7.384 | 7.393 |
| T 2g(R) | 9.218 | 9.007 | 8.758 | 8.833 |
| T 2g(R) | 10.230 | 9.358 | 8.906 | 9.025 |
| T 2g(R) | 12.105 | 10.048 | 9.476 | 9.617 |
| T 2g(R) | 12.169 | 11.723 | 11.804 | |
| E g(R) | 4.014 | 4.262 | 4.510 | 4.500 |
| E g(R) | 6.142 | 6.113 | 5.938 | 6.031 |
| E g(R) | 7.884 | 8.303 | 8.210 | 8.283 |
| E g(R) | 10.419 | 10.043 | 9.438 | 9.612 |
| A 1g(R) | 7.723 | 7.741 | 7.748 | 7.911 |
| A 1g(R) | 9.494 | 9.330 | 8.750 | 9.016 |
| A 1g(R) | 12.145 | 11.406 | 10.684 | 10.900 |
| T 2u | 2.734 | 2.735 | 2.662 | 2.895 |
| T 2u | 3.915 | 3.838 | 3.147 | 3.650 |
| T 2u | 4.575 | 4.526 | 4.671 | 4.682 |
| T 2u | 5.815 | 5.682 | 5.660 | 5.693 |
| T 2u | 6.064 | 6.277 | 6.432 | 6.335 |
| T 2u | 7.324 | 7.101 | 7.336 | 7.220 |
| T 2u | 8.391 | 8.238 | 8.080 | 8.186 |
| T 2u | 11.457 | 11.603 | 11.206 | 11.284 |
| T 1g | 3.503 | 3.637 | 3.570 | 3.755 |
| T 1g | 4.752 | 4.722 | 4.876 | 4.872 |
| T 1g | 4.869 | 4.974 | 5.132 | 5.064 |
| T 1g | 6.749 | 7.045 | 6.916 | 7.021 |
| T 1g | 7.290 | 7.215 | 7.436 | 7.281 |
| T 1g | 10.544 | 10.663 | 10.326 | 10.374 |
| E u | 3.876 | 3.698 | 2.782 | 3.345 |
| E u | 4.315 | 4.427 | 4.571 | 4.569 |
| E u | 5.587 | 5.940 | 5.597 | 5.847 |
| E u | 7.760 | 7.023 | 6.817 | 6.741 |
| E u | 8.302 | 8.741 | 8.697 | 8.695 |
| E u | 10.043 | 9.582 | 8.879 | 9.024 |
| A 2u | 3.840 | 5.772 | 7.021 | 6.694 |
| A 2u | 7.389 | 7.661 | 7.484 | 7.424 |
| A 2u | 8.892 | 8.492 | 7.716 | 7.816 |
| A 2u | 9.767 | 9.132 | 8.702 | 8.949 |
| A 2u | 11.975 | 11.659 | 10.909 | 11.083 |
| A 2g | 2.902 | 2.741 | 2.705 | 2.757 |
| A 1u | 4.902 | 5.093 | 5.411 | 5.331 |
Depending on the occupation of the 8a site significant changes in total Z(ω) are observable at ℏω ≲ 20 meV (≲5 THz). At ℏω > 20 meV only a subtle renormalization of the response can be identified. As expected, at ℏω ≲ 20 meV the cation vibrations dominate the inelastic response. Their coupling to each of the unique atoms is significantly different having the strongest effect on the Al(16c) dynamics. Al(16c) exhibits a localized density of states peaking at around 16 meV in the binary compound. In ScV2Al20 the localized ZAl(16c)(ω) splits into two bands with characteristic energies of about 16 meV and 24 meV. These bands are renormalized to 12 and 30 meV in LaV2Al20 and to 15 and 28.5 meV in CeV2Al20. As can be seen from the texture of the partial densities of states, the renormalization of the low-energy maximum is due to a strong hybridization with the A(8a) vibrations. To quantify these findings the mean energies Ēn and the variances Ẽn of A(8a) and Al(16c) were calculated as
They are listed in Table 5. Averaged velocities of sound vav and Debye temperatures ΘD calculated from the Debye-level of limω→0Z(ω)/ω2 are listed as well.
| □ | Sc | La | Ce | |
|---|---|---|---|---|
| Ē Al(16c) [meV] | 16.8 | 18.9 | 18.1 | 19.7 |
| Ẽ Al(16c) [meV2] | 12.8 | 28.4 | 69.2 | 45.0 |
| Ē A(8a) [meV] | — | 9.0 | 13.8 | 13.6 |
| Ẽ A(8a) [meV2] | — | 33.6 | 28.7 | 21.1 |
| v av [m s−1] | 4866 | 4420 | 4641 | 4726 |
| Θ D [K] | 563 | 520 | 540 | 551 |
A concomitant hybridization of A(8a) vibrations is formed with the Al(48f) and Al(96g) dynamics leading to a mode deficiency around 17 meV in LaV2Al20 and CeV2Al20. This effect is as well visualized by their phonon dispersions in Fig. 4 through a concentration of localized eigenmodes at 2.7–3.5 THz (11.2–14.5 meV) in LaV2Al20, and at 2.8–3.8 THz (11.6–15.7 meV) in CeV2Al20. Effectively and unlike ZAl(16c)(ω), ZAl(48f)(ω) and ZAl(96g)(ω) are distributed over the entire range of eigenmodes. In accordance with Z(ω) they exhibit only a weak renormalization at ℏω > 20 meV for different occupants of the 8a sites. The dynamics of vanadium (16d) is in line with these results. However, for ℏω ≲ 20 meV its density of states is characterized by a low, flat and textureless profile.
The most distinct influence on the collective vibrations is generated by the inclusion of Sc. In ScV2Al20 its characteristic frequencies are located below the first optic modes of the binary compound. These optic modes are dominated by Al(96g) vibrations and can be identified from the first strong peak at about 11.6 meV (2.8 THz) in the densities of states in Fig. 5 as well as by the flat phonon dispersions at this energy in Fig. 4. Thus, Sc hybridizes weakly with the V2Al20 vibrations forming the additional dispersionless optic phonons at energies down to 5 meV (1.2 THz). Small peaks in ZAl(16c)(ω) and ZAl(96g)(ω) matching the texture of ZSc(8a)(ω) give evidence of this weak hybridization.
We indicate by the red dashed line drawn with the phonon dispersion of ScV2Al20 in Fig. 4 the boundary below which the Sc generated optic phonons dominate the collective dynamics. Unlike in □V2Al20, LaV2Al20, and CeV2Al20 in which the Γ-point modes of lowest energy are optically silent (T2u, A2g symmetries) as indicated in Table 3, in ScV2Al20 they are infra-red (T1u) and Raman (T2g) active eigenstates.
C. Atomic potentials and force constants
Some features of the established collective dynamics can be broken down to the shape of atomic potentials approximated on the DFT level and to force constants determining the LDC. Atomic potentials U(Δx) of Al(16c) and A(8a) are reported in Fig. 6. Table 6 reports parameters obtained from approximating the potentials as U(Δx) = AΔx2 + BΔx4 within the extensive displacement range of [−0.25, 0.25] Å. | ||
| Fig. 6 Atomic potentials U(Δx) of Al(16c) and A(8a) computed from DFT in the directions x00 and xxx. | ||
| Compound | A Al x00 | B Al x00 | A Al xxx | B Al xxx | A A x00 | B A x00 | A A xxx | B A xxx |
|---|---|---|---|---|---|---|---|---|
| □V2Al20 | 0.9420(3) | 1.102(6) | 0.84(2) | 0.0 | — | — | — | — |
| ScV2Al20 | 1.24 | 0.861(2) | 1.834(1) | 0.756(7) | 0.610(1) | 2.03(1) | 0.61(3) | 2.1(4) |
| LaV2Al20 | 1.284(1) | 0.63(2) | 2.71 | 1.0186(1) | 3.624(1) | 1.367(2) | 3.624(1) | 1.5(1) |
| CeV2Al20 | 1.395(6) | 0.64(9) | 2.495(4) | 0.98(7) | 3.441(5) | 1.22(7) | 3.44(2) | 1.3(3) |
The occupation of the 8a site by the different cations has two effects on the harmonic part (A parameters) of the Al(16c) potentials. Firstly, the restoring forces are gradually augmented in both monitored directions in the sequence of Sc, Ce and La occupants. Thereby AAlxxx is approximately tripled in LaV2Al20 and CeV2Al20. AAlx00 is increased by about 50% only. Secondly, a moderate anisotropy present in □V2Al20 with AAlx00 ≳ AAlxxx is enhanced simultaneously. It takes on the highest value in LaV2Al20 whereby AAlx00 ≪ AAlxxx. This anisotropy and its systematic variation are the origin of the formation and shifting of the two maxima in ZAl(16c)(ω) shown in Fig. 5.
In contrast to the Al(16c) potentials, the harmonic contribution to U(Δx) of A(8a) is isotropic. AAx00 and AAxxx do not change systematically with AAlx00 and AAlxxx in the respective compounds but take on a minimum for Sc and a six times higher maximum for La. Since the mass ratio of La and Ce with Sc corresponds only to about three (see Table 1) the characteristic frequency of the heavy cations La and Ce is to be expected at higher values as evidenced by the ZA(8a)(ω) in Fig. 5.
In the binary compound the potential of Al(16c) appears to be considerably anharmonic in x00 direction. This anharmonicity is progressively suppressed in the ternary compounds following the sequence of Sc, Ce and La occupants. On the other hand the potential appears to be perfectly harmonic in xxx direction with BAlxxx = 0.
However, the most striking result of the potential analysis is the distinctive anharmonicity of Sc. As can be seen in Fig. 6 the U(Δx) of Sc is strongly reminiscent of a flat bottom potential. Note that the quality of the match of the quartic analytical function does not depend significantly on the fitting range, as we have probed in different fitting approaches not discussed here. Clearly, the quartic term is found to be intrinsic to the DFT-computed Sc potential. Terms of higher order such as of sextic proved to be redundant. Apart from its indispensable significance for the modelling of the Sc potential the quartic term proved to be of relevance to improve the fit quality for Al(16c) in □V2Al20 along x00.
The parameters A should reflect the harmonic forces derived from the Hellmann–Feynman forces through the LDC. The nonzero components of the 3 × 3 force matrix Fij are listed in Table 7. They match the expected relations of 2Ax00 = Fii and 2Axxx = Fii + 2Fij with i, j = x, y, z and prove the consistence of the potential analysis.
| Compound | F Al(16c) ii | F Al(16c) ij | F A(8a) ii |
|---|---|---|---|
| □V2Al20 | 1.897 | −0.100 | — |
| ScV2Al20 | 2.489 | 0.594 | 1.234 |
| LaV2Al20 | 2.571 | 1.423 | 7.266 |
| CeV2Al20 | 2.792 | 1.096 | 6.885 |
D. Inelastic neutron scattering and powder average lattice dynamics
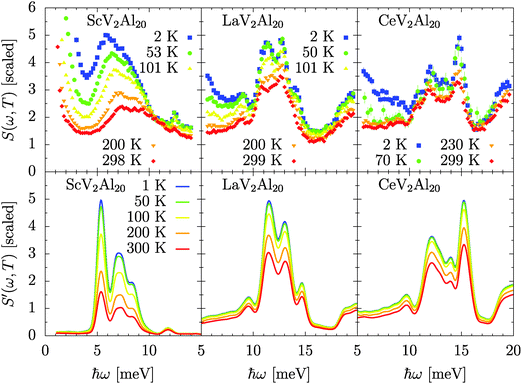
Fig. 7 depicts the phonon formfactor of ScV2Al20 at T = 300 K and the corresponding relative Debye–Waller factor (DWF) computed by PALD. The effect of the elevated temperature is visualized by the decrease of the DWF towards high wave vectors Q. This decrease is particularly pronounced for vibrational modes to which Sc contributes with high amplitudes, i.e. to modes at 4 ≲ ℏω ≲ 10 meV. In INS experiments the phonon intensity is determined by F(Q,ω,T) comprising the DWF.40 Thence, the characteristics of the Sc dynamics are detectable at low Q only evidenced by the pronounced signal localized at 1 ≲ Q ≲ 5 Å−1 and 4 ≲ ℏω ≲ 10 meV in F(Q,ω,T = 300 K) in Fig. 7.Fig. 8 reports the generalized densities of states G(ω) derived from INS experiments at IN6@ILL and from according PALD calculations G′(ω). The phase space covered by the experiment as well as exploited for the PALD is sketched in Fig. 7. The scatter towards high energies of the experimental data taken at 100 K results from reduced intensity due to the lowered Bose–Einstein occupation number. Note that at 100 K a peak around 22 meV becomes detectable stemming from elastic second-order scattering of the spectrometer's monochromator.
We find an overall good match between the experimental and PALD data sets. In any of the measured G(ω) pronounced low-energy peaks are identified giving evidence of the localization of the Sc, La and Ce dominated vibrations at low energies as discussed above. In particular for LaV2Al20 and CeV2Al20 the overall spectral distribution, the characteristic peaks and their relative intensities are well reproduced by the PALD. Note that the distinguished maximum at about 30 meV present only in G(ω) of LaV2Al20 and CeV2Al20 corresponds to the characteristic maximum in ZAl(16c)(ω) in these compounds.
Despite the overall good approximation of the ScV2Al20 INS response the match is less satisfactory for two reasons. Firstly, the pronounced low-energy peak dominated by Sc dynamics is shifted towards low energies in the PALD data. Although, the experimental results give evidence of a positive anharmonicity dω(T)/dT > 0 of this peak between 100 and 300 K, this anharmonicity is too small to compensate for the overall mismatch of this peak even at base temperature. Secondly, the spectral shape of the PALD distribution indicates better resolved peaks than found in the experimental G(ω). Obviously the analytically approximated energy-dependent resolution function of the spectrometer, which has been convoluted with the PALD results, is not fully sufficient to account for the broadening of peaks in the experimental signal of ScV2Al20.
To shed more light on the anharmonicity of the Sc-, La- and Ce-dominated low-energy modes and their spectral distribution Fig. 9 reports the Q-averaged dynamic structure factors S(ω,T) derived from IN4@ILL experiments. S(ω,T) has been corrected for the Bose–Einstein occupation number, thence, the intensity changes reflect the T dependence of the DWF only.
The INS derived S(ω,T) are affected by the following experimental effects. Bragg reflections are mediated through the energy resolution of the spectrometer and disguise the inelastic signal at ℏω → 0 for T → 0 as evidenced in Fig. 9. In general, lattice dynamics calculations do not account for elastic signals. Moreover, the compounds incoherent scattering mainly given by vanadium (see Table 1) contributes to the INS response. It is not accounted for by our PALD approach as it contributes monotonically as a flat background to the signal in the energy ranges considered in Fig. 9.
Aside from these effects, the PALD approach reproduces the properties of the low-energy modes with high quality. For LaV2Al20 and CeV2Al20 the spectral shape and its T response are captured in detail. Weak anharmonicity is revealed by the experiment evidenced by a smearing and a weak red-shift dω(T)/dT < 0 of peaks upon heating. Within the quality of the present data we quantify this shift to about −0.2(1) meV between 2 and 300 K. However, this shift does not apply universally to all identified peaks. We highlight only the behaviour of the small peak at about 14.5 meV in LaV2Al20 response whose T shift is roughly doubled. According to Zn(ω) it is dominated by Al(96g) vibrations. A similar conclusion can be drawn for the peak around 12 meV in CeV2Al20.
For ScV2Al20 the IN4@ill data firm up the observations made with the IN6@ILL measurements. As expected from the PALD calculations the intensity loss due to the T-dependence of the DWF is strongest for ScV2Al20, in spite of the smaller Q range monitored. In comparison to the PALD results the Sc-dominated modes are localized at higher energies and specific peaks, although implied in the low-energy maximum, barely resolved. Upon increasing T this maximum exhibits a pronounced blue-shift dω(T)/dT > 0 in contrast to the LaV2Al20 and CeV2Al20 response.
To quantify the anharmonic response of ScV2Al20 the low-energy part of G(ω) has been matched by a set of Gaussians and a Debye ω2 contribution. Two Gaussians are sufficient to approximate the IN4@ILL results, whereby the anti-Stokes line which is not shown here has been exploited separately down to 50 K. IN6@ILL results have been approximated by three Gaussians one explicitely dedicated to match a peak around 11.5 meV. This peak is identified by lattice dynamics calculation in Fig. 5 being dominated by Al(96g) dynamics and marked by the red dotted line in Fig. 8. The results are displayed in Fig. 10.
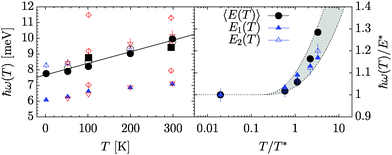 | ||
| Fig. 10 Left, temperature dependence of the characteristic low-energy peaks in the inelastic response of ScV2Al20. Large symbols represent the momenta 〈E(T)〉 of the approximated spectral density derived from the IN4@ILL Stokes line (●), anti-Stokes line (○), and IN6@ILL anti-Stokes line (■). The two characteristic energies E1(T) and E2(T) identified in the Stokes line of IN4@ILL data are discriminated by △ and ▲, respectively. Anti-Stokes line data are characterized by ▽ for IN4@ILL data and ◊ for IN6@ILL data. The full line represents a linear fit to all 〈E(T)〉 data. Right, comparison of the characteristic energies with the anharmonic model by Dahm and Ueda of ref. 69. The gray shaded area is given by the anharmonicity parameter 0.15 ≲ β ≲ 0.5. | ||
We report the energy positions of the peaks with the Stokes-line data explicitely discriminated as E1(T) and E2(T) as well as the moments of energy 〈E(T)〉 computed from the 2- and 3-Gaussian spectra, respectively. The entire set of 〈E(T)〉 has been matched by a linear T-dependence E(T) = E* + C·T with E* = 7.745 meV and C = 0.007379 meV K−1 as indicated by the solid line in Fig. 10. To classify the strength of the anharmonicity we interprete the values of E1(T), E2(T) and 〈E(T)〉 in terms of the Dahm and Ueda model (DUM) introduced in ref. 69. As indicated by the gray shaded area in Fig. 10 the evolution of the entire set of data is in agreement with an anharmonicity parameter β in the range of 0.15–0.5.
The T-variation of the low-energy modes in ScV2Al20 evidences the presence of a term surmounting the cubic term characteristic of thermal expansion.41 It is thus in agreement with a strong quartic anharmonic term in the Sc potential as discussed in Section IIIC. In contrast, for La and Ce the cubic term is obviously balancing out any other contribution of higher order.
Within the single particle DUM the prefactors A and B obtained for Sc result with the free mass of Sc in the characteristic energy  and the anharmonicity parameter βDUM ≈ 0.05. These values are close to the characteristic energy ĒSc ≈ 9.0 meV calculated from ZSc(ω) and to the β range estimated from experimental data. The correspondance of βDUM with the experimental data can be improved by taking into account the low-energy modes identified in G(ω) and thus ZSc(ω) only. It is then quantified to the range of 0.15–0.2.
and the anharmonicity parameter βDUM ≈ 0.05. These values are close to the characteristic energy ĒSc ≈ 9.0 meV calculated from ZSc(ω) and to the β range estimated from experimental data. The correspondance of βDUM with the experimental data can be improved by taking into account the low-energy modes identified in G(ω) and thus ZSc(ω) only. It is then quantified to the range of 0.15–0.2.
E. Thermal displacement parameters
Fig. 11 depicts the element specific thermal displacement parameters Uniso(T) derived from the partial phonon densities of states Zn(ω) through eqn (2). Note, that UAliso(T) and UViso(T) of the □V2Al20 compound are not explicitely displayed as they are very similar to and well represented by the corresponding values determined for ScV2Al20. | ||
| Fig. 11 Atomic thermal displacement parameters Uniso(T) computed from partial Zn(ω) within the harmonic approximation. Linestyle and color schemes are indicated in the subfigures. Symbols report literature data derived from single crystal diffraction experiments by Kangas et al. (●) in ref. 70, Moze et al. (□) in ref. 71 and in this work (large ○). Corresponding color schemes are chosen. Additional USciso(T) was computed for scandium corrected for the anharmonic temperature shift (Sc*) from ZSc[ω(T)]. | ||
We exploited in addition the experimentally determined energy shift E(T) shown in Fig. 10 to reconstruct an effective Z[ω(T)] which respects the renormalization of the low-energy modes in ScV2Al20. Thereby, an effective ZSc[ω(T = 0)] was generated to which only the localized signal between 4.9 and 10.4 meV in ZSc(ω) was assigned to, with the energy shift Δℏω(T) = CT with C = 0.007379 meV K−1. The weakly textured signal at ℏω ≤ 10.4 meV in ZAl(ω) + ZV(ω) was replaced by a Debye-like ∝ω2 signal respecting ΘD listed in Table 5. Finally, Z[ω(T)] was reconstructed from both contributions respecting their expected relative number of vibrational modes.
In the present X-ray diffraction experiments on powder materials the partial occupancies and site disorder in the AV2Al20 compounds as well as the low contrast of aluminum lead to high uncertainties and Uniso(T) values. They are one order of magnitude higher than values obtained with single crystals and for this reason they are not discussed here. The single crystal data shown in Fig. 11, however, match reasonably well with the DFT results and trends in the atomic displacements. Taking as well into consideration the data of Kangas et al. established in ref. 70 and Moze et al. (□) presented in ref. 71Uniso(T) of the different Al sites seem to scatter around Uniso(T) in such a way so as to balance out each other for an overall reasonable fit.
Data on Al0.2V2Al20 from neutron diffraction experiments by Safarik et al. discussed in ref. 23 show a reasonable match with the DFT results of □V2Al20. The experimentally established T-dependent deviation from a harmonic behavior of the Al(8a) displacement parameter in Al0.2V2Al20 is qualitatively in accordance with the estimated behaviour of USciso(T) in ScV2Al20.
F. Heat capacity
Fig. 12 shows the heat capacities derived from Z(ω) through eqn (3). The right subfigure focuses on the low T region and highlights the excess of vibrational modes on the heat capacity of ScV2Al20 in equivalence to the properties of Al and Ga containing compounds.22–24 The difference between CV(T) of ScV2Al20 and LaV2Al20 indicates by its negative values from about 80 K that the cumulative number of vibrational modes in LaV2Al20 is higher when integrated up to 12–18 meV.With the DFT derived data we report as well the effect of phonon renormalization on CV(T)/T data for ScV2Al20 calculated using Z[ω(T)]. Despite the visible access of intensity at low T in ScV2Al20 its CV(T)/T does not display a pronounced shoulder as evidenced for Ga and Al containing V2Al20.4,22–24 This can be expected as the characteristic modes of Sc are located at higher energies than those of Ga and Al, and, moreover, the energy shift upon T-variation of Al-dominated vibrations is supposed to be enhanced.4 The variation brought about by Z[ω(T)] is rather subtle. It is detectable as a dilution of the difference amplitude with respect to LaV2Al20 albeit a higher signal towards low T is present.
G. Grüneisen parameters and thermal expansion
Fig. 13 shows the mode Grüneisen parameter γ(ωi), the thermodynamic Grüneisen parameter Γ(T) and the coefficient of linear thermal expansion α(T) calculated through eqn (4)–(6). In full accordance with the reconstruction of an effective Z[ω(T)] of ScV2Al20 we carried out a renormalization of the two low-energy Γ-point frequencies. The corresponding Γ(T) and α(T) are as well displayed in Fig. 13.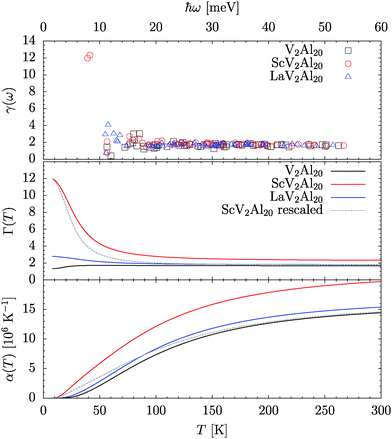 | ||
| Fig. 13 From top to bottom, the mode Grüneisen parameter γ(ωi), thermodynamic Grüneisen parameter Γ(T), and coefficient of linear expansion α(T) of □V2Al20, ScV2Al20, and LaV2Al20. | ||
The properties of γ(ωi) are correlated with the partial contributions of the elements to the eigenmodes. Vibrations at energies above 20 meV which are dominated by the amplitudes of Al(48f), Al(96g) and V tend to take on γ(ωi) values between 1.5 and 2.0. In the energy range of strong Al(16c) participation γ(ωi) increases to about 3 as can be specifically seen with the modes between 16 and 18 meV in □V2Al20 as well as below 15 meV in LaV2Al20. The effect of the A(8a) contribution to γ(ωi) is moderate in the LaV2Al20 whereas in ScV2Al20 values of about 12 are derived for the two low-energy modes.
As an effect of the pristine LDC results the enhanced anharmonicity in ScV2Al20 increases visibly Γ(T) and α(T) above the ones of □V2Al20 and LaV2Al20. High-T values of Γ(T) correspond to 1.7, 2.3 and 1.8 for □V2Al20, ScV2Al20 and LaV2Al20, respectively. The relative behaviour of α(T) at elevated T follows accordingly. At low-T the deviation of the ScV2Al20 properties is amplified as the anharmonicity is only strong for the low-energy modes.
Calculations with the renormalized low-energy modes result in high-T responses of ScV2Al20 very comparable to the ones of the other compounds. Γ(T) reaches a value of 1.8 and α(T) arrives close to the level of □V2Al20. Hence, the properties of ScV2Al20 are corrected by about 25% by the phonon renormalization.
The overall behaviour of the LDC derived Γ(T) and α(T) is in good agreement with experimental data on Al0.2V2Al20.23 Towards low T the Γ(T) of Al0.2V2Al20 shows an excess about four times stronger than that in ScV2Al20. Taking into consideration the exceeding energy shift of the characteristic Al(8a) modes in AlxV2Al20 this result could be conjectured.4 To reproduce at low T a significant shoulder in α(T) as established by Safarik et al. for Al0.2V2Al20 accounting for stronger anharmonicity is required. The same can be stated for the slightly higher signals of Γ(T) and α(T) towards high T in the experimental data, such as Γ(T) ≈ 2.
IV. Discussion and conclusions
To start with some generalities we highlight the good agreement of the DFT and LDC results with data and conclusions drawn from computer studies on other Einstein solids such as skutterudites and clathrates published in the literature.15,16,30,31,37,39,72 Experimentally established inelastic responses are reproduced satisfactorily with no negative eigenfrequencies indicative of an instability of the computer generated compounds. The electropositive elements A = Sc, La and Ce occupy the center positions in the voids of the polyanionic matrix V2Al20. Low-energy excitations are identified as hybrid eigenmodes of A with V2Al20 to which A contributes with higher amplitudes. As a consequence of the hybridization the eigenmodes dominated by A are distinctly dispersive leading to a number of van Hove singularities in the low-energy region of the vibrational density of states of the compounds.From the analysis of the static, local potentials it follows that anharmonicity is enhanced for the weaker coupling and, thus, for smaller restoring forces acting on Sc. An estimation of the anharmonicity as a response to T variations by means of the DUM anharmonic model introduced in ref. 69 indicates a positive frequency shift in the order of the detected renormalization of low-energy modes in ScV2Al20. This shift was approximated from INS data to 2 meV upon heating the compound from 2 to 300 K which corresponds to an anharmonicity parameter β = 0.15–0.5 of the model. DFT derived potentials are in agreement with β = 0.05–0.2. Equivalent data analysis had been performed for the T response of INS data for the compounds YbFe4Sb12 with β ≈ 0.014 in ref. 36 and AOs2O6 with β ranging between 0.025 and about 1 for different A = K, Rb, and Cs in ref. 14. Thus, the amplitude of the phonon renormalization and the values of the β parameter in those compounds render the property of ScV2Al20.
We exploited the positive mode shift of ScV2Al20 to correct LDC derived data on USciso(T) and CV(T), as well as Γ(T) and α(T) derived from volume dependent DFT calculations. The agreement with data available in the literature on AV2Al20 is convincing on qualitative and quantitative grounds.4,22–25 In particular, the applied correction proves to be essential to arrive at reasonable values of Γ(T) and α(T) at high temperatures and discloses thus the significance of the enhanced positive anharmonicity of the low-energy modes in ScV2Al20. The high-T behaviour of Γ(T) and α(T) shows a propensity to slightly reduced values, e.g. α(T) is smaller by 10% when compared with experimental results and the DFT derived pressure derivative B′. Nonetheless, it is necessary to recall that the presented thermodynamic responses were modelled with ground state parameters Vo, Bo and ground state Γ-point distributions ωoi, and the applied renormalization of low-energy modes was based on the idea of decoupled and harmonic vibrations of Sc, on the one hand, and V2Al20, on the other.
The importance of coupling and anharmonicity can be judged upon from the properties of LaV2Al20. Unlike in ScV2Al20 the low-energy vibrations in LaV2Al20 show a weak softening upon heating, however, the enhanced low-T Γ(T) values and the augmented α(T) behaviour rather suggest a weak positive mode-shift upon heating. This apparent contrast can be explained by the thermal expansion of LaV2Al20 balancing out the quartic term identified in the La potential as a ground-state property. The spectral densities do not shift uniformly and different peaks in G(ω) and S(ω,T) show different sensitivities upon T variations. An equivalent observation is reported in the literature for the dynamics of skutterudites and clathrates.16,33,36,72
There is a dynamic feature in the response of ScV2Al20 which may underline the coupling properties of this compound and is worth speculating about. The shift of the mean energy 〈E(T)〉 of the Sc-dominated peak does not follow strictly the prediction of the DUM but tends towards higher values at higher T as shown in Fig. 10. INS data for KOs2O6 show a corresponding behaviour.14 Obviously higher restoring forces than those predicted by the static quartic potential at T = 0 are at work at higher T. This finding is supported by the recently discussed thermal effects of the Al0.33W1.67O6 matrix on the effective potential of K derived through molecular dynamics simulations by Shoko et al. in ref. 73. If it was correct, it would be in line with the conjecture of an effective sextic term dominating the thermal displacement parameter UAl(8a)iso(T) in Al0.2V2Al20 as discussed in ref. 23. Interestingly, we concluded as well a noticeable anharmonicity in the DFT computed Al(16c) potential akin to the one communicated by Safarik et al. for Al0.2V2Al20.
The anharmonic effects discussed so far cannot explain the weak definition of peaks in the INS response of ScV2Al20. Assuming a strict correctness of our DFT and LDC results we expect characteristic peaks in ScV2Al20 to be as well resolved by INS as they are in LaV2Al20 and CeV2Al20. It is tempting to assign the broadening of the INS data to defects and disorder in the ScV2Al20 compound. However, the validity of this assignment remains an open question here as we could not quantify a possible amount of defects in the specimen. A defective crystalline structure becomes noticeable by a reduction of its Bragg peak intensities equivalent to the impact of enhanced thermal displacements Uniso(T). With the performed X-ray diffraction experiments we could not discriminate these effects. Temperature dependent neutron diffraction enhancing the contrast between Sc and Al and total scattering experiments could be of help and will be tackled in future.
Finally we highlight that the core of this study is the establishment of the microscopic dynamics of AV2Al20 with the temperature dependent effects being computed as a consequence of the ground state properties of the DFT approximated compounds. Consequently, the results do not explain the thermal conductivity data for ScV2Al20 and LaV2Al20 in quantitative measures as reported in Fig. 2. Nonetheless we identify two properties of the microscopic dynamics which lead to a reduced thermal conductivity in crystals and could account for the particular behaviour of κl(T) of ScV2Al20 on qualitative grounds. Number one is the formation of hybrid modes of low-dispersion located within the energy range of acoustic phonons of the binary compound. Thereby, the average energy of the hybrid modes is bisected in ScV2Al20 when compared to LaV2Al20 disrupting propagating modes of longer wavelength and thus indicating an overall lowered κl(T). Number two is the enhanced mode Grüneisen parameter of the hybrid modes which is highly augmented in the Sc containing compound facilitating shorter phonon lifetimes and leading to lowered κl(T). With an increase of T the low-energy hybrid modes of ScV2Al20 are renormalized approaching energies of the LaV2Al20 hybrid modes thence being indicative of a progressive reduction of the difference in κl(T) between these two compounds. In summary, the measured κl(T) plotted in Fig. 2 is qualitatively in line with the properties of the microscopic dynamics established experimentally by INS and through DFT and LDC.
V. Summary
We have shown that the microscopic dynamics of AV2Al20 (A = Sc, La, and Ce) which was monitored by inelastic neutron scattering experiments can be approximated by a set of vibrational eigenmodes derived through density finctional theory (DFT) and lattice dynamics calculations (LDC). Structural properties studied experimentally have been equally matched on qualitative and quantitative grounds by the computer modelling. The propensity of the DFT-derived potential of A(8a) and Al(16c) sites to anharmonicity with a significant quartic term has been established and experimentally confirmed in ScV2Al20 by a positive renormalization of Sc-dominated modes upon heating in INS experiments. It has been demonstrated for ScV2Al20 that with the aid of DFT and LDC-derived mode Grüneisen parameters and the experimentally deduced mode shift optimization of the characterization of thermal displacements, heat capacities, thermodynamic Grüneisen parameters and thermal expansions can be performed.References
- B. C. Sales, Handbook on the Physics and Chemistry of the Rare Earths, 2002 Search PubMed.
- G. S. Nolas, D. T. Morelli and T. M. Tritt, Annu. Rev. Mater. Sci., 1999, 29, 89 CrossRef CAS.
- G. S. Nolas, J. Sharp and H. J. Goldsmid, Thermoelectrics Basic Principles and New Materials Developments, Springer, 2001 Search PubMed.
- A. D. Caplin and L. K. Nicholson, J. Phys. F: Met. Phys., 1978, 8, 51 CrossRef , http://stacks.iop.org/0305-4608/8/i=1/a=010.
- V. Keppens, D. Mandrus, B. C. Sales, B. C. Chakoumakos, P. Dai, R. Coldea, M. B. Maple, D. A. Gajewski, E. J. Freeman and S. Bennington, Nature, 1998, 395, 876 CrossRef CAS PubMed.
- R. P. Hermann, R. Jin, W. Schweika, F. Grandjean, D. Mandrus, B. C. Sales and G. J. Long, Phys. Rev. Lett., 2003, 90, 135505 CrossRef.
- R. Viennois, L. Girard, D. Ravot, H. Mutka, M. Koza, F. Terki, S. Charar and J.-C. Tedenac, Physica B, 2004, 350, e403 CrossRef CAS PubMed.
- R. Viennois, L. Girard, M. M. Koza, H. Mutka, D. Ravot, F. Terki, S. Charar and J.-C. Tedenac, Phys. Chem. Chem. Phys., 2005, 7, 1617 RSC.
- M. Christensen, F. Juranyi and B. B. Iversen, Phys. B, 2006, 385–386(part 1), 505 CrossRef CAS PubMed , ISSN 0921-4526, proceedings of the Eighth International Conference on Neutron Scattering, http://www.sciencedirect.com/science/article/pii/S092145260601132X.
- R. Viennois, P. Toulemonde, M. Koza, H. Mutka, A. S. Miguel and R. Lortz, J. Phys.: Conf. Ser., 2007, 92, 012121 CrossRef , http://stacks.iop.org/1742-6596/92/i=1/a=012121.
- N. Melnychenko-Koblyuk, A. Grytsiv, L. Fornasari, H. Kaldarar, H. Michor, F. Rhrbacher, M. Koza, E. Royanian, E. Bauer and P. Rogl, et al., J. Phys.: Condens. Matter, 2007, 19, 216223 CrossRef , http://stacks.iop.org/0953-8984/19/i=21/a=216223.
- N. Melnychenko-Koblyuk, A. Grytsiv, P. Rogl, M. Rotter, E. Bauer, G. Durand, H. Kaldarar, R. Lackner, H. Michor and E. Royanian, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 144118, DOI:10.1103/PhysRevB.76.144118.
- R. Lortz, R. Viennois, A. Petrovic, Y. Wang, P. Toulemonde, C. Meingast, M. M. Koza, H. Mutka, A. Bossak and A. S. Miguel, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224507, DOI:10.1103/PhysRevB.77.224507.
- H. Mutka, M. M. Koza, M. R. Johnson, Z. Hiroi, J.-I. Yamaura and Y. Nagao, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 104307 CrossRef.
- M. M. Koza, L. Capogna, A. Leithe-Jasper, H. Rosner, W. Schnelle, H. Mutka, M. R. Johnson, C. Ritter and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 174302 CrossRef.
- M. M. Koza, M. R. Johnson, H. Mutka, M. Rotter, N. Nasir, A. Grytsiv and P. Rogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 214301, DOI:10.1103/PhysRevB.82.214301.
- M. Christensen, S. Johnsen and B. B. Iversen, Dalton Trans., 2010, 39, 978 RSC.
- A. D. Caplin, G. Grüner and J. B. Dunlop, Phys. Rev. Lett., 1973, 30, 1138, DOI:10.1103/PhysRevLett.30.1138.
- K. Iwasa, M. Kohgi, H. Sugawara and H. Sato, Physica B, 2006, 378–380, 194 CrossRef CAS PubMed.
- C. Lee, I. Hase, H. Sugawara, H. Yoshizawa and H. Sato, J. Phys. Soc. Jpn., 2006, 75, 123602 CrossRef.
- Z. Hiroi, J.-I. Yamaura and K. Hattori, J. Phys. Soc. Jpn., 2012, 81, 011012, DOI:10.1143/JPSJ.81.011012.
- Z. Hiroi, A. Onosaka, Y. Okamoto, J.-i. Yamaura and H. Harima, J. Phys. Soc. Jpn., 2012, 81, 124707 CrossRef.
- D. J. Safarik, T. Klimczuk, A. Llobet, D. D. Byler, J. C. Lashley, J. R. O'Brien and N. R. Dilley, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 014103, DOI:10.1103/PhysRevB.85.014103.
- A. Onosaka, Y. Okamoto, J.-i. Yamaura and Z. Hiroi, J. Phys. Soc. Jpn., 2012, 81, 023703 CrossRef.
- A. Onosaka, Y. Okamoto, J.-i. Yamaura, T. Hirose and Z. Hiroi, J. Phys. Soc. Jpn., 2012, 81, 123702 CrossRef.
- T. Isono, D. Iguchi, T. Matsubara, Y. Machida, B. Salce, J. Flouquet, H. Ogusu, J.-i. Yamaura, Z. Hiroi and K. Izawa, J. Phys. Soc. Jpn., 2013, 82, 114708, DOI:10.7566/JPSJ.82.114708.
- N. Bernstein, J. L. Feldman and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 134301 CrossRef.
- B. Huang and M. Kaviany, Acta Mater., 2010, 58, 4516 CrossRef CAS PubMed.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843, 10.1039/C1JM11754H.
- J. L. Feldman, P. Dai, T. Enck, B. C. Sales, D. Mandrus and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014306 CrossRef.
- P. Ghosez and M. Veithen, J. Phys.: Condens. Matter, 2007, 19, 096002 CrossRef.
- S. Tsutsui, H. Kobayashi, D. Ishikawa, J. P. Sutter, A. Q. R. Baron, T. Hasegawa, N. Ogita, M. Udagawa, Y. Yoda and H. Onodera, et al., J. Phys. Soc. Jpn., 2008, 77, 033601 CrossRef.
- M. M. Koza, M. R. Johnson, R. Viennois, H. Mutka, L. Girard and D. Ravot, Nat. Mater., 2008, 7, 805 CrossRef CAS PubMed.
- M. Christensen, A. B. Abrahamsen, N. B. Christensen, F. Juranyi, N. H. Andersen, K. Lefmann, J. Andreasson, C. R. H. Bahl and B. B. Iversen, Nat. Mater., 2008, 7, 811 CrossRef CAS PubMed.
- D. Wee, B. Kozinsky, N. Marzari and M. Fornari, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 045204 CrossRef.
- M. M. Koza, A. Leithe-Jasper, H. Rosner, W. Schnelle, H. Mutka, M. R. Johnson, M. Krisch, L. Capogna and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 014306 CrossRef.
- H. Euchner, S. Pailhès, L. T. K. Nguyen, W. Assmus, F. Ritter, A. Haghighirad, Y. Grin, S. Paschen and M. de Boissieu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 224303, DOI:10.1103/PhysRevB.86.224303.
- S. Tsutsui, H. Uchiyama, J. P. Sutter, A. Q. R. Baron, M. Mizumaki, N. Kawamura, T. Uruga, H. Sugawara, J.-i. Yamaura and A. Ochiai, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195115, DOI:10.1103/PhysRevB.86.195115.
- M. Marek Koza, D. Adroja, N. Takeda, Z. Henkie and T. Cichorek, J. Phys. Soc. Jpn., 2013, 82, 114607, DOI:10.7566/JPSJ.82.114607.
- M. M. Koza, A. Leithe-Jasper, H. Rosner, W. Schnelle, H. Mutka, M. R. Johnson and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 014302, DOI:10.1103/PhysRevB.89.014302.
- N. Ashcroft and N. Mermin, Solid State Physics, Saunders College Philadelphia, USA, 1976 Search PubMed.
- S. R. Elliott, The Physics and Chemistry of Solids, John Wiley and Sons, 1998ISBN 047198194x; 0471981958 Search PubMed.
- G. Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications, Inc., Mineola, New York, 1996 Search PubMed.
- S. Lovesey, Theory of Neutron Scattering from Condensed Matter, Oxford Science Publications, Oxford, UK, 1984 Search PubMed.
- B. C. Sales, B. C. Chakoumakos, B. Mandrus and J. W. Sharp, J. Solid State Chem., 1999, 146, 528 CrossRef CAS.
- W. Schnelle, A. Leithe-Jasper, H. Rosner, R. Cardoso-Gil, R. Gumeniuk, D. Trots, J. A. Mydosh and Y. Grin, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094421 CrossRef.
- K. Matsuhira, C. Sekine, M. Wakeshima, Y. Hinatsu, T. Namiki, K. Takeda, I. Shirotani, H. Sugawara, D. Kikuchi and H. Sato, J. Phys. Soc. Jpn., 2009, 78, 124601 CrossRef.
- G. P. Meisner, D. T. Morelli, S. Hu, J. Yang and C. Uher, Phys. Rev. Lett., 1998, 80, 3551 CrossRef CAS.
- H. Kim, M. Kaviany, J. C. Thomas, A. Van der Ven, C. Uher and B. Huang, Phys. Rev. Lett., 2010, 105, 265901 CrossRef.
- H. Chi, H. Kim, J. C. Thomas, X. Su, S. Stackhouse, M. Kaviany, A. Van der Ven, X. Tang and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195209, DOI:10.1103/PhysRevB.86.195209.
- L. G. Akselrud, P. Y. Zavalii, Y. Grin, V. K. Pecharsky, B. Baumgartner and E. Wölfel, Mater. Sci. Forum, 1993, 133–136, 335 CrossRef CAS.
- G. M. Sheldrik, SHELXL-97, University of Göttingen, Göttingen, 1997 Search PubMed.
- V. F. Sears, Neutron News, 1992, 3, 26 CrossRef.
- M. M. Bredov, B. A. Kotov, N. M. Okuneva, V. S. Oskotskii and A. L. Shakh-Budagov, Sov. Phys. Solid State, 1967, 9, 214 Search PubMed.
- V. S. Oskotskii, Sov. Phys. Solid State, 1967, 9, 420 Search PubMed.
- P. E. Bloechl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- G. Kresse and J. Furthmueller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71, 809, DOI:10.1103/PhysRev.71.809.
- K. Parlinski, Neutrons and numerical methods N2M (Am. Inst. Phys. Conference Proceedings 479, 1999).
- K. Parlinski, Z.-Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- A. Kontio and E. D. Stevens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 623 CrossRef.
- M. Jahnátek, M. Krajčí and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 024101, DOI:10.1103/PhysRevB.71.024101.
- J. Wang, S.-L. Shang, Y. Wang, Z.-G. Mei, Y.-F. Liang, Y. Du and Z.-K. Liu, Calphad, 2011, 35, 562 CrossRef CAS PubMed , ISSN 0364-5916, World Round Robin Seminar 2010, http://www.sciencedirect.com/science/article/pii/S036459161100099X.
- T. Dahm and K. Ueda, Phys. Rev. Lett., 2007, 99, 187003 CrossRef.
- M. J. Kangas, D. C. Schmitt, A. Sakai, S. Nakatsuji and J. Y. Chan, J. Solid State Chem., 2012, 196, 274 CrossRef CAS PubMed.
- O. Moze, L. Tung, J. Franse and K. Buschow, J. Alloys Compd., 1998, 268, 39 CrossRef CAS , ISSN 0925-8388, http://www.sciencedirect.com/science/article/pii/S0925838897005860.
- S. Christensen, L. Bjerg, A. Kaltzoglou, F. Juranyi, T. Fssler, T. Unruh and M. Christensen, J. Appl. Phys., 2013, 113, 084902 CrossRef PubMed.
- E. Shoko, Y. Okamoto, G. J. Kearley, V. K. Peterson and G. J. Thorogood, J. Appl. Phys., 2014, 115, 033703 CrossRef PubMed , http://scitation.aip.org/content/aip/journal/jap/115/3/10.1063/1.4861641.
- S. Samson, Acta Crystallogr., 1958, 11, 851, DOI:10.1107/S0365110X58002425.
- P. J. Brown, Acta Crystallogr., 1957, 10, 133 CrossRef CAS.
- P. I. Kripyakevich and O. S. Zarechnyuk, Dopov. Akad. Nauk Ukr. RSR, Ser. A: Fiz.-Tekh. Mat. Nauki, 1968, 30, 364 CAS.
- M. Jahnátek, M. Krajci and J. Hafner, J. Phys.: Condens. Matter, 2003, 15, 5675 CrossRef.
- V. M. T. Thiede, W. Jeitschko, S. Niemann and T. Ebel, J. Alloys Compd., 1998, 267, 23 CrossRef CAS.
| This journal is © the Owner Societies 2014 |