Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigations into the nature of spontelectrics: nitrous oxide diluted in xenon
Andrew
Cassidy
a,
Oksana
Plekan†
a,
Jack
Dunger
a,
Richard
Balog
a,
Nykola C.
Jones
b,
Jérôme
Lasne
c,
Alexander
Rosu-Finsen
c,
Martin R. S.
McCoustra
c and
David
Field
*a
aDepartment of Physics and Astronomy, Aarhus University, DK-8000 Aarhus C, Denmark. E-mail: dfield@phys.au.dk
bISA, Department of Physics and Astronomy, Aarhus University, DK-8000 Aarhus C, Denmark
cInstitute of Chemical Sciences, Heriot-Watt University, Riccarton, EH14 4AS Edinburgh, UK
First published on 24th September 2014
Abstract
The recent discovery of a new class of solids displaying bulk spontaneous electric fields as high as 108 V m−1, so-called ‘spontelectrics’, poses fundamental and unresolved problems in solid state physics. The purpose of the present work is to delve more deeply into the nature of the interactions which give rise to the spontelectric effect in films of nitrous oxide (N2O), by observing the variation of the spontaneous field as the N2O molecules are physically removed from one another by dilution in Xe. Data, obtained using the ASTRID storage ring, are presented for films diluted by factors ξ = Xe/N2O of 0.9 to 67, at deposition temperatures of 38 K, 44 K and 48 K, where films are laid down by deposition from a gas mixture. Results show that the spontelectric field decreases as ξ increases and that at ξ = 67 for 44 K deposition, the spontelectric effect is absent. Reflection–absorption infrared spectroscopy (RAIRS) data are also reported, providing insight into the structure of Xe/N2O films and specifically showing that N2O remains dispersed in the Xe/N2O films prepared here. A simplified theoretical model is developed which illustrates that electric fields can be understood in terms of dilution-dependent dipole orientation. This model is used to reproduce experimental data up to an average molecular separation, s, of ≥1.25 nm apart, ∼4 times that associated with pure solid N2O. The disappearance of the spontelectric effect at larger average distances of separation, between s = 1.25 nm and s = 1.75 nm, is a phenomenon which cannot be described by any existing model but which shows that dipole–dipole interactions are an essential ingredient for the creation of the spontelectric state.
1 Introduction
Spontelectrics form a new group of solid state materials,1–7 whose salient characteristic is that they exhibit a spontaneous electric field within the bulk of the solid. The spontelectric state is unique in the physics of solids and shows characteristics quite distinct from any other known solids, such as the ferroelectric state of matter.1 The fundamental interactions which govern the nature of the spontelectric state and the processes whereby the spontelectric state is created remain however elusive. It is the purpose of this paper to shed additional light on the nature of the spontelectric state. Experimental results reported here for the spontelectric material N2O diluted in Xe, further characterize the spontelectric state and place additional constraints on any future ab initio models of the structure or dynamical models of the creation of this state.For the present, it is evident that the properties of spontelectrics arise through collective effects resulting in the orientation of permanent dipole moments of the constituent species. However it remains unclear whether dipole–dipole interactions between the active species are an essential ingredient of the physics which leads to this orientation. From hereon, dipole orientation refers to the tendency of dipoles to align in energetically unfavourable configurations in which δ+ lies on average closer to another δ+ and correspondingly δ− to δ−, where δ+ and δ− refer to opposite dipolar ends of the species.
Here we address the following questions: (i) how does the degree of dipole orientation change as the spontelectric species are removed physically from one another by dilution in a solid matrix of an inert gas? (ii) Is there some average physical separation between species at which the spontelectric effect can no longer be observed? The latter is the major qualitative aim of the present work and essentially tests the hypothesis that dipole–dipole interactions are necessary to the spontelectric effect – and it is found that they are necessary.
Questions (i) and (ii) are addressed by studying films of N2O diluted in Xe in which, with increasing dilution, the N2O molecules are increasingly further apart and are thus more weakly interacting. N2O is known to exhibit the spontelectric effect and it has been investigated in considerable detail in earlier work.1,2,4 Indeed it was the first species which was shown to exhibit this effect.2
A parameterized model is developed which adequately addresses question (i) posed above. This model quantitatively reproduces observations of a reduction in the spontaneous electric field in films of N2O with increasing dilution in Xe. The answer to question (ii), as we have indicated, is that when the dilution and the corresponding average separation of dipolar species is sufficient, there is no evidence of a spontaneous field within the film. This occurs for a factor of dilution of between 26 and 67 for N2O in Xe deposited at 44 K. We estimate the critical separation of N2O species for the loss of the spontelectric effect to lie between 1.25 and 1.75 nm.
The characteristics of spontelectrics in pure films have recently been reviewed in ref. 1. In brief, the spontelectric effect is experimentally characterized by the following properties:
• On forming a film by gas phase deposition under ultra-high vacuum (UHV) of a spontelectric material, a polarization potential, typically of several volts, appears spontaneously on the surface of the film.
• This potential, linearly proportional to the thickness of the film, may be either positive or negative and gives rise to a corresponding spontelectric field in the film.
• The spontelectric field depends on both the nature of the material which is deposited and on the temperature at which the film is deposited. The field for any substance is in general less for higher temperatures (save for methyl formate deposited at ≥80 K).
• At greater than a certain temperature of deposition, no spontelectric effect can be observed.
• Warming of a spontelectric film causes at first little change in the spontaneous potential on the surface of the film, but a critical temperature is reached at which the spontelectric effect decays abruptly.
• The nature of the substrate surface, upon which spontelectric films are deposited, has essentially no bearing on the value of the spontelectric field within the film.7
Materials which show the spontelectric effect are very diverse1 and include species such as nitrous oxide, propane, toluene or chlorotrifluoromethane. Films of material may contain electric fields which can exceed 108 V m−1, noting that breakdown fields of solids lie between 108 to 109 V m−1. These fields are spontaneous, created without any external stimulus, such as an applied electric field; hence the term ‘spontelectric’.
Spontelectric films constitute a form of the solid state in which both non-linear effects and non-local, collective effects operate. The spontelectric effect is non-linear in the sense that in the steady state the degree of dipole orientation and the spontelectric field are related in a manner such that one depends upon the other: that is, the degree of dipole orientation depends upon an expansion in powers of the local field at any dipole and the local field itself depends on the degree of dipole orientation (see for example ref. 1 and eqn (1) and (2) in Section 3.1).
The spontelectric effect is non-local since it is a bulk phenomenon which cannot be described in terms of local interactions alone. Rather, the spontelectric field permeates the entire thickness of the film and assumes a value which is due to a combination of interactions which extend both over the entire film as well as through pair-wise or few-body local intermolecular interactions. In this connection, we observe experimentally that in general a certain thickness of the sample is required before the spontelectric effect develops. It is found for example that isoprene deposited at 70 K requires >50 monolayers (ML) or toluene at 75 K requires >100 ML to develop a substantial electric field (Fig. 4 and 5 of ref. 1). In this respect the spontelectric effect is unique in solid state physics since the steady-state structures with which it is associated depend upon effects of long range feedback. This feedback results in such counter-intuitive behaviour as the increase in dipole orientation, seen in methyl formate, with increasing temperatures of deposition above 80 K.5
Our current qualitative understanding of the spontelectric phenomenon is as follows. On deposition of a dipolar gas to form a film, species adjust such that dipoles should tend to be configured on average in head to tail configurations, that is, δ+ to δ−. However thermal fluctuations may give rise to temporary configurations in which are found local average excess of δ+ close to δ+ rather than δ− and correspondingly an excess of δ− close to δ−, that is, net dipole orientation. Here, fluctuations play the role of the externally applied field in the standard description of dielectric polarization.
Such dipole aligned configurations are evidently accompanied by a local energy deficit due to repulsions between molecules. These configurations will create a fleeting and spatially localised electric field which tends to oppose the orientation. There are now two possibilities. In the first place, the effect may remain a local fluctuation which continually forms, dies away and is resurrected, with dipole orientation averaging to zero over time and space. In the second, given a large enough local fluctuation, there may be a macroscopic switch to a dipole orientation opposing that set up through thermal fluctuation. This opposing dipole orientation then propagates throughout the system via the corresponding opposing electric field. This is posited to occur since, outside the immediate region of the fluctuation, there is instantaneously no, or less, net dipole orientation. In this model, the opposing field, in a region exterior to the fluctuation, sets up dipole orientation in the opposite sense to the fluctuation itself. It is dipole orientation in this opposite sense which gives rise to the observed spontelectric field. Note that the film is not itself an isolated system but is fed by an external cooling system. Moreover the spontelectric state would not appear to be a minimum energy state, but rather a metastable state into which the system becomes lodged in its exploration of the phase space on its journey towards the lowest energy configuration. Having entered the spontelectric state, there are substantial local barriers to the equilibrium state, much as there are in, say, amorphous water ice whose minimum energy configuration, unattainable on any practical timescale at low temperature, is hexagonal ice.
With regard to this qualitative model of the generation of spontelectrics, an electric field must of course be described by two regions of established potential and, within the above model, these locations may instantaneously be within a region of a fluctuation and outside of it. As an important, perhaps crucial, special case, one of these regions may be the surface–vacuum interface, the nature of which may determine the sign of the spontelectric field. Thus N2O at the surface is configured with the terminal N atom, which is δ+, pointing into the vacuum whereas, for example, CF3Cl is configured with the Cl atom pointing outwards, giving a spontelectric field of the opposite sign.6
In addition, the dynamical model put forward above implies that the presence of thermal fluctuations alone may be sufficient in causing the spontelectric phenomenon. However the dynamics of the constituent species will be modulated by local dipole–dipole interactions. Our present work shows that such dipole–dipole interactions play a fundamental role in creating the spontelectric effect and that a model based solely upon independent fluctuations of the active species is insufficient.
2 Experimental method and results
2.1 The experimental method
Surface potential measurements were performed on the SGM2 beamline at the ASTRID synchrotron storage ring at Aarhus University (http://www.isa.au.dk). The experimental chamber operates under ultra-high vacuum conditions, with a base pressure of ∼2 × 10−10 mbar. Films were grown on a polycrystalline Au substrate which was cooled via a closed cycle He cryostat to a minimum temperature of 38 K. Before film growth the substrate was cleaned by annealing to 700 K using a cartridge heater. Background vapour deposition was used to grow all films with the substrate fixed at a chosen temperature.Throughout, film thicknesses are described in monolayers (ML), where one ML of coverage was calibrated from temperature programmed desorption (TPD) experiments. A single ML of nitrous oxide (or xenon) refers to the number of species required to saturate adsorption sites on the polycrystalline Au surface. The residual gas pressure in the chamber during dosing was measured using a quadrupole mass spectrometer, so that a given background pressure could be correlated to a dosing rate. The residual gas pressure method was used to fine-tune actual final dosing rates while dosing gas mixtures for the creation of diluted films. Dilution ratio is defined here as the effective number of ML of Xe divided by the number of ML of nitrous oxide.
Gas mixtures were prepared in an adjacent gas-line, also under UHV, before admission to the experimental chamber. Nitrous oxide (≥99.998%) and xenon (99.99%) were used as received from Sigma Aldrich. Nitrous oxide was loaded into an initially isolated gas-line, using a continuous flow of gas, until the pressure required to maintain the dosing flux for a required dose rate (ML min−1), known from our calibration experiments, was achieved. Xenon gas was then mixed into the continuous flow of nitrous oxide until the required dilution, again estimated from initial calibration experiments, was achieved. Thus the gases were pre-mixed in a known ratio in a flowing system. This flow was then exposed to the cold substrate in the experimental chamber for an appropriate time to create a mixed film corresponding to any selected dilution. Films were built up by the sequential deposition of layers of the xenon–nitrous oxide matrix. The rate of deposition was typically 5 to 10 ML min−1. In earlier work we have tested the hypothesis that values of surface potential may be dependent on deposition rate, by varying the rate through a factor of ten. No effects were found and no further checks of this sort were carried out here.
As far as was practically possible, the nitrous oxide fluence, in terms of number of ML, was kept constant for all experiments at both different temperatures and dilutions. Thus for any deposition step, a fluence of ∼50 ML of nitrous oxide was deposited, with the xenon fluence adjusted to give the desired degree of dilution. This technique ensured that for separate experiments performed, say, with increasing dilution, the layer of material contained always the same total number of N2O molecules, but separated from one another by an increasing distance by intervening Xe atoms. Thus the column density of N2O remains approximately constant in all experiments whereas the column length, that is the film thickness, becomes increasingly greater with greater dilution. For the present we view N2O as remaining mixed with Xe, rather than separated from Xe in the deposited film. We return to this point in detail below. The quoted absolute film thicknesses are accurate to within 20–30%, but relative thicknesses for any experiment for a specific dilution and deposition temperature are accurate to within a few per cent.
Details of the experimental method for measurement of film surface potentials have been described elsewhere.1 In brief, using synchrotron radiation from ASTRID, low energy electrons were produced by photoionization of Ar gas at ∼5 meV above threshold (78.56 nm) in a source chamber and with an energy spread given by that of the photoionizing radiation, set here to be ∼1.5 meV. These low energy electrons were extracted, via a series of lenses, and formed into a beam. The potentials on the film surfaces are estimated using the principle that an electron beam formed at the potential of the centre of the photoionization chamber can just reach another point, for example the surface of a film or of clean gold, at the same potential, potential barriers apart. Thus if electrons are formed at a known potential, the potential of their destination can be measured by the bias that must be applied, either to their point of formation or their destination, such that a current just begins to flow.
The spontaneous potential appearing on the surface of spontelectric films is measured by applying such a bias potential to the system and effectively adjusting this bias in order to null the current. Since electrons are formed at nominally zero volts with an energy of ∼5 meV, the beam should therefore just be able to reach a clean Au target when the target is itself at this same nominal zero (less 5 mV). If the target were covered with a film of spontelectric material and its surface were not at zero but rather, say, at +5 volts, due to the spontaneous formation of an electric field within the film, then in order to ensure that the electrons only just reach the target, it would be necessary to bias the target, or the point of formation of the electrons, by 5 volts. Measurement of the bias required to locate the onset of a measureable current (∼2 fA) therefore gives the potential on the surface of the film. A small correction is made to establish a true zero difference between the clean gold substrate and the potential of formation of the electrons. This arises from the difference between the work function of the gold substrate and the graphite-covered walls of the photoionization chamber in which electrons are formed. This difference is measured for each series of experiments; a typical value of ∼0.25 V is found, in agreement with standard figures. As emphasized in earlier work, we interrogate the material while perturbing it to a minimum. This was ensured by using very small currents, typically of 100–200 fA, in order not to reduce significantly the spontaneous polarization of the film surface or introduce negative charging. These low currents were detected using a Keithley 6340 femtoammeter.
2.2 Results
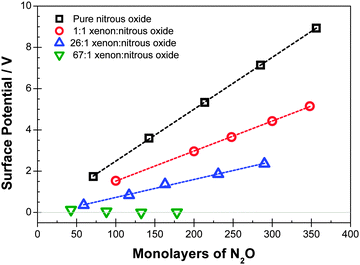
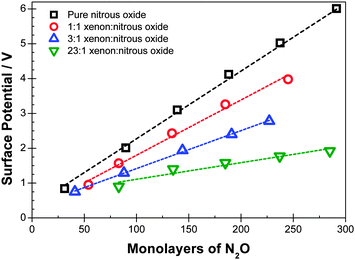
Experimental data are shown in Fig. 1 and 2 for deposition of diluted films at temperatures of 44 K and 48 K respectively. Fig. 3 shows data at 38 K, 44 K and 48 K with dilutions of 2.1, 2.2 and 2.8 respectively. Corresponding voltages per ML of N2O added are shown in Tables 1–3.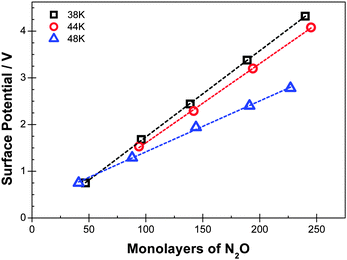 | ||
| Fig. 3 Surface potentials measured for mixtures of N2O and Xe deposited at 38 K, 44 K and 48 K at dilutions of 2.1, 2.2 and 2.8 respectively (see Table 3). The thickness of the layer is expressed as the equivalent number of ML of N2O deposited, excluding Xe. | ||
| Deposition temperature (K) | Dilution ξ: Xe/N2O | mV per equivalent ML of N2O |
|---|---|---|
| 44 | 0 | 25 |
| 44 | 1.0 | 15 |
| 44 | 26 | 9 |
| 44 | 67 | 0 |
| Deposition temperature (K) | Dilution ξ: Xe/N2O | mV per equivalent ML of N2O |
|---|---|---|
| 48 | 0 | 21 |
| 48 | 0.9 | 16 |
| 48 | 2.8 | 12 |
| 48 | 23 | 7 |
| Deposition temperature (K) | Dilution ξ: Xe/N2O | mV per equivalent ML of N2O |
|---|---|---|
| 38 | 2.1 | 18 |
| 44 | 2.2 | 16 |
| 48 | 2.8 | 12 |
2.3 The nature of Xe/N2O films; reflection–absorption infrared spectroscopy studies
As mentioned above, we have taken the view that films laid down from gas mixtures of Xe and N2O are themselves mixed and do not segregate into pure Xe and N2O phases. The only evidence for this is that previous studies8,9 have shown that at low concentrations, that is, ξ = 729 to 1000 and temperatures of 16 to 45 K, N2O does not segregate from Xe matrices and remains in the form of monomers. However a simple argument, given below, shows the experimental data presented in Fig. 1 to 3 illustrate that Xe and N2O remain mixed for the much lower values of dilution used here.It is known from other work that deposition of N2O onto a Xe layer or deposition of Xe on top of a N2O layer has no measureable effect on the spontelectric field in the N2O.1 Thus segregation into pure Xe and N2O phases in the present work would result in a lack of any dependence of the spontelectric field on the value of the dilution, in clear contrast to observation. This provides conclusive evidence that Xe and N2O do not segregate in the films studied here.
This qualitative result still leaves open the question of clustering in mixed films. For lower values of ξ it is inevitable that N2O species must find themselves juxtaposed to form dimers, trimers etc. In order to investigate this more subtle effect on film structure with dilution, experiments were performed using reflection–absorption infrared spectroscopy (RAIRS) at Heriot-Watt University.10 These confirm that nitrous oxide molecules were dispersed in the film on deposition of the gas mixture and did not segregate from the Xe matrix when laid down from a gas mixture. Experiments also demonstrate the juxtaposition, and thus association, to form dimers, trimers etc. of N2O within Xe.
RAIRS experiments were performed as follows. Mixtures with ξ = 5 were prepared in a gas line maintained under vacuum and in dark conditions to avoid photodissociation. The mixing ratio was determined using a capacitance manometer and confirmed using a quadrupole mass spectrometer (Hiden Analytical Ltd, HAL301) inside the chamber. Thick films were grown by background dosing of the Xe–N2O mixture onto a copper substrate coated with 300 nm silica. Film thicknesses in ML were determined from the TPD of N2O from the silica-coated substrate. RAIR spectra were recorded over the range 400–4000 cm−1 at a resolution of 1 cm−1 using a Fourier-transform infrared spectrometer (Varian 670-IR) set at a grazing incidence of 75° with respect to the normal of the substrate. We note that the spontelectric effect does not depend on the nature of the substrate on which the films are deposited.7 Therefore the RAIRS results on a silica substrate remain relevant to the surface potential measurements on polycrystalline Au performed at the ASTRID laboratory.
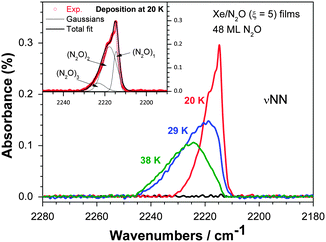
Initially a ξ = 5 film containing the equivalent of 48 ML of N2O was deposited at 20 K on silica and monitored with RAIRS. This film gives rise to a single partially resolved set of features around 2220 cm−1 belonging to the adsorbate, over the 400–4000 cm−1 range investigated. Fig. 4 shows this set of features, where the lowest frequency, centered at 2214.5 cm−1, corresponds to the NN stretching mode of the isolated N2O monomer in Xe as discussed below.8,9 Spectra of films deposited at 29 K and 38 K are also shown in Fig. 4. We note that TPD experiments on Xe films adsorbed on silica show that Xe does not stick efficiently to silica above 42 K, precluding deposition studies at higher temperatures.
Fig. 4 shows that as the deposition temperature is raised, the intensity on the low wavenumber side of the band (2210–2220 cm−1) decreases, while intensity is gained on the high wavenumber side (2220–2245 cm−1). A similar change of the RAIR spectra is observed when the film is deposited at 19 K and annealed to 49 K, just below the onset of Xe desorption at 50 K. Significantly however, the νNN bands of a pure N2O multilayer, characterized by bands at 2260 and 2235 cm−1 in RAIR spectra recorded on non-metallic surfaces,11–13 are absent from the spectra in Fig. 4 or in similar spectra for annealing of mixtures up to 49 K (not shown). This demonstrates the major result of the RAIRS study that N2O does not separate from Xe to form a pure solid layer but remains dispersed within the xenon matrix for ξ = 5 and temperatures between 20 K and 38 K for deposition, and 49 K for annealing.
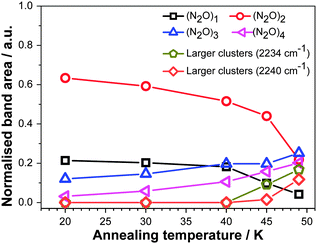
To obtain the relative contributions from N2O monomer, dimer etc., the band centered at 2220 cm−1 for both deposition data (Fig. 4) and annealing data was fitted using the addition of varying proportions of four bands in the form of gaussian functions, where each gaussian centre corresponds to an absorption frequency of (N2O)x, where x ranges from 1–4. For the monomer in a Xe matrix, the relevant frequency is 2214.5 cm−1.8,9 To the best of our knowledge, the absorption frequencies for x = 2, 3 and 4 in a Xe matrix are not available and we set out to estimate them here. Kudoh et al.14 isolated N2O in an argon matrix and observed the monomer band at 2218.6 cm−1. From this value, the difference between the matrix shifts in Xe and Ar for the νNN band of N2O is taken to be −4.1 cm−1 in Xe relative to Ar. This gives access to estimates of dimer and trimer band frequencies in Xe since the bands of N2O dimer and trimer in Ar have been reported.14,15 Given our estimated matrix shift difference of −4.1 cm−1, frequencies of 2218.0 and 2223.4 cm−1 may be assigned to N2O dimers and trimers in Xe respectively, using the available Ar data. In addition, the N2O tetramer has been observed in a supersonic helium jet expansion with a strong Q-branch at 2237.43 cm−1.16 Given the gas phase nature of the jet expansion environment, a matrix shift for Xe of Δν(gas – Xe) = 8.9 cm−1 for the νNN band of N2O9 may be applied and gives an expected band at 2228.5 cm−1 for (N2O)4 in Xe, the value therefore assigned to this tetramer.
Adopting the above values for vibrational frequencies of (N2O)x, respectively 2214.5 cm−1, 2218 cm−1, 2223.4 cm−1 and 2228.5 cm−1, and FWHMs of 9.4 cm−1 for all bands except the monomer band (FWHM = 3.5 cm−1), a fit is shown in the inset of Fig. 4 for data obtained for deposition at 19 K, noting that this case involves negligible tetramer contribution. We note the appearance of a shoulder at 2216.5 cm−1. This does not relate to any known N2O–N2O interaction and may be due to an impurity. This shoulder is not found in spectra taken for higher temperature films.
Fits of the RAIR spectra with the contributions assigned to N2O monomer, dimer, trimer and tetramer can be adjusted to give good agreement at 20 K of deposition and up to 30 K of annealing. For deposition at 29 K and above however, a better fit may be obtained by including an additional contribution on the high wavenumber side. This contribution, composed of two peaks at 2234 and 2240 cm−1 (FWHMs = 9.4 cm−1), most likely arises from associations (or ‘clusters’) larger than the tetramer. There remains however, as noted above, no contribution from a pure N2O phase since the characteristic doublet bands at 2260 and 2235 cm−1 are absent.
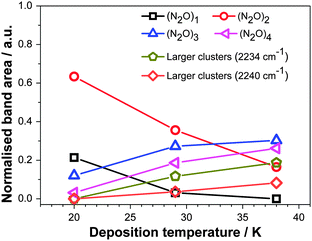
The area of the gaussians used to fit the RAIR spectra is taken to be proportional to the amount of N2O in each configuration, that is, monomer, dimer etc., on the assumption that the strength of the νNN band in each configuration is similar. To allow the comparison between data from experiments performed on films held at different temperatures, the areas were normalised to the total area of the νNN band for every deposition temperature. The resulting quantities, proportional to the number of N2O molecules in each configuration, are given in Fig. 5. This shows the prominence of isolated N2O monomers and dimers in the ξ = 5 mixtures deposited at 20 K. Increasing the deposition temperature of the film leads to an increase of the amount of trimers, tetramers and larger associations at the expense of monomers and dimers – but not to the segregation of N2O from Xe. This reiterates the most significant result of the RAIRS data, that is, the absence of segregation. Fig. 6 shows equivalent data for annealing.
Our present results are consistent with the conclusions drawn in ref. 8 and 9 and extend these conclusions to much higher mixing ratios. N2O monomers, dimers, trimers and tetramers are observed to remain dispersed in the lattice, while a higher deposition temperature (or annealing) allows more association and cluster formation. The latter effect reflects the increased ability for mutual diffusion of Xe and N2O at higher temperatures but does not suggest any fundamental structural changes as the temperature of deposition is raised.
3 A theoretical description
3.1 A model of diluted spontelectrics
A mean-field model is used here to describe the spontelectric steady state. This model was originally introduced in ref. 4 and is set out in detail in ref. 1. The model is based on the concept that the net z-component of the electric field within a spontelectric film and normal to the plane of the film, Ez, is composed of a local symmetrical part, defining the interactions which bind layers to one another, and an asymmetrical part due to the infinite range field which permeates the film. The symmetrical part is expressed as a constant term plus a dipole–dipole term, proportional to (〈μz〉/μ)2 and representing average intermolecular dipole–dipole interactions. Here 〈μz〉/μ, the degree of dipole orientation, is the ratio of the average z-component of the dipole moment and the total dipole moment of the molecular species in the solid state. The form of this term describing dipole–dipole interactions reflects the fact that all such interactions, involving dipole-image charge, extended dipoles and arrays of dipoles, follow a squared relation.17–19 The ζ(〈μz〉/μ)2 term in eqn (1) below may be interpreted as a measure of the tendency of one dipolar species to restrict the angular motion of another, a ‘locking’ term or, as it is sometimes called, a ‘frustration’ term.The symmetrical part of the contribution to Ez is related to the ‘local field’ at any molecular site as defined in standard texts.20 The asymmetrical part, 〈Easym〉〈μz〉/μ, is found only in the description of spontelectrics and has no direct counterpart for any other form of material. This asymmetrical part however resembles the Weiss field in ferromagnetism, which is assumed to be proportional to the magnetisation.21 Here, read degree of dipole orientation for magnetisation and read polarisation field for the Weiss field. We emphasise that the polarisation field, that is, the spontelectric field, is self-generated within the spontelectric material and takes the place of an external field imposed on the film. The polarization field acts in opposition to the symmetrical part and represents the infinite range field created by the average dipoles and experienced by an average dipole.
Hence, using atomic units throughout,
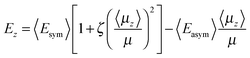 | (1) |
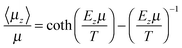 | (2) |
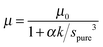 | (3) |
This theoretical model is now adapted to cover the case in which N2O is diluted in Xe. The RAIRS data in Fig. 5 and 6 reveal the complication that associations of N2O of larger size increasingly form as the temperature is raised. However for simplicity we ignore any compositional changes associated with different temperatures and we describe the films as two component mixtures of Xe and an average N2O species, without explicit reference to temperature. Thus the composition of the film is treated as an average over the data between 38 K and 49 K in Fig. 6. We therefore derive below expressions for the variation of the parameter ζ (eqn (1)), the dipole moment of N2O and the degree of dipole orientation which contains only dilution dependence, effectively averaging over the temperature dependence of composition. The justification for this approach is that, though inexact, it turns out to give considerable insight into the nature of diluted spontelectrics, with a minimum of parameterization.
In keeping with the mean field approach which allows for only one type of active species, we treat the system of N2O configurations (monomers, dimers, timers etc.) as consisting of a set of randomly dispersed and identical N2O species. A dimer, (N2O)2 in Fig. 5 and 6, is viewed as forming by a chance juxtaposition of two N2O monomers, a trimer, (N2O)3 in Fig. 5 and 6, as a chance juxtaposition of three N2O monomers and so on. Pure N2O is the limit in which all N2O neighbours are themselves N2O molecules. Given this, the dipole moment of N2O in the solid mixture should be expected to increase towards the gas phase value for N2O as ξ increases, on the assumption that Xe perturbs N2O only weakly. For lack of other information, and again in the interests of keeping the number of adjustable parameters to a minimum, N2O in its various mutual configurations is assumed to have the molecular volume and the related polarizability associated with N2O monomers.
On this basis, there are three interrelated parameters which need to be adjusted according to the experimental dilution of N2O in Xe. These are the average distance apart of the N2O species for a specific dilution, the value of ζ (eqn (1)), which determines the strength of the interaction between adjacent N2O species, and the value of the average dipole moment of N2O species relevant to the diluted solid mixtures, μξ, where the subscript ξ refers throughout to the value of any parameter associated with a particular dilution.
Recollect here that we define the dilution in the film as the ratio of the number of atoms of Xe and of molecules of N2O condensed upon the Au substrate ratio, that is, ξ = nXe/nN2O. The fraction of the total volume of the film taken up by N2O is then given by
| nN2OΩN2O/(nN2OΩN2O + nXeΩXe) |
| nXeΩXe/(nN2OΩN2O + nXeΩXe) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4/3π
4/3π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (rN2O)3 whereas, if diluted, the same number of molecules of N2O may be found in a volume ξnN2OΩXe + nN2OΩN2O. Thus one molecule of N2O may be found in a volume of the solid film of 4/3πrξ3 for a film composed of a mixture of N2O and Xe with a dilution ξ. Hence nN2O4/3πrξ3, the total volume of the film, may be expressed as ξnN2OΩXe + nN2OΩN2O which yields
(rN2O)3 whereas, if diluted, the same number of molecules of N2O may be found in a volume ξnN2OΩXe + nN2OΩN2O. Thus one molecule of N2O may be found in a volume of the solid film of 4/3πrξ3 for a film composed of a mixture of N2O and Xe with a dilution ξ. Hence nN2O4/3πrξ3, the total volume of the film, may be expressed as ξnN2OΩXe + nN2OΩN2O which yields| rξ = (ξrXe3 + rN2O3)1/3 |
From this it follows the average distance apart of two N2O molecules, 2rξ, previously spure (eqn (3)), but now sξ, is given by 2(ξrXe3 + rN2O3)1/3. The lattice constant of pure solid Xe on a FCC lattice yields rXe = 0.219 nm and, for pure N2O, rN2O has been estimated to be 0.16 nm,4 giving values of sξ as a function of ξ.
We turn now to the evaluation of ζξ. The potential between two dipoles, at an angle θ to one another, is given by −μξ2/8εrξ3(1–3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) where ε is some permittivity. The latter quantity, at the low temperatures encountered here, should to a good approximation be independent of ξ. It then follows that ζξ/ζN2O, that is, the ratio of the value of ζ in the mixture of monomers, dimers, trimers etc. of N2O and that in the pure state, is given by
θ) where ε is some permittivity. The latter quantity, at the low temperatures encountered here, should to a good approximation be independent of ξ. It then follows that ζξ/ζN2O, that is, the ratio of the value of ζ in the mixture of monomers, dimers, trimers etc. of N2O and that in the pure state, is given by
| ζξ/ζN2O = rN2O3μξ2/rξ3μN2O2 | (4) |
Using eqn (3), which relates the solid state dipole moment to the gas phase value, with eqn (4) and inserting sξ = 2rξ = 2(ξrXe3 + rN2O3)1/3 derived above, we obtain
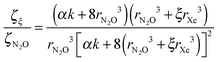 | (5) |
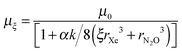 | (6) |
| Temperature/K | E obs/V m−1 | ξ = nXe/nN2O | s ξ /nm | ζ ξ | μ ξ /au |
|---|---|---|---|---|---|
| 38 | 1.189 × 108 | Zero | 0.320 | 43.8 | 0.03214 |
| 44 | 7.889 × 107 | Zero | 0.320 | ||
| 48 | 6.616 × 107 | Zero | 0.320 | ||
| 38 | 3.032 × 107 | 2.1 | 0.594 | 22.23 | 0.05785 |
| 44 | 2.769 × 107 | 2.2 | 0.602 | 21.62 | 0.05819 |
| 48 | 1.899 × 107 | 2.8 | 0.645 | 18.54 | 0.05980 |
| 44 | 3.026 × 107 | 1.0 | 0.489 | 31.89 | 0.05176 |
| 44 | 6.230 × 106 | 26 | 1.304 | 2.801 | 0.06685 |
| 44 | Zero | 67 | 1.782 | 1.119 | 0.06752 |
| 48 | 3.407 × 107 | 0.9 | 0.477 | 33.12 | 0.05083 |
| 48 | 1.899 × 107 | 2.8 | 0.645 | 18.54 | 0.05980 |
| 48 | 5.378 × 106 | 23 | 1.253 | 3.147 | 0.06671 |
Values in Table 4 reflect our intuition that the value of ζξ drops with increasing dilution, ξ, in the limit that, as dilution tends to infinity, so dipole–dipole interactions tend to zero. Again the increasing average distance between N2O molecules, associated with increasing dilution, creates a dipole moment in the solid which approaches that in the gas phase of 0.0684 au (0.167 D), as indicated through eqn (6). This incidentally exposes an additional hidden assumption that the presence of Xe perturbs negligibly the electronic structure of N2O, an assumption supported for example by results in ref. 9. In this connection one may note that although Xe is a highly polarizable atom, with α = 4.01 × 10−30 m3, it can readily be shown that the dipole generated in Xe by the presence of N2O is only of the order of 0.002 D, making a negligibly small contribution to the field at N2O.
3.2 Comparison of model and experimental values
Results in Table 5 give the values of parameters required exactly to reproduce the values of electric field, Eobs, in rows 4–6 of Table 4 (also shown in Table 5 for convenience). This is achieved by varying only the value of 〈Esym〉, where 〈Esym〉, or more properly 〈Esym〉ξ, is defined in connection with eqn (1). Recollecting that 〈Easym〉ξ = μξ/ε0Ω where Ω is the molecular volume (= 37.79 Å3)1 a value of the degree of dipole orientation 〈μz〉/μξ follows, since Eobs = 〈Easym〉ξ〈μz〉/μξ. As seen in Table 5, values of 〈μz〉/μξ, corresponding to the values of the fitting parameter 〈Esym〉ξ, lie between 0.01 to 0.02 with a dilution of 2 to 3, very much less than the values for the pure material1 of 0.08 to 0.15 shown in the last column of Table 5. In connection with values in Table 5, Eobs is found to be only very weakly sensitive to variation of the value of ζξ which have therefore been held at the values computed from eqn (5) and given in Table 4.
| Temperature/K | E obs/V m−1 | ξ | 〈Esym〉ξ/V m−1 | Diluted N2O 〈μz〉/μξ | Pure N2O 〈μz〉/μ |
|---|---|---|---|---|---|
| 38 | 3.032 × 107 | 2.1 | 1.252 × 108 | 0.0207 | 0.1552 |
| 44 | 2.769 × 107 | 2.2 | 1.094 × 108 | 0.0188 | 0.0981 |
| 48 | 1.899 × 107 | 2.8 | 8.128 × 107 | 0.0125 | 0.0826 |
| Temperature/K | E obs/V m−1 | ξ | 〈Esym〉ξ/V m−1 | Diluted N2O 〈μz〉/μξ | Pure N2O 〈μz〉/μ |
|---|---|---|---|---|---|
| 44 | 3.026 × 107 | 1 | 1.405 × 108 | 0.0231 | 0.0981 |
| 44 | 2.769 × 107 | 2.2 | 1.094 × 108 | 0.0188 | |
| 44 | 6.230 × 106 | 26 | 3.117 × 107 | 0.0037 | |
| 44 | Zero | 67 | 1.381 × 107 | 0 | |
| 48 | 3.407 × 107 | 0.9 | 1.602 × 108 | 0.0265 | 0.0826 |
| 48 | 1.899 × 107 | 2.8 | 8.128 × 107 | 0.0125 | |
| 48 | 5.378 × 106 | 23 | 2.808 × 107 | 0.0032 | |
In connection with results in Tables 4–6, we note that for the pure material it proved possible to fit the variation of the observed spontelectric field with temperature of deposition with a single value of 〈Esym〉 = 5.43 ± 0.2 × 108 V m−1.1,4 Results in Table 5 tend to confirm this for a diluted sample; the relatively small variation in 〈Esym〉ξ may be put down to the variation in values of dilution, ξ, encountered in these experiments. Results in Table 6 however show a large drop in 〈Esym〉ξ as dilution is increased. This reflects the property that atoms of Xe create a much weaker local field than that created by dipole–dipole, polarisation, dispersion and covalent forces between molecules of N2O.
| 〈μz〉/μξ ∼ κξ−λ | (7) |
| μξ〈Esym〉ξ ∼ σξ−τ | (8) |
Recollecting that values of 〈μz〉/μξ and μξ〈Esym〉ξ are themselves derived from a model represented by eqn (1) to (6) above, our purpose here is to show that the relationships (7) and (8) are as far as possible in algebraic agreement with the model embodied in eqn (1) to (6). This acts as a check on the self-consistency of our analysis.
We now introduce two approximations both of which may be justified numerically in the present case. The first is that coth(x) −1/x = x/3 in eqn (2) and the second derives from an algebraic analysis, based on the first approximation, which shows that the degree of dipole orientation 〈μz〉/μξ may be expressed as d3d4/2d2 where
| d1 = rN2O3 + ξrXe3 |
| d2 = 256πμ02d12 + 3TΩ(8d1 + αk)2 |
| d3 = 4σ2d1ζξΩ2ξ−2τ(8d1 + αk)2(8rN2O3 + αk)2/rN2O3 |
| d4 = rN2O3ξτ/[2σd1ζξΩ(8rN2O3 + αk)2] |
We then find that:
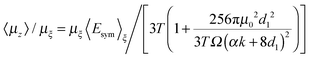 | (9) |
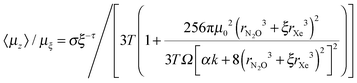 | (10) |
For eqn (7) and (8) to be consistent as desired, it should be possible approximately to represent eqn (10) by κξ−λ such that κ ∼ 0.0246 and λ ∼ 0.6533 when σ ∼ 1.51 × 10−5 and τ ∼ 0.45, as derived empirically. If for example we hold κ and λ at the empirical values and allow σ and τ to vary, we find that for σ = 1.45 × 10−5 and τ = 0.59 we obtain 〈μz〉/μξvs. ξ in better than 1% agreement at low dilution rising to ∼6.5% for ξ = 23. Alternatively, consistency of eqn (7) and (8) can for example be achieved within 3% for all values of ξ by varying all four parameters, κ, λ, σ and τ with κ = 0.028 and λ = 0.6 when σ = 1.43 × 10−5 and τ = 0.5.
This brief analysis demonstrates that the parameterization introduced intuitively into the theoretical model, in particular in developing eqn (5) and (6) for ζξ and μξ, is consistent with the observed exponentially decreasing behaviour of the degree of dipole orientation with dilution.
Eqn (9) can also be used for comparison with data for the temperature dependence of the degree of dipole orientation for a similar value of ξ. This is shown in Table 7. For 38 K, an average value of σ for 44 K and 48 K has been used and a smaller value of τ has been estimated, referring to parameters in eqn (7) and (8). Results for 〈μz〉/μξ(calc) are insensitive to these choices.
| Temperature/K | ξ | σ | τ | 〈μz〉/μξ(calc) | 〈μz〉/μξ(obs) |
|---|---|---|---|---|---|
| 38 | 2.1 | 1.52 × 10−5 | 0.350 | 0.0224 | 0.0207 |
| 44 | 2.2 | 1.53 × 10−5 | 0.400 | 0.0191 | 0.0188 |
| 48 | 2.8 | 1.51 × 10−5 | 0.453 | 0.0149 | 0.0125 |
As shown in Table 4, ζξ has been estimated to fall to 1.119 at ξ = 67. This may be compared with the value of ζξ = 2.801 for the ξ = 26 or ζξ = 43.8 in the pure material. Thus we suggest that somewhere between these two figures of ζξ of 1.119 and 2.801, the strength of the dipole–dipole interaction becomes sufficiently weak, at 44 K deposition temperature, that collective dipole orientation becomes unattainable. In this connection, the increase in the strength of the dipole is negligible, lying at 1% over the range of the layer spacing sξ of 1.304 nm for ξ = 26 to 1.782 nm for ξ = 67 (Table 4).
To substantiate the absence of a spontelectric field, it is now shown, on the basis of the theoretical description given above, that the observed electric field for ξ = 67 should be quite substantial and a potential should readily be measured, if the material were spontelectric in the manner described for lower dilutions. First we note that the observed spontelectric field, Eobs, is given by the second term in eqn (1), that is, 〈Easym〉〈μz〉/μ, (see Section 4.1 of ref. 1) and thus:
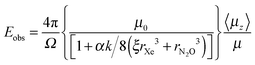 | (11) |
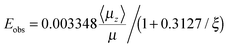 | (12) |
Experiments have for example been performed for a total column density of 175 ML of N2O equivalent to a total film thickness of 175 × 1.782 = 312 nm (see Table 2, 44 K, ξ = 67). This would yield a potential on the surface of ∼1.16 V given a field of 3.74 × 106 V m−1. We find a measurement of zero within experimental error, whereas if the material remained spontelectric at this dilution, the above estimate shows that a value in excess of 1 V should be observed. Hence the lack of detection of a spontelectric effect at ξ = 67 clearly shows that the spontelectric effect is switched off at sufficiently high dilution.
4 Concluding remarks
At the outset two questions were posed whose answers had as their object the provision of greater insight into the nature of the spontelectric state. These questions were (i) how does the degree of dipole orientation change as the spontelectric species are removed physically from one another? (ii) Is there some physical separation between species or species dilution at which the spontelectric effect can no longer be observed?With respect to the first question, we find that dipole orientation is reduced on dilution of N2O in Xe. Thus for the same column density of material, a smaller spontaneous electric field is generated when the N2O molecules are positioned on average further apart. With respect to the second, we find that given sufficient dilution, the spontelectric effect is no longer present.
There are two factors at play here in the context of both the questions posed and the answers given. First, we recollect that the dipole term in eqn (1), 〈Esym〉ζ(〈μz〉/μ)2 may be interpreted as a measure of the tendency of one dipole to restrict the angular motion of another. The first term of eqn (1), simply 〈Esym〉, also effectively attempts to hold the dipole in a vice-like grip, that is, from both sides, restricting any form of motion. The relative importance of these two terms, 〈Esym〉 and 〈Esym〉ζ(〈μz〉/μ)2, is strongly dependent on the degree of dilution. For example at zero dilution the dipole–dipole interaction is 30% (at 48 K) to 45% (at 44 K) of the total symmetric field 〈Esym〉⌊1 + ζ(〈μz〉/μ)2⌋, whereas at high dilution, ξ = 23 to 26, this reduces to 0.003% to 0.004% (and, at ξ = 67, to zero at 44 K). At the same time the total symmetrical field falls by a factor of ∼25 from between 7.13–7.85 × 108 V m−1 for pure N2O1 to 2.8–3 × 107 V m−1 for ξ = 23 to 26, where figures span the range 48 K to 44 K. This reflects both the drop in dipole–dipole interactions and the weaker interaction between N2O with Xe, compared with N2O with itself, as dilution is increased. This is itself accompanied by an increase in effective dipole moment in the solid by a factor of ∼2.1, resulting in a net decrease in 〈Esym〉ξ·μξ by a factor of ∼12 on dilution from pure N2O to ξ = 23–26. Thus in diluted mixtures of N2O and Xe, the N2O molecules sit in a well which restricts rotation whose depth is an order of magnitude smaller at ξ = 23 to 26 compared with pure N2O or a factor of ∼5 between ξ = 0.9 to 1 and 23 to 26.
At high dilution, rotational motion is therefore much less restricted and thermal energy can overpower 〈Esym〉ξ·μξ. For example for ξ = 26 at 44 K, 〈Esym〉ξ·μξ is ∼3% of kT whereas the figure for ξ = 1 is ∼10% and for pure N2O is ∼25%. Given that average dipole orientation in the steady state is in part related to competition between random thermal motion and the restriction of rotational motion, it is therefore evident why 〈μz〉/μ falls to small values at high dilution. For ξ = 67 for 44 K, 〈Esym〉ξ·μξ is ∼1.3% of kT indicating that at some point where the 〈Esym〉ξ·μξ electrical interaction lies between 1 and 3% of kT, the spontelectric effect is altogether inhibited. The conclusion is that a local field of sufficient strength to restrict rotation is necessary to the development of the non-local many body collective physics associated with spontelectrics and that the local field-dipole interaction must be at least 1 to 3% of kT. This is not reflected in the theoretical description of spontelectrics presented here, which makes the assumption that a spontelectric state may always be achieved. However it sets a goal for molecular dynamics simulations of the spontelectric effect.
Second, results may be understood in the context of the model involving fluctuating motions of dipoles, put forward in the introduction, to illustrate how the spontelectric state may form dynamically. Some fluctuation, whose average physical extent depends on the temperature of deposition and the degree of dilution, leads to local dipole orientation 〈μz〉/μ, which we note will be in the opposite sense to that encountered in the spontelectric state. A fluctuation is therefore able to create a fleeting polarisation, (〈μz〉/μ)ξ. (μξ/Ω), and thus a field will briefly arise. We suggest that the more dilute the material the less the value of dipole orientation which will be formed through fluctuations. This arises because of the greater freedom of rotational movement associated with greater dilution, as described above in relation to the spontelectric state but equally applicable here. The compensating field, the spontelectric field, will be correspondingly less as dilution is increased.
Acknowledgements
We gratefully acknowledge support of the staff of the Aarhus Synchrotron Radiation Laboratory (ISA), the Danish Research Council, a Marie Curie Intra-European Fellowship 009786 (RB), the European Community FP7-ITN Marie-Curie Programme (LASSIE project, grant agreement #238258) (AC, JL), the Lundbeck Foundation (RB) and Heriot-Watt University for a James Watt scholarship (ARF).Notes and references
- D. Field, O. Plekan, A. Cassidy, R. Balog, N. C. Jones and J. Dunger, Int. Rev. Phys. Chem., 2013, 32, 345–392 CrossRef CAS.
- R. Balog, P. Cicman, N. Jones and D. Field, Phys. Rev. Lett., 2009, 102, 2–5 CrossRef.
- D. Field, O. Plekan, A. Cassidy, R. Balog and N. Jones, Europhys. News, 2011, 42, 32–35 CrossRef CAS PubMed.
- O. Plekan, A. Cassidy, R. Balog, N. C. Jones and D. Field, Phys. Chem. Chem. Phys., 2011, 13, 21035–21044 RSC.
- O. Plekan, A. Cassidy, R. Balog, N. C. Jones and D. Field, Phys. Chem. Chem. Phys., 2012, 14, 9972–9976 RSC.
- A. Cassidy, O. Plekan, R. Balog, N. C. Jones and D. Field, Phys. Chem. Chem. Phys., 2012, 15, 108–113 RSC.
- A. Cassidy, O. Plekan, R. Balog, J. Dunger, N. C. Jones and D. Field, J. Phys. Chem. A, 2014, 118, 6615–6621, DOI:10.1021/jp503332x.
- H. Krueger and E. Weitz, J. Chem. Phys., 1992, 96, 2846 CrossRef CAS PubMed.
- W. G. Lawrence and V. A. Apkarian, J. Chem. Phys., 1992, 97, 2224 CrossRef CAS PubMed.
- H. J. Fraser, M. P. Collings and M. R. S. McCoustra, Rev. Sci. Instrum., 2002, 73, 2161 CrossRef CAS PubMed.
- A. Łapiński, J. Spanget-Larsen, J. Waluk and J. G. Radziszewski, J. Chem. Phys., 2001, 115, 1757 CrossRef PubMed.
- D. Fulvio, B. Sivaraman, G. A. Baratta, M. E. Palumbo and N. J. Mason, Spectrochim. Acta, Part A, 2009, 72, 1007–1013 CrossRef CAS PubMed.
- The νNN band of the pure N2O multilayer is split into longitudinal and transverse modes in RAIR spectra. Both modes are visible when the spectra are recorded at non-normal incidence and the film is deposited on a non-metallic substrate,11,12 as is the case here. The behaviour of these LO and TO bands has been thoroughly investigated and will be presented in a separate publication on the nature of the spontelectric effect in pure N2O.
- S. Kudoh, K. Onoda, M. Takayanagi and M. Nakata, J. Mol. Struct., 2000, 524, 61–68 CrossRef CAS.
- J. Sodeau and R. Withnall, J. Phys. Chem., 1985, 89, 4484–4488 CrossRef CAS.
- J. N. Oliaee, M. Dehghany, N. Moazzen-Ahmadi and A. R. W. McKellar, J. Chem. Phys., 2011, 134, 074310 CrossRef PubMed.
- E. Cohen de Lara and J. Vincent-Geisse, J. Phys. Chem., 1976, 80, 1922–1927 CrossRef CAS.
- B. L. Maschhoff and J. P. Cowin, J. Chem. Phys., 1994, 101, 8138 CrossRef CAS PubMed.
- D. Fernández-Torre, O. Kupiainen, P. Pyykkö and L. Halonen, Chem. Phys. Lett., 2009, 471, 239–243 CrossRef PubMed.
- C. Kittel, Introduction to Solid State Physics, Wiley, 3rd edn, 2005 Search PubMed.
- H. Kliem, M. Kuehn and B. Martin, Ferroelectrics, 2010, 400, 41–51 CrossRef CAS.
- J. Topping, Proc. R. Soc. London, Ser. A, 1927, 114, 67–72 CrossRef.
Footnote |
| † Present address: Sincrotrone Trieste, S.C.p.A. di Interesse Nazionale, 34149 Basovizza, Trieste, Italy. |
| This journal is © the Owner Societies 2014 |