 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The dependence of surface tension on surface properties of ionic surfactant solution and the effects of counter-ions therein
Chuangye
Wang
*a and
Harald
Morgner
b
aDepartment of Chemistry, School of Science, China University of Petroleum (East China), Changjianxi Road 66, 266580 Tsingtao, China. E-mail: chwang@upc.edu.cn
bWilhelm-Ostwald Institute for Physical and Theoretical Chemistry, Department of Chemistry and Mineralogy, University Leipzig, Linnestrasse 2, D-04103 Leipzig, Germany
First published on 17th September 2014
Abstract
In the present paper, we aim to investigate the dependence of surface tension on the surface properties and reveal the counter-ion effects on the adsorption of ionic surfactants on the solution surface. The surface tension, surface excess and surface concentration (defined as the amount of surfactant adsorbed in the surface phase divided by the surface area) of two anionic surfactants, namely dodecyl sulfate sodium and dodecyl sulfate caesium, dissolved in non-aqueous polar solvent formamide have been separately measured at 6 °C through independent experiments. Then, the correlation of surface tension with surface concentration and that of surface tension with surface excess is inspected in detail. It was found that there is a linear relationship between the surface tension and the surface concentration for the pure solutions of each surfactant, but their surface tension and surface excess cannot be correlated linearly. It is striking that the same surface tension–surface concentration linearity holds for two different surfactants, although they have apparently distinct counter-ions. Based on this finding, it is derived that the surface tension is decided by surface concentration of the surface active ions. After analyzing the surface structure, it is concluded that the counter-ions affect the surface tension indirectly through modifying the adsorption amount of the surface active ions in the surface layer.
Introduction
The surface tension of liquid surfaces has been investigated intensively since more than a century, due to its tight relationship with industrial technologies and commercial products. However, the relationship between the surface tension of solution and other surface properties, for instance, the surface fraction and the surface concentration of the components, has been studied for a long time, and the related attempts are still in progress.1–5 On the other hand, many publications on ionic surfactant solution surfaces have investigated the relationship between surface tension and surface concentration, and many adsorption models have been derived in this framework.6–10 However, in most cases surface excess has been calculated using the Gibbs equation and then treated as the amount of surfactant in the entire surface phase, namely surface concentration. Here, it is of importance to note that the surface excess is not the population of the surfactant at the surface but rather it is the mole of surfactant molecules at the surface minus the number of surfactants in a bulk volume of the solution that contains the same number of solvent molecules at the surface. In some systems the measured surface concentrations of the surfactants agree well with those obtained theoretically from the Gibbs adsorption isotherms.11–15 However, this is attributed to the fact that the bulk concentration of surfactant is so dilute that the difference between surface excess and surface concentration can be neglected. The attempts to correlate surface tension with surface concentration would fail in those cases, since no significant deviations between surface excess and surface concentration can be observed. In some systems where the ionic surfactants have high bulk concentrations,16 the difference between the surface concentration and the surface excess cannot be ignored anymore, otherwise, apparent deviations would be caused. This will be explained further in the following.The relationship between surface tension and surface excess of a solution containing multiple components is ref. 17 as follows:
 | (1) |
For a binary solution [solvent (1) + solute (2)], eqn (1) can be rearranged into
| −dσ = Γ1dμ1 + Γ2dμ2. | (2) |
If the position z0 of the dividing plane is chosen to make Γ1 = 0, then Γ2 is the excess of solute per unit surface area. This surface excess, Γ2, is denoted by Γexcess2, and it can be integrated with
 | (3) |
The surface concentration of surfactant, here, denoted by Γs2, for the sake of being distinguished from proceeding surface excess Γexcess2, is defined as the amount of surfactant accumulated within the entire surface phase divided by the surface area, in the unit of mol m−2. For the surface phase with thickness, it can be calculated by
 | (4) |
 | (5) |
In the above two equations, Γs2 is the surface concentration, ns the amount of surfactant accumulated in the solution surface layer, V the volume and VB that of the surface phase the boundary between which and the bulk phase is located at the depth of zB, c(z) in unit of mol m−3 is the concentration of surfactant varying with the depth z, and A is the surface area. Therefore, the difference between the surface excess Γexcess2 and the defined surface concentration Γs2 is
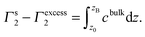 | (6) |
When the bulk concentration is not so dilute as can be neglected, the surface concentration Γs2 is substantially different from the surface excess Γexcess2, and can not be replaced by the latter. If one studies the surface properties, like the area occupied by each adsorbed molecule and the orientation of those surfactant molecules at the surface, the amount of the accumulated substance, Γs2, which is the indicator of the surface density and is an entity reflecting the surface composition but not the surface excess Γexcess2, should be employed.
From the above explanation, surface excess Γexcess2and surface concentration Γs2 have clearly different physical meanings, but in most cases such as dilute surfactant solution the surface concentration is substituted by the surface excess which is popularly determined through the surface tension isotherm by
 | (7) |
Interesting is whether there is an intrinsic relationship between the surface tension and the surface excess or there is one between the surface tension and the surface concentration. This question is much attractive to us and motivated us to solve this issue. On the other hand, it has been proved that the adsorption behaviours of ionic surfactants are different when the counter-ions have identical bulk concentrations. What is the situation in case they have the same surface concentration? To answer this question, we conducted this investigation. The organization of this paper is as follows. At first, we use the pure solutions of two ionic surfactants with different counter-ions dissolved in polar solvent formamide as the objects. This solvent possesses a high polarity (3.73 Debye) and surface tension (58.2 mN m−1 at 20 °C). Its relative permittivity (εr = 84) is much similar to that of water (εr = 81). Moreover, compared to water it can accommodate more surfactant molecules to form concentrated solution. Importantly, due to its low vapour pressure (6 × 10−3 mBar at 6 °C) it can be applied to the vacuum-based surface analytical technique. The surface tension, surface excess and the surface concentration of those solutions are independently measured. Then, the relation between the surface tension and surface excess, as well as that between the surface tension and surface concentration, is established and analyzed. Finally, the effects of counter-ions on the structure of the surface layer are checked. The results could be much valuable for the establishment of the adsorption model of the ionic surfactants on the liquid surfaces.
Experimental section
a. Investigated systems
The investigated systems are the pure non-aqueous solutions of two anionic surfactants, namely dodecyl sulfate sodium (SDS) and dodecyl sulfate caesium (CDS). They contain the same surface active anion, namely dodecyl sulfate, but have different counter-ions, sodium and caesium separately. The polar solvent is formamide. SDS was bought from Acros with purity higher than 99% and was purified by warm absolute ethanol (Merck 99.9%). CDS was synthesized with dodecanol and chlorosulfonic acid, and caesium carbonate in the medium of dichloromethane. The product was then purified by crystallization with water and ethanol alternatively, for three cycles. More details about these two substances can be found in a previous reference.18b. Surface tension
The surface tension data of two series of solutions with varying bulk concentrations have been determined by the method of Wilhelmy plate (Kruess, Germany) at the temperature of 279.15 K in nitrogen atmosphere. More detailed information on that can be found in ref. 18. Still, here we quote partially those data in the following section and plot them in Fig. 1. | ||
| Fig. 1 Surface tension isotherms of CDS and SDS dissolved in formamide at 6 °C and the fittings to experimental data. | ||
c. Surface excess and surface concentration
The surface excess of surfactant, Γexcess2, can be determined through measuring surface tension of ideal solutions, and in most investigations is also used as surface density. In recent decades, some potential instruments like neutron reflection,15,19,20 second harmonic generation21,22 and sum frequency generation,23–25 meta-stable induced electron spectroscopy26 have been employed to measure the surface density of the surfactant precisely. Here, the surface excess Γexcess2, as well as surface concentration Γs2, is determined directly through measuring the concentration-depth profiles of the surfactant ions in the vicinity of the surface, by the method of neutral impact collision ion scattering spectroscopy (NICISS).This technique utilizes the helium ions as a probe and can determine the concentration-depth profiles of elements heavier than helium near the solution surface with a thickness of up to 200 Å in a good resolution of few angstroms. Briefly, in this instrument, the pulsed ionized helium beam is accelerated to a kinetic energy of several keV, and then is directed onto the target. Those projectiles, helium ions, will be back scattered by atoms in the targeted surface layer if they are heavier than helium. During the projectiles hit the atoms and are back scattered, they lose kinetic energy. The extent of the energy loss is dependent on both the mass of the hit atoms and the depth they travel in the sample. Some of those back scattered projectiles enter a drift tube and their flight time is detected by a channel plate mounted at the end of this drift tube, to form the spectrum I(t) with respect to the element i. The primary kinetic energy of the projectiles and the distance between the target and the detector are known, therefore, the energy loss spectrum of element i, I(E), can be obtained by
 | (8) |
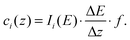 | (9) |
With this NICISS apparatus, we obtained the distributions, namely the concentration-depth profiles, of solvents, of cations and of anions, in the surface-near region. With those profiles, both the surface excess Γexcess2 and surface concentration Γs2 of the surfactant can be determined through integrating the density profiles of the relevant ions along the depth scale. The depth profiles of solvent and of the sulfur which is used to identify the surface active dodecyl sulfate ion, as shown in Fig. 2, are chosen to illustrate the determination process of the surface excess and the surface concentration. The Gibbs dividing plane is first chosen to make the surface excess of solvent zero. The area surrounded by the profile and the dividing plane equal to the value of surface excess is calculated using eqn (3).
Concerning the surface concentration, the amount of surfactant in the entire surface phase divided by the surface area, as proceeding definition, it is equal to the area surrounded by the profiles and the phase boundary which is located at the depth of zB. The surfactant recovers its bulk concentration there. In the current investigation, the shape of the concentration curve is not perfectly smooth due to its statistic characteristic, such that zB cannot be determined by the differential of the concentration profile. In practice, however, the location of zB is quantitatively determined by the arithmetical mean of a series of successive concentration data of the profiles. Briefly, the arithmetical mean concentration ![[c with combining overline]](https://www.rsc.org/images/entities/i_char_0063_0305.gif) i is calculated by
i is calculated by
 | (10) |
![[c with combining overline]](https://www.rsc.org/images/entities/i_char_0063_0305.gif) j is then compared to the bulk concentration cbulk. When the deviation between them is sufficiently tiny, lower than 5%, the correspondent depth zj is then defined as the surface–bulk boundary zB. In the present work, we assigned 20 to the step width l, and find the location of zB for each solution. Due to the blurring of the projectile energy and the broadened energy loss distribution during the measurement,29 it has to be mentioned that the real thickness of the surface layer is thinner than this measured value. Importantly, this spreading of the profiles along the depth scale only makes those measured profiles broader than the real ones, but does not change the value of surface excess and that of surface concentration in any way. Therefore, the surface concentration could be calculated with eqn (5).
j is then compared to the bulk concentration cbulk. When the deviation between them is sufficiently tiny, lower than 5%, the correspondent depth zj is then defined as the surface–bulk boundary zB. In the present work, we assigned 20 to the step width l, and find the location of zB for each solution. Due to the blurring of the projectile energy and the broadened energy loss distribution during the measurement,29 it has to be mentioned that the real thickness of the surface layer is thinner than this measured value. Importantly, this spreading of the profiles along the depth scale only makes those measured profiles broader than the real ones, but does not change the value of surface excess and that of surface concentration in any way. Therefore, the surface concentration could be calculated with eqn (5).
Results and discussion
The surface tension isotherms of the pure solutions of two surfactants dissolved in formamide have been measured and are plotted in Fig. 1 dependent on bulk concentration c. The exponential function can describe better than the polynomial the relation among the surface tension and bulk concentration.| σ = (A0 − A1) + A1·exp[−(B·c + C·c2)]. | (11) |
A 0, A1, B and C are, respectively, the fitting parameters and their values are listed in Table 1.
| Isotherms | A 0 [mN m−1] | A 1 [mN m−1] | B [kg mmol−1] | C [kg2 mmol−2] |
|---|---|---|---|---|
| CDS | 60.33 | 16.516 | 0.0100 | 5.735 × 10−5 |
| SDS | 60.33 | 13.4013 | 0.0124 | 6.017 × 10−5 |
The relationship between the surface excess and bulk concentration for two surfactant solutions as shown in Fig. 3 can be well described using exponential functions in the form of
| Γexcess2 = α − α·exp[−(β1·c + β2·c2 + β3·c3)]. | (12) |
α, β1, β2 and β3 are the fitting parameters and their values are listed in Table 2.
| Isotherms | α [mol m−1] | β 1 [kg mmol−1] | β 2 [kg2 mmol−2] | β 3 [kg3 mmol−3] |
|---|---|---|---|---|
| CDS | 1.798 × 10−6 | 1.651 × 10−2 | 9.3288 × 10−5 | 2.2346 × 10−6 |
| SDS | 1.815 × 10−6 | 1.636 × 10−2 | 1.3849 × 10−4 | −1.0441 × 10−6 |
Combining the fitted surface tension–bulk concentration and surface excess–bulk concentration relations, we correlate the surface tension to the surface excess for CDS and SDS solutions in Fig. 4. The surface concentration isotherms are determined and plotted as a function of bulk concentration in Fig. 5. According to the surface tension–bulk concentration relation, the correlation of surface tension with surface concentration is achieved and plotted in Fig. 6.
 | ||
| Fig. 4 Surface tension of SDS and CDS as a function of surface excess. The upper panel is for the entire measured range whereas the lower one focuses on the course of low surface excess. | ||
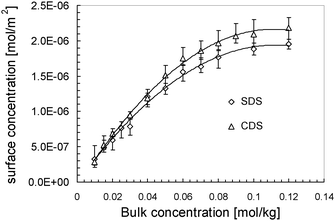 | ||
| Fig. 5 Surface concentration of surfactants dissolved in solvent as a function of bulk concentration. The lines are added to guide the sight. | ||
It can be seen clearly from Fig. 4, in the region of low surface excess, those two series of data are coincident quite well, implying that those two surfactants behave in the same way. That means, in this specific regime, the different counter-ions do not cause significant deviation in the item of surface tension. However, in the regime of high surface excess, those two surfactants show significantly different trends. SDS has comparatively lower surface tension than CDS as their surface excesses are identical, and it drops more sharply. From another perspective, when two series of solutions reach the same surface tension, CDS possesses a higher surface excess. That seems opposite to the situation occurring in surface tension–bulk concentration isotherms, in which the difference between two surface tension isotherms emerges from the most dilute concentration. This notion will be discussed in combination with the surface tension–surface concentration relation in the following section.
Fig. 6 shows an identical linear relationship between the surface tension and the surface concentration. Their behaviours coincide much well within the experimental error bars, and can be fitted with the linear line
 | (13) |
 | (14) |
| (σ0 − σ)A = qRT. | (15) |
It is striking that two surfactants, CDS and SDS, obey the same linearity in the surface tension dependence on surface concentration. In a previous study,18 we have found that the surface excess, surface tension and the structure of the surface layer are much different if their bulk concentrations are identical, indicating that the counter-ions, namely, caesium ion and sodium ion, exert profound effects on the adsorption behaviour of those two ionic surfactants. At first glance, the present finding looks contradictory to this previous conclusion. However, it will be easy to understand if we recall the concept that the surface excess is not the actual density but rather the relative density of the surfactant at the surface with respect to its bulk density. Here, we particularly investigate the effects of the surface composition on the surface tension, but not the properties of the bulk phase which can be, though, related to those of the surface phase thermodynamically.
If the components keep the surface tensions at their pure states, the surface tension would be composed of the products of surface tension of each pure component σi timing their individual molar fraction xi at the surface as
| σ = ∑σi·xi. | (16) |
This equation provides a linear relationship between surface tension and the constituents of the surface phase.
With the surface concentration as we defined proceeding, the molar fraction of the surfactant in the surface layer is
 | (17) |
Thereby, eqn (16) turns into
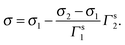 | (18) |
It is reasonable to predict that the surface tensions of two surfactants in the pure state are different, since they are not the identical chemicals due to the distinct counter-ions. According to eqn (16), combined with the coincident linearity found for two surfactants, the surface tension is composed of that of pure solvent and that of adsorbed substance, i.e. the surface active ion. That means, as long as SDS and CDS possess the same surface active ion concentration, the surface tensions of two solutions are identical. Therefore, from the observation of the coincident surface tension–surface concentration dependencies of SDS and CDS, one important conclusion can be drawn. That is, the surface tension is dependent on surface concentration of the surface active anion, but not controlled by the types of counter-ions. The counter-ion, indeed, can influence the surface tension of the solution, however, its influences are exerted in an indirect way through modifying the surface concentration of surface active ion. The larger solvated counter-ion, for example sodium ion but not caesium ion, possesses lower ability of neutralizing the aggregated opposite charges generated by the adsorbed surface active ion in the surface layer, hindering the further accumulation of the surface active ions, therefore, under same bulk concentration the solution containing this ion has comparably lower surface tension as seen in Fig. 1.
It is worthy of attention that CDS and SDS have the same surface tension–surface concentration relation does not unambiguously lead to the argument that two types of counter-ions distribute identically in the vicinity of surface if only their surface concentrations are the same. Reversely, their distributions with same surface concentration deviate much from each other. Fig. 7 gives an experimentally obtained picture of the surface structure, in which the distance between the maxima of concentration-depth profiles of alkali ions and of dodecyl sulfate ions in formamide (Fig. 8) is plotted as a function of surface concentration. The distance between the maxima of ionic peaks of CDS is clearly closer than that of SDS, evidencing that the alkali ions in the surface layer distribute distinctly under fixed surface concentration indeed. That means that the surface structures of CDS and SDS solutions under identical surface concentration are significantly different. This finding endorses a previous computer simulation study,30 in which the alkali ions in the surface layer are found distributing distinctly under the identical surface concentrations. This difference in spatial distributions of the counter-ion does not cause any deviation in surface tension. But, this factor indeed leads to different surface potentials. Thereby, the surface structure of ionic surfactant solution cannot be derived solely from surface tension data, even for inorganic salt solution.31 Although those proposed models may be fulfilled perfectly by surface tension data, the adjustable parameters embedded therein reduce their accurateness, and other parameters like surface potential have to be taken into account if the adsorption model is to be established.
 | ||
| Fig. 7 The distance between the density maxima of cation and of anion as a function of surface concentration. The straight lines are added to guide the sight. | ||
 | ||
| Fig. 8 The distance is calculated as the depth difference of the peaks of profiles. For the sake of precision the peaks of the profiles are fitted with Gaussian curves. | ||
The factor in the Gibbs equation for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ionic surfactant solution has been debated. The prevailing argument is factor 2, which is not appropriate. Besides the uncertainty dissociation of ionic surfactant molecules on the surface, one of well-founded grounds is factor 2 implying that the counter-ion contributes to the surface tension as much as the surface active ion though those two species have distinct surface activity and different sizes.32 Seen from our experimental finding, the counter-ions do not affect the surface tension once the surface concentration of surface active ion is fixed. From this point, it does not need to revise the factor in the Gibbs equation. However, more experiments and theories should be developed in order to give a deeper insight into this topic.
1 ionic surfactant solution has been debated. The prevailing argument is factor 2, which is not appropriate. Besides the uncertainty dissociation of ionic surfactant molecules on the surface, one of well-founded grounds is factor 2 implying that the counter-ion contributes to the surface tension as much as the surface active ion though those two species have distinct surface activity and different sizes.32 Seen from our experimental finding, the counter-ions do not affect the surface tension once the surface concentration of surface active ion is fixed. From this point, it does not need to revise the factor in the Gibbs equation. However, more experiments and theories should be developed in order to give a deeper insight into this topic.
Conclusions and outlook
In the current work, we have investigated the dependence of surface tension on surface excess and surface concentration for two alkali dodecyl sulfate salts. Those three parameters are measured independently, and the comparisons are done without any extra assumptions. The results evidence that the surface excess and surface concentration have different values as the surfactant solutions have identical bulk concentrations, reminding one of the fact that the surface excess is an excess quantity with respect to the bulk concentration. The surface excess can be approximated by the surface concentration when the bulk concentration is low, however, in case the bulk concentration is high the deviation between those two emerges and becomes significant. Importantly, two series of solutions show the coincident linear dependencies of surface tension on surface concentration, but this case does not hold for their surface tension–surface excess relations. From this finding, an important conclusion can be drawn that the surface tension is decided by the surface concentration of the surface active ion, but not its surface excess which is just an excess quantity thermodynamically with respect to the bulk concentration. This notion implies, when one investigates the topics like molecular orientation on the surface, which relates to the surface population of the adsorbed molecules, it is the surface concentration but not the surface excess that is more appropriate to be employed. The present investigation on the structure of the electric double layer indicates as well that the same surface tension is not equivalent to the same distribution of hydrophilic counter-ions in the surface layer.It is necessary to explain further the definition of the surface–bulk phase boundary zB. Emphatically, this is not a parameter chosen freely to fulfil the linearity between the surface tension and surface concentration. We have defined it in a vague way as the depth from where the surfactant begins to relax to its bulk concentration. Therefore, its value can be determined unambiguously through the shape of the concentration profile of the surfactant using eqn (10). As a result, the surface concentration can be determined accurately by integrating the concentration profile until zB. Due to the concentration profile levels off smoothly to the value in bulk, the depth of zB is a bit blurred. Nevertheless, the deviation of surface concentration caused by this uncertainty is evaluated to be less than 1%, and this factor has been incorporated into the error bar in those displayed diagrams.
In the proceeding investigation,4 the surface fraction of the outmost layer taken by the species has been related to the surface tension and a linear relationship among them has been found in several binary systems. The current investigation is focused on the composition of the surface layer affecting the surface tension and the surface structure, for the pure solutions of two ionic surfactants. Whether this linear surface tension–surface concentration relationship holds in all binary ionic surfactant solutions, for example, cationic surfactant solutions, needs further investigations. It would also be worth employing meta-stable induced electron spectroscopy, which determines just the outmost surface structure to correlate the surface fraction to the surface concentration of the component. Certainly, the methods incorporating molecular dynamics simulation, which is able to reveal the surface structure, as well as the evaporation experiment of solvent relating to the surface coverage, are expected to be employed in further investigations as well.
Acknowledgements
The financial support from Natural Science Foundation of China (No. 21203251) and from Ministry of Education of China (The Scientific Research Foundation for Returned Scholars and PhD Programs Foundation No. 20120133120008) is gratefully acknowledged. The Fund for Distinguished Young Scientists of Shandong Province (No. BS2013NJ008) is also thanked.References
- J. A. V. Butler, Proc. R. Soc. A, 1932, 135, 348 CrossRef CAS.
- R. Knapikowski, U. Messow, P. Braueer and K. Quitzsch, Colloid Polym. Sci., 1996, 274, 461 CAS.
- A. Schmidt, U. Messow, P. Braueer, C. Bilke-Kraus and K. Quitzsch, Chem. Tech., 1997, 49, 274 CAS.
- K. Kirmse and H. Morgner, Langmuir, 2006, 22, 2193 CrossRef CAS PubMed.
- Y. He, Y. Shang, H. Liu, D. Langevin and A. Salonen, Langmuir, 2012, 28, 3146 CrossRef PubMed.
- R. P. Borwankar and D. T. Wasan, Chem. Eng. Sci., 1986, 41, 199 CrossRef CAS.
- V. V. Kaliinin and C. J. A. Radke, Colloids Surf., A, 1996, 114, 337 CrossRef.
- P. Warszynski, W. Barzyk, K. Lunkenheim and H. Fruhner, J. Phys. Chem. B, 1998, 102, 10948 CrossRef CAS.
- P. Warszynski, K. Lunkenheim and G. Czichocki, Langmuir, 2002, 18, 2506 CrossRef CAS.
- T. Gilanyi, I. Varga and R. Meszaros, Phys. Chem. Chem. Phys., 2004, 6, 4338 RSC.
- K. Tajima, M. Muramatsu and T. Sasaki, Bull. Chem. Soc. Jpn., 1970, 43, 1991 CrossRef CAS.
- K. Tajima, Bull. Chem. Soc. Jpn., 1970, 43, 3063 CrossRef CAS.
- K. Tajima, Bull. Chem. Soc. Jpn., 1971, 44, 1767 CrossRef CAS.
- K. Tajima, M. Iwahashi and T. Sasaki, Bull. Chem. Soc. Jpn., 1971, 44, 3251 CrossRef CAS.
- J. Eastoe, S. Nave, A. Downer, A. Paul, A. Rankin, K. Tribe and J. Penfold, Langmuir, 2000, 16, 4511 CrossRef CAS.
- G. Andersson, T. Krebs and H. Morgner, Phys. Chem. Chem. Phys., 2006, 5, 136 Search PubMed.
- E. A. Guggenheim and N. K. Adam, Proc. R. Soc. A, 1933, 139, 218 CrossRef CAS.
- C. Wang and H. Morgner, Langmuir, 2010, 26, 3121 CrossRef CAS PubMed.
- S. W. An, J. R. Lu and R. K. Thomas, Langmuir, 1996, 12, 2446 CrossRef CAS.
- J. Eastoe, J. Dalton, P. Rogueda, D. Sharpe, J. Dong and J. R. P. Webster, Langmuir, 1996, 12, 2706 CrossRef CAS.
- P. Koelsch and H. Motschmann, Langmuir, 2005, 21, 3436 CrossRef CAS PubMed.
- J. Song and M. W. Kim, J. Phys. Chem. B, 2011, 115, 1856 CrossRef CAS PubMed.
- Y. Rao, X. Li, X. Lei, S. Jockusch, M. W. George, N. J. Turro and K. B. Eisenthal, J. Phys. Chem. C, 2011, 115, 12064 CAS.
- Z. Lu, A. Karakoti, L. Velarde, W. Wang, P. Yang, S. Thevuthasan and H. Wang, J. Phys. Chem. C, 2013, 117, 24329 CAS.
- S. Song, P. Koelsch, T. Weidner, M. Wagner and D. Castner, Langmuir, 2013, 29, 12710 CrossRef CAS PubMed.
- H. Pohl and H. Morgner, J. Phys. Chem. B, 2010, 114, 12847 CrossRef CAS PubMed.
- G. Andersson and H. Morgner, Surf. Sci., 1998, 405, 138 CrossRef CAS.
- G. Andersson and H. Morgner, Surf. Sci., 2000, 445, 89 CrossRef CAS.
- G. Andersson and H. Morgner, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 032904 CrossRef.
- G. Hantal, L. Partay, I. Varga, P. Jedlovszky and T. Gilanyi, J. Phys. Chem. B, 2007, 111, 1769 CrossRef CAS PubMed.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2002, 106, 6361 CrossRef CAS.
- S. Bae, K. Haage, K. Wantke and H. Motschmann, J. Phys. Chem. B, 1999, 103, 1045 CrossRef CAS.
| This journal is © the Owner Societies 2014 |



