Optical excitation of MgO nanoparticles; a computational perspective

Abstract

The optical absorption spectra of magnesium oxide (MgO) nanoparticles, along with the atomic centres responsible, are studied using a combination of time-dependent density functional theory (TD-DFT) and coupled-cluster methods. We demonstrate that TD-DFT calculations on MgO nanoparticles require the use of range-separated exchange–correlation (XC-) functionals or hybrid XC-functionals with a high percentage of Hartree–Fock like exchange to circumvent problems related to the description of charge-transfer excitations. Furthermore, we show that the vertical excitations responsible for the experimentally studied range of the spectra of the MgO nanoparticles typically involve both 3-coordinated corner sites and 4-coordinated edge sites. We argue therefore that to label peaks in these absorption spectra exclusively as either corner or edge features does not provide insight into the full physical picture.

---

1 Introduction

Magnesium oxide, MgO, is perhaps the simplest of oxides and has traditionally been the proverbial guinea pig of computational solid-state chemists and physicists. However, besides use as a model system, MgO also displays technologically interesting physics and chemistry. Lithium doped MgO, for example, acts as a catalyst for the oxidative coupling of methane,^1–3 while small MgO nanoparticles absorb ultraviolet light and reemit it quite efficiently in the visible spectrum.⁴ An analysis of the optical properties of MgO nanoparticles, especially the absorption in the ultraviolet, is the subject of this computational paper.

Cubic nanoparticles of MgO and the other alkaline earth oxides, so-called MgO nanocubes or, more strictly, nanocuboids, are observed to absorb light well below the band-gap of the bulk oxide; e.g. 3 nm MgO^4,5 nanoparticles absorb at 220 and 270 nm (5.6 and 4.6 eV) compared to 160 nm (7.8 eV) for the bulk.⁶ After absorption they display luminescence with a significant Stokes' shift; e.g. luminescence at ∼370 nm (∼3.6 eV) for the same 3 nm MgO nanoparticles with thus a Stokes' shift of approximately 1–2 eV.^5,7 Experimentally it is found that the absorption and luminescence spectra of nanoparticles of a given alkaline earth oxide can be successfully tuned by varying the nanoparticle size⁵ and/or by the partial substitution of the alkaline earth for other divalent cations, e.g. the incorporation of small amounts of Zn²⁺ in MgO.⁸

In contrast to nanoparticles made from small band-gap semiconductor materials, the alkaline earth oxides are wide band-gap insulators and display no quantum confinement behavior. Besides the fact that the absorption on-set of nanoparticles is smaller than the bulk band-gap, discussed above, it also shifts to the blue with increasing particle size^4,5,9 rather than the red shift expected from quantum confinement. The optical properties of the alkaline earth oxide nanoparticles, especially the absorption of light below the bulk band-gap and luminescence with a large Stokes' shift, has instead been proposed to find its origin in the low-coordinated atoms on the surface of the nanoparticles,^5,7 such as 3-coordinated (3-C) atoms on the corners, 4-coordinated (4-C) atoms on the edges and flat (100) surfaces with 5-coordinated (5-C) atoms. Also, as the spectroscopic experiments referenced above are typically performed in high vacuum on samples that have previously been annealed at high temperature, the effect of absorbed molecules can most likely be ignored, except in selected cases were such molecules are intentionally added as part of the spectroscopic experiment (e.g. H₂¹⁰).

Computational global optimization studies using an empirical interatomic potential have suggested that the global minima of MgO nanoparticles of eighteen formula units and larger already generally have rocksalt derived structures.^11–13 The adoption of the bulk crystal structure for such small particles is rather advantageous from a computational point of view as it suggests that the results for relatively small nanoparticles can also give insight into the properties of much larger structures. The optical spectra associated with corner and edge sites of large MgO particles were previously studied computationally by Sushko and co-workers^10,14 and McKenna and co-workers^15,16 using an embedded cluster approach. Here the region around the 3-C, 4-C or 5-C atoms was explicitly modeled quantum mechanically while the remainder of the particle was described by classical point charges. The lowest excitations of Zn doped small MgO clusters – (Zn_1−xMg_xO)₄, (Zn_1−xMg_xO)₈ – were also recently predicted by Woodley and co-workers.¹⁷

In this paper we focus on the evolution of the absorption spectrum of MgO nanoparticles with particle size. In contrast to the embedded cluster calculations discussed above, we treat the whole nanoparticle quantum mechanically. While this limits the size of particle we can consider, it does specifically allow us to compare the absorption spectra of particles of different shapes and sizes. Just as in the work by McKenna and co-workers on MgO, that of Woodley and co-workers on doped MgO, as well as the work by others^18–21 and us^22–26 on the excited state properties of other inorganic nanomaterials, we use time-dependent density functional theory (TD-DFT) to predict the optical spectra of different MgO nanoparticles.

We first consider small nanoclusters of up to six formula units. We use these model clusters to validate the suitability of TD-DFT for describing optical excitations of MgO nanoparticles by comparing the TD-DFT results with those obtained using the inherently more accurate but also computationally much more expensive Equation-of-Motion Coupled Cluster (EOM-CC) methods. After we have assured ourselves of the suitability of TD-DFT and which exchange–correlation (XC-) functional gives the best results relative to EOM-CC and experimental data, we consider the absorption on-set, spectra and nature of the excited state in rocksalt nanocuboids of eighteen to one hundred and eight formula units as well as some clusters with alternative topologies. Amongst other things, we will use this information to put forward a more complete identification of the absorption peaks observed experimentally. We also briefly comment on the optical properties of alternative non-nanocuboid rocksalt particles with (111) faces and particles with completely different topologies; e.g. tubes and bubbles.

2 Computational details

In this study, the ground state geometries of the (MgO)_n nanoparticles were optimised using density functional theory (DFT) and their lowest vertical excitation energies calculated using two distinctly different approaches. Firstly, for all particles the lowest vertical excitation energies were obtained from TD-DFT calculations. Secondly, where it was computationally feasible (n ≤ 6), EOM-CC with singles and doubles or singles, doubles and triples (EOM-CCSD/T) calculations of the lowest vertical excitation energies were also undertaken.

The DFT and TD-DFT calculations were performed with different approximations to the XC-functional; PBE,²⁷ B3LYP,^28–31 and BHLYP^28,32 as implemented in the TURBOMOLE^33–39 6.3 code, and CAM-B3LYP,⁴⁰ as incorporated in GAMESS-US⁴¹ (1 OCT 2010 – R1). These XC-functionals differ in the percentage of Hartree–Fock like exchange (HFLE) included (PBE 0%, B3LYP 20%, BHLYP 50%), while CAM-B3LYP is a range-separated functional that includes a different amount of HFLE at short distance (19%) than at long distance (65%). The triple-ζ def2-TZVP basis set⁴² was used in all (TD-) DFT calculations, except when comparing with the largest (MgO)₁₀₈ nanoparticle, where for reasons of computational tractability the smaller double-ζ D(Z)DP⁴³ basis-set was used. In the remainder of the text we will refer to these basis-sets as TZ and DZ respectively.

The vertical excitation energies of the four lowest-lying excited singlet states for the DFT ground state geometries have also been calculated using different variants of coupled cluster theory; the EOM-CCSD and EOM-CCSDT methods. For all systems the TZ basis is used in these coupled cluster calculations. Moreover, for selected systems we have also used a triple-ζ aug-cc-pVTZ⁴⁴ basis set (further referred to as ATZ). The majority of the coupled cluster calculations, for reasons of computational tractability, employed the frozen core approximation, where only the valence electrons are correlated (i.e., the 1s orbitals of the oxygen atoms and the 1s to 2p orbitals of the magnesium atoms are frozen in the (EOM-) CC calculations). For the smallest structure in this work ((MgO)₁, (MgO)₂) we were able to obtain the vertical excitation at the EOM-CCSD/T level of theory without making the frozen core approximation (i.e. in which all electrons were correlated) using the TZ and ATZ basis-sets (referred to as aeTZ and aeATZ respectively). All coupled cluster calculations were performed using the Tensor Contraction Module of NWChem⁴⁵ 6.1.

The TD-DFT results were analysed in terms of the Kohn–Sham orbitals contributing to excitations, excited and ground state charge differences, and the density differences between the excited and ground state. Moreover, the Λ diagnostic of Peach et al.⁴⁶ to identify potentially problematic charge-transfer excitations was calculated for selected particles. Ground and excited State NBO charges⁴⁷ as well as density differences between the excited and ground state were obtained directly from Turbomole. Λ values were obtained straight from GAMESS-US.

3 Results and discussion

In this section we will discuss our results and contrast them with both experimental data^{4,5,7,8,48,49} and results from previous computational work.^{14–16,50–52}

3.1 TD-DFT vs. EOM-CC

In our comparison of TD-DFT with EOM-CC, we focused on five small MgO nanoclusters; the tentative global minima structures of (MgO)₁, (MgO)₂, (MgO)₄, (MgO)₆ (hexagonal), and the cubic isomer of (MgO)₆ (see Fig. 1 for the nanocluster structures). In each case we compare results for the B3LYP optimized ground state geometry. In the EOM-CC calculations, we obtained the lowest excitation energies of (MgO)₁ and (MgO)₂ structures with EOM-CCSDT/TZ and those of (MgO)₁, (MgO)₂, (MgO)₄, and (MgO)₆ clusters with EOM-CCSD/TZ. In the case of TD-DFT we consider results calculated with the non-hybrid XC-functional PBE, the hybrid XC-functionals B3LYP and BHLYP, and the range-separated XC-functional CAM-B3LYP.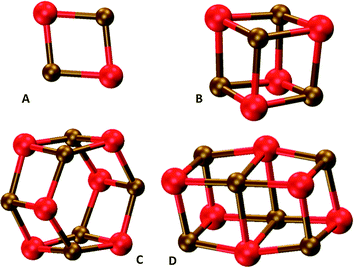

Fig. 1 DFT optimised structures of (A) (MgO)₂, (B) (MgO)₄, (C) hexagonal (MgO)₆ and (D) cubic (MgO)₆ particles.

Fig. 2 shows a comparison of the five lowest excited states of (MgO)₂ as calculated with the different TD-DFT XC-functionals and EOM-CC approaches. All methods agree on the energetic ordering of the lowest two excited states and the presence of a 0.5–0.7 eV gap with the next set of excited states. There is a minor disagreement about the character of the third and fourth excited states but this discrepancy most likely stems from the presence of a manifold of excited states lying very close in energy (<0.1 eV). In terms of the absolute values of the excitation energies the TD-CAM-B3LYP values lie closest to those obtained with EOM-CCSDT/TZ, while the TD-PBE values lie ∼0.7 eV lower, the TD-B3LYP values ∼0.4 eV lower and the TD-BHLYP values ∼0.4 eV higher in energy. The (MgO)₂ results shown in Fig. 2, finally, are characteristic for all MgO nanoclusters considered in terms of the fit between results obtained with the different XC-functionals and EOM-CC (see Fig. S1 and S3–S5 of the ESI† for a comparison between TD-DFT and EOM-CC for the other clusters).

Fig. 2 Excitation energies of the five lowest excitations of the (MgO)₂ cluster as calculated using TD-DFT and EOM-CC. Blue diamonds 1-¹b_1g state, orange squares 1-¹b_3u state, green crosses 1-¹b_1u state, yellow circles 1-¹a_u state, and grey triangles 1-¹b_1g state.

The EOM-CC data shown in Fig. 2 were obtained using the frozen core approximation, which makes EOM-CC calculations on clusters larger than (MgO)₂ tractable. All-electron calculations that do not make this assumption (see Fig. S2 of the ESI†) for (MgO)₂ yield excitation energies that generally lie less than 0.1 eV below their frozen-core counterparts, suggesting that this is a sensible approximation to make.

Fig. 3 shows the lowest vertical excitation energy (LVEE) of the five nanoclusters calculated with EOM-CCSD/TZ and TD-DFT as a function of nanocluster size. All methods agree on the fact the LVEE smoothly increases with cluster size and that the LVEE of the cubic (MgO)₆ cluster lies below its hexagonal counterpart. Moreover, for all clusters the EOM-CCSD/TZ data‡ is found to lie in between the CAM-B3LYP and BHLYP TD-DFT results. Overall, TD-DFT thus seems to display sensible behaviour for these small clusters, where XC-functionals with a higher percentage of HFLE (CAM-B3LYP, BHLYP) yield values that lie closer to the EOM-CC benchmark than XC-functionals with no or a low percentage of HFLE (PBE, B3LYP).

Fig. 3 Lowest vertical excitation energy (LVEE) of (MgO)₁ to (MgO)₆ calculated using TD-DFT and EOM-CCSD. Red circles represent TD-PBE results, orange squares TD-B3LYP results, grey triangles TD-BHLYP results, green diamonds TD-CAM-B3LYP results and blue crosses EOM-CCSD results. Open symbols correspond to LVEE of cubic (MgO)₆ cluster.

3.2 TD-DFT vs. experiment

In the next step we calculated the LVEE of the (MgO)₂₄, (MgO)₃₂, (MgO)₄₀, and (MgO)₄₈ nanocuboids where the LVEE values for these particles correspond to the absorption on-set, as in all cases the lowest excitation is dipole-allowed. Fig. 4 shows the structures of these nanoparticles and Fig. 5 the trend in predicted LVEE with particle size for these nanocuboids and the smaller rocksalt derived nanoclusters ((MgO)₂, (MgO)₄ and the cubic isomer of (MgO)₆). Due to the relative computational cost of the code used for the (TD-)CAM-B3LYP calculations, we focus in these calculations on particles up to (MgO)₃₂.

Fig. 4 DFT optimised structures of (A) (MgO)₁₈, (B) (MgO)₂₄, (C) (MgO)₃₂, (D) (MgO)₄₀ and (E) (MgO)₄₈ particles.

Fig. 5 Lowest vertical excitation energy (LVEE) of (MgO)₄ to (MgO)₄₀ nanocubes calculated using TD-DFT with different XC-functionals. Red circles represent TD-PBE results, orange squares TD-B3LYP results, green diamonds TD-CAM-B3LYP results, grey triangles TD-BHLYP results and the dashes lines the experimental absorption on-set of 3 nm particles.

From the data in Fig. 5 it is clear that TD-PBE and TD-B3LYP show a slightly different behavior than TD-CAM-B3LYP and TD-BHLYP. While the latter show a smooth trend that suggests that the LVEE converges to a values of ∼4.7 eV (260 nm) and ∼5.1 eV (240 nm) respectively, the TD-PBE and TD-B3LYP results are less smooth and show a dip for (MgO)₂₄. Of the four XC-functionals the TD-BHLYP and TD-CAM-B3LYP results in Fig. 5 also lie closest to the experimental absorption on-set of 3 nm MgO particles^4,5 (∼3000 MgO formula units, absorption on-set indicated in Fig. 5 by a dashed line: discussion of the full absorption spectra is given in Section 3.5). The largest particle studied here using the TZ basis-set still has sides of only 0.6 nm (see Table S1 in the ESI† for a summary of the edge lengths and body diagonal of all cuboid particles considered), but the observed LVEE plateau suggests that such a comparison should be non problematic. These observations are reinforced by Fig. S5 in the ESI,† the DZ equivalent of Fig. 5, which also includes the LVEE of the (MgO)₁₀₈ particle with sides of 1 nm. Fig. S5 (ESI†) specifically shows that the LVEE only increases by 0.01 eV for TD-B3LYP and 0.09 eV for TD-BHLYP when increasing the particle size from (MgO)₃₂ to (MgO)₁₀₈.

TD-CAM-B3LYP thus seems to gives the best match to both the EOM-CC results for small clusters and the experimental absorption on-set for the larger particles. TD-BHLYP consistently, over the whole size range studied, predicts LVEE values that are blue shifted by 0.4–0.5 eV relative to the TD-CAM-B3LYP values. However, the difference between TD-CAM-B3LYP and TD-PBE/TD-B3LYP LVEE values increases dramatically with particle size. For example, while for the small model clusters, the difference between the LVEE values predicted by TD-CAM-B3LYP and TD-B3LYP is similar in magnitude to that between TD-CAM-B3LYP and TD-BHLYP but opposite in sign, for the large particles the difference between TD-CAM-B3LYP and TD-B3LYP increases to more than 1 eV. TD-B3LYP as a result also severely underestimates the absorption on-set compared with experiment. Similarly the difference between TD-CAM-B3LYP and TD-PBE increases from 0.7 to more than 2 eV. Clearly, for reasons we will discuss below, the performance of TD-PBE and TD-B3LYP deteriorates dramatically with increasing particle size.

3.3 Origin of the problematic description of excitations in the MgO nanocuboids

The observations above about the use of TD-PBE and TD-B3LYP yielding radically too low excitation energies are reminiscent of the underestimation of the excitation energy of charge transfer (CT-) excitation, observed for many organic molecules and more recently by us also in TiO₂ nanoparticles.²⁵ Here a combination of (i) negligible overlap between initial and final orbitals involved in the electronic excitations, and (ii) the use of non-hybrid (e.g. PBE) or hybrid XC-functionals with a low percentage of HFLE (e.g. B3LYP), leads to a spurious stabilisation of CT-excitations relative to more local excitations. Use of hybrid XC-functionals with a larger percentage of HFLE (e.g. BHLYP) or range separated XC-functionals (e.g. CAM-B3LYP) is well known to minimize such problems with the description of CT-excitations,^46,53–55 and it could be that we are observing something similar here.

To probe if issues with CT-excitations could indeed explain the observed problems with TD-PBE and TD-B3LYP, we calculated for selected systems the Λ diagnostic of Peach et al.,⁴⁶ which ranges from 1, complete overlap between initial and final orbitals, and 0, no overlap. Low values of the Λ diagnostic suggest that an excitation has strong CT-character and is likely to be underestimated when using non-hybrid or hybrid XC-functionals with a low percentage of HFLE. Table 1 shows that the Λ diagnostic is ∼0.3 for all small clusters but considerably lower, ∼0.14, for the larger nanocubes, and appears to decrease for the latter particles with increasing particle size. The exact Λ value below which one is likely to be dealing with a problematic CT-excitation is probably to a degree system dependent – work on organic systems for TD-B3LYP suggest Λ < 0.3⁴⁶ while our work on TiO₂ suggest Λ < 0.15.²⁵ However, the Λ values of the lowest excitations for the nanocuboids are suggestive of CT-problems being the origin of the underestimation observed for TD-PBE and TD-B3LYP. In the remainder of the manuscript we hence focus on results obtained with TD-BHLYP and TD-CAM-B3LYP.

Table 1 TD-B3LYP Λ values of the lowest vertical excitation for a range of particles

	(MgO)2	(MgO)4	(MgO)6	(MgO)12	(MgO)24	(MgO)32
a Cubic structure. b Hexagonal structure. c Bubble structure.
Λ	0.30	0.32	0.34 (0.33^a)	0.35^b (0.34)^c	0.15	0.13

---

3.4 Nanocuboids with odd-numbered faces

Besides nanocuboids with faces containing even number of atoms, like the ones considered above, nanocuboids with faces with odd number of atoms are also possible. The smallest possible nanocube that is not a slab, (MgO)₁₈, belongs to this category, having two faces with an odd number (nine) of atoms, where one of the odd faces has an excess magnesium atom and the other an excess oxygen atom. (MgO)₁₈ is predicted to have a considerably lower LVEE than the other nanocubes (see Fig. 6 and Fig. S6 in the ESI† for its TD-CAM-B3LYP equivalent). The same holds for another example from this class; (MgO)₂₇, which has an even more red-shifted LVEE. We suspect that this downward LVEE shift is related to the very large ground state dipole moment of these particles; 17 and 31 Debye respectively, which are in turn a direct result of the faces with odd numbers of atoms. While these (100) faces are non-polar in the traditional sense,⁵⁶ the fact that they are comprised of an odd number of atoms makes them effectively behave as if polar. Finally, the (MgO)₁₈ nanocube has been suggested in the literature to be the global minimum for this particle size,¹³ but this naively appears at odds with the presence of these intrinsically polar surfaces and its large associated dipole and we wonder if there exists a yet undiscovered lower energy structure for this particle size that is not a simple cut of the rocksalt structure.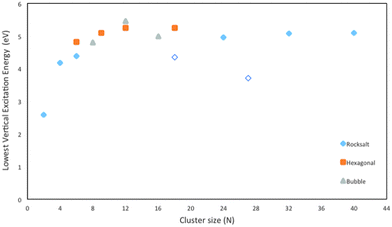

Fig. 6 Lowest vertical excitation energy (LVEE) of (MgO)₁ to (MgO)₄₀ calculated using TD-BHLYP. Open symbols correspond to particles with faces containing odd number of atoms.

3.5 Calculated optical absorption spectra

In the next step we calculated the optical absorption spectra of the (MgO)₂₄, (MgO)₃₂, (MgO)₄₀, and (MgO)₄₈ particles with TD-BHLYP. Fig. 7 shows the TD-BHLYP predicted absorption spectra of the particles, which include a Gaussian smearing of 0.05 eV, as well as the absorption spectrum measured experimentally for MgO particles with an average size of 3 nm.⁵ The TD-BHLYP spectra in Fig. 7 also include an additional rigid red-shift of 0.5 eV. The latter shift is inspired by the fact that in Fig. 5 the LVEE predicted by TD-BHLYP lies approximately 0.5 eV above the experimental absorption on-set (see Fig. S7 in the ESI† for the unshifted spectra). The rigidly shifted predicted spectra and the experimentally measured spectrum are very similar; a low peak at ∼265–285 nm (4.7–4.3 eV) followed by a stronger peak at ∼220–240 nm (5.6–5.2 eV). The clearest difference between the experimental and predicted spectra is that the latter display more fine structure, i.e. the shoulders between ∼240–260 nm (5.2–4.8 eV), although this depends on the degree of Gaussian smearing employed. The most likely explanation for this difference is that the experimentally measured spectrum is that of an ensemble of particles and that the splitting predicted theoretically is not visible in the experimental spectrum as a result of inhomogeneous broadening stemming from the particle size distribution.

Fig. 7 TD-BHLYP calculated absorption spectra (including the 0.5 eV rigid red-shift discussed in the text) of (MgO)₂₄, (MgO)₃₂, (MgO)₄₀ and (MgO)₄₈. Experimental absorption spectrum of 3 nm particles, taken from ref. 5, included for comparison.

A comparison of the predicted spectra for the different particles shows that in line with what is observed for the LVEE the whole spectrum of the larger particles is shifted slightly to the blue. More specifically, the position of the peak maximum of the first low-intensity peak at ∼265–285 nm (4.7–4.3 eV) shifts to shorter wavelength with increasing particle size. The peaks in the spectrum of the larger particle are also generally narrower, while the intensity of the shoulder in the ∼240–260 nm (5.2–4.8 eV) region of the spectra relative to that of the main ∼220–240 nm (5.6–5.2 eV) peak decreases in the order (MgO)₂₄, (MgO)₄₀, (MgO)₄₈, (MgO)₃₂. The decrease in the intensity of the shoulder appears to at least partly result from the lower symmetry of (MgO)₂₄, (MgO)₄₀ and (MgO)₄₈, all D_2h, compared with T_d for (MgO)₃₂. In a lower symmetry point group a greater variety of excitations are symmetry-, and potentially dipole-, allowed.

To further investigate the effect of particle size, we have also calculated the absorption spectrum of the larger (MgO)₁₀₈T_d-symmetry nanocube with 1 nm sides. For these calculations we had to use, as discussed above, the smaller DZ basis-set to make the calculations numerically tractable. Fig. 8 compares the predicted TD-BHLYP absorption spectrum of (MgO)₁₀₈ and (MgO)₃₂, both obtained using the DZ basis-set and both including the same 0.5 eV rigid red-shift as the TZ spectra. The DZ (MgO)₃₂ spectrum is very similar to its TZ equivalent in Fig. 7 (see Fig. S8 in the ESI†). Relative to the (MgO)₃₂ spectrum, the (MgO)₁₀₈ spectrum displays a blue-shift of the low intensity peak in the 265–285 nm (4.7–4.3 eV) part of the spectrum and the appearance of a second strong peak in the 220–240 nm (5.6–5.2 eV) range. The low intensity peak also appears to gain intensity relative to the strong peaks. The latter, however, is an artifact of the specific choice of the Gaussian broadening parameter. The ratio of the sum of oscillator strength above and below 260 nm (4.8 eV), which does not depend on the choice of broadening and is given in Table 2, decreases when going from (MgO)₃₂ to (MgO)₁₀₈, in line with what is seen in experiment.

Fig. 8 TD-BHLYP/DZ calculated absorption spectra (including the 0.5 eV rigid red-shift discussed in the text) of (MgO)₃₂ and (MgO)₁₀₈. Experimental absorption spectrum of 3 nm particles, taken from ref. 5, included for comparison.

Table 2 Ratios of summed oscillator strength above and below 260 nm (R) as calculated with TD-B3LYP/DZ(D)P

	(MgO)32	(MgO)108
R	0.072	0.062

---

As previous authors have used TD-B3LYP it is interesting to compare the unshifted TD-B3LYP spectra with the rigidly red-shifted TD-BHLYP and experimental spectra. The (MgO)₃₂ spectrum calculated with TD-B3LYP (see Fig. S9 in the ESI†) is very similar to that reported by McKenna and co-workers^15,16 for larger particles using their embedded cluster approach on a cluster centered around a 3-C corner atom; a low peak at ∼350 nm (3.5 eV) and a stronger intensity peak at ∼270 nm (4.6 eV). Now, as the latter peak, without any energy shift, lies very close to the experimental shoulder at 270 nm (4.6 eV), it is tantalizing to assume that the TD-B3LYP ∼270 nm (4.6 eV) peak equals the experimental 270 nm (4.6 eV) shoulder and that the predicted ∼350 (3.5 eV) nm peak is too weak to be observed experimentally. In this scenario, the higher energy 230 nm (5.4 eV) experimental peak might then be due to, for example, purely edge based excitations. We, however, think differently, because we believe that, at least in our whole particle calculations, the TD-B3LYP spectra suffers from charge-transfer problems, as discussed above, and that the predicted ∼350 nm (3.5 eV) peak in particular is an artifact. Furthermore, we prefer to make no assumptions about the relative intensities of experimentally visible peaks. The ∼350 (3.5 eV) nm TD-B3LYP peak is predicted to have intensity less than an order of magnitude lower than the ∼270 nm (4.6 eV) peak for the particles, and so is by no definition inherently dark.

3.6 Character of the excitations

Having demonstrated that we can successfully reproduce the type of spectra measured experimentally, we turn our focus to the atomistic origin of the light absorption, i.e. the atoms involved with the excitations. One can analyze the character of excitations, from which atom to which atom electron density moves, by comparing for a given excitation the ground and excited state charges for each of the atoms in the different particles and the percentage contribution of each atom to the total charge difference for either sub-lattice (∑Δq_Mg, ∑Δq_O). This analysis can then be further complemented by plotting the excited state – ground state density difference. We start by considering excitations of the perfectly cubic (MgO)₃₂ and (MgO)₁₀₈ particles before discussing the other cuboid particles, and focus in all cases on the optically allowed excitations responsible for the absorption spectra.

For (MgO)₃₂ the excitation responsible for the ∼270 nm (4.6 eV) peak corresponds to an excitation that primarily moves an electron from the four oxygen corner atoms (92% of ∑Δq_O) to the twelve magnesium edge atoms directly coordinated to these oxygen corner atoms (70% of the ∑Δq_Mg) with a minor contribution of the four magnesium corner atoms (a further 17%). Fig. 9A shows a plot of the density difference between the ground and excited state for the same excitation, which yields a very similar picture as obtained using the charge differences, except that the magnesium contribution is less apparent. The longer wavelength excitation of the two major excitations that contribute to the ∼240 nm (5.2 eV) shoulder has a similar character to the ∼270 nm excitation. The shorter wavelength contribution to the ∼240 nm shoulder predominantly involves an electron being moved from the oxygen corner atoms (84% of ∑Δq_O) to the magnesium corner atom (60% of ∑Δq_Mg), with more minor contributions of the oxygen and magnesium edge atoms (11% of ∑Δq_O and 35% of ∑Δq_Mg). This excitation has characteristics of a CT-excitation, with 0.6 nm between the main sites involved. Finally, the 230 nm (5.4 eV) peak corresponds to the transfer of an electron from the oxygen edge atoms surrounding the magnesium corner atoms (70% of ∑Δq_O) to these magnesium corner atoms (88% of ∑Δq_Mg), with a minor contribution of the four 6-C oxygen atoms in the centre of particle (a further 18% of ∑Δq_O). Fig. 9B shows a plot of the density difference between the ground an excited state for this excitation, which again yields a similar picture as obtained using the charge differences. In the excitations responsible for the longer wavelength (lower energy) peak the hole is thus localized over fewer atoms than the excited electron, while in the excitation that underlie the shorter wavelength (higher energy) peak and shoulder the excited electron is localized over less atoms than the hole. Also, most excitations are found to be local, in the sense that neighboring atoms are involved, with the exception of the one state with clear CT-character.

Fig. 9 TD-BHLYP excited state – ground state density difference for the excitations corresponding to the 270 (A) and 230 (B) nm peaks of (MgO)₃₂ (blue, excess of electrons in the excited state; excited electron/green, deficit of electrons in the excited state; hole). The numbers indicate the most significant differences in NBO charge of the excited state and ground state charge, as well as the multiplicity of each site.

For (MgO)₁₀₈, we find, similarly to (MgO)₃₂, that the excitation responsible for the long wavelength peak at ∼270 nm (4.6 eV) corresponds to an excitation that moves an electron from the four oxygen corner atoms (86% of ∑Δq_O) to the twelve magnesium edge atoms directly coordinated to these oxygen corner atoms (77% of ∑Δq_Mg). The same holds for the excitation that is the strongest contribution to the ∼240 nm (5.2 eV) shoulder. The first of the two strong peaks in the 220–240 nm (5.6–5.2 eV) part of the spectrum, corresponds to excitations that transfer an electron from the twelve oxygen edge atoms surrounding the magnesium corner atoms (60% of ∑Δq_O) to these four magnesium corner atoms (86% of ∑Δq_Mg), with a minor contribution of the four 6-C oxygen atoms closest to the magnesium corner atoms (20% of ∑Δq_O). The second strong peak is a combination of a number of excitations where an electron moves from a combination of oxygen corner atoms (10–30% of ∑Δq_O) and oxygen edge atoms (∼60% of ∑Δq_O) to the magnesium corner atoms (40–50% of ∑Δq_Mg), with a more minor involvement of magnesium edge atoms (30–40% of ∑Δq_Mg). Of all the excitations, the latter ones are those with the most CT-character, and appear related to the CT-excitation observed for (MgO)₃₂, only with a much larger contribution of both oxygen and magnesium edge atoms.

For cuboid (MgO)₂₄ analysis of the charge differences suggests that the 265–285 nm (4.7–4.3 eV) peak corresponds to excitations that move an electron from the four oxygen corner atoms (91% of ∑Δq_O) to magnesium corner (45% of ∑Δq_Mg) and edge atoms (44% of ∑Δq_Mg). Compared with (MgO)₃₂ the magnesium corner atoms play a more important role here; 45% compared with 17% in the case of (MgO)₃₂. The shoulder at ∼240 nm (5.2 eV) and the peak at ∼230 nm (5.4 eV), in contrast, correspond to excitations that shift an electron from oxygen corner (30–55% of ∑Δq_O) and edge atoms (30–45% of ∑Δq_O) to magnesium corner atoms (80–95% of ∑Δq_Mg). Again the difference with (MgO)₃₂ is the involvement of corner atoms, in this case the oxygen corner atoms. Just as for (MgO)₃₂, at long wavelength/low energy the hole is localized on the least number of atoms while at short wavelength/higher energy the excited electron exhibits this characteristic. However, clearly going from perfect cubes to cuboids slightly complicates the picture. Calculations on the (MgO)₄₀ and (MgO)₄₈ particles, with longer edges, yield essentially the same picture.

In none of the particles considered did we observe any of the symmetry allowed excitations in the studied excitation energy range to correspond to pure edge excitations; i.e. where an electron gets excited from a 4-C oxygen edge atom to a 4-C magnesium edge atom. The same holds for pure corner excitations. What we do observe is a significant increase in the participation of edge atoms in higher energy/shorter wavelength excitations upon going from (MgO)₃₂ to (MgO)₁₀₈. For much larger particle (≫1 nm), beyond the size range we can currently study computationally, the edge contribution might thus become the dominant contribution to such short wavelength excitations.

The above analysis into the origin of the peaks in the absorption spectra agrees with the experimental observation,^5,7,48 obtained on the basis of the evolution of the shape of the absorption spectra with particle size, that the ∼270 nm (4.6 eV) peak involves excitation of an electron from oxygen 3-C corner atoms. Our analysis is also consistent with the experimental interpretation that the 220–240 nm (5.6–5.2 eV) peak involves excitations of an electron from oxygen 4-C edge atoms. However, we believe it is, at least for particles up to 1 nm, misleading to identify these features exclusively as either a corner or edge features, based on the coordination number of the oxygen atoms involved. As shown above, the sites from which an electron gets excited from and the site it gets excited to often differ in coordination number, and both might even correspond to mixtures of sites with different coordination numbers. The latter was previously hypothesized experimentally in order to explain the luminescence spectrum of MgO nanoparticles exposed to molecular hydrogen,¹⁰ something we plan to study in future work.

It is interesting to also consider the prediction of the character of the lowest optically allowed excitation of the (MgO)₃₂ particle in TD-B3LYP and to contrast it with the TD-BHLYP prediction discussed above. TD-B3LYP predicts, in line with the Λ value in Table 1, the lowest excitation to be a CT-excitation in which an electron moves from the corner oxygen atoms (89% of ∑Δq_O) to the corner magnesium atoms particle (71% of ∑Δq_Mg). See Fig. 10 for a plot of the density difference between the ground an excited state for this excitation, which shows the same picture. As discussed above, TD-BHLYP also predicts such a CT-excitation, but not as lowest excitation. There is thus both a change in the character of the lowest optically allowed excited state and swap in ordering of excited states when going from TD-B3LYP to TD-BHLYP. This is all, in our opinion, further evidence for our hypothesis outlined in Section 3.3 that TD-B3LYP fails to correctly describe the excitation spectra of MgO nanocuboids due to its inability to accurately describe excited states with CT-character.

Fig. 10 TD-B3LYP excited state – ground state density difference for the excitations corresponding to the 350 nm charge-transfer peak of (MgO)₃₂ (blue, excess of electrons in the excited state; excited electron/green, deficit of electrons in the excited state; hole). The numbers indicate the most significant differences in NBO charge of the excited state and ground state charge, as well as the multiplicity of each site.

Embedded cluster calculations centered on an oxygen corner atom can by definition not yield the sort of CT-excited state we find as the lowest excited state for (MgO)₃₂ with TD-B3LYP because of the absence of magnesium corners. As a result in the embedded cluster calculation in the literature a lowest excited state of different character is found^10,14–16 than that obtained here for the whole (MgO)₃₂ particle, even if TD-B3LYP was used in both cases. The lowest TD-B3LYP excited state in the embedded cluster calculation resembles that found here for the (MgO)₃₂ particle with TD-BHLYP but with an excitation energy similar to that predicted for the lowest TD-B3LYP CT-excited state (3.6–3.8 eV).

3.7 Beyond nanocuboids

Experimental Transmission Electron Microscopy (TEM) micrographs of MgO nanoparticles appear to show exclusively nanocuboids. However, in principle stoichiometric rocksalt cuts with other shapes are also possible, which expose other faces than (100), as well as particles with completely different structures. Examples of the former include cuboctahedral and octahedral particles terminated with a mixture of (100) and (111) faces and exclusively (111) faces respectively, while examples of the latter include tube-like particles, built for example by stacking the hexagonal (MgO)₆ cluster, and bubble-like particles.

Focusing first on the rocksalt particles with different shapes than nanocuboids, atoms on (111) faces are 3-coordinated and hence such particles might have a much higher concentration of 3-C sites than nanocuboids. It is thus interesting to speculate if such particles have as a result fundamentally different absorption spectra than nanocuboids. In an attempt to probe this issue we calculated the TD-BHLYP LVEE of a cuboctahedral (MgO)₂₈ particle (see Fig. 11). The LVEE of this particle is considerably lower (3.6 eV, 340 nm, see Fig. 6) than that predicted for similar sized nanocubes as well as the experimentally measured absorption on-set. There is also a fundamental difference in the nature of the excitation, which in the case of (MgO)₂₈ tends to involve all atoms in the (111) face (see Fig. 12). This delocalization is probably related to, if not the origin of, the LVEE red shift. The smallest octahedral particle (MgO)₁₆ appears unstable and spontaneously converts into the (MgO)₁₆ bubble.

Fig. 11 DFT optimized structure of the (MgO)₂₈ cuboctahedral particle.

Fig. 12 TD-BHLYP excited state – ground state density difference for the excitation corresponding to the 350 nm peak of cuboctahedral (MgO)₂₈ (blue, excess of electrons in the excited state; excited electron/green, deficit of electrons in the excited state; hole).

The LVEE values of the selected tube-like clusters in Fig. 6 appear to show a similar convergence as the nanocubes, albeit to a slightly higher energy plateau. The bubble-like clusters show, however, a different behaviour. Just as previously observed for ZnS,²² the LVEE values increase from (MgO)₈ to (MgO)₁₂ to only decreases again when going to (MgO)₁₆.

4 Conclusions

In this paper we have studied the use of TD-DFT to predict and rationalize the optical absorption spectra of cubic and cuboid MgO nanoparticles. We have shown that vertical excitations in this system are surprisingly difficult to describe accurately and requires the use of range-separated XC-functionals, e.g. CAM-B3LYP, or hybrid XC-functionals with a high percentage of Hartree–Fock like exchange, e.g. BHLYP. We demonstrate that this issue most likely stems from charge-transfer excitations involving the corners of the nanoparticles, which are erroneously energetically stabilized by low HFLE XC-functionals. The description of similar charge-transfer excitations might also lead to problems for other ionic materials that crystallize in the rocksalt structure. We demonstrate that the low-energy long-wavelength excitations responsible for the absorption of light between 200 and 300 nm typically involve both 3-coordinated corner sites and 4-coordinated edge sites. We would therefore argue that to label peaks in the absorption spectrum exclusively as either a corner or edge feature based on the coordination number of the oxygen atoms involved is, at least for particles up to 1 nm, misleading. For the largest particles studied, we find that edge-atoms start to contribute significantly to excitations at the lower end of the wavelength range studied. Finally, we show that particles that expose other faces than (100), e.g. cuboctahedral and octahedral particles (also) exposing (111) faces, or have faces with odd number of atoms, are likely to have considerably different absorption spectra.

Acknowledgements

Dr. Keith McKenna, Dr. Karol Kowalski, Prof. Alex Shluger, Prof. Marek Sierka, Dr. Carmen Sousa, Dr. Slavica Stankic and Dr. Scott Woodley are kindly acknowledged for stimulating discussion. M.A.Z. and A.K. acknowledge the UK Engineering and Physical Sciences Research Council (EPSRC) for a Career Acceleration Fellowships (Grants EP/I004424/1 and EP/J002208/1). Computational time on the computers of the Legion High Performance Computing Facility at University College London (Legion@UCL), the IRIDIS regional high-performance computing service provided by the e-Infrastructure South Centre for Innovation (EPSRC Grants EP/K000144/1 and EP/K000136/1) and on HECToR and ARCHER the UK's national high-performance computing service (via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC grants EP/F067496/1 and EP/L000202/1) is gratefully acknowledged.

References

1. D. W. Lewis and C. R. A. Catlow, Top. Catal., 1994, 1, 111–121.
2. S. Arndt, G. Laugel, S. Levchenko, R. Horn, M. Baerns, M. Scheffler, R. Schlögl and R. Schomäcker, Catal. Rev., 2011, 53, 424–514.
3. G. J. Hutchings, M. S. Scurrell and J. R. Woodhouse, Chem. Soc. Rev., 1989, 18, 251.
4. A. Sternig, S. Stankic, M. Müller, J. Bernardi, E. Knözinger and O. Diwald, Adv. Mater., 2008, 20, 4840–4844.
5. S. Stankic, M. Müller, O. Diwald, M. Sterrer, E. Knözinger and J. Bernardi, Angew. Chem., Int. Ed., 2005, 44, 4917–4920.
6. R. C. Whited, C. J. Flaten and W. C. Walker, Solid State Commun., 1973, 13, 1903–1905.
7. S. Stankic, J. Bernardi, O. Diwald and E. Knözinger, J. Phys. Chem. B, 2006, 110, 13866–13871.
8. S. Stankic, A. Sternig, F. Finocchi, J. Bernardi and O. Diwald, Nanotechnology, 2010, 21, 355603.
9. S. Coluccia, A. M. Deane and A. J. Tench, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 2913–2922.
10. M. Müller, S. Stankic, O. Diwald, E. Knözinger, P. V. Sushko, P. E. Trevisanutto and A. L. Shluger, J. Am. Chem. Soc., 2007, 129, 12491–12496.
11. R. Dong, X. Chen, X. Wang and W. Lu, J. Chem. Phys., 2008, 129, 044705.
12. Y. Zhang, H. S. Chen, B. X. Liu, C. R. Zhang, X. F. Li and Y. C. Wang, J. Chem. Phys., 2010, 132, 194304.
13. S. T. Bromley, I. D. P. R. Moreira, K. M. Neyman and F. Illas, Chem. Soc. Rev., 2009, 38, 2657–2670.
14. P. E. Trevisanutto, P. V. Sushko, A. L. Shluger, K. M. Beck, M. Henyk, A. G. Joly and W. P. Hess, Surf. Sci., 2005, 593, 210–220.
15. K. P. McKenna, D. Koller, A. Sternig, N. Siedl, N. Govind, P. V. Sushko and O. Diwald, ACS Nano, 2011, 5, 3003–3009.
16. A. Sternig, D. Koller, N. Siedl, O. Diwald and K. McKenna, J. Phys. Chem. C, 2012, 116, 10103–10112.
17. S. B. Woodley, A. A. Sokol, C. R. A. Catlow, A. A. Al-Sunaidi and S. M. Woodley, J. Phys. Chem. C, 2013, 117, 27127–27145.
18. D. Sundholm, Phys. Chem. Chem. Phys., 2004, 55, 2044–2047.
19. X. Wang, R. Q. Zhang, S. T. Lee, T. A. Niehaus and T. Frauenheim, Appl. Phys. Lett., 2007, 90, 123116.
20. Y. Wang, R. Zhang, T. Frauenheim and T. A. Niehaus, J. Phys. Chem. C, 2009, 113, 12935–12938.
21. V. E. Matulis, D. M. Palagin and O. A. Ivashkevich, Russ. J. Gen. Chem., 2010, 80, 1078–1085.
22. M. A. Zwijnenburg, Nanoscale, 2011, 3, 3780–3787.
23. M. A. Zwijnenburg, F. Illas and S. T. Bromley, Phys. Chem. Chem. Phys., 2011, 13, 9311–9317.
24. M. A. Zwijnenburg and S. Bromley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–9.
25. E. Berardo, H.-S. Hu, K. Kowalski and M. A. Zwijnenburg, J. Chem. Phys., 2013, 139, 064313.
26. E. Berardo, H.-S. Hu, S. A. Shevlin, S. M. Woodley, K. Kowalski and M. A. Zwijnenburg, J. Chem. Theory Comput., 2014, 10, 1189–1199.
27. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
29. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
30. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
31. A. D. Becke, Phys. Rev., 1988, 38, 3098–3100.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
33. R. Ahlrichs, M. Bär, H. Marco, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
34. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
35. R. Bauernschmitt, M. Häser, O. Treutler and R. Ahlrichs, Chem. Phys. Lett., 1997, 264, 573–578.
36. M. von Arnim and R. Ahlrichs, J. Chem. Phys., 1999, 111, 9183.
37. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433.
38. F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772.
39. C. van Wuellen, J. Comput. Chem., 2011, 32, 1195–1201.
40. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
41. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. U. Shyjun, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
42. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
43. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
44. C. Hättig, Phys. Chem. Chem. Phys., 2005, 7, 59–66.
45. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489.
46. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118.
47. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
48. A. Sternig, S. Stankic, M. Müller, N. Siedl and O. Diwald, Nanoscale, 2012, 4, 7494–7500.
49. S. Stankic, M. Sterrer, P. Hofmann, J. Bernardi, O. Diwald and E. Knözinger, Nano Lett., 2005, 5, 1889–1893.
50. M. Sterrer, T. Berger, O. Diwald, E. Knözinger, P. V. Sushko and A. L. Shluger, J. Chem. Phys., 2005, 123, 64714.
51. A. L. Shluger, P. V. Sushko and L. N. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 2417–2430.
52. L. N. Kantorovich, A. L. Shluger, P. V. Sushko, J. Günster, P. Stracke, D. W. Goodman and V. Kempter, Faraday Discuss., 1999, 114, 173–194.
53. M. J. G. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585.
54. P. Wiggins, J. A. G. Williams and D. J. Tozer, J. Chem. Phys., 2009, 131, 091101.
55. D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2000, 2117–2121.
56. P. W. Tasker, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp03442b

‡ EOM-CCSDT/TZ calculations were only computationally feasible for (MgO)₁ and (MgO)₂ and hence are not shown in Fig. 3.

---