Supramolecular self-assembled network formation containing N⋯Br halogen bonds in physisorbed overlayers

Abstract

The formation of a halogen bonded self-assembled co-crystal physisorbed monolayer containing N⋯Br interactions is reported for the first time. The co-crystal monolayer is identified experimentally by synchrotron X-ray diffraction and the structure determined. Density functional theory (DFT) calculations are also employed to assess the magnitudes of the different interactions in the layer. Significantly, compared to other halogen bonds in physisorbed monolayers we have reported recently, the N⋯Br bond here is found to be non-linear. It is proposed that the increasing importance of the lateral hydrogen bond interactions, relative to the halogen bond strength, leads to the bending of the halogen bonds.

---

Introduction

The study of supramolecular self-assembled networks held together by non-covalent interactions is currently of great interest. These overlayers are not covalently bound to the substrate (like thiols on gold) but are only weakly physisorbed. This means that the adsorbate–adsorbate interactions dominate the behaviour leading to a much richer surface phase behaviour as several different phases can have similar energies. There are a number of non-covalent interactions that might be used to control the self-assembly process. In particular those with a strength and directionality which can be used to control materials properties such as corrosion resistance, wettability^1–3 and the formation of templated monolayer structures for recognition by molecular engineering.

In bulk three-dimensional (3D) crystal engineering, multicomponent co-crystals have become a popular means of modulating the physicochemical properties of molecular solids⁴via complementary interactions between the constituent molecules. Similar principles have been utilised in the design of two-dimensional (2D) physisorbed co-layers. Typically, hydrogen bonding is the interaction of choice for controlling both hetero- and homomolecular assembly in two dimensions. Indeed, hydrogen bond formation among a variety of molecules has been extensively studied in physisorbed layers, including alcohols,^5–11 fatty acids^12–16 and amides.^17–20

A variety of other non-covalent interactions have also been observed in physisorbed layers, including halogen–halogen interactions.^21–24 An extension of this, the halogen bond – the electrostatic interaction between a halogen atom and a Lewis base – represents an important alternative and complement to the hydrogen bond.^25–27 The halogen bond is increasingly recognised as an important non-covalent interaction in 3D crystal engineering due to a strength, directionality and robustness comparable to the hydrogen bond.^28,29 Furthermore, the halogen bond provides a parallel set of non-covalent interactions to the hydrogen bond, and has even been demonstrated to be stronger than hydrogen bonding in some self-assembly processes.³⁰

Interestingly one could combine halogen and hydrogen bonds in a single structure each performing separate tasks, without the present level of confusion when hydrogen bonds are used to do both. For example one could consider forming a 2D molecular frame work using the stronger of the halogen bonds and separately include hydrogen bonds for recognition of other species without compromising the frame integrity.

We have previously reported the formation of a 1 : 1 stoichiometry co-layer of 4,4′-bipyridine (BPY – Fig. 1a) and 1,4-diiodotetrafluorobenzene (DITFB – Fig. 1b) physisorbed on a graphite surface.³¹ In this co-layer, the molecules form extended linear chains of alternating DITFB and BPY, with evidence of halogen bond formation between the iodine atoms of DITFB and the nitrogen atoms of BPY, as deduced by the short internuclear separation; this is further supported by recent simulation work.³² This structure is in good agreement with the bulk behaviour, where halogen bond formation is also observed.³³ Interestingly, we have recently demonstrated that 1,4-diiodobenzene (DIB – Fig. 1c), the non-fluorinated analogue of DITFB, does not form a halogen bonded co-layer with BPY when physisorbed on graphite.³² This contrasts with the bulk behaviour, where a BPY–DIB co-crystal is observed.³³ The lack of halogen bond formation in the mixed overlayer of DIB–BPY has been attributed to the weaker halogen bonds formed by DIB compared to DITFB, relative to the energies of the two separate materials, a conclusion supported by DFT calculations.³²

Fig. 1 The molecular structure of (a) 4,4′-bipyridine (BPY); (b) 1,4 diiodotetrafluorobenzene (DITFB); (c) 1,4-diiodobenzene (DIB); and (d) 1,4-dibromotetrafluorobenzene (DBTFB).

First principles calculations performed on complexes of pyridine and aryl halides suggest that the halogen bond between BPY and 1,4-dibromotetrafluorobenzene (DBTFB – Fig. 1d) should be intermediate in strength between the BPY–DITFB and BPY–DIB interactions.³⁴ However, there is some experimental evidence from IR vibrational frequencies that might suggest that the BPY–DIB halogen bond is stronger than the BPY–DBTFB interaction.³⁵ The results above illustrate that the formation of halogen bonded co-layers in physisorbed systems appears very sensitive to the halogen bond interaction strength.

Hence, in this work we report the phase behaviour of the mixed overlayer of BPY–DBTFB to test the prediction from the DFT calculations. This work will also provide quantitative measure of the BPY–DBTFB halogen bond strength as a robust interaction for controlling self-assembly in physisorbed layers.

Methods

Experimental

The experimental approach employed in this work to obtain diffraction patterns from physisorbed overlayers on graphite has been detailed elsewhere.²⁰ The graphite substrate used was Papyex, an exfoliated recompressed graphite foil from Le Carbon. Papyex is a compressed powder of graphite crystallites, which have had a preferred orientation imparted to them from the manufacturing process. This preferred orientation was used to maximise the recorded intensity from the adsorbed layer by concentrating scattering from the overlayer into the detector plane. The batch of Papyex used was determined to have a surface area of 27.5 m² g⁻¹ by nitrogen adsorption.

BPY and DBTFB were purchased from Sigma Aldrich with respective purities of 99.9% determined by GLC, and 99.7% determined by GC as stated on the certificate of analysis. Both were used without further purification. The shapes of the DBTFB and BPY molecules were initially used to estimate the quantity of adsorbate required based on the specific surface area of the graphite. Subsequent calculations using the experimentally determined overlayer structures give the coverages as 0.519 equivalent monolayers (ML) and 0.497 ML respectively for the co-layer and pure DBTFB layer, well within the sub-monolayer regime (where the equivalent monolayer is defined by the number of molecules required to fully cover the surface of the substrate based on the specific surface area of the substrate and the area of each adsorbate).

Dosing was performed through the vapour phase. For the co-layer, graphite (3.06 g) was dosed with a 1 : 1 ratio of BPY (8.78 mg) and DBTFB (16.98 mg); for the pure DBTFB layer, graphite (3.40 g) was dosed with DBTFB (40.07 mg). The graphite and adsorbates were loaded into Pyrex tubes, which were evacuated to a pressure of ∼0.1 mbar and sealed under vacuum. The tubes were annealed for 3 hours at 485 K and 295 K for the co-layer and pure DBTFB layer respectively, before being allowed to cool slowly to room temperature over the course of ∼8 hours. After cooling, the tubes were broken open and the dosed graphite recovered.

In this study, diffraction patterns were recorded on Beamline I11 at Diamond Light Source, UK.³⁶ The X-ray wavelength used was 1.033787 Å with a detector zero angle offset of 0.00803° for the co-layer, and 1.054700 Å with a detector offset of 0.05899° for the pure DBTFB layer as determined by Rietveld refinement of a silicon standard (NIST SRM 640c). The dosed graphite was cut into 3 mm diameter discs and loaded into a glass capillary such that the plane of preferred orientation of the graphite was aligned with the scattering plane. The samples were rotated on the diffractometer at ∼100 rpm to enhance powder averaging, and the diffraction pattern recorded over the angular range 1° to 91° in 2θ using the position sensitive detector.³⁷ The sample temperature was controlled with a nitrogen cryostream (Oxford Cryostreams, UK).

Experimentally, data can only be recorded over a limited range of momentum transfer, Q. Hence, there are only a limited number of diffraction peaks available for analysis, and so the fitting process must ideally be constrained as much as possible. Therefore, rather than refining individual atomic positions, the structures of the BPY and DBTFB molecules used in the fitting process have been taken unchanged from the 3D crystal structure (Cambridge crystallographic database refcode IKUJUT), and only rigid body rotations and translations of these molecules have been considered. In addition, high symmetry plane groups, in which molecules have fewer degrees of freedom, were considered in preference to lower symmetry structures.

There are several analytical models to account for the saw-tooth shape of the 2D diffraction peaks. In this work, we have considered the Gaussian, Lorentzian and Lorentzian-squared lineshapes of Schildberg and Lauter.³⁸ The Lorentzian-squared peak shape produced the closest match to the experimental peaks, and so was used for the final refinement. The model includes terms for the size and preferential orientation of the graphite crystallites, which were fitted to the experimental data. A single temperature factor set to unity was used. The agreement between the experimental and calculated fit was compared using R and the reduced chi-squared.³⁹

Computational method

In the present work we use density functional theory (DFT) calculations to quantify the energetics and the intermolecular bonding in the BPY–DBTFB overlayer. For this purpose we employ CASTEP, a periodic boundary condition DFT code.⁴⁰ Here we have performed two sets of calculations, with and without explicit inclusion of the graphitic substrate in the model. Previous work with related systems have indicated that is not unreasonable to model the supramolecular interactions in halogen bonded networks without explicitly accounting for the substrate, because graphite is a very inert surface, and therefore one does not expect the relatively weak substrate–adsorbate interactions to play a significant role in determining the symmetry and dimension of the surface unit cell, relative to the much stronger adsorbate–adsorbate interactions.^32,41 Therefore in the first set of calculations we have optimized the structure of the commensurate and non-commensurate co-layer without including the substrate.

In the second set of calculations, we estimated the variations in the adsorption of the isolated BPY and DBTFB monomers along the graphitic surface by adsorbing a single molecule on a 6 × 6 graphene cell including the full graphite carbon interactions with the overlayer, including surface periodicity. For this set of calculations we used a (2 × 2 × 1) Monkhorst–Pack⁴²k-point grid. The calculations were converged as a function of k-point sampling and cut-off energy. The optimized graphene lattice parameter (2.439 Å) was found to be in good agreement with the reported value (2.46 Å).⁴³ For the surface calculations both the molecule and the substrate atomic positions were left unconstrained.

Details of the DFT calculations are discussed in two recent publications,^32,41 and therefore we summarize here only the most important computational parameters. The GGA formalism was adopted through the Perdew–Burke–Ernzerhof exchange correlation functional⁴⁴ and combined with ultrasoft pseudopotentials.⁴⁵ The plane wave basis was truncated at a kinetic energy cut-off of 340 eV. Long-range intermolecular interactions⁴⁶ are accounted through the TS correction method of Tkatchenko and Scheffler.⁴⁷ All the structural optimizations were converged to a maximum force tolerance of 0.05 eV Å⁻¹, while the electronic energy tolerance during the SCF cycles was set to 10⁻⁶ eV.

Results

Synchrotron X-ray diffraction

DBTFB–BPY. Fig. 2 shows the diffraction patterns for the overlayers of pure BPY (bottom) and pure DBTFB (second from bottom). The data in these figures are obtained after the subtraction of the graphite substrate alone⁴⁸ and hence represents the scattering from the adsorbed monolayer. The characteristic asymmetric peaks in these patterns are indicative of the formation of solid monolayers at these temperatures and coverages. The diffraction pattern from a mixture of these two species is also given in Fig. 2. Once again the characteristic asymmetric peaks in this pattern are also indicative of the formation of a solid monolayer.

Fig. 2 Overlayer diffraction patterns of BPY (blue – bottom), DBTFB (red – second from bottom), the 1 : 1 mixed co-layer (green – second from top). The pattern expected for phase separation of BPY and DBTFB is shown in purple at the top. All patterns were recorded at a similar coverage and temperature.

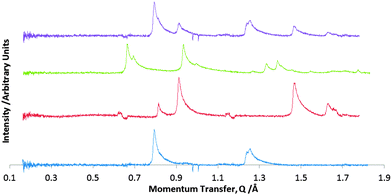
The nature of the mixed monolayer can be deduced by comparison with the two patterns of the pure monolayers. If these species do not mix on the surface, but phase separate, then the diffraction pattern from the co-layer should simply be the sum of the patterns for the two pure overlayers. This predicted pattern is shown at the top of Fig. 2. The experimental pattern for the co-layer is shown second from top in Fig. 2. The experimental pattern differs significantly from the anticipated case for phase separation, indicating that the two species are not phase separated but do interact to form a co-crystal in these physisorbed layers.

Diffraction patterns were recorded over the temperature range 200–294 K. At ∼275 K, the peaks indicative of the DBTFB–BPY co-layer disappeared and were replaced by peaks corresponding to a pure overlayer of BPY. This sharp transition is indicative of a mixed co-layer (rather than solid solution) that underwent incongruent melting to form crystalline BPY and liquid DBTFB, with a melting point of ∼275 K. This compares with the bulk melting point of 383–388 K,³⁵ meaning that the overlayer melting point is 0.7 of that of the bulk. This behaviour is fairly typical for a number of physisorbed overlayers with non-covalent interactions.^32,41,49

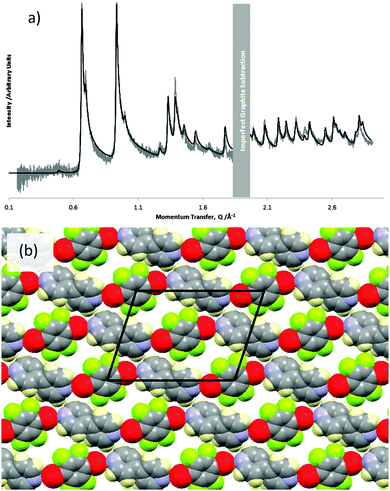
The experimental pattern for the co-crystal was indexed with an oblique unit cell of dimensions a = 19.13(7) Å, b = 13.61(5) Å, ν = 29.7(2)°. Other higher symmetry rectangular unit cells were considered. However, the splitting of the lowest angle peaks can only be reasonably accounted for by a small oblique unit cell. This unit cell is only large enough to accommodate one pair of DBTFB and BPY molecules. Assuming the cell has p2 symmetry, the highest symmetry that an oblique cell can possess, the two-fold rotation axes of the molecules must coincide with the two-fold rotation axes of the unit cell. In this case it was found that the molecules are centred at the cell origin and (1/2, 0). This effectively constrains the translations of the molecules, meaning that only the three rotations of each molecule need be considered.

The best fit to the experimental pattern of the co-crystal is shown in Fig. 3(a), and the corresponding structure is shown in Fig. 3(b). The BPY molecules have a torsion angle of ∼35° between the two pyridine rings. In this structure, the BPY molecules lie so that their mean plane is parallel to the graphite surface. In contrast, the DBTFB molecules do not appear to lie exactly “flat” on the surface: the fit is slightly improved by allowing a rotation of ∼15° ± 15° about the Br–Br axis, and canting the Br–Br axis up from the substrate plane by ∼10° ± 10°. However, as noted previously, diffraction patterns from adsorbed layers are fairly insensitive to changes in structure normal to the surface.⁴¹ This means that the magnitude of small rotations that only move molecules slightly out of the plane parallel to the substrate cannot be determined accurately, and, in addition, the sense of the rotation cannot be inferred from the experimental data.

Fig. 3 (a) The overlayer diffraction pattern of the 1 : 1 stoichiometry co-layer of BPY and DBTFB at a coverage of 0.519 ML and a temperature of 200 K. The experimental pattern is shown in grey, and the calculated fit in black. (b) The overlayer structure corresponding to this fit. In this and subsequent figures, atom colours are: grey = carbon, blue = nitrogen, white = hydrogen, green = fluorine, bronze = bromine. The unit cell is shown in black.

A comparison of the overlayer lattice parameters with those of the graphite lattice (a_g = 2.46 Å and √3 × a_g = 4.26) indicates that the lattice parameters of a doubled overlayer cell are reasonably close to integer multiples of the graphite lattice parameters (2 × 19.13 Å ≈ 9 × 4.26 Å and 2 × 13.61 Å ≈ 11 × 2.46 Å). In addition, the angle between the axes of the overlayer cell is close to 30°, which is the angle between the a_g and √3 × a_g directions of the graphite lattice. This suggests that the overlayer could well be commensurate with the underlying substrate. Here we can only identify a similarity of lattice parameters between the overlayer and substrate and cannot confirm that the layers are commensurate.

Typically, two adsorbed species will tend to phase separate unless very similar in size.^50–53 Hence, the formation of the co-crystal, rather than phase separation of the components, implies that there is some significant non-covalent halogen bonding in this overlayer. However, we note that halogen bond in this overlayer does not appear to be linear, as we have observed previously,³¹ but significantly bent.

DBTFB. We also present here the structure of the pure DBTFB monolayer at a coverage of 0.496 ML (the structure of the BPY monolayer has been published previously⁵⁴). Diffraction patterns were recorded over the temperature range 100–285 K. The evolution of the pattern with temperature is shown in Fig. 4; the patterns have had the substrate subtracted similarly to the co-layer described above. This figure shows that this physisorbed monolayer freezes at a temperature of ∼180 K to form a solid overlayer. At ∼130 K several of the peaks begin to split, indicating a solid–solid phase transition to a different structure at lower temperatures.

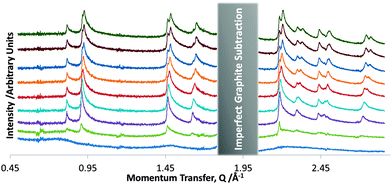Fig. 4 The overlayer diffraction pattern of DBTFB at 0.497 ML coverage at selected temperatures. Temperatures from bottom to top are: 202 K, 177 K, 154 K, 137 K, 125 K, 115 K, 108 K, 103 K, 100 K.

The overlayer diffraction pattern of the high temperature polymorph of DBTFB is shown in grey in Fig. 5. This pattern was indexed using a rectangular unit cell of dimensions a = 15.50(7) Å, b = 7.72(6) Å and ν = 90.0(5)°. Based on the size of this unit cell, it can contain two DBTFB molecules with their planes parallel to the substrate.

Fig. 5 (a) The overlayer diffraction pattern of DBTFB at 0.497 ML coverage and a temperature of 130–160 K. The experimental pattern is shown in grey, and the calculated fit in black. (b) The overlayer diffraction pattern of DBTFB at 0.497 ML coverage and a temperature of 100 K. The experimental pattern is shown in grey, and the calculated fit in black. (c) The structure corresponding to the fit in part (a).

The highest symmetry that a rectangular cell can possess is c2mm. With this symmetry, a structure composed of two molecules per unit cell physisorbed parallel with the surface has no degrees of freedom: the positions of the molecules are constrained so that the two-fold rotation axes of the molecules align with the two-fold rotation axes of the cell at the origin and (1/2, 1/2), and the rotation about the z-axis (the surface normal) is constrained so that the mirror planes of the molecule align with the mirror planes of the unit cell. This structure produces a good fit to the experimental pattern, with R = 0.54 and X_red² = 496.

The fit can be somewhat improved by allowing the molecules to tilt up from the surface, so that the overlayer is no longer “flat”. Maintaining the symmetry constraints on translation and rotation about the z-axis, the best fit structure has a rotation of ∼10° ± 10° about the Br–Br axis, and ∼10° ± 5° about the perpendicular in the molecular plane. This structure gives a fit with R = 0.39 and X_red² = 284; the fit is shown in Fig. 5(a) and the corresponding structure in Fig. 5(c).

The constraint on rotation about the z-axis can be lifted by lowering the symmetry of the cell to p2gg (in this case, the two molecules are not rotated independently, but instead the rotations are coupled via the glide symmetry of the cell). However, after refinement, the molecular rotations do not deviate significantly from the c2mm structure, indicating that the higher symmetry cell is the correct one.

As b ≈ 0.5a, a higher symmetry square supercell doubled in the b direction was also considered. However, square cells have four-fold rotational symmetry, and it was not possible to find a structure that satisfied this symmetry constraint.

Unlike for the co-layer, a comparison of the overlayer lattice parameters with those of the graphite lattice does not reveal any simple integer relationship that might indicate commensurability. We note that a trebled unit cell in the a-direction would be commensurate to within the error in a (3 × 15.5 Å ≈ 19 × 2.46 Å = 46.72 Å). However, this would be a rather long-range commensurability, and there is no similar relationship for the b-direction.

The experimental diffraction pattern of the low temperature polymorph (at 100 K) is shown in grey in Fig. 5(b). The splitting of the peaks in the low temperature phase is interpreted as a reduction of symmetry as the structure moves from a rectangular cell to a very slightly oblique cell (this is not uncommon when monolayer systems are cooled^32,54). The pattern was indexed with an oblique cell of dimensions a = 15.46(6) Å, b = 7.63(3) Å and ν = 89.2(4)°. This represents a slight contraction of the unit cell, which is also to be expected upon cooling.

The structure of this phase was refined assuming p2 symmetry, the highest possible symmetry that an oblique cell can formally possess. This means each molecule has three independent rotations, but the positions of the molecules are constrained to the origin and (1/2, 1/2). However, the unit cell is still very close to rectangular at 100 K, and upon fitting it became apparent that the overlayer maintains a quasi-c2mm structure virtually identical to the high temperature rectangular phase above. For comparison, the fitted pattern is shown in black in Fig. 5(a). The structure is not shown, as it is essentially indistinguishable from that in Fig. 5(c).

Density functional theory

DBTFB–BPY. The energy landscape of the BPY–DBTFB co-layer was explored in proximity of the experimentally determined ‘best fit’ structure above. Essentially we performed geometry optimizations for a series of trial initial structures in which both the unit cell parameters and atom positions were allowed to vary. Similarly to our previous BPY–DITFB calculations,³² the DFT calculations produce again remarkably similar lattice parameters for the co-crystal monolayer structures when compared with the experimental structure. For a given set of initial cell lattice parameters we considered two main molecular arrangements, one with the same small molecular tilt observed experimentally and one with the molecules perfectly flat. The “flat” geometry turned out to be energetically preferred (by only 2 meV). The lattice parameters were found to agree within 3.3% (−1.75% a, −3.30% b, −0.06% γ) for the tilted geometry and within 3.1% (−1.84% a, −3.07% b, −0.44% γ) for the “flat” molecular arrangement.

The experimental results suggest that the overlayer lattice could be commensurate with the top-layer graphitic honeycomb lattice. Hence, by allowing the cell parameters to relax we have ignored any geometrical constraints deriving from the graphite periodicity. We therefore performed the same geometry optimization, but this time fixed the unit cell parameters at the commensurate values (a = 19.1832 Å, b = 13.5366 Å, γ = 30°) to evaluate how the overlayer energetics would be affected by the imposed periodicity. Interestingly, this geometry optimisation produced a only slightly higher energy structure (by 44 meV) than the non-commensurate “flat” structure described above, although the resulting structures are similar in both cases (less than 2.6% difference in the lattice parameters).

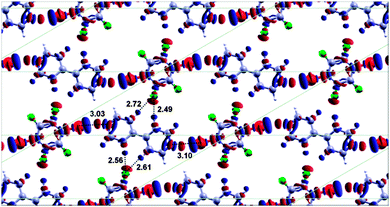
Even for a commensurate cell the binding energy is found to be almost unaffected by the variation of the relative azimuthal angle between the monomers, with the “flat” arrangement being only 2 meV more stable than the tilted (∼15°) commensurate arrangement. Fig. 6 shows the electron density difference map for the optimised commensurate flat BPY–DBTFB co-layer. Since DFT predicts a very small energy difference between the commensurate and non-commensurate lattice and since the experimental data suggest the co-layer may be commensurate, in the following discussion we therefore have taken the flat, commensurate, structure to be the “global” minimum for the purposes of this discussion. Although the almost commensurate structure has a slightly lower energy than a perfectly commensurate structure, in the following section we will see that accounting for the interactions with the substrate will provide further evidence for a commensurate cell.

Fig. 6 DFT electron density difference for BPY–DBTFB monolayer. Red regions show increase of electron density relative to the separate molecules and blue indicates a decrease of electron density relative to the separate molecules (the isosurface level is set to 0.005 e Å⁻³). The lines indicate the unit cell.

The DFT calculations relative to the flat commensurate structure (Fig. 6) show that the total intermolecular bonding energy (including hydrogen bonding, halogen bonding and vdW dispersion force corrections) per cell is 0.786 eV. By fixing the geometry of the BPY and DBTFB molecules in the unit cell and expanding the lateral separation between the BPY–DBTFB molecular chain and the periodically repeated images in the neighbouring cells, we can then estimate the contribution to the intermolecular binding energy per cell coming from the inter-chain H-bonding alone to be approximately 60 meV each. This energy is less than 4% smaller than that observed for BPY–DITFB (62 meV). In addition, the halogen bond was found to contribute only 271 meV (136 meV for each Br⋯N per cell), half of the energy of the I–N bond in the BPY–DITFB co-layer. The results are summarised in Table 1 column (a). This dramatic decrease in the halogen bond strength points to a greater relative importance of the lateral interactions between the fluorine atoms of DBTFB and the hydrogen atoms of BPY.

Table 1 The contributions to the total binding energy for different configurations of the BPY–DBTFB co-layer (see text)

	(a) Experiment-based non-linear commensurate geometry/meV	(b) Hypothetical linear geometry/meV
Halogen bonding	271	296
Interchain H-bonding	240	169
van der Waals	275	285
Total	786	750

---

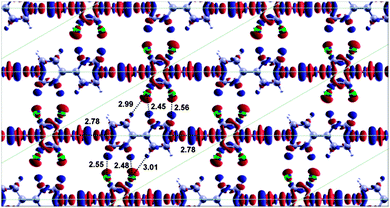
The closely related BPY–DITFB co-layer³¹ forms a structure with a linear arrangement of molecules, resulting in a halogen bond with the “optimum” bond angle of ∼180° (as opposed to the non-linear halogen bonds observed experimentally for this BPY–DBTFB co-layer). To rationalise why the BPY–DBTFB co-layer forms non-linear halogen bonds, we have repeated the DFT calculations for BPY–DBTFB using a linear molecular geometry (Fig. 7) isomorphic with the BPY–DITFB commensurate co-layer.

Fig. 7 DFT electron density difference for the hypothetical BPY–DBTFB linear monolayer. Red regions show increase of electron density relative to the separate molecules and blue indicates a decrease of electron density relative to the separate molecules (the isosurface level is set to 0.005 e Å⁻³).

For the linear arrangement, the total binding energy is 750 meV, about 4% lower than the non-linear geometry. The halogen bonding contribution to the total energy is about 148 meV per bond, while the lateral interactions between fluorine and hydrogen atoms accounts to a total of 169 meV (see Table 1 column (b)). The results of these calculations show that the non-linear arrangement is the most favourable when the cell is constrained to the commensurate geometry and the optimal lateral interactions in the non-linear arrangement are a significant factor for determining the orientation of the molecules – the structure is not simply dominated by the halogen bond. The energy of the non-linear (commensurate) structure is overall about 36 meV lower than that of the linear structure, hence the results of the DFT calculations are consistent with the presence of a (commensurate) overlayer with non-linear halogen bonds. When the lattice parameters are allowed to relax the non-commensurate oblique structure is still more favourable than the linear structure, but only by 18 meV. Clearly, the very small energy difference between the commensurate and non-commensurate unit cells and between the flat and titled configurations indicates a very flat energy landscape (low energy corrugation). Nevertheless the calculations show a small preference for the non-linear arrangement observed experimentally.

When comparing the relative stabilities of different possible overlayers it is important to consider the conditions of the system. In the present case (i) the amount of graphite surface was much larger than the total overlayer area (coverage of approximately 0.5). Hence the most stable overlayer structure is the lowest energy structure. In the case (ii) where the adsorbate is present in excess, the overlayer structure with the greatest specific energy (energy density per unit cell) will be favoured. Experimentally, working at sub-monolayer coverage implies the first regime, and the calculations have been interpreted accordingly. In a recent paper³² we included an interpretation based on the second case. However, using the approach of case (i) also leads to the same conclusion (that a BPY–DIB halogen-bonded co-layer is unfavourable, by 21 meV per cell).

Commensurability. As there is some indication that the overlayer may be commensurate with the graphite substrate, we have attempted to explore the driving force behind any commensurability.

Although it is at present computationally unfeasible to model the co-layer explicitly accounting for the molecule to substrate interactions (the dimensions of the commensurate unit cell are about 130 Ų), we explore here the adsorption of single BPY and DBTFB molecules on the graphitic surface by calculating the variation of the adsorption energy of the monomers on a 6 × 6 graphene cell. We only considered adsorption structures with the phenyl and pyridyl rings lying flat on the surface (this is the most common adsorption orientation for many aromatic molecules^{31,32,39,41,54–56}). The results are summarized in Fig. 8 and 9.

Fig. 8 Optimized structures of DBTFB on graphene. Relative adsorption energies (ΔE) are reported. The most stable adsorption site (c) is for DBTFB adsorbed with the Br atoms approximately on hollow sites and the centre of the ring atop a carbon atom of the substrate.

Fig. 9 Optimized structures of BPY on graphene. Relative adsorption energies (ΔE) are reported. The most stable adsorption site (c) is for BPY adsorbed with the centre of each ring atop a carbon atom of the substrate.

The energy difference between the most stable adsorption site and the most unfavourable is about 70–90 meV for the two adsorbates. The height of the molecules over the surface is essentially independent of the adsorption site. Interestingly, we did not observe any charge transfer between the surface and the adsorbates, indicating again that the substrate is essentially chemically inert with respect to the overlayer molecules. The small, but not negligible, adsorption energy variation along the surface suggests that the molecules could provide a small driving force towards self-assembly into a commensurate overlayer. The small energy difference between the commensurate and non-commensurate oblique cell (43 meV) is lower than the average energetic corrugation for DBTFB (50 meV) and BPY (56 meV), therefore the small energetic preference for the two molecules to sit on top sites may drive the self-assembly process towards a commensurate lattice.

As in previous work, the present study concerns physisorbed overlayers supported on a graphite substrate; as such, they are not truly two-dimensional. There clearly is a role of the graphite in the adsorption, but as these DFT calculations suggest, the substrate does not greatly influence the adsorbate commensurability or structure. The flat orientation of these aromatic molecules may be favoured by the graphite substrate. However, we cannot experimentally observe the overlayer without the graphite support and any changes to the overlayer that may result.

Discussion

We have identified the formation of a halogen bonded co-crystal of BPY and DBTFB. Significantly the overlayer structure has been determined and the C–Br⋯N halogen bond angle between the bromine and the nitrogen (as determined from the overlayer X-ray diffraction structure) is found to be approximately 158° and not linear. The DFT results are in reasonable agreement (4.5% error) with this conclusion, also indicating a bent bond angle of 163.4° after geometry optimisation.

Interestingly this combination of species is also found to form non-linear halogen bonds in the bulk, although the halogen bond in the monolayer is somewhat less linear (−8%) than in the bulk structure (176.40°/177.71°), although very similar to some of the halogen bond angles observed for related perfluoroaryl bromide species (∼163°).³⁵ This halogen bond angle is also much less linear than that observed for analogous halogen bonded co-layer of BPY–DITFB, which was essentially linear with a bond angle of ∼180°.

The presence of an electropositive region, the σ-hole,⁵⁷ (visible as a blue cloud atop the Br atom in the electron density difference plot in Fig. 6) confirms this topological feature as a signature for halogen bonding interactions. Both the non-linear molecular geometry and the relatively long (on average, 3.07 Å from DFT and 3.19 Å experimentally – 8% shorter than the sum of the vdW radii) internuclear separation (DFT calculations suggest 15% longer than in the BPY–DITFB monolayer³²) between the bromine and the nitrogen atoms point to the presence of a halogen bond weaker than for the BPY–DITFB case. This is confirmed by the DFT results, which indicate that each halogen bond imparts a stabilisation of 136 meV, about a 46% smaller energy contribution than for the N⋯I halogen bond in the BPY–DITFB co-layer.

The lateral interchain H-bonding interactions in the BPY–DBTFB monolayer are somewhat different from the BPY–DITFB monolayer. In the BPY–DBTFB co-layer there is a bifurcated H-bond between one of the DBTFB fluorines and two of the BPY hydrogens with an average length of 2.595 Å after DFT geometry optimisation, and an energy of 60 meV each, making the total binding energy contribution from the lateral interactions almost equivalent (12% smaller) to that provided by the weak N⋯Br halogen bonds. In the BPY–DITFB co-layer there are lateral hydrogen bonds of about the same average length (∼2.52 Å) but with a total energy (248 meV), approximately half of the bonding energy coming from two strong N⋯I halogen bond (498 meV). This suggests that the non-linear orientation of BPY and DBTFB molecules arises from more important lateral interactions (the F–H hydrogen bonds) with weaker N⋯Br halogen bonding, than in the BPY–DITFB co-layer. This is confirmed by a comparison with calculations for the hypothetical linear BPY–DBTFB structure, which show that the small increase in halogen bond strength resulting from linear bonds is more than offset by the decrease in interchain H-bonding, resulting in a less stable structure overall. These results are consistent with the general trend that correlates halogen bonding strength with atomic polarisability (increasing from bromine to bromine due to the increasing dimension of the halogen atoms). We also note that experimentally and theoretically there is some tentative evidence to suggest that the co-layer could be commensurate, which was not observed for the BPY–DITFB co-layer.

In an attempt to understand which halogen bonds have the directionality and robustness to overcome other intermolecular interactions and be used reliably for controlling molecular self-assembly in physisorbed layers, we can combine these results with previous studies to begin to construct a hierarchy of different halogen bonds in physisorbed monolayers. The results so far for BPY-based halogen bonds are listed in Table 2 and indeed follow the trends outlined above.

Table 2 The calculated halogen bond strength of complexes of BPY with halobenzenes when physisorbed on a graphite surface at ∼0.5 monolayer coverage

Interaction		Halogen bond strength per bond/meV	DFT		Diffraction
			Bond angle (degrees)	Bond length/Å	Bond angle (degrees)	Bond length/Å	% of sum of vdW radii
a This co-layer has not been observed experimentally, and the strength of the halogen bond has been calculated to be too weak to drive the formation of a mixed layer. Instead, values have been calculated using DFT for a hypothetical (metastable) structure isomorphic with the BPY–DITFB co-layer.
BPY–DITFB		249	178	2.67	180	2.84	80
BPY–DBTFB		136	163	3.07	158	3.19	92
BPY–DIB^a		125	179	2.86	—	—	—

---

Acknowledgements

We acknowledge financial support for AB from EPSRC DTA award from the Department of Chemistry, University of Cambridge. We acknowledge Diamond Light Source for time on beamline I11 under proposals EE6511 and EE7761.

References

1. J. A. A. W. Elemans and S. De Feyter, Structure and function revealed with submolecular resolution at the liquid-solid interface, Soft Matter, 2009, 5, 721–735.
2. S. De Feyter and F. C. De Schryver, Two-dimensional supramolecular self-assembly probed by scanning tunneling microscopy, Chem. Soc. Rev., 2003, 32, 139–150.
3. T. Kudernac, S. Lei, J. A. A. W. Elemans and S. De Feyter, Two-dimensional supramolecular self-assembly: nanoporous networks on surfaces, Chem. Soc. Rev., 2009, 38, 402–421.
4. D. Braga, F. Grepioni, L. Maini and M. Polito, Molecular Networks, Springer, Berlin, 2009.
5. K. Morishige and T. Kato, Chain-length dependence of melting of n-alcohol monolayers adsorbed on graphite: n-hexanol, n-heptanol, n-octanol and n-nonanol, J. Chem. Phys., 1999, 111, 7095–7102.
6. K. Morishige and Y. Sakamoto, Melting of n-butanol and n-pentanol monolayers adsorbed on graphite: effects of molecular length on melting, J. Chem. Phys., 1995, 103, 2354–2360.
7. L. Messe, S. M. Clarke, A. Inaba, T. Arnold, C. C. Dong and R. K. Thomas, The Mixing Behaviour at the Solid/Liquid Interface: Binary Monolayers of Linear Alcohol Adsorbed on Graphite, Langmuir, 2002, 18, 4010–4013.
8. L. Messe, S. M. Clarke, A. Inaba, C. C. Dong, R. K. Thomas, M. A. Castro and M. Alba, Mixing Behaviour at the Solid/Liquid Interface: Binary Alcohol Monolayers on Graphite, Langmuir, 2002, 18, 9429–9433.
9. K. Morishige, Y. Takami and Y. Yokota, Structures of alkanes and alkanols adsorbed on graphite in solution: comparison with scanning tunneling microscopy images, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 8277–8281.
10. C. L. Claypool, F. Faglioni, W. A. Goddard III, H. B. Gray, N. S. Lewis and R. A. Marcus, Source of image contrast in STM images of functionalized alkanes on graphite: a systematic functional group approach, J. Phys. Chem. B, 1997, 101, 5978–5995.
11. D. M. Cyr, B. Venkataraman, G. W. Flynn, A. Black and G. M. Whitesides, Functional Group Identification in Scanning Tunneling Microscopy of Molecular Adsorbates, J. Phys. Chem., 1996, 100, 13747–13759.
12. A. K. Bickerstaffe, N. P. Cheah, S. M. Clarke, J. E. Parker, A. Perdigon, L. Messe and A. Inaba, The Crystalline Structures of Carboxylic Acid Monolayers Adsorbed on Graphite, J. Phys. Chem. B, 2006, 110, 5570–5575.
13. M. Hibino, A. Sumi and I. Hatta, Molecular arrangements of fatty acids and cholesterol at liquid graphite interface observed by STM, Jpn. J. Appl. Phys., 1995, 34, 3354–3359.
14. M. Hibino, A. Sumi, H. Tsuchiya and I. Hatta, Microscopic origin of the odd even effect in monolayer of fatty acids formed on a gaphite surface by STM, J. Phys. Chem. B, 1998, 102, 4544–4547.
15. E. Kishi, H. Matusda, R. Kuroda, K. Takimoto, A. Yamano, K. Eguchi, K. Hatanaka and T. Nakagiri, Barrier-height imaging of fatty acid Langmuir-Blodgett films, Ultramicroscopy, 1992, 42–44, 1067–1072.
16. R. Kuroda, E. Kishi, A. Yamano, K. Hatanaka, H. Matsuda, K. Eguchi and T. Nakagiri, Scanning tunneling microscope images of fatty acid Langmuir-Blodgett bilayers, J. Vac. Sci. Technol., B, 1991, 9, 1180–1183.
17. T. Arnold and S. M. Clarke, Thermodynamic Investigation of the Adsorption of Amides on Graphite from Their Liquids and Binary Mixtures, Langmuir, 2008, 24, 3325–3335.
18. K. S. Mali, B. Van Averbeke, T. Bhinde, A. Y. Brewer, T. Arnold, R. Lazzaroni, S. M. Clarke and S. De Feyter, To Mix or Not To Mix: 2D Crystallization and Mixing Behavior of Saturated and Unsaturated Aliphatic Primary Amides, ACS Nano, 2011, 5, 9122–9137.
19. T. Bhinde, A. Y. Brewer, S. M. Clarke, T. K. Phillips, T. Arnold and J. E. Parker, Adsorption of Unsaturated Amides on a Graphite Surface: trans-Unsaturated Amides, J. Phys. Chem. C, 2011, 115, 6682–6689.
20. T. Bhinde, S. M. Clarke, T. K. Phillips, T. Arnold and J. E. Parker, Crystalline Structures of Alkylamide Monolayers Adsorbed on the Surface of Graphite, Langmuir, 2010, 26, 8201–8206.
21. R. E. Bucknall, S. M. Clarke, R. A. Shapton and R. K. Thomas, The structure of a methyl iodide monolayer adsorbed on graphite, Mol. Phys., 1989, 67, 439–446.
22. S. M. Clarke and R. K. Thomas, The structure of a bromomethane monolayer adsorbed on graphite, Mol. Phys., 1991, 72, 413–423.
23. K. Morishige, Y. Tajima, S. Kittaka, S. M. Clarke and R. K. Thomas, The structure of chloromethane monolayers adsorbed on graphite, Mol. Phys., 1991, 72, 395–411.
24. A. Inaba, H. Chihara, S. M. Clarke and R. K. Thomas, The structure and heat capacity of fluoromethane monolayers adsorbed on graphite, Mol. Phys., 1991, 72, 109–120.
25. R. Gutzler, O. Ivasenko, C. Fu, J. L. Brusso, F. Rosei and D. F. Perepichka, Halogen bonds as stabilizing interactions in a chiral self-assembled molecular monolayer, Chem. Commun., 2011, 47, 9453–9455.
26. X. Yang, F. Wang, Q. Chen, L. Wang and Z. Wang, Halogen bonded two-dimensional supramolecular assemblies studied by high resolution scanning tunneling microscopy, Chin. Sci. Bull., 2007, 52, 1856–1859.
27. Q. Chen, T. Chen, X. Zhang, L.-J. Wan, H.-B. Liu, Y.-L. Li and P. Stang, Two-dimensional OPV4 self-assembly and its coadsorption with alkyl bromide: from helix to lamellar, Chem. Commun., 2009, 3765–3767.
28. A. C. Legon, The halogen bond: an interim perspective, Phys. Chem. Chem. Phys., 2010, 12, 7736–7747.
29. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Halogen Bonding Based Recognition Processes: A World Parallel to Hydrogen Bonding, Acc. Chem. Res., 2005, 38, 386–395.
30. E. Corradi, S. V. Meille, M. T. Messina, P. Metrangolo and G. Resnati, Halogen Bonding versus Hydrogen Bonding in Driving Self-Assembly Processes, Angew. Chem., Int. Ed., 2000, 39, 1782–1786.
31. S. M. Clarke, T. Friscic, W. Jones, A. Mandal, C. Sun and J. E. Parker, Observation of a two-dimensional halogen-bonded cocrystal at sub-monolayer coverage using synchrotron X-ray diffraction, Chem. Commun., 2011, 47, 2526–2528.
32. M. Sacchi, A. Y. Brewer, S. J. Jenkins, J. E. Parker, T. Friščić and S. M. Clarke, Combined Diffraction and Density Functional Theory Calculations of Halogen-Bonded Cocrystal Monolayers, Langmuir, 2013, 29, 14903–14911.
33. R. B. Walsh, C. W. Padgett, P. Metrangolo, G. Resnati, T. W. Hanks and W. T. Pennington, Crystal Engineering through Halogen Bonding: Complexes of Nitrogen Heterocycles with Organic Iodides, Cryst. Growth Des., 2001, 1, 165–175.
34. S. Tsuzuki, A. Wakisaka, T. Ono and T. Sonoda, Magnitude and Origin of the Attraction and Directionality of the Halogen Bonds of the Complexes of C6F5X and C6H5X (X = I, Br, Cl and F) with Pyridine, Chem. – Eur. J., 2012, 18, 951–960.
35. A. De Santis, A. Forni, R. Liantonio, P. Metrangolo, T. Pilati and G. Resnati, N⋯Br Halogen Bonding: One-Dimensional Infinite Chains through the Self-Assembly of Dibromotetrafluorobenzenes with Dipyridyl Derivatives, Chem. – Eur. J., 2003, 9, 3974–3983.
36. S. P. Thompson, J. E. Parker, J. Potter, T. P. Hill, A. Birt, T. M. Cobb, F. Yuan and C. C. Tang, Beamline I11 at diamond: a new instrument for high resolution powder diffraction, Rev. Sci. Instrum., 2009, 80, 075107.
37. S. P. Thompson, J. E. Parker, J. Marchal, J. Potter, A. Birt, F. Yuan, R. D. Fearn, A. R. Lennie, S. R. Street and C. C. Tang, Fast X-ray powder diffraction on I11 at diamond, J. Synchrotron Radiat., 2011, 18, 637–648.
38. H. P. Schildberg and H. J. Lauter, Lineshape calculations for two-dimensional powder samples, Surf. Sci., 1989, 208, 507–532.
39. A. Y. Brewer, T. Friscic, G. M. Day, L. M. Overvoorde, J. E. Parker, C. N. Richardson and S. M. Clarke, The monolayer structure of 1,2-bis(4-pyridyl)ethylene physisorbed on a graphite surface, Mol. Phys., 2012, 111, 73–79.
40. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
41. A. Y. Brewer, M. Sacchi, J. E. Parker, C. L. Truscott, S. J. Jenkins and S. M. Clarke, The crystalline structure of the phenazine overlayer physisorbed on a graphite surface, Mol. Phys., 2013, 111, 3823–3830.
42. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
43. T. P. Hardcastle, C. R. Seabourne, R. Zan, R. M. D. Brydson, U. Bangert, Q. M. Ramasse, K. S. Novoselov and A. J. Scott, Mobile metal adatoms on single layer, bilayer, and trilayer graphene: an ab initio DFT study with van der Waals corrections correlated with electron microscopy data, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195430.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
45. D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
46. E. R. McNellis, J. Meyer and K. Reuter, Azobenzene at coinage metal surfaces: role of dispersive van der Waals interactions, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
47. A. Tkatchenko and M. Scheffler, Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005.
48. A. Guinier and G. Fournet, Small-angle scattering of X-rays, Wiley, New York, 1955.
49. T. K. Phillips, S. M. Clarke, T. Bhinde, M. A. Castro, C. Millan and S. Medina, Monolayer structures of alkyl aldehydes: odd-membered homologues, Thin Solid Films, 2011, 519, 3123–3127.
50. S. M. Clarke, L. Messe, J. Adams, A. Inaba, T. Arnold and R. K. Thomas, A quantitative parameter for predicting mixing behaviour in adsorbed layers: the 2D isomorphism coefficient, Chem. Phys. Lett., 2003, 373, 480–485.
51. J. E. Parker and S. M. Clarke, Mixing in Adsorbed Monolayers: Perfluorinated Alkanes, Langmuir, 2008, 24, 4833–4844.
52. A. K. Bickerstaffe and S. M. Clarke, The interpretation of mixing behaviour in carboxylic acid monolayers adsorbed on graphite using a regular solution description, Colloids Surf., A, 2007, 298, 80–82.
53. T. Arnold, J. E. Parker and P. Macdonald, Investigation of the Adsorption of Alkanes on Hexagonal Boron Nitride from Their Liquids and Binary Mixtures, J. Phys. Chem. C, 2012, 116, 10599–10606.
54. S. M. Clarke, T. Friščić, A. Mandal, C. Sun and J. E. Parker, Monolayer structures of 4,4′ bipyridine on graphite at sub-monolayer coverage, Mol. Phys., 2011, 109, 477–481.
55. P. Meehan, T. Rayment, R. K. Thomas, G. Bomchil and J. W. White, Neutron diffraction from benzene adsorbed on graphite, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 2011–2016.
56. I. Gameson and T. Payment, Confirmation of the √7 × √7 commensurate structure of a benzene monolayer adsorbed on graphite, Chem. Phys. Lett., 1986, 123, 150–153.
57. P. Politzer, P. Lane, M. Concha, Y. Ma and J. Murray, An overview of halogen bonding, J. Mol. Model., 2007, 13, 305–311.

---