Probing the dynamics of plasmon-excited hexanethiol-capped gold nanoparticles by picosecond X-ray absorption spectroscopy

Abstract

Picosecond X-ray absorption spectroscopy (XAS) is used to investigate the electronic and structural dynamics initiated by plasmon excitation of 1.8 nm diameter Au nanoparticles (NPs) functionalised with 1-hexanethiol. We show that 100 ps after photoexcitation the transient XAS spectrum is consistent with an 8% expansion of the Au–Au bond length and a large increase in disorder associated with melting of the NPs. Recovery of the ground state occurs with a time constant of ∼1.8 ns, arising from thermalisation with the environment. Simulations reveal that the transient spectrum exhibits no signature of charge separation at 100 ps and allows us to estimate an upper limit for the quantum yield (QY) of this process to be <0.1.

---

1 Introduction

The surface of a catalyst is required to promote the formation of intermediate species that exhibits moderate stability. In this respect the chemical inertness of gold (Au) would appear to render it unsuitable for catalysis.¹ Indeed, bulk Au adsorbs neither hydrogen nor oxygen to any significant extent at ambient temperatures and it is therefore unable to act as a hydrogenation or oxidation catalyst. However, distinct from its bulk properties, Au nanoparticles (especially on high surface area oxide supports^2–5) possess remarkable catalytic properties in both the gas and liquid phases. This has led to them becoming a central focus of heterogeneous catalytic research⁶ with a wide range of applications in photocatalysis,^7–9 pollution control,^10,11 sensors and fuel cell technology,^12,13 and biomedicine.^14–16 In addition, because the surfaces of Au nanoparticles (NPs) can be easily functionalised with various organic and biomolecular ligands, there has also been extensive research into capped Au NPs with a particular focus upon biomedical applications.^17–19

Central to their applications in photocatalysis is the surface plasmon resonance (SPR) exhibited by Au NPs. This collective resonant oscillation of the outer electrons has a good overlap with the solar spectrum making Au NPs very effective sun light absorbers.²⁰ In conjunction with their chemical stability arising from the d¹⁰ electronic configuration, Au NPs are strong candidates as sensitisers for metal oxides, such as TiO₂. Indeed, Au-sensitised TiO₂ NPs were recently used to significantly enhance the efficiency of the water splitting process,^21,22 first reported by Fujishima.²³ However, despite this success the mechanism(s) behind the energy transfer from the metal to the semiconductor NPs is not completely understood. The most likely mechanism is that the energy is transferred via coupling of hot electrons on the surface of the Au NP to the TiO₂ substrate. This leads to electrons being injected into the conduction band, initiating the catalysis.^24,25

Charge separation following photoexcitation of the plasmon resonance has also been predicted in the absence of a semiconductor substrate for functionalised Au NPs²⁶ and other noble metal NPs.^27,28 Recently, Aprile et al.²⁶ studied the charge separation in 5 nm Au NPs stabilised by hexanethiol, octadecanethiol or dodecanethiol. They reported that laser excitation of Au NPs leads to electron ejection into the environment, with the lifetime of this charge separation state extending to milliseconds. However, they found that this process was strongly dependent on both the polarity of the medium, which stabilises the ejected electron, and the length of the long alkyl chains that inhibits the recombination of the electrons.

These studies highlight that for developing possible applications it is important to understand the response of SPR-excited Au NPs, which can be qualitatively described as follows. Upon excitation, the energy of light is efficiently transferred to the electrons, which gives rise to excited electrons often described in terms of electronic temperature. The relaxation processes start to thermalise the electrons via electron–electron scattering and electron scattering with the surface. This thermalization process occurs in a few hundreds of femtoseconds.^29,30 The second relaxation step is energy transfer to the lattice, via the electron–phonon coupling, resulting in a large temperature jump of the lattice.^31,32 These temporal evolutions of the electronic and lattice temperatures are generally described using the two-temperature model.³³ The final step is energy transfer to the surrounding matrix. This process corresponds to the heat transfer from the metal particles to the environment, whose rate exhibits a strong dependence on the size of the nanoparticle^34,35 and the thermal conductivity of the surrounding medium.³⁶

The structural dynamics of the Au NPs following energy transfer from the electronic subsystem to the lattice has been studied by Plech et al.³⁷ using time-resolved X-ray diffraction. They found that at lower excitation power the initial lattice heating is followed by cooling on the nanosecond time scale. They also reported that the expansion of the lattice increased linearly with excitation power, up to an excitation power corresponding to a lattice temperature increase of 529 K. At higher temperatures the Bragg peaks were lost as pre-melting of the NPs broke the long-range order. At the bulk melting temperature, complete melting occurs within the first 100 ps after laser excitation. Recently, Ruan et al.³⁸ used ultrafast electron crystallography to study size-selected Au NPs (2–20 nm) supported on a self-assembled molecular interface. They reported size-dependent effects on the maximum change in the bond lengths, which was ∼6% at 2 nm and 3.5% at 20 nm, corresponding to a laser fluence of 75 mJ cm⁻², which is above the melting threshold. Interestingly, they also reported a strong variance of the maximum bond length change with the fluence as a function of size. For instance, at 31 mJ cm⁻² and 75 mJ cm⁻² the structural change in the 20 nm nanoparticle was the same, however, this significantly differed for the 2 nm nanoparticle implying that melting occurs only in the latter and strongly suggesting that the size plays a significant role in the thermodynamics of the NP.^34,35

The studies described above highlight that for describing the catalytic activity of gold, a detailed understanding of the interplay of the structural and electronic properties of nanoparticles is important. In this regard, for determining both the local geometric and the electronic structure of Au NPs, time-resolved X-ray absorption spectroscopy (XAS) is ideal^39,40 since it is element-specific and strongly sensitive to the short-range order within the NPs. Indeed, a number of recent works have highlighted the effectiveness of picosecond XAS applied to study photoinduced dynamics in NPs.^41–44 Consequently, in this contribution, we report a time-resolved XAS study of the photoexcited dynamics of Au nanoparticles functionalised with hexanethiol chains. By monitoring the temporal evolution of the X-ray absorption near-edge structure (XANES) and using theoretical simulations to analyse the data around the Au-L₃ edge, we demonstrate that an 8% lattice expansion is accompanied by a melting of the nanoparticles. Finally, our transient spectrum exhibits no clear signature for a charge transfer at 100 ps and allows us to estimate an upper limit for the quantum yield (QY) of this process to be <0.1.

2 Samples, experiments and computations

2.1 Samples

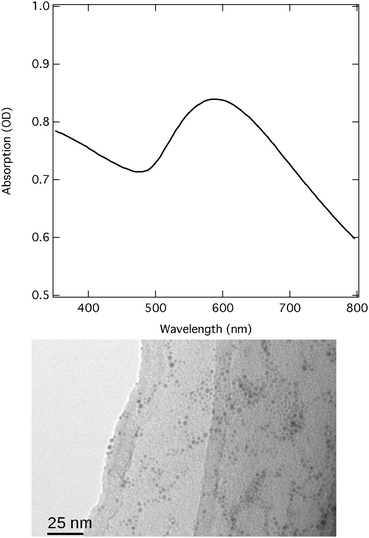
Commercially available (Nanopartz Inc.) Au NPs of about 1.8 nm diameter suspended in ethanol were functionalised with hexanethiol chains (C₆H₁₄S). The concentration used in the experiment was about 3 mM, corresponding to an absorption of about 1 OD for the pump wavelength used. Fig. 1 shows the UV-Vis absorption spectrum and a TEM image of the sample prior to the experiment. The SPR of the gold nanoparticles is clearly visible as a peak in the range between 500 and 700 nm.

Fig. 1 Upper panel: the UV-vis absorption spectrum of the hexanethiol functionalised Au NPs. The cuvette thickness was 1 mm. The SPR of the gold nanoparticles is clearly visible as a peak in the range between 500 and 700 nm. Lower panel: the corresponding TEM image with a resolution bar of 25 nm.

2.2 Laser and synchrotron light

A high repetition-rate picosecond laser system (Duetto from Time-Bandwidth Products AG, 10 ps pulse duration, 260 kHz rep rate, 6.15 W power, 25 μJ per pulse, 532 nm wavelength, focused on a spot size of 150 μm to reach a flux of 110 mJ cm⁻²) was used to optically pump the AuNPs. The laser pulses were synchronised to the camshaft of the synchrotron to probe the excited sample at short time scales (80 ps time resolution). The liquid jet had a diameter of 1 mm. The flow velocity was about 3 m s⁻¹: by considering the laser spot size and the repetition rate, it results that each laser shot shone on about 10% of the new sample. Part of the tubes in the liquid jet circuit was put in a sonicator bath to avoid the collapsing of the nanoparticles. The Au-L₃ edge (11.919 keV) was used to monitor the transient behaviour of the AuNP. We used an APD as a detector coupled with an aluminium Soller slit and a Ge filter (80 μm thick). Secondary Al-Kα photons were suppressed by placing 80 μm thick Kapton foil directly in front of the APD. The setup has been thoroughly characterised and described elsewhere.⁴⁵ The experiment was performed at the SuperXAS beamline of the Swiss Light Source at PSI, Switzerland.

2.3 Computational details

Calculations of the above-edge region of the spectrum were performed using full multiple scattering and a self-consistent field (SCF) potential as implemented within FEFF9.⁴⁶ The SCF loop is initialised by the construction of muffin-tin (MT) potentials where the MT-radii are chosen according to the Norman criterion.⁴⁷ A radius of 7.0 Å around the absorbing atom was used. A Debye–Waller factor (DWF) was included to reflect the fluctuation of atoms in the nanoparticle about their mean positions. In the ground state the DWF was 0.05 Ų, while for the transient spectrum this was 0.1 Ų. Both of these values are consistent with mean-square displacements obtained from molecular dynamics simulations.⁴⁸

Due to the limitations of the MT approximation close to the ionisation potential, calculations of the edge region of the spectrum were performed using the finite difference method as implemented within the FDMNES package⁴⁹ using a free form SCF potential of radius 7.0 Å around the absorbing atom including scalar relativistic effects. Broadening due to the finite mean-free path of the photoelectron and to the core–hole lifetime were accounted for using an arctangent convolution.⁵⁰

The Au NPs used have a diameter of 1.8 nm corresponding to about 250 atoms. This means that 60% of the atoms are at the surface and the remaining 40% are bulk. Consequently, all presented calculations are a linear combination of the spectrum arising from atoms at the surface (×0.6) and those in the bulk (×0.4). It was found that the effect of the sulphur atoms added to the surface to mimic the effect of capping of the Au surface by 1-hexanethiol was only small for the ground state spectrum and negligible for the transient spectrum. Therefore, the capping groups were neglected in the calculations. To simulate the charge separated state, only the absorbing atom was placed in an electronically excited electronic configuration (i.e. Au 5d¹⁰ 6s¹ → Au 5d¹⁰ 6s⁰).

3 Results

Fig. 2 (red line) shows the normalised Au L₃-edge ground-state spectrum of the 1-hexanethiol functionalised Au NPs in ethanol. The spectrum is characterised by an absorption onset just below ∼11.92 keV and a white line transition, typical for the L_2,3-edge of transition metals,^51,52 which appears at 11.925 keV. The intensity of the latter is very weak. Indeed, the d¹⁰ electronic configuration of Au suggests that the white line should in fact be absent. However, for small NPs both the quantum-size and the surface effects (including functionalisation) result in electronic redistribution (e.g., s–d hybridisation in d-band metals).⁵³ The more intense white line in this case, compared to Au foil⁵³ therefore reflects an increase in d-hole population arising from hybridisation.

Fig. 2 Normalised Au L₃-edge ground state (red) and the difference XAS spectrum – pumped minus umpumped – (black) of hexanethiol functionalised Au NPs in ethanol measured 100 ps after excitation. The signal was recorded in fluorescence yield mode (converted to absorption units), at a fluence of 110 mJ cm⁻² and at a repetition rate of 260 kHz.

The difference X-ray absorption spectrum (i.e. excited minus unexcited) at a time delay of 100 ps is also shown in Fig. 2 (black line) and exhibits changes which correspond to about 4% of the signal intensity. Around the edge a derivative profile is observed implying a red shift of the absorption edge. While shifts of the absorption edge are quite commonly assigned to changes in oxidation state, such shifts are also indicative of bond length changes. The 1/r² relationship between the bond length and the edge position⁵⁴ means that this red shift likely points to an increase in the Au–Au distance. At higher energies a distinct oscillatory structure is observed in the difference spectrum, from inspection this appears to be out of phase with the features appearing in the ground state spectrum, pointing to a damping in the excited state consistent with an increase in disorder.

Fig. 3 shows the temporal evolution of the feature at 11.924 keV. By fitting the kinetic trace we observe a pulse-width limited signal rise (∼80 ps) followed by a recovery of the ground state with a decay constant of 1.8 ± 0.2 ns. This latter timescale is consistent with thermalisation with the environment.³⁸

Fig. 3 Kinetic trace of the Au L₃-edge at 11.924 keV for hexanethiol functionalised Au NPs in ethanol. The fit show a pulse-width limited signal rise (<80 ps) followed by a decay of 1.8 ± 0.2 ns.

4 Analysis of the spectrum

Fig. 4 reproduces the ground state experimental spectrum compared to the spectra simulated using FEFF (blue line) and FDMNES (red line). As the advantage of the latter resides in going beyond the MT approximation for the near-edge structure, the spectral range of this calculation is limited to <11.96 keV. The experimental spectrum exhibits four main features highlighted by the dashed lines. The features occurring at 11.935 keV, just below 11.95 keV and at 11.97 keV, are structural and are principally sensitive to the Au–Au bond distance, while the feature at 11.925 keV corresponds to the white line and therefore reflects the number of d-holes. In the near-edge region, the features appearing in both simulations achieve agreement with the experimental spectrum. We observe, in terms of the spectra intensity, the largest deviation between the experiment and the FEFF simulations, which is expected to be due to the limitations of the MT potential. However, although the agreement is better, deviations are still observed for the FDMNES simulations, especially at around 11.925 keV. Zhang et al.⁵⁵ have previously concluded that because S is slightly more electronegative than Au, there is a charge transfer from the surface Au atoms to the S. For particles of ∼1.6 nm diameter they reported a 11% increase of d-holes compared to bulk Au. Using FDMNES, we found that the addition of alkanethiolate chains to the surface Au atoms did not have a strong effect on the spectra and therefore we expect the difference between the calculated and the experimental spectrum at 11.925 keV is reflecting the fact that the calculations have not captured these charge-transfer effects.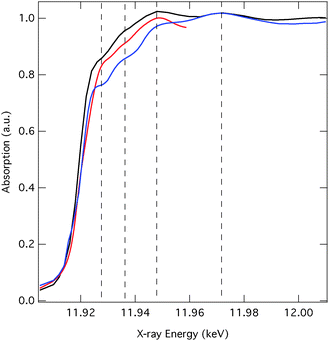

Fig. 4 Measured (black line) and calculated (FEFF: blue, FDMNES: red) Au L₃-edge absorption spectra of hexanethiol capped Au NPs in ethanol.

As previously stated, the difference spectrum in Fig. 2 shows that the spectral changes in the above-edge region correspond to a damping of the features in the ground-state spectrum. This would appear to be indicative of a significant increase of disorder expected for the pump fluence used (110 mJ cm⁻²), which is above the threshold fluence for melting of the NPs. Fig. 5 shows the above-edge region of the difference spectrum compared to the calculated difference spectra for three different lattice expansions. Interestingly, besides the feature appearing at 11.94 keV, we observe negligible differences between the simulated spectra for the different lattice expansions. This demonstrates that above-edge transient features are therefore primarily only sensitive to the changes in disorder, i.e. the Debye–Waller factor, rather than the structural changes. Consequently, to extract information about the lattice expansion and electronic structure changes following SPR excitation, we focus upon the analysis of the edge region of the spectrum.

Fig. 5 Comparison of the experimental Au L₃-edge difference spectrum of hexanethiol-capped Au NPs in ethanol with the FEFF simulated spectra (for three different lattice expansions) in the above-edge region of the spectrum.

Fig. 6a shows a zoom of the edge-region of the difference spectrum compared to the simulated difference spectra for selected lattice expansions. This shows that the best agreement with the experimental spectrum is achieved for a lattice expansion of 8%, corresponding to a bond length change from 2.826 Å to 3.052 Å. This change is large, but consistent with results of Ruan et al.,³⁸ who for laser fluences of 31 mJ cm⁻² and 75 mJ cm⁻² observed lattice expansions of 1.5% and 6%, respectively. Here, our present laser fluence of 110 mJ cm⁻², which results in a lattice expansion of 8%, demonstrates that the lattice expansion of Au NPs continues to rise linearly with excitation power above the melting threshold.

Fig. 6 Comparison of the experimental Au L₃-edge difference spectrum of hexanethiol-capped Au NPs in ethanol with FDMNES simulated spectra: (a) calculated spectra for a range of lattice expansions. (b) Calculated spectra assuming a lattice expansion of 8% together with a charge transfer for different QYs.

It is important to notice that at the high temperature reached by the Au NPs (>1500 K),³⁸ the thiol groups could undergo desorption from the surface, which is expected to occur at about 500 K.^56,57 However, in this case the ultrafast nature of the heating leads to ballistic energy transfer along the chains.⁵⁸ While this significantly increases the disorder of the thiol chains, the Au–S bonds remain intact. This is supported by the recovery of the kinetic trace shown in Fig. 3. In addition, Plech et al.³⁷ reported that molten Au NPs undergo some fragmentation, nanoseconds after photoexcitation. In this present study our transient data exhibits no evidence of this, however this is expected because we used much smaller NPs (1.8 nm vs. 100 nm diameter), which favours a faster dissipation of the excess heat. Transient picosecond bleaching, as reported by François et al.,⁵⁹ should have played a secondary role for the small NPs we used: according to that work, for NPs of comparable size (2.5 nm), the use of much higher fluences was needed to detect bleaching.

Finally, the good agreement between the experimental difference spectrum and the simulated spectrum for an 8% lattice expansion (Fig. 6a) suggests that the present difference XAS spectrum does not exhibit any electronic effects, such as charge separation, previously predicted for alkanethiolate-capped Au NPs²⁶ and for other noble metal NPs.^27,28 However, this does not exclude the occurrence of such processes, implying that our present spectra might not possess the necessary sensitivity to detect them. Fig. 6b shows the simulated difference spectra (assuming an 8% lattice expansion) combined with a difference spectrum corresponding to a charge separated configuration for different values for the quantum yields. This shows that a quantum yield of <0.1 would not exhibit significant changes on our transient spectra. This puts an upper limit on the magnitude of charge separation, which is consistent with the optical work of Aprile et al.,²⁶ who reported a quantum yield of 0.12. We note here that the quantum yield might have also been influenced by a charge transfer lifetime shorter than the temporal resolution of the experiment (80 ps).

5 Conclusions

Using picosecond X-ray absorption spectroscopy we have investigated the electronic and structural dynamics following photoexcitation of the SPR of hexanethiol-capped Au nanoparticles. At a time delay of 100 ps, the difference signal exhibits signatures of nanoparticle melting accompanied by a significant lattice expansion. Using first principles simulations, we demonstrated that this corresponds to an ∼8% expansion of the Au–Au bond length, arising from the anharmonicity of the bonding potential. In conjunction with recent electron diffraction experiments,³⁸ these results demonstrate that the lattice expansion of Au NPs continues to rise linearly with excitation power above the melting threshold.

Besides the lattice expansion, our transient spectrum exhibits no evidence of charge separation. While this has been previously postulated for Au metal NPs,²⁶ the absence of any effect on the transient X-ray signal enables us to put an upper limit of the quantum yield of charge separation as 0.1 at the time scale of the measurements.

Acknowledgements

We thank the staff (Olga Safonova and Grigory Smolentsev) of the SuperXAS beamline at the SLS, PSI, Villigen, Switzerland. This work was performed under the auspices of the FAST program (Switzerland). J. A. vB. and M. C. acknowledge funding by the Swiss NSF through the NCCR MUST ‘Molecular ultrafast science and technology’.

References

1. G. Bond, Gold Bull., 1972, 5, 11–13.
2. D. Cha and G. Parravano, J. Catal., 1970, 18, 200–211.
3. S. Galvano and G. Parravano, J. Catal., 1978, 55, 178–190.
4. G. C. Bond, P. A. Sermon, G. Webb, D. A. Buchanan and P. B. Wells, J. Chem. Soc., Chem. Commun., 1973, 444b–445b.
5. G. Bond and P. Sermon, Gold Bull., 1973, 6, 102–105.
6. G. C. Bond, C. Louis and D. T. Thompson, Catalysis by gold, Imperial College Press, 2006.
7. P. A. Brugger, P. Cuendet and M. Graetzel, J. Am. Chem. Soc., 1981, 103, 2923–2927.
8. S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921.
9. X. Zhang, Y. L. Chen, R.-S. Liu and D. P. Tsai, Rep. Prog. Phys., 2013, 76, 046401.
10. I. Ojea-Jimenez, X. Lopez, J. Arbiol and V. Puntes, ACS Nano, 2012, 6, 2253–2260.
11. H. Qian, L. A. Pretzer, J. C. Velazquez, Z. Zhao and M. S. Wong, J. Chem. Technol. Biotechnol., 2013, 88, 735–741.
12. K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Chem. Rev., 2012, 112, 2739–2779.
13. A. N. Shipway, M. Lahav and I. Willner, Adv. Mater., 2000, 12, 993–998.
14. P. K. Jain, X. Huang, I. H. El-Sayed and M. A. El-Sayed, Acc. Chem. Res., 2008, 41, 1578–1586.
15. E. C. Dreaden, A. M. Alkilany, X. Huang, C. J. Murphy and M. A. El-Sayed, Chem. Soc. Rev., 2012, 41, 2740–2779.
16. E. C. Dreaden, M. A. Mackey, X. Huang, B. Kang and M. A. El-Sayed, Chem. Soc. Rev., 2011, 40, 3391–3404.
17. K. G. Thomas and P. V. Kamat, Acc. Chem. Res., 2003, 36, 888–898.
18. G. Han, P. Ghosh and V. M. Rotello, Nanomedicine, 2007, 2, 113–123.
19. P. Ghosh, G. Han, M. De, C. K. Kim and V. M. Rotello, Adv. Drug Delivery Rev., 2008, 60, 1307–1315.
20. C. F. Bohren, Am. J. Phys., 1983, 51, 323.
21. D. B. Ingram and S. Linic, J. Am. Chem. Soc., 2011, 133, 5202–5205.
22. C. Gomes Silva, R. Juarez, T. Marino, R. Molinari and H. Garcia, J. Am. Chem. Soc., 2011, 133, 595–602.
23. A. Fujishima, Nature, 1972, 238, 37–38.
24. A. Furube, L. Du, K. Hara, R. Katoh and M. Tachiya, J. Am. Chem. Soc., 2007, 129, 14852–14853.
25. S. Mubeen, J. Lee, N. Singh, S. Krämer, G. D. Stucky and M. Moskovits, Nat. Nanotechnol., 2013, 1–5.
26. C. Aprile, M. Á. Herranz, E. Carbonell, H. Garcia and N. Martn, Dalton Trans., 2009, 134–139.
27. R. Philip, G. R. Kumar, N. Sandhyarani and T. Pradeep, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13160–13166.
28. P. V. Kamat, M. Flumiani and G. V. Hartland, J. Phys. Chem. B, 1998, 102, 3123–3128.
29. J. Cao, Y. Gao, H. E. Elsayed-Ali, R. Miller and D. A. Mantell, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 10948.
30. E. Knoesel, A. Hotzel and M. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 12812.
31. J. H. Hodak, I. Martini and G. V. Hartland, J. Phys. Chem. B, 1998, 102, 6958–6967.
32. T. V. Shahbazyan, I. E. Perakis and J.-Y. Bigot, Phys. Rev. Lett., 1998, 81, 3120–3123.
33. R. Fang, H. Wei, Z. Li and D. Zhang, Solid State Commun., 2012, 152, 108–111.
34. P. Buffat and J.-P. Borel, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 2287–2298.
35. G. Allen, R. Bayles, W. Gile and W. Jesser, Thin Solid Films, 1986, 144, 297–308.
36. M. B. Mohamed, T. S. Ahmadi, S. Link, M. Braun and M. A. El-Sayed, Chem. Phys. Lett., 2001, 343, 55–63.
37. A. Plech, V. Kotaidis, S. Grésillon, C. Dahmen and G. Von Plessen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 195423.
38. C.-Y. Ruan, Y. Murooka, R. K. Raman and R. A. Murdick, Nano Lett., 2007, 7, 1290–1296.
39. T. Penfold, C. Milne and M. Chergui, Adv. Chem. Phys., 2013, 153, 1–41.
40. S. Bordiga, E. Groppo, G. Agostini, J. A. van Bokhoven and C. Lamberti, Chem. Rev., 2013, 113, 1736–1850.
41. X. Zhang, G. Smolentsev, J. Guo, K. Attenkofer, C. Kurtz, G. Jennings, J. V. Lockard, A. B. Stickrath and L. X. Chen, J. Phys. Chem. Lett., 2011, 2, 628–632.
42. M. Rittmann-Frank, C. Milne, J. Rittmann, M. Reinhard, T. Penfold and M. Chergui, Angew. Chem., Int. Ed., 2013, 53, 5858–5862.
43. J. Huang, O. Buyukcakir, M. W. Mara, A. Coskun, N. M. Dimitrijevic, G. Barin, O. Kokhan, A. B. Stickrath, R. Ruppert, D. M. Tiede, J. F. Stoddart, J.-P. Sauvage and L. Chen, Angew. Chem., Int. Ed., 2012, 51, 12711–12715.
44. J. E. Katz, X. Zhang, K. Attenkofer, K. W. Chapman, C. Frandsen, P. Zarzycki, K. M. Rosso, R. W. Falcone, G. A. Waychunas and B. Gilbert, Science, 2012, 337, 1200–1203.
45. G. Smolentsev, A. Guda, M. Janousch, C. Frieh, G. Jud, F. Zamponi, M. Chavarot-Kerlidou, V. Artero, J. A. van Bokhoven and M. Nachtegaal, Faraday Discuss., 2014 10.1039/C4FD00035H.
46. J. Rehr, J. Kas, M. Prange, A. Sorini, Y. Takimoto and F. Vila, C. R. Phys., 2009, 10, 548.
47. J. G. Norman, Mol. Phys., 1976, 31, 1191–1198.
48. F. Kirchhoff, M. J. Mehl, N. I. Papanicolaou, D. A. Papaconstantopoulos and F. S. Khan, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 195101.
49. Y. Joly, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125120.
50. O. Bunău and Y. Joly, J. Phys.: Condens. Matter, 2009, 21, 345501.
51. A. El Nahhas, R. M. van der Veen, T. J. Penfold, V. T. Pham, F. A. Lima, R. Abela, A. M. Blanco-Rodriguez, S. Zalis, A. Vlcek, I. Tavernelli, U. Rothlisberger, C. J. Milne and M. Chergui, J. Phys. Chem. A, 2013, 117, 361–369.
52. R. van der Veen, C. Milne, A. el Nahhas, F. Lima, V. Pham, J. Best, J. Weinstein, C. Borca, R. Abela, C. Bressler and M. Chergui, Angew. Chem., 2009, 48, 2711–2714.
53. P. Zhang and T. Sham, Phys. Rev. Lett., 2003, 90, 245502.
54. C. Natoli, in EXAFS and Near Edge Structure III, ed. K. O. Hodgson, B. Hedman and J. E. Penner-Hahn, Springer Proceedings in Physics, 1984, pp. 38–42.
55. P. Zhang and T. Sham, Phys. Rev. Lett., 2003, 90, 245502.
56. R. G. Nuzzo, B. R. Zegarski and L. H. Dubois, J. Am. Chem. Soc., 1987, 109, 733–740.
57. R. G. Nuzzo, L. H. Dubois and D. L. Allara, J. Am. Chem. Soc., 1990, 112, 558–569.
58. Z. Wang, J. A. Carter, A. Lagutchev, Y. K. Koh, N.-H. Seong, D. G. Cahill and D. D. Dlott, Science, 2007, 317, 787–790.
59. L. François, M. Mostafavi, J. Belloni and J. A. Delaire, Phys. Chem. Chem. Phys., 2001, 3, 4965–4971.

---

Footnotes

† These authors contributed equally to the present work.

‡ Present address: Institut für Physik und Astronomie, University of Potsdam, Germany. E-mail: flavio.zamponi@uni-potsdam.de

§ Present address: Max-Born-Institut, Berlin, Germany.

---