A face-sharing bi-icosahedral model for Al₂₃⁻

Abstract

A face-sharing bi-icosahedral motif is proposed as a candidate structure of the magic cluster, Al₂₃⁻, on the basis of DFT calculations. The structure can be viewed as a quasi-molecule made of two Al₁₃ (D_3d) superatoms with an open electronic configuration via constructive overlap of 1F and 2P superatomic orbitals. A face-sharing tri-icosahedral motif is also predicted for Al₃₃⁻.

---

Introduction

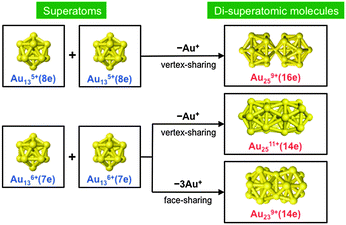
A cluster of simple metals can be viewed as a “superatom” since valence electrons confined in a jellium-like potential field are accommodated in a series of quantized orbitals. These superatomic orbitals (SAOs) are named 1S, 1P, 1D, 2S, 1F, 2P, 1G, 2D, 3S, 1H, 1I, etc., in order of energy, where S, P, D, F, G, H, and I represent the angular momenta, L = 0, 1, 2, 3, 4, 5, and 6, respectively.¹ The superatom concept has been verified experimentally and successfully used to explain the magic numbers of clusters of s-electron (ref. 1) metals, such as Na (ref. 2) and Au,^3,4 and trivalent Al.⁵ For example, the well-known magic cluster, Al₁₃⁻, can be viewed as a superatom with an icosahedral motif and a closed electronic shell with 40 valence electrons.⁵ With the prospect that superatoms will serve as the building blocks of novel nanomaterials, considerable effort has been made to develop Au superatoms protected by ligands, such as thiolates (RS) and phosphines (PR₃).^6,7 For example, Au₁₁³⁺(8e)^8,9 and Au₁₃⁵⁺(8e)^10–13 superatoms protected by ligands have been isolated. Their high stability has been explained by an extended version of the superatomic concept that takes into account electron transfer from the Au cores to the ligands.¹⁴

An interesting challenge is to construct a new class of pseudo-molecules from superatoms (superatomic molecules) by their direct connection or partial fusion.¹⁵ So far, three types of ligand-protected Au superatomic molecules with bi-icosahedral motifs have been synthesized (Chart 1). The Au₂₅⁹⁺(16e) core of [Au₂₅(SR)₅(PR′₃)₁₀Cl₂]²⁺ comprises two Au₁₃⁵⁺(8e) superatoms with the closed electronic configuration (1S)²(1P)⁶ by sharing a vertex atom.¹⁶ The Au₂₃⁹⁺(14e) core of Au₃₈(SR)₂₄ (ref. 17) and the Au₂₅¹¹⁺(14e) core of Au₂₅(SR)₁₁ (ref. 18) are constructed from two Au₁₃⁶⁺(7e) superatoms with an open electronic configuration of (1S)²(1P)⁵ by sharing a facet and vertex, respectively. Yang and Cheng developed the super valence bond (SVB) model to explain the bonding of two superatoms in Au₂₃⁹⁺(14e) and found similarities with the bonding in F₂.^19,20 The production of poly-Au₁₃ icosahedra with different bonding schemes has been theoretically proposed.^21,22

Chart 1 Examples of Au superatomic molecules.

In contrast, Al₁₃-based superatomic molecules corresponding to those in Chart 1 have not been synthesized so far, although mass spectrometry has demonstrated the formation of a variety of superatomic complexes, including Al₁₃Na,²³ Al₁₃I⁻,²⁴ Al₁₃X (X = H, Au, and alkali metals),²⁵ Al₁₃(OAl)_n,²⁶ Cs⁺B@Al₁₂⁻, and F⁻P@Al₁₂⁺.²⁷ Assemblies of endohedral Al clusters, X@Al₁₂–Y@Al₁₂ (X–Y = Si–Si, B–P, Al–P), were predicted theoretically.²⁸ The present work is focused on the structure of one of the magic clusters Al₂₃⁻, which also exhibits high stability towards O₂ like Al₁₃⁻.⁵ Previous experimental and theoretical studies have proposed that Al₂₃⁻ has an octupolar-deformed shape (structure 2 in Fig. 1)^29,30 and a closed electronic configuration. We propose using DFT calculations the possibility of a face-sharing bi-icosahedral motif for Al₂₃⁻ and the generalized bonding scheme of multiple Al₁₃ units based on the structure of Al₂₃⁻.

Fig. 1 Optimized structures of Al₂₃⁻.

Calculation procedure

The fully optimized structures, formation energies, and SAO structures of face-sharing bi-icosahedral Al₂₃⁻ and tri-icosahedral Al₃₃⁻ were obtained at the B3LYP/6-311++G** level using the Gaussian09 package.³¹ As references, we also optimized the structures of Al₂₃⁻ with deformed octupolar²⁹ and fcc-based motifs³⁰ and Al₁₃⁻ with the icosahedral (I_h) motif. Frequency analysis of the obtained structures showed no imaginary values indicating that they are local minima in energy. The SAOs were visualized by using the Gaussview program with the isovalue of 0.020, otherwise noted. The nature of SAOs of the Al₁₃⁻ (D_3d) moiety of bi-icosahedral Al₂₃⁻ (3) was studied by monitoring how the energies of the SAOs were changed during the optimization to Al₁₃⁻ (I_h).

Results and discussion

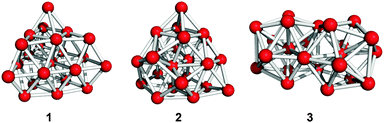
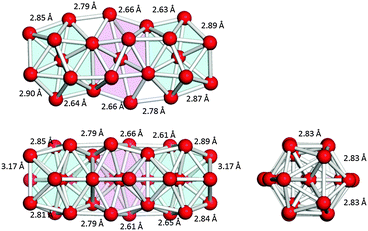
Fig. 1 shows the geometries of three optimized Al₂₃⁻ structures (1–3) in the singlet electronic state. Vibrational analysis confirmed that the geometries are local minima. The atomic coordinates of 1–3 are given in Tables S1–S3 (ESI†), respectively. Structures 1 and 2 are similar to structures reported previously.^29,30 Newly-found structure 3 retains a face-sharing bi-icosahedral motif. Fig. 2 shows the structure of 3 in the third angle projection and the optimized structure of Al₁₃⁻ (I_h). The average Al–Al bond lengths at the joint (3.44 Å) and the facets at both ends (3.17 Å) are significantly elongated compared with that (2.82 Å) of Al₁₃⁻ (I_h). The symmetry of the Al₁₃ moiety of 3 was reduced to D_3d.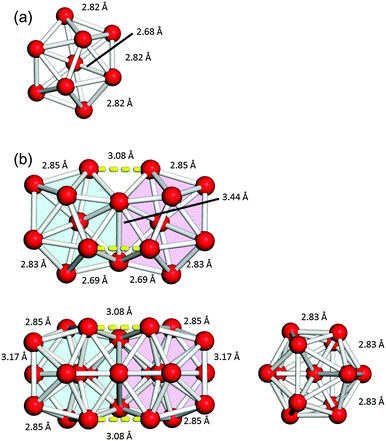

Fig. 2 The structures of (a) Al₁₃⁻ (I_h) and (b) Al₂₃⁻ (3) in the third angle projection. Three bonds between the two Al₁₃ units in 3 are shown by yellow dashed lines.

Table 1 compares the relative stability of 1–3. Structures 1 and 2 have comparable stability,²⁹ whereas structure 3 is less stable than 1 and 2 by 0.97 eV. Nevertheless, we cannot exclude the possibility that structure 3 is produced under certain experimental conditions given that structure 3 is isolated from 1 and 2 by significant energy barriers. Table 1 also lists the vertical detachment energy (VDE), which is defined as the energy difference between the neutral and anionic states at the optimized structures of the anion. The VDE values of 1–3 are comparable to the experimental value (3.57 eV).²⁹

Table 1 Relative stability, vertical detachment energy, and the HOMO–LUMO gap of Al₂₃⁻ (1–3)

Structure	1	2	3
a Experimental value: 3.57 eV (ref. 29).
ΔE (eV)	0.00	0.05	0.97
VDE (eV)^a	3.16	3.28	3.17
HOMO–LUMO gap (eV)	1.63	1.83	1.55

---

Energy diagrams of SAOs of 1–3 are shown in Fig. 3. Large HOMO–LUMO gaps for all the structures (Table 1) indicate that their high stability originates from their closed electronic shells. The electronic structures of 1 and 2 are similar and the energy diagrams of 1 and 2 indicate that they can be viewed as superatoms with nearly spherical morphologies and a closed electronic configuration of (1S)²(1P)⁶(1D)¹⁰(2S)²(1F)¹⁴(2P)⁶(1G)¹⁸(2D)¹⁰(3S)². In contrast, the electronic structure of 3 is significantly different from those of 1 and 2. The occupied SAOs of 3 are named #116–#150 in order of energy (Fig. 3) and their shapes are visualized in Fig. S1 and S2 (ESI†). In the following, we attempt to interpret the electronic structure of 3 in the framework of the SVB model¹⁹ rather than that of a deformed (elongated) superatom. According to the SVB model,¹⁹ the face-sharing bi-icosahedral Al₂₃⁻ (3) is constructed from two Al₁₃⁴⁺(35e) superatoms with an open electronic configuration,

Al₂₃⁻(70e) = 2 × Al₁₃⁴⁺(35e) − 3Al³⁺. (1)

The physical meaning of removing 3Al³⁺ nuclei is the reduction of the electron confinement volume. To gain an insight into the bonding scheme between two Al₁₃⁴⁺ superatoms in Al₂₃⁻ (3), we consider how the SAOs of 3 are constructed from those of Al₁₃⁴⁺ by comparing their shapes. In the following, Al₁₃⁻ with the same geometry (D_3d) as Al₂₃⁻ (3) was considered as the building unit, instead of Al₁₃⁴⁺. The nature of the SAOs of Al₁₃⁻ (D_3d) was characterized by correlation with those of Al₁₃⁻ (I_h) (Fig. S3, ESI†), which was established by following the evolution of the SAOs over the course of structural optimization from Al₁₃⁻ (D_3d) to Al₁₃⁻ (I_h) (Fig. S4–S6, ESI†).

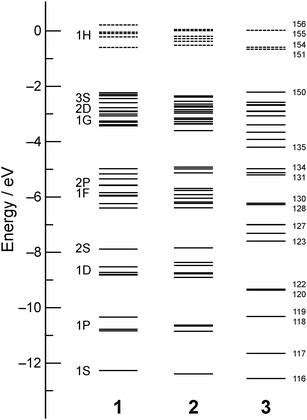Fig. 3 Energy diagram of SAOs of 1–3. The solid and dotted lines represent occupied and unoccupied orbitals, respectively.

The correlation between the SAOs of 3 (#116–#150) and those of Al₁₃⁻ (D_3d) is summarized in Table 2. The construction of the low-lying SAOs (Fig. S1, ESI†) is straightforward. For example, SAOs #116 and #117 are assigned to bonding and anti-bonding orbitals, respectively, constructed by interactions of SAO #66 of Al₁₃⁻ with 1S nature (Table 2 and Fig. S3, ESI†). SAOs #118–#134 and #143 are constructed from the SAO of Al₁₃⁻ with 1P, 1D, and 2S nature. The high-lying SAOs #135–#150 except #143 (Fig. S2, ESI†) are made from the SAOs of Al₁₃⁻ with 1F and 2P nature (Table 2 and Fig. S3, ESI†). In 3, SAOs #142, #145, and #146 with bonding nature are occupied whereas their anti-bonding counterparts #151, #155, and #156 are unoccupied (Table 2). The occupation of SAOs #142, #145, and #146 is responsible for the bonding interaction between the two Al₁₃ superatoms. SAOs #142, #145, and #146 are constructed from the SAO of Al₁₃⁻ with 2P, 1F, and 1F nature, respectively, as shown in Fig. 4. The bond order (BO) for Al₂₃⁻ (3) is estimated to be 3 according to the definition in conventional VB theory. Note that the BO value for Al₂₃⁻ (3) is larger than that (BO = 1) of Au₂₃⁹⁺ (Chart 1).

Table 2 Correlation of SAOs of Al₂₃⁻ (3) and SAO of Al₁₃⁻ (D_3d)

SAO of Al23^− (3)^a		SAO of Al13^− (D3d)^c
Bonding	Anti-bonding
a The SAOs in brackets are unoccupied orbitals. The notations in parentheses (1Σ, 2Σ, …) indicate orbital symmetries numbered in the order of energy in the same symmetry. b LUMO of Al23^− (3). c The orbital symmetries shown in parentheses are those of the corresponding SAOs of Al13^− (Ih) (Fig. S3, ESI).
116 (1Σ)	117 (2Σ)	66 (1S)
118, 119 (1Π)	121, 122 (2Π)	67, 68 (1Px,y)
120 (3Σ)	123 (4Σ)	69 (1Pz)
124, 125 (1Δ)	128, 129 (2Δ)	70, 71 (1D)
126, 127 (3Π)	132, 133 (4Π)	72, 73 (1D)
130 (5Σ)	131 (6Σ)	74 (2S)
134 (7Σ)	143 (9Σ)	75 (1Dz)
136, 137 (3Δ)	149, 150 (4Δ)	76, 77 (1F)
135 (1Φ)	141 (3Φ)	78 (1F)
138 (2Φ)	144 (4Φ)	79 (1F)
139, 140 (5Π)	147, 148 (7Π)	80, 81 (2Px,y)
145, 146 (6Π)	[155, 156] (8Π)	82, 83 (1F)
142 (8Σ)	[151]^b (10Σ)	84 (2Pz)

---

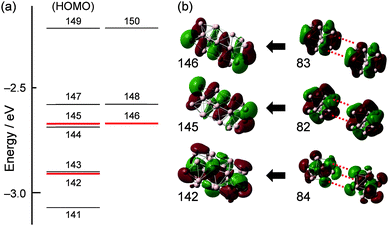Fig. 4 (a) Energy diagram of SAOs of Al₂₃⁻ (3). (b) Schematic representation of the bonding interaction between two SAOs of Al₁₃⁻ (D_3d).

We can rewrite eqn (1) as follows by considering Al₁₃⁻(40e) as a superatomic unit,

Al₂₃⁻(70e) = [2 × Al₁₃⁻(40e) − 3Al³⁺] − 10e = Al₂₃¹¹⁻(80e) − 10e. (2)

This indicates that two Al₁₃⁻(40e) superatoms are bonded by sharing 10 electrons for each superatomic bond. Counterintuitively, the BO of Al₂₃⁻ (3) is not 5, but 3. This suggests that 8 and 2 electrons are removed from anti-bonding and bonding orbitals of a putative Al₂₃¹¹⁻(80e), respectively. By extending this idea, we can predict a series of sizes for the linear polymers of Al₁₃(40e) which are connected by sharing the facet as follows,

Al₃₃⁻(100e) = 3 × Al₁₃⁻(40e) − 2 × 3Al³⁺ − 2 × 10e (3)

Al₄₃⁻(130e) = 4 × Al₁₃⁻(40e) − 3 × 3Al³⁺ − 3 × 10e (4)

Interestingly, it was reported that Al₃₃⁻ is stable against etching by O₂.³² The stability of Al₃₃⁻(100e) cannot be explained by the number of effective valence electrons since superatomic shell closure under spherical potential is accomplished at n* = 92 and 106. Thus, formation of a linear trimer is a possible explanation for the chemical stability of Al₃₃⁻. To test this hypothesis, we conducted structural optimization of Al₃₃⁻ with a tri-icosahedral motif. We obtained a local minimum structure as shown in Fig. 5. The atomic coordinates of the optimized Al₃₃⁻ are given in Table S4 (ESI†).

Fig. 5 Optimized structure of tri-icosahedral Al₃₃⁻ in the third angle projection.

Conclusions

DFT calculations allowed us to propose face-sharing bi- and tri-icosahedral motifs as possible structures of the magic clusters, Al₂₃⁻ and Al₃₃⁻. Constructive overlap of 1F and 2P superatomic orbitals of deformed Al₁₃ (D_3d) units is responsible for the bonding of two Al₁₃ superatoms. Fabrication of these unique Al clusters is a future challenge required to establish this building-up principle and to develop new functional materials with a ubiquitous element.

Acknowledgements

This research was financially supported by the Funding Program for Next Generation World-Leading Researchers (NEXT Program) (GR-003), the “Elements Strategy Initiative for Catalysts & Batteries (ESICB),” supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. We thank Dr Hironori Tsunoyama (Keio Univ.) and Ms Tomomi Watanabe (The Univ. of Tokyo) for their contribution at the initial stage of this research.

Notes and references

1. W. A. de Heer, Rev. Mod. Phys., 1993, 65, 611.
2. W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141.
3. K. J. Taylor, C. L. Pettiette-Hall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319.
4. L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038.
5. R. E. Leuchtner, A. C. Harms and A. W. Castleman, Jr., J. Chem. Phys., 1989, 91, 2753.
6. R. Jin, Nanoscale, 2010, 2, 343.
7. P. Maity, S. Xie, M. Yamauchi and T. Tsukuda, Nanoscale, 2012, 4, 4027.
8. Y. Yanagimoto, Y. Negishi, H. Fujihara and T. Tsukuda, J. Phys. Chem. B, 2006, 110, 11611.
9. B. S. Gutrath, U. Englert, Y. Wang and U. Simon, Eur. J. Inorg. Chem., 2013, 2002.
10. C. E. Briant, B. R. C. Theobald, J. W. White, L. K. Bell, D. M. P. Mingos and A. J. Welch, J. Chem. Soc., Chem. Commun., 1981, 201.
11. M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754.
12. M. C. Zhu, M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883.
13. Y. Shichibu and K. Konishi, Small, 2010, 6, 1216.
14. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157.
15. J. Nishigaki, K. Koyasu and T. Tsukuda, Chem. Rec. DOI:10.1002/tcr.201402011 , in press.
16. Y. Shichibu, Y. Negishi, T. Watanabe, N. K. Chaki, H. Kawaguchi and T. Tsukuda, J. Phys. Chem. C, 2007, 111, 7845.
17. H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132, 8280.
18. J. Nishigaki, S. Yamazoe, S. Kohara, A. Fujiwara, W. Kurashige, Y. Negishi and T. Tsukuda, Chem. Commun., 2014, 50, 839.
19. L. Cheng, C. Ren, J. Zhang and X. Yang, Nanoscale, 2013, 5, 1475.
20. Y. Yuan, L. Cheng and J. Yang, J. Phys. Chem. C, 2013, 117, 13276.
21. K. Nobusada and T. Iwasa, J. Phys. Chem. C, 2007, 111, 14279.
22. D. Jiang, K. Nobusada, W. Luo and R. L. Whetten, ACS Nano, 2009, 3, 2351.
23. A. Nakajima, K. Hoshino, T. Naganuma, Y. Sone and K. Kaya, J. Chem. Phys., 1991, 95, 7061.
24. D. E. Bergeron, P. J. Roach, A. W. Castleman, Jr., N. O. Jones and S. N. Khanna, Science, 2005, 307, 231.
25. Y. J. Ko, A. Shakya, H. Wang, A. Grubisic, W. Zheng, M. Götz, G. Ganteför, K. H. Bowen, P. Jena and B. Kiran, J. Chem. Phys., 2010, 133, 124308.
26. T. Watanabe and T. Tsukuda, J. Phys. Chem. C, 2013, 117, 6664.
27. M. Akutsu, K. Koyasu, J. Atobe, N. Hosoya, K. Miyajima, M. Mitsui and A. Nakajima, J. Phys. Chem. A, 2006, 110, 12073.
28. T. Iwasa and A. Nakajima, J. Phys. Chem. C, 2013, 117, 21551.
29. J. Akola, M. Manninen, H. Häkkinen, U. Landman, X. Li and L.-S. Wang, Phys. Rev. B, 2000, 62, 13216.
30. A. Aguado and J. M. López, J. Chem. Phys., 2009, 130, 064704.
31. M. J. Frisch, et al., Gaussian 09, Revision C.01, (see ESI† for full citation).
32. R. L. Hettich, J. Am. Chem. Soc., 1989, 111, 8582.

---

Footnote

† Electronic supplementary information (ESI) available: Full citation of ref. 31, full list of atomic coordinates and orbital energy levels with SAOs of the three isomers of Al₂₃⁻ and Al₃₃⁻, and the energy diagram with SAOs of distorted Al₁₃⁻. See DOI: 10.1039/c4cp03199g

---