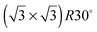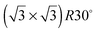The role of lattice parameter in water adsorption and wetting of a solid surface

Abstract

Ice formation is a complex cooperative process that is almost invariably catalysed by the presence of an interface on which ice crystals nucleate. As yet there is no clear picture of what factors make a surface particularly good at nucleating ice, but the importance of having a template with a suitable lattice parameter has often been proposed. Here we report the contrasting wetting behaviour of a series of pseudomorphic surfaces, designed to form an ordered template that matches the arrangement of water in a bulk ice Ih(0001) bilayer. The close-packed M(111) surfaces (M = Pt, Pd, Rh, Cu and Ni) form a 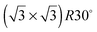Sn substitutional alloy surface, with Sn atoms occupying sites that match the symmetry of an ice bilayer. The lattice constant of the alloy changes from 4% smaller to 7% greater than the lateral spacing of ice across the series. We show that only the PtSn surface, with a lattice parameter some 7% greater than that of a bulk ice layer, forms a stable water layer, all the other surfaces being non-wetting and instead forming multilayer ice clusters. This observation is consistent with the idea that the repeat spacing of the surface should ideally match the O–O spacing in ice, rather than the bulk ice lattice parameter, in order to form a continuous commensurate water monolayer. We discuss the role of the lattice parameter in stabilising the first layer of water and the factors that lead to formation of a simple commensurate structure rather than an incommensurate or large unit cell water network. We argue that lattice match is not a good criteria for a material to give low energy nucleation sites for bulk ice, and that considerations such as binding energy and mobility of the surface layer are more relevant.

---

Introduction

Ice nucleation is a complex process whose mechanism, including the size and structure of the critical nuclei, remains uncertain.¹ Ice crystallisation is unusual in that freezing is associated with a large decrease in density, and requires considerable co-operative rearrangement of the water, resulting in a large critical nucleus size for homogeneous nucleation. As a result, pure water can be supercooled well below its freezing point¹ and, in most environments, ice formation is instead initiated by the presence of a suitable solid surface on which ice can nucleate. The differing ability of surfaces to inhibit or encourage nucleation is exploited in many different biological environments, for example to encourage ice formation and promote rainout of airborne bacteria,² or to hinder freezing and ice damage on plants or animals.³ Formation of ice particles in the atmosphere relies strongly on heterogeneous nucleation of ice on dust particles^4,5 and plays a role in determining the atmosphere's albedo.⁶ The nucleation mechanism depends on the humidity and thermal history of the sample, with deposition nucleation occurring just above water saturation, homogeneous nucleation below about 235 K and immersion or contact freezing occurring at higher saturation.⁴ The nature of the dust particles also influences the degree of supercooling that occurs before clouds precipitate, with particular materials being more susceptible to ice nucleation than others and so influencing the conditions under which ice clouds form.⁷

Although there have been numerous theoretical simulations of ice nucleation at surfaces, there is so far no simple picture of what makes a surface particularly good at initiating ice formation. One concept that has repeatedly been invoked is that the surface should have a lattice parameter that matches that of bulk ice, providing a template on which the ice film can grow. It was this idea that originally led to the use of AgI as an agent to seed rain clouds,⁸ while other features, such as steps, kinks and pores have also been invoked as active nucleation sites.⁴ The idea that a suitable commensurate template would stabilise an ice layer was also used to explain how water adsorbs on metal surfaces.⁹ Early observations suggested that water formed a 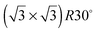structure on a series of close packed transition metal surfaces and, since this unit cell matches closely that of bulk ice, it was assumed that adsorbed water adopted a commensurate bulk ice structure, compensating any difference in lattice parameter by minor changes in the buckling of the ‘ice-like’ water bilayer.¹⁰ More recent experiments have shown that this is not the case,¹¹ with water adopting much more complex structures on transition metal surfaces, usually with large unit cells^12–14 containing a mixture of 5, 6 and 7 member rings.^15–18 Since the first layer of water adopts a structure that is quite unlike a bulk ice layer, formation of a continuous multilayer film is inhibited by the need to reconstruct the first layer to hydrogen bond to the multilayer ice.^14,19–23 There is therefore little experimental evidence that directly addresses the role that lattice parameter itself plays in mediating water adsorption, despite a number of theoretical papers addressing this question.^24–26

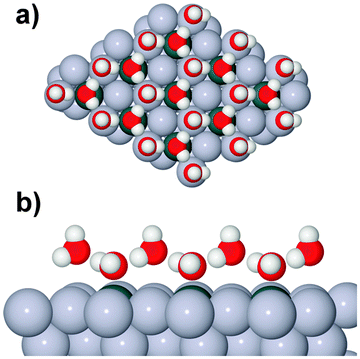
One difficulty in examining the role of lattice parameter experimentally is that changing the substrate also introduces changes in the electronic structure of the solid. Recently we reported the adsorption of an ordered water layer on a SnPt alloy template,²⁷ chosen to match the adsorption geometry required to form a simple water ice bilayer, Fig. 1. This study showed that water forms a well defined wetting layer on the 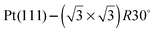Sn alloy surface, with a hexagonal network of hydrogen bonded water bonded atop the Sn atoms in a simple, commensurate arrangement. The water structure shows long range order in both the lateral O location and in the height of O above the surface, implying a simple proton ordered ice film with just two distinct water environments – something that appears to be unique compared to water adsorption on other plane metal surfaces.^11,28 A structural analysis shows that water is adsorbed in a flattened layer, with half the water bonded directly to the Sn atoms via the O atom, while the other half completes the H-bonding network. This structure has the same symmetry as an ice bilayer but instead of the non-hydrogen bonded H atoms pointing ‘up’ away from the surface, as they would if water adopted the tetrahedral geometry expected for the classic ice bilayer shown in Fig. 1, they are instead oriented pointing ‘down’, towards the metal. This H-down arrangement places the H atoms close to the metal surface, allowing the metal to screen the OH dipole effectively. Changing the symmetry of the Sn template to a (2 × 2) arrangement completely disrupts the water layer, with water instead forming a complex structure with a large unit cell.²⁷

Fig. 1 Schematic showing Sn atoms (dark grey) substituted into a close packed M(111) surface in a surface alloy. An idealised, hexagonal ‘ice-like’ bilayer is illustrated on the surface, adsorbed with the O atoms bonded to Sn and the un-coordinated H atoms pointing ‘up’, away from the surface, into the vacuum.

In this paper we compare the behaviour of water adsorbed on a series of 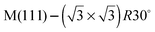Sn substitutional alloy surfaces, where M = Pt, Pd, Rh, Cu and Ni. The lattice parameter of these alloy surfaces varies from 2.49 Å for Ni(111) up to 2.78 for Pt(111), spanning the lateral spacing of the O atoms in an ice Ih(0001) layer (2.61 Å). Water adsorption is carried out at temperatures below 150 K, corresponding to low temperature deposition nucleation of ice. We find that water does not wet any of these surfaces except that with the largest lattice spacing, PtSn(111), supporting the idea that the ideal template for water adsorption should match the O–O spacing of bulk ice and not the ice lattice parameter, and is in agreement with recent molecular dynamics simulations.^25,26 Based on calculations comparing water adsorption on the SnM alloy series, we examine the role of lattice parameter and corrugation in stabilising the first layer of water and discuss to what extent we would expect the lattice parameter to influence the formation of 3D bulk ice clusters over other considerations.

Experimental

Experiments were conducted in an ultra high vacuum (UHV) chamber with base pressure ≤3 × 10⁻¹¹ mBar. The fcc (111) surfaces (Pt, Pd, Rh, Cu and Ni, Surface Preparation Lab.) were polished to within ±0.25° of the (111) face and attached via short Ta heating wires to Ta posts cooled by a liquid nitrogen dewar type manipulator. This arrangement gave a temperature range of 90 to 1200 K, measured with a K type thermocouple, and allowed sample heating rates up to 20 K s⁻¹ with minimal degassing of anything except the sample. The surfaces were cleaned by cycles of Ar⁺ ion sputtering and annealing, with oxygen treatment to remove carbon. Tin forms a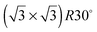 substitutional surface alloy, hereafter referred to as the 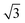alloy, on all five surfaces. The 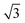alloy was prepared by dosing slightly in excess of 0.33 ML Sn (where 1 ML or monolayer is defined as one adsorbate per surface atom) and annealing to 750 K to order the surface alloy and desorb any excess Sn. Surface quality was determined by low energy electron diffraction (LEED), by water temperature programmed desorption (TPD) using a quadrupole mass spectrometer, or in some cases by in situ He atom scattering to confirm the alloy ordering. Water layers were dosed via a collimated molecular beam and the relative coverage calculated by integrating the water TPD signal, with one layer being defined as the coverage just prior to the appearance of a multilayer desorption peak. Formation of a stable water film was investigated by TPD and using low current LEED (<1 nA), with a dual-MCP amplifier to minimise electron dose and prevent damage.²⁷ In addition to the 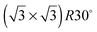Sn substitutional surface alloys discussed here, several other ordered alloys were observed and their wetting behaviour is described elsewhere.²⁹

Results and discussion

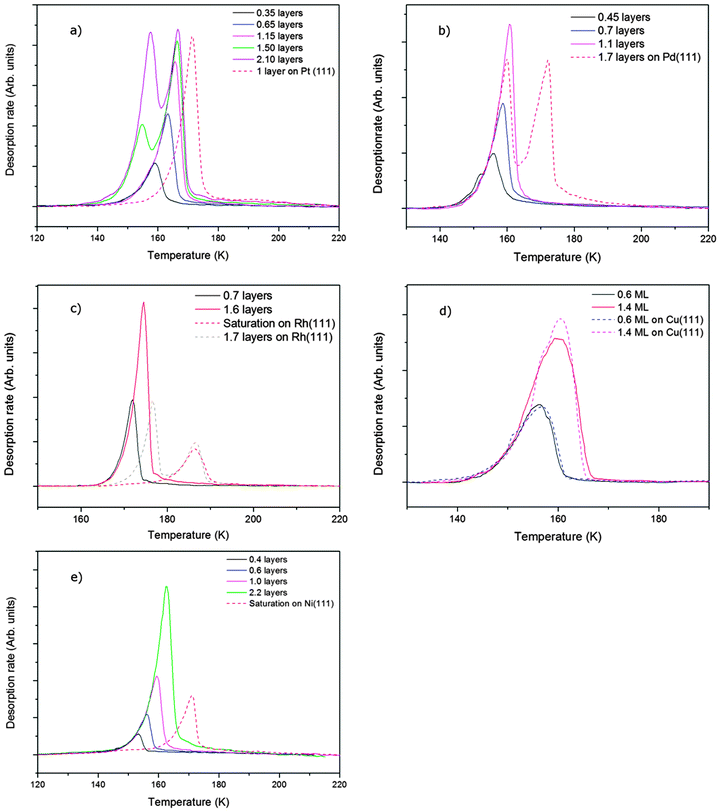
Water adsorption on solid surfaces is stabilised by a combination of direct water–surface bonding and hydrogen bonding to other water molecules. When the adsorption temperature is below 120 K an amorphous ice film is formed on metal surfaces^30,31 but above ca. 135 K water is sufficiently mobile that it either forms a continuous H-bonded layer or, if the surface is non-wetting, nucleates multilayer ice clusters.²⁸ The growth of a 2D film can be distinguished from that of ice clusters by measuring the desorption rate. Water that is bound to the surface as part of a 2D wetting film is stabilised compared to water in a 3D ice cluster and desorbs from the surface at a higher temperature than from the clusters. Fig. 2 shows the temperature programmed desorption behaviour of water from five different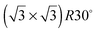 Sn alloy surfaces (solid lines) and from the parent metal surface (dashed lines). Of the pure metal surfaces, only Cu(111) is non-wetting,³² forming multilayer clusters that desorb above 140 K, forming a TPD peak near 160 K (Fig. 2e). All the other pure metal surfaces show a water desorption peak at 170 K or above, followed by the appearance of a second multilayer peak at lower temperature as the water coverage is increased and multilayers form. LEED and helium atom scattering also provide evidence for the formation of extended 2D water films on Ni(111),¹⁴ Rh(111)^33,34 and Pt(111)^12,13,19,35 surfaces. In each case the simple metal LEED pattern is replaced by a complex diffraction pattern indicating formation of a 2D water network with a large unit cell. On Cu(111) the metal LEED pattern disappears only slowly as water clusters grow, eventually disappearing after many 10's of water layers have been adsorbed (depending on the exact temperature used for growth) as the clusters eventually cover the entire surface.

Fig. 2 Temperature programmed desorption of water from (a) SnPt(111), (b) SnPd(111), (c) SnRh(111), (d) SnCu(111), (e) SnNi(111). The coverage of water given in the figure legends are with respect to saturation on the relevant clean metal surface, (except Cu, where the number is with respect to an ideal commensurate structure). The dashed lines show the desorption behaviour of water from the pure metal surface in the absence of the Sn. Water was dosed at ca. 120 K and the heating rates used were 0.8 K s⁻¹ for SnPt, 0.65 K s⁻¹ for SnRh and SnPd, 0.5 K s⁻¹ for SnCu and 0.7 K s⁻¹ for SnNi.

Alloying of the parent metal surfaces to form the 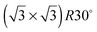SnM(111) structure causes the water TPD behaviour to change, as shown by the corresponding solid lines in Fig. 2. On 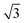SnPt(111) water forms a well defined first layer desorption peak near 165 K (solid lines, Fig. 2a), just 5 K below the corresponding clean surface Pt(111) desorption peak, while adsorption of further water results in the appearance of a multilayer peak near 150 K. Helium atom scattering and LEED show this first water layer consists of a commensurate proton ordered 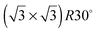water network²⁷ which completely covers the surface. The behaviour of all the other 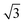SnM alloy surfaces studied here is different from SnPt. On CuSn(111) (Fig. 2d) the water desorption peak occurs at the same temperature as that of the 3D ice clusters formed on the non-wetting Cu(111) surface, while on PdSn(111), RhSn(111) and NiSn(111) (Fig. 2b, c and e respectively) the water desorbs at a temperature similar to that of multilayer ice, with no evidence for formation of a stable 2D wetting layer. LEED patterns observed after water adsorption on these surfaces show only integer order metal beams, which slowly become weaker as the water coverage is increased. Complete disappearance of the substrate spots only occurs for water layers with an average thickness of several tens of layers, confirming formation of 3D water clusters rather than a uniform film. This behaviour is similar to that seen for water adsorption on other non-wetting structures.^21–23,36 We conclude that, under conditions where water is sufficiently mobile that it can form ordered water films on other metal surfaces, the Pd, Rh, Cu and Ni–Sn alloys do not wet and instead form 3D water clusters on the bare surface, with only the SnPt(111) surface forming a stable, commensurate 2D water layer.

Table 1 shows the range of lattice spacing of the alloy surfaces investigated here, along with the buckling of Sn out from the surface metal layer. As the lateral spacing of the host metal is reduced along the sequence Pt to Ni, the mismatch between the lateral repeat of the Sn template and that of bulk ice changes from 7% greater than bulk ice Ih(0001) for the Pt alloy to 4% less for the Ni alloy respectively. Formation of a continuous commensurate ice layer would require a corresponding expansion of the lateral separation of water in an ice layer on Pt, Pd and Rh, but a compression on the Cu and Ni alloys. Although it has often been proposed that templates that have a close match to the lattice spacing of bulk ice will preferentially wet, instead we find that the SnM alloy surfaces that have lattice parameters close to that of ice are non-wetting – only the surface with the largest Sn spacing studied, SnPt (which has a lateral spacing 7% greater than that of ice Ih(0001)), forms a stable, hexagonal 2D water network. The hydrogen bonded structure formed on this surface has O almost coplanar,²⁷ with the uncoordinated H atoms pointing down towards the surface instead of into the vacuum and an O–O separation just 2% greater than found in bulk ice (2.72 Å at 100 K), matching the template periodicity exactly. This result does not support the idea that an ideal ice template should match the lateral lattice parameter of bulk ice; instead it suggests that water preferentially forms a stable 2D layer when the template matches the O–O separation, not the lateral spacing of bulk ice. Molecular dynamics simulations of water films have also found a preference for ordered hexagonal water networks to form when the spacing of the surface matches the O–O hydrogen bonding separation for water, rather than the smaller lateral spacing of a 3D crystalline ice structure. Cox et al.²⁵ showed that a good match between the substrate and the nearest neighbour oxygen–oxygen distance is a better descriptor for the structures formed than a good match to the bulk ice lattice constant, while Zhu et al.²⁶ found that changing the lattice constant of a hydrophilic surface introduced a change in the wetting, with a contact-angle minimum when the lattice constant matches the oxygen–oxygen distance of bulk water.

Table 1 Lateral spacing, compression/expansion compared to ice and Sn vertical buckling for the bare alloy surfaces

surface	Sn/M buckling (Å)	a 0 host metal (Å)	Expansion vs. a0 ice (%)	Expansion vs. d(O–O) ice (%)
a Ref. 37 and 38. b No experimental data published; unpublished results indicate the SnPd buckling is reduced compared to the other alloys.^39 c Ref. 40. d Ref. 38. e Ref. 41. f Ref. 38 and 42.
Sn/Pt(111)	0.22^a	2.78	7.0	2.0
Sn/Pd(111)	—^b	2.75	6.1	1.1
Sn/Rh(111)	0.29 ± 0.05^c	2.69	3.7	−1.1
Sn/Cu(111)	0.39^d	2.56	−1.5	−6.0
Sn/Ni(111)	0.45 ± 0.03,^e 0.46^f	2.49	−3.9	−8.4

---

In order to investigate the role that lattice spacing plays in more detail, we performed density functional theory calculations (DFT) to optimise the geometry of a 2D water film adsorbed on the different templates. Fig. 3 shows how the predicted geometry of a commensurate 0.67 ML water film changes as we cross the alloy series; the corresponding binding energies are given in Table 2. Calculations were done in a 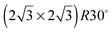unit cell, using various different starting configurations for the uncoordinated H atoms to allow the water film the flexibility to distort from a flat structure when this becomes favourable. In the case of the stable water layer formed on SnPt, the DFT calculations match closely with the structure of the water layer found from experiment.²⁷ Water forms a flattened layer, with one water bound flat atop Sn, with d_Sn–O = 2.68 Å, and the other almost coplanar, tilted so that one H points down towards the metal surface. The DFT calculations reproduce closely the structure obtained experimentally by LEED IV^27,43 and give a calculated binding energy of 0.600 eV, very similar to the energy calculated for water in bulk ice.^44–46 Although this structure has the same symmetry as an ice bilayer, it has a much lower O corrugation (0.44 ± 0.09 Å, cf. 1 Å for an ice bilayer) having lost the tetrahedral arrangement found in bulk ice (Fig. 1) to allow the uncoordinated H atoms to point towards the surface. This flat, H-down structure optimises bonding to the surface by allowing water to sit flat in its favoured adsorption site above Sn, with the uncoordinated H atom close to the surface (d_H–Pt = 2.61 Å) such that the metal electrons screen the OH dipole effectively.

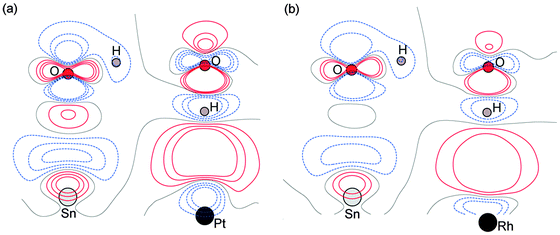
Fig. 3 Calculated minimum energy structures for a 0.67 ML water layer on the SnM surfaces (left to right, top row Pt, Pd, Rh, bottom row Cu and Ni). The calculations find that Pt, Pd and Rh favour a simple H-down structure, similar to that found to be stable on SnPt surface,²⁷ whereas a more complex, buckled structure with some water displaced away from the surface is formed on the Cu and Ni alloy templates. The host atoms are depicted in pale grey, with Sn in dark grey, O atoms in red and H in white.

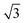Table 2 Calculated binding energies, E_ad (eV per H₂O) for continuous 2D water layers on SnM alloys. All models were calculated using a 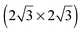unit cell and 0.67 ML coverage

Surface	E ads (eV)	O–Sn (Å)	〈dO–O〉 (Å)
Sn/Pt(111)	0.600	2.68	2.78
Sn/Pd(111)	0.522	3.14	2.75
Sn/Rh(111)	0.565	2.78	2.69
Sn/Cu(111)	0.535	2.82–4.52	2.71
Sn/Ni(111)	0.547	2.55–4.64	2.66

---

Calculations for the SnPd and SnRh alloys, Fig. 3, which have a lateral Sn spacing within ±1% of the expected O–O hydrogen bonding separation in ice, predict a 2D water layer would adopt a very similar minimum energy structure to that found on SnPt, with the O–O separation matching the Sn spacing on both surfaces. Fig. 4 compares the change in electron density as the water layer is brought into contact with the SnPt and SnRh templates respectively. Whereas there is a clear increase in electron density between O and Sn on the SnPt surface, indicative of a bonding interaction, the corresponding SnRh surface shows only a small increase in electron density. On both surfaces there is a substantial reduction in electron density on the H atom that points towards the metal, accompanied by an increase in electron density between H and the metal as the metal electrons screen the OH dipole. This increase in OH polarisation when in contact with the metal is analogous to the increase in OH dipole seen in liquid or gas phase water clusters as the number of hydrogen bonds is increased, indicating that the water which points down to the surface forms an ‘agostic’ bond.⁴⁷ The reduced interaction between water and the SnRh (or SnPd) surfaces is reflected in an increased Sn–O separation (2.78 Å for SnRh, cf. 2.68 Å for SnPt) and a reduced binding energy (0.565 eV per water, cf. 0.600 eV per water for SnPt, Table 2). Despite having a lattice spacing only slightly less than the O–O spacing in ice, and a very similar Sn corrugation and calculated water geometry for a 2D layer, the water–metal interaction on SnRh is sufficiently weak that the 2D water layer is unstable with respect to 3D ice cluster formation and so the surface does not wet.

Fig. 4 Calculated electron density difference plots showing the changes induced by adsorption of a 2D water layer on (a) SnPt(111) and (b) SnRh(111). Red contours indicate an increase in electron density and blue a decrease.

The behaviour of water on the SnCu and SnNi templates, where the lattice spacing is significantly smaller than the O–O spacing of bulk ice, is qualitatively different, as shown in Fig. 3. Calculations predict that water cannot form a flat 2D water layer, instead the structure buckles, displacing some of the flat lying water away from the Sn and reducing the number of Sn–O bonds. Again, these structures maintain all the uncoordinated H atoms pointing down towards the metal surface, even at the expense of losing metal–O bonding. It is not favourable to buckle the water structure to bind water in a second layer with OH pointing away from the surface, as it would in a tetrahedral bulk ice structure, Fig. 1, or to compress the O–O spacing in order to maintain the flat H-down structure observed for SnPt. The resulting 2D water layers are disordered, with an average O–O separation that is larger than the lateral spacing of the template (Table 2) and similar to the spacing of the O atoms in bulk ice. The calculated 2D water networks are less stable than bulk ice, so these surfaces would again be expected to form 3D ice clusters in preference to a wetting layer, as is found experimentally.

Calculations for commensurate water structures on non-alloyed metal surfaces also find that a flattened, H-down bilayer (Fig. 3, top) is more stable than the icelike bilayer shown in Fig. 1,^46,48–50 but, without a regular alternation in the nature of the adsorption sites created by the 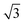alloy, other hexagonal water networks are yet more stable, including networks based on flat chains or rings of flat water linked by H-down waters.^51,52 On Ru(0001), where the first water layer has no free OH groups available to bond second layer water and is relatively tightly bound,⁵³ water multilayers form clusters that do not wet the surface, suggesting the first layer is unable to restructure to bind to an ice film and stabilize the solid-ice interface.²² Similarly, the OH–water network formed on Pt(111) has no free OH groups and does not relax to stabilize a multilayer ice film.²³ On Pt(111) and Pd(111) water forms complex networks containing water hexamers bound flat atop the metal atoms, linked into an extended network by 5, 6 and 7 membered water rings containing H-down water.¹⁶ The H-down water molecules are free to adopt an incommensurate adsorption site, allowing the structure to optimize the overall hydrogen bonding network to form a unit cell with a suitable period to match the metal lattice parameter. Just as for the simple 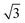water structure formed on SnPt(111), these large unit cell structures are quite different from the structure of an ice bilayer and are therefore not optimized to bond to multilayer water. Water multilayers grown on Pt(111) and Ni(111) form islands that are preferentially aligned to the close packed metal directions,^14,21,35 not the water monolayer, with a repeat that is incommensurate with the solid surface. This implies that the first layer must reconstruct as the multilayer forms, adopting a particular alignment to the close packed metal surface in order to stabilize the interface between the solid surface and the ice lattice.^16,20,36,54 Although the structure of this interfacial water is not known, we can assume the structure rearranges to form hydrogen bonds to the ice network while optimizing the metal–water bonding by its choice of local arrangement and metal binding sites. Thürmer et al.^20,55 have followed the ice growth process in detail on Pt(111) by STM and discuss how the bulk ice cluster thickness depends on the relative free energy of the metal wetting layer, the metal-ice and ice-vacuum interfaces. Unlike Pt(111), the first layer of water adsorbed on Ni(111) is relatively disordered and labile, being completely covered by a second layer of water before the multilayer forms,¹⁴ indicating some difference in the surface free energies and growth behavior compared to Pt(111).

For a strongly corrugated adsorption template, such as the alloy surfaces discussed here, the template can be chosen to match the lateral O–O spacing, e.g. on SnPt(111), promoting formation of a flat first water layer only at the expense of forming a structure that cannot then easily reconstruct to bind to an incommensurate multilayer ice film, which has a smaller lateral period. Alternatively, if the template is chosen to match the bulk ice spacing, formation of the first water layer is inhibited by the inability to form a flat structure binding to multiple Sn adsorption sites, making it more difficult to nucleate a multilayer. For this reason, choosing a material as a potential ice seed on the basis of its lattice parameter is simplistic, even when a deposition mechanism for ice nucleation is appropriate. The original choice of AgI as a nucleation agent was in retrospect fortuitous; pristine AgI is actually a rather poor nucleation agent and only when the surface is disordered by photolysis or other atmospheric processing does it become effective.⁵⁶ Rather than a corrugated template, such as SnPt, which is inflexible and can't accommodate the different lateral spacing needed by the first water layer and by a 3D ice film, an ideal surface for ice nucleation should have a binding energy for water that is sufficient to wet but still form a water layer that is able to relax easily, with minimal free energy cost, to match the solid surface to the bulk 3D ice structure. This implies that such a surface will be relatively un-structured, able to accommodate different lateral water spacings and not pin the first layer water into any rigid framework. On that basis plane metal surfaces, which have relatively little variation in water binding energy with site and are able to relax the geometrical arrangement and proton ordering of the first layer with minimal energy cost, should be better surfaces for ice nucleation than a corrugated structure such as SnPt. Although these results are most directly relevant to deposition nucleation on (ideal) surfaces, the structure of the first layer is also expected to be important in determining the behavior of thicker water films,^25,26 and therefore similar considerations can be expected to play a role during ice nucleation via condensation nucleation, although the size of the critical nucleus makes experimental study difficult.

On the SnPt(111) surface, further water adsorption forms an ordered film with a 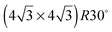diffraction pattern, Fig. 5. This structure persists from 2 to ca. 30 layers of water, slowly reverting to a diffuse 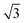pattern, suggesting the eventual formation of an incommensurate ice film. The structure of this 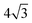multilayer is unknown, but since the film initially retains the period of the underlying lattice, rather than adopting the lattice parameter of a bulk ice film, it is expected to be quite unlike a bulk ice Ih(0001) surface. Efforts to understand how water grows on this well-defined first layer water structure may reveal more insights into the nucleation and growth process and the role of the first water layer.

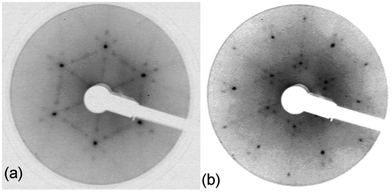Fig. 5 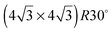LEED pattern for 3.9 layers of water adsorbed on the SnPt(111) alloy recorded at 44 eV (a) and 90 eV (b). Water was dosed at 135 K.

Conclusion

We have shown that only the SnPt(111) surface forms a stable 2D water layer, with the corresponding Pd, Rh, Sn and Ni alloys being non-wetting and forming 3D clusters. The Sn spacing on SnPt(111) closely matches the O–O spacing in bulk ice, allowing the first layer to adopt a flattened structure with the O atoms almost coplanar. Calculations show that commensurate water structures adsorbed on surfaces with a lateral spacing close to that of bulk ice, form highly buckled water structures that are not stable. Rather than having a template that matches the O–O separation, which is inflexible and cannot accommodate the different spacing needed by the first layer and a 3D ice film, an ideal surface for ice nucleation should rather have a binding energy for water just sufficient to wet and form a water structure that is still able to relax, at minimal energy cost, to match the solid surface to an incommensurate bulk ice structure.

Acknowledgements

This work was supported by an EPSRC studentship to F McBride.

References

1. E. B. Moore and V. Molinero, Nature, 2011, 479, 506.
2. V. R. Despres, J. A. Huffman, S. M. Burrows, C. Hoose, A. S. Safatov, G. Buryak, J. Frohlich-Nowoisky, W. Elbert, M. O. Andreae, U. Poschl and R. Jaenicke, Tellus, Ser. B, 2012, 64, 15598.
3. V. Haridas and S. Naik, RSC Adv., 2013, 3, 14199.
4. C. Hoose and O. Moehler, Atmos. Chem. Phys., 2012, 12, 9817.
5. E. J. Murray, B. J. Murray and V. Sivakumar, Chem. Soc. Rev., 2013, 42, 9571.
6. T. Storelvmo, C. Hoose and P. Eriksson, J. Geophys. Res.: Atmos., 2011, 116, D05207.
7. J. D. Atkinson, B. J. Murray, M. T. Woodhouse, T. F. Whale, K. J. Baustian, K. S. Carslaw, S. Dobbie, D. O'Sullivan and T. L. Malkin, Nature, 2013, 498, 355.
8. B. Vonnegut, J. Appl. Phys., 1947, 18, 593.
9. D. L. Doering and T. E. Madey, Surf. Sci., 1982, 123, 305.
10. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211.
11. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667.
12. A. Glebov, A. P. Graham, A. Menzel and J. P. Toennies, J. Chem. Phys., 1997, 106, 9382.
13. S. Haq, J. Harnett and A. Hodgson, Surf. Sci., 2002, 505, 171.
14. M. Gallagher, A. Omer, S. Haq and A. Hodgson, Surf. Sci., 2007, 601, 268.
15. P. J. Feibelman, N. C. Bartelt, S. Nie and K. Thurmer, J. Chem. Phys., 2010, 133, 154703.
16. S. Nie, P. J. Feibelman, N. C. Bartelt and K. Thurmer, Phys. Rev. Lett., 2010, 105, 026102.
17. S. Standop, A. Redinger, M. Morgenstern, T. Michely and C. Busse, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161412.
18. S. Maier, I. Stass, T. Mitsui, P. J. Feibelman, K. Thurmer and M. Salmeron, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 155434.
19. G. A. Kimmel, N. G. Petrik, Z. Dohnálek and B. D. Kay, Phys. Rev. Lett., 2005, 95, 166102.
20. K. Thürmer and N. C. Bartelt, Phys. Rev. Lett., 2008, 100, 186101.
21. G. Zimbitas and A. Hodgson, Chem. Phys. Lett., 2006, 417, 1.
22. S. Haq and A. Hodgson, J. Phys. Chem. C, 2007, 111, 5946.
23. G. Zimbitas, M. E. Gallagher, G. R. Darling and A. Hodgson, J. Chem. Phys., 2008, 128, 074701.
24. D. R. Nutt and A. J. Stone, Langmuir, 2004, 20, 8715.
25. S. J. Cox, S. M. Kathmann, J. A. Purton, M. J. Gillan and A. Michaelides, Phys. Chem. Chem. Phys., 2012, 14, 7944.
26. C. Q. Zhu, H. Li, Y. F. Huang, X. C. Zeng and S. Meng, Phys. Rev. Lett., 2013, 110, 126101.
27. F. McBride, G. R. Darling, K. Pussi and A. Hodgson, Phys. Rev. Lett., 2011, 106, 226101.
28. A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64(9), 381.
29. F. McBride, PhD thesis, The University of Liverpool, 2012.
30. K. P. Stevenson, G. A. Kimmel, Z. Dohnalek, R. S. Smith and B. D. Kay, Science, 1999, 283, 1505.
31. G. A. Kimmel, N. G. Petrik, Z. Dohnálek and B. D. Kay, J. Chem. Phys., 2006, 125, 124702.
32. B. J. Hinch and L. H. Dubois, Chem. Phys. Lett., 1991, 181, 10.
33. A. Beniya, Y. Sakaguchi, T. Narushima, K. Mukai, Y. Yamashita, S. Yoshimoto and J. Yoshinobu, J. Chem. Phys., 2009, 130, 034706.
34. A. Beniya, S. Yamamoto, K. Mukai, Y. Yamashita and J. Yoshinobu, J. Chem. Phys., 2006, 125, 054717.
35. G. Zimbitas, S. Haq and A. Hodgson, J. Chem. Phys., 2005, 123, 174701.
36. G. A. Kimmel, N. G. Petrik, Z. Dohnalek and B. D. Kay, J. Chem. Phys., 2007, 126, 114702.
37. S. H. Overbury, D. R. Mullins, M. T. Paffett and B. E. Koel, Surf. Sci., 1991, 254, 45.
38. S. H. Overbury and Y. S. Ku, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7868.
39. A. Massey, G. R. Darling, K. Pussi, M. Taylor and A. Hodgson, unpublished results.
40. Y. D. Li, M. R. Voss, N. Swami, Y. L. Tsai and B. E. Koel, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15982.
41. E. A. Soares, C. Bittencourt, E. L. Lopes, V. E. de Carvalho and D. P. Woodruff, Surf. Sci., 2004, 550, 127.
42. Y. S. Ku and S. H. Overbury, Surf. Sci., 1992, 273, 341.
43. F. McBride, G. R. Darling, K. Pussi, C. A. Lucas, Y. Grunder, M. Darlington, A. Brownrigg and A. Hodgson, J. Phys. Chem. C, 2013, 117, 4032.
44. J. Klimes and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
45. B. Santra, A. Michaelides, M. Fuchs, A. Tkatchenko, C. Filippi and M. Scheffler, J. Chem. Phys., 2008, 129, 194111.
46. P. J. Feibelman, Science, 2002, 295, 99.
47. T. Jacob and W. A. Goddard, J. Am. Chem. Soc., 2004, 126, 9360.
48. H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102.
49. A. Michaelides, A. Alavi and D. A. King, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 113404.
50. S. Meng, E. G. Wang and S. W. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195404.
51. M. Gallagher, A. Omer, G. R. Darling and A. Hodgson, Faraday Discuss. Chem. Soc., 2009, 141, 231.
52. S. Haq, C. Clay, G. R. Darling, G. Zimbitas and A. Hodgson, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115414.
53. C. Clay, S. Haq and A. Hodgson, Chem. Phys. Lett., 2004, 388, 89.
54. S. Nie, N. C. Bartelt and K. Thurmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035420.
55. K. Thürmer and N. C. Bartelt, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195425.
56. S. C. Rowland, R. G. Layton and D. R. Smith, J. Atmos. Sci., 1964, 21, 698.

---