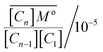Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-assembly and mesophase formation in a non-ionic chromonic liquid crystal system: insights from dissipative particle dynamics simulations
Martin
Walker
a,
Andrew J.
Masters
b and
Mark R.
Wilson
*a
aDepartment of Chemistry, Durham University Science Laboratories, South Road, Durham, DH1 3LE, UK. E-mail: mark.wilson@durham.ac.uk; Tel: +44 (0)191 384 1158
bSchool of Chemical Engineering and Analytical Science, University of Manchester, Manchester, M13 9PL, UK. E-mail: andrew.masters@manchester.ac.uk; Tel: +44 (0)161 2754679
First published on 9th September 2014
Abstract
Results are presented from a dissipative particle dynamics (DPD) simulation of a model non-ionic chromonic system, TP6EO2M, composed of a poly(ethylene glycol) functionalised aromatic (triphenylene) core. The simulations demonstrate self-assembly of chromonic molecules to form single molecule stacks in solution at low concentrations, the formation of a nematic mesophase at higher concentrations and a columnar phase in the more concentrated regime. The simulation model used allows very large system sizes, of many thousands of particles, to be studied. This provides, for the first time, an opportunity to study chromonic phase behaviour by simulation without severe restrictions imposed by system size. In the low concentration limit, the simulations demonstrate approximate isodesmic association from which a binding energy can be obtained, allowing the simulations to be tuned to reproduce the behaviour of the real experimental system.
1 Introduction
Chromonic liquid crystals are a sub-class of the lyotropic liquid crystal family.1,2 The molecular features that drive the formation of chromonic phases are a polyaromatic core, with polar or solubilising groups at the periphery. In water, although in principle other dispersing media could be used, chromonic molecules self-assemble to form stacks with single3–5 or multiple-molecule cross-sections.6–8 Upon aggregation, aromatic groups are aligned into a stack (or column), limiting unfavourable interactions with the solvent.3 At higher concentrations, when aggregates are sufficiently long, mesophase formation occurs from entropy-driven alignment of the long anisotropic columns, resulting in a nematic (N) phase composed of stacks with a size distribution that is dependent upon temperature and concentration. At still higher concentrations a chromonic M phase can form, with a regular two-dimensional packing of columns on a hexagonal lattice.2 There is considerable current interest in chromonics because of applications in areas such as thin film fabrication,9 real-time microbial sensors,10,11 and controllable side-by-side or end-to-end assembly of gold nanorods.12Chromonic mesogens tend to have a strong enthalpic contribution towards the self-assembly process. They aggregate in a reversible manner, with aggregation occurring in the absence of a critical micelle concentration, and often at extremely low concentrations.13 The favourable enthalpic interactions are usually attributed to π–π stacking of the aromatic cores, leading to the growth of linear aggregates. Since aggregation is a one-dimensional process (for simple single molecule stacks) each molecule only interacts strongly with its two neighbours, above and below in the stack. Molecules at the end of the stack interact strongly with only one neighbouring molecule. This configuration implies an isodesmic binding model; that is the binding environment does not change as the aggregates grow in size.14 Adding a molecule to the stack increases the stack size, and replaces the end of the stack with another identical to its predecessor. This is distinctly different from micellar growth. As a micelle grows the curvature of the interface of the micelle changes, leading to a different binding environment for each additional molecule.
Most identified chromonics fall under the banner of ionic chromonics, with a large chromonic ion that self-assembles, which is responsible for the shape of aggregates in solution, and a dissociated solvated counter ion. Here, counter ions are well-solvated and appear to be only partially associated with the aggregate species.3 Far less studied are non-ionic chromonics, which tend to have far larger aromatic cores with a number of solubilising groups attached that stabilise the molecule in solution.15,16
This study considers the non-ionic chromonic 2,3,6,7,10,11-hexa-(1,4,7-trioxaoctyl)-triphenylene, TP6EO2M (Fig. 1). TP6EO2M is a neutral molecule with D3h symmetry, and is composed of a triphenylene core with six ethylene oxide arms (each ethylene oxide oligomer unit is terminated with a methyl group). Previous studies17,18 have shown that TP6EO2M in water has a stable nematic phase, which extends from 14 wt% to 51.2 wt%, depending on temperature, with a hexagonal columnar phase at higher concentrations. An isodesmic binding model has been suggested for the formation of TP6EO2M aggregates.19
Simulation studies have provided some useful insights into chromonic behaviour.14,19,20 In recent work Chami and Wilson3 have provided one of the first detailed atomistic studies, looking at the structure and dynamics of molecules within a chromonic column in water and the structure of a (pre-assembled) N phase. However, for a molecule as large as TP6EO2M such studies are limited, by computational expense, to a relatively small number of molecules in water; and cannot be used to study bulk phase behaviour or to look at aggregation as a function of concentration.
In the current work, we use the dissipative particle dynamics (DPD)21 technique to study a model for TP6EO2M at a coarse-grained level. We show how altering the ethylene oxide arm length has subtle effects on local packing, and greatly impacts on the phase behaviour of the system in water. Additionally we show how DPD parameters can be tuned to fit binding energies and reproduce experimental phase behaviour.
2 Computational methods
2.1 DPD model
DPD has been successfully applied to simulate a number of soft matter systems: block co-polymers,22–24 colloidal suspensions,25 lipid bilayers,26,27 nanoparticles28,29 and liquid crystalline phases30,31 including those formed from complex polyphilic molecules.32–35 Molecular systems are readily coarse-grained to a DPD representation by replacing multi-atom chemical groups with simple, single-site microphase segregating groups (beads). The beads then interact through space with three simple forces acting along the inter-bead vector: a conservative force (FC), a dissipative force (FD) and a random force (FR).| FC = aij(1 − rij/rcut) for |rij| < rcut |
| FC = 0 for |rij| ≥ rcut | (1) |
| FD = −γω2rij(rij·vij) for |rij| < rcut |
| FD = 0 for |rij| ≥ rcut; | (2) |
 | (3) |
In principle, non-ionic chromonic molecules can be represented by two types of chemical group: an unsaturated aromatic-like group that can be used to represent the core and a hydrophilic group to represent peripheral solubilising groups. In the case of TP6EO2M, in order to properly capture molecular structure (and hence self-assembly behaviour) it is necessary to include additional bonding and angle parameters to accurately represent the molecular shape. The coarse-graining scheme used in this work is shown in Fig. 1. We used a rigid disc-like core, composed of 19 aromatic type beads arranged hexagonally in 2 dimensions, surrounded with six flexible arms (see Fig. 1) each represented by L beads. We note that while the D3h symmetry of the atomistic representation has been increased to D6h within the coarse-grained model, this (38 bead) model is still able to capture the key interactions of TP6EO2M responsible for self-assembly and mesophase formation.
We have also carried out test calculations of a more fine-grained representation of TP6EO2M with D3h symmetry. However, here a larger number of beads is required to represent the reduced, D3h, symmetry of the core. This, combined with additional intramolecular interaction terms to maintain geometry, necessitates the use of a smaller DPD time-step. Hence, as the self-assembly behaviour was very similar in the two models in initial tests, we have concentrated on the more coarse-grained representation in the work presented here.
The usual reduced DPD units were employed throughout. Distances were scaled by unit length, l = 1, we used beads of size rcut/l = 1 with a reduced mass of m = 1. Energies were scaled by unit energy, ε = 1 and temperature was measured in units of T* = kBT/ε. Our simplified TP6EO2M core maintained rigidity with harmonic springs binding beads at an ideal distance of r/l = 0 using the repulsive DPD potential to provide the repulsive component of the “bonding” potential (and hence a finite bond length). Harmonic angle potentials were used to link any three linear adjacent beads (in Fig. 1) with an ideal angle of 180°. The force constants for these two interactions were set to κbond/(ε l−2) = 20, κangle/(ε rad2) = 20 respectively. The ethylene oxide units are represented by simple beads bonded with the same harmonic potentials described for the core, no angle potentials were imposed on the ethylene oxide units.
The properties of the two types of coarse-grained groups aim to mimic the properties of the aromatic-core and the ethylene oxide chains within TP6EO2M, and so, in the first instance the DPD parameters, aij were selected to encourage microphase segregation, allowing the ethylene oxide arm and water to freely mix but, keeping the aromatic core separate. The corresponding parameter set was aij/ε = 25 when i = j, or i = water and j = ethylene oxide, and aij/ε = 45 for all other interactions.
As the coarse-graining scheme used is relatively crude, we initially varied the ethylene oxide chain length L from zero to 5 units. Treating L in this way, for fixed values of aij allow us to obtain a chain length that best matches experimental15 data for TP6EO2M.
1000 molecules of TP6EO2M were placed at random positions and orientations within a cubic simulation box. The required concentration was then obtained by adding an appropriate number of water beads in random positions. To explore the influence of arm length, simulations were performed on molecules with an arm length L = 0–5, over the range of concentrations 25 wt%, 50 wt%, 75 wt% and 100 wt% (no water). To study binding energies additional longer simulations at 10 wt% were also performed to minimise the influence of highly fluctuating larger aggregates. Given the uniform mass of DPD beads used in these simulations, the weight percent can be mapped in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 manner with the volume fraction.
1 manner with the volume fraction.
Equations of motion were solved using the Velocity Verlet integration algorithm, using the DPD module of the DL_MESO37,38 program (DL_MESO_DPD) in the constant-NVT (canonical) ensemble. In each case, simulations were started from a random configuration, which was quenched to the desired temperature (T* = 1). More complicated cooling procedures were found to be unnecessary, since the unbound water content allowed for sufficient system flexibility to equilibrate under any set of conditions without the equilibrium configuration depending on thermal history (or nucleation events). We found that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with a time step of τ/(l/(m/ε)1/2) = 0.02 was sufficient to ensure a well equilibrated phase in most cases. The parameter slowest to equilibrate was the cluster size/distribution, simulations where this distribution was found unequilibrated were continued for a further 1
000 steps with a time step of τ/(l/(m/ε)1/2) = 0.02 was sufficient to ensure a well equilibrated phase in most cases. The parameter slowest to equilibrate was the cluster size/distribution, simulations where this distribution was found unequilibrated were continued for a further 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibrated steps. The DPD parameter for noise amplitude was taken to be σ = 3.6710. All simulations were performed at a particle site density ρ/l3 = 3.0.
000 equilibrated steps. The DPD parameter for noise amplitude was taken to be σ = 3.6710. All simulations were performed at a particle site density ρ/l3 = 3.0.
Simulations of ordered phases (nematic, columnar and crystal phases) started from a random arrangement of molecules often failed to equilibrate, resulting in linear aggregates with no long range positional, or orientational order. These aggregates were often locked into position by periodic boundary conditions, and could not dynamically reorient due to packing restraints of adjacent aggregates. To aid the equilibration of ordered phases we investigated the influence of a pseudo magnetic field, applied to orient the discs in a single direction. Once a phase formed, the field was removed and a further 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 equilibration time steps were performed to study a field free simulation. To impose a field we first calculated the normal vector to the plane defined by three of the corner aromatic beads, a, b and c (Fig. 1). The field acted to align this vector to the z-axis of the simulation cell. The energy due to the field is:
000 equilibration time steps were performed to study a field free simulation. To impose a field we first calculated the normal vector to the plane defined by three of the corner aromatic beads, a, b and c (Fig. 1). The field acted to align this vector to the z-axis of the simulation cell. The energy due to the field is:
| |Emag| = 0.5kfield(θ − θeqm) | (4) |
 , θeqm = 0, with a field director D = (001). A field strength of kfield/(ε/l−1 rad−2) = 2.0 was selected as sufficiently large to align the short molecular axis but sufficiently small to minimise the effects of the field on phase boundaries. The presence of the field did not influence phase stability for any of the systems in water. However, without a field it was difficult for long columns formed from self-assembly of an initial random configuration of mesogens to fully align because of the possibility of long aggregates interacting with themselves across periodic boundary conditions. For thermotropics the field helped stabilize mesophases for two systems, as described below.
, θeqm = 0, with a field director D = (001). A field strength of kfield/(ε/l−1 rad−2) = 2.0 was selected as sufficiently large to align the short molecular axis but sufficiently small to minimise the effects of the field on phase boundaries. The presence of the field did not influence phase stability for any of the systems in water. However, without a field it was difficult for long columns formed from self-assembly of an initial random configuration of mesogens to fully align because of the possibility of long aggregates interacting with themselves across periodic boundary conditions. For thermotropics the field helped stabilize mesophases for two systems, as described below.
2.2 Analysis of simulations
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time steps.
000 time steps.
3 Results and discussion
3.1 Arm length L = 0
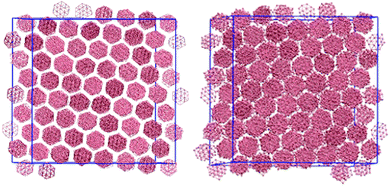
An arm length of zero at 100 wt% corresponds to a simulation of a thermotropic polyaromatic discotic liquid crystal. The polyaromatic mesogen shows no clear ordering upon cooling, short linear aggregates form, but fail to equilibrate on any reasonable timescale. To aid in equilibration a weak field (kfield/(ε/l−1 rad−2) = 2.0) was used to align the molecular short axis, inducing a series of transitions: isotropic–nematic (T* = 1.9), nematic–columnar (T* = 1.5), columnar–crystalline (T* = 0.7). For the columnar phase (Fig. 2) each molecule has the freedom to rotate giving each column a circular cross section, whereas in the crystalline phase the molecular rotations are frozen such that each column maintains a hexagonal cross-section. The transition between the two highly ordered phases can easily be distinguished through analysis of the g(u,v) plots (Fig. 3). g(u,v) for the crystal phase which show long range in-plane orientational order, whereas the columnar mesophase shows hexagonal packing of columns but exhibits in-plane molecular rotations. This leads to a loss of the sharp peaks within the rings that arise from the hexagonal tiling. At higher temperature, the columnar phase melts to give a discotic nematic, with no hexagonal order.Removal of the field from each equilibrated phase resulted in loss of both the nematic and columnar phases, only the crystal and isotropic phases remained stable with a single transition crystal–isotropic phase transition at T* = 0.8.
Since there are no ethylene oxide arms to aid solvation in water, upon addition of water, one would expect any ordered phase to swell, to accommodate minimum amounts of water, then phase separate to form a two phase region. This does indeed occur and is seen at the next concentration increment (75 wt%). A biphasic region in the phase diagram becomes evident with the two phases corresponding to a region of pure water and a region of essentially pure chromonic material.
3.2 Arm length L = 1
Adding six ethylene oxide arms each with a length of a single bead, reduces phase transition temperatures slightly but does not dramatically change the thermotropic phase behaviour. Once again no ordering was observed on cooling from an isotropic liquid. However, for the solventless system, in an aligning field, transitions occur at T* = 1.6 (isotropic–nematic), T* = 1.4 (nematic–columnar), T* = 0.6 (columnar–crystalline). In comparison to the L = 0 system the only notable differences are seen in a slight increase in the column spacing in the crystal and columnar phases, and a change in the in-plane ordering within the crystal. To accommodate the ethylene oxide groups the columns are spaced further apart. Additionally, since a single bead arm has very little conformational freedom, it fills space without distorting the molecule. Consequently, the columns are reorientated by approximately 20 degrees relative to the L = 0 crystal (as seen in Fig. 3). In the columnar phase increases in the spacing between columns leads to more diffuse peaks in g(u,v) and less orientational order relative to the L = 0 model.Removal of the field only affected the thermotropic nematic phase stability. Both the crystal and columnar phases were stable with and without an aligning field; with the columnar phase melting directly to an isotropic phase on increasing temperature.
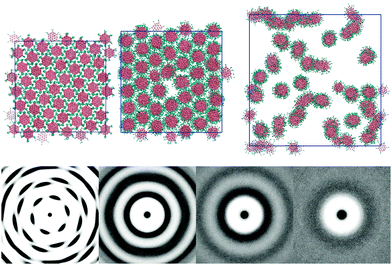
The L = 1 system displays further phase changes upon the addition of water. The ethylene oxide arms add a favourable interaction between the molecule and water, stabilising the inclusion of water within a single phase. No two phase regions were observed, even down to a 25 wt% concentration. The columns clearly interact less with each other as the amount of solvent increases (see Fig. 4). At 75 wt% the 2d-orientational correlation of the pure melt has been lost. The ring pattern seen in g(u,v) is commensurate with a chromonic M phase (hexagonally arranged columns). At 50 wt% (N phase) the hexagonal arrangement of columns has disappeared. However, a ring structure persists, indicating that there is a weak column–column interaction. At 25 wt% (nematic–isotropic phase transition) all structure in the pair distribution function is lost apart from an exclusion zone around each core unit that no other columns can enter; indicating the columns randomly fill space.
3.3 Arm length L = 2–3
Increasing the arm length to two beads per arm adds a soft, distortable corona around each molecule. 2d-orientational order between columns is now lost for the thermotropic case: even at low temperatures (T* = 0.5) each molecule within a column has freedom to rotate around the molecular primary axis. At low temperatures we see therefore only a columnar phase (see Fig. 5). This phase can accommodate water by swelling to give both M (at 75 wt%) and N phases. The system shows a nematic phase at 50 wt% and 25 wt% but orientational ordering of columns is lost at 10 wt% giving an isotropic arrangement of aggregates.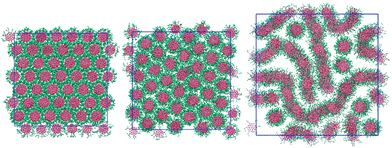 | ||
| Fig. 5 Configurations of the L = 2 model at 100 wt% (left), 75 wt% (middle) and 50 wt% (right). T* = 1.0. | ||
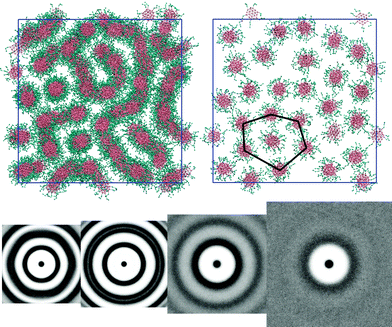
Molecules with L = 3 arms exhibit a very similar trend to the L = 2 system. The exception occurs at 50 wt% concentration. Here, the phase is nematic but shows local hexagonal arrangement of columns for thin slices parallel to the director (see Fig. 6: top); suggesting that 50 wt% is on the cusp of a hexagonal–nematic columnar transition. The g(u,v) (see Fig. 6: bottom) shows that in the thermotropic melt there is no in-plane orientational order within a column but the ring pattern and intensity corresponds to a hexagonal columnar phase. At 50 wt% the water volume reduces the packing forces between columns, allowing columns a greater configurational freedom and resulting in a pattern in which the columns appear to form strings in the 2D projections (Fig. 5 and 6). However, each column is fully solvated by water and remains independent of adjacent columns. The M phase is evident at 75 wt% and, as before, at 25 wt% the pair distribution function shows no positional order in the cross section normal to the columnar director.
3.4 Arm length L = 4–5
Arm lengths of L = 4 and L = 5 show similar behaviour to the L = 3 system, with the exception that at 50 wt% an M phase is seen. There are two competing factors responsible for the stabilisation of ordered phases at lower concentrations: as the arms increase in length the fraction of rigid core present in the system decreases, acting to destabilise the phases relative to water content, this is counteracted by the longer arms allowing a higher capacity for swelling of a phase, and thereby incorporating more solvent.3.5 Aggregation at low concentrations
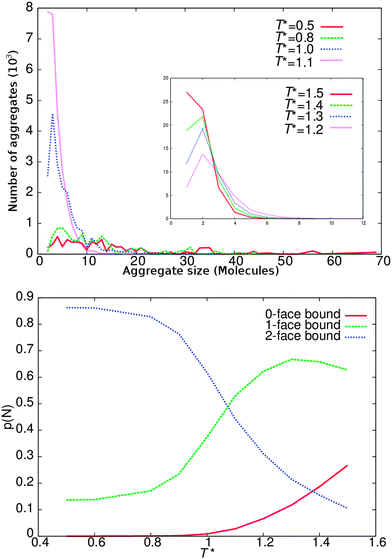
To test the self-assembly properties of our model against experimental behaviour and to show how DPD parameters can be fine-tuned for chromonic systems, an additional series of lower concentration calculations were performed. Simulations with arm length of 3 beads (L = 3) were selected for this experiment, since the behaviour of the L = 3 model best represents our target experimental system TP6EO2M.15 Simulations were performed at a concentration of 10 wt%, in the isotropic phase. At this concentration columns are sufficiently short to remove the possibility of periodically infinite columns and to reduce the frequency of any poorly sampled, larger aggregates.The standard isodesmic model assumes that the equilibrium constant for binding an additional molecule is the same across each n-mer for each further binding event. This leads to the production of an exponential distribution of monomers in aggregates. In Fig. 7, we show the distribution of cluster sizes for different temperatures. At higher temperatures (T* ≥ 1.5) monomers dominate, while at lower temperatures (T* < 1.1) larger aggregates dominate. In between there is a regime where the number of dimers exceeds the number of bare monomers.
The lower part of Fig. 7 shows the probability of finding molecules with zero bound faces i.e. monomers, molecules with one face bound representing either dimers or molecules at the end of an aggregate, and aggregates molecules with two bound faces. At high temperatures (T* = 1.5) ∼30% of the molecules are monomers, with ∼65% end aggregate molecules and ∼5% mid aggregate molecules. As the temperature decreases we initially observe an increase in both forms of bound molecules and an associated decrease in monomers; indicating that more aggregates form and aggregates also increase in size. As the temperature is reduced further the monomer numbers continue to decrease while the number of molecules in a mid aggregate configuration increases. However, the number of end aggregate molecules decreases also; indicating (for fixed number of molecules) that fewer but larger aggregates have formed. At lower temperatures still (T* = 0.8) there are effectively no monomers remaining and only a small number of end aggregate molecules.
It is interesting to compare the results seen here with the Monte Carlo simulations of a simple disc model for a chromonic system by Edwards et al.19 They note that a modification to the usual isodesmic association model is required to explain their results, whereby the equilibrium constant becomes concentration dependent. However, the results in the current study are more consistent with a different type of modification to isodesmic association, in which there is more than one binding event. In our case initial formation of dimers is favoured over addition of further monomers. The latter appears also to be seen in some experimental systems. For sunset yellow, Chami and Wilson3 have attempted to quantify this by calculating free energies of binding to aggregate stacks within an atomistic simulation model. In their work a small preference is seen (∼ of 2 kJ mol−1) for aggregation of two monomers to form a dimer, in comparison to addition of a monomer to a larger (dimer or above) aggregate. In the DPD model used here, all interactions are repulsive, consequently a small preference arises naturally for dimer formation due to the absence of next nearest neighbour repulsions (particularly arising from the flexible chains).
To quantify this further we define equilibrium constants for the binding process
 | (5) |
For a standard constant-NpT simulation binding enthalpies can be extracted directly from the slope of a Van't Hoff plot. Our DPD simulations are in the constant-NVT ensemble but given
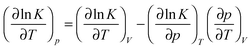 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K/∂p)T is small, and additionally our system size is relatively large, we can neglect the second term on the right hand side of eqn (6), writing
K/∂p)T is small, and additionally our system size is relatively large, we can neglect the second term on the right hand side of eqn (6), writing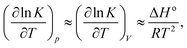 | (7) |
 | (8) |
The association enthalpy in our model is easily tuned by the DPD repulsion parameter aij. This means that it should, in future work, be possible to tune the association behaviour of models such as this by reference to small atomistic simulations in dilute solution.
4 Conclusions
A simple DPD model has been developed to study chromonic self-assembly and phase formation in the non-ionic chromonic TP6EO2M. The computational speed of the model allows the phase diagram to be probed across a range of concentrations from pure mesogen to dilute solution. Depending on concentration and the length of the hydrophilic chain, we see the formation of a crystal phase, a columnar phase, and a stable chromonic nematic phase; in addition to association to give an isotropic arrangement of chromonic aggregates at low concentrations.In dilute solution, association behaviour is approximately isodesmic, leading to an approximate exponential distribution of monomers in aggregates. However, we note a small deviation from isodesmic behaviour in the case of dimers. Here, as in some experimental systems, entropic factors lead to the association of two monomers being slightly more favourable than aggregate growth. This probably arises because chains belonging to a molecule in the middle of a stack are restricted by the presence of two neighbours, whereas chains belonging to end molecules are only restricted by a neighbour on one side.
Acknowledgements
The authors would like to acknowledge the support of the Engineering and Physical Sciences Research Council (EPSRC) in the UK through grants EP/J004413/1 and EP/J004707/1.References
- J. Lydon, Curr. Opin. Colloid Interface Sci., 2004, 8, 480–490 CrossRef CAS PubMed.
- J. Lydon, J. Mater. Chem., 2010, 20, 10071–10099 RSC.
- F. Chami and M. R. Wilson, J. Am. Chem. Soc., 2010, 132, 7794–7802 CrossRef CAS PubMed.
- D. J. Edwards, J. W. Jones, O. Lozman, A. P. Ormerod, M. Sintyureva and G. J. T. Tiddy, J. Phys. Chem. B, 2008, 112, 14628–14636 CrossRef CAS PubMed.
- V. R. Horowitz, L. A. Janowitz, A. L. Modic, P. A. Heiney and P. J. Collings, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041710 CrossRef.
- M. R. Tomasik and P. J. Collings, J. Phys. Chem. B, 2008, 112, 9883–9889 CrossRef CAS PubMed.
- A. J. Dickinson, N. D. LaRacuente, C. B. McKitterick and P. J. Collings, Mol. Cryst. Liq. Cryst., 2009, 509, 9/[751]–20/[762] Search PubMed.
- D. Perahia, E. J. Wachtel and Z. Luz, Liq. Cryst., 1991, 9, 479–492 CrossRef CAS.
- K. V. Kaznatcheev, P. Dudin, O. D. Lavrentovich and A. P. Hitchcock, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 061703 CrossRef CAS.
- S. V. Shiyanovskii, O. D. Lavrentovich, T. Schneider, T. Ishikawa, I. I. Smalyukh, C. J. Woolverton, G. D. Niehaus and K. J. Doane, Mol. Cryst. Liq. Cryst., 2005, 434, 587–598 CAS.
- S. V. Shiyanovskii, T. Schneider, I. I. Smalyukh, T. Ishikawa, G. D. Niehaus, K. J. Doane, C. J. Woolverton and O. D. Lavrentovich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 020702 CrossRef CAS.
- H. S. Park, A. Agarwal, N. A. Kotov and O. D. Lavrentovich, Langmuir, 2008, 24, 13833–13837 CrossRef CAS PubMed.
- E. A. Mills, M. H. Regan, V. Stanic and P. J. Collings, J. Phys. Chem. B, 2012, 116, 13506–13515 CrossRef CAS PubMed.
- P. K. Maiti, Y. Lansac, M. A. Glaser and N. A. Clark, Liq. Cryst., 2002, 29, 619–626 CrossRef CAS.
- Z. H. Al-Lawati, B. Alkhairalla, J. P. Bramble, J. R. Henderson, R. J. Bushby and S. D. Evans, J. Phys. Chem. C, 2012, 116, 12627–12635 CAS.
- R. E. Hughes, S. P. Hart, D. A. Smith, B. Movaghar, R. J. Bushby and N. Boden, J. Phys. Chem. B, 2002, 106, 6638–6645 CrossRef CAS.
- N. Boden, R. J. Bushby, L. Ferris, C. Hardy and F. Sixl, Liq. Cryst., 1986, 1, 109–125 CrossRef CAS.
- R. Hentschke, P. J. B. Edwards, N. Boden and R. J. Bushby, Macromol. Symp., 1994, 81, 361–367 CrossRef CAS.
- R. G. Edwards, J. R. Henderson and R. L. Pinning, Mol. Phys., 1995, 86, 567–598 CrossRef CAS.
- P. Prybytak, W. J. Frith and D. J. Cleaver, Interface Focus, 2012, 2, 651–657 CrossRef CAS PubMed.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, EPL, 1992, 19, 155 CrossRef.
- R. D. Groot, T. J. Madden and D. J. Tildesley, J. Chem. Phys., 1999, 110, 9739–9749 CrossRef CAS PubMed.
- A. A. Gavrilov, Y. V. Kudryavtsev and A. V. Chertovich, J. Chem. Phys., 2013, 139, 224901 CrossRef PubMed.
- L. He, Z. Chen, R. Zhang, L. Zhang and Z. Jiang, J. Chem. Phys., 2013, 138, 094907 CrossRef PubMed.
- E. S. Boek, P. V. Coveney, H. N. W. Lekkerkerker and P. van der Schoot, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3124–3133 CrossRef CAS.
- S. Yamamoto, Y. Maruyama and S. Hyodo, J. Chem. Phys., 2002, 116, 5842–5849 CrossRef CAS PubMed.
- J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061 CrossRef CAS PubMed.
- H. Xu, Q. Zhang, H. Zhang, B. Zhang and C. Yin, J. Theor. Comput. Chem., 2013, 12, 1250111 CrossRef.
- X. Chen, F. Tian, X. Zhang and W. Wang, Soft Matter, 2013, 9, 7592–7600 RSC.
- A. AlSunaidi, W. K. Den Otter and J. H. R. Clarke, Philos. Trans. R. Soc., A, 2004, 362, 1773–1781 CrossRef CAS PubMed.
- A. AlSunaidi, W. K. den Otter and J. H. R. Clarke, J. Chem. Phys., 2013, 138, 154904 CrossRef CAS PubMed.
- M. Bates and M. Walker, Soft Matter, 2009, 5, 346–353 RSC.
- M. A. Bates and M. Walker, Phys. Chem. Chem. Phys., 2009, 11, 1893–1900 RSC.
- M. A. Bates and M. Walker, Mol. Cryst. Liq. Cryst., 2010, 525, 204–211 CrossRef CAS.
- M. A. Bates and M. Walker, Liq. Cryst., 2011, 38, 1749–1757 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS PubMed.
- M. A. Seaton, R. L. Anderson, S. Metz and W. Smith, Mol. Simul., 2013, 39, 796–821 CrossRef CAS.
- DL_MESO is a mesoscale simulation package written by R. Qin, W. Smith and M. A. Seaton and has been obtained from STFC's Daresbury Laboratory via the website http://www.ccp5.ac.uk/DL_MESO.
- S. D. Stoddard, J. Comput. Phys., 1978, 27, 291–293 CrossRef.
| This journal is © the Owner Societies 2014 |