Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unimolecular reaction chemistry of a charge-tagged beta-hydroxyperoxyl radical†
Sui
So
a,
Benjamin B.
Kirk‡
bc,
Adam J.
Trevitt
bc,
Uta
Wille
cd,
Stephen J.
Blanksby
bce and
Gabriel
da Silva
*a
aDepartment of Chemical and Biomolecular Engineering, The University of Melbourne, VIC 3010, Australia. E-mail: gdasilva@unimelb.edu.au
bSchool of Chemistry, University of Wollongong, NSW 2522, Australia
cARC Centre of Excellence for Free Radical Chemistry and Biotechnology, Hosted by The University of Melbourne, Victoria 3010, Australia
dSchool of Chemistry and Bio21 Institute, The University of Melbourne, VIC 3010, Australia
eCentral Analytical Research Facility, Institute for Future Environments, Queensland University of Technology, QLD 4001, Australia
First published on 9th October 2014
Abstract
β-Hydroxyperoxyl radicals are formed during atmospheric oxidation of unsaturated volatile organic compounds such as isoprene. They are intermediates in the combustion of alcohols. In these environments the unimolecular isomerization and decomposition of β-hydroxyperoxyl radicals may be of importance, either through chemical or thermal activation. We have used ion-trap mass spectrometry to generate the distonic charge-tagged β-hydroxyalkyl radical anion, ˙CH2C(OH)(CH3)CH2C(O)O−, and investigated its subsequent reaction with O2 in the gas phase under conditions that are devoid of complicating radical–radical reactions. Quantum chemical calculations and master equation/RRKM theory modeling are used to rationalize the results and discern a reaction mechanism. Reaction is found to proceed via initial hydrogen abstraction from the γ-methylene group and from the β-hydroxyl group, with both reaction channels eventually forming isobaric product ions due to loss of either ˙OH + HCHO or ˙OH + CO2. Isotope labeling studies confirm that a 1,5-hydrogen shift from the β-hydroxyl functionality results in a hydroperoxyalkoxyl radical intermediate that can undergo further unimolecular dissociations. Furthermore, this study confirms that the facile decomposition of β-hydroxyperoxyl radicals can yield ˙OH in the gas phase.
Introduction
β-Hydroxyperoxyl radicals containing the![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) C(O2˙)–C(OH)
C(O2˙)–C(OH)![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) moiety are oxidation intermediates of unsaturated volatile organic compounds (VOCs) in the atmosphere, where they are formed by sequential addition of the hydroxyl radical (˙OH) and O2 to a carbon–carbon double bond. During combustion of ethanol and larger alcohol fuels β-hydroxyperoxyl radicals can also form via hydrogen atom loss (abstraction or bond homolysis) followed by subsequent O2 addition. β-Hydroxyperoxyl radicals will be consumed by competing bimolecular and unimolecular reactions in the atmosphere and in combustion environments.
moiety are oxidation intermediates of unsaturated volatile organic compounds (VOCs) in the atmosphere, where they are formed by sequential addition of the hydroxyl radical (˙OH) and O2 to a carbon–carbon double bond. During combustion of ethanol and larger alcohol fuels β-hydroxyperoxyl radicals can also form via hydrogen atom loss (abstraction or bond homolysis) followed by subsequent O2 addition. β-Hydroxyperoxyl radicals will be consumed by competing bimolecular and unimolecular reactions in the atmosphere and in combustion environments.
Isoprene is the second most emitted VOC to the atmosphere, following methane, and it is the most emitted biogenic VOC. Isoprene, along with its primary oxidation products methacrolein (MACR) and methyl vinyl ketone (MVK),1–3 possess sites of unsaturation that allow for the formation of β-hydroxyperoxyl radicals. The chemistry of β-hydroxyperoxyl radicals thus plays a key role in understanding and modeling the composition of the atmosphere. Isoprene photooxidation particularly dominates the chemistry in the forested planetary boundary layer where isoprene emissions are concentrated. Here, the photochemical oxidation of isoprene is critical to determining ozone and aerosol formation,4–6 HOx radical (˙OH + HO2˙) levels and the rate of ˙OH consumption (i.e., ˙OH reactivity).7
Over the last decade, field campaigns conducted over remote forested environments, which are characterized by large isoprene emission sources and relatively low levels of NOx (NO˙ + NO2˙), have reported higher-than-predicted ˙OH concentrations (ca. 107 molecule cm−3 or 0.4 ppt) along with high HO2˙![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ˙OH ratios (ca. 100).8 It has recently emerged that isoprene derived β-hydroxyperoxyl radicals can undergo unimolecular decomposition to replenish ˙OH.9,10 These reactions have been proposed as contributors to elevated oxidative capacities in remote forested regions of the troposphere.9 However, there has been relatively little experimental work on the unimolecular chemistry of β-hydroxyperoxyl radicals.
˙OH ratios (ca. 100).8 It has recently emerged that isoprene derived β-hydroxyperoxyl radicals can undergo unimolecular decomposition to replenish ˙OH.9,10 These reactions have been proposed as contributors to elevated oxidative capacities in remote forested regions of the troposphere.9 However, there has been relatively little experimental work on the unimolecular chemistry of β-hydroxyperoxyl radicals.
The current study utilizes ion-trap mass spectrometry to investigate the reaction of a model distonic β-hydroxyalkyl radical anion with O2, and probe the unimolecular reaction chemistry of the resultant β-hydroxyperoxyl radical. Quantum chemical calculations and master equation kinetic modeling are performed to gather insight into the reaction dynamics. This distonic radical ion approach to studying peroxyl radical chemistry has recently proven useful in the investigation of peroxyl radical reactions relevant to combustion, biochemistry, and atmospheric science.11–16 It allows for definitive assignment of the mass of reaction products while avoiding complicating peroxyl radical cross and self-reactions.
Methods
Experiments
Reaction rates for formation of the peroxyl radical anions were determined without additional neutral reagents added to the helium buffer gas. Instead, the ion-trapping region contains a small quantity of O2 due to transmission from the atmospheric pressure ionization source. The concentration of O2 throughout these experiments was determined by a calibration reaction (3-carboxylatoadamantyl + O2) to be (3.1 ± 0.1) × 109 molecules cm−3.18 Reaction times between 30–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ms are set using the activation time parameter within the Xcalibur instrument control software (Thermo Fisher Scientific, San Jose CA) with the excitation energy set at zero (arbitrary units). All spectra presented are the average of at least 50 scans.
000 ms are set using the activation time parameter within the Xcalibur instrument control software (Thermo Fisher Scientific, San Jose CA) with the excitation energy set at zero (arbitrary units). All spectra presented are the average of at least 50 scans.
The reaction efficiency can be calculated by first plotting the natural logarithm of the precursor ion concentration at different reaction times ([R]t) relative to the initial concentration ([R]0). This gives a straight line where the slope equals the pseudo first-order rate coefficient (k1), which is illustrated in eqn (1). With a measured O2 concentration, the second-order rate coefficient (k2) can be obtained by eqn (2). Finally, by calculating the collision rate coefficient (kcoll) using the trajectory collision rate theory, the reaction efficiency (ϕ) can be determined using eqn (3).
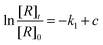 | (1) |
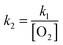 | (2) |
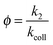 | (3) |
Theory
Wells and transition states are modeled following standard statistical mechanical formulae, with internal degrees of freedom described as harmonic oscillators and external rotations treated as a separable active 1D K-rotor and inactive 2D J-rotor. Densities and sums of states were solved for energies up to 2000 cm−1 with a grain size of 10 cm−1. The continuum master equation was then extended up to 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.
Collisional energy transfer between the bath gas helium and the C5H8O5˙− reaction intermediate is approximated using the single-exponential down model, with a constant value of ΔEdown, the average energy transferred in deactivating collisions. We found that in order to achieve agreement with experiment (in which no collisionally stabilized C5H8O5˙− adduct ion was detected), a ΔEdown of around 10 cm-1 was required. Note that recent modeling of energy transfer in collisions of similarly sized cations with helium has required ΔEdown values on the order of 100–300 cm−1,13,30 which is considerably larger than that seen in the present anionic system. The latter is more consistent with accurate ΔEdown values recently reported for the methane–helium system at room temperature.31
The Lennard-Jones model is used to approximate the frequency of bath gas collisions, with σ and ε/kb for all wells estimated as 6.3 Å and 800 K, respectively, using additivity procedures based on partial molar volumes.32 Microcanonical rate coefficients k(E) are determined from sums and densities of states along with calculated barrier heights using RRKM theory.
For barrierless association of the ˙CH2C(OH)(CH3)CH2C(O)O− radical anion with O2, the restricted Gorin model has been used to generate a representative transition state structure. Here, the high-pressure limit rate coefficient was set at the parameterized trajectory theory collision rate of 5.9 × 10−10 cm3 molecule−1 s−1 at 307 K. A Morse function is used to model the dissociation potential by fitting the adiabatic 2D J-rotor of the transition state. The method employed by Golden33 is then used to estimate the centre of mass distance at equilibrium from the reduced mass and 1D K-rotor of the complex. The restricted Gorin transition state is subsequently constructed from the 1D and 2D external rotors and the four extra degrees of freedom representing the internal rotations, along with the vibrational frequencies of the dissociated fragments.
Stochastic master equation simulations were conducted under conditions representative of the ion-trap: 307 K and 2.5 mTorr of helium. Each simulation featured 107 trials, which allowed us to obtain reliable statistics on channels with low yields.
Results and discussion
Mass spectrometry
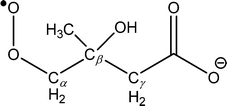
The approach used to synthesize and isolate the ˙CH2C(OH)(CH3)CH2C(O)O− radical anion in the gas phase is summarized in Scheme 1. The dicarboxylate dianion at m/z 80 is generated by subjecting a methanolic solution of 3-hydroxy-3-methylglutaric acid to electrospray ionization. The target radical anion is formed by mass-selecting the m/z 80 dianion population and subsequently irradiating it with a 266 nm laser pulse. Electron photodetachment and prompt decarboxylation result, yielding the product detected at m/z 116. Fig. 1 provides mass spectra demonstrating (A) isolation of the 3-hydroxy-3-methylglutaric acid dianion, (B) subsequent collision-induced dissociation (CID) and (C) photodetachment (PD) of the isolated dianion. While PD of the m/z 80 ion yields only the target ion at m/z 116 as the major product (Fig. 1C), the less-selective CID (Fig. 1B) approach predominantly leads to even-electron dissociation processes yielding product ions at m/z 59 (C2H3O2−) and 101 (C4H5O3−). In order to further investigate the nature of the m/z 116 radical anion produced according to the steps outlined in Scheme 1, it was isolated in the ion-trap and subjected to CID (see ESI,† Fig. S1). This predominantly resulted in loss of C3H6O to yield a product ion of m/z 58, consistent with β-scission of the target distonic radical anion. These data indicate that the product ion at m/z 116 is most likely the desired γ-carboxylate isomer and not the resonance stabilized α-carboxylate radical anion isomer, which cannot undergo a direct bond homolysis to lose C3H6O. We have assigned the product ion at m/z 58 as the ˙CH2C(O)O− acetate radical anion. This assignment is supported by experiments in which the m/z 58 anion was re-isolated in the presence of O2, where it reacted to yield a product at m/z 60, consistent with the known reaction of the acetate radical anion to form CO3˙−.17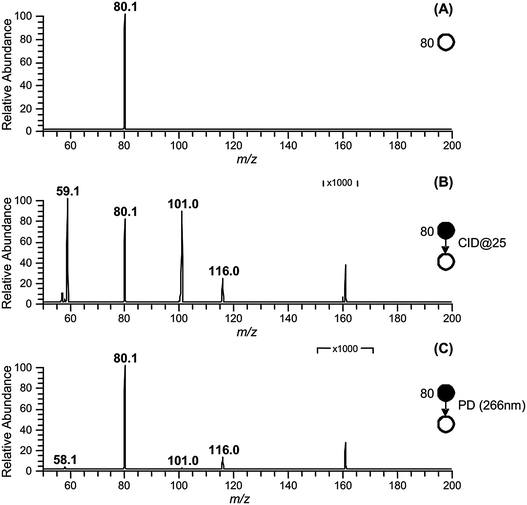 | ||
| Fig. 1 (A) Isolation of the 3-hydroxy-3-methylglutaric acid dianion (m/z 80) in the gas-phase. (B) Collision induced dissociation (CID) of m/z 80. (C) Photodissociation (PD) of m/z 80. | ||
Isolation of the ˙CH2C(OH)(CH3)CH2C(O)O− radical anion (m/z 116) in the presence of O2 for 10 s resulted in the mass spectrum depicted in Fig. 2. The dominant reaction products are ions corresponding to loss of 29 Da [+O2 –˙CHO3] at m/z 87 and loss of 15 Da [+O2 –˙CH3O2] at m/z 101, along with a small peak at m/z 131 corresponding to [+O2 –˙OH]. Reaction is postulated to proceed via the ˙O2CH2C(OH)(CH3)CH2C(O)O− peroxyl radical intermediate depicted in Scheme 2, although there was no evidence of a product ion with mass of the stabilized peroxyl radical [+O2] at m/z 148. The assignment of the radical anion to the γ-carboxylate isomer, rather than the α-carboxylate isomer, is further supported by the absence of a carbonate radical anion signal at m/z 60 in the O2 reaction experiments. Decay of the parent ion with respect to time was followed over the course of 10 s, with the kinetics found to exhibit good pseudo first-order behavior (ESI†). These observations further support the assertion that the m/z 116 ion population consists of a single reactive isomer assigned here to the γ-carboxylate radical ion shown in Scheme 2. Finally, given the known O2 concentration of (3.1 ± 0.1) × 109 molecule cm−3 and measured first-order rate coefficient of 0.071 ± 0.001 s−1, the second-order rate coefficient for the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction can be deduced as (2.3 ± 0.1) × 10−11 cm3 molecule−1 s−1. Considering the ion–molecule collision rate of 5.9 × 10−11 cm3 molecule−1 s−1, the reaction efficiency is determined to be 3.9%.
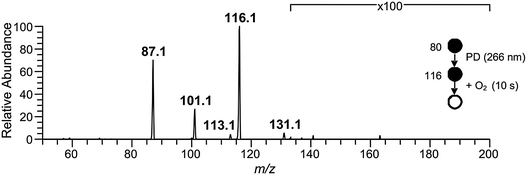 | ||
| Fig. 2 Mass spectrum resulting from the ˙CH2C(OH)(CH3)CH2C(O)O− (m/z 116) radical anion reaction with O2 after 10 s of reaction time. The m/z 116 ion was synthesized in the gas-phase following Scheme 1, and was isolated in the presence of 3.1 × 109 molecule cm−3 O2. | ||
We hypothesize that the products detected in the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction arise from chemically activated fragmentation of the ˙O2CH2C(OH)(CH3)CH2C(O)O− peroxyl radical intermediate within the low pressure conditions of the ion-trap. Vide infra, the product ion at m/z 87 is suggested to arise from concerted loss of ˙OH and formaldehyde (i.e., +O2 –˙OH –HCHO), whereas the product ion at m/z 101 is attributed to a two-stage reaction in which the ˙OH radical is first eliminated, followed by rapid decarboxylation from the vibrationally hot m/z 131 product ion population (i.e., + O2 –˙OH –CO2). The product detected at m/z 131 is suggestive of minor collisional deactivation of these [+O2 –˙OH] ions prior to decarboxylation, or the formation of a stable [+O2 –˙OH] isomer in small yield.
To gain insight into the reaction mechanism and assist with product assignments, experiments utilizing 18O2 and the deuterated isotopologue ˙CH2C(OD)(CH3)CH2C(O)O− were carried out, and the resulting mass spectra are provided in the ESI.† When ˙CH2C(OH)(CH3)CH2C(O)O− was isolated in the presence of 18O2, the major product ion previously identified at m/z 87 shifts to 89, whereas the product observed at m/z 101 remains unchanged. This indicates that the m/z 87 product is incorporating one of the oxygen atoms from 18O2, whereas the m/z 101 product does not contain any oxygen from 18O2. Note also that the minor peak observed at m/z 131 shifts to 133, consistent with loss of ˙18OH from a peroxyl radical intermediate. Exchange of the hydroxyl group to deuterated hydroxyl (OD) was achieved by electrospray of the precursor in D1-methanol. Reaction of ˙CH2C(OD)(CH3)CH2C(O)O− with O2 reveals that the product ions previously observed at m/z 87 and 101 actually each comprise two separable isomers, with peaks now appearing at m/z 87, 88, 101 and 102. Relative intensities for the m/z 87 and 88 peaks and for the m/z 101 and 102 peaks are of similar magnitude. This indicates that reactions are proceeding at similar rates via reaction at the OD group and via some other mechanism involving C–H bond activation. The minor product channel previously observed at m/z 131 remains largely unchanged, indicating that it predominantly corresponds to ˙OD loss from the peroxyl radical intermediate.
Reaction mechanism
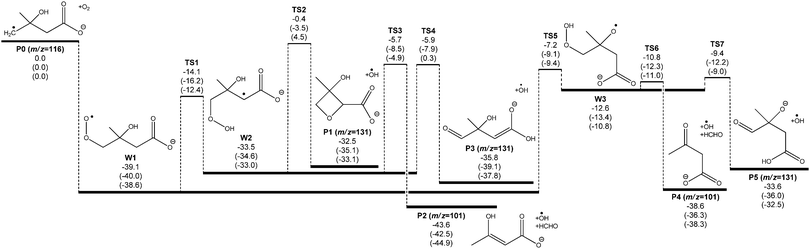
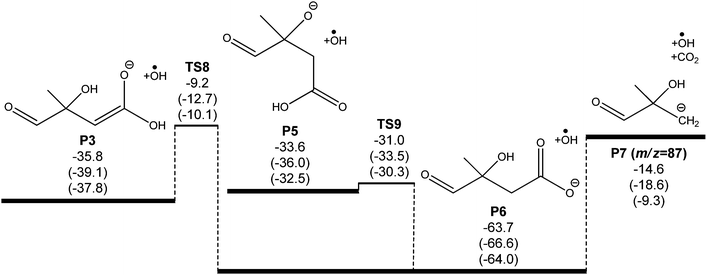
A potential energy surface for the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction system is provided in Fig. 3. Secondary decarboxylation reactions for the initial reaction products leading to CO2 loss, as will be discussed below, are demonstrated in Fig. 4. Optimized structures of the wells and transition states at the M06-2X/aug-cc-pVTZ level of theory are illustrated in Fig. 5 and 6 respectively. As can be seen in Fig. 3 and 4, the three theoretical methods are in relatively good agreement, with the G4 to G3SX and G4 to M06-2X average deviations being 2.2 kcal mol−1 and 1.6 kcal mol−1 respectively. These are consistent with the expected mean errors of 1–2 kcal mol−1.22,25,26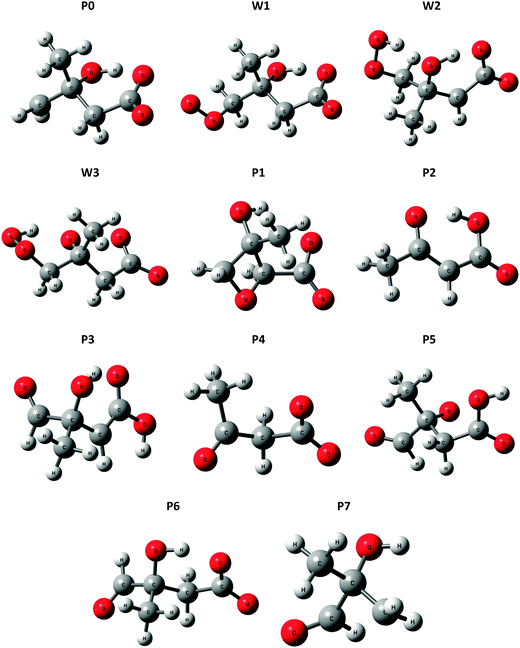 | ||
| Fig. 5 Optimized structures for wells (Wn) and product ions (Pn) in the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction system, at the M06-2X level of theory. | ||
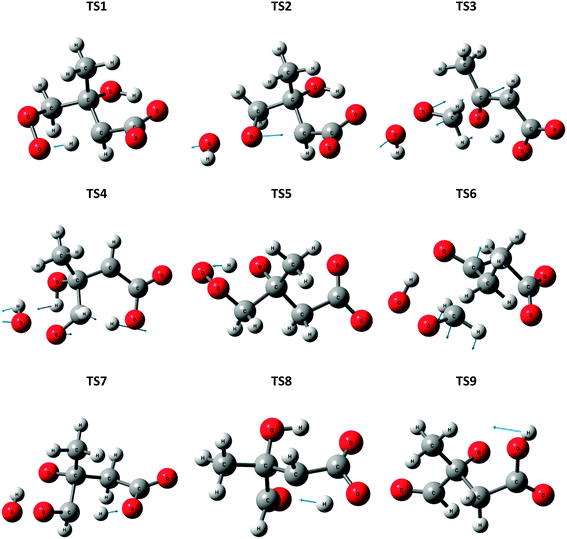 | ||
| Fig. 6 Optimized structures for transition states (TSn) in the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction system, at the M06-2X level of theory. Displacement vectors for imaginary frequencies are shown. | ||
Fig. 3 shows that the initial reaction begins with barrierless addition of O2 to the radical, resulting in formation of the β-hydroxyperoxyl radical ˙O2CH2C(OH)(CH3)CH2C(O)O− (W1). This reaction is exothermic by 39 kcal mol−1, providing the chemically activated peroxyl radical intermediate with considerable excess vibrational energy. W1 may then proceed with a series of unimolecular transformations, encountering barriers at around or below the entrance channel energy. Specifically, two branches were identified for the subsequent reactions of W1 (see Scheme 2 for nomenclature) that lead to expulsion of ˙OH through 1,5-hydrogen shifts from the γ-methylene group (Cγ abstraction) and from the β-hydroxyl group (OH abstraction).
1,5-Hydrogen abstraction from the γ-methylene group proceeds viaTS1, with a barrier around 14 kcal mol−1 below the initial reactants (or 25 kcal mol−1 above the W1 energy). This reaction produces a hydroperoxide-substituted radical anion (W2) which can decompose to three distinct product sets, labeled P1 + ˙OH, P2 + ˙OH + HCHO and P3 + ˙OH. First, homolytic substitution via the hydroperoxide group results in the four-member ring structure P1 + ˙OH. This reaction has a barrier predicted to be around that of the reactants (only 0.4 kcal mol−1 below the reactants at the G4 level) and is thus unlikely to be of major significance. Second, HCHO and ˙OH can be eliminated from W2 by β-scission (TS3), leading to an enol (P2) + ˙OH + HCHO. The barrier height here is calculated to be about 6 kcal mol−1 below the reactants. Third, an ˙OH elimination reaction – which is effectively a proton transfer from the alkyl peroxide moiety to the carboxylate group coupled with electron transfer – can also transpire (TS4), leading to an enolate anion (P3) + ˙OH. This process has analogy to the hydroxide elimination of alkyl hydroperoxides, which is driven by the weak O–O bond in the hydroperoxide group.34 The barrier associated with TS4 is very similar to that for TS3, except at the M06-2X level of theory, where it is 0.3 kcal mol−1 above the reactants. From the Cγ abstraction channel, product sets P2 + ˙OH + HCHO and P3 + ˙OH would be expected to dominate, with the relative energies of TS3 and TS4 controlling the reaction flux and subsequent branching ratios for these channels.
The significantly higher relative energy for TS4 at the M06-2X level of theory, in comparison to the composite G4 and G3SX energies is intriguing and worthy of closer examination. Our kinetic modeling (vide infra) points to a TS4 energy that should be below that of TS3, whereas the M06-2X calculations place it 5 kcal mol−1 higher. The G4 and G3SX calculations, on the other hand, result in energies for TS3 and TS4 that are almost identical. Examining the composite energy calculations, the CCSD(T) and MP4(SDTQ) energy components demonstrate an unusually large contribution from triple excitations. This component of the correlation energy dominates the other terms and is on average about 6 kcal mol−1 greater (more stabilizing) than the same triples energies in the reactant (W2) energy calculations. We suggest that the DFT calculation fails to capture a substantial component of this correlation energy resulting in a significant overestimation of the barrier height. Indeed the composite energy calculations may themselves be underestimating this correlation energy, given that the experiments suggest that TS4 is more stable than TS3.
The 1,5-hydrogen shift from the β-hydroxyl group yields a hydroperoxyalkoxyl radical anion (W3) through TS5. The barrier height is calculated to be 7 kcal mol−1 below the reactants using G4 energies, and it is about 32 kcal mol−1 above the peroxyl radical. This places it very close in energy to the controlling transition states (TS3 and TS4 in particular) in the competing Cγ abstraction channel. The hydroperoxyalkoxyl intermediate (W3) lies just below the energy of TS5, and it can also undergo a variety of fragmentations. Simple β-scission in W3viaTS6 leads to product ion P4via concerted loss of HCHO and ˙OH. The barrier height for TS6 is only 2 kcal mol−1 above W3. Alternatively, another proton transfer from the γ-methylene to the carboxylate group is available viaTS7, releasing ˙OH and yielding an oxyanion compound (P5) and ˙OH. The barrier of this reaction is also small; it is about 1 kcal mol−1 greater than the energy of TS6 but still below the energy for the initial 1,5-hydrogen shift. For the OH abstraction channel, we observe that TS5 is likely to dominate the transmission of overall reaction flux, whereas TS6 and TS7 will ultimately control the branching to products. One should also notice that other potential β-fragmentation may occur. The hydroperoxyalkoxyl radical anion (W3) can also decompose to lose ˙CH3 and ˙CH2C(O)O−. However, calculations show that the corresponding transition states for these processes are above the reactant energies and therefore not competitive. This is consistent with the experimental results observed, where there is an absence of peaks at m/z 133 and 58 respectively.
Considering the entire mechanism developed for the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction, the four expected dominant product sets originate via transition states that are all very close in energy, grouped at 5 to 10 kcal mol−1 below the reactant energies. This mechanism can explain the experimental observation of an m/z 101 product anion [+O2 –˙OH –HCHO] in the mass spectrometry experiments. However it also seems to suggest substantial formation of an m/z 131 anion [+O2 –˙OH], as opposed to the major m/z 87 product anion that is detected. This apparent discrepancy can be resolved by considering further CO2 elimination from the dominant closed-shell anions that arise from ˙OH loss in the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction (P3 and P5). An energy diagram for this process is depicted in Fig. 4, where all energies are relative to the initial reactants (˙CH2C(OH)(CH3)CH2C(O)O− + O2). Note that the ˙OH radical is included in the energy calculations (and therefore energy diagram) only so that energies are relative to the initial reactants. The ˙OH radical here is an infinitely separated product.
The oxyanion structure (P5) can readily undergo internal proton transfer (TS9) to yield a significantly more stable carboxylate anion (P6). The transition state structure here is peculiar, as the imaginary frequency corresponds to internal rotation about the carboxyl C–OH bond. Referring to Fig. 7, intrinsic reaction coordinate scans reveal that following internal rotation the proton spontaneously migrates to the O− site, exothermically generating the carboxylate anion structure (P6). From here, barrierless C–C bond scission releases CO2, leaving a carbanion (P7). This final step proceeds with the highest energy, but is about 15 kcal mol−1 below the initial ˙CH2C(OH)(CH3)CH2C(O)O− + O2 energy. Assuming prompt internal energy redistribution, and that little energy is lost via collisional deactivation or to translational energy upon ˙OH ejection, it is plausible that a significant portion of the vibrationally-hot product ion population arising from TS7 will have sufficient energy to undergo this further decarboxylation mechanism, consistent with the experimental observations. It is anticipated, however, that following dissociation the depicted carbanion (P7) would rearrange to the more stable alkoxide form CH(O)C(CH3)2O− to yield the actual product anion observed at m/z 87.
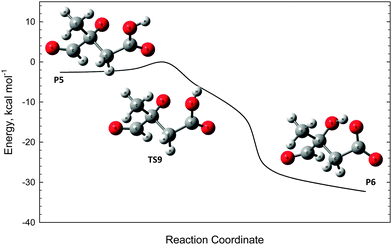 | ||
| Fig. 7 Intrinsic reaction coordinate scan for the ambiguous transition state structure TS9. The scan confirms the connectivity of TS9 to the reactant P5 and product P6. | ||
For the enolate anion (P3) produced via ˙OH loss through TS4 in the primary ˙CH2C(OH)(CH3)CH2C(O)O− + O2 mechanism, a similar decarboxylation process is available. Here, the proton transfer viaTS8 required to yield the intermediate P6 has a considerable barrier, at 10 kcal mol−1 below the starting reactants, and is likely to be the rate controlling step for decarboxylation. However, this mechanism does again provide an explanation for the observation of an m/z 87 product ion (and not m/z 131) in the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction.
The potential energy diagram can explain all major products observed experimentally from the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction. Based on the mass spectrometry analysis, the three major products from the reaction of the radical anion ˙CH2C(OH)(CH3)CH2C(O)O− + O2 have m/z of 131, 101, and 87, which corresponds to [+O2 –˙OH], [+O2 –˙OH –HCHO], and [+O2 –˙OH –CO2] respectively. The proposed mechanism is also consistent with the 18O2 experiments, with the product sets corresponding to m/z 101 (P2 + ˙OH + HCHO and P4 + ˙OH + HCHO) formed through loss of both of the added oxygen atoms, whereas the product corresponding to m/z 87 (CH(O)C(CH3)2O− + ˙OH + CO2) retains one of the atoms from O2. Because the two proposed product channels accessed via initial Cγ abstraction and OH abstraction channels yield isobaric ions, they cannot be differentiated in the mass spectrometry experiments using unlabelled ˙CH2C(OH)(CH3)CH2C(O)O−, although they can be identified in the deuterated isotopologue case (˙CH2C(OD)(CH3)CH2C(O)O−). For the latter, initial reaction via OD abstraction would always result in ˙OD loss, whereas initial abstraction from the Cγ group would yield ˙OH (see ESI† for reaction schemes). Our experiments therefore provide evidence for ˙OH (then CO2) and ˙OH + HCHO loss in the chemically activated peroxyl radical proceeding via both 1,5-hydrogen atom transfer mechanisms.
It is of interest to relate the calculations reported here to the analogous neutral peroxyl radical ˙O2CH2C(OH)(CH3)CH2C(O)OH, in which the carboxylate group has been protonated. Calculations show that the relevant product channels are still accessible, with transition states being below the entrance channel. The G4 reaction barriers of TS1 and TS5 (see Fig. 3) are 25.0 kcal mol−1 and 31.9 kcal mol−1 for the radical anion respectively. These barriers are calculated to be 28.2 kcal mol−1 and 27.7 kcal mol−1 for the neutral radical form.
Reaction kinetics
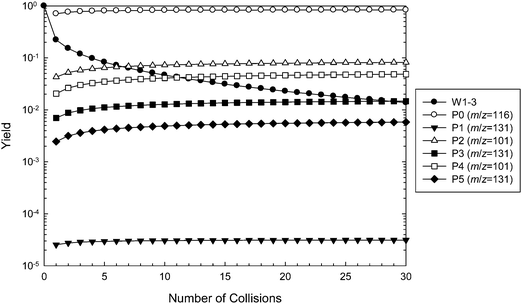
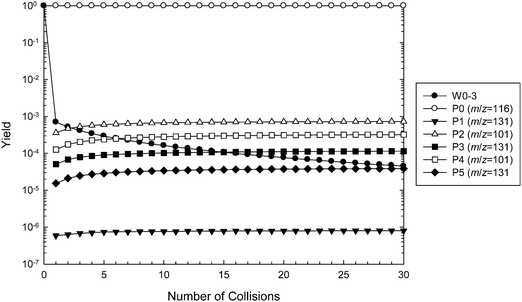
Master equation simulations were performed to further investigate the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction system and validate the theoretically proposed reaction mechanism. The M06-2X structures were used in all simulations, along with barrier heights evaluated at the three tested levels of theory (M06-2X, G3SX and G4). The simulated time evolution of the wells and products using G4 energies is illustrated in Fig. 8, with the corresponding figures using M06-2X and G3SX energies provided in ESI.† The results of these calculations are tabulated in Table 1, where they are also compared with the experimental data. The master equation modeling applies to the dissociation of initially activated ˙O2CH2C(OH)(CH3)CH2C(O)O− (W1), which can be collisionally deactivated as any of the interconnected wells (W1, W2, W3), undergo reverse reaction to ˙CH2C(OH)(CH3)CH2C(O)O− + O2, or dissociate to the five product sets corresponding to the [+O2 –˙OH –HCHO] (m/z 101) and [+O2 –˙OH] (m/z 131) channels. Note that the subsequent decarboxylation reactions of the hot m/z 131 anions are not included in the master equation modeling, and we make the assumption that this process occurs quantitatively.| k (cm3 molecule−1 s−1) | ϕ (%) | ˙OH loss (%) | ˙OH, HCHO loss (%) | |
|---|---|---|---|---|
| Experiment | 2.3 × 10−11 | 3.9 | 73 | 27 |
| Theory (G4) | 9.5 × 10−11 | 16.2 | 14 | 85 |
| Theory (G4 + pre) | 7.6 × 10−13 | 0.1 | 13 | 87 |
| Theory (G3SX) | 3.4 × 10−10 | 57.8 | 8 | 91 |
| Theory (M06-2X) | 2.1 × 10−10 | 34.8 | 7 | 90 |
Referring to Fig. 8, the relative concentration (yield) of all intermediate wells and product sets involved in the reaction are plotted as a function of number of collisions (the sum of yields is 100% at any given time). The majority (80%) of the excited adduct population dissociates back to the reactants, resulting in a predicted reaction efficiency of about 20%. This result is relatively insensitive to the level of theory. Using G4 energies, about two-thirds of the remaining peroxyl radical population is predicted to react via the Cγ abstraction channel to produce P2 + ˙OH + HCHO (54%, m/z 101) and P3 + ˙OH (10%, m/z 131), with the rest proceeding through the OH abstraction channel to yield P4 + ˙OH + HCHO (33%, m/z 101) and P5 + ˙OH (4%, m/z 131). Again, similar results are obtained at the other levels of theory. The prediction of relatively similar branching ratios between the alternative Cγ and OH abstraction channels is consistent with the isotope labeling studies. Referring to Table 1, all simulations favor the [+O2 –˙OH –HCHO] (m/z 101) product channels over [+O2 –˙OH –CO2] (m/z 87) following both hydrogen abstraction pathways, whereas the experiments find the opposite. This can be attributed to the similarity in the energies of TS3 and TS4, and TS6 and TS7, where differences are within the expected accuracy of the theoretical methods. Decarboxylation would be expected to dominate if the barriers associated with TS4 and TS7 were above those of TS3 and TS6, respectively. However, G4 energy calculations find that TS3 is 0.2 kcal mol−1 above TS4, whereas TS7 is 1.4 kcal mol−1 above TS6. Note also that in order for these results to be compatible with the experimental observations, we must assume that the vibrationally excited m/z 131 anions corresponding to product sets P3 + ˙OH and P5 + ˙OH undergo further decarboxylation to the m/z 87 product + ˙OH + CO2 almost completely. The experimental detection of some small yield of an m/z 131 product ion could perhaps be explained by P1 + ˙OH, which has a relatively large barrier height, or more likely by minor collisional deactivation of the m/z 131 ions arising from P3 + ˙OH and P5 + ˙OH.
The predicted reaction efficiency and, therefore, the rate coefficient obtained from the master equation simulations is much higher than that found experimentally. The low reaction efficiency identified for this reaction is similar to values obtained for other distonic radical reactions with O2.35 However, it is discordant with the high efficiencies measured for related α-carboxylate radical anion reactions with O2.13 Indeed, in the glycyl radical anion + O2 reaction the reaction efficiency was measured as being effectively 100%, and this number could be accurately reproduced by master equation simulations similar to those carried out here.13 The low reaction efficiency measured in the present work indicates some additional restriction to peroxyl radical formation, resulting in significant reflection of the nascent [C5O5H8˙−]* adduct population back to ˙CH2C(OH)(CH3)CH2C(O)O− + O2 before the peroxyl radical can form and subsequently dissociate to new products. To incorporate this phenomenon into our reaction rate model we investigated the possibility of a pre-reaction complex occurring along the O2⋯˙CH2C(OH)(CH3)CH2C(O)O− reaction coordinate. Although a pre-reaction complex was not identified at the M06-2X/6-31G(2df,p) level of theory, one could be located when diffuse basis functions were added to the basis set (i.e., 6-31+G(2df,p)). Referring to Fig. 9, this pre-reaction complex sits at 0.7 kcal mol−1 below the reactant energy. A transition state structure was also identified just 0.06 kcal mol−1 above the complex energy, or 0.15 kcal mol−1 below it when zero point energies are included. It is of relevance to note that the inclusion of diffuse functions has a negligible effect on both structure and energy of the reactants ˙CH2C(OH)(CH3)CH2C(O)O− + O2 or the peroxyl radical CH2C(OH)(CH3)CH2C(O)O− themselves.
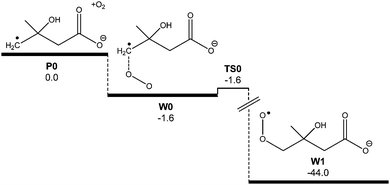 | ||
| Fig. 9 Ab initio potential energy surface of the proposed pre-reaction complex W0. Energies at 0 K (E0) are provided at the M06-2X/6-31+G(2df,p) level of theory in kcal mol−1. | ||
This new two-transition-state model of ˙O2CH2C(OH)(CH3)CH2C(O)O− formation was incorporated into the master equation model. The results of the new simulations are depicted in Fig. 10 using G4 energies, and are also included in Table 1. We now observe major reflection of the chemically activated peroxyl radical population back to the reactants, with only around 0.1% of the adduct going on to form new products. All other product channels are predicted to form in the same preferential order as shown in Fig. 9. This presence of the pre-reaction complex dramatically reduces the calculated rate coefficient, with the predictions now being slower than expected. This would appear to support the presence of a lower lying pre-reaction complex than that identified here, or merely an inflection on the bond dissociation potential, and more in-depth variational transition state theory modeling may be necessary to better describe this behavior.
Conclusion
A distonic β-hydroxylalkyl radical analogue ˙CH2C(OH)(CH3)CH2C(O)O− has been generated by ion-trap mass spectrometry. Reaction of the β-hydroxylalkyl radical in the presence of O2 proceeded with a second order rate of 2.3 × 10−11 cm3 molecule−1 s−1 corresponding to a reaction efficiency of 3.9%. Products were identified consistent with initial formation of a β-hydroxyalkylperoxyl radical that may undergo facile unimolecular decomposition reactions via 1,5-hydrogen atom abstractions from the γ-methylene and β-hydroxyl positions to yield ions at m/z 131, 101 and 87 due to neutral loss of ˙OH, ˙OH + HCHO, and ˙OH + CO2, respectively. A theoretical study of the reaction mechanism revealed pathways to all major experimental products, and master equation simulations were performed to gain further insight into the reaction kinetics and product branching. In several of the mechanisms identified, the charge tag (–CO2−) does not participate directly in the transformation (pathways to P1, P2 and P4 formation in Fig. 3) suggesting that these pathways may have analogy for the neutral system. While we are cognizant that even remote anions can influence radical stability and thus energetics,36,37 the proposed reaction mechanism of the ˙CH2C(OH)(CH3)CH2C(O)O− + O2 reaction still serves as a model to reveal the unimolecular decomposition chemistry of peroxyl radicals formed in biogenic VOC oxidation that can replenish ˙OH in the troposphere.Acknowledgements
The authors are grateful to the Australian Research Council for funding through the Discovery Project (DP110103889 [GdS], DP140101237 [SJB], DP130100862 [AJT & GdS]), Centre of Excellence Grant (CE0561607 [SJB]) and Future Fellowship (FT130101304 [GdS]) schemes.References
- D. Pierotti, S. Wofsy, D. Jacob and R. Rasmussen, J. Geophys. Res., 1990, 95, 1871–1881 CrossRef CAS.
- S. Montzka, M. Trainer, P. Goldan, W. Kuster and F. Fehsenfeld, J. Geophys. Res., 1993, 98, 1101–1111 CrossRef CAS.
- C. Warneke, R. Holzinger, A. Hansel, A. Jordan, W. Lindinger, U. Pöschl, J. Williams, P. Hoor, H. Fischer and P. Crutzen, J. Atmos. Chem., 2001, 38, 167–185 CrossRef CAS.
- M. Claeys, B. Graham, G. Vas, W. Wang, R. Vermeylen, V. Pashynska, J. Cafmeyer, P. Guyon, M. O. Andreae and P. Artaxo, Science, 2004, 303, 1173–1176 CrossRef CAS PubMed.
- J. H. Kroll, N. L. Ng, S. M. Murphy, R. C. Flagan and J. H. Seinfeld, Environ. Sci. Technol., 2006, 40, 1869–1877 CrossRef CAS.
- D. K. Henze and J. H. Seinfeld, Geophys. Res. Lett., 2006, 33, L09812 CrossRef.
- N. Poisson, M. Kanakidou and P. J. Crutzen, J. Atmos. Chem., 2000, 36, 157–230 CrossRef CAS.
- D. Tan, I. Faloona, J. B. Simpas, W. Brune, P. B. Shepson, T. L. Couch, A. L. Sumner, M. A. Carroll, T. Thornberry, E. Apel, D. Riemer and W. Stockwell, J. Geophys. Res., 2001, 106, 24407–24427 CrossRef CAS.
- G. da Silva, C. Graham and Z. F. Wang, Environ. Sci. Technol., 2009, 44, 250–256 CrossRef PubMed.
- J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939 RSC.
- B. B. Kirk, D. G. Harman and S. J. Blanksby, J. Phys. Chem. A, 2009, 114, 1446–1456 CrossRef PubMed.
- B. B. Kirk, D. G. Harman, H. I. Kenttämaa, A. J. Trevitt and S. J. Blanksby, Phys. Chem. Chem. Phys., 2012, 14, 16719–16730 RSC.
- G. da Silva, B. B. Kirk, C. Lloyd, A. J. Trevitt and S. J. Blanksby, J. Phys. Chem. Lett., 2012, 3, 805–811 CrossRef CAS.
- M. B. Prendergast, P. A. Cooper, B. B. Kirk, G. da Silva, S. J. Blanksby and A. J. Trevitt, Phys. Chem. Chem. Phys., 2013, 15, 20577–20584 RSC.
- C. H. Li, G. N. Khairallah, A. K. Lam, R. A. O'Hair, B. B. Kirk, S. J. Blanksby, G. da Silva and U. Wille, Chem. – Asian J., 2013, 8, 450–464 CrossRef CAS PubMed.
- G. N. Khairallah, R. A. O'Hair and U. Wille, J. Phys. Chem. A, 2014, 118, 3295–3306 CrossRef CAS PubMed.
- T. Ly, B. B. Kirk, P. I. Hettiarachchi, B. L. Poad, A. J. Trevitt, G. da Silva and S. J. Blanksby, Phys. Chem. Chem. Phys., 2011, 13, 16314–16323 RSC.
- D. G. Harman and S. J. Blanksby, Org. Biomol. Chem., 2007, 5, 3495–3503 CAS.
- T. Ly and R. R. Julian, Angew. Chem., Int. Ed., 2009, 48, 7130–7137 CrossRef CAS PubMed.
- T. Y. Kim, M. S. Thompson and J. P. Reilly, Rapid Commun. Mass Spectrom., 2005, 19, 1657–1665 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern, K. Raghavachari and J. A. Pople, J. Chem. Phys., 2001, 114, 108 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126, 084108 CrossRef PubMed.
- J. MultiWell-2013 Software, designed and maintained by J. R. Barker with contributors N. F. Ortiz, J. M. Preses, L. L. Lohr, A. Maranzana, P. J. Stimac, T. L. Nguyen and T. J. Dhilip Kumar, University of Michigan, Ann Arbor, MI; http://aoss.engin.umich.edu/multiwell/.
- J. R. Barker, Int. J. Chem. Kinet., 2001, 33, 232–245 CrossRef CAS.
- J. R. Barker, Int. J. Chem. Kinet., 2009, 41, 748–763 CrossRef CAS.
- A. K. Y. Lam, C. Li, G. Khairallah, B. B. Kirk, S. J. Blanksby, A. J. Trevitt, U. Wille, R. A. J. O'Hair and G. da Silva, Phys. Chem. Chem. Phys., 2012, 14, 2417–2426 RSC.
- D. M. Golden, Int. J. Chem. Kinet., 2013, 45, 213–220 CrossRef CAS.
- H. Durchschlag and P. Zipper, Ultracentrifugation, Springer, 1994, pp. 20–39 Search PubMed.
- D. M. Golden, Int. J. Chem. Kinet., 2009, 41, 573–581 CrossRef CAS.
- S. J. Blanksby, G. B. Ellison, V. M. Bierbaum and S. Kato, J. Am. Chem. Soc., 2002, 124, 3196–3197 CrossRef CAS PubMed.
- B. B. Kirk, A. J. Trevitt, B. L. Poad and S. J. Blanksby, Int. J. Mass Spectrom., 2013, 351, 81–94 CrossRef CAS PubMed.
- G. Gryn'ova, D. L. Marshall, S. J. Blanksby and M. L. Coote, Nat. Chem., 2013, 5, 474–481 CrossRef PubMed.
- G. Gryn'ova and M. L. Coote, J. Am. Chem. Soc., 2013, 135, 15392–15403 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Mass spectrometry of the photodissociation and collision induced dissociation to produce the target radical anion. Master equation simulation with and without pre-reaction complex using M06-2X and G3SX barrier heights at 307 K and 2.5 mTorr He. Optimized geometries, vibrational frequencies and moments of inertia of the wells and transition states at M06-2X level of theory. Reaction schemes of the isotope labeling experiments. See DOI: 10.1039/c4cp02981j |
| ‡ Present address: Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. |
| This journal is © the Owner Societies 2014 |