Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct observation of OH formation from stabilised Criegee intermediates†
A.
Novelli
,
L.
Vereecken
,
J.
Lelieveld
and
H.
Harder
*
Atmospheric Chemistry Dept., Max Planck Institute for Chemistry, 55128 Mainz, Germany. E-mail: hartwig.harder@mpic.de
First published on 7th August 2014
Abstract
The syn-CH3CHOO Criegee intermediate formed from the ozonolysis of propene and (E)-2-butene was detected via unimolecular decomposition and subsequent detection of OH radicals by a LIF-FAGE instrument. An observed time dependent OH concentration profile was analysed using a detailed model focusing on the speciated chemistry of Criegee intermediates based on the recent literature. The absolute OH concentration was found to depend on the steady state concentration of syn-CH3CHOO at the injection point while the time dependence of the OH concentration profile was influenced by the sum of the rates of unimolecular decomposition of syn-CH3CHOO and wall loss. By varying the most relevant parameters influencing the SCI chemistry in the model and based on the temporal OH concentration profile, the unimolecular decomposition rate k (293 K) of syn-CH3CHOO was shown to lie within the range 3–30 s−1, where a value of 20 ± 10 s−1 yields the best agreement with the CI chemistry literature.
Introduction
Criegee intermediates (CI, carbonyl oxides) are key intermediates in the atmospheric ozonolysis of unsaturated compounds. This class of reactions has been studied for many years1 because of its importance in the oxidation of volatile organic compounds (VOC) in the boundary layer, and plays a key role in the formation of free radicals and secondary organic aerosol.2 Ozonolysis of alkenes in the gas phase proceeds via the Criegee mechanism3,4 depicted in Fig. 1. The addition of ozone across the double bond forms a primary ozonide (POZ) which quickly decomposes forming a Criegee intermediate (CI) and a carbonyl compound. The fate of the Criegee intermediate depends on its nascent energy content, which we broadly divide in two populations:4–6 thermally stabilized and chemically activated. The chemically activated Criegee intermediate has a high energy content and therefore a comparatively short lifetime. Typically, it will decompose through the vinyl hydroperoxide (VHP) or ester channels discussed below, though depending on the reaction rates at the given energy and the rate of energy loss in collisions with the bath gas, it can form a stabilised Criegee intermediate (SCI). For example, chemically activated CH2OO will mostly decompose, as the internal energy is distributed across only a few degrees of freedom, leading to very fast unimolecular reactions, while larger CI such as those obtained from terpenoid ozonolysis will mostly stabilise at 1 atm. The SCI has a longer lifetime owing to its lower thermal energy content: in the atmosphere its fate depends on the competition between unimolecular decomposition and reaction with atmospheric trace gases. The two main unimolecular decomposition channels accessible to both chemically activated and stabilised CI are the ester and the VHP channel, whose contributions depends on the substituents on the carbonyl carbon atom and their orientation relative to the outer CI oxygen atom7 (Fig. 1). CI can isomerise by ring closure, forming a dioxirane that in turn re-isomerizes to an ester or an acid; for small alkenes these latter compounds will receive enough internal energy to immediately decompose forming CO2, OH, CO, HO2, H2O and alkyl fragments. If the outer oxygen is pointing towards a suitable H-atom such as in an alkyl group (syn-CI) a faster 1,4-H-shift is accessible, yielding a vinyl hydroperoxide which promptly decomposes forming OH and a vinoxy radical.2,5,8,9 This path is a major non-photolytic source of OH radicals in the atmosphere10–12 and appears to be especially important during winter, at night and indoors.13 CI with more complex substituents are subject to additional unimolecular rearrangements.7 For the CI discussed in this paper, syn-CI yield OH radicals through the VHP channel, while anti-CI and CH2OO rearrange through the ester channel. | ||
| Fig. 1 Cycloaddition of ozone across an unsaturated compound and potential fates of the Criegee intermediate formed. | ||
Historically2 it was assumed that the fate of SCI formed in the atmosphere would mainly be reaction with water or unimolecular decomposition.14 Several laboratory studies during the last two years15–22 report measured rate coefficients for the reaction between SCI and several atmospheric trace gases such as SO2, NO, NO2, H2O, acetone, acetaldehyde and organic acids. For some coreactants, these studies have reported larger rate coefficients than expected.23 Likewise, CI photolysis reactions were shown to occur24,25 on a time scale similar to measured CI decomposition.26,27 Theoretical work7,28–31 suggested the possible importance of reactions between SCI and ozone, RO2, alcohols, OH, HO2, and self reaction. The use of these updated rate coefficients in simple model analysis13,20,32–37 reveals how, depending on the environment, the loss of some of the SCIs analysed is not only caused by reaction with water, but includes a number of other trace gases, indicating that SCIs might impact oxidation processes in the atmosphere. As highlighted by Taatjes et al.13 SCI have not yet been directly observed in the atmosphere. Still, SCI have been invoked to explain additional oxidation of SO2 in the boreal forest,38 and as the cause of internally generated OH within a LIF (laser induced fluorescence) FAGE (fluorescence assay by gas expansion) instrument39 measuring in a forest. During ambient measurements using a LIF-FAGE system we also detected a sizable background signal in a number of environments,40 which may owe its presence to the detection of ozonolysis products.
In this paper, we demonstrate the direct formation of OH radicals from SCI decomposition within a LIF-FAGE instrument, presenting results from the reaction of ozone with propene, (E)-2-butene and ethene as SCI sources. The time-dependent OH profiles are analyzed using a detailed chemical model including updated chemistry of CI, yielding an upper and lower limit for the syn-SCI decomposition rate. The relevance for atmospheric chemistry and for OH measurements based on LIF-FAGE instruments is discussed.
Methodology
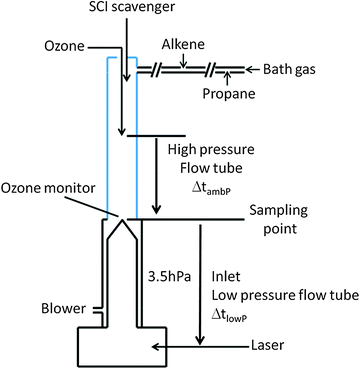
a. Laboratory instrumentation
The ozonolysis experiments (Fig. 2) were carried out in a quartz flow tube (inner diameter 4.5 cm; length 50 cm) at ambient pressure (980 hPa) and temperature (293 K) using nitrogen (Westfalen, 99.999%) with 5% of oxygen (Westfalen, 99.999%) as a bath gas. The flow tube is directly connected to the inlet of the LIF-FAGE instrument used to measure the concentration of OH during the experiments. A blower was connected to the base of the flow tube after the sampling position of the LIF-FAGE instrument in order to assure sampling from the center and reduce wall effects. The resulting gas flow of nitrogen in the flow tube was 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 sccm. By titrating OH with methane at the flow conditions described above, the residence time in the flow tube at ambient pressure (ΔtambP) was measured to be 2.5 s. Ozone was produced outside the tube by passing pure oxygen in front of a mercury UV lamp (Hg(Ar) Pen Ray lamp) and was injected together with nitrogen to improve the mixing in the center of the flow tube. The initial ozone concentration in the flow tube was monitored using an ultraviolet photometric ozone analyser (Thermo Environmental Instruments: 49C) by measuring the attenuation of light in the absorption cell at a wavelength of 254 nm.
000 sccm. By titrating OH with methane at the flow conditions described above, the residence time in the flow tube at ambient pressure (ΔtambP) was measured to be 2.5 s. Ozone was produced outside the tube by passing pure oxygen in front of a mercury UV lamp (Hg(Ar) Pen Ray lamp) and was injected together with nitrogen to improve the mixing in the center of the flow tube. The initial ozone concentration in the flow tube was monitored using an ultraviolet photometric ozone analyser (Thermo Environmental Instruments: 49C) by measuring the attenuation of light in the absorption cell at a wavelength of 254 nm.
The alkenes tested were ethene (Air Liquide, 99.99+%), propene (pure, Aldrich 295663, 99+% and Air Liquide 10% in nitrogen) and (E)-2-butene (Sigma-Aldrich, 295086, 99+%). The alkenes were added via a MFC and injected in a stream flow of nitrogen to enhance the mixing and then injected at the top of the tube. Additionally, propane (Westfalen 3.5, 99.95% purity) was used to scavenge the OH radicals formed at ambient pressure in the flow tube and was added directly in the stream flow of nitrogen. A mixture of SO2 in synthetic air (Air Liquide, 2%) was used as a SCI scavenger during some experiments as well as acetic acid (AppliChem, 96%) and water vapor. The flow of SO2 was controlled with an MFC and injected at the top of the flow tube, while acetic acid vapour was added to the flow tube by passing a small flow of nitrogen through a bubbler filled with bulk acetic acid. Water vapor was produced by passing nitrogen through a bubbler filled with deionized water and the concentration of water vapor in the flow tube was measure with a high-precision chilled mirror dew point hygrometer (Michell Instruments, model S4000).
The OH concentration was measured with HORUS (Hydroxyl Radical Measurement Unit based on fluorescence Spectroscopy), the LIF-FAGE instrument in use at the Max Planck Institute for Chemistry in Mainz described in detail elsewhere.40,41 Only a brief description highlighting the features particularly relevant for the current experiments is given. The inlet sampled the reaction mixture with a 1 mm nozzle pinhole from the centre of the flow tube. The OH radical was detected in the low-pressure segment of the instrument (∼3.50 hPa) by measuring the fluorescence signal after excitation with a UV pulsed light at around 308 nm. The temperature in the low-pressure segment of the instrument was measured with a thermistor positioned in the center of the air flow and, at a distance of 13 cm from the pinhole and beyond, is equal to ambient temperature, ∼293 K. Shorter distances could not be examined due to practical limitations. The pressure in the detection axis was sufficiently low to prevent most of the bimolecular reactions (see below). In order to avoid formation of OH radical in the detection cell of the instrument via reactions initiated by the laser beam, such as photolysis of ozone, and formation of OH radicals after reaction of O(1D) with water molecules, the repetition rate of the Nd:YAG laser was 1500 Hz. With this repetition rate, the residence time of the air sample in the detection cell was five times shorter than the time period between two laser pulses.
By using different inlet lengths it was possible to measure the concentration of OH after different “residence” times inside the low pressure segment of the instrument (ΔtlowP), between the sampling point and the laser beam. To characterize the residence time, a Nd:YAG laser (Quantel Brilliant) at 266 nm and with a 6 ns laser pulse was used to produce OH directly in front of the inlet nozzle by photolysis of ozone and the subsequent reaction of O(1D) with water. The residence time of the OH produced was measured using a Turbo-MCS (multichannel scaler, EG&G ORTEC's) and by starting the scan at the pulse of the Brilliant laser. An OH concentration profile in time was obtained and the maximum occurrence of OH concentration was adopted as the residence time. The test was repeated for all inlet lengths used during the experiments and results are shown in Fig. S1 (ESI†).
b. Characterization of wall losses
In order to improve the understanding about the origin of the OH signal in the LIF-FAGE instrument and to better characterize the evolution of the hydroxyl radicals (HOx) in the low-pressure region of the instrument, tests to determine the losses of OH and hydroperoxyl radical (HO2) inside the instrument have been performed. The HOx radicals have been produced before the inlet by passing humidified air in front of a mercury lamp with a known actinic flux and in the setup used to calibrate the instrument for field measurement, as described elsewhere.41 OH was detected as described in the previous section while HO2 was detected as OH after reaction with nitric oxide (NO) injected immediately before the detection cell.42 Wall losses of radicals as a function of residence time were determined by varying the injection position at a constant radical concentration and the results are shown in Fig. S2 and S3 (ESI†) for OH and HO2 respectively. By using a chi-square fit an effective “unimolecular” loss rate on walls of 55 s−1 for OH and 26 s−1 for HO2 was extrapolated.c. Box model
The results obtained from the different experiments were compared against the results of a box model based on the Master Chemical Mechanism (MCM) version 3.2,43,44 available at http://mcm.leeds.ac.uk/MCM, and the simulations were integrated using FACSIMILE.45 To simulate our experiments, ethene, propene and (E)-2-butene MCM schemes were modified and extended to fully describe production and destruction of speciated stabilized and excited CI formed in the ozonolysis. The full mechanism for the alkenes studied is presented in the ESI.† The main extensions concerning the CI formation are the inclusion of direct formation of thermal SCI, and explicit speciation of different CI conformers (syn and anti) which effectively act as different species owing to the high barrier (over 20 kcal mol−1) for syn–anti isomerisation.7,46 The yields of formation of OH and SCIs were guided by the values used in the MCM scheme (Table 1). As there is quite a large uncertainty between different studies on the SCI yields we allowed the value to change between 0.3547 and 0.548 for ethene, 0.1649 and 0.3548 for propene and 0.1549 and 0.426 for (E)-2-butene in the sensitivity studies on model parameters (Table 1). Yields of formation of syn relative to anti SCI were based on theoretical50,51 and experimental52 studies when available (Table 1). Given the high uncertainty we varied these yields in the sensitivity study by a factor of 4 to estimate their impact on the model results. Another important difference with the MCM is the inclusion of a larger number of bimolecular reactions involving SCI based on recent experiments16,17,19,21,26 and theoretical studies28,31,33 (Table 2). In Table 2 the values of the CI-specific rate coefficients with H2O and (H2O)2, the relative rate predictions by Anglada et al.53 and Ryzhkov and Ariya,54 were scaled to match the absolute value for anti-CH3CHOO + H2O as measured by Taatjes et al.16 The unimolecular decomposition rate coefficient of SCI is highly uncertain, with literature data16,26,48,55 spanning well over an order of magnitude; we estimate this rate parameter from the comparison of model and experiment together with wall losses of SCI, which could not be experimentally determined; these two parameters are strongly coupled in our analysis (see below). Wall-losses of OH (55 s−1) and HO2 (26 s−1) in the low-pressure segment of the instrument as determined earlier were also included in the model. The concentrations of alcohols, aldehydes, ketones, organic acids and peroxides formed during the ozonolysis were summed to allow for their reactions with SCI. The initial conditions for each of the experiments, as shown in Table 3, were used for the initialization of the corresponding box models. The box model runs are not used to obtain optimal fits of kinetic parameters to the observations; rather, we adhere as much as possible to the available literature data, and analyze the experimental data against this model, within the respective margins of the uncertainty, to elucidate the underlying chemistry and to obtain uncertainty intervals for the rate of unimolecular decomposition.| Alkenes | SCIa | SCI yield rangeb | Ratio range a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cb,c (ref. 50–52) cb,c (ref. 50–52) |
|---|---|---|---|
| a As used in the MCM mechanism. b Range of values examined for the SCI yield, and for the ratios of the different SCI during the sensitivity study of the model (see main text). c The yields are showed as a fraction of the total SCI yield. | |||
| Ethene | 0.4 | 0.35–0.5 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0–1 0–1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| Propene | 0.24 | 0.16–0.35 | 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0–0.5 0.0–0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 0.4 |
| (E)-2-Butene | 0.18 | 0.15–0.4 | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2–0 0.2–0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 0.8 |
| Coreactants | CI | k (298 K) | Ref. |
|---|---|---|---|
| a Range of values from experimental studies. | |||
| H2O | H2COO | 2 × 10−16 cm3 s−1 | 41 |
| syn-CH3CHOO | 2 × 10−19 cm3 s−1 | 53 | |
| anti-CH3CHOO | 1 × 10−14 cm3 s−1 | 16 | |
| (H2O)2 | H2COO | 7 × 10−11 cm3 s−1 | 33, 54, 73 |
| syn-CH3CHOO | 3 × 10−14 cm3 s−1 | 33, 54, 73 | |
| anti-CH3CHOO | 5 × 10−11 cm3 s−1 | 33, 54, 73 | |
| Ketones | All | 2 × 10−13 cm3 s−1 | 17 |
| Aldehydes | All | 1 × 10−12 cm3 s−1 | 19 |
| Hydroxyl compounds | All | 5 × 10−12 cm3 s−1 | 33 |
| Carboxylic acids | All | 2.5 × 10−10 cm3 s−1 | 22 |
| Ethene | H2COO | 6 × 10−16 cm3 s−1 | 21 |
| Propene | H2COO | 2 × 10−15 cm3 s−1 | 21 |
| syn-CH3CHOO | 2 × 10−18 cm3 s−1 | 28 | |
| anti-CH3CHOO | 9 × 10−15 cm3 s−1 | 28 | |
| (E)-2-Butene | syn-CH3CHOO | 1.7 × 10−19 cm3 s−1 | 28 |
| anti-CH3CHOO | 1.4 × 10−15 cm3 s−1 | 28 | |
| NO2 | All | 2 × 10−12 cm3 s−1 | 16, 19 |
| SO2 | H2COO | 4 × 10−11 cm3 s−1 | 15 |
| syn-CH3CHOO | 2 × 10−11 cm3 s−1 | 16 | |
| anti-CH3CHOO | 7 × 10−11 cm3 s−1 | 16 | |
| O3 | All | 4 × 10−13 cm3 s−1 | 74 |
| CO | All | 4 × 10−14 cm3 s−1 | 33 |
| OH | All | 5 × 10−12 cm3 s−1 | 33 |
| HO2 | All | 5 × 10−12 cm3 s−1 | 33 |
| RO2 | All | 5 × 10−12 cm3 s−1 | 33 |
| Organic peroxides | All | 3 × 10−12 cm3 s−1 | 74 |
| Decomposition | All syn-CI | 3–76a s−1 | 48, 55 |
| H2COO | H2COO | 4 × 10−10 cm3 s−1 | 30 |
| CI + CI | All | 3 × 10−11 cm3 s−1 | 21 |
| Species | Alkenes [molecules cm−3] | SCI scavengera |
|---|---|---|
| Propane and ozone concentrations were 2.5 × 1016 and 1.3 × 1013 molecules cm−3, respectively, for all experiments unless indicated.a Added during some experiments. | ||
| Ethene | 1.1 × 1016 | Water vapor |
| Propene | 3.5 × 1015 | Water vapor, SO2 |
| 1.8 × 1015 | ||
| (E)-2-Butene | 1.4 × 1015 | SO2, acetic acid |
Results
a. Comparison of model and experiment
The qualitative comparison of the kinetic box model results against the experimental data is based on the absolute OH concentration and its time dependence. As shown below for each of the reaction systems, the OH concentration time profile in the low pressure flow tube is determined primarily by (pseudo) first order reaction kinetics, i.e., wall losses and unimolecular decay of SCI and OH radicals. Hence, the absolute height of the OH profile predicted by the model is determined mainly by the SCI steady state concentration [SCI]SS at the sample point. Many kinetic parameters in the model that determine this steady state concentration carry a comparatively large uncertainty: rate coefficients for SCI unimolecular and bimolecular reactions, the yield of SCI and its speciation into syn- and anti-SCI in the ozonolysis reaction, etc. The uncertainties of each of these parameters only affect the model to experiment intercomparison to the extent to which they affect [SCI]SS, and hence can be lumped into an uncertainty factor governing this [SCI]SS. In this work, we allow for the steady state concentration to be adjusted by a small factor to fit the absolute profile heights.The time profile of the OH signal shows a steep rise of the OH concentration by SCI decomposition until steady state is reached with OH loss processes, followed by a slower decay of the steady-state OH signal by depletion of the SCI. This time dependence is determined mostly by the ratio of total SCI loss to OH loss rates, where the OH wall loss has been measured directly, and the bimolecular reactions of OH operate under pseudo first order conditions and have well known rate coefficients. This indicates that the uncertainty of the time dependence in our model is sensitive mostly to the sum kuni(SCI → OH) + kwall(SCI) of unimolecular SCI decomposition to OH and wall losses, respectively. The contribution of each parameter in this sum affects the absolute OH signal, but this cannot be distinguished from uncertainties of [SCI]SS at the sample point; this makes it infeasible to derive an accurate unimolecular rate coefficient for OH formation from syn-SCI from our present set of data.
A quantitative uncertainty analysis is given below.
b. Propene
Fig. 3 shows a typical evolution of the OH radical concentration measured with our LIF-FAGE instrument averaged over several experiments of propene ozonolysis (red bullets), and compared to a model simulation (black line). The model reproduces the experimental data within their uncertainty ranges, as discussed in more detail below. The model adequately simulates the observed data with injection of different propane concentrations in the flow tube (Fig. S4, ESI†). The modelling study shows that at ambient pressure the OH radical (Fig. S5a, ESI†) is formed mainly by unimolecular decomposition of chemically activated syn-CH3CHOO, and removed quickly by propene and propane scavengers, leading to a negligible OH concentration. Stabilized syn-CH3CHOO (Fig. S6a, ESI†) formed in the ozonolysis of propene attains a slowly decreasing steady state concentration, where the relative contributions of the individual loss reactions change with time owing to the change in concentration of the bimolecular coreactants. The main loss paths are unimolecular decomposition and reaction with ozone, whereas reaction with organic peroxy radicals (RO2), alcohols, aldehydes and organic peroxides become more important at later reaction times. As the rate coefficients for these reactions are uncertain, a number of different scenarios will be discussed in detail later. In the low pressure region inside the inlet (Fig. S6b, ESI†) the ozonolysis reaction is effectively stopped, such that there is no additional formation of SCIs. Their losses are governed by the unimolecular decomposition and wall losses. Unimolecular decomposition of syn-CH3CHOO is the dominant source, >95%, of the OH radicals observed, while OH loss is determined by residual scavenging by propene and propane, and by wall loss (Fig. S5b, ESI†). The degree of OH scavenging was varied in a series of experiments with lower propene concentrations and with different addition of propane (Fig. S7, ESI†). By using lower concentrations of propene, the OH concentration profile shows a less steep decrease slope as implied by the reduced removal of OH. The box model again reproduces these data, indicating that OH loss is simulated realistically. Table S1 (ESI†) lists the predicted concentrations of SCIs at the sampling point together with the peak concentration of OH observed for the different experiments. | ||
| Fig. 3 Temporal profile of the OH signal (red bullets) inside the detection cell of the LIF-FAGE instrument for the ozonolysis reaction of propene, and the model simulation (black line). | ||
c. (E)-2-Butene
Fig. 4 shows the evolution of the average OH radical concentration measured with our LIF-FAGE instrument during several experiments of ozonolysis of (E)-2-butene (red bullet) compared with a model simulation (black line). The agreement between the experimental data and the model simulation is good for different amounts of propane (Fig. S8, ESI†) and (E)-2-butene (Fig. S9, ESI†). The reactions impacting the steady state concentration of OH radicals at ambient and low pressure are analogous to the propene experiment, as well as the profile of the syn-CH3CHOO at low pressure. Likewise, the factors influencing the steady state concentration of the SCI in the ambient pressure region are similar (Fig. S10, ESI†) with unimolecular decomposition and reaction with O3 and RO2 being the main loss processes for syn-CH3CHOO at the beginning of the flow tube, and with the relative importance of reactions with aldehydes, alcohols and peroxides increasing when approaching the sample point. Similar to the propene experiment the relative importance and contribution of the coreactants towards the total losses of syn-CH3CHOO depends on its unimolecular decomposition rate, and different scenarios will be discussed later. Table S2 (ESI†) lists the predicted concentrations of SCIs at the sampling point together with the peak concentration of OH observed for the different experiments.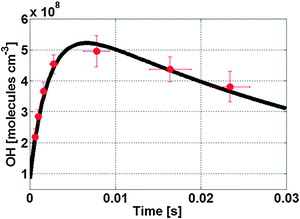 | ||
| Fig. 4 Temporal profile of the OH signal (red bullets) inside the detection cell of the LIF-FAGE instrument for the ozonolysis reaction of (E)-2-butene, and model simulation (black line). | ||
d. Ethene
The ozonolysis reaction of ethene does not form SCI that are expected to decompose thermally to OH, and hence this reaction serves as a blank experiment quantifying the formation of OH from the basic alkene ozonolysis reaction intermediates and from the CH2OO SCI also formed in propene ozonolysis. Fig. S11 (ESI†) shows that the OH concentration quickly grows to 6.5 × 106 molecules cm−3, observed after ∼1 ms, and then decreases quickly. These concentrations are a factor of 20–100 below those observed for propene and (E)-2-butene, indicating that this OH contribution is negligible in the latter experiments. By increasing the amount of propane injected in the flow tube (Fig. S12, ESI†) we observe a decrease in the measured OH concentration, showing clearly that some residual OH scavenging occurs in the low pressure region of the LIF-FAGE, affecting the OH time profile.e. Experiments with SCI scavengers
In some experiments water vapor, SO2 and acetic acid were used to scavenge the SCIs: water vapor reacts with different Criegee intermediate conformers at different rates spanning from 1 × 10−14 cm−3 molecules−1 s−1 for the reaction with anti-CH3CHOO16 to less than 4 × 10−15 cm−3 molecules−1 s−1 and 9 × 10−17 cm−3 molecules−1 s−1 for reaction with syn-CH3CHOO16 and CH2OO,19 respectively. SO2 and acetic acid both react very fast with SCI,16,22 ∼4 × 10−12 cm−3 molecules−1 s−1 and ∼2.5 × 10−10 cm−3 molecules−1 s−1, respectively, and do not show a large difference in rate between different SCI conformers. These experiments were completed with the inlet length normally used during measurements of OH radicals in the atmosphere (14 cm inlet, 2.4 ms residence time). Fig. S13 (ESI†) shows the decay of the OH signal observed during ozonolysis of propene with addition of water vapor between 0 and 2.3 × 1017 molecules cm3. With the addition of similar concentrations of water vapor no change in the OH signal was detected during the ozonolysis of ethene. Fig. S14 (ESI†) shows the disappearance of the OH peaks over the background spectrum with the addition of SO2 during ozonolysis of propene. Precise determination of the OH concentration was not possible due to the spectral interference of SO2 at the wavelength of detection of OH (308 nm). Fig. S15 (ESI†) shows the decay of OH radical during ozonolysis of (E)-2-butene during the addition of acetic acid.Discussion
Fig. 3 and 4 show the OH signal during ozonolysis of different alkenes, and how the OH concentration depends strongly on the residence time within the LIF-FAGE instrument: in all experiments OH increase steeply to a maximum value followed by a more gradual decrease. This OH formation process has recently been suggested39,40 as a source of interference in the measurement of ambient OH concentrations using LIF-FAGE instruments. The signal was proposed to originate from SCI decomposition, which would imply that Criegee intermediates are present in the troposphere in sufficiently high concentrations to affect the chemistry. Here, we present the first experimental evidence showing that the source of the OH is indeed unimolecular decomposition of syn-CH3CHOO, followed by our analysis of the reaction kinetics involving SCI chemistry.a. SCI as the OH source
Firstly, we can rule out that the observed OH is sampled from the high pressure flow tube, as OH is scavenged by the alkene and the added propane OH scavenger; residual OH would also not increase initially, but start at a maximum value and decrease monotonically. Secondly, the source of OH cannot be a bimolecular reaction. The pressure in the low pressure section of the instrument during the experiment was ∼3.5 hPa, diluting the concentrations of all species by a factor of 300, therefore most bimolecular reactions would decline or be fully prohibited. Especially for the ozonolysis of the alkenes studied, a well-known source of OH, the reaction is too slow to be relevant at such pressure producing less than 5% of the total OH observed inside the instrument. For the reactants with highest concentrations, i.e., alkenes and propane, we observe some residual scavenging in the low pressure region, which is due to their high rate of reaction with OH. Any other molecule, apart from the initial reagents, can only be present in a concentration that is several orders of magnitude lower and therefore cannot be significant in the low pressure segment of the instrument. The OH within the instrument thus originates from the unimolecular decomposition of a transient species formed in the ozonolysis of the alkene. Theoretical7,11 and experimental4,6,9 studies strongly suggest that syn-CH3CHOO is the source of OH by 1,4-H-migration, forming vinyl hydroperoxide that quickly decomposes to vinoxy radicals + OH. However, we cannot a priori preclude the possibility of other compounds decomposing to OH. These pathways include hot acid decomposition from dioxirane formed in the ester channel of all CIs, and thermal decomposition of stabilized ROOH hydroperoxide (including VHP). In order to confirm the role of syn-CH3CHOO in the formation of OH in the instrument, we performed several experiments with SO2, water vapor, and acetic acid, known SCI scavengers. SO2 was shown experimentally to react very fast with all CI,16 but unfortunately it causes a high spectral interference in the OH measurements. By recording fluorescence spectra during the ozonolysis of propene before and after the addition of different concentrations of SO2 (Fig. S14, ESI†) it is possible to observe how even a small concentration of SO2 strongly influences the OH spectrum and removes the OH peaks superimposed on the background, for all concentrations of SO2 used. The concentration of SO2 added in the flow tube was small enough to avoid OH scavenging by SO2, i.e., the OH radical lifetime was a factor of 50 smaller towards reaction with SO2 compared to propene, indicating that the disappearance of the OH signal is not due to removal of OH radical by SO2. While these experiments strongly point towards SCI scavenging, the spectral interference makes the results harder to interpret quantitatively, e.g., it is not possible to reliably derive a relative rate coefficient for SCI + SO2 (see ESI†). SO2 is not expected to react at an appreciable rate with ROOH molecules or any traditional intermediates formed in the ozonolysis of alkenes, leaving SCI, or products derived directly from SCI chemistry as OH sources. Similar experiments with added acetic acid (Fig. S15, ESI†) also show a fast decrease in generated OH, but difficulties in quantifying the added concentrations of acetic acid prohibits the rate analysis of SCI scavenging. As with SO2, we propose that acetic acid does not readily react with any intermediates other than SCI, again pointing to SCI as the likely source of OH.The decay of the OH concentration with the addition of water vapor during the ozonolysis of propene (Fig. S13, ESI†) likewise is consistent with SCI scavenging with a rate coefficient of SCI loss towards H2O of ∼3 × 10−17 cm3 molecules−1 s−1, in agreement with the upper limit of 4 × 10−15 cm3 molecules−1 s−1 measured by Taatjes et al.16 and in fair agreement with the (scaled) theoretical predictions listed in Table 2. A more detailed discussion is available in the ESI.† The rate coefficient between H2O and anti-CH3CHOO has been measured16 at 1 × 10−14 cm3 molecules−1 s−1, which is too fast to explain the water-dependent signal decrease observed during our experiment. Hence, the OH we observe does not originate from anti-CH3CHOO, and hence also not from dioxiranes or hot acid decomposition formed in the SCI ester channel. This is also in agreement with the very small yields of OH formation observed in ozonolysis reaction of ethene, a source of CH2OO. Most of the literature data7 point to VHP as a very short-lived species that promptly decomposes to vinoxy radical + OH upon formation from the higher energy syn-SCI prior to collisional thermalization. Drozd et al.56 observed secondary OH formation in chamber experiments on a time scale of 0.5 s, which was attributed to some VHP stabilization aided by the existence of a (small) energy barrier in the VHP decomposition channel. However, given our residence time of the order of milliseconds, we would not be sensitive to OH formation on this timescale. We thus conclude that the LIF-FAGE instrument is sensitive only to syn-CH3CHOO, and generally SCI that decompose thermally to OH via the VHP channel.
b. Box model results
The time dependence of the OH concentration in the low pressure section of the instrument is largely determined by the ratio of total SCI loss to OH loss rates; the OH loss rates are known given that the OH wall loss was measured directly, and the bimolecular reactions of OH occur under pseudo first order conditions and have well known rate coefficients. As shown in Fig. 5 and 6, by changing the total loss of syn-CH3CHOO in the model simulation a change in the shape of the time dependence OH concentration was obtained. Within the error bounds of our experimental results we obtain a total SCI loss rate of 23 ± 7 s−1. Using literature data for the bimolecular reaction rates in the high pressure section, the model also reproduces the absolute OH concentrations within a factor 1.8 (propene) and 1.7 ((E)-2-butene), indicating that the model is remarkably accurate relative to the a priori uncertainties on the steady state SCI concentration at the sample point. Given that the total loss is the sum of the unimolecular decomposition rate and wall losses, the highest total SCI loss of 30 s−1 thus translates into an upper limit for the unimolecular decomposition rate of syn-CH3CHOO of 30 s−1; faster unimolecular rates would lead to disagreement of the time-dependent OH concentration profile between experimental data and model (Fig. 5 and 6). The available experimental data on the unimolecular decomposition rate of CH3CHOO are few and span a large range: the values reported from experimental studies are 2.5 s−1,57 2.9 s−1,58 76 s−1,55 and <250 s−1.16 A direct comparison of these rates against our results is difficult as most of the experimental data lump syn- and anti-CH3CHOO, regardless of their strongly differing chemistry. The results by Fenske et al.55 of 76 s−1, the only experimental value unambiguously higher than our rate, results in clear disagreement with our observed time-dependence (Fig. 5 and 6). It is important to note that the reported uncertainty of the latter decomposition rate is a factor of 3 and therefore the upper limit determined in this study lies within the uncertainty range. Our upper limit result is also in agreement with theoretical calculations from Kuwata et al.59 who estimate a unimolecular decomposition rate for syn-CH3CHOO and anti-CH3CHOO of 24 s−1 and 64 s−1, respectively, though with a high degree of uncertainty. The unimolecular decomposition rate is expected to be strongly dependent on temperature.60 The strong pressure drop while sampling the air into the instrument leads to expansion cooling of the gas. The air quickly returns to ambient temperatures; we have established that at most at 13 cm (∼1 millisecond) behind the pinhole the ambient temperature is regained. The expansion cooling therefore affects at most the first two points measured closest to the pinhole. These points have a negligible impact on our analysis of the time profile (Fig. 5 and 6), well below the uncertainties induced by other aspects of this work, and thus do not affect the conclusions applicable to 293 K.Determining a lower limit on the unimolecular rate, while maintaining a total loss rate of 30 s−1, is less straightforward. The model contains a set of bimolecular reactions involving SCIs, where the coreactants are the initial reactants or are formed in the ozonolysis reaction, and thus have concentrations changing in time. Unfortunately there are only few accurate measurements of rate coefficients for different CI isomers. Some experimental data is available for CH2OO chemistry, and with the help of theoretical studies it is possible to extrapolate these rate coefficients to several other reactants and SCI although with high uncertainty. In addition, the yields of SCI are uncertain and the relative yields of syn and anti have not yet been measured. We estimate a lower limit for the unimolecular decomposition rate of syn-CH3CHOO by maximally decreasing the SCI losses by removing all bimolecular reactions, while increasing the yield to a reasonable maximum, i.e., the SCI is formed as 100% syn-CH3CHOO, while the SCI yield is increased to the high end of the IUPAC recommendation uncertainty interval (Table 1). Using this scenario, it was no longer possible to match the OH time profile with unimolecular decomposition rates below 3 s−1. This is a very conservative lower limit as many of the bimolecular reaction rates of SCI were measured, and often appear to be faster than theoretical predictions. We therefore performed a sensitivity analysis with the model using more realistic uncertainty intervals on the kinetic parameters, i.e., varying the bimolecular reactions rates by a factor of 3 and the SCI yields and the syn-SCI yield within the total SCI yields in the range listed in Table 1. We find that the combined uncertainty of the SCI concentration at the sample point under this error model is only a factor 1.5 to 3, depending on the unimolecular decomposition rate adopted.
The best agreement between the absolute OH concentrations measured and model predicted is well within this factor of 3, for unimolecular decomposition rates closer to our upper limit, 30 s−1. To reproduce the absolute OH concentrations using our lower limit of 3 s−1, one would need significant downscaling of the bimolecular rate coefficients, with significant deviations from the literature data by up to orders of magnitude. We therefore propose a less stringent lower limit of 10 s−1 for the syn-CH3CHOO unimolecular decomposition rate coefficient, which is the lowest value that still allows us to model the absolute OH concentrations with a deviation equal to the more realistic error simulation obtained above. It should be emphasized that this limit is not based on direct experimental observations but rather on achieving reasonable agreement between our experiment and the available literature data.
c. Contributions under atmospheric conditions
The inferred unimolecular decomposition rate coefficient for syn-CH3CHOO of 20 ± 10 s−1 together with the most recent rate coefficients for reactions between SCI and atmospheric trace gas species (Table 2) allow us to improve our earlier assessment28,33 of the relative contribution of many coreactants in the atmosphere to the atmospheric fate of a set of SCI. The major differences are a higher unimolecular decomposition rate for the different SCI and a significantly faster reaction rate with organic acids as recently measured by Welz et al.22 As no direct measurements are available for the unimolecular rate decomposition of CH2OO, anti-CH3CHOO and (CH3)2COO we used the value of 20 s−1 measured for syn-CH3CHOO for CH2OO and (CH3)2COO. In the case of CH2OO this rate is likely an overestimate as most of theoretical calculations7 predict a higher energy barrier for CH2OO decomposition compared to syn-CH3CHOO. For (CH3)2COO the barrier heights derived theoretically7 are a bit lower than those for syn-CH3CHOO possibly indicating the unimolecular decomposition rate of 20 s−1 might be an underestimation. For anti-CH3CHOO the value of 60 s−1 was used as calculated by Kuwata et al.;59 the value predicted in their study for syn-CH3CHOO, 24 s−1, is in fair agreement with the value measured in this study.Table 4 lists the predicted contributions of the various loss processes in different environments as defined earlier28,33,42,61–69 updated by using carboxylic acid concentrations from Limón-Sánchez et al.70 for urban conditions and Grossmann et al.71 for the rural Europe environment, respectively. Compared to these earlier estimates, even with a faster unimolecular rate for both CH2OO and anti-CH3CHOO and a very fast reaction rate with organic acids, these two SCIs are still found to be lost mainly via reaction with water dimers both during day and nighttime. Recent studies72 show that this reaction is indeed very fast at least for CH2OO, with k(SCI + H2O)2/k(SCI + SO2) = 0.29. Therefore, model studies on the impact of CI on the chemistry of the atmosphere should incorporate water dimer reactions. As the unimolecular decomposition rate and the reaction rate with organic acids are very fast for both syn-CH3CHOO and (CH3)2COO, these become the main loss path in all environmental conditions analysed contributing for up to 80% of the total loss of the two conformers. Reaction with SO2 still occurs even though it only represents a very minor SCI loss. During nighttime, as the concentrations of most coreactants are lower than during daytime, the main loss for both syn-CH3CHOO and (CH3)2COO is represented by unimolecular decomposition via the VHP channel, representing a potentially important source of ambient OH radical.
| H2COO | Boreal forest | Tropical forest | Mega city | Rural Europe | ||
|---|---|---|---|---|---|---|
| Day | Night | Day | Day | Day | Night | |
| H2O | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | |
| (H2O)2 | 0.99 | 0.99 | 1 | 0.98 | 0.99 | 0.99 |
| Ester channel | 0.01 | |||||
| anti-CH3CHOO | ||||||
| H2O | 0.25 | 0.39 | 0.18 | 0.35 | 0.26 | 0.46 |
| (H2O)2 | 0.75 | 0.6 | 0.82 | 0.63 | 0.73 | 0.52 |
| Ester channel | 0.01 | 0.01 | 0.01 | 0.02 | ||
| Carboxylic acids | 0.01 | |||||
| syn-CH3CHOO | ||||||
| H2O | 0.01 | |||||
| (H2O)2 | 0.11 | 0.08 | 0.3 | 0.03 | 0.14 | 0.03 |
| VHP | 0.42 | 0.77 | 0.45 | 0.27 | 0.57 | 0.85 |
| NO2 | 0.02 | 0.02 | ||||
| SO2 | 0.01 | 0.01 | 0.03 | 0.01 | ||
| O3 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | |
| Carbonyl compounds | 0.01 | 0.01 | ||||
| Carboxylic acids | 0.42 | 0.12 | 0.22 | 0.57 | 0.27 | 0.09 |
| Hydroxyl compounds | 0.02 | 0.01 | 0.01 | 0.06 | ||
| (CH3)2COO | ||||||
| H2O | 0.02 | 0.03 | 0.04 | 0.01 | 0.02 | 0.01 |
| (H2O)2 | 0.01 | 0.01 | ||||
| VHP | 0.47 | 0.82 | 0.62 | 0.28 | 0.64 | 0.87 |
| NO2 | 0.02 | |||||
| SO2 | 0.01 | 0.01 | 0.03 | 0.01 | ||
| O3 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 | |
| Carbonyl compounds | 0.01 | 0.01 | ||||
| Carboxylic acids | 0.47 | 0.12 | 0.32 | 0.58 | 0.30 | 0.09 |
| Hydroxyl compounds | 0.02 | 0.01 | 0.01 | 0.06 | ||
Conclusions
A LIF-FAGE instrument, normally operated for in situ atmospheric OH measurements, was used to observe directly, for the first time, the OH formation from unimolecular decay of syn-CH3CHOO Criegee intermediates generated in the ozonolysis reaction of a set of alkenes. Using scavenging experiments and extensive comparison with the available literature data on CI chemistry we could exclude other reactions and compounds as the potential OH source. In particular, CH2OO and anti-CH3CHOO are not the source of the OH, in agreement with mechanistic understanding of carbonyl oxide chemistry.A clear time dependence of the OH signal was observed, showing a fast rise to the steady state concentration, followed by a more gradual decay following depletion of the SCI reactants. Based on the shape of this temporal OH profile, we determined the syn-SCI decomposition rate coefficient k (293 K) to be within the range of 3 to 30 s−1. The lower limit of this interval is increased to 10 s−1 based on the level of agreement between measured and modelled absolute OH concentrations, where the higher values yield the best correspondence with the literature data on SCI formation and bimolecular reactions.
The formation of OH from syn-SCI decomposition within the FAGE instrument corroborates earlier reports on interferences of the OH measurements.39,40 It was recently proposed to estimate and correct for this by pulsed scavenging of the OH to distinguish the background, SCI-generated OH from the atmospheric OH. The observed time dependence of the OH signal in the current work also suggests that very short inlets would be less affected by the interference, though the interfering signal is strictly speaking only eliminated at zero length. For all other inlet lengths the amount of SCI-generated OH depends on the concentration of syn-SCI within the reactant mixture and the rate coefficients for decomposition for each of the SCI in the sampled air. As this reaction system is currently insufficiently characterized, it is recommended that FAGE measurements incorporate blank measurements by OH scavenging techniques to improve the reliability of the ambient OH detection. Our current experiments do not fully exclude other interferences in FAGE OH measurements that cannot be eliminated with the proposed technique.
Acknowledgements
LV is supported by the Max Planck Graduate Center with the Johannes Gutenberg-Universität Mainz (MPGC). The authors thank John Crowley for help with the accurate characterization of the residence time.References
- R. Atkinson and J. Arey, Chem. Rev., 2003, 103, 4605–4638 CrossRef CAS PubMed.
- D. Johnson and G. Marston, Chem. Soc. Rev., 2008, 37, 699–716 RSC.
- R. Criegee, Angew. Chem., Int. Ed. Engl., 1975, 14, 745–752 Search PubMed.
- N. M. Donahue, G. T. Drozd, S. A. Epstein, A. A. Presto and J. H. Kroll, Phys. Chem. Chem. Phys., 2011, 13, 10848–10857 RSC.
- G. T. Drozd and N. M. Donahue, J. Phys. Chem. A, 2011, 115, 4381–4387 Search PubMed.
- J. H. Kroll, S. R. Sahay, J. G. Anderson, K. L. Demerjian and N. M. Donahue, J. Phys. Chem. A, 2001, 105, 4446–4457 CrossRef CAS.
- L. Vereecken and J. S. Francisco, Chem. Soc. Rev., 2012, 41, 6259–6293 RSC.
- L. Lu, J. M. Beames and M. I. Lester, Chem. Phys. Lett., 2014, 598, 23–27 Search PubMed.
- S. E. Paulson, M. Y. Chung and A. S. Hasson, J. Phys. Chem. A, 1999, 103, 8125–8138 CrossRef CAS.
- J. M. Anglada, P. Aplincourt, J. M. Bofill and D. Cremer, ChemPhysChem, 2002, 3, 215–221 CrossRef CAS.
- R. Gutbrod, E. Kraka, R. N. Schindler and D. Cremer, J. Am. Chem. Soc., 1997, 119, 7330–7342 CrossRef CAS.
- K. T. Kuwata, L. C. Valin and A. D. Converse, J. Phys. Chem. A, 2005, 109, 10710–10725 CrossRef CAS PubMed.
- C. A. Taatjes, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2014, 16, 1704–1718 RSC.
- D. Johnson, A. G. Lewin and G. Marston, J. Phys. Chem. A, 2001, 105, 2933–2935 Search PubMed.
- O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207 CrossRef CAS PubMed.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, A. M. Scheer, D. E. Shallcross, B. Rotavera, E. P. Lee, J. M. Dyke, D. K. Mok, D. L. Osborn and C. J. Percival, Science, 2013, 340, 177–180 CrossRef CAS PubMed.
- C. A. Taatjes, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, E. P. F. Lee, J. M. Dyke, D. W. K. Mok, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2012, 14, 10391–10400 RSC.
- Y. Liu, K. D. Bayes and S. P. Sander, J. Phys. Chem. A, 2014, 118, 741–747 CrossRef CAS PubMed.
- D. Stone, M. Blitz, L. Daubney, N. U. Howes and P. Seakins, Phys. Chem. Chem. Phys., 2014, 16, 1139–1149 RSC.
- B. Ouyang, M. W. McLeod, R. L. Jones and W. J. Bloss, Phys. Chem. Chem. Phys., 2013, 15, 17070–17075 RSC.
- Z. J. Buras, R. M. Elsamra, A. Jalan, J. E. Middaugh and W. H. Green, J. Phys. Chem. A, 2014, 118, 1997–2006 Search PubMed.
- O. Welz, A. J. Eskola, L. Sheps, B. Rotavera, J. D. Savee, A. M. Scheer, D. L. Osborn, D. Lowe, A. Murray Booth, P. Xiao, M. Anwar, H. Khan, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Angew. Chem., 2014, 126, 4635–4638 Search PubMed.
- S. Hatakeyama, H. Kobayashi, Z. Y. Lin, H. Takagi and H. Akimoto, J. Phys. Chem., 1986, 90, 4131–4135 CrossRef CAS.
- J. M. Beames, F. Liu, L. Lu and M. I. Lester, J. Chem. Phys., 2013, 138, 244307 CrossRef PubMed.
- F. Liu, J. M. Beames, A. M. Green and M. I. Lester, J. Phys. Chem. A, 2014, 118, 2298–2306 CrossRef CAS PubMed.
- T. Berndt, T. Jokinen, R. L. Mauldin, T. Petaja, H. Herrmann, H. Junninen, P. Paasonen, D. R. Worsnop and M. Sipila, J. Phys. Chem. Lett., 2012, 3, 2892–2896 Search PubMed.
- O. Horie, P. Neeb and G. K. Moortgat, Int. J. Chem. Kinet., 1997, 29, 461–468 Search PubMed.
- L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2014, 16, 4039–4049 RSC.
- H. G. Kjaergaard, T. Kurten, L. B. Nielsen, S. Jorgensen and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 2525–2529 CrossRef CAS.
- Y. T. Su, H. Y. Lin, R. Putikam, H. Matsui, M. C. Lin and Y. P. Lee, Nat. Chem., 2014, 6, 477–483 CrossRef CAS PubMed.
- A. Mansergas and J. M. Anglada, J. Phys. Chem. A, 2006, 110, 4001–4011 CrossRef CAS PubMed.
- C. J. Percival, O. Welz, A. J. Eskola, J. D. Savee, D. L. Osborn, D. O. Topping, D. Lowe, S. R. Utembe, A. Bacak, G. McFiggans, M. C. Cooke, P. Xiao, A. T. Archibald, M. E. Jenkin, R. G. Derwent, I. Riipinen, D. W. Mok, E. P. Lee, J. M. Dyke, C. A. Taatjes and D. E. Shallcross, Faraday Discuss., 2013, 165, 45–73 RSC.
- L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2012, 14, 14682–14695 RSC.
- J. R. Pierce, M. J. Evans, C. E. Scott, S. D. D'Andrea, D. K. Farmer, E. Swietlicki and D. V. Spracklen, Atmos. Chem. Phys., 2013, 13, 3163–3176 Search PubMed.
- M. Boy, D. Mogensen, S. Smolander, L. Zhou, T. Nieminen, P. Paasonen, C. Plass-Dülmer, M. Sipilä, T. Petäjä, L. Mauldin, H. Berresheim and M. Kulmala, Atmos. Chem. Phys., 2013, 13, 3865–3879 Search PubMed.
- G. Sarwar, K. Fahey, R. Kwok, R. C. Gilliam, S. J. Roselle, R. Mathur, J. Xue, J. Yu and W. P. L. Carter, Atmos. Environ., 2013, 68, 186–197 CrossRef CAS PubMed.
- G. Sarwar, H. Simon, K. Fahey, R. Mathur, W. S. Goliff and W. R. Stockwell, Atmos. Environ., 2014, 85, 204–214 CrossRef CAS PubMed.
- R. L. Mauldin III, T. Berndt, M. Sipilä, P. Paasonen, T. Petaja, S. Kim, T. Kurten, F. Stratmann, V. M. Kerminen and M. Kulmala, Nature, 2012, 488, 193–196 CrossRef PubMed.
- J. Mao, X. Ren, L. Zhang, D. M. Van Duin, R. C. Cohen, J. H. Park, A. H. Goldstein, F. Paulot, M. R. Beaver, J. D. Crounse, P. O. Wennberg, J. P. DiGangi, S. B. Henry, F. N. Keutsch, C. Park, G. W. Schade, G. M. Wolfe, J. A. Thornton and W. H. Brune, Atmos. Chem. Phys., 2012, 12, 8009–8020 CAS.
- A. Novelli, K. Hens, C. Tatum Ernest, D. Kubistin, E. Regelin, T. Elste, C. Plass-Dülmer, M. Martinez, J. Lelieveld and H. Harder, Atmos. Meas. Tech. Discuss., 2014, 7, 819–858 Search PubMed.
- M. Martinez, H. Harder, D. Kubistin, M. Rudolf, H. Bozem, G. Eerdekens, H. Fischer, T. Klupfel, C. Gurk, R. Konigstedt, U. Parchatka, C. L. Schiller, A. Stickler, J. Williams and J. Lelieveld, Atmos. Chem. Phys., 2010, 10, 3759–3773 CrossRef CAS.
- K. Hens, A. Novelli, M. Martinez, J. Auld, R. Axinte, B. Bohn, H. Fischer, P. Keronen, D. Kubistin, A. C. Nölscher, R. Oswald, P. Paasonen, T. Petäjä, E. Regelin, R. Sander, V. Sinha, M. Sipilä, D. Taraborrelli, C. Tatum Ernest, J. Williams, J. Lelieveld and H. Harder, Atmos. Chem. Phys. Discuss., 2013, 13, 28561–28629 Search PubMed.
- M. E. Jenkin, S. M. Saunders and M. J. Pilling, Atmos. Environ., 1997, 31, 81–104 CrossRef CAS.
- S. M. Saunders, M. E. Jenkin, R. G. Derwent and M. J. Pilling, Atmos. Chem. Phys., 2003, 3, 161–180 CrossRef CAS.
- A. R. Curtis and W. P. Sweetenham, Harwell Laboratory, Oxfordshire, 1987 Search PubMed.
- M. Nakajima and Y. Endo, J. Chem. Phys., 2014, 140, 011101 CrossRef PubMed.
- H. Niki, P. D. Maker, C. M. Savage and L. P. Breitenbach, J. Phys. Chem., 1981, 85, 1024–1027 Search PubMed.
- O. Horie and G. K. Moortgat, Atmos. Environ., Part A, 1991, 25, 1881–1896 CrossRef.
- A. R. Rickard, D. Johnson, C. D. McGill and G. Marston, J. Phys. Chem. A, 1999, 103, 7656–7664 Search PubMed.
- W. C. D. Rathman, T. A. Claxton, A. R. Rickard and G. Marston, Phys. Chem. Chem. Phys., 1999, 1, 3981–3985 Search PubMed.
- J. D. Fenske, K. T. Kuwata, K. N. Houk and S. E. Paulson, J. Phys. Chem. A, 2000, 104, 7246–7254 CrossRef CAS.
- J. H. Kroll, N. M. Donahue, V. J. Cee, K. L. Demerjian and J. G. Anderson, J. Am. Chem. Soc., 2002, 124, 8518–8519 CrossRef CAS PubMed.
- J. M. Anglada, J. Gonzalez and M. Torrent-Sucarrat, Phys. Chem. Chem. Phys., 2011, 13, 13034–13045 RSC.
- A. B. Ryzhkov and P. A. Ariya, Phys. Chem. Chem. Phys., 2004, 6, 5042–5050 RSC.
- J. D. Fenske, A. S. Hasson, A. W. Ho and S. E. Paulson, J. Phys. Chem. A, 2000, 104, 9921–9932 CrossRef CAS.
- G. T. Drozd, J. Kroll and N. M. Donahue, J. Phys. Chem. A, 2011, 115, 161–166 Search PubMed.
- O. Horie, C. Schäfer and G. K. Moortgat, Int. J. Chem. Kinet., 1999, 31, 261–269 CrossRef CAS.
- O. Horie, P. Neeb and G. K. Moortgat, Int. J. Chem. Kinet., 1997, 29, 461–468 Search PubMed.
- K. T. Kuwata, M. R. Hermes, M. J. Carlson and C. K. Zogg, J. Phys. Chem. A, 2010, 114, 9192–9204 Search PubMed.
- T. Berndt, T. Jokinen, M. Sipilä, R. L. Mauldin III, H. Herrmann, H. Junninen and M. Kulmala and, Atmos. Environ., 2014, 89, 603–612 CrossRef CAS PubMed.
- J. Lelieveld, T. M. Butler, J. N. Crowley, T. J. Dillon, H. Fischer, L. Ganzeveld, H. Harder, M. G. Lawrence, M. Martinez, D. Taraborrelli and J. Williams, Nature, 2008, 452, 737–740 CrossRef CAS PubMed.
- H. Junninen, A. Lauri, P. Keronen, P. Aalto, V. Hiltunen, P. Hari and M. Kulmala, Boreal Environ. Res., 2009, 14, 447–457 CAS.
- T. Petäjä, R. L. Mauldin, E. Kosciuch, J. McGrath, T. Nieminen, P. Paasonen, M. Boy, A. Adamov, T. Kotiaho and M. Kulmala, Atmos. Chem. Phys., 2009, 9, 7435–7448 CrossRef.
- A. T. Case Hanks, Doctor of Philosophy, Georgia Institute of technology, 2008 Search PubMed.
- E. C. Wood, S. C. Herndon, T. B. Onasch, J. H. Kroll, M. R. Canagaratna, C. E. Kolb, D. R. Worsnop, J. A. Neuman, R. Seila, M. Zavala and W. B. Knighton, Atmos. Chem. Phys., 2009, 9, 2499–2516 CrossRef CAS.
- T. R. Shirley, W. H. Brune, X. Ren, J. Mao, R. Lesher, B. Cardenas, R. Volkamer, L. T. Molina, M. J. Molina, B. Lamb, E. Velasco, T. Jobson and M. Alexander, Atmos. Chem. Phys., 2006, 6, 2753–2765 CrossRef CAS.
- E. C. Fortner, J. Zheng, R. Zhang, W. Berk Knighton, R. M. Volkamer, P. Sheehy, L. Molina and M. André, Atmos. Chem. Phys., 2009, 9, 467–481 Search PubMed.
- G. M. Handisides, C. Plass-Dülmer, S. Gilge, H. Bingemer and H. Berresheim, Atmos. Chem. Phys., 2003, 3, 1565–1588 Search PubMed.
- W. Birmili, H. Berresheim, C. Plass-Dülmer, T. Elste, S. Gilge, A. Wiedensohler and U. Uhrner, Atmos. Chem. Phys., 2003, 3, 361–376 CrossRef CAS.
- M. T. Limón-Sánchez, J. L. Arriaga-Colina, S. Escalona-Segura and L. G. Ruíz-Suárez, Sci. Total Environ., 2002, 287, 203–212 CrossRef.
- D. Grossmann, G. K. Moortgat, M. Kibler, S. Schlomski, K. Bächmann, B. Alicke, A. Geyer, U. Platt, M. U. Hammer, B. Vogel, D. Mihelcic, A. Hofzumahaus, F. Holland and A. Volz-Thomas, J. Geophys. Res., 2003, 108, 8250 CrossRef.
- T. Berndt, J. Voigtlander, F. Stratmann, H. Junninen, R. L. Mauldin, M. Sipila, M. Kulmala and H. Herrmann, Phys. Chem. Chem. Phys., 2014 10.1039/c4cp02345e.
- A. B. Ryzhkov and P. A. Ariya, Chem. Phys. Lett., 2006, 419, 479–485 CrossRef CAS PubMed.
- L. Vereecken, H. Harder and A. Novelli, Geophysical Research Abstracts, 2014, 16, EGU2014-3788 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp02719a |
| This journal is © the Owner Societies 2014 |