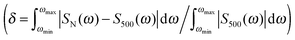Multi-scale modeling of electronic spectra of three aromatic amino acids: importance of conformational averaging and explicit solute–solvent interactions

Abstract

Electronic transitions in the ultraviolet and visible spectral range can reveal a wealth of information about biomolecular geometry and interactions, such as those involved in protein folding. However, the modeling that provides the necessary link between spectral shapes and the structure is often difficult even for seemingly simple systems. To understand as to how conformational equilibria and solute–solvent interaction influence spectral intensities, we collected absorption (UV-vis), electronic circular dichroism (ECD), and magnetic circular dichroism (MCD) spectra of phenylalanine (Phe), tyrosine (Tyr) and tryptophan (Trp) zwitterions in aqueous solutions, and compared them with quantum-chemical simulations. These aromatic amino acids provide a relatively strong signal in the accessible wavelength range. At the same time, they allow for a relatively accurate modeling. Energies and intensities of spectral bands were reproduced by the time-dependent density functional theory (TD DFT). The solvent was approximated by a continuum as well as clusters containing solvent molecules from the first hydration sphere. The ECD signal was found to be strongly dependent on molecular conformation, and the dependence was much weaker in UV-vis and MCD spectra. All spectral intensities, however, were significantly affected by the solvent approximation; especially for ECD and MCD the usual polarizable continuum solvent model did not yield satisfactory spectral shapes. On the other hand, averaging of the clusters obtained from molecular dynamics simulations provided an unprecedented agreement with the experiment. Proper modeling of the interactions with the environment thus makes the information about the molecular structure, as obtained from the electronic spectra, more accurate and reliable.

---

Introduction

Biological functions of peptides and proteins are determined by their structure and interactions, which can be conveniently studied by optical spectroscopic methods. They are relatively cheap, simple, and enable a variety of experimental conditions. In particular, the electronic circular dichroism (ECD, detecting the difference in absorption of left- and right-circularly polarized light) proved to be a very sensitive probe of peptides' secondary structure and molecular conformation in general.^1,2 In the last decade, the possibility to reliably model^3–7 the spectra renewed interest also in the magnetic circular dichroism (MCD). This technique measures the dichroism induced by the magnetic field parallel to the light beam; unlike natural ECD it is exhibited by both chiral and non-chiral molecules.

Most conveniently, the spectra involving electronic transitions are modeled using the time-dependent density functional theory (TD DFT), accessible for relatively sizable systems.^8,9 However, the flexibility and variety of the peptide molecules containing both hydrophilic and hydrophobic parts make the direct application of TD DFT difficult.^10–18 Semiempirical models already indicated that a large number of geometries were needed to reproduce peptide ECD.¹⁹ The need to average over many geometries, to account for the molecular motion, makes quantum-mechanical computations demanding in terms of computer time and other resources.²⁰ The natural aqueous solvent strongly interacts with the amide groups or polar side chains, which limits the applicability of the solvent polarizable continuum model (PCM).^21–24 Practically, the computations are not directly applicable either to interpret experimental spectra of larger molecules, or to smaller systems such as single amino acids. In some sense, smaller molecules are more problematic than bigger ones, due to their flexibility and lack of regular structure.^25–28

In the present study, we measured, modeled and analyzed the absorption, ECD and MCD of three aromatic amino acids, Phe, Tyr and Trp, aiming to better understand the relationship between the spectrum and the structure, including the effects of the environmental factors. The very presence of the aromatic residue lends the molecules a relatively strong signal in the accessible wavelength range. Although the zwitterions do not possess amide groups, their polarity is relevant to the strongest solute–solvent interactions in peptides as well. Additionally, tertiary structural analyses of proteins are often aided by the large ECD and MCD signals provided by the aromatic residues.^29–34

In particular, factors important for the protein MCD signal have been explored only sporadically so far. We consider this to be important as the technique has been applied to a large scale of systems, namely organic dyes, such as porphyrins,³⁵ phthalocyanines³⁶ and metalloproteins.^37–39 In proteins, MCD also proved to be useful in estimating the tryptophan contents or the tryptophan/tyrosine ratio.^34,40–42 As shown below, these results suggest that the sensitivity of MCD to environmental factors and the conformation is somewhere between the absorption and ECD spectroscopies.

The solvent studies are enhanced by the latest quantum-mechanical codes that made it possible to compute absorption, ECD and MCD spectral intensities relatively quickly,^3–7 thus paving the way for explicitly including the solvent in the computation. In the spirit of the “multi-scale” (QM/MM) approach we average the spectra simulated for solute–solvent clusters obtained from molecular dynamics (MD).⁴³

Unlike for ECD, the dependence of the MCD signal on the conformation has not been satisfactorily addressed yet, as far as we are aware. MCD formally stems from transition electric dipoles perturbed by the external magnetic field,⁴⁴ and ECD involves both transition electric and magnetic dipoles.^45–47 Computations of both spectral intensities thus involve similar operators, and their relative conformational sensitivity is not apparent beforehand. As shown below, for our systems, MCD is not that sensitive to the conformation, but both techniques do sensitively reflect the molecular environment.

Methods

Spectral measurement

Commercial (Sigma-Aldrich) Phe, Tyr and Trp amino acids were dissolved in miliQ water to concentrations of 0.05–0.20 mg ml⁻¹. The pH of ∼4.7 for all samples stabilized the zwitterionic forms. Absorption, ECD and MCD spectra were recorded at room temperature (298 K) on a Jasco J-5 spectrometer (Japan) equipped with a 1.5 T permanent magnet. A quartz cell of 1 mm optical pathlength, a scanning speed of 10 nm min⁻¹, a 0.05 nm data pitch, a 32 s response time, and 4 accumulations were used. ECD was obtained as an average, and MCD as a difference of the CD signal obtained with the two magnet orientations. The baseline correction was performed by subtracting the signal of pure solvent.

Computations

For phenylalanine, tyrosine, and tryptophan relaxed potential energy surface (PES) scans were performed for the two side chain torsion angles χ₁ and χ₂ (Fig. 1, 15° increments), using the MP2⁴⁸/PCM, B3LYP-D^49,50/PCM, B3LYP/PCM, B3LYP-D/SMD and B3LYP/SMD methods with a standard 6-31++G** basis set. The MP2 method was chosen as a standard comprising the dispersion interaction, independent of the DFT parameterization.^51,52 To DFT, the empirical dispersion correction indicated by “-D” uses the Grimme “D2” method.⁵³ Two continuum solvent models were used, PCM⁵⁴ and SMD,⁵⁵ the latter presumably better accounts for the solvent dispersion interactions. Water was used as a solvent in the continuum solvent models, while employing the atomic radii derived from the universal force field (UFF) to construct solvent cavities. For geometries near the local energy minima unconstrained optimizations were performed as well. The Gaussian program, revision D01,⁵⁶ was used for the DFT computations.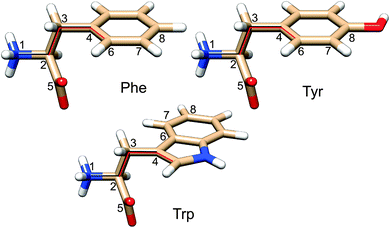

Fig. 1 Phe, Tyr and Trp zwitterions. The side chain dihedral angles were defined as χ₁ (1–2–3–4) and χ₂ (2–3–4–6).

Molecular dynamics simulations were employed to estimate the effect of explicit hydrogen bonds, presumably described only incompletely by the continuum solvent models. The simulations were performed within the Amber10 program.⁵⁷ Each amino acid was placed in a (20 Å)³ cubic box otherwise filled with water molecules, then the energy of the system was minimized and the dynamics equilibrated during 10⁶ steps, using the Amber03^58,59 force field, the nVT ensemble, temperature T of 300 K, and a 1 fs integration step. Relative conformer energies (ΔG_MD) were obtained from average conformer populations η_i as , where R is the universal gas constant.

During the following production runs, each of the 10⁸ MD steps, 500 snapshots evenly distributed in time were saved for spectral computations. In the snapshots, water molecules farther away than 3.4 Å from the amino acid were deleted. To reduce the MD geometry dispersion and thus to speed up the averaging convergence⁶⁰ the resultant clusters were partially optimized (ten steps only) using the vibrational normal mode coordinates^61–63 and the HF/PCM method, with the standard 6-31++G** and 6-31G basis sets applied to the solute and water atoms, respectively. The HF method was used as it provided a more reliable convergence than DFT, especially on geometries significantly distorted (too long bond lengths, etc.) during MD. It is known that HF and DFT geometries are different;⁶⁴ however, these differences (e.g. 2% in bond lengths) do not significantly influence the electronic transitions.²⁰

For the equilibrium geometries and MD clusters, absorption, ECD and MCD spectra were calculated at the B3LYP/6-31++G**(solute)/6-31G(solvent)/PCM level, using the time-dependent DFT.^65,66 This level provided realistic electronic spectra before; in particular the 6-31++G** basis set appeared to be sufficient for the amide group modeling.²⁰ Aromatic π-systems could be reasonably-well modeled even with a smaller basis set.^47,67 Natural bond orbitals (NBOs)⁶⁸ were plotted as obtained using the Gaussian⁵⁶ software.

For several trial systems MCD spectra were calculated using the complex polarization propagator³ (CPP, implemented in the Dalton⁶⁹ program) and the sum-over-states⁷ (SOS) methods. As these two approaches provided similar results, the SOS method was used to average over many cluster geometries as it is faster. Gaussian curves (a full width at half maximum of 0.1 eV) were used for the spectra generation, presented in units of cm⁻¹ mmol⁻¹ dm³ (ε, absorption), cm⁻¹ mol⁻¹ dm³ (Δε, ECD), and cm⁻¹ mol⁻¹ dm³ Tesla⁻¹ (Δε, MCD).

Results and discussion

Geometry

The energy landscape of the three molecules is relatively simple. Characteristic torsional angles and relative energies of individual conformers calculated by the MP2, B3LYP and B3LYP-D methods are listed in Table 1. In the last column, Gibbs energies obtained from average conformer populations during the free molecular dynamics are added. For all compounds three χ₁ values generating stable conformations are possible, approximately corresponding to the canonical values of 60°, −60° and 180°. All compounds also seem to prefer the “−60°” value of a “puckered” conformation where the aromatic ring points between the NH₃⁺ and the COO⁻ group. For χ₁ ∼ 180° the aromatic residue points in the opposite direction than NH₃⁺, and the least probable (with highest relative energy) is a conformation where the aromatic ring points between the NH₃⁺ and ^αH groups (χ₁ ∼ 60°, opposite to COO⁻).

Table 1 Characteristic torsional angles (deg.) and relative energies (kJ mol⁻¹) of Phe, Tyr and Trp conformers^a

Conformer	MP2				B3LYP			B3LYP-D			MD
	χ 1	χ 2	ΔE	ΔG	χ 1	χ 2	ΔG	χ 1	χ 2	ΔG	ΔGMD
a The 6-31++G**/PCM level was used for all methods; ΔE and ΔG are, respectively, the electronic and Gibbs energies.
Phe
I	−58	107	0	1	−59	109	0	−61	99	0	3
II	41	71	6	0	53	78	4	62	86	3	4
III	179	76	9	6	−174	71	10	−177	73	7	0
Tyr
I	−57	−70	0	3	−58	−70	1	−61	−75	0	3
I′	−57	107	0	2	−59	110	0	−60	102	1	4
II	53	−103	5	1	51	−103	3	60	−92	1	5
II′	53	75	5	0	51	76	3	60	85	3	7
III	175	76	9	10	−174	72	9	−177	79	5	0
III′	175	−100	9	10	−175	−109	9	−177	−100	7	1
Trp
I	−57	−67	0	2	−57	−72	0	−60	−69	0	0
I′	−54	90	8	6	−55	98	5	−57	88	7	0
II	47	76	9	0	47	79	5	55	82	3	3
II′	54	−91	10	1	52	−99	4	62	−86	6	1
III	177	70	12	10	−175	72	11	−176	67	11	1
III′	174	−92	17	12	−176	−103	15	−180	−88	13	2

---

For Tyr (with a specific rotation of the OH group) and Trp, another set of conformers is generated by a rotation of their aromatic rings by about 180°. As expected, energy differences caused by the different orientation of the OH group in Tyr are much smaller than those caused by rotation of the larger Trp residue. Within a few kJ mol⁻¹, the MP2 results correspond to B3LYP, and the empirical dispersion correction (in B3LYP-D) does not significantly affect conformer ordering. We note, however, that the torsional angles calculated e.g. by the B3LYP and B3LYP-D methods are slightly different, by up to 15° for conformer III′ of Trp.

Comparison of the electronic and Gibbs energies (listed for the MP2 level in Table 1) suggests an important effect of the vibronic motions on conformational equilibria, although the dynamical contributions based on the ideal gas model may not be applicable to our systems.^70,71 The most striking inconsistency is thus the very different conformer ordering for Phe and Tyr, and to a lesser extent also for Trp, as obtained from molecular dynamics (cf. ΔG_MD). For Phe, for example, conformer III, least favored by the B3LYP and B3LYP-D methods, becomes the preferential one in MD.

This contrast is also apparent in the two-dimensional (χ₁, χ₂) potential energy surfaces (PES) presented in Fig. 2. MD predicts for Phe and Tyr the most probable χ₁ value of about 180°, whereas the electronic methods rather prefer the puckered value (χ₁ ∼ −60°) and χ₁ ∼ 60°. For Trp, the MD PES suggests a larger conformational flexibility than DFT, with conformer populations spread more evenly among the three canonical χ₁ values. As expected, addition of the dispersion (in the MP2 or B3LYP-D methods) favors the puckered conformer, as opposed to B3LYP. As only minor differences were observed between the SMD and PCM solvent models, only the PCM results are shown.

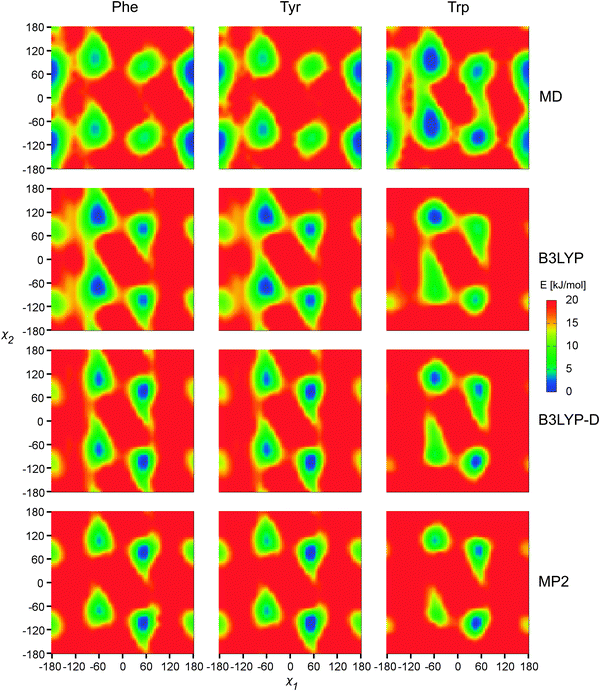Fig. 2 Calculated MD free energies and electronic energies, as dependent on two torsional angles (χ₁ and χ₂). The 6-31++G** basis set and PCM were used in the electronic computations.

By analyzing the MD trajectories, we could construct average water densities with respect to a given orientation of the NH₃⁺–CH–COO⁻ parts of the amino acids (Fig. 3). The first hydration spheres are well-developed. They are compact, and structured both radially and angularly with respect to the charged centers. They do not seem to be significantly dependent on the aromatic residues, although the side chain clearly perturbs the hydration sphere more strongly in Trp than in Phe and Tyr.

Fig. 3 Hydration spheres (isodensity surfaces) obtained by an MD run with the Amber03 force field.

Spectra of individual conformers

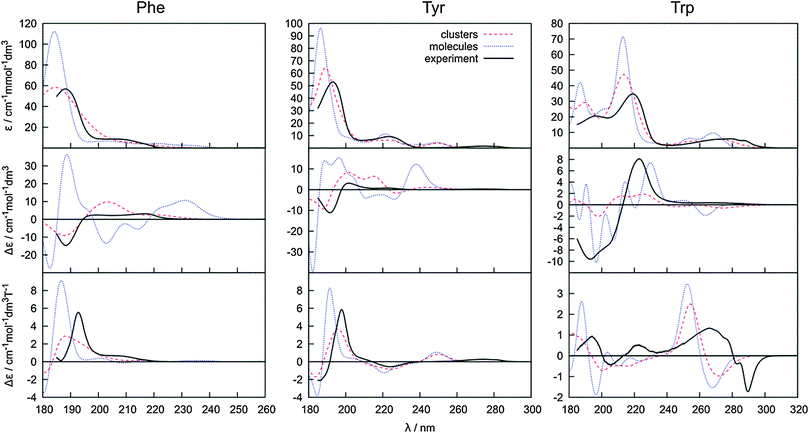
Absorption, CD, and MCD spectra calculated for individual Phe, Tyr and Trp conformers are displayed with the experiment in Fig. 4. As discussed before³¹ the electronic spectra of these amino acids can be understood to a large extent based on the dominant signal of the benzene, phenol and indole models. For example, experimental positions of the longest-wavelength absorption bands (240, 275 and 278 nm, Fig. 4) correspond to the CASPT2 predictions of 263, 274 and 283 nm, respectively. Likewise, absorption of benzene is very similar to phenol, at longer wavelengths (∼270 nm) indole absorbs much more than benzene, around 200 nm indole absorption is about half of that of benzene, etc.³¹ Around 200–220 nm, a significant contribution of the carboxyl group is assumed.⁷²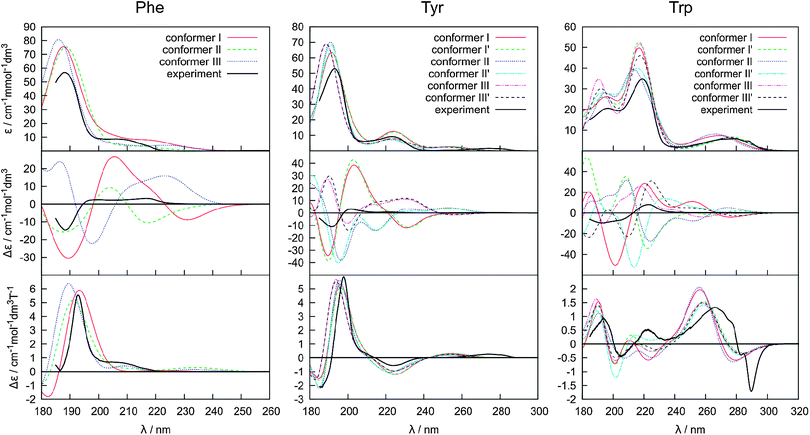

Fig. 4 Calculated absorption (top), ECD (middle) and MCD (bottom) spectra of individual conformers of Phe (left), Tyr (middle), and Trp (right), and the experiment.

The experimental absorption spectra of all the zwitterionic amino acids are well-reproduced by the TDDFT computations presented in Fig. 4, with a main peak position within a 2–10 nm distance from the experiment. As expected, the absorption is relatively independent of the conformation. Conformer I of Phe and conformers I and I′ of Tyr absorb much more strongly around 220 nm than the other conformers. On the other hand, the single peak around 190 nm does not seem to be particularly affected by the conformation. For Trp, the differences are most apparent in the 180–230 nm region comprising two strong absorption bands. Also the longer-wavelength signal at ∼280 nm has the potential to distinguish the conformation.

The MCD spectra (bottom row in Fig. 4) exhibit only slightly greater conformational sensitivity than the absorption spectra, although a closer look does reveal distinct patterns. For Phe, a weak band at around 235 nm is apparent for conformer II only. At around 188 nm the relative MCD differences in the intensity and apparent peak positions between the conformers are about twice as large as that for the absorption (e.g. MCD maxima vary between 5 and 6 cm⁻¹ mol⁻¹ dm³ Tesla⁻¹, while absorption maxima between 75 and 80 cm⁻¹ mmol⁻¹ dm³). Tyr behaves similar to Phe, although the differences between the conformers seem to be smaller. In contrast to Phe and Tyr, the Trp MCD signal is quite conformer-dependent, although also for this molecule all conformers have a positive signal at around 190 nm, a weak one within the 200–240 nm interval, and a positive/negative MCD at 260/275 nm. However, at around 220 nm, for example, even the MCD sign of conformer II′ is clearly different from the others.

The ECD spectra (middle of Fig. 4) are most dependent on the conformation. This reflects the characteristic mechanism of the ECD phenomenon intimately linked to a molecular conformation,^45,73 more so than in MCD. One can realize, for example, that the planar aromatic and COO⁻ residues provide most of the MCD signal, whereas without coupling to the rest of the molecule their ECD would be zero. However, in the chiral amino acids, electronic transitions within the planar chromophores may be the main source of ECD as well, as these are perturbed by covalent bonding, electrostatic interaction and mutual polarization with the chiral part of the molecule.⁴⁷ In Tyr the change in the χ₁ torsion angle causes much larger intensity changes than χ₂ variation, whereas in Trp the relative influence of the two angles varies throughout the spectrum.

The key to a faithful reproduction of the experimental ECD thus seems to be proper conformer weighting. The spectra were calculated at the B3LYP/6-31++G**/PCM level and averaged using the Boltzmann factors, and MP2, B3LYP, B3LYP-D and MD conformer energies (Fig. 5). The MD conformer populations provide the best results when compared to the experiment, probably because the MD model better reproduces both the real conformer ordering and magnitudes of the energy differences. The span of the MD relative conformer energies is indeed much smaller than for the electronic methods (cf.Table 1), so that individual conformers are more evenly populated and the averaged ECD spectra are weaker, closer to the experiment. Yet even for the simplest Phe molecule the simulated intensities are more than twice as large as the experimental ones in the longer-wavelength region. The MP2 conformer energies provide the least satisfactory spectral curves, most probably due to an overestimation of the dispersion and correlation effects by this method.^50,74 Indeed, the dispersion-corrected B3LYP-D with a more balanced dispersion⁷⁵ often provides more realistic results.

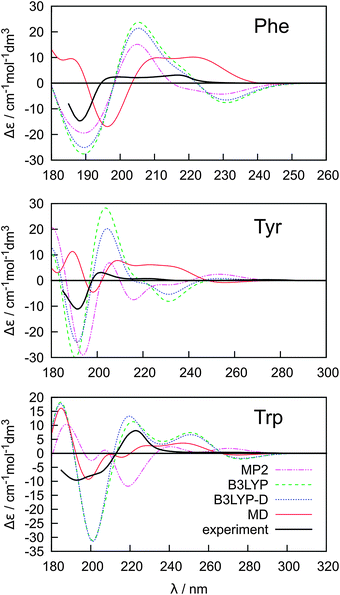Fig. 5 Calculated (B3LYP/6-311++G**/PCM) ECD spectra of Phe, Tyr and Trp based on Boltzmann averaging using MP2, B3LYP, B3LYP-D and MD relative conformer energies.

However, the conformer weighting alone does not suffice for a reliable modeling of the electronic spectra. The water molecules present in the clusters obtained from MD and explicitly comprised in the quantum-chemical computations have an additional potential to modulate the spectral curves. The absorption, ECD and MCD spectra obtained using the B3LYP functional as an average from 500 snapshots are plotted in Fig. 6. We also explored the CAM-B3LYP functional recommended as a more universal tool comprising also charge-transfer excitations.⁷⁶ In our case its performance was clearly inferior to B3LYP (data not shown). In particular, the transition wavelengths were too low.

Fig. 6 Absorption, ECD and MCD spectra obtained by averaging of 500 amino acid–water clusters, 500 conformers of a bare amino acid molecule (both obtained during the same molecular dynamics) and the experiment.

On the other hand, the B3LYP method and the averaging with explicit water molecules (red curve in Fig. 6) makes especially the ECD intensities more realistic compared to the PCM solvent model (Fig. 4 and 5). The greatest deviations between the theory and experiment appear in the longest-wavelength region. Most probably, the inaccuracy of the B3LYP functional, as well as the rovibronic effects,⁷⁷ not comprised in the ab initio modeling are to a large extent responsible for the rest of the error.

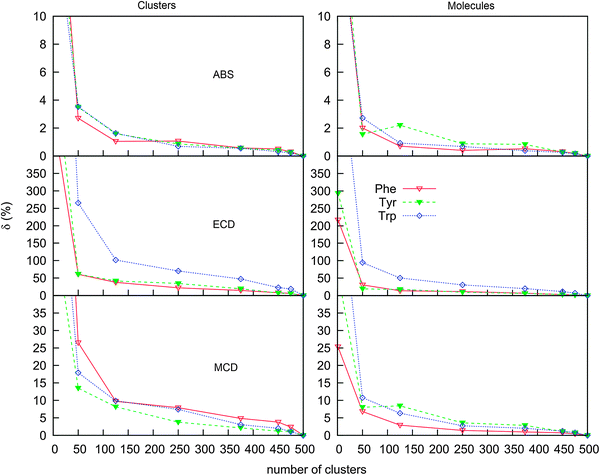
The water molecules cause a large dispersion of spectral intensities and peak frequencies, and a high number of clusters is required for results to converge, similarly previously found, e.g., for modeling of vibrational optical activity.^78–81 This is also documented in Fig. 7, where dependencies of spectral errors measured against the 500 cluster average are plotted as a function of the number of averaged clusters. The 500 cluster ensemble provides a reference allowing to estimate the minimal error of the computation. Note that more clusters may in principle be needed for absolute convergence. From the dependence, we can see that only few clusters are necessary to achieve a converged absorption intensity, whereas MCD and ECD require a much more extensive averaging.

Fig. 7 Error of the absorption, ECD and MCD spectra as dependent on the number of averaged snapshots, for both clusters and bare molecules, the integration ran over the whole calculated region of ∼180–320 nm.

For 100 clusters, for example, the error (δ) for absorption already approaches 1%. A reasonable convergence is also exhibited by the MCD spectra, although the error (∼10%) is about ten times larger. For ECD, the corresponding error of 100% in intensities for Trp is not acceptable, except for an approximate reproduction of the main spectral features. It is also noteworthy that when the water molecules are removed from the clusters before averaging (right-hand side of Fig. 7), the ECD error drops at least to one half. We thus can conclude that both the conformational dispersion and solute–solvent interaction contribute approximately equally to the dispersion and inhomogeneous broadening of spectral lines. The drop of MCD error is rather unexpected when the water molecules are removed, which suggests that, unlike absorption, both ECD and MCD are very sensitive to the interaction of the solvated molecules with the aqueous environment.

For a more detailed insight into the effects of the solvent and conformational changes on the spectra, we ran molecular dynamics with a fixed geometry of Phe. The 25 and 50-cluster averages are compared with an implicit PCM model in Fig. 8. Clearly, even with fixed Phe geometry, the water molecules explicitly involved in the electronic computations are needed to yield a realistic spectral profile; the PCM model provides a reasonable absorption spectral shape, but rather unrealistic magnitudes of ECD intensities. As discussed elsewhere^22,23,82 the continuum PCM approximation is not suitable to reproduce in full the strong solvent–solute interaction, in particular the hydrogen bonding, for the zwitterions. In extreme case, improper solvent modeling can lead to a wrong conclusion about molecular conformation or even absolute configuration derived from ECD. The cluster spectra are much closer to the experiment (cf., e.g., Fig. 5). We also see that in spite of the high integral error (Fig. 7) a few tens of the clusters suffice for a reasonably accurate prediction of the ECD shape. This is similar as found in previous studies for the vibrational optical activity.⁸⁰ However, for the vibrational spectra, the PCM model was found to be sufficient as a reasonable computationally cheap approximation,⁸¹ which is something that cannot be concluded from our results simulating the electronic optical activity.

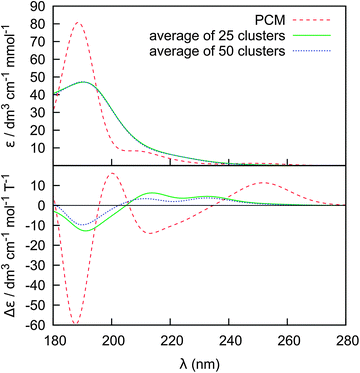Fig. 8 ECD and absorption spectra for a randomly chosen Phe conformer (χ₁ = −163, χ₂ = 72): average of 25 and 50 clusters from MD run with fixed Phe geometry.

The modeling thus shows that water molecules directly participate in the electronic transitions, which is consistent with previous observations of similar systems.²⁰ Indeed, as apparent from two randomly chosen snapshots of Phe and the closest water molecules (Fig. 9), the frontier orbitals most strongly contributing to the measured spectral signal are in some cases dramatically modified by the presence of water. By comparing the first and third column of the orbitals in Fig. 9, we can also notice the significant conformational dependence even for a bare Phe molecule, i.e. without water. The orbital energies are not that different if calculated for different conformers and clusters, which indicates the relative stability of the absorption spectra. The “different chemistry” of the vacuum and hydrated Phe molecule is also reflected in the NBO orbitals⁶⁸ plotted in Fig. 10. The lowest unoccupied NBO, for example, is virtually unchanged, except for a phase factor, while the highest occupied, and the highest occupied – 3 one switch their positions, being alternately localized near the phenyl and carboxyl residues.

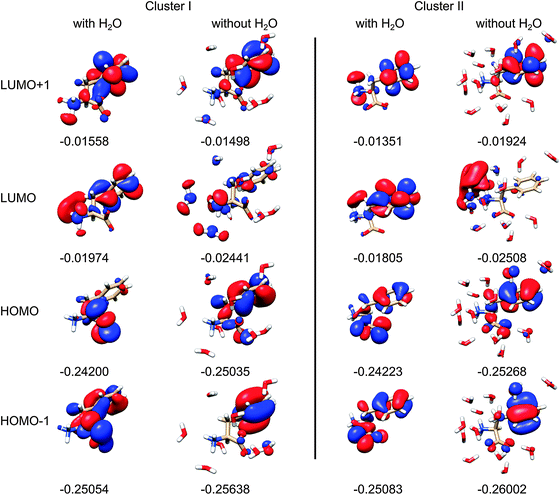Fig. 9 Selected Phe canonical molecular orbitals of two clusters, with and without water (left and right, for each cluster), with orbital energies in atomic units, for the isodensity value of 0.25.

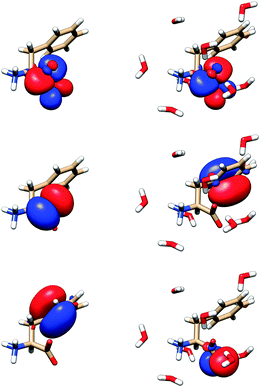Fig. 10 Selected natural bond orbitals for Phe (left) and its MD cluster with water (right). From top to bottom: lowest unoccupied, highest occupied, and highest occupied – 3 NBO.

Conclusions

To understand the multitude of factors affecting the electronic spectra of aromatic amino acids, we compared experimental absorption, electronic circular dichroism, and magnetic circular dichroism spectra of Phe, Tyr and Trp with a series of model computations. ECD was found to be the most sensitive method reflecting molecular conformation and interaction with the environment, followed by MCD and absorption. Conformer averaging based on molecular dynamics provided much better results than the ab initio conformer energies obtained with dielectric solvent models. However, explicit water molecules had to be included in the computations to achieve more realistic simulations of spectral intensities. Rather surprisingly, MCD intensities were not much influenced by the conformation, but were found to be significantly affected by the solute–solvent interaction. As the most important result we thus consider consistent comparison of the three types of spectra with respect to their solvent and conformational sensitivity, and evaluation of the role of solvent molecules implicitly involved in the computations. A further improvement of the computational methodology is needed for reliable interpretations of spectra, needed for determination of structure and interaction of biologically relevant molecules with the environment.

Acknowledgements

The work was supported by the Grant Agency of the Czech Republic (13-03978S, P208/11/0105), Academy of Sciences (M200550902), Grant Agency of Charles University (711012), and Ministry of Education (LH11033, LM2010005, CZ.1.05/3.2.00/08.0144). We thank Jiří Kessler for the help with the MD computations and Radek Pelc for the discussion on the manuscript.

References

1. Circular Dichroism Principles and Applications, ed. N. Berova, K. Nakanishi and R. W. Woody, Wiley-VCH, New York, 2000.
2. W. C. Johnson, Proteins, 1999, 35, 307–312.
3. H. Solheim, K. Ruud, S. Coriani and P. Norman, J. Chem. Phys., 2008, 128, 094103.
4. H. Solheim, K. Ruud, S. Coriani and P. Norman, J. Phys. Chem. A, 2008, 112, 9615–9618.
5. M. Seth, J. Autschbach and T. Ziegler, J. Chem. Theory Comput., 2007, 3, 434–447.
6. M. Seth, M. Krykunov, T. Ziegler, J. Autschbach and A. Banerjee, J. Chem. Phys., 2008, 128, 144105.
7. P. Štěpánek and P. Bouř, J. Comput. Chem., 2013, 34, 1531–1539.
8. F. Furche, R. Ahlrichs, C. Wachsmann, E. Weber, A. Sobanski, F. Vögtle and S. Grimme, J. Am. Chem. Soc., 2000, 122, 1717–1724.
9. M. Pecul, K. Ruud and T. Helgaker, Chem. Phys. Lett., 2004, 388, 110–119.
10. T. Fukuyama, K. Matsuo and K. Gekko, Chirality, 2011, 23, E52–E58.
11. M. R. Poopari, Z. Dezhahang, G. C. Yang and Y. J. Xu, ChemPhysChem, 2012, 13, 2310–2321.
12. P. Y. Zhu, G. C. Yang, M. R. Poopari, Z. Bie and Y. J. Xu, ChemPhysChem, 2012, 13, 1272–1281.
13. T. Fukuyama, K. Matsuo and K. Gekko, J. Phys. Chem. A, 2005, 109, 6928–6933.
14. M. Knapp-Mohammady, K. J. Jalkanen, F. Nardi, R. C. Wade and S. Suhai, Chem. Phys., 1999, 240, 63–77.
15. M. D. Kundrat and J. Autschbach, J. Chem. Theory Comput., 2008, 4, 1902–1914.
16. A. Osted, J. Kongsted, K. V. Mikkelsen and O. Christiansen, Chem. Phys. Lett., 2006, 429, 430–435.
17. S. Qiu, G. N. Li, P. Wang, J. Zhou, Z. C. Feng and C. Li, J. Phys. Chem. A, 2011, 115, 1340–1349.
18. J. E. Rode, J. C. Dobrowolski and J. Sadlej, J. Phys. Chem. B, 2013, 117, 14202–14214.
19. X. Daura, D. Bakowies, D. Seebach, J. Fleischhauer, W. F. van Gunsteren and P. Krüger, Eur. Biophys. J., 2003, 32, 661–670.
20. J. Šebek, Z. Kejík and P. Bouř, J. Phys. Chem. A, 2006, 110, 4702–4711.
21. V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417.
22. B. Mennucci, C. Cappelli, R. Cammi and J. Tomasi, Chirality, 2011, 23, 717–729.
23. M. Caricato, F. Ingrosso, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 154501.
24. R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513.
25. J. Kapitán, V. Baumruk, V. Kopecký, Jr. and P. Bouř, J. Phys. Chem. A, 2006, 110, 4689–4696.
26. V. Parchaňský, J. Kapitán, J. Kaminský, J. Šebestík and P. Bouř, J. Phys. Chem. Lett., 2013, 4, 2763–2768.
27. V. Madison and J. Schellman, Biopolymers, 1970, 9, 511–567.
28. K. I. Oh, J. Han, K. K. Lee, S. Hahn, H. Han and M. Cho, J. Phys. Chem. B, 2006, 110, 13335–13365.
29. R. W. Woody, Eur. Biophys. J., 1994, 23, 253–262.
30. R. A. Sendak, D. M. Rothwarf, W. J. Wedemeyer, W. A. Houry and H. A. Scheraga, Biochemistry, 1996, 35, 12978–12992.
31. D. M. Rogers and D. M. Hirst, Biochemistry, 2004, 43, 11092–11102.
32. D. M. Rogers, N. A. Besley, P. O'Shea and J. D. Hirst, J. Phys. Chem. B, 2005, 109, 23061–23069.
33. A. Roy, P. Bouř and T. A. Keiderling, Chirality, 2009, 21, E163–E171.
34. C. Djerassi, G. Barth, R. Records, E. Bunnenberg and W. Voelter, J. Am. Chem. Soc., 1971, 93, 2545–2547.
35. J. Mack, M. J. Stillman and N. Kobayashi, Coord. Chem. Rev., 2007, 251, 429–453.
36. J. Mack and M. J. Stillman, Coord. Chem. Rev., 2001, 219, 993–1032.
37. E. I. Solomon, K. M. Light, L. V. Liu, M. Srnec and S. D. Wong, Acc. Chem. Res., 2013, 46, 2725–2739.
38. E. I. Solomon, M. J. Baldwin and M. D. Lowery, Chem. Rev., 1992, 92, 521–542.
39. E. I. Solomon, T. C. Brunold, M. I. Davis, J. N. Kemsley, S. K. Lee, N. Lehnert, F. Neese, A. J. Skulan, Y. S. Yang and J. Zhou, Chem. Rev., 2000, 100, 235–349.
40. B. Holmquis and B. L. Vallee, Biochemistry, 1973, 12, 4409–4417.
41. G. Barth, E. Bunnenberg and C. Djerassi, Anal. Biochem., 1972, 48, 471–479.
42. G. Barth, W. Voelter, E. Bunnenbe and C. Djerassi, J. Am. Chem. Soc., 1972, 94, 1293–1298.
43. J. Kessler, M. Dračínský and P. Bouř, J. Comput. Chem., 2013, 34, 366–371.
44. P. J. Stephens, J. Chem. Phys., 1970, 52, 3489–3516.
45. L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2004.
46. E. Charney, The Molecular Basis of Optical Activity, Wiley-Interscience, New York, 1979.
47. J. Šebek and P. Bouř, J. Phys. Chem. A, 2008, 112, 2920–2929.
48. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
49. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
51. I. Dabkowska, H. V. Gonzalez, P. Jurečka and P. Hobza, J. Phys. Chem. A, 2005, 109, 1131–1136.
52. V. Parchaňský, P. Matějka, B. Dolenský, M. Havlík and P. Bouř, J. Mol. Struct., 2009, 934, 117–122.
53. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
54. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
55. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D01, Gaussian, Inc., Wallingford, CT, 2009.
57. D. A. Case, I. T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, J. K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
58. N. Kamiya, Y. S. Watanabe, S. Ono and J. Higo, Chem. Phys. Lett., 2005, 401, 312–317.
59. Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. M. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. M. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012.
60. M. Dračínský, J. Kaminský and P. Bouř, J. Phys. Chem. B, 2009, 113, 14698–14707.
61. P. Bouř and T. A. Keiderling, J. Chem. Phys., 2002, 117, 4126–4132.
62. J. Hudecová, K. H. Hopmann and P. Bouř, J. Phys. Chem. B, 2012, 116, 336–342.
63. P. Bouř, Collect. Czech. Chem. Commun., 2005, 70, 1315–1340.
64. A. A. El-Azhary and H. U. Suter, J. Phys. Chem., 1996, 100, 15056–15063.
65. C. Jamorski, M. E. Casida and D. R. Salahub, J. Chem. Phys., 1996, 104, 5134–5147.
66. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 116, 7433–7447.
67. P. Štěpánek, V. Andrushchenko, K. Ruud and P. Bouř, J. Phys. Chem. A, 2012, 116, 778–783.
68. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
69. C. Angeli, K. L. Bak, V. Bakken, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, T. Enevoldsen, B. Fernandez, C. Haettig, K. Hald, A. Halkier, H. Heiberg, T. Helgaker, H. Hettema, H. J. A. Jensen, D. Jonsson, P. Joergensen, S. Kirpekar, W. Klopper, R. Kobayashi, H. Koch, O. B. Lutnaes, K. V. Mikkelsen, P. Norman, J. Olsen, M. J. Packer, T. B. Pedersen, Z. Rinkevicius, E. Rudberg, T. A. Ruden, K. Ruud, P. Salek, A. Sanchez de Meras, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. O. Sylvester-Hvid, P. R. Taylor, O. Vahtras, D. J. Wilson and H. Agren, Dalton 2011, a molecular electronic structure program, University of Oslo, Oslo, 2005–2009.
70. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
71. K. H. Hopmann, J. Šebestík, J. Novotná, W. Stensen, M. Urbanová, J. Svenson, J. S. Svendsen, P. Bouř and K. Ruud, J. Org. Chem., 2012, 77, 858–869.
72. H. Suzuki, Electronic absorption spectra and geometry of organic molecules: An application of molecular orbital theory, Academic Press Inc., New York, 1967.
73. P. J. Stephens, Adv. Chem. Phys., 1976, 35, 197–264.
74. P. Hobza, H. L. Selze and E. W. Schlag, J. Phys. Chem., 1996, 100, 18790–18794.
75. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
76. T. Yanai, D. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
77. G. Pescitelli, D. Padula and F. Santoro, Phys. Chem. Chem. Phys., 2012, 15, 795–802.
78. J. R. Cheeseman, M. S. Shaik, P. L. A. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991–4997.
79. K. J. Jalkanen, R. M. Nieminen, K. Frimand, J. Bohr, H. Bohr, R. C. Wade, E. Tajkhorshid and S. Suhai, Chem. Phys., 2001, 265, 125–151.
80. K. H. Hopmann, K. Ruud, M. Pecul, A. Kudelski, M. Dračínský and P. Bouř, J. Phys. Chem. B, 2011, 115, 4128–4137.
81. A. Ganesan, M. J. Brunger and F. Wang, Eur. Phys. J. D, 2013, 67, 229–240.
82. P. Bouř, D. Michalík and J. Kapitán, J. Chem. Phys., 2005, 122, 144501.

---