 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Loading of ionic compounds into metal–organic frameworks: a joint theoretical and experimental study for the case of La3+†
Wei
Guo
a,
Jinxuan
Liu
a,
Peter G.
Weidler
a,
Jianxi
Liu
a,
Tobias
Neumann
b,
Denis
Danilov
b,
Wolfgang
Wenzel
b,
Claus
Feldmann
c and
Christof
Wöll
*a
aKarlsruhe Institute of Technology, Institute of Functional Interfaces (IFG), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: christof.Woell@kit.edu; Fax: +49-(0)721-608-23478; Tel: +49-(0)721-608-23775
bKarlsruhe Institute of Technology, Institute of Nanotechnologie (INT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
cKarlsruhe Institute of Technology, Institute of Inorganic Chemistry, Engesserstraße 15, 3. OG, Room 330, 76344 Karlsruhe, Germany
First published on 10th July 2014
Abstract
Crystalline, highly orientated surface-anchored MOF thin films, grown on Au substrates, were prepared using liquid-phase epitaxy (LPE). The successful loading of La3+ ions into the Cu3(BTC)2 (HKUST-1) SURMOFs (surface-mounted metal–organic frameworks) was monitored using X-ray diffraction (XRD). Theoretical calculations using classical force-field based Monte Carlo simulations yield a structure with two La3+ ions within the large Cu3(BTC)2 pores, in full agreement with experimental results on the composition of these films and the relative intensities of the XRD peaks. Implications of these findings for using MOF thin films for electronic applications are briefly discussed.
Introduction
Among highly porous crystalline materials, presently metal–organic frameworks (MOFs)1–3 attract increasing amount of attention resulting from their flexible pore sizes and large loading capacity for guest species,4 in particular metals and metal ions.5 During the past decade, a huge number of metal@MOF systems (for metals like Au,6 Zn,7 Pd8) have been reported, with the metal guests rendering fascinating properties [e.g., such as hydrogen storage,9,10 catalysis (e.g. CO oxidation,11,12 alcohol oxidation13)] to the host MOF material. Particularly attractive are the cases where the loading of the metal guest species not only changes the crystal structure of the host material but also modifies their properties (e.g. electrical conductivity,14 capacity of ion absorption,15 optical properties).16,17 For a number of applications, e.g. electric/electronic devices,18 information storage,19 electrochemistry,20 heterogeneous catalysts,21 MOF thin films,22,23 the ability to load this MOF-coatings with metals is important.In the present work we focus on a special type of MOF coatings, surface-mounted metal–organic frameworks (SURMOFs). They represent a particularly important class of MOF thin films since they are crystalline, oriented and exhibit a well-defined thickness. They can be manufactured with thicknesses in the micrometer-regime, allowing the application of standard methods to determine their mechanical,24 optical17 and electrical and electrochemical14,20 properties. The loading of Eu3+ ions into HKUST-I SURMOFs has been shown to result in interesting optical properties, it could be shown that optical excitations resulting from absorption in the MOF ligands could be transferred to the embedded Eu ions.25
In the present paper we investigate the loading of La3+ cations into HKUST-1 or Cu3(BTC)2 (BTC, 1,3,5-benzenetricarboxylic acid), a popular MOF-material with fairly large (∼1 nm) pore sizes.26 Since we target applications in electrochemistry, information storage and sensors, here we focus on MOF thin films, SURMOFs. Investigations are carried out using X-ray diffraction (XRD), while quantitative information on the Cu/La-ratio is obtained from ICP-OES (Inductively Coupled Plasma Optical Emission Spectrometry) and XPS (X-ray Photoelectron Spectrum) data. In addition, force-field calculations are carried out to obtain the precise positions of the metal cations and their corresponding counter ions in the lattice. Interestingly, these calculations reveal a rather pronounced binding energy of the metal ions within the MOF cavities brought about by the fairly substantial cations–BTC ligand interaction. Knowledge about the precise structure of metal ion-loaded MOF thin films is crucial for understanding electrical transport,14 electrochemical behaviour20 and metal ion diffusion19 in MOFs and SURMOFs.
Experimental
Preparation of gold substrates
Gold substrates were obtained from PVD Beschichtungen (Silz, Germany). Thin polycrystalline gold films were prepared by thermal vapor deposition of 100 nm gold (99.995%, Chempur) onto polished silicon wafers (Wacker) precovered with a 5 nm titanium adhesion layer. Evaporation was carried out at a pressure of 2 × 10−7 mbar and a deposition rate of 0.5 nm s−1, yielding a root-mean-square roughness of the Au films of about 1 nm. The gold substrates were kept in an argon atmosphere until use.Preparation of COOH-terminated self-assembled monolayers (SAMs)
The 16-mercaptohexadecanoic acid (MHDA, 99%, Aldrich) solution was prepared by dissolving MHDA in a 5% (by volume) solution of acetic acid in ethanol (Merck) to reach the desired concentration of 20 μM.27 A clean gold substrate was placed in this solution for 72 h and then rinsed with ethanol and gently dried under nitrogen flux.Fabrication of Cu3(BTC)2 SURMOFs
All Cu3(BTC)2 thin films used in the present work were grown on modified Au substrates using the liquid-phase epitaxy (LPE) method, which yields highly oriented and well-defined MOF coatings and can be applied to a variety of substrates. In contrast to the conventional bulk solvothermal MOF synthesis, where reactants are mixed to initiate the reaction, the layer-by-layer growth of Cu3(BTC)2 SURMOFs proceeds in two steps comprising a sequential spray solution of the individual reactants. For the present experiments the SURMOFs were grown on a COOH-terminated organic surface on Au.The SURMOFs were fabricated using the following diluted ethanolic solutions: copper acetate hydrate (1 mM, Aldrich) and BTC (1,3,5-benzenetricarboxylic acid) (0.2 mM, Aldrich). For the SURMOF deposition, we used a spray system (Fig. S1, ESI†), as described in detail in an earlier publication.28 The spray times were 15 s for the copper acetate solution and 25 s for the BTC solution. Each spray step was followed by a rinsing step (3 s) with pure ethanol to remove residual reactants. A total of 20 growth cycles were used for all SURMOFs investigated in this work. Before further experiment, all SURMOF samples were activated by ultrasound in dichloromethane solution for 5 min to remove residual solvent from the SURMOF pores and finally checked by XRD.
Characterization of Cu3(BTC)2 SURMOFs was carried out using X-ray diffraction (XRD) (Fig. 1c) and Infrared (IR) spectroscopy (Fig. S2, ESI†). The presence of a broad and strong band at 1700–1300 cm−1 is assigned to vibrations of COO− of Cu3(BTC)2.29 The SEM (Scanning Electron Microscope) picture (Fig. S3, ESI†) shows that the thickness of SURMOFs is nearly about 100 nm.
Preparation of the La(OTf)3@Cu3(BTC)2 SURMOF
First, a Cu3(BTC)2 thin film on the gold substrate was put into a 250 ml flask and then evacuated to 0.2 kPa at room temperature for 30 min. Subsequently, the sample was immersed in a freshly prepared solution of La(OTf)3 [lanthanum(III) trifluoromethanesulfonate] in ethanol (1 mM, Aldrich) kept at 65 °C. After an immersion time of 12 h the sample was removed from the solution, rinsed with pure ethanol, and finally dried in a flux of nitrogen gas.The characteristic R-SO3− vibration at 1042 cm−1 appears after immersing the Cu3(BTC)2 SURMOFs in a La(OTf)3 solution (Fig. S2, ESI†), this observation provides strong support for the hypothesis presented above, namely, that the (OTf) anion is adsorbed in the SURMOFs. Upon immersing the La(OTf)3@Cu3(BTC)2 SURMOF in dichloromethane under ultrasonic conditions for 15 min, the XRD pattern has no significant change (Fig. S4, ESI†) suggesting an irreversible loading of the SURMOF with La(OTf)3.
Modelling
Molecular modeling simulations were performed using a Monte Carlo algorithm implemented in the simulation package SIMONA.30 In order to avoid the trapping of the system in metastable conformations, the basin hopping approach31–33 with consecutive simulated annealing cycles was used to obtain the lowest energy for the system. Each simulated annealing cycle consists of a series of Metropolis Monte Carlo steps starting at high temperature, where the molecule can escape local minima and traverse energy barriers. Throughout the simulation the temperature is lowered according to: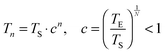 | (1) |
The interaction between the atoms was modeled by the classical electrostatic potential:
 | (2) |
 | (3) |
We used standard parameters of the Lennard-Jones interaction for all atoms except La. In order to determine the LJ parameters for La3+ we performed Metropolis Monte Carlo simulations of La3+ with 3(OTf) at constant low temperature (T = 1 K) and varied the La-parameters until the distance between oxygen and La3+ reached the equilibrium distance obtained from ab initio calculations. The resulting parameters for La3+ are ε = 0.15 kcal mol−1 and σ = 3.425 Å. Partial charges were calculated using the ESP fit implemented in the DFT code TURBOMOLE34 using SV(P) basis and b3-lyp functional (see ESI† for details, Fig. S5).
To screen possible configurations a system consisting of two neighboring cavities (the medium and the large cavity of the MOF) was constructed. Each cavity was loaded with up to four La(OTf)3 molecules resulting in 24 different model systems. To prevent the ions from leaving the complex we applied a strong restraining force to particles outside the cavities:
| Uconfine(q) = k(q − x0)2, q > x0 or q < −x0, q = x, y, z |
The simulations consisted of 10 simulated annealing runs with N = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Metropolis Monte-Carlo steps each, starting at TS = 750 K and ending at TE = 300 K using rigid body translation for La3+ and (OTf) and in addition rigid body rotation and rotation around dihedral angles in the (OTf) ions. The step size for the random rigid translations was drawn from a random uniform distribution between 0 and 1 Å, the angle of the rigid rotations from a random uniform distribution between 0° and 180°.
000 Metropolis Monte-Carlo steps each, starting at TS = 750 K and ending at TE = 300 K using rigid body translation for La3+ and (OTf) and in addition rigid body rotation and rotation around dihedral angles in the (OTf) ions. The step size for the random rigid translations was drawn from a random uniform distribution between 0 and 1 Å, the angle of the rigid rotations from a random uniform distribution between 0° and 180°.
Results and discussion, experimental
Experiments
The out-of-plane XRD data for the pristine HKUST-1 SURMOFs are shown in Fig. 1c (black). The (002) and (004) peaks are well-defined and sharp, their relative intensity agrees with that observed for bulk MOF powders obtained from simulations using the well-established bulk structure of HKSUST-1 (Fig. 1a). The absence of diffraction peaks for other crystallographic directions in the out-of-plane data reveals that that the SURMOF growth proceeds only along the (001) direction on the MHDA SAM. The in-plane XRD data showing only the (200) and (220) direction also support this orientation structure (Fig. 1c, red). XRD data recorded after immersion into the La(OTf)3 solution are shown in Fig. 1c (out-of-plane, blue; in-plane, dark yellow). No new diffraction peaks appeared revealing that the structure of the MOF lattice has remained unchanged. However, the form factor is strongly different, after loading the ratio of (002)/(004) (out-of-plane data) has decreased from 1.1 for the pristine film to 0.7 for the La loaded film. Also the in-plane XRD data reveal pronounced changes: the ratio of (200)/(400) has dropped from 1.6 to 0.1. Longer immersion times did not lead to a further change of the relative XRD peak intensities.The same loading process has also been carried out for powder Cu3(BTC)2 MOF. The changes in relative peak intensities observed for the powders were similar to that seen for the SURMOFs (Fig. S6, ESI†). The ratio of (002)/(004) has dropped from 2.15 to 1.21 after loading La(OTf)3.
This significant change in relative intensities of XRD-peaks directly demonstrates that La3+ ions are loaded in virtually every pore of the SURMOF (and MOF powders), a decoration of the outer surface only would not be compatible with the change of diffraction peak relative intensities.
The results of the XPS analysis are shown in Fig. 2. Clearly, after loading the data recorded for the La(OTf)3@Cu3(BTC)2 SURMOFs show distinctive La peaks.35 A quantitative analysis reveals that the total copper and lanthanum content of the SURMOFs after loading are 4.3% and 0.8%, respectively (Table S2, ESI†).
 | ||
| Fig. 2 X-ray photoelectron spectrum (XPS) of (a) Cu 2p and (b) La 3d of the La(OTf)3@Cu3(BTC)2 MOF thin films. | ||
The metal ion concentration curves from inductively coupled plasma optical emission spectrometry (ICP-OES) measurement are shown in Fig. 3. By calculation of the integrated area of the measured curves, the copper and lanthanum concentration after loading the sample are 6.6 mg L−1 and 0.9 mg L−1, respectively (Table S3, ESI†), the calculated ratio of Cu/La amounts to 7.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is close to the value calculated from XPS data.
1, which is close to the value calculated from XPS data.
 | ||
| Fig. 3 Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES) of (a) Cu2+ and (b) La3+ of the La(OTf)3@Cu3(BTC)2 MOF thin films. | ||
Simulations
In order to complement the experimental data to obtain detailed information regarding the positions of the molecules within the MOF pores we have carried out force-field based Monte Carlo simulations for different numbers of La(OTf)3 embedded in Cu3(BTC)2. First, simulations of up to four La(OTf)3 moieties within a single Cu3(BTC)2 unit cell were performed and the binding energies were calculated. To confine the La(OTf)3 moieties to the cavity an additional harmonic penalty potential (confining potential) was introduced for particles outside the cavity. Results for binding energies and the confining harmonic potential of the lowest energy state are reported in Table 1. The binding energy decreases with an increase in the number of moieties for up to four molecules, as repulsive interactions between the molecules compete with attractive interactions with the MOF. We note that the confining potential at the energy minimum is increased significantly when more than three La(OTf)3 are loaded in each per cavity, which indicates that not more than 3 molecules can fit one pore. There is a substantial binding energy associated with the loading, which mainly results from the dispersive interaction of the La3+ ion, which is moved close to the central phenyl ring of one of the BTC ligands at the energy minimum (Fig. S7, ESI†). Because this interaction may not be fully represented in the force field, we have performed additional DFT calculations to obtain the binding between La3+ and the phenyl rings and obtained a binding energy of −7.84 eV which is approximately 300 times kBT at room temperature.| Cu3(BTC)2 of La(OTf)3 | Binding energy/kcal mol−1 | Confining potential |
|---|---|---|
| 1 | −837.33 | 6.53 |
| 2 | −1235.38 | 49.08 |
| 3 | −1482.21 | 47.34 |
| 4 | −1559.74 | 152.89 |
In order to compare with the experimental data both cavities were loaded with different numbers of La(OTf)3 and simulation with 10 SA-cycles with 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MC steps each, starting at T = 750 K and cooling down to T = 300 K, was carried out. The optimized structure with possible locations and numbers (1, 2, 3, 4) of La(OTf)3 in the large pore of Cu3(BTC)2 MOF is presented in Fig. 4a and Fig. S6 (ESI†). The simulated out-of-plane XRD data for a (001) growth direction for the optimized structures obtained from the calculations are shown in Fig. 4b.
000 MC steps each, starting at T = 750 K and cooling down to T = 300 K, was carried out. The optimized structure with possible locations and numbers (1, 2, 3, 4) of La(OTf)3 in the large pore of Cu3(BTC)2 MOF is presented in Fig. 4a and Fig. S6 (ESI†). The simulated out-of-plane XRD data for a (001) growth direction for the optimized structures obtained from the calculations are shown in Fig. 4b.
The increase of the (004) peak relative to the (002) peak in the calculated XRD data when adding the first La ion close to the Cu2+ ions can be rationalized by considering the fact that this structure can (to first approximation) be described as an F lattice, and the intensity of the (002) peaks has to increase because placing the La3+ ion close to the Cu ions effectively increases the electron density around these Cu position. When additional La3+ ions are placed more close to the middle of the major pore (as in the structures of the 2 and 3 ions by the structure optimizations) the F-lattice is effectively changed into an I-lattice (Fig. S6, ESI†). The extinction rules for I-lattices lead to a decrease of the (002) peak intensity, as is evident from the figure for the case of 2 and 3 La3+ ions. Further increase of the La content in the unit cell leads to an increase of the intensity. This can be explained by the higher atomic scattering factor of the La and its position. The former Cu F-lattice transforms into a La F-lattice (or even P-lattice) with some admixtures of Cu in the I-lattice positions. The atomic scattering factor for Cu cannot fully compensate the La contributions to the scattered intensity. The effect explaining the intensity decrease for the 1La and 2La loading state applies also for the higher loading states for La, hence, an initial Cu dominated structure is not transformed into a La dominated structure. This result fits very well with the experiment data. The results for the two and three ions are very similar in the out-of-plane data.
By comparing with the results of structure optimizations, loading with a single La ion can be ruled out because for the poor agreement of the simulated with the experimental XRD data. On the other hand a loading with 3 ions per HKUST-1 unit cell can be ruled out because of the poor agreement with the ICP-OES data. We thus conclude that in the loaded structure 2La3+ ions are hosted within the pore of Cu3(BTC)2. This finding is fully consistent with all available experimental and theoretical information.
Conclusions
In conclusion, La(OTf)3 was successfully loaded into Cu3(BTC)2 SURMOF via a solution impregnation method as evidenced by XPS, ICP-OES and IR data. By additionally considering the results of theoretical structure optimizations using a refined force-field analysis, we find a loading with two La-ions per unit cell to give the best agreements. This structure is stabilized by pronounced dispersive interactions between the La ion and the phenyl ring of a BTC ligand. The resultant loading of La (and other noble metal) species into the porous solid is of pronounced interest with regard to using MOF thin films for applications. Loading with metal ions and subsequently using redox-chemistry to create new species inside the MOF have recently received substantial attention in the context of information storage.19 In future work we plan to study the electrochemical properties of the loaded SURMOFs, which also offer rich potential for catalysis applications.Acknowledgements
We thank Vanessa Trouillet (Institute for Applied Materials – Energy Storage Systems (IAM-ESS), Karlsruhe Institute of Technology, Germany) for the XPS measurement, Marita Heinle (Institute of Functional Interfaces (IFI), Karlsruhe Institute of Technology, Germany) for the ICP-OES measurements and Stefan Heißler (Institute of Functional Interfaces (IFG), Karlsruhe Institute of Technology, Germany) for the fluorescence measurements. Financial support from Deutsche Forschungsgemeinschaft (DFG) within the Priority Program Metal Organic Frameworks (SPP 1362) is gratefully acknowledged. The authors acknowledge the financial support of the Chinese Scholarship Council (CSC).Notes and references
- H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279 CrossRef CAS PubMed.
- R. Makiura, S. Motoyama, Y. Umemura, H. Yamanaka, O. Sakata and H. Kitagawa, Nat. Mater., 2010, 9, 565–571 CrossRef CAS PubMed.
- C. Mellot-Draznieks, J. Dutour and G. R. Ferey, Angew. Chem., Int. Ed., 2004, 43, 6290–6296 CrossRef CAS PubMed.
- J. Liu, B. Lukose, O. Shekhah, H. K. Arslan, P. Weidler, H. Gliemann, S. Braese, S. Grosjean, A. Godt, X. Feng, K. Muellen, I.-B. Magdau, T. Heine and C. Wöll, Sci. Rep., 2012, 2, 921 Search PubMed.
- M. Meilikhov, K. Yusenko, D. Esken, S. Turner, G. Van Tendeloo and R. A. Fischer, Eur. J. Inorg. Chem., 2010, 3701–3714 CrossRef CAS.
- D. Esken, S. Turner, O. I. Lebedev, G. Van Tendeloo and R. A. Fischer, Chem. Mater., 2010, 22, 6393–6401 CrossRef CAS.
- D. Esken, H. Noei, Y. M. Wang, C. Wiktor, S. Turner, G. Van Tendeloo and R. A. Fischer, J. Mater. Chem., 2011, 21, 5907–5915 RSC.
- D. Esken, X. Zhang, O. I. Lebedev, F. Schroder and R. A. Fischer, J. Mater. Chem., 2009, 19, 1314–1319 RSC.
- S. Proch, J. Herrmannsdorfer, R. Kempe, C. Kern, A. Jess, L. Seyfarth and J. Senker, Chem. – Eur. J., 2008, 14, 8204–8212 CrossRef CAS PubMed.
- S. J. Yang, J. H. Cho, K. S. Nahm and C. R. Park, Int. J. Hydrogen Energy, 2010, 35, 13062–13067 CrossRef CAS PubMed.
- J. Y. Ye and C. J. Liu, Chem. Commun., 2011, 47, 2167–2169 RSC.
- H. L. Jiang, B. Liu, T. Akita, M. Haruta, H. Sakurai and Q. Xu, J. Am. Chem. Soc., 2009, 131, 11302–11303 CrossRef CAS PubMed.
- T. Ishida, M. Nagaoka, T. Akita and M. Haruta, Chem. – Eur. J., 2008, 14, 8456–8460 CrossRef CAS PubMed.
- A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. El Gabaly, H. P. Yoon, F. Leonard and M. D. Allendorf, Science, 2014, 343, 66–69 CrossRef CAS PubMed.
- J. He, M. Q. Zha, J. S. Cui, M. Zeller, A. D. Hunter, S. M. Yiu, S. T. Lee and Z. T. Xu, J. Am. Chem. Soc., 2013, 135, 7807–7810 CrossRef CAS PubMed.
- S. Y. Jin, H. J. Son, O. K. Farha, G. P. Wiederrecht and J. T. Hupp, J. Am. Chem. Soc., 2013, 135, 955–958 CrossRef CAS PubMed.
- E. Redel, Z. B. Wang, S. Walheim, J. X. Liu, H. Gliemann and C. Wöll, Appl. Phys. Lett., 2013, 103, 091903 CrossRef PubMed.
- M. D. Allendorf, A. Schwartzberg, V. Stavila and A. A. Talin, Chem. – Eur. J., 2011, 17, 11372–11388 CrossRef CAS PubMed.
- S. M. Yoon, S. C. Warren and B. A. Grzybowski, Angew. Chem., Int. Ed., 2014, 53, 4437–4441 CrossRef CAS PubMed.
- A. Dragasser, O. Shekhah, O. Zybaylo, C. Shen, M. Buck, C. Wöll and D. Schlettwein, Chem. Commun., 2012, 48, 663–665 RSC.
- X. W. Dong, T. Liu, Y. Z. Hu, X. Y. Liu and C. M. Che, Chem. Commun., 2013, 49, 7681–7683 RSC.
- O. Shekhah, J. Liu, R. A. Fischer and C. Wöll, Chem. Soc. Rev., 2011, 40, 1081–1106 RSC.
- H. Gliemann and C. Wöll, Mater. Today, 2012, 15, 110–116 CrossRef CAS.
- S. Bundschuh, O. Kraft, H. K. Arslan, H. Gliemann, P. G. Weidler and C. Wöll, Appl. Phys. Lett., 2012, 101, 101910 CrossRef PubMed.
- H. C. Streit, M. Adlung, O. Shekhah, X. Stammer, H. K. Arslan, O. Zybaylo, T. Ladnorg, H. Gliemann, M. Franzreb, C. Wöll and C. Wickleder, ChemPhysChem, 2012, 13, 2699–2702 CrossRef CAS PubMed.
- S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS.
- M. Kind and C. Wöll, Prog. Surf. Sci., 2009, 84, 230–278 CrossRef CAS PubMed.
- H. K. Arslan, O. Shekhah, J. Wohlgemuth, M. Franzreb, R. A. Fischer and C. Wöll, Adv. Funct. Mater., 2011, 21, 4228–4231 CrossRef CAS.
- O. Zybaylo, O. Shekhah, H. Wang, M. Tafipolsky, R. Schmid, D. Johannsmann and C. Wöll, Phys. Chem. Chem. Phys., 2010, 12, 8092–8097 RSC.
- T. Strunk, M. Wolf, M. Brieg, K. Klenin, A. Biewer, F. Tristram, M. Ernst, P. J. Kleine, N. Heilmann, I. Kondov and W. Wenzel, J. Comput. Chem., 2012, 33, 2602–2613 CrossRef CAS PubMed.
- S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680 CAS.
- Z. Q. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS.
- R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- V. V. Atuchin, A. V. Kalinkin, V. A. Kochubey, V. N. Kruchinin, R. S. Vemuri and C. V. Ramana, J. Vac. Sci. Technol., A, 2011, 29, 021004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp02285h |
| This journal is © the Owner Societies 2014 |


