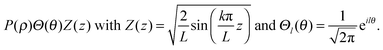Open Access Article
Open Access ArticleA particle on a hollow cylinder: the triple ring tubular cluster B27+†
Long Van
Duong
a,
Hung Tan
Pham
a,
Nguyen Minh
Tam
ab and
Minh Tho
Nguyen
*b
aInstitute for Computational Science and Technology (ICST), Quang Trung Software City, Ho Chi Minh City, Vietnam
bDepartment of Chemistry, University of Leuven, B-3001 Leuven, Belgium. E-mail: minh.nguyen@chem.kuleuven.be
First published on 29th July 2014
Abstract
We determined the geometries and chemical bonding phenomena of the B27 system in its dicationic, cationic, neutral, anionic and dianionic states using DFT computations. In both cationic and neutral states, the triple ring tubular forms correspond to the lowest-energy isomers, especially in B27+. The cation B27+ represents the first stable hollow cylinder having a triple ring among the pure boron clusters. In the anionic and dianionic states, the quasi-planar structures are favoured due to a charge effect. In the triple ring tube B27+, strong diatropic responses to external magnetic field occur in both radial and tangential types of electrons, and thus confer it a characteristic tubular aromaticity. The presence of a consistent aromatic character contributes to its high thermodynamic stability. The shapes of calculated MOs of B27+ TR can be predicted by the eigenstates of a simple model of a particle on a hollow cylinder. The number of electrons in a hollow cylinder should attain a number of (4N + 2M) with M = 0 and 1 for both radial and tangential electrons, depending on the number of non-degenerate MOs occupied, in order to properly fulfill the closed electron shells. In the case of B27+, M = 0 for radial electrons and M = 1 for tangential electrons.
1. Introduction
Boron is an interesting electron deficient element in the Periodic Table. The lack of five electrons in its 2p valence shell allows boron to receive electrons forming high coordination states. In addition, the characteristically short covalent radius of boron frequently leads to formation of strong and non-classical chemical bonds. Boron elements are thus able to build up compounds with unlimited sizes by covalently binding to themselves. A plethora of boron clusters featuring two-dimensional (2D, planar and quasi-planar) and three-dimensional (3D, tube, convex, cage, sphere, fullerene...) shapes have been predicted on the basis of the ‘Aufbau principle’,1 and some of them have experimentally been identified.2,3 This suggests an overlap of several different growth patterns of boron clusters. Extensive efforts have therefore been devoted to the search for new forms of boron allotropes, nanocages,4,5 and nanotubes6 and as a matter of fact, most boron clusters appear to exhibit polymorphism and multi-center bonding.7Boron has been proved to be a rare element whose atomic clusters Bn retain either planar or quasi-planar (QP) geometries even when the cluster size n goes up beyond >20, depending on the charge state. Except for B14, which has a fullerene-like shape,8 most small bare boron clusters up to B19 have also been identified to have planar or quasi-planar structures.9 The corresponding cations Bn+ prefer to adopt 3D structures at smaller sizes (at n < 18),10,11 whereas the anions Bn− and dianions Bn2− species tend to exhibit planar or QP structures with n being up to >30.3. There is an effective charge effect in which addition of extra electrons allows a redistribution of chemical bonds and thereby consistently favours QP boron cluster anions, and removal of electrons leads to 3D cations.12 A Frank–Condon effect is fully operative in which geometry relaxation turns out to be extremely important following addition or removal of electrons from neutral boron clusters in order to stabilize the resulting ions. In other cases, Jahn–Teller and pseudo-Jahn–Teller effects are also of primordial importance in the stabilization of boron clusters yielding lower symmetry structures.13–15
Regarding the tubular forms of boron clusters, the neutral B20 was found to be the first size having a double ring tube (DR) in which the two ten-membered rings are connected together in an antiprism bonding motif.16–18 This DR was calculated to be a few kcal mol−1 more stable than the quasiplanar isomer.16 Similar to B20, each of the neutrals B22, B24, B26 and B28 were also found to exist in a DR ground state.17,19,20 These observations resulted in a popular belief that intermediate-sized Bn with n ≥ 30 still prefers tubular geometries. Nevertheless, we recently demonstrated that B30 exhibits rather a bowl structure,21 which is composed of a pentagon background and successively built up by two strings of 10 and 15 boron atoms yielding a five-fold symmetry (C5v). This bowl built up by 5@10@15 strings turns out to be ∼5 kcal mol−1 more stable than the 3 × 10 triple ring tube (TR). The slightly higher thermodynamical stability of the bowl B30 was shown to arise in part from its disk aromatic character.22,23 In spite of its non-planarity, the 20 π-type electrons of the bowl B30 are distributed in a way similar to those of the planar disk aromatic B202− dianion.22,23
Previous computations also predicted that the neutral B32 has a DR shape composed of two 16-membered rings.24 In contrast, the neutral B36 was again found by computations, and confirmed by experimental spectroscopy, to have a bowl structure which is based on a hexagonal background and successively capped on it by two strings of 12 and 18 boron atoms.3 The 6@12@18 strings thereby lead to a six-fold symmetry (C6v) bowl form which is calculated to be the lowest-lying structure being ∼20 and ∼32 kcal mol−1 more stable than the TR 3 × 12 tube and QP (having a hexagon and a heptagon) isomers, respectively.3 Recently, we found that a TR tube formed by a superposition of three 14 boron cyclic strings is the global minimum of the neutral B42 cluster, again being a few kcal mol−1 more stable than the planar disk 7@14@28 with a heptagon base.25
Nevertheless, a TR tube at a size of 42 atoms is relatively large, and an intermediate size can be expected to exist in the growth paths leading to boron tubes. In this context, a pertinent question is as to whether a TR tube could exist as a global minimum at a smaller size. A tubular form, longer than a DR, constitutes a following necessary precursor for the building-up of boron tubes. Motivated by such an issue, we set out to perform in the present work a search for Bn clusters having a stable TR tube. Using density functional theory (DFT) methods, a TR tube is found as the lowest-lying isomer at the size n = 27 in its cationic state. In the present paper we report for the first time some geometrical features of the cation B27+ having a TR tubular shape, and also an analysis of its chemical bonding and electronic structure. For the latter purpose, we attempt to formulate a simple model based on the behaviour of a particle on a hollow cylinder. In addition, we make use of the partition of the electron densities into bonded and non-bonded electron pairs, as well as the computation of magnetic ring currents, in order to probe further the bonding pattern and aromatic character of the TR tubular cluster B27+.
2. Computational methods
Standard electronic structure calculations are carried out using the Gaussian 09 program.26 As the reliability of DFT functionals has extensively been tested in previous studies for boron clusters,8,9,11,12 we employ in this work the hybrid TPSSh and the PBE functionals in the search for equilibrium structures, and subsequent determination of their relative energies. The search for energy minima is conducted using two different approaches. In the first, we use a stochastic genetic algorithm to generate possible structures.12,27 The equilibrium structures that are initially optimized using computations with small basis sets, are reoptimized using larger basis sets. In the second approach, initial structures of a B27 cluster are manually constructed by adding necessary B-atoms at possible positions on the surfaces of the smaller Bn (n ∼ 20–26) clusters. The use of the genetic algorithm is effective for producing non-classical structures whereas the manual protocol allows a more focused search to be performed. Although the large number of initial structures makes the genetic search more tedious, only a combination of different search approaches allows new structures to be discovered, and a consistent set of lower-energy structures for a size to be obtained.While computations on initial guess geometries are carried out using both TPSSh and PBE functionals,26 in conjunction with the 3-21G and 6-31G(d) basis sets, selected equilibrium geometries with relative energies of up to ∼3 eV are fully reoptimized using the same functional but with the larger 6-311+G(d) basis set.28 In order to confirm the identity of the local minima obtained, their harmonic vibrational frequencies are also calculated at the same levels of theory. For the analysis of chemical bonding, in particular the aromaticity, we make use of canonical MOs, electron localization function (ELF)29 and electron localizability indicator (ELI-D)30 maps, as well as the ring current approach31,32 along with the ipsocentric model.33–35 Calculations of the ring current are carried out using the CTOCD-DZ method32 implemented in the SYSMO program,36,37 which is connected to the GAMESS-UK package.38
3. Results and discussion
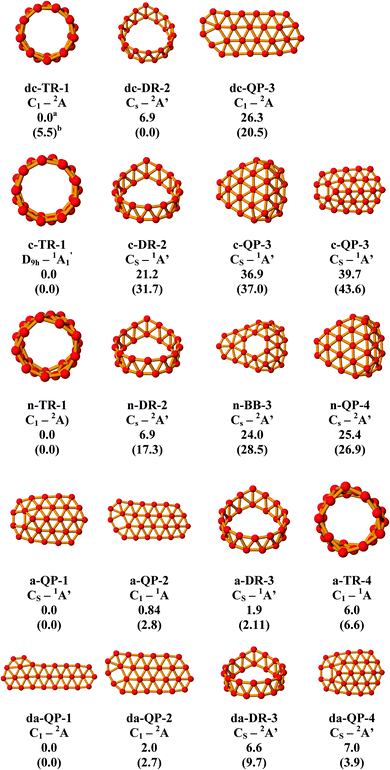
The calculated results are mainly presented in the figures and table described in the following sections.3.1 Lower-lying isomers of the B27 clusters in five charge states
Let us first analyze the structures of the B27 system in five different charge states including the dication, cation, neutral, anion and dianion. To simplify the presentation of data, only a few lower-lying isomers in each charge state will be displayed in Fig. 1, which summarizes the structural shapes and relative energies of the B27 system in five charge states ranging from −2 to +2. As a convention, each structure will be labeled as x-Y, in which x = n (neutral), c (cation), dc (dication), a (anion) and da (dianion), and Y = QP (quasiplanar), DR (double ring tube), TR (triple ring tube), BB (broken bowl). Cartesian coordinates of the optimized geometries of these structures are collected in Table S1 of the ESI† file.In order to understand the influence of electron removal and addition, the adiabatic (IE) and vertical ionization energy (VIE), adiabatic (EA) and vertical electron affinity (VEA) are calculated and reported here. The adiabatic results are obtained from fully optimized geometries, IE = E(B27+) − E(B27) and EA = E(B27) − E(B27−). The VIE and VEA values are defined as the energy differences between neutral and ionic states, with both energies at the optimized geometry of the neutral B27 tube. The value IE(B27) = 6.0 eV and VIP(B27) = 6.3 eV are obtained. Likewise, the adiabatic and vertical electron affinity values of B27 are calculated to be 2.7 and 2.5 eV, respectively. Consequently, the nuclear configuration relaxation induces only a small change in the energy following electron removal and addition.
It is clear that in this size, the cationic state B27+ having a closed-shell electronic state and a triple ring cylinder shape c-TR, which is formed by a regular and high symmetry tubular form, turns out to be the energetically lowest-lying isomer. As far as we are aware, this represents the first TR tube as a global minimum among the small sized boron clusters.
The structures found in both cationic and dicationic clusters confirm the trend observed before pointing that removal of electrons from boron clusters tends to favour the 3D isomers.12
Of particular interest for the present work are the two lower-lying tubular forms, with c-TR representing a typical triple ring tube.
Overall, it appears that in both cationic and neutral states, the TR tube is identified to be among the lowest-lying isomer, in particular the cation B27+ which is characterized by a clear-cut energy separation with the remaining isomers. Accordingly, this (3 × 9-membered ring) species can be regarded as a representative of the smallest boron clusters featuring a triple ring tubular shape. Therefore in the following analysis, we only focus on this cationic triple ring cluster B27+.
3.2 The model of a particle on a hollow cylinder
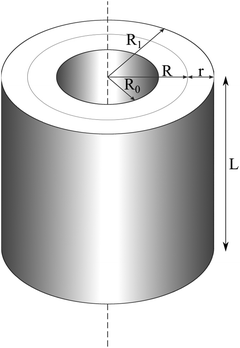
In order to rationalize the high stability of the TR B27+ cluster, and in particular to understand the distribution of its electrons, we propose herewith a simple model of a particle in a hollow cylinder. We first present in this section the solutions of the corresponding wave functions, and subsequently a comparison of these model solutions with the molecular orbitals actually computed using DFT methods.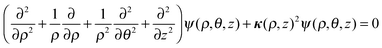 | (1) |
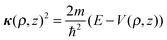 | (2) |
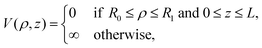 | (3) |
The solutions for eqn (1) were previously proposed by Gravesen and co-workers.39 Accordingly, the wave function ψ(ρ,θ,z) can be written as:
The Z(z) function responds to the boundary conditions at two surfaces z = 0 and z = L in such a way that the rational quantum number k must be a positive integer (1, 2, 3,…). In addition, the Θ(θ) function must satisfy the periodic boundary conditions that lead to the rotational quantum number l must be integer (0, ±1, ±2,…). States with non-zero values for l will be twofold degenerate.
A solution of the P(ρ) function with the vanished boundary conditions at inner and outer radii positions (ρ = R0 and ρ = R1) is a Bessel function, which is written in eqn (4):
| Jl(klnR(1 + ε))Yl(klnR(1 − ε)) − Jl(klnR(1 − ε))Yl(klnR(1 + ε)) = 0 | (4) |
Eqn (4) is a three-parameter, l, klnR and ε equation. Jl and Yl are the Bessel functions of order l with the first and the second kind, respectively. l is known as the rotational quantum number. 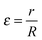 is the pseudo-radius of the hollow cylinder. Determination of the klnR parameter allows the eigenvalues (energies) of the eqn (1) to be derived as given in eqn (5):
is the pseudo-radius of the hollow cylinder. Determination of the klnR parameter allows the eigenvalues (energies) of the eqn (1) to be derived as given in eqn (5):
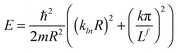 | (5) |
If the pseudo-radius ε and the rotational quantum number l are known, we can then plot the f(klnR) and thereby determine the value of klnR for which f(klnR) = 0.
As a simple illustration, Fig. 3 shows the first three values of klnR when ε = 0.5 and l = ±1. This implies that eqn (4) can be solved for klnR, with n is the nth zero of this equation. This gives rise to the third quantum number in the hollow cylinder model, namely the radial (n = 1, 2, 3,…) quantum number. We see that E varies as a function of klnR, k, and Lf. As mentioned above, the klnR varies with respect to ε, l and n. In such a context, the eigenstates (wavefunctions) in the HCM are characterized by three quantum numbers, including a rational (k = 1, 2, 3,…), a rotational (l = 0, ±1, ±2, ±3,…), and a radial (n = 1, 2, 3,…) quantum number. Accordingly, the eigenstates in an ascending order will be changed following any change of the values of ε or Lf.
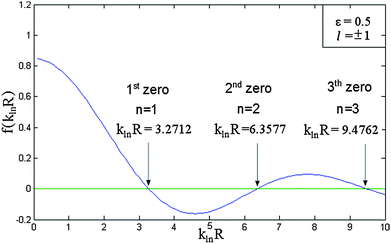 | ||
| Fig. 3 Method for the determination of the parameter klnR. The graph shows the first three klnR values of the eqn (4) when ε = 0.5 and l = ±1. | ||
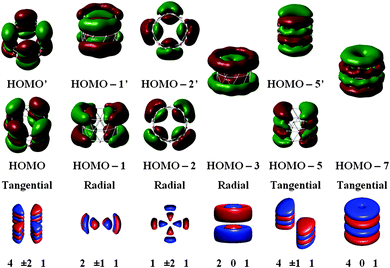
(i) MOs from numbers 28 to 46: these 19 MOs are essentially formed from the s atomic orbitals (AO) of boron corresponding thus to the deep MO region having low orbital energies. These MOs are expected to have small contributions to the molecular ring current; and
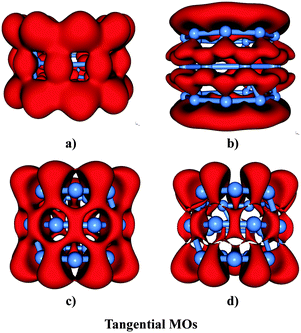
(ii) MOs from numbers 47 to 67: these 21 MOs are mainly formed from the p AOs. These MOs can be divided for their part into two different classes depending on the orientation of the p-lobes, namely the radial MOs (denoted as r-MOs) and tangential MOs (t-MOs).18 In more popular terms, the radial MOs correspond to π-MOs, whereas the tangential MOs can be assigned as σ-MOs.
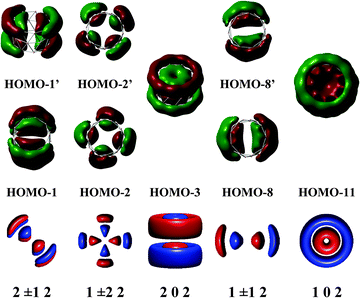
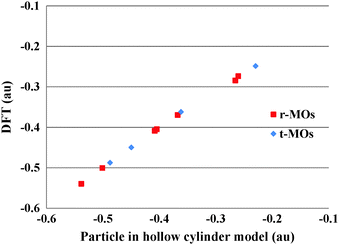
To facilitate comprehension, we plot in Fig. 4–6 a comparison of representative delocalized MOs of the TR B27+ tube calculated by the DFT method with the corresponding HCM solutions. Fig. 7 illustrates a correlation between DFT-computed and HCM-predicted MO energies. It is clear from Fig. 4 that the shape of the delocalized HOMOs of the TR tube can perfectly be predicted by the HCM, irrespective of the degeneracy of the MO.
Most orbitals of the tangential MOs set are formed from 2pz or 2spz hybridized AOs having their axis parallel to the tube's axis. In this case, the number of radial nodes has only one value n = 1. The number of rational node k is consistently greater than the ring number of the tube. In addition, the eigenstates (MOs) in the t-MO set with k = 5 are anti-bonding MOs. The number of rotational node l also could not be greater than the number atoms in each ring. In the B27+ tube case, we thus have k = 4, 5,… and l = 0, ±1, ±2,…, ±9 and n = 1.
For t-MOs of B27+, we can determine that the hollow cylinder with εσ, Lfσ satisfies the above conditions.
Fig. 7 shows a correlation between the calculated t-MOs orbital energies to the spectrum derived from HCM for B27+. A good correlation can be found for these orbital energies. Due to the character of the t-MO set of the TR tube, we can see that the ascending order of MOs in this set apparently obeys a certain rule. As shown in Fig. 5, the (401) state is the ground state in this set. The (501) state is the next non-degenerate state, but it is an anti-bonding MO when applied to a boron TR structure. The doubly degenerate MOs corresponding to value l ≠ 0 are occupied by 4N electrons. Thus, the tangential σ-MO set simply follows the classical electron counting rule of (4N + 2) if only the (401) eigenstate is fully occupied or 4N if the (401) and (501) eigenstates are fulfilled. The B27+ TR has two electrons occupied in HOMO − 7, which corresponds to the (401) eigenstate of the HCM, and 8 electrons occupied in two doubly degenerate MOs involving the HOMO (HOMO′) and HOMO − 5 (HOMO − 5′) corresponding to the (4±11) and (4±21) solutions of the HCM. Consequently, the t-MO set satisfies this electron counting rule with 10 electrons.
Another application of the HCM can be considered is the neutral B42 triple ring. Our recent results illustrate that the B42 TR is calculated to be the most stable isomer at the size of 42 B atoms. The total number of electrons occupied in tangential MOs set involves of two electrons corresponding to the (401) eigenstate and 12 electrons filling 3 doubly degenerate MOs corresponding to value l ≠ 0. Thus, the t-MOs of the neutral B42 TR satisfy the (4N + 2) counting rule with 14 electrons.
When using chemical characters to limit the possible values for quantum numbers, we find a hollow cylinder with pseudo-radius ε and pseudo-height Lf in such a way that an ascending order of the quantum numbers and their energies coincides well with the ascending order of the node and energies of actually calculated MOs. In the radial MOs of B27+, we can determine that the hollow cylinder with the values επ, Lfπ fully satisfies the above conditions. As shown in Fig. 6, the MO shape of the hollow cylinder, including their rational, rotational, and radial nodes, are concordant with those effectively computed by DFT for the radial-MO set. A comparison of the orbital energies displayed in Fig. 7 indeed shows a quite good correlation for this set of orbitals as well.
The radial r-MOs for TR tubes point out that the increasing ordering of MOs in this set again obey a certain rule. The (102) state turns out to be the ground state in this set. Along with the eigenstates (202) and (302), the whole series of eigenstates have the rotational number l = 0. Located between the (102) and (202) states, and the (202) and (302) states, and located above the (302) state are the states characterized by l ≠ 0. These are known as twofold degenerate states whose numbers appeared in the above positions, are variable of the size of the hollow cylinder considered (pseudo-radius and pseudo-height). The electrons needed to fill the shell of r-MOs will be 4N if the (202) and (102) eigenstates are fulfilled. Otherwise, the number of electrons is 4N + 2 if only the lower-lying (102) state or all eigenstates having l = 0 are fully occupied. As shown in Fig. 6, the triple ring B27+ has 16 radial electrons of which 4 electrons occupied in HOMO − 11 and HOMO − 3 correspond to the (102) and (202) eigenstates of the model. The remaining electrons are distributed in 3 doubly degenerate MOs (HOMO − 1,1′, HOMO − 2,2′ and HOMO − 8,8′). As a consequence, the radial MOs of the cation B27+ apparently satisfy the electron counting rule 4N with N = 4. The same result is again reproduced when applying this to the neutral B42 TR. The radial MOs of the neutral B42 TR are also fulfilled by 28 electrons, which obey the 4N rule because the (202) eigenstate is doubly occupied.
Overall, the cylinder model excellently predicts the r-MOs and t-MOs both in terms of irreducible representations and eigenvalues of MOs. This is quite remarkable as according to the HCM, each eigenvalue depends not on one quantum number such as in the case of the circular disk,22,23 but on three quantum numbers k, l and n. Both tangential and radial MOs satisfy the electron sequences obtained from the HCM. In this context, the number of electrons involved in a hollow cylinder in order to properly close an electron shell structure can be either 4N or (4N + 2), depending on the occupancy of non-degenerate states. In fact, one non-degenerate state accounts for the value 2 of this electron counting rule. Such a representational tower of the cylindrical symmetry group was briefly mentioned by Ceulemans et al.40 but no details were reported on hollow cylinders.
With a formula of (4N + 2M), with M = 0 or 1, depending on the number of non-degenerate MOs that are fulfilled, for both radial and tangential electrons, we can recover the classical 4N and (4N + 2) Hückel rules. However this is only an apparent similarity. The main difference is that in a cylinder, both sets of 4N and (4N + 2) electrons can attain a properly closed shell structure.
The cation B27+ can be regarded as the smallest TR boron tube which exhibits enough electrons to fill the shell for each set of MOs and accordingly, its electrons fully obey the (4N + 2M) rule, with M = 0 for radial MOs set, and M = 1 in case of tangential MOs set (Table 1).
| Radial-MOs | Tangential-MOs | ||
|---|---|---|---|
| kln | n. e | kln | n. e |
| 102 | 2 | 401 | 2 |
| 1±12 | 6 | 4±11 | 6 |
| 202 | 8 | 4±21 | 10 |
| 1±22 | 12 | 4±31 | 14 |
| 2±12 | 16 | 501 | 16 |
| 1±32 | 20 | 5±11 | 20 |
| 2±22 | 24 | 5±21 | 24 |
| 302 | 26 | 4±41 | 28 |
| ⋮ | ⋮ | ⋮ | ⋮ |
3.3 B27+ triple ring: tubular aromaticity
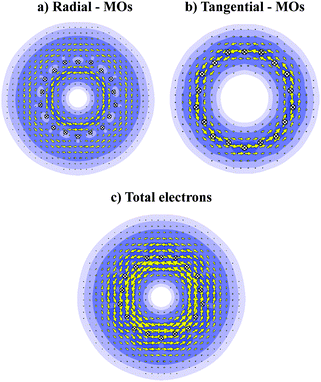
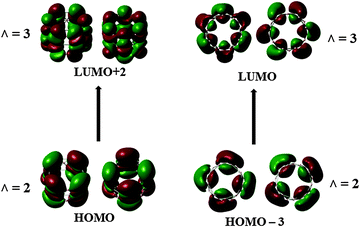
In order to probe further the electron distribution of B27+, we plot the ring current maps in the cut plans using the B3LYP densities,37 with the 6-31G(d), 6-311+G(d) and cc-pVTZ basis sets. The results obtained using these basis sets emphasize some small variations in the intensities of the currents, but the main conclusions about the magnetic responses, implying the direction of the density currents remain valid when using the smaller basis set.Fig. 8 displays the maps of magnetic ring currents of B27+c-TR that are derived from the contributions of radial π electrons (Fig. 8b), tangential σ electrons (Fig. 8a), and of the total electron density (Fig. 8c). It is obvious that consistent and unambiguous responses occur in this tubular cation inducing strong diatropic current, irrespective of the electron type. A diatropic ring current suggests an aromatic character of the hollow cylinder considered.20 The energy gap between both frontier orbitals of c-TR amounts to ∼2.6 eV. Electronic excitations within the frontier orbitals, as shown in Fig. 9, namely HOMO → LUMO + 2 and HOMO − 3 → LUMO, bring in the essential contributions to the magnetic responses. It is known that the current intensity is inversely proportional to the energy gap.35 The change of the Λ number accompanying these electronic transitions obeys the selection rule ΔΛ = 1, thus making the TR B27+ tube aromatic. A similar situation was previously observed in the boron toroids, which are in fact the double ring structures of B20, B24, B28 characterized by a double aromaticity.18 These results suggest that the B27+ TR exhibits a tubular aromaticity, which is seemingly a general feature of boron hollow cylinders. Such an aromatic character contributes to a thermodynamic stability rendering the boron tubes the lower-lying isomers at each of the sizes considered.
Fig. 10 displays the ELI-D and ELF maps of the cation B27+c-TR considering both types of electrons. It is clear from the Fig. 10c and d that the B27+ triple ring has one localization domain which is delocalized over the whole system at the bifurcation value of 0.70, and split into smaller domains at the ELF value of 0.75. As a result, the electrons of (3 × 9) B27+ cationic tube are likely to move cylindrically within the whole tube.
Its total density is accordingly divided into radial and tangential electrons. The radial MOs, arising from radial AOs, are mostly delocalized along each atom string but pointing toward outside the tubular surface (Fig. 10a and b). These radial MOs have localization pattern involving both outer and inner surfaces, in which the outer surface is apparently more delocalized than the inner counterpart. The tangential electrons are mainly located in tangential orbitals, connecting the B-atom of each string (Fig. 10c and d). The localization domains of tangential MOs comprise four domains that are delocalized over the whole (3 × 9) tube. The sum of contributions of both types of electrons result in the basins located between each boron–boron bond within either each string or between two strings. Overall, the delocalization pattern of both radial and tangential MOs suggests that the electrons occupying these MOs will move cylindrically over the whole (3 × 9) tube.
4. Concluding remarks
In the present theoretical study, we determined the geometries and chemical bonding phenomena of the B27 system in their dicationic, cationic, neutral, anionic and dianionic states using quantum chemical computations. The most important results emerge as follows:(i) In both cationic and neutral states, the triple ring tube forms correspond to the lowest-energy isomers. This is more obvious in the cation B27+. This cation represents the first stable hollow cylinder having a triple ring of the pure boron clusters.
(ii) In the anionic and dianionic states, the quasi-planar shapes are favoured over other isomers, following a typical charge effect in which addition of extra electron stabilizes the quasi-planar forms.
(iii) The shapes of molecular orbitals of the B27+ TR calculated using DFT methods can be predicted by the eigenstates of a simple model of a particle on a hollow cylinder.
(iv) The number of electrons in a hollow cylinder should attain a number of (4N + 2M) with M = 0 or 1, depending on the number of non-degenerate MOs, in order to properly fulfill the closed electron shells. In the case of B27+, M = 0 for radial MOs set, and M = 1 for tangential MOs set.
(v) In the triple ring tube B27+, strong diatropic responses to external magnetic field occur in both radial and tangential types of electrons, thus suggesting a typical tubular aromaticity. Such an aromatic character contributes to its high thermodynamic stability.
Overall, stabilized tubular cylinders are frequently occurred in boron clusters in the large size range, and their formation and specific bonding foreshadow a typical growth pattern leading to larger boron tubes. Further investigation of the latter could allow these patterns to be established.
Acknowledgements
We are grateful to the Department of Science and Technology of Ho Chi Minh City, Vietnam, for granting major research projects at ICST. MTN thanks ICST for making his stays in Vietnam enjoyable. We are indebted to KU Leuven Research Council (GOA and IDO programs) for continuing support. We greatly appreciate the help of Dr Remco Havenith for allowing us to plot the ring current maps using his computers at the University of Groningen, The Netherlands.References
- I. Boustani, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 16426 CrossRef CAS.
- B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961 CrossRef CAS PubMed.
- Z. A. Pizza, H. Hu, W. Li, Y. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113 Search PubMed and references therein.
- I. Boustani, A. Quandt, E. Hernandez and A. Rubio, J. Chem. Phys., 1999, 110, 3176 CrossRef CAS PubMed.
- J. T. Muya, E. Lijnen, M. T. Nguyen and A. Ceulemans, ChemPhysChem, 2013, 14, 346 CrossRef CAS PubMed and references therein.
- D. Ciuparu, R. F. Klie, Y. Zhu and L. Pfefferte, J. Phys. Chem. B, 2004, 108, 3867 Search PubMed.
- P. Boulanger, M. Moriniere, L. Genovese and P. Pochet, J. Chem. Phys., 2013, 138, 184302 CrossRef PubMed and references therein.
- L. Cheng, J. Chem. Phys., 2012, 136, 104301 CrossRef PubMed.
- T. B. Tai, N. M. Tam and M. T. Nguyen, Chem. Phys. Lett., 2012, 530, 71 CrossRef CAS PubMed.
- E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503 CrossRef CAS PubMed.
- T. B. Tai, N. M. Tam and M. T. Nguyen, Theor. Chem. Acc., 2012, 131, 1241 CrossRef PubMed.
- H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, Chem. Phys. Lett., 2013, 577, 32 CrossRef CAS PubMed.
- J. T. Muya, G. Gopakumar, E. Lijnen, M. T. Nguyen and A. Ceulemans, Vibronic Interactions and the Jahn-Teller Effects: Theory and Applications, Progress in Theoretical Chemistry and Physics, ed. M. Atanasov, 2011, ch. 14, vol. 23, pp. 265–278 Search PubMed.
- J. T. Muya, T. Sato, M. T. Nguyen and A. Ceulemans, Chem. Phys. Lett., 2012, 543, 111 CrossRef CAS PubMed.
- J. T. Muya, H. Ramanantoanina, C. Daul, M. T. Nguyen, G. Gopakumar and A. Ceulemans, Phys. Chem. Chem. Phys., 2013, 15, 2829 RSC.
- W. An, S. Bulusu, Y. Gao and X. C. Zeng, J. Chem. Phys., 2006, 124, 154310 CrossRef PubMed.
- M. P. Johanssen, J. Phys. Chem. C, 2009, 113, 524 Search PubMed.
- D. E. Bean and P. W. Fowler, J. Phys. Chem. C, 2009, 113, 15569 CAS.
- W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202 CrossRef CAS PubMed.
- D. E. Bean, J. T. Muya, P. W. Fowler, M. T. Nguyen and A. Ceulemans, Phys. Chem. Chem. Phys., 2011, 13, 20855 RSC.
- T. B. Tai, L. V. Duong, H. T. Pham, D. T. T. Mai and M. T. Nguyen, Chem. Commun., 2014, 50, 1558 RSC.
- T. B. Tai, A. Ceulemans and M. T. Nguyen, Chem. – Eur. J., 2012, 18, 4510 CrossRef CAS PubMed.
- T. B. Tai, R. H. W. Havenith, J. L. Teunissen, A. R. Dok, S. D. Hallaert, M. T. Nguyen and A. Ceulemans, Inorg. Chem., 2013, 52, 10595 CrossRef CAS PubMed.
- I. Boustani, A. Rubio and J. A. Alonso, Chem. Phys. Lett., 1999, 311, 21 CrossRef CAS.
- H. T. Pham, L. V. Duong, N. M. Tam, M. P. Pham-Ho and M. T. Nguyen, Chem. Phys. Lett., 2014, 608, 295 CrossRef CAS PubMed.
- M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant and J. Millam, et al., Gaussian 09 Revision: B.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. B. Tai and M. T. Nguyen, J. Chem. Theory Comput., 2011, 7, 1119 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265 CrossRef CAS PubMed.
- B. Silvi and A. Savin, Nature, 1994, 371, 683 CrossRef CAS.
- M. Kohut, F. R. Wagner and Y. Grin, Int. J. Quantum Chem., 2006, 106, 1499 CrossRef PubMed.
- R. Zanasi, J. Chem. Phys., 1996, 105, 1460 CrossRef CAS PubMed.
- P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299 CrossRef CAS.
- E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553 CrossRef CAS.
- T. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223 CrossRef CAS.
- P. Lazzeretti, M. Malagoli and R. Zanasi, J. Chem. Phys., 1995, 102, 9619 CrossRef PubMed.
- P. Lazzeretti, M. Malagoli and R. Zanasi, SYSMO package, Technical Report “Sistemi Informatici e Calcolo Parallelo”, CNR Italy (1991). Research Report number 1/67. Additional routines by P. W. Fowler, E. Steiner, R. W. A. Havenith and A. Soncini.
- R. W. A. Havenith and P. W. Fowler, Chem. Phys. Lett., 2007, 449, 347 CrossRef CAS PubMed.
- M. F. Guest, et al., Gamess-UK, Mol. Phys., 2005, 103, 719 CrossRef CAS.
- J. Gravesen, M. Willatzen and L. C. L. Y. Voon, J. Math. Phys., 2005, 46, 012107 CrossRef PubMed.
- A. Ceulemans, S. Compernolle and E. Lijnen, Phys. Chem. Chem. Phys., 2004, 6, 238 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Tables listing the Cartesian coordinates of optimized geometries of the B27 isomers in different charge states considered. See DOI: 10.1039/c4cp01996b |
| This journal is © the Owner Societies 2014 |