Computational study of structural properties of lithium cation complexes with carbamate-modified disiloxanes

Abstract

Lithium cation solvation structures [Li(S)_n=1–4]⁺ with ligands of cyclic or noncyclic carbamate-modified disiloxanes are optimized at B3LYP level of theory and compared to their corresponding simplified carbamates and to the organic carbonates ethylene carbonate (EC) and dimethyl carbonate (DMC). The electrostatic potentials (ESP) of these investigated carbonyl-containing solvents are mapped on the electron density surface. The maximum ESP is located at the C=O-oxygen, whereas the disiloxane functionality represents an unpolar residue. Natural Bond Orbitals (NBO) analysis reveals strong n(N) → π(C=O) donor–acceptor interactions in carbamates which outrun dipolar properties. As a result, higher total binding energies (ΔE_B) for solvation of Li⁺ in carbamates (−148 kcal mol⁻¹) are found than for carbonates (−137 kcal mol⁻¹). Furthermore, the disiloxane moiety with its Si–O bond is stabilized by n(O) → σ*(Si–C) hyperconjugation that provides additional electron density to a nearby SiCH₃ methyl group thus supporting an additional SiCH₂–H⋯Li⁺ coordination. The formation of all investigated solvation structures is exothermic. Owing to steric hindrance of noncyclic carbonyl-containing ligands and the bulky disiloxane functionality, the solvation structure [Li(S)₃]⁺ is the preferred structure according to Gibbs free energy ΔG_B results.

---

Introduction

Liquid blends of organic carbonates, e.g. ethylene carbonate (EC; 1), propylene carbonate (PC), dimethyl carbonate (DMC; 2) or diethyl carbonate (DEC), are typical examples for non-aqueous solvents of liquid electrolytes used in lithium-ion battery systems.¹ There have been large numbers of reports discussing these solvents and their electrochemical properties, decomposition,^2–5 cycling behaviour and formation of first-shell solvation structures with lithium cations.⁶ Regarding the development of alternative liquid electrolytes to improve safety, low viscosity silicon-containing liquids have drawn much attention due to their nontoxic nature and reduced flammability. So far, published results mainly focus on carbonate-modified^7–9 and ethylene glycol-modified^10–15 di-/trisiloxanes and silyl ether compounds.^16–18 Their structure derived from EC/PC, and from poly(ethylene oxide) (PEO), an ion-conducting polymer already widely used in solid polymer electrolytes (SPE) since 1973.¹⁹

Further improvement of safety issues may be achieved by application of SPEs since they replace flammable liquids completely.^20,21 But so far, they suffer from poor ionic conductivity in a magnitude of 10⁻⁵ S cm⁻¹ at ambient temperature. In order to increase the ionic conductivity of polysiloxane-based SPE systems, mixed ethylene glycol- and carbonate-modified polysiloxanes were prepared to introduce a high ability to dissociate lithium salts and increase the concentration of free ions in a polymer matrix.^22,23

Nevertheless, the incorporated carbonate-moiety decreased the ionic conductivity due to increased viscosity and reduced segmental motion of the polymer matrix. The ionic transport properties of the SPE were inhibited by strong dipole–dipole interactions between the carbonate components.²³

Recently, we have reported the synthesis of novel liquid carbamate-modified disiloxanes,²⁴ as well as their application in porous PVDF-HFP membranes.²⁵ These liquid materials reach an ionic conductivity in the magnitude of 10⁻⁴ S cm⁻¹ at ambient temperature and are electrochemically stable up to 4.5 V vs. Li/Li⁺. Beside their application as alternative liquid electrolytes, we considered carbamate-modified disiloxanes as model compounds for the development of future SPEs, due to the decreased dielectric constant ε of their lead structure N-methyloxazolidin-2-one (NMO, 3; ε = 78).¹ Therefore, compared to 1 (ε = 90)¹ and various carbonate-modified poly-/di-/trisiloxanes, weaker dipole–dipole interactions might arise in carbamate-modified polysiloxane-based SPEs.

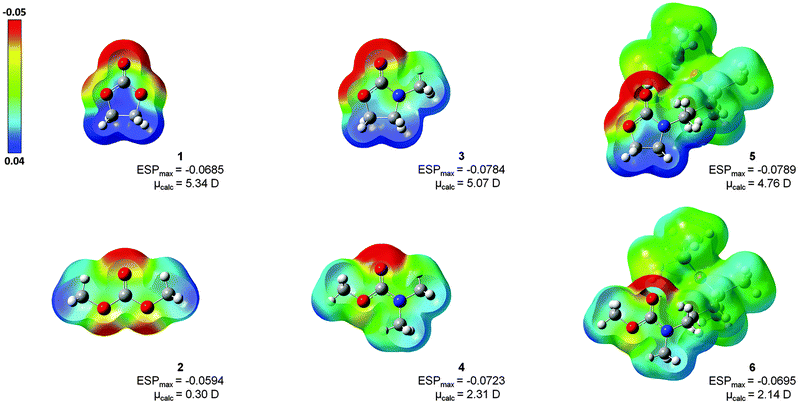
Herein, quantum-chemical calculations employing the density functional theory (DFT) have been performed to calculate the character and strength of the binding between the lithium ion and a number of carbonate and carbamate containing solvents (S = 1–6; Fig. 1). Furthermore, electrostatic properties and population analysis were examined for all solvents. The organic carbonates 1 and 2 were considered as conventional references. The carbamates 3 and the noncyclic methyl dimethylcarbamate (4) were investigated as simplified carbamate models to identify influences of the disiloxanes functionality in their corresponding carbamate-modified disiloxanes 3-(3-(1,1,3,3,3-pentamethyldisiloxanyl)propyl)oxazolidin-2-one (5) and N-methyl methyl(3-(1,1,3,3,3-pentamethyldisiloxanyl)propyl) carbamate (6). In addition, the impact of cyclic and noncyclic carbonyl structures on the formation of Li⁺ solvation structures was examined, directly. The computed properties may be helpful for the understanding of complex formation of carbamates and carbamate-modified disiloxanes, as well as for the development of future siloxane containing polymer electrolyte systems.

Fig. 1 Structures of investigated solvents (S = 1–6), including organic carbonates 1 and 2, simplified carbamates 3 and 4, and the corresponding carbamate-modified disiloxanes 5 and 6.

Computational methodology

All calculations were performed with the Gaussian 09 program package.²⁶ The electronic ground state geometries of the studied lithium ion solvation structures [Li(S)_n=1–4]⁺ (S = 1–6; Fig. 1) were optimized in gas phase at Becke's three-parameter hybrid method²⁷ with the Lee–Yang–Parr correlation functional²⁸ (B3LYP) level of theory without the presence of a counter anion. In order to verify the relative energy sequence of the optimized complexes, their single point energies were also calculated using ab initio HF and MP2 methods. All calculations were performed using the 6-311G(d,p) basis set²⁹ providing a qualitative understanding of the complex energetics. The stability of all optimized solvation structures was verified by vibrational analysis; no imaginary vibrational frequencies were detected. No basis superposition error (BSSE) corrections have been applied.

Population analysis was performed by Natural Bond Orbital (NBO)^30–34 analysis and by analysis of electrostatic potential-derived charges (ESP) according to Merz–Singh–Kollman scheme.^35,36 ESP results were used to compute maps of electrostatic potential.

Results and discussion

Structures and geometries

First, formations of the lithium ion solvation structures [Li(S)_n=1–4]⁺ (S = 1–6) were analysed. All investigated solvents contain a carbonyl group that reacts as a ligand by interacting with the cation via C=O-oxygen. This is consistent with other theoretical and spectroscopic IR and Raman studies regarding mixtures of lithium salts in 1 or PC.^37,38 As revealed by IR²⁵ and NMR²⁴ results examined for solvent 5, the carbamate moiety interacts with a lithium ion, similarly.

By coordinating the lithium ion and acting as a ligand, the solvent molecules 1–6 are deformed including a slightly stretched C=O bond (see Fig. S1 of ESI†). The strongest deformation of the ligands C=O geometry in comparison to the free solvent molecule was found for the structure [Li(S)₁]⁺. Owing to a weaker interaction of the ligand with the cation, the deformation decreases with increasing coordination number. This result is consistent with the Li–O bond length, as listed in Table 1, and has already been observed in other calculated lithium ion complex structures.^2,39 The proportionality between the coordination numbers and the averaged Li–O bond lengths may be described, as for dimethyl sulfoxid (DMSO) solvation structures,³⁹ by the exponential function

d̄_Li–O = a exp(bn)

where a = 1.663 Å, b = 0.037 for 1, a = 1.649 Å, b = 0.041 for 2, a = 1.666 Å, b = 0.038 for 3, a = 1.617 Å and b = 0.046 for 4, a = 1.669 Å, b = 0.037 for 5 and a = 1.644 Å and b = 0.042 for 6, respectively. Considering the structure of the coordinating ligands 1–6, values of b = 0.0375 ± 0.005 were found for cyclic carbonyl moieties 1, 3 and 5, whereas a value of b = 0.043 ± 0.0026 was determined for the noncyclic carbonyls 2, 4 and 6.

Table 1 Li–O bond lengths and O–Li–O angles of complex structures optimized at B3LYP/6-311G(d,p) level of theory

Complex	Solvent S
	1	2	3	4	5	6
Li–O bond lengths (Å)
[Li(S)1]^+	1.733	1.729	1.730	1.705	1.739	1.736
[Li(S)2]^+	1.786	1.780	1.794	1.763	1.784	1.763
	1.786	1.780	1.794	1.763	1.795	1.760
[Li(S)3]^+	1.850	1.851	1.860	1.842	1.869	1.841
	1.850	1.851	1.868	1.842	1.849	1.841
	1.851	1.848	1.870	1.843	1.866	1.85
[Li(S)4]^+	1.940	1.942	1.944	1.958	1.917	1.964
	1.942	1.962	1.942	1.956	1.953	1.976
	1.943	1.961	1.935	1.960	1.947	1.963
	1.937	1.961	1.921	1.962	1.950	1.958
O–Li–O angles (deg)
[Li(S)2]^+	180.0	180.0	179.5	178.5	170.7	177.4
[Li(S)3]^+	119.7	120.0	120.0	119.4	118.9	121.7
	120.0	120.0	119.0	119.8	120.0	118.5
	120.3	120.0	121.0	120.8	121.0	119.7
[Li(S)4]^+	107.4	110.3	112.3	110.9	109.8	110.4
	108.1	109.3	108.2	107.5	107.5	111.9
	107.7	108.5	103.7	111.7	108.4	109.7
	113.5	116.6	110.6	106.7	117.9	105.4
	106.9	108.5	112.3	110.9	105.4	106.1
	113.3	103.5	112.7	109.9	107.3	113.4

---

No symmetry was imposed in the geometry optimizations of the complexes [Li(S)_n]⁺. According to O–Li–O angles of approximately ≈109°, ≈120° and ≈180° a tetrahedral, trigonal planar and linear geometry were obtained for n = 4 → 2, respectively.

In Fig. 2, the optimized geometries of solvation structures [Li(5)_n=1–4]⁺ are illustrated. The carbamate functionality interacts with Li⁺via C=O-oxygen, whereas the disiloxane moieties with its SiCH₃-groups are rearranged with minimal repulsion around the complex centre. Furthermore, the linear nature of the Si–O–Si functionality with approximately 160°–180° is visible.^40,41 This solvation structure is consistent with previously presented results regarding the ionic conductivity of carbamate-modified disiloxanes.²⁴ Since Li⁺ transport in liquids occurs mostly by diffusion of ions including their first shell of solvation (vehicular mechanism),²¹ the bulky disiloxane moiety increases the size of the solvation structure significantly (see Table T2 of ESI†). A larger solvation structure is equivalent to a larger van der Waals surface for intermolecular interactions and therefore increases the viscosity and decreases the vehicular diffusion, respectively. Comparing the ionic conductivity of 5 and 6 (10⁻⁴ S cm⁻¹ at ambient temperature) to conventional liquid electrolytes composed of blends of 1 and 2 (10⁻²–10⁻³ S cm⁻¹), the deviation in performance is a result of the different sizes of their corresponding Li⁺ solvation structures.

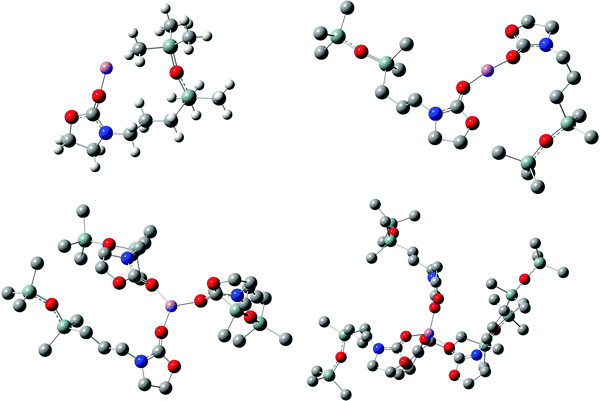Fig. 2 Geometries of solvation structures [Li(5)_n=1–4]⁺ optimized at B3LYP/6-311G(d,p) level of theory. Hydrogen atoms are not shown in all structures for clarity.

Analysis of electronic structures

The electronic structure of solvents 1–6 has been analysed using two different approaches: (a) via NBO and (b) ESP. The NBO method examines the charge distribution close to the atom centres, whereas the ESP method is better suited to reproduce the coulombic effects of the adjacent ligands coordinating the lithium ion.

In Fig. 3, the isodensity surfaces (isoval = 0.002) of the B3LYP-optimized structures of solvents 1–6 were mapped with their computed electrostatic potentials. The highest negative potential (red) is always located at the C=O functionality. An increase in ESP_max is observed in the ranking 2 < 1 < 6 < 4 < 3 ≈ 5, which indicates a structural relation: (a) carbonates 1 and 2 have lower potentials than carbamates 3–6, (b) noncyclic compounds 2, 4 and 6 have lower potentials than their cyclic counterparts 1, 3 and 5. Furthermore, in the five-membered ring structures of 1, 3 and 5, the potentials are clearly polarized with the lowest values (blue) located at the CH₂–CH₂ moieties. This result illustrates the dipolar character of commercially available solvents 1 and 3, which corresponds to their large dipole moments of 4.6 D and 4.5 D, respectively.¹ In noncyclic solvents 2, 4 and 6 the charge polarization appears less pronounced, indicating lower dipole moments (0.8 D for 2)¹ which results in inert properties. Additionally, the ESP maps verify that the dipolar properties of the oxazolidinone moiety in 5, as well as the inert character of the carbamate moiety in compound 6, remain unaffected by the disiloxane functionality. According to the colour code, the disiloxane with its SiCH₃-groups represents an unpolar region (green), predominantly.

Fig. 3 Electron density maps from total SCF B3LYP density (isoval = 0.002; mapped with ESP) for investigated solvents 1–6 with their values of maximum ESP (ESP_max) and calculated dipole moments (μ_calc).

Regarding NBO population analysis, the charges of the N–C(O)–O fragment in the corresponding pairs of isolated 3/5 and 4/6 are almost identical (see Table T1 in ESI†). The atomic charges of C=O-oxygen and Li⁺ of the isolated solvents and their solvation structures [Li(S)_n=1–4]⁺ (S = 1–6) are plotted in Fig. 4a and b, respectively. By comparing C=O-oxygen charge values, structural relations become evident again: (a) carbamate C=O-oxygens are more negative than in carbonates and (b) in noncyclic compounds the C=O-oxygen is more negative than in cyclic carbonyl structures (+I effect). As a result, an increase in negative atomic charge at this oxygen is observed in the ranking 1 < 3 ≈ 5 < 2 < 4 ≈ 6. For solvation structures of n = 1, the lowest NBO charge in the magnitude of −0.8 to −0.9 were observed. With n = 2 → 4 the negative charge values decrease reaching a magnitude of −0.6 to −0.7. This result is consistent with the described geometry changes. In complexes of type [Li(S)₁]⁺ the C=O-oxygen of a single ligand provides electrons for a strong, short, dative bond to the cation, which requires a high negative charge at this oxygen-position. Compared to donor–acceptor interactions, the carbamate unit has two resonance forms, Fig. 5. The lone pair of the sp² hybridized nitrogen (sp^1.8 according to NBO analysis) overlaps effectively with the carbonyl group and provides additional electron density by n(N) → π(C=O) donor–acceptor interactions, causing a delocalization of the nitrogen's lone pairs into the π-system. By increasing the C=N double bond character (II), the electron density at the C=O-oxygen is maximized. According to NBO analysis, resonance structure II is only preferred in complexes of [Li(S)₁]⁺ (S = 3, 4), whereas carbamate-modified disiloxanes (S = 5, 6) prefer resonance structure I. Moreover, the NBO charge at Li⁺ is reduced by 7% in presence of a single disiloxane ligand (Fig. 4b). This is due to an additional stabilization of Li⁺ by intramolecular donor–acceptor interactions between two hydrogens H^a of a SiCH₃ group and the cation (Fig. 6 and Table 2). Via this SiCH₂–H⋯Li⁺ interaction, the cation polarizes the Si–C bond. In order to provide the required electron density in the donating methyl group, the contribution of the Si atom in the corresponding Si–C bond decreases from ≈29% to 24% (Table 3). In return, the Si contribution to the σ*(Si–C) increases from 71% to 76%, stabilized by a preferred n(O) → σ*(Si–C) hyperconjugation of the nearby Si–O bond (>8.1 kcal mol⁻¹).

Fig. 4 NBO atomic charges of (a) C=O-oxygen and (b) Li⁺.

Fig. 5 Resonance structures for the carbamate group in 3–6.

Fig. 6 Coordination of Li⁺ by interacting with a carbamate-modified disiloxane. The interaction stabilizes the solvation structures [Li(S)₁]⁺ (S = 5, 6) by the given energies.

Table 2 Atomic charges from NBO method for simplified carbamate solvents 3 and 4 and carbamate-modified disiloxanes 5 and 6 in their [Li(S)₁]⁺ solvation structures. Hydrogens H^a of a SiCH₃-group provide additional electron density to interact with Li⁺

[Li(S)1]^+	Li^+	C=O	H^a	H^b	SiCH^a2H^b
S = 3, 4	0.95	−0.62	—	—	—
S = 5, 6	0.88	−0.67	0.20	0.24	−1.13

---

Table 3 Contributions of the Si atom in bonds with normal (CH₃) and a donating methyl group (CH^a₂H^b), and energy of stabilization by hyperconjugation E_H in kcal mol⁻¹

	Pure 5, 6	[Li(S)1]^+ (S = 5, 6)
	SiCH3	SiCH3	SiCH^a2H^b
σ(Si–C)	28%	29%	24%
σ*(Si–C)	72%	71%	76%
E H(n(O) → σ*(Si–C))	6.6–7.3	7.1–8.0	8.1–8.6

---

Similar to literature,⁴¹ the NBO analysis of the Si–O–Si unit reveals a single Si–O bond with only 14% contribution of the Si atoms. Additionally, the Si–O bond is stabilized by n(O) → σ*(Si–C) hyperconjugation implying a partial double bond character of Si–O. This is consistent with the observed linear nature of the Si–O–Si bond. Depending on the exact angle, each hyperconjugation stabilizes the disiloxane by 6 to 8 kcal mol⁻¹. An angle of nearly 180° is favoured due to better interaction of n(O) → σ*(Si–C) causing higher stabilization energies.

For n = 2 → 4, the NBO charge of Li⁺ decreases due to more ligands providing electron density for the dative bond to the cation. This is consistent with geometry results. For all carbamates, resonance structure I is preferred for all corresponding complexes.

Energetics and cluster stabilization

In order to estimate the energetic aspects of [Li(S)_n=1–4]⁺ (S = 1–6) formation, the total binding energies (ΔE_B) of the solvation structures were calculated by subtracting the energy of a given cluster from the summed energies of its constituting ingredients:

ΔE_B = E[Li⁺(S)_n] − (E[Li⁺] + E[S] × n)

The computed binding energies ΔE_B of B3LYP/6-311G(d,p) optimized solvation structures are shown in Fig. 7 and listed in Table 4 alongside their single point energies at HF/6-311G(d,p)//B3LYP/6-311G(d,p) and MP2/6-311G(d,p)//B3LYP/6-311G(d,p) levels of theory. The coordination number of the central lithium cation is directly related to the stability of the cluster. The larger the number of Li–O interactions n = 1 → 4, the more stable the cluster is, as implied by more negative values of ΔE_B. Energies calculated by the HF-method are similar to B3LYP-results with a deviation of 2 kcal mol⁻¹ at maximum. For MP2-results, a more significant deviation up to 9% compared to B3LYP-results was obtained. Nevertheless, the ranking of energies for complexes with n = 2 → 4 2 < 1 ≈ 6 ≈ 4 < 3 ≈ 5 was observed for the B3LYP-, HF- and MP2-methode, which verifies the structural relation implied by analysis of the electronic structure: (a) ΔE_B of carbonates 1 and 2 are weaker than those of carbamates 3–6 and (b) ΔE_B of noncyclic carbonyls 2, 4 and 6 are weaker than for their cyclic counterparts 1, 3 and 5.

Fig. 7 Total binding energies ΔE_B of [Li(S)_n=1–4]⁺ (S = 1–6) as a function of coordination number obtained from B3LYP/6-311G(d,p) calculations.

Table 4 Energy analysis for all [Li(S)_n]⁺ clusters: total (ΔE_S) and relative (ΔΔE_S) solvent–solvent interactions, total (ΔE_M) and relative (ΔΔE_M) solute–solvent interactions and total (ΔE_B) and relative (ΔΔE_B) binding energies; thermodynamic analysis at 298.15 K: total (ΔH_B) and relative (ΔΔH_B) heats of solvation and total (ΔG_B) and relative (ΔΔG_B) Gibbs free energies of solvation. All energies (in kcal mol⁻¹) were calculated using basis set 6-311G(d,p)

Complex	HF	MP2	B3LYP
	ΔEB	ΔEB	ΔEB	ΔΔEB	ΔES	ΔΔES	ΔEM	ΔΔEM	ΔHB ^a	ΔΔHB	ΔGB ^b	ΔΔGB
a ΔHB = H[Li^+(S)n=1–4] − (H[Li^+] + H[S] × n). b ΔGB = G[Li^+(S)n=1–4] − (G[Li^+] + G[S] × n).
[Li(1)n]^+
n = 1	−55.2	−50.6	−54.4		3.4		−57.8		−53.2		−46.6
n = 2	−97.2	−90.3	−95.5	−41.1	7.8	4.3	−103.2	−45.4	−92.6	−39.4	−78.5	−31.9
n = 3	−122.9	−117.1	−121.2	−25.7	13.9	6.1	−135.1	−31.8	−118.0	−25.4	−93.2	−14.7
n = 4	−138.4	−137.3	−137.4	−16.3	19.8	5.9	−157.2	−22.1	−132.4	−14.4	−98.7	−5.5
[Li(2)n]^+
n = 1	−47.4	−43.5	−47.6		3.4		−51.0		−46.8		−39.7
n = 2	−87.2	−81.7	−86.3	−38.7	5.1	1.7	−91.4	−40.4	−82.6	−35.9	−69.6	−30.0
n = 3	−111.0	−107.8	−109.5	−23.2	8.2	3.2	−117.8	−26.4	−103.9	−21.3	−82.5	−12.8
n = 4	−122.4	−128.1	−121.7	−12.2	8.2	0.0	−130.0	−12.2	−114.2	−10.3	−81.6	0.9
[Li(3)n]^+
n = 1	−61.6	−57.5	−61.3		3.5		−64.8		−60.0		−53.4
n = 2	−107.1	−101.4	−106.3	−45.0	8.7	5.1	−115.0	−50.1	−103.2	−43.2	−88.9	−35.4
n = 3	−133.3	−129.8	−132.7	−26.4	16.5	7.8	−149.2	−34.2	−128.1	−24.9	−104.7	−15.8
n = 4	−148.0	−151.1	−148.5	−15.8	13.4	−3.1	−161.9	−12.7	−142.7	−14.5	−109.0	−4.3
[Li(4)n]^+
n = 1	−57.0	−53.8	−57.5		3.1		−60.6		−56.9		−48.4
n = 2	−99.9	−95.6	−100.1	−42.6	6.8	3.7	−106.9	−46.3	−97.1	−40.2	−81.8	−33.4
n = 3	−124.4	−123.2	−124.5	−24.4	11.6	4.8	−136.0	−29.2	−120.0	−23.0	−96.8	−15.0
n = 4	−136.6	−146.2	−138.2	−13.8	13.4	1.8	−151.6	−15.6	−132.4	−12.4	−95.7	1.1
[Li(5)n]^+
n = 1	−70.7	−68.8	−72.3		6.5		−78.8		−71.0		−61.2
n = 2	−106.3	−101.9	−106.2	−33.9	10.9	4.5	−117.1	−38.3	−103.2	−32.2	−87.0	−25.8
n = 3	−132.2	−133.9	−132.8	−26.7	17.9	6.9	−150.7	−33.6	−128.3	−25.1	−101.0	−14.0
n = 4	−147.1	−152.8	−148.1	−15.2	25.7	7.8	−173.8	−23.0	−144.3	−16.0	−100.3	0.7
[Li(6)n]^+
n = 1	−68.4	−66.7	−70.3		6.2		−76.5		−69.0		−59.0
n = 2	−101.9	−97.8	−102.0	−31.7	9.1	2.9	−111.1	−34.6	−99.3	−30.3	−83.2	−24.2
n = 3	−125.1	−125.8	−125.1	−23.2	14.4	5.3	−139.6	−28.5	−120.9	−21.7	−94.5	−11.3
n = 4	−135.5	−149.7	−137.2	−12.1	18.1	3.6	−155.3	−15.7	−131.7	−10.8	−92.6	2.0

---

In fact, ΔE_B of the noncyclic carbamates 4 and 6 are similar to that of 1. This result is quite surprising, because it indicates that donor properties, as revealed by NBO analysis, even of noncyclic carbamates 4 and 6 outrun the higher dipolar character of 1.

For a better understanding of the driving factors leading to formation of solvation structures, the total binding energy was separated in terms of solvent–solvent interactions, ΔE_S,

ΔE_S = E[(S)_n*] − E[S] × n

and solute–solvent interactions, ΔE_M,

ΔE_M = E[Li⁺(S)_n] − (E[Li⁺] + E[(S)_n*])

in accordance with a sequential energy decomposition scheme.^42,43

Here, single point calculations of a supermolecule [(S)_n*] were performed with the lithium cation removed at fixed geometry of [Li(S)_n]⁺. Since B3LYP is known for insufficient description of dispersive forces,⁴⁴ ΔE_S represents repulsive interaction energies among the solvent molecules in the solvation structures, as well as their deformation energies. For n = 1, ΔE_S is equivalent to the deformation energy of the single solvent molecules. Thus, deformation energies of 3 to 3.5 kcal mol⁻¹ were examined for solvents 1–4, whereas the n = 1 structures of the disiloxanes 5 and 6 are slightly folded to enable SiCH₂–H⋯Li⁺ interaction (6.2 to 6.5 kcal mol⁻¹). ΔE_M is the interaction energy between the prepared solvent supermolecule and the lithium cation. The sum of both terms gives the total binding energy, ΔE_B:

ΔE_B = ΔE_S + ΔE_M

The calculated energies, ΔE_B, ΔE_S and ΔE_M, for ligands 1–6 are listed in Table 4. In general, lager magnitudes of the electrostatic solvent–solute interactions ΔE_M make them the major stabilizing interactions for all solvation structures. But some differences in the energetic point of view were recognized. For instance, although structure [Li(3)₄]⁺ presents a more negative ΔE_B than structure [Li(3)₃]⁺, the latter is predicted to have a more positive ΔE_S, indicating a less stable (3.1 kcal mol⁻¹) supermolecule structure of [(3)₃*] compared to [(3)₄*]. This observation remarks a notable impact of the carbamate structure in the study of clusters with ligands 3 and 4, because for noncyclic carbamate 4 the energies of the triangular supermolecule is slightly lower (1.8 kcal mol⁻¹) than those of the tetrahedral, n = 4, counterpart. Comparing ΔE_S of carbamate-modified disiloxanes 5 and 6 with simplified carbamates 3 and 4, values of 18.1–25.7 kcal mol⁻¹ were reached by 6 and 5, respectively, due to much stronger repulsion of their adjacent, bulky disiloxane functionalities.

Regarding solvent–solute interactions ΔE_M, further differences between cyclic and noncyclic carbamate structure are noticeable. Energies ΔE_M for [Li(3)_n]⁺ are quite large (−65 to −162 kcal mol⁻¹) whereas values for 4 were calculated to be in a range of −61 to −152 kcal mol⁻¹. A similar effect of the ligand structure has been observed for carbonates where 1 represents a cyclic carbonyl and 2 its noncyclic counterpart.

According to computed heat of solvation ΔH_B, the formation of the complexes [Li(S)_n=1–4]⁺ (S = 1–6) is exothermic. For carbonate 1, the calculated values of ΔΔH_B agree with results predicted at B3PW91/6-31G(d) level of theory.² In Fig. 8, the Gibbs free energies of reaction ΔG_B of solvation structures [Li(S)_n=1–4]⁺ (S = 1–6) are shown. Since thermochemical properties of all solvation structure were calculated at a temperature of 25 °C (298.15 K), entropy effects were recognizable. The relative Gibbs free energies of solvation ΔΔG_B for 2, 4, 5 and 6 at n = 4 are positive or similar to values at n = 3, which indicates that their preferred solvation structure is the three-coordinated complex. For 2 and 4, this is caused by the steric hindrance of the noncyclic carbonyl functionality, whereas 6 additionally, and 5 obviously suffer from the bulky disiloxane moiety. As expected, the four-coordinated complex is preferred for 1² and 3.

Fig. 8 Gibbs free energies of solvation ΔG_B of [Li(S)_n=1–4]⁺ (S = 1–6) as a function of the coordination number at 298.15 K obtained from B3LYP/6-311G(d,p) frequency calculations.

Conclusions

Computed lithium cation solvation structures with carbamate-modified disiloxanes 5 and 6 were compared to their simplified carbamates 3 and 4, and to conventional liquid electrolyte components 1 and 2. Geometries of all investigated solvation structure were analysed. As visualized by ESP mapping, for all investigated solvents 1–6 the highest electron density is located at the C=O-oxygen, where the coordination to the lithium cation occurs. Furthermore, the solvents with cyclic carbonyl moieties 1, 3 and 5 have more dipolar characters than noncyclic carbonyls 2, 4 and 6. The disiloxane functionality has no effect on the electronic structure of the carbamate moiety. Instead, the Si–O–Si stabilizes donor–acceptor interactions between hydrogens of a SiCH₃ methyl group and the cation. As examined by NBO analysis, the required electron density of the σ(Si–C) bond is polarized towards the C atom, reducing the Si contribution to the Si–C bond by 5%. Therefore, the n(O) → σ*(Si–C) hyperconjugation of a Si–O bond interacts predominantly with the corresponding σ*(Si–C) orbitals. Considering results of Si–O–Si stabilized interactions between anions and a disiloxane functionality,⁴¹ the herein described stabilization of a lithium cation by SiCH₂–H⋯Li⁺ interaction remarks a notable capability of siloxane-containing electrolytes.

As a result of delocalization of the nitrogen's lone pair into the C=O π-system, n(N) → π(C=O), and the +I effect of methyl groups nearby the noncyclic carbonyl moiety, higher atomic NBO charges for the C=O-oxygen were calculated for carbamates in the ranking 1 < 3 ≈ 5 < 2 < 4 ≈ 6. According to the ranking 2 < 1 < 4 ≈ 3 < 6 ≈ 5 of total binding energies ΔE_B for solvation structures with n = 1 → 2, the greater atomic charge/electron density at C=O-oxygens of carbamates 3–6 caused formation of more stable Li⁺ solvation structures. For solvation structures with n = 3 → 4, calculated values of ΔG_B indicated an increasing influence of steric hindrance in noncyclic carbonyl ligands 2, 4 and 6 as well as bulky disiloxanes 5 and 6.

According to analysis of solvent–solvent, ΔE_S, and solute–solvent, ΔE_M, interactions, formation of solvent supermolecules requires energy due to repulsive forces, attenuating the electrostatic interactions ΔE_M which are the major stabilizing effects. Further investigations with different DFT-methods to improve understanding of dispersive and repulsive contributions to ΔE_S and ΔE_M are currently in progress.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (DFG) under grant “Functional Materials and Materials Analysis for Lithium-High-Performance Batteries” (PAK 177 – Wi 952-7/1), and the German Federal Ministry of Education and Research.

Notes and references

1. K. Xu, Chem. Rev., 2004, 104, 4303–4418.
2. Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708–11718.
3. J. M. Vollmer, L. A. Curtiss, D. R. Vissers and K. Amine, J. Electrochem. Soc., 2004, 151, A178–A183.
4. V. S. Bryantsev and M. Blanco, J. Phys. Chem. Lett., 2011, 2, 379–383.
5. L. Xing and O. Borodin, Phys. Chem. Chem. Phys., 2012, 14, 12838.
6. K. Tasaki, A. Goldberg and M. Winter, Electrochim. Acta, 2011, 56, 10424–10435.
7. T. Takeuchi, S. Noguchi, H. Morimoto and S. Tobishima, J. Power Sources, 2010, 195, 580–587.
8. X. J. Wang, H. S. Lee, H. Li, X. Q. Yang and X. J. Huang, Electrochem. Commun., 2010, 12, 386–389.
9. Y. Takei, K. Takeno, H. Morimoto and S. Tobishima, J. Power Sources, 2013, 228, 32–38.
10. H. Nakahara, S.-Y. Yoon and S. Nutt, J. Power Sources, 2006, 158, 600–607.
11. H. Nakahara and S. Nutt, J. Power Sources, 2006, 158, 1386–1393.
12. H. Nakahara, M. Tanaka, S.-Y. Yoon and S. Nutt, J. Power Sources, 2006, 160, 645–650.
13. H. Nakahara and S. Nutt, J. Power Sources, 2006, 160, 1355–1360.
14. H. Nakahara, S.-Y. Yoon and S. Nutt, J. Power Sources, 2006, 160, 548–557.
15. T. Inose, S. Tada, H. Morimoto and S. Tobishima, J. Power Sources, 2006, 161, 550–559.
16. Z. Chen, H. H. Wang, D. R. Vissers, L. Zhang, R. West, L. J. Lyons and K. Amine, J. Phys. Chem. C, 2008, 112, 2210–2214.
17. L. Zhang, Z. Zhang, S. Harring, M. Straughan, R. Butorac, Z. Chen, L. Lyons, K. Amine and R. West, J. Mater. Chem., 2008, 18, 3713–3717.
18. L. Zhang, L. Lyons, J. Newhouse, Z. Zhang, M. Straughan, Z. Chen, K. Amine, R. J. Hamers and R. West, J. Mater. Chem., 2010, 20, 8224–8226.
19. D. E. Fenton, J. M. Parker and P. V. Wright, Polymer, 1973, 14, 589.
20. V. Di Noto, S. Lavina, G. A. Giffin, E. Negro and B. Scrosati, Electrochim. Acta, 2011, 57, 4–13.
21. D. T. Hallinan and N. P. Balsara, Annu. Rev. Mater. Res., 2013, 43, 503–525.
22. Z. Zhu, A. G. Einset, C.-Y. Yang, W.-X. Chen and G. E. Wnek, Macromolecules, 1994, 27, 4076–4079.
23. Z. Zhang, L. J. Lyons, R. West, K. Amine and R. West, Silicon Chem., 2007, 3, 259–266.
24. S. Jeschke, A.-C. Gentschev and H.-D. Wiemhöfer, Chem. Commun., 2013, 49, 1190–1192.
25. S. Jeschke, M. Mutke, Z. Jiang, B. Alt and H.-D. Wiemhöfer, ChemPhysChem, 2014 DOI:10.1002/cphc.201400065.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
30. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
31. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
32. A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1746.
33. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
34. J. E. Carpenter and F. Weinhold, THEOCHEM, 1988, 169, 41–62.
35. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145.
36. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439.
37. Z. Wang, W. Gao, X. Huang, Y. Mo and L. Chen, J. Raman Spectrosc., 2001, 32, 900–905.
38. P. Johansson, M. Edvardsson, J. Adebahr and P. Jacobsson, J. Phys. Chem. B, 2003, 107, 12622–12627.
39. V. Sládek, V. Lukeš, M. Breza and M. Ilčin, Comput. Theor. Chem., 2011, 963, 503–509.
40. S. Grigoras and T. H. Lane, J. Comput. Chem., 1987, 8, 84–93.
41. H. Niedermeyer, M. A. Ab Rani, P. D. Lickiss, J. P. Hallett, T. Welton, A. J. P. White and P. A. Hunt, Phys. Chem. Chem. Phys., 2010, 12, 2018–2029.
42. K. Hashimoto and T. Kamimoto, J. Am. Chem. Soc., 1998, 120, 3560–3570.
43. J. Romero, A. Reyes, J. David and A. Restrepo, Phys. Chem. Chem. Phys., 2011, 13, 15264–15271.
44. L. F. Holroyd and T. van Mourik, Chem. Phys. Lett., 2007, 442, 42–46.

---

Footnote

† Electronic supplementary information (ESI) available: C=O bond lengths, C=O-oxygen charges, cavity volumes and images of computed solvation structures. See DOI: 10.1039/c4cp01837k

---