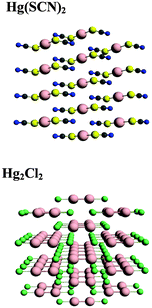Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calculation of chemical-shift tensors of heavy nuclei: a DFT/ZORA investigation of 199Hg chemical-shift tensors in solids, and the effects of cluster size and electronic-state approximations†
Fahri
Alkan
and
C.
Dybowski
*
Department of Chemistry and Biochemistry, University of Delaware, Newark, DE 19716-2522, USA. E-mail: dybowski@udel.edu
First published on 2nd June 2014
Abstract
Calculations of the nuclear magnetic resonance chemical-shielding tensors of a suite of mercury-containing materials using various cluster models for the structures provide a stringent test of the procedures for forming models and for calculation with various methods. The inclusion of higher co-ordination shells in the molecular clusters permits quantum chemical calculations of 199Hg chemical-shielding tensor elements within 3% of the experimental values. We show that it is possible to reduce the size of computationally expensive molecular-cluster calculations with limited effect on calculated NMR parameters by carefully introducing the frozen core approximation. The importance of the relativistic Hamiltonian for accurate predictions of chemical-shielding values is demonstrated within the molecular cluster approach. The results demonstrate that careful design of a cluster to represent the solid-state structure, inclusion of relativistic components in the Hamiltonian at least at the spin–orbit level, and judicious use of approximations are essential to obtain good agreement with experimental results.
1. Introduction
Nuclear magnetic resonance (NMR) chemical shieldings and quadrupolar couplings provide a means of examining the electronic state of a material. The full tensor interaction, available in the solid, gives a description of the three-dimensional electronic structure.1,2 The connection between the electronic state and these parameters is embodied in complex equations that rely on accurate models of the electronic wave function. In general, very good approximate computational predictions of isotropic NMR parameters for light nuclei such as 13C and 1H in molecules have become routine nowadays, and such calculations of the parameters are often a part of the assignment of spectra.3,4 Prediction of NMR parameters of heavier nuclei such as 199Hg, 205Tl, and 207Pb is usually limited to prediction of properties of isolated structures in the gas phase5–8 and in the solution phase.8–11The experimentally determined ranges of chemical shieldings (chemical shifts) for heavy nuclei like 199Hg and 207Pb are generally much larger than the ranges for lighter nuclei such as 13C and 1H. For example, the range of experimental principal components for 199Hg in the various materials studied is almost 4500 ppm. The range of experimental principal components for 207Pb is almost 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ppm.12
700 ppm.12
Calculations of NMR parameters of heavy nuclei in a solid have two obstacles not generally encountered in “standard” quantum chemical calculations on molecules in solution or the gas phase. First, some, if not all, of the electrons must be treated as relativistic particles, in part because of the high nuclear charge.13,14 Second, the local intermolecular environment with its periodic structure has geometric effects that are not averaged by rapid motion.15 To address the latter, two methods have been proposed to calculate NMR parameters of nuclei in solids: (1) use of periodic boundary conditions based on the full crystal symmetry, and (2) treatment of model molecular clusters that define the local environment.
In the last ten years, periodic-boundary calculations have become popular for estimating NMR parameters in solids of known structure. An important method which employs periodic boundary conditions was developed by Sebastiani et al.16,17 with the use of localized Wannier orbitals as implemented in the program CPMD.18 Another popular formalism is the Gauge Included Projected Augmented Wave (GIPAW) method of Pickard and Mauri.19 The general theory and applications to solid-state NMR of the GIPAW method have been reviewed recently.20
The GIPAW method is currently not very suitable for calculation of the NMR parameters of heavy nuclei for the following two reasons. First, such calculations are computationally very expensive for unit cells with large numbers of electrons, which is usually the case for systems containing heavy nuclei like 207Pb and 199Hg. Second, relativistic effects, which can be very important for heavy nuclei, are treated in a limited manner (or not at all) in codes that employ periodic-boundary conditions.
Calculations using model clusters that simulate the local solid-state environment are an alternative to the periodic-boundary approach. In early studies, Tossell et al. investigated the effects of next-nearest neighbors on NMR chemical shielding for 15N and 23Na by employing molecular clusters to mimic the solid-state structure.21–23 Similarly, Valerio et al. employed molecular-cluster-based calculations for NMR chemical shielding of 29Si and 27Al in zeolite structures.24,25 In these cases, it was shown that more accurate chemical-shift and quadrupolar parameters result when the cluster size is sufficient to reflect the nature of local structure on the electronic state. More recently, 19F chemical shifts have been computed for several different fluorine sites with the cluster approach.26 Another attempt at using cluster models to mimic the solid-state structure involves embedding a cluster in a point-charge field.27–29
The cluster-based approach has been employed in some cases to obtain solid-state NMR parameters of heavy nuclei such as 207Pb and 199Hg.30–39 In general, NMR calculations on clusters have centered on the effects of nearest neighbors, principally due to the large number of electrons in these systems. The agreement with experimental data is usually qualitative.
There are important issues in employing molecular clusters to simulate the solid-state environment. For example, there is frequently a large number of parameters (charge of the cluster, dangling bonds, etc.) which must be optimized to give reasonable results. One important challenge in a cluster-based approach is to define the co-ordination sphere of the NMR nucleus and the appropriate size of the cluster. Some differences between cluster and periodic-boundary calculations for determining NMR parameters have been summarized in a recent article.29
In this contribution, we report calculations of NMR chemical-shielding tensors for a series of solid mercury compounds, in which we use the cluster approach. We systematically evaluate the effect of molecular-cluster size on NMR parameters of a suite of 199Hg-containing materials. We examine the effect of application of the frozen core approximation (FCA) in calculating NMR chemical shielding using molecular clusters, and we examine the effect of neglect of various parts of the relativistic Hamiltonian in NMR calculations by treating the molecular clusters at different levels of theory. Our aim is to provide examples of how various approximations affect the calculation of NMR parameters in a variety of solids.
2. Calculational protocols
The formal definition of the chemical-shielding interaction is given by the components of a rank-2 three-dimensional Cartesian tensor, σ: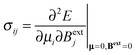 | (1) |
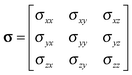 | (2) |
In one specific co-ordinate system, the principal-axis system (PAS), the chemical-shielding tensor is diagonal. These principal components are conventionally assigned as: σ11 ≤ σ22 ≤ σ33, which is known as the frequency-ordered convention. The chemical-shielding tensor in other co-ordinate systems may be derived from this tensor in the PAS by rotational transformation between the two co-ordinate systems.
The absolute chemical shielding is not measured in a NMR experiment. Instead, the chemical shift, the shielding relative to some reference material, is generally reported. The principal components of the chemical shielding and the observable principal chemical-shift components are related by eqn (3).
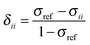 | (3) |
In principle, one defines the chemical-shift tensor experimentally with the three principal components, δ11, δ22, and δ33. There are several other descriptions in use. In one convention, the tensor is expressed in terms of its irreducible spherical-tensor components.40 Another convenient description for spectra of powders is given by the Maryland convention, a set of three NMR parameters describing the shape of the spectrum of a random powder, the isotropic chemical shift (δiso), the span (Ω), and the skew (κ).43 These three parameters are related to the principal components of the chemical-shift tensor by the following relations:
| δiso = ⅓(δ11 + δ22 + δ33) | (4) |
| Ω = |δ11 − δ33| | (5) |
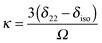 | (6) |
All computations were performed using the ADF (ADF v2010 and ADF v2013) suite of programs.44–46 Calculations were carried out at the DFT/BP86 level.47,48 For the results in Sections 3.1 and 3.2, the TZ2P/all-electron (AE) basis set is used for all atoms in the cluster. Relativistic effects are treated with the ZORA Hamiltonian at the spin–orbit level.49–52 For the calculations in Section 3.3, the TZ2P/AE basis set is employed for atoms in the near vicinity of the NMR nucleus of interest, including the nearest neighbors, and the frozen core approximation53,54 (FCA) is used with TZP- and DZ-type basis sets for the remainder of the cluster. For the calculations in Section 3.4, we examine how inclusion of various relativistic terms affects the NMR parameters by comparison to results that neglect these effects. In all cases, NMR parameters are computed within the GIAO formalism.11,55,56
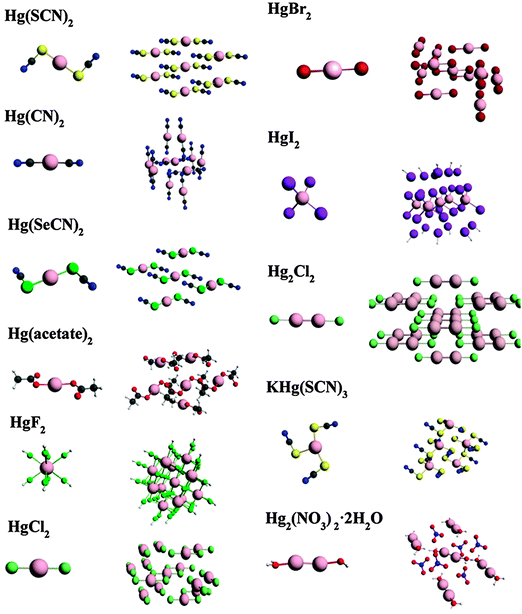
An important issue in calculations of NMR parameters of molecular clusters is the size of the cluster and how it affects predicted parameters. All clusters examined are formed from experimental X-ray geometries found in the literature (Table 1). The set includes materials with relatively small first-coordination shells, and does not contain examples of large mercury-containing complexes. For the solid systems with hydrogen atoms [Hg(acetate)2 and Hg2(NO3)2·2H2O], an optimization was carried out on hydrogen positions of small clusters at the ZORA/scalar level with the BP86 density functional and TZ2P/AE basis set. For HgF2 and HgI2, the clusters are terminated with protons to reduce the charge on the cluster and obtain SCF convergence.
| Crystal system | Reference code | Space group |
|---|---|---|
| a Codes from the inorganic crystal structure database,59 or structures are from the literature where no code is given. | ||
| Hg(SCN)2 | 10304a | C12/m1 |
| Hg(CN)2 | 412315a | I42d |
| Hg(SeCN)2 | Bowmaker et al.57 | P21/c |
| Hg(CO2CH3)2 | Allmann et al.58 | P21/a |
| HgF2 | 33614a |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
| HgCl2 | 23277a | Pnma |
| HgBr2 | 39319a | Cmc21 |
| HgI2 | 2224a | P42/nmc |
| Hg2Cl2 | 23720a | I4/mmm |
| K[Hg(SeCN)3] | Bowmaker et al.57 | P21/n |
| Hg2(NO3)2·2H2O | 1958a | P121/n1 |
To specify the agreement or lack of agreement between calculated shifts and experimental observations, we report the residual, the square root of the sum of the squares of the deviations of the calculated principal components from the experimental values. The smaller the residual, the better a model agrees with experiment.
3. Results and discussion
3.1. The effect of size and charge
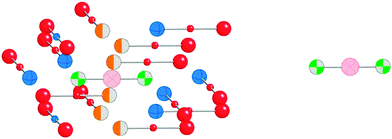
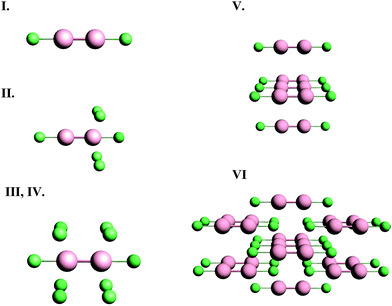
Although NMR chemical shielding is known to be primarily a local property, the electronic state from which one derives chemical shielding is influenced strongly by long-range interactions, especially in solids. To check for the importance of this long-range effect, we evaluate chemical shielding for two types of molecular clusters (called, respectively, small and large clusters). Small clusters consist of only the atoms with NMR-active nuclei (199Hg) and the nearest neighbors (ligands). Large clusters include the extended co-ordination shell, next-nearest neighbors, and the rest of the molecule of which the next-nearest neighbors and extended co-ordination shell atoms are a part. Pictorial representations of the small and large clusters of HgCl2 are given in Fig. 1.We investigated the nature of cluster size on the NMR chemical shielding of Hg2Cl2 described by various clusters formed from the X-ray crystal structure of the compound (Fig. 2). All calculations were performed within the ZORA/SO framework while employing a TZ2P/AE basis set. For convenience, the predicted NMR chemical-shift principal components were referenced to a single value, the calculated chemical shielding of the isolated dimethylmercury (DMM) molecule at the same level of theory, 7965 ppm. The calculated NMR parameters are tabulated in Table 2, along with the experimental results. For cluster I, which consists of the isolated Hg2Cl2 unit, the calculated isotropic shift is about 580 ppm more negative than the experimental value, whereas the span is in error by almost 2000 ppm. This error in the span mostly arises from an error in the δ33 component of the chemical-shielding tensor, whereas the other two components are within 100 ppm of the respective experimental values.
| Model cluster | δ 11 (ppm) | δ 22 (ppm) | δ 33 (ppm) | δ iso (ppm) | Ω (ppm) | Residuala |
|---|---|---|---|---|---|---|
a
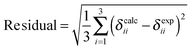 . .
|
||||||
| Experiment | 236 | 236 | −3452 | −993 | 3688 | — |
| Cluster I | 285 | 285 | −5280 | −1570 | 5520 | 1056 |
| Cluster II | −1588 | −1588 | −3541 | −2239 | 1937 | 1490 |
| Cluster III | −803 | −804 | −3859 | −1822 | 3031 | 881 |
| Cluster IV | −1 | −1 | −4063 | −1355 | 4030 | 402 |
| Cluster V | 598 | 598 | −5113 | −1306 | 5665 | 1003 |
| Cluster VI | −66 | −66 | −3676 | −1269 | 3582 | 278 |
Cluster II includes the extended co-ordination shell of the NMR nucleus of interest. The added atoms (compared to cluster I) are the four Cl− ions. The distance from the mercury nucleus to these additional chlorine centers is 0.321 nm, compared to the Hg–Cl bond distance of 0.243 nm. The addition of these four chlorine centers significantly improves the calculated value of δ33 relative to the neglect of these centers in cluster I. The introduction of these centers, however, causes significant errors in the values of δ11 and δ22 that were not seen for cluster I. The calculated span is much smaller than the experimental span. Cluster II does not have certain symmetry elements that cluster I does have, in particular the mirror plane between the two Hg centers. It appears that this lack of symmetry is one possible cause of the difference between the values of these two components for cluster I and cluster II.
Cluster III adds elements to include the mirror symmetry that was lost in the definition of cluster II. Compared to cluster II, cluster III has four additional chlorine centers present. Calculations on cluster III give an isotropic shift that is 800 ppm more negative than the experimental value, whereas the span is underestimated by about 700 ppm. In general, all the calculated principal components of cluster III are more shielded than the experimental values. This observation is often the fingerprint of excess charge on the molecular cluster, which is the case for both cluster II and cluster III, having charges of −4 and −8, respectively.
Cluster IV is designed to compensate charge by termination with hydrogen atoms. These hydrogen atoms were inserted along the mercury–chlorine bond axis at 0.127 nm from the chlorine. This position maintains the symmetry at the mercury site whose NMR parameters we calculate. The compensation of charge, while maintaining the symmetry, decreases the isotropic shielding of the Hg center compared to that of cluster III. Additionally, residuals of the principal components are much smaller than those of cluster III. Saturation of the dangling bonds to decrease charge on the cluster is important in using clusters to model the local structure in solids for calculating NMR parameters, as these calculations show. However, in such treatments, the calculated chemical-shielding tensor is usually dependent on the positions of the hydrogen atoms.
In cluster V, we include only the Hg2Cl2 units which contain the four next-nearest Hg atoms to the NMR nucleus of interest. The Hg–Hg distances between the Hg2Cl2 units are 0.448 nm. As expected, inclusion of next-nearest Hg centers has a smaller effect on NMR parameters than inclusion of the next-nearest Cl centers, since the Hg–Hg distance is larger than the Hg–Cl distance. Moreover, since the next-nearest chlorines are missing in this cluster, the agreement between experiment and calculation is not good. Compared to cluster I, there is a considerable difference between the principal components, which indicates that next-nearest Hg atoms should be included in the extended co-ordination shell in designing the cluster.
In cluster VI, not only is the first co-ordination shell present, but the extended co-ordination shell and next-nearest neighbors are also included. Additionally, the structure is completed by adding atoms to produce uncharged Hg2Cl2 units, as shown in Fig. 1. Inclusion of these additional centers improves the calculated values of the chemical-shift tensor components, so that the residual is the smallest of any of the clusters examined. We have found that, with available computational resources to create clusters, a residual of 200 ppm or less for these kinds of heavy atoms indicates a reasonable model cluster. With this accuracy and the known wide ranges of shifts for 199Hg, calculation with these cluster models allows assignment of shifts to nuclei in unique structural motifs.
3.2. Calculations on clusters in the all-electron basis
We report NMR parameters for a series of mercury compounds, using large-cluster models and small-cluster models (Fig. 3). The calculated NMR chemical-shift parameters are tabulated in Table 3, along with reported experimental values. (The calculated chemical shieldings from which these shifts are derived are in Table S1 in the ESI.†) σref for determining chemical shifts is taken as the intersection of the best-fit linear correlation for each type of cluster (Fig. 4a and b). These values are 7853 ppm and 8043 ppm for small and large clusters, respectively.| Model clusters | δ 11 (ppm) | δ 22 (ppm) | δ 33 (ppm) | δ iso (ppm) | Ω (ppm) | Residual |
|---|---|---|---|---|---|---|
| a Ref. 60. b Ref. 61. c Ref. 57. d Ref. 62. e Actual principal elements cannot be determined from the line shape.62 | ||||||
| Hg(SCN)2 | ||||||
| Experimenta | −81 | −328 | −3390 | −1300 | 3309 | — |
| Small cluster | 351 | −1154 | −4694 | −1832 | 5006 | 926 |
| Large cluster | 198 | −501 | −3663 | −1322 | 3830 | 246 |
| Hg(CN)2 | ||||||
| Experimentb | −33 | −381 | −3773 | −1396 | 3740 | — |
| Small cluster | −101 | −106 | −5490 | −1899 | 5347 | 1005 |
| Large cluster | 51 | −3 | −4081 | −1344 | 4099 | 286 |
| Hg(SeCN)2 | ||||||
| Experimentc | −503 | −1337 | −3440 | −1760 | 2937 | — |
| Small cluster | −617 | −1176 | −4601 | −2131 | 3953 | 680 |
| Large cluster | −503 | −1339 | −3434 | −1759 | 2908 | 4 |
| Hg(acetate)2 | ||||||
| Experimenta | −1859 | −1947 | −3685 | −2497 | 1826 | — |
| Small cluster | −1757 | −2052 | −4688 | −2832 | 2908 | 585 |
| Large cluster | −1948 | −2076 | −3639 | −2554 | 1678 | 94 |
| HgF2 | ||||||
| Experimentd | −2826 | −2826 | −2826 | −2826 | 0 | — |
| Small cluster | −3754 | −3754 | −3754 | −3754 | 1 | 928 |
| Large cluster | −2867 | −2868 | −2868 | −2868 | 1 | 42 |
| HgCl2 | ||||||
| Experimenta | −282 | −573 | −4019 | −1625 | 3737 | — |
| Small cluster | −134 | −135 | −5369 | −1598 | 5194 | 765 |
| Large cluster | −242 | −299 | −4311 | −1617 | 4036 | 232 |
| HgBr2 | ||||||
| Experimentd | −1945 | −1945 | −3293 | −2394 | 1348 | — |
| Small cluster | −2128 | −2128 | −5331 | −3195 | 3178 | 1186 |
| Large cluster | −1898 | −1930 | −3383 | −2403 | 1473 | 59 |
| HgI2 | ||||||
| Experimentd,e | −3131 | <100 | — | |||
| Small cluster | −3619 | −4475 | −4530 | −4208 | 904 | — |
| Large cluster | −2689 | −2729 | −3280 | −2899 | 586 | — |
| Hg2Cl2 | ||||||
| Experimentd | 236 | 236 | −3452 | −993 | 3688 | — |
| Small cluster Hg(1) | 172 | 172 | −5392 | −1683 | 5520 | 1121 |
| Small cluster Hg(2) | 172 | 172 | −5392 | −1683 | 5520 | 1121 |
| Large cluster Hg(1) | 13 | 12 | −3598 | −1191 | 3582 | 201 |
| Large cluster Hg(2) | 42 | 42 | −3598 | −1172 | 3611 | 180 |
| K[Hg(SCN)3] | ||||||
| Experimentc | 49 | −323 | −1941 | −738 | 1990 | — |
| Small cluster | −169 | −710 | −2373 | −1084 | 2187 | 358 |
| Large cluster | 161 | −201 | −1808 | −616 | 1953 | 123 |
| Hg2(NO3)2·2H2O | ||||||
| Experimenta | −435 | −497 | −3669 | −1534 | 3234 | — |
| Small cluster Hg(1) | −1614 | −1676 | −5215 | −2835 | 3572 | 1312 |
| Small cluster Hg(2) | −1551 | −1656 | −5214 | −2807 | 3635 | 1288 |
| Large cluster Hg(1) | −988 | −1078 | −4058 | −2042 | 3045 | 515 |
| Large cluster Hg(2) | −813 | −1092 | −4056 | 1987 | 3217 | 464 |
In general, calculations on small clusters predict isotropic chemical shifts (δiso) to within 300–1000 ppm of the experimental values. As seen in Table 3, the deviations of the principal components of the chemical-shift tensor calculated for small clusters are often more severely in error (relative to experimental data) than the isotropic shifts. The differences between computed spans (which do not depend on errors in referencing) and experimental spans often exceed 1000 ppm. For this reason, conclusions about the quality of models based on the near agreement of a calculated isotropic chemical shift with an experimental chemical shift can be misleading. More importantly, the principal components of a chemical-shift tensor reflect important properties of the electronic structure that cannot be discerned by concentrating on the isotropic chemical shift alone. For example, the isotropic chemical shift of HgCl2 calculated with a small cluster is only 27 ppm from the experimental value, but the calculated span deviates by 1457 ppm from the experimental value.
The spans calculated for large clusters are closer to the experimental values for all cases we have examined. Additionally, there is better agreement between experimental and predicted isotropic chemical shifts, as well as better agreement between calculated and experimental principal components of the shift tensor, as can be discerned from the smaller residuals for the large clusters. With the exception of the hydrated mercurous nitrate, the residuals of all the large-cluster-model calculations are near or below 200 ppm, which seems to be some limit for clusters of this size for these systems. But, even for the hydrated mercurous nitrate, the large-cluster model gives better agreement with experiment than the small-cluster model.
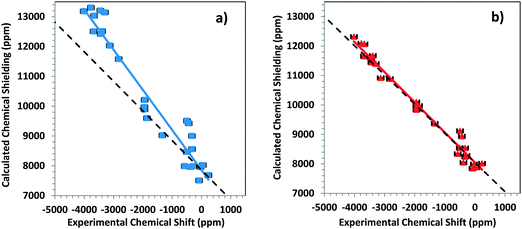
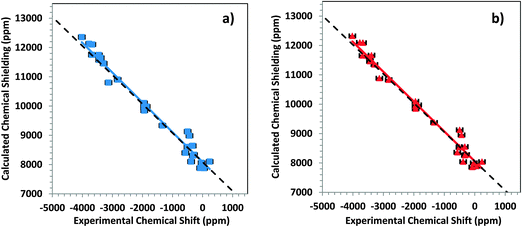
The performance of small- and large-cluster models is shown graphically in Fig. 4a and b. In Fig. 4a, the correlation between calculated chemical-shielding tensor components and experimental chemical-shift tensor components is shown for small clusters. In Fig. 4b, the same correlation is shown for large clusters. The correlation for the large clusters has a slope that deviates by only 2.3% from the ideal slope of −1, whereas the linear correlation for the small clusters deviates by 36% from this ideal value.
From the intersection of the best-fit linear correlation lines in Fig. 4a and b, the absolute shielding of DMM can be estimated within the two-component ZORA/SO framework for large and small clusters. Within this framework, the absolute shielding of DMM is predicted to be 7853 ppm by the small clusters and 8043 ppm by the large clusters. In separate calculations on an isolated DMM molecule at the same level of theory and with either (a) a fully optimized geometry or (b) the experimental geometry63 with optimized hydrogen positions, the predicted isotropic shielding in case (a) was 8120 ppm, and in case (b) it was 7965 ppm. In a previous study, Taylor et al.33 showed (with the same level of theory) that the absolute shielding of DMM was between 7929 and 8095 ppm.
The shielding constant of DMM has also been calculated by means of four-component relativistic methods.64,65 Within the four-component DFT theory, the absolute shielding of DMM is found to be 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 299 ppm, whereas the Dirac–Hartree–Fock (DHF) formalism gives a value of 12
299 ppm, whereas the Dirac–Hartree–Fock (DHF) formalism gives a value of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 417 ppm. Wodynski et al.66 report that ZORA reproduces only 75–79% of the shielding values of the four-component results for the heavy metals of the sixth row of the periodic table. Despite the underestimation of the shielding constants, Arcisauskaite et al.64 showed that 199Hg shielding constants calculated with ZORA/SO and with four-component DFT follow a similar trend, and the chemical shifts calculated with these two methods are in agreement within 60 ppm. Autschbach shows that the valence–shell properties such as chemical shift and J coupling are well described in the ZORA formalism.67,68 This observation is supported by our findings that calculations using ZORA produce results in agreement with experiment.
417 ppm. Wodynski et al.66 report that ZORA reproduces only 75–79% of the shielding values of the four-component results for the heavy metals of the sixth row of the periodic table. Despite the underestimation of the shielding constants, Arcisauskaite et al.64 showed that 199Hg shielding constants calculated with ZORA/SO and with four-component DFT follow a similar trend, and the chemical shifts calculated with these two methods are in agreement within 60 ppm. Autschbach shows that the valence–shell properties such as chemical shift and J coupling are well described in the ZORA formalism.67,68 This observation is supported by our findings that calculations using ZORA produce results in agreement with experiment.
In Ramsey's formulation,69 the shielding is evaluated as an integral of operators which vary as 1/r3, where r is the distance from the electron to the nucleus of interest. One expects that major contributions to NMR shielding are predominantly from orbitals that place the electron near the nucleus. For solids, the positions of nearby nuclei are exceedingly important in determining the general structure of orbitals. Comparison of the results for small and large clusters shows that medium-to-long-range effects must be taken into account to determine meaningful NMR tensor parameters.
There are two factors that contribute to the difference between the results for small clusters and for large clusters. First, missing atoms in the near region in the small cluster for a 199Hg-containing system may affect the chemical shielding. A secondary effect results from the fact that the nearest neighbors of the ligands are not included in the small clusters. As a result, the molecular orbitals (MOs) forming Hg–L bonds are largely localized, which would not adequately represent the structural effects on NMR chemical shielding. Both effects depend on the crystal structure, and they contribute differently to the 199Hg shielding in the two models.
3.3. The use of the frozen core approximation
The frozen core approximation (FCA) is commonly used in many applications to trim the computational time. It is generally thought that the deep core electrons are not strongly influenced by changes that may influence the valence electrons. We have investigated whether use of the FCA for these clusters yields reliable NMR parameters by the following procedure. For the large clusters of Fig. 3, the electrons of the first co-ordination shell near the nucleus of interest were treated with an all-electron (AE) basis set, whereas the rest of the cluster was treated with the FCA. TZP and DZ basis sets with a frozen large core are used in the part of the cluster treated with the FCA. (The details of the frozen core basis sets are given in Table S2 of the ESI.†)The results of these calculations are given in Table 4 for various mercury-containing solids. (The corresponding chemical-shielding values are given in Table S3, ESI.†) Fig. 5a and b show the correlation of the calculated FCA/AE principal components with the experimental chemical-shift principal components. From the correlation, σref is found to be 8056 ppm or 8087 ppm, respectively, for FCA(TZP)/AE and FCA(DZ)/AE basis sets. The results determined with FCA(TZP)/AE are closer to the all-electron results, as expected. The difference between principal components calculated with FCA(TZP)/AE and the AE basis sets does not exceed 25 ppm for most cases. The largest differences are 113 ppm for δ33 of HgI2 and 69 ppm for δiso (= δ11 = δ22 = δ33 for this case) of HgF2. The differences between principal components determined with FCA(DZ)/AE compared to the all-electron basis set are slightly larger. Nevertheless, given the accuracy of the NMR calculations on heavy nuclei, calculations using the FCA for the remote atoms and calculations with the full all-electron basis set produce almost the same NMR parameters. In fact, Fig. 5a and b show that the correlation for results using the FCA is slightly closer to the ideal case than for results using the full all-electron basis set for the large clusters. This difference is within the uncertainty of the experimental measurements. The two calculations essentially give the same results within experimental error.
| Model clusters | δ 11 (ppm) | δ 22 (ppm) | δ 33 (ppm) | δ iso (ppm) | Ω (ppm) | Residual |
|---|---|---|---|---|---|---|
| Hg(SCN)2 | −81 | −328 | −3390 | −1300 | 3309 | |
| FCA(DZ)/AE | 209 | −557 | −3588 | −1312 | 3766 | 242 |
| FCA(TZP)/AE | 197 | −503 | −3644 | −1316 | 3810 | 240 |
| All-electron | 198 | −501 | −3663 | −1322 | 3830 | 246 |
| Hg(CN)2 | −33 | −381 | −3773 | −1396 | 3740 | |
| FCA(DZ)/AE | 29 | −13 | −4072 | −1352 | 4068 | 276 |
| FCA(TZP)/AE | 53 | 12 | −4080 | −1339 | 4099 | 292 |
| All-electron | 51 | −3 | −4081 | −1344 | 4099 | 286 |
| Hg(SeCN)2 | −503 | −1337 | −3440 | −1760 | 2937 | |
| FCA(DZ)/AE | −516 | −1256 | −3516 | −1763 | 2975 | 64 |
| FCA(TZP)/AE | −484 | −1332 | −3436 | −1751 | 2928 | 12 |
| All-electron | −503 | −1339 | −3434 | −1759 | 2908 | 4 |
| Hg(Acetate)2 | −1859 | −1947 | −3685 | −2497 | 1826 | |
| FCA(DZ)/AE | −1908 | −2030 | −3691 | −2543 | 1768 | 38 |
| FCA(TZP)/AE | −1935 | −2061 | −3629 | −2542 | 1681 | 85 |
| All-electron | −1948 | −2076 | −3639 | −2554 | 1678 | 94 |
| HgF2 | −2826 | −2826 | −2826 | −2826 | 0 | |
| FCA(DZ)/AE | −2837 | −2837 | −2838 | −2837 | 1 | 12 |
| FCA(TZP)/AE | −2798 | −2799 | −2799 | −2798 | 1 | 28 |
| All-electron | −2867 | −2868 | −2868 | −2868 | 1 | 42 |
| HgCl2 | −282 | −573 | −4019 | −1625 | 3737 | |
| FCA(DZ)/AE | −249 | −316 | −4303 | −1622 | 4021 | 222 |
| FCA(TZP)/AE | −232 | −309 | −4305 | −1615 | 4040 | 226 |
| All-electron | −242 | −299 | −4311 | −1617 | 4036 | 232 |
| HgBr2 | −1945 | −1945 | −3293 | −2394 | 1348 | |
| FCA(DZ)/AE | −1867 | −1895 | −3395 | −2386 | 1516 | 80 |
| FCA(TZP)/AE | −1894 | −1922 | −3324 | −2380 | 1418 | 37 |
| All-electron | −1898 | −1930 | −3383 | −2403 | 1473 | 59 |
| HgI2 | −3131 | <100 | ||||
| FCA(DZ)/AE | −2571 | −2610 | −3025 | −2736 | 451 | — |
| FCA(TZP)/AE | −2675 | −2719 | −3167 | −2854 | 487 | — |
| All-electron | −2689 | −2729 | −3280 | −2899 | 586 | — |
| Hg2Cl2 | 236 | 236 | −3452 | −993 | 3688 | |
| FCA(DZ)/AE Hg(1) | −21 | −21 | −3687 | −1243 | 3636 | 250 |
| FCA(DZ)/AE Hg(2) | −5 | −5 | −3687 | −1232 | 3652 | 239 |
| FCA(TZP)/AE Hg(1) | −2 | −3 | −3582 | −1196 | 3551 | 209 |
| FCA(TZP)/AE Hg(2) | 28 | 28 | −3582 | −1176 | 3581 | 186 |
| All-electron Hg(1) | 13 | 12 | −3598 | −1191 | 3582 | 201 |
| All-electron Hg(2) | 42 | 42 | −3598 | −1172 | 3611 | 180 |
| K[Hg(SCN)3] | 49 | −323 | −1941 | −738 | 1990 | |
| FCA(DZ)/AE | 214 | −221 | −1772 | −593 | 1970 | 148 |
| FCA(TZP)/AE | 164 | −210 | −1807 | −617 | 1955 | 121 |
| All-electron | 161 | −201 | −1808 | −616 | 1953 | 123 |
| Hg2(NO3)2·2H2O | −435 | −497 | −3669 | −1534 | 3234 | |
| FCA(DZ)/AE Hg(1) | −990 | −1014 | −4047 | −2017 | 3032 | 489 |
| FCA(DZ)/AE Hg(2) | −820 | −1084 | −4048 | −1984 | 3201 | 461 |
| FCA(TZP)/AE Hg(1) | −993 | −1069 | −4070 | −2044 | 3053 | 516 |
| FCA(TZP)/AE Hg(2) | −820 | −1090 | −4066 | −1992 | 3220 | 468 |
| All-electron Hg(1) | −988 | −1078 | −4058 | −2042 | 3045 | 515 |
| All-electron Hg(2) | −813 | −1092 | −4056 | −1987 | 3217 | 464 |
Although there are very small differences in the computed NMR parameters, there is a substantial difference in computational time that favors using the FCA. In Table 5, we compare the computational time and number of Cartesian functions employed for selected calculations, when using the all-electron basis set versus the FCA(TZP)/AE and FCA(DZ)/AE basis sets. The calculations with the triple-zeta basis set generally take longer than those with the double-zeta basis set, but they are both substantially shorter than a calculation on the same cluster using the all-electron wave function. For example, the all-electron calculation for a large cluster of Hg2Cl2 took nearly 2.5 days, whereas the FCA(TZP)/AE treatment of the same cluster required 3.6 hours and the FCA(DZ)/AE treatment took only 35 minutes. These results indicate that the FCA can be applied to the peripheral portions of large clusters in solid-state NMR calculations with minimal introduction of significant errors.
| AE | FCA(TZP)/AE | FCA(DZ)/AE | ||||
|---|---|---|---|---|---|---|
| Model clusters | # of cf | CT (s) | # of cf | CT (s) | # of cf | CT (s) |
| Hg2Cl2 | 4264 | 209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
2584 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 020 |
2080 | 1037 |
| HgF2 | 3606 | 111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 960 |
2322 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
1566 | 3660 |
| Hg(CN)2 | 2706 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 240 |
1716 | 3540 | 1206 | 1200 |
| HgBr2 | 2409 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
1822 | 2460 | 1432 | 600 |
An important criterion in the cluster-based approaches is the convergence of NMR parameters with increasing cluster size. Since the computational requirements are relatively low at the FCA level of theory, it is possible to investigate whether calculated parameters are converged with these larger clusters. For this reason, we calculated the shielding values for Hg(SCN)2 and Hg2Cl2 at the FCA(TZP)/AE level of theory, and with molecular clusters which are extended another co-ordination shell from the ‘large clusters’ (which we call extended clusters). (Fig. 6) Table 6 shows the comparison of chemical shielding components for large clusters and extended clusters of Hg(SCN)2 and Hg2Cl2. For Hg(SCN)2, the large cluster and the extended cluster produce similar results. The differences between σ33 and σ11 are 22 ppm and 9 ppm, whereas σ22 is the same for the large cluster and the extended cluster. The difference in σiso is only 4 ppm. For Hg2Cl2, the differences are slightly larger than those of Hg(SCN)2. The largest difference is for the σ33. (79 ppm) On the other hand, the differences for σiso are 5 ppm and 13 ppm for Hg(1) and Hg(2) respectively. For all calculated principal components, the variations between the two clusters are less than 1%, which would be a valid convergence criterion for heavy-nucleus shieldings.
| Model clusters | σ 11 (ppm) | σ 22 (ppm) | σ 33 (ppm) | σ iso (ppm) |
|---|---|---|---|---|
| Hg(SCN)2 | ||||
| Large cluster | 7860 | 8554 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
9361 |
| Extended cluster | 7869 | 8554 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 648 648 |
9357 |
| Hg2Cl2 | ||||
| Large cluster Hg(1) | 8058 | 8058 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
9242 |
| Large cluster Hg(2) | 8028 | 8028 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
9222 |
| Extended cluster Hg(1) | 8089 | 8090 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 531 |
9237 |
| Extended cluster Hg(2) | 8088 | 8088 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 530 |
9235 |
3.4. Effect of level of relativistic theory on NMR parameters
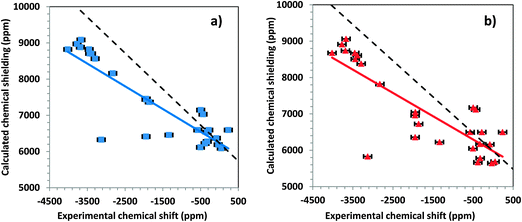
An important consideration in the calculation of chemical shielding of heavy nuclei such as 199Hg, 207Pb, and 119Sn is the inclusion of relativistic effects.7 Including relativistic terms in the Hamiltonian increases the computational time, which makes it of some practical importance to determine how significantly these affect the calculated chemical shielding. We investigated these effects by comparing results of calculations that (a) neglect all relativistic terms (nonrelativistic results) with (b) results of calculations that include only scalar relativistic corrections, and with (c) results of calculations that include the full spin–orbit interaction for large clusters.Fig. 7a shows the correlation between calculated chemical shieldings and experimental chemical shifts for all tensor components of the large clusters, when the system is treated with only nonrelativistic terms. The linear correlation has a slope of −0.6274 and an intercept of 6232 ppm. Fig. 7b shows a similar correlation for the same systems when only scalar relativistic corrections are considered. The slope of the linear correlation is −0.6697 for this system and the intercept is 5976 ppm. The inclusion of the scalar relativistic terms improves agreement with the experimental data marginally over the nonrelativistic results.
The data of Fig. 5b show the result of inclusion of relativistic effects at the spin–orbit level. The slope of the linear correlation line is −1.0234 and the intercept is 8043 ppm. Thus, within less than 3%, the slope of this linear trend is correct. In addition, comparison of Fig. 7 and 4b shows that scatter about the ideal line is much smaller when the ZORA spin–orbit Hamiltonian is used. Significantly, there is a systematic error of approximately 2000 ppm in the predicted value of the chemical shielding of DMM when the spin–orbit terms are neglected. From these calculations, it is clear that one must include spin–orbit relativistic terms in the Hamiltonian when calculating chemical shieldings of mercury-containing solids.
4. Conclusions
We have used the cluster-model approach to predict 199Hg NMR parameters of eleven Hg-containing solids. The comparison of results on small clusters (often a single isolated unit) with large clusters demonstrates that to predict the NMR chemical shielding accurately, one must take into account the effects of the surrounding environment, and specifically one must treat the problem with a large cluster that maintains symmetry at the site of the nucleus of interest. We have found that, in some cases, the isotropic shift may be fortuitously predicted for an isolated unit, but that the tensor components may be in substantial error. The cluster model must be chosen so that the local site symmetry at the nucleus of interest is maintained, which determines the minimal size. Care must be taken to ensure that the charge on a cluster (which is sometimes necessary) is not too large. The situation for large organomercury complexes may involve the higher coordination shells to a lesser degree than for the small molecules investigated here, in which case a single molecule model may be adequate. Of concern in calculation of chemical shielding in these heavy-nucleus-containing materials is the computation time that a large-cluster model may require. We examined the use of the frozen core approximation (FCA) for atomic centers removed from the locality of interest as a means to shorten this calculation time. The calculations show that using the FCA on more remote centers makes a minimal difference in computed NMR parameters, compared to calculations with models using the full all-electron basis set. The use of the FCA for these more remote centers presents a substantial savings in computational time when compared with the all-electron approach, and we suggest that using the FCA in this manner for computation of NMR parameters may allow one to specify the environment with larger clusters that better define the effects of structure, without sacrificing much accuracy.The impact of relativistic terms in the Hamiltonian is significant for these heavy nuclei. In particular, inclusion of spin–orbit terms is essential to get chemical shieldings that reflect the experimental data. Total neglect of relativistic terms is the poorest approximation, inclusion of scalar relativistic terms improves the calculation slightly, but for the highest accuracy, one must include spin–orbit components in the Hamiltonian.
Acknowledgements
This work was supported by the National Science Foundation under Grant CHE-0956006. We thank Dr Shi Bai, Mr Sean Holmes, and Professor Jochen Autschbach for helpful discussions.References
- E. D. Becker, High Resolution NMR: Theory and Chemical Applications, Academic Press, San Diego, 3rd edn, 2000 Search PubMed.
- M. J. Duer, Introduction to Solid-State NMR Spectroscopy, Wiley-Blackwell, Oxford, 2nd edn, 2005 Search PubMed.
- J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 5399–5418 RSC.
- J. C. Facelli, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 58, 176–201 CrossRef PubMed.
- R. Fukuda, M. Hada and H. Nakatsuji, J. Chem. Phys., 2003, 118, 1027–1035 CrossRef CAS PubMed.
- A. Bagno, G. Casella and G. Saielli, J. Chem. Theory Comput., 2006, 2, 37–46 CrossRef CAS.
- J. Autschbach and S. Zheng, Annu. Rep. NMR Spectrosc., 2009, 67, 1–95 CrossRef CAS.
- J. Autschbach, Philos. Trans. R. Soc., A, 2014, 372, 39 CrossRef PubMed.
- L. A. Truflandier and J. Autschbach, J. Am. Chem. Soc., 2010, 132, 3472–3483 CrossRef CAS PubMed.
- S. H. Zheng and J. Autschbach, Chem. – Eur. J., 2011, 17, 161–173 CrossRef CAS PubMed.
- S. K. Wolff, T. Ziegler, E. van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689–7698 CrossRef CAS PubMed.
- K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Elsevier Science, Amsterdam, 2002 Search PubMed.
- P. Pyykko, Chem. Rev., 1988, 88, 563–594 CrossRef CAS.
- J. Autschbach, J. Chem. Phys., 2012, 136, 15 CrossRef PubMed.
- A. M. Orendt and J. C. Facelli, Annu. Rep. NMR Spectrosc., 2007, 62, 115–178 CrossRef CAS.
- D. Sebastiani and M. Parrinello, J. Phys. Chem. A, 2001, 105, 1951–1958 CrossRef CAS.
- D. Sebastiani, G. Goward, I. Schnell and M. Parrinello, Comput. Phys. Commun., 2002, 147, 707–710 CrossRef CAS.
- J. H. M. Parrinello, D. Marx, P. Focher, M. Tuckerman, W. Andreoni, A. Curioni, E. Fois, U. Roetlisberger, P. Giannozzi, T. Deutsch, A. Alavi, D. Sebastiani, A. Laio, J. Van de Vondele, A. Seitsonenet al., CPMD 3.11, MPI fur Festkorperforschung Stuttgart, 1997–2001, IBM Corp., 1990–2006 technical report, 2006.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 13 CrossRef.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS PubMed.
- J. A. Tossell, J. Magn. Reson., 1997, 127, 49–53 CrossRef CAS.
- J. A. Tossell, Chem. Phys. Lett., 1999, 303, 435–440 CrossRef CAS.
- J. A. Tossell, Phys. Chem. Miner., 1999, 27, 70–80 CrossRef CAS.
- G. Valerio, A. Goursot, R. Vetrivel, O. Malkina, V. Malkin and D. R. Salahub, J. Am. Chem. Soc., 1998, 120, 11426–11431 CrossRef CAS.
- G. Valerio and A. Goursot, J. Phys. Chem. B, 1999, 103, 51–58 CrossRef CAS.
- M. Body, G. Silly, C. Legein and J. Y. Buzare, J. Phys. Chem. B, 2005, 109, 10270–10278 CrossRef CAS PubMed.
- Y. Zhang and E. Oldfield, J. Phys. Chem. B, 2004, 108, 19533–19540 CrossRef CAS.
- D. Stueber, Concepts Magn. Reson., Part A, 2006, 28, 347–368 Search PubMed.
- J. Weber and J. Gunne, Phys. Chem. Chem. Phys., 2010, 12, 583–603 RSC.
- G. G. Briand, A. D. Smith, G. Schatte, A. J. Rossini and R. W. Schurko, Inorg. Chem., 2007, 46, 8625–8637 CrossRef CAS PubMed.
- O. Dmitrenko, S. Bai, P. A. Beckmann, S. van Bramer, A. J. Vega and C. Dybowski, J. Phys. Chem. A, 2008, 112, 3046–3052 CrossRef CAS PubMed.
- O. Dmitrenko, S. Bai and C. Dybowski, Solid State Nucl. Magn. Reson., 2008, 34, 186–190 CrossRef CAS PubMed.
- R. E. Taylor, C. T. Carver, R. E. Larsen, O. Dmitrenko, S. Bai and C. Dybowski, J. Mol. Struct., 2009, 930, 99–109 CrossRef CAS PubMed.
- B. J. Greer, V. K. Michaelis, M. J. Katz, D. B. Leznoff, G. Schreckenbach and S. Kroeker, Chem. – Eur. J., 2011, 17, 3609–3618 CrossRef CAS PubMed.
- A. J. Rossini, A. W. Macgregor, A. S. Smith, G. Schatte, R. W. Schurko and G. G. Briand, Dalton Trans., 2013, 42, 9533–9546 RSC.
- R. E. Taylor, F. Alkan, D. Koumoulis, M. P. Lake, D. King, C. Dybowski and L.-S. Bouchard, J. Phys. Chem. C, 2013, 117, 8959–8967 CAS.
- M. Gerken, P. Hazendonk, A. Iuga, J. Nieboer, M. Tramsek, E. Goreshnik, B. Zemva, S. H. Zheng and J. Autschbach, Inorg. Chem., 2007, 46, 6069–6077 CrossRef CAS PubMed.
- J. Vicha, M. Patzschke and R. Marek, Phys. Chem. Chem. Phys., 2013, 15, 7740–7754 RSC.
- B. E. G. Lucier, K. E. Johnston, W. Q. Xu, J. C. Hanson, S. D. Senanayake, S. Y. Yao, M. W. Bourassa, M. Srebro, J. Autschbach and R. W. Schurko, J. Am. Chem. Soc., 2014, 136, 1333–1351 CrossRef CAS PubMed.
- U. Haeberlen, High Resolution NMR in Solids, Academic Press, New York, 1976 Search PubMed.
- J. Autschbach, A. M. Kantola and J. Jokisaari, J. Phys. Chem. A, 2007, 111, 5343–5348 CrossRef CAS PubMed.
- J. Jokisaari, S. Jarvinen, J. Autschbach and T. Ziegler, J. Phys. Chem. A, 2002, 106, 9313–9318 CrossRef CAS.
- J. Mason, Solid State Nucl. Magn. Reson., 1993, 2, 285–288 CrossRef CAS.
- ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 CAS.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- E. Vanlenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS PubMed.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef PubMed.
- E. v. Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef PubMed.
- E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, Int. J. Quantum Chem., 1996, 60, 753–766 CrossRef CAS.
- J. Autschbach and E. Zurek, J. Phys. Chem. A, 2003, 107, 4967–4972 CrossRef CAS.
- G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606–611 CrossRef CAS.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- G. A. Bowmaker, A. V. Churakov, R. K. Harris, J. A. K. Howard and D. C. Apperley, Inorg. Chem., 1998, 37, 1734–1743 CrossRef CAS.
- R. Allmann, Z. Kristallogr., Kristallgeom., Kristallphys., Kristallchem., 1973, 138, 366–373 CrossRef CAS.
- The Inorganic Crystal Structure Database is copyrighted by the Fachinforationszentrum Karlsruhe and the National Institute of Standards and Technology. Information on the data base is available at http://icsd.fiz-karlsruhe.de.
- G. A. Bowmaker, R. K. Harris and D. C. Apperley, Inorg. Chem., 1999, 38, 4956–4962 CrossRef CAS PubMed.
- G. A. Bowmaker, R. K. Harris and S. W. Oh, Coord. Chem. Rev., 1997, 167, 49–94 CrossRef CAS.
- R. E. Taylor, S. Bai and C. Dybowski, J. Mol. Struct., 2011, 987, 193–198 CrossRef CAS PubMed.
- K. Kashiwabara, S. Konaka, T. Iijima and M. Kimura, Bull. Chem. Soc. Jpn., 1973, 46, 407–409 CrossRef CAS.
- V. Arcisauskaite, J. I. Melo, L. Hemmingsen and S. P. A. Sauer, J. Chem. Phys., 2011, 135, 11 CrossRef PubMed.
- J. Roukala, A. F. Maldonado, J. Vaara, G. A. Aucar and P. Lantto, Phys. Chem. Chem. Phys., 2011, 13, 21016–21025 RSC.
- A. Wodynski, M. Repisky and M. Pecul, J. Chem. Phys., 2012, 137, 11 CrossRef PubMed.
- J. Autschbach, Theor. Chem. Acc., 2004, 112, 52–57 CrossRef CAS PubMed.
- J. Autschbach, Mol. Phys., 2013, 111, 2544–2554 CrossRef CAS.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp01682c |
| This journal is © the Owner Societies 2014 |