Understanding composition–property relationships in Ti–Cr–V–Mo alloys for optimisation of hydrogen storage in pressurised tanks

Abstract

The location of hydrogen within Ti–Cr–V–Mo alloys has been investigated during hydrogen absorption and desorption using in situ neutron powder diffraction and inelastic neutron scattering. Neutron powder diffraction identifies a low hydrogen equilibration pressure body-centred tetragonal phase that undergoes a martensitic phase transition to a face-centred cubic phase at high hydrogen equilibration pressures. The average location of the hydrogen in each phase has been identified from the neutron powder diffraction data although inelastic neutron scattering combined with density functional theory calculations show that the local structure is more complex than it appears from the average structure. Furthermore the origin of the change in dissociation pressure and hydrogen trapping on cycling in Ti–Cr–V–Mo alloys is discussed.

---

Introduction

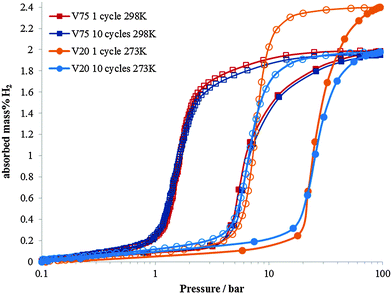
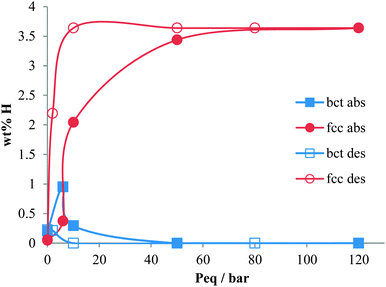
The necessity for alternative energy sources for vehicle applications is a critical area of scientific and engineering development.^1,2 In the field of hydrogen storage for automotive applications, a large part of the periodic table has been studied in the quest for high gravimetric and volumetric hydrogen densities, and operating conditions that are appropriate for fuel cell applications.^3–8 Often these materials are powders which have an intrinsic volumetric density limitation owing to the packing efficiencies of the particles. In order to achieve higher hydrogen densities, use of a metal hydride within a pressurised hydrogen tank enables the full volume of the tank to be utilised.^9–11 For this application, the metal hydrides ideally should have high hydrogen capacity and also high dissociation pressures. A high dissociation pressure ensures hydrogen can be readily supplied even at low temperatures, and also reduces the reaction heat during hydrogen desorption, thus facilitating heat exchange during hydrogen charging and discharging. Research into this area has mainly focussed on the first row transition metals with predominantly V or Ti based alloys. V is known for its high hydrogen diffusion rate and has been studied extensively since the 1970's.^12–21 Alloying with other transition metals has also been investigated in order to tailor the properties of metal hydride for maximising the hydrogen content, hydrogen diffusion rate or hydrogen dissociation pressure (or plateau pressure). For instance, the addition of Ti (which has a lower diffusion coefficient) to V reduces the rate of hydrogen diffusion in the V–Ti alloy, but increases the maximum hydrogen content compared to pure V,^22–24 although this is not maintained on cycling.¹¹ Conversely, Cr has been found to reduce hydrogen uptake and diffusion rate, but increase the hydrogen plateau pressure (or dissociation pressure).²⁵ Dissociation pressure is also increased on the inclusion of a small atom% of Mo in TiCrV alloys.²⁶ Furthermore the importance of thermal stability during hydrogen absorption and desorption in determining the properties of the alloy has also been highlighted.²⁷

The two alloys that have been investigated in this study are Ti₂₅Cr₅₀V₂₀Mo₅ (referred to as V₂₀) (max 2.4 wt% H₂, dissociation pressure = 11 bar) and Ti₁₀Cr₁₀V₇₅Mo₅ (referred to as V₇₅) (max 2.0 wt% H₂, dissociation pressure = 1.5 bar). The Ti–Cr–V–Mo elemental combination has been shown to have considerable potential as a hydrogen store for use in pressurised tanks,²⁶ but the composition of the alloys greatly influences their properties. V₂₀ has a higher maximum capacity and a higher dissociation pressure, it also shows significant degradation in the hydrogen capacity on cycling.²⁸ V₇₅ has a slightly lower maximum capacity, a significantly lower dissociation pressure, but does not show significant degradation in capacity on cycling (Fig. 1).

Fig. 1 Hydrogen pressure–composition isotherm for Ti₂₅Cr₅₀V₂₀Mo₅ (V₂₀) at 273 K and Ti₁₀Cr₁₀V₇₅Mo₅ (V₇₅) at 298 K for 1 cycle and 10 cycle samples during hydrogen absorption (filled data points) and desorption (empty data points). At 298 K and 273 K the V₇₅ and V₂₀ samples respectively achieve their maximum H₂ absorption at approximately 100 bar P_eq. The higher dissociation pressure and reduced capacity on cycling can be observed for V₂₀.

To examine the structure and dynamics of the hydrogen in these alloys we have collected synchrotron X-ray diffraction (XRD) and in situ neutron powder diffraction (NPD) data for the V₇₅ sample and inelastic neutron scattering (INS) data for the V₂₀ and V₇₅ samples across a range of temperatures and hydrogen equilibration pressures (P_eq) on hydrogen absorption and desorption. Protic hydrogen has been used owing to the differences in site occupation observed between deuterium and hydrogen.¹⁴In situ NPD measurements enable the preferred absorption site within the alloy to be determined as a function of hydrogen equilibration pressure. In situ INS informs us regarding the strengths of the interatomic interactions and the dynamics of the hydrogen within the alloy, from which the local geometry of the hydrogen absorption sites can be inferred. Using the results from these complementary techniques the origin of the degradation in hydrogen capacity and different dissociation pressures for the alloys are discussed.

Experimental

Sample synthesis

Pure titanium, vanadium, chromium and molybdenum were used as the starting materials. Granular- or sponge-shape metals were weighed with the stoichiometric ratio to the formula of V₇₅ and V₂₀. The total amount of the mixture was about 50 g for each sample. The mixture was then arc-melted in an argon atmosphere eight times in order to improve homogeneity. The obtained alloy ingot was heat-treated at 1473 K for 2 hours in an argon atmosphere. Finally, the heat-treated ingot was mechanically pulverized to coarse particles with the diameters around 0.5–1.0 mm.

Pressure–composition (PC) isotherms

A 2 g sample of the alloy particles was placed into a stainless-steel cell to measure the pressure–composition (PC) isotherms of the alloys on a Sievert's type apparatus (Suzuki Shokan Co.). PC isotherm measurements were performed for hydrogen pressures in the range 0.1 to 96 bar at 273 K for the V₂₀ sample and at 298 K for the V₇₅ sample. For the 10 cycles samples, the hydrogen absorption and desorption reactions were performed for 10 cycles using the same apparatus.

Synchrotron X-ray powder diffraction (XRD)

Synchrotron XRD data were collected at beam-line BL19B2 in SPring-8, Japan, using a large Debye–Scherrer camera with an image plate detector.²⁹ Treatment of the samples by an aqueous solution of chromic acid³⁰ was used to prevent the alloy particles releasing hydrogen during XRD measurements. The treated powder samples were inserted into a glass capillary (diameter: 0.2 mm). The powder X-ray diffraction data were measured at room temperature (300 K) with an incident X-ray of wavelength 0.80 Å. The diffraction data were collected with a 0.01° step from 8.0° to 78.0° in 2θ. The structural parameters were extracted from the data using Rietveld refinement within TOPAS.³¹

Neutron powder diffraction (NPD)

In situ variable pressure neutron powder diffraction data were collected on the General Materials Diffractometer (GEM) at the ISIS Neutron Facility at Harwell Oxford (UK). The V₇₅ sample that had been cycled once ex situ (one hydrogen absorption and desorption to 100 bar; referred to as the V₇₅ 1 cycle sample) was loaded into a cylindrical aluminium alloy high pressure cell in an argon glove box and then attached to a gas handling centre-stick and pressure intensifier. Care was taken to change the hydrogen gas pressure slowly during absorption and desorption to maintain the sample temperature at ambient temperature and to ensure sample equilibration. The sample was left for 30 minutes after dosing for equilibration; data collections lasted ∼4 hours. The diffraction data were processed using Mantid, and Rietveld refinements were performed using TOPAS.³¹

Inelastic neutron scattering (INS)

INS data were collected on the indirect geometry spectrometer TOSCA³² at the ISIS Neutron Facility at Harwell Oxford (UK), which has an energy range of −2.5–1000 meV and an energy resolution of ∼1.25% of the energy transfer. The V₇₅ sample that had been cycled once and the V₇₅ sample that had been cycled ten times (referred to V₇₅ 1 cycle and V₇₅ 10 cycle samples respectively), and the V₂₀ sample that had been cycled once and the V₂₀ sample that had been cycled ten times (referred to as the V₂₀ 1 cycle and V₂₀ 10 cycle samples respectively) were each loaded separately into an aluminium alloy high pressure cell or a stainless steel high pressure cell in an argon glove box, and then attached to a gas handling centre-stick and gas panel. All gas loadings were performed at 300 K. Data collections were made across the temperature range 5–300 K facilitated by the TOSCA cryostat, and lasted between 4 and 12 hours depending on temperature and hydrogen content. Conversion from time-of-flight to energy transfer was carried out using Mantid.

Periodic density functional theory (DFT) calculations

The periodic density functional theory calculations were carried out using a plane wave basis-set and pseudopotentials as implemented in the CASTEP code.^33,34 Two models were used. The first was a vanadium-only model which used a 2 × 2 × 2 multiplication of the bct unit cell to generate a supercell of the bct structure with each hydrogen site obtained from the NPD data occupied fully (i.e. no partially occupied sites). The appropriate number of hydrogen atoms were then removed from the supercell to give the correct hydrogen stoichiometry. The second model used a 4 × 4 × 4 supercell with full occupancy by vanadium and hydrogen. In this case, vanadium atoms were selected at random and changed to Ti, Cr, or Mo to generate the stoichiometry of Ti₁₃Cr₁₃V₉₆Mo₅ (equivalent to a Ti : Cr : V : Mo ratio of 10.2 : 10.2 : 75.6 : 3.9 respectively; owing to the size of the unit cell it was not possible to generate the precisely equivalent ratio Ti₁₀Cr₁₀V₇₅Mo₅). Sufficient hydrogen atoms were then removed at random to generate Ti₁₃Cr₁₃V₉₆Mo₅H₈₀. Random numbers were generated using atmospheric noise by the site: http://www.random.org.

Test calculations with spin polarised structures showed no unpaired electrons, so all subsequent calculations assumed spin-paired structures. The generalised gradient approximation Perdew–Burke–Ernzerhof functional was used in conjunction with optimised norm-conserving pseudopotentials with a plane-wave cut-off energy of 770 eV. Phonon modes were calculated using density-functional perturbation-theory.³⁵ As a prerequisite to any lattice dynamics calculation a full geometry optimization of the internal atomic co-ordinates was performed. The output of the phonon calculation includes atomic displacements of the atoms in the mode. The visualisations of the modes were carried out in Materials Studio (Accelrys)³⁶ and the INS spectra were generated with ACLIMAX.³⁷

Results and discussion

Structural analysis

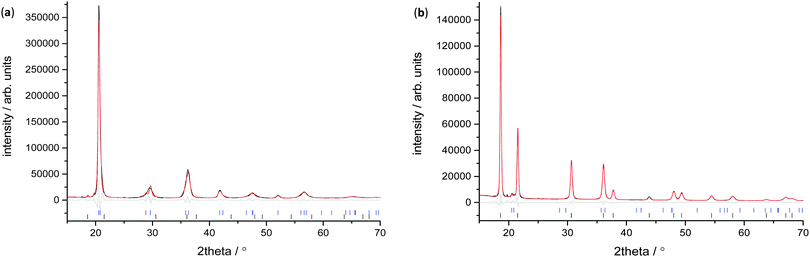
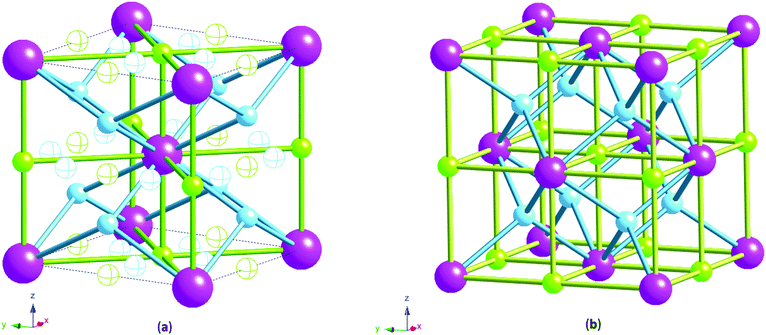
X-ray measurements were used to determine the structure of the V₇₅ metal lattice; owing to the high vanadium content and the low coherent neutron scattering cross-section of vanadium, the XRD data provide a more reliable assessment of the long range structure of the metal lattice. The NPD data, on the other hand, provide information about the long range ordering of the hydrogen atoms within the metal lattice.

XRD data of the 1 cycle V₇₅ samples after degassing to 1 × 10⁻⁶ bar show a body centred tetragonal (bct) phase with a very small amount of the face centred cubic phase (fcc) also present (Fig. 2a). The assignment of the major phase as bct in space group I4/mmm was determined after also attempting fitting in the body centred cubic space group Im3̄m (commonly assigned as the disordered α-phase for mono-metal hydrogen solid solutions¹²). The bcc space group resulted in a worse fit as it does not account for the asymmetrical peak shapes and shoulders arising from the distortion of the unit cell. Indeed, at intermediate hydrogen contents (e.g. VH_x 0 < x < 1.1) a tetragonally distorted phase has been observed for pure-V, V–Cr and V–Mo alloys.^25,26,38,39 The breadth of the peaks observed in the X-ray data suggest that while I4/mmm is a satisfactory assignment of the long range order of the phase, the local structure might be different owing to the number of elements present in the alloy. This is discussed further later. The bct phase exhibits distortion with a c/a ratio of 1.027, which is slightly larger than that observed for the V₂₀ sample after 1 cycle²⁸ (refined structural parameters for the X-ray data are listed in the ESI,† Table S1). The conversion of the bct to the fcc phase follows a Bains transformation (martensite–austenite phase transformation). This transformation relates the fcc phase to the bct phase as a significantly more distorted bct cell where the c/a ratio is 1.247 (ESI,† Fig. S1). The distortion of the bct phase yields two interstitial distorted tetrahedral sites with slightly different environments (Fig. 3a): the 4d site has D_2d point group symmetry, with equal nearest neighbour M–H distances and 2 sets of M–H–M angles, while the 8j site has C_2v point group symmetry with 2 sets of nearest neighbour M–H distances and M–H–M angles. Two octahedral sites also exist; both have D_2h point group symmetry with regular M–H–M bond angles but the equatorial nearest neighbour M–H bond lengths are longer than the axial M–H bond lengths. This is more pronounced for the 4c site than the 2b. Kamazawa et al.²⁸ highlight that the nearest neighbour tetrahedral and octahedral sites cannot co-exist in the bct phase, owing to spatial constraints, and therefore can be grouped together to form disc sites after determining the site occupancies from Rietveld refinement. The disc sites occur around the 2b octahedral site, also known as the O_z site, which has been found to be the primary location of the hydrogen atoms in the bct β-phase of V₂H, and is the cause of the anisotropic cell expansion from the bcc α-phase.^14,25 The channel sites (4c and 4d) occur along the faces of the cell, running parallel to the c-axis. In the fcc phase, the interstitial sites are the conventional larger octahedral, O, (4b) and smaller tetrahedral, T, (8c) sites (Fig. 3b).

Fig. 2 XRD data and fit for V₇₅ (a) 1 cycle sample at 1 × 10⁻⁶ bar P_eq, and (b) 1 cycle sample at 100 bar hydrogen P_eq. At 1 × 10⁻⁶ bar P_eq the sample predominantly consists of the bct phase, while at 100 bar the sample is mainly the fcc phase. Data are shown in black, the calculated pattern from the refined model in red, the difference in grey and tic marks for bct and fcc in blue and black respectively.

Fig. 3 (a) bct phase tetrahedral and octahedral sites: tetrahedral site 4d in solid blue, tetrahedral site 8j in blue line, octahedral site 2b (O_z) in solid green, octahedral site 4c in green line. Note the complete coordination spheres for the sites are not shown. For clarity, only M–H co-ordination is shown for sites 4d and 2b which were found to be occupied by hydrogen. (b) fcc phase tetrahedral, T, (blue) and octahedral, O, (green) interstitial hydrogen atom sites with co-ordination to metal atoms (purple) shown.

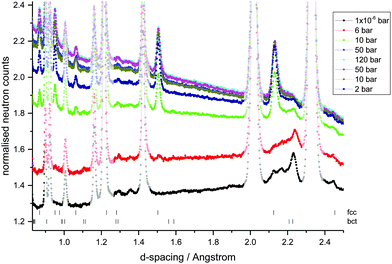
In order to investigate the location of the hydrogen atoms in the alloy, in situ variable hydrogen gas pressure neutron powder diffraction data (NPD) were collected on the GEM diffractometer at ISIS (UK) (Fig. 4). Using the metal lattice structures known from the XRD data, the hydrogen occupancies of the interstitial sites, the phase fractions and change in lattice parameters on hydrogen absorption and desorption were determined from the NPD data using Rietveld refinement (Table 1). The degassed sample shows a small amount of hydrogen in the octahedral O_z (2b) site of the bct phase, in keeping with the location of hydrogen in the bct phase of V₂H. A very small amount of hydrogen is also observed in the channel tetrahedral site (4d), although there is a large error associated with this value indicating its poor reliability and potentially low significance. Hydrogen occupation of both the tetrahedral and octahedral sites has, however, also been observed in a bct V_0.9Mo_0.1H_0.68 alloy where the authors attribute the change in site occupation to the addition of the larger Mo metal atoms thus reducing the size of the O_z site.²⁶ The degassed sample also contains a low proportion of the fcc phase, which contains some residual hydrogen in the tetrahedral site. This is in keeping with hydrogen being located on the T site in the fcc phase of VH₂, TiH₂, CrH₂ and Ti_1−xV_xH₂ alloys.^40–43

Fig. 4 NPD data collected on GEM, ISIS, at variable hydrogen gas pressures at 300 K (absorption up to 120 bar, followed by desorption to 2 bar). Data were collected in a high pressure aluminium alloy cell which produces the large peaks present in all plots; these were included in the background during Rietveld refinement.

Table 1 Change in hydrogen content, location of the hydrogen, phase fraction and fcc lattice parameter obtained from in situ neutron powder diffraction measurements. The bct 8j and 4c and the fcc 4b sites were found to be unoccupied and are therefore not included

H2Peq/bar	PC wt% H2	NPD wt% H2	bct phase (wt%)	bct 2b occ H/M (atm)	bct 4d occ H/M (atm)	bct c/a ratio	fcc phase (wt%)	fcc T occ H/M (atm)	fcc a axis (Å)
1 × 10^−6		0.14	84(4)	0.11(6)	0.02(3)	1.017	16(4)	0.17(3)	4.2429(81)
6	0.70	0.71	75(5)	0.62(8)	0.06(7)	1.021	25(5)	0.79(2)	4.2427(67)
10	1.48	1.21	20(2)	0.72(6)	0.06(6)	1.019	80(2)	1.39(2)	4.2476(5)
50	1.92	1.78	0.0				100.0	1.89(4)	4.2480(5)
120	1.96	1.89	0.0				100.0	2.00(4)	4.2485(5)
80	1.96	1.89	0.0				100.0	2.00(4)	4.2474(5)
50	1.96	1.89	0.0				100.0	2.00(4)	4.2472(5)
10	1.91	1.89	0.0				100.0	2.00(4)	4.2452(4)
2	1.50	1.25	14(2)	0.70(8)	0.12(8)	1.022	86(2)	1.39(1)	4.2452(4)
1 × 10^−6		0.15	84(4)	0.12(7)	0.02(3)	1.021	16(4)	0.18(3)	4.2407(74)

---

At low hydrogen gas pressures (1 × 10⁻⁶ bar < P_eq ≤ 10 bar), a significant increase in the occupancy of the octahedral O_z site is observed together with a small increase in the distortion of the bct phase. This increase in the length of the c-axis and decrease in the a- and b-axes result in the M–H distances becoming more evenly matched for the O_z octahedral site as the longitudinal distance increases while the opposite occurs for the 4c octahedral site. More significantly, on increasing P_eq the occupancy of the fcc T site increases and the phase fraction of the fcc phase increases. The hydrogen content of the sample therefore exists predominantly in the T sites of the fcc phase. At higher hydrogen gas pressures (P_eq > 10 bar), the bct phase converts completely to the fcc phase and the fcc T site is completely occupied. On filling of the fcc interstitial sites, the fcc lattice parameter is seen to increase.

On decreasing hydrogen pressure, the hysteresis observed in the PC isotherms is also observed in the bct and fcc phase fractions and the hydrogen site occupancies (Fig. 5). Hydrogen desorption appears to follow the process of hydrogen absorption in reverse. The fcc phase mainly converts back to the bct phase, which again shows the hydrogen to predominantly occupy the O_z site, but the conversion is not complete. On degassing the sample, a small amount of hydrogen is retained in the material which is mainly located in the bct phase O_z site. This is less than is observed in the V₂₀ sample where at least twice as much hydrogen is retained after cycling.²⁸ The fcc T site also contains some residual hydrogen, but owing to the small fcc phase fraction in the sample, this does not contribute significantly to the overall residual hydrogen content. The resulting hydrogen wt% during absorption and desorption agrees well with that obtained from the PC isotherms at each hydrogen pressure.

Fig. 5 Atomic hydrogen wt% in the sample contributed by the bct and fcc phases on absorption and desorption at variable hydrogen pressures (i.e. takes into account the hydrogen occupancy per metal atom, and the phase fraction in the sample). The lines are shown as a guide to the eye.

The absorption and desorption of hydrogen in V₇₅ shows some similarities to the absorption and desorption of hydrogen in V₂₀ – in the fcc phase, the hydrogen occupies the T site, and at low hydrogen pressures and low hydrogen content, both the bct and fcc phases are observed simultaneously. However, complete conversion to the fcc phase is observed in the V₇₅ data which is not observed in the V₂₀ sample.²⁸ This frustrated precipitation of the high hydrogen content phase is caused by hydrogen trapping from lattice defects and impurities (including atom substitution as is observed in alloys, lattice inhomogeneity and hydrogen occupying interstitials) and has been noted in a number of systems including Nb_0.8Mo_0.2H_x⁴⁴ and α-LaNi₅.^45,46 The effects of hydrogen trapping are also expressed in the maximum capacity and absorption pressures of the alloys; the V₂₀ sample shows a higher hydrogen uptake (i.e. hydrogen solubility) than the V₇₅ sample and requires higher pressures for hydrogen absorption.

Dynamics of hydrogen in the alloys – inelastic neutron scattering studies

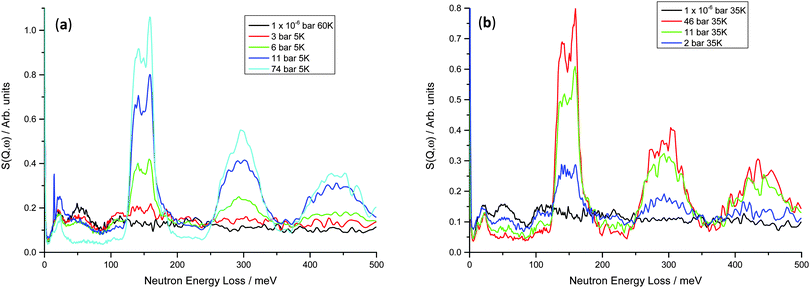
Inelastic neutron scattering data were collected for both the V₇₅ and V₂₀ samples at variable temperature and pressure, in order to investigate the dynamics of the hydrogen atoms on loading, and also the effect of temperature on their motion. As is often the case for hydrogen in metal systems, the INS spectra show only a small difference on heating from base temperature to 200 K, but on heating above 300 K the peaks became much smaller and broader, and only the large peaks at higher hydrogen P_eq can be clearly distinguished (ESI,† Fig. S2). This lack of spectral degradation from 4 to 200 K is partly due to the total mean square vibration of the hydrogen atom being dominated by the optic modes, but also suggests the hydrogen motion is localised within the metal structure. The breadth of the peaks at low temperatures suggests that the geometry of the oscillators is not well defined indicating that the local structure is not well defined and there are varying degrees of geometrical distortion of the sites.

The INS data for the V₇₅ 1 and 10 cycle samples are shown in Fig. 6. At 1 × 10⁻⁶ bar hydrogen P_eq, a peak centred at approximately 20 meV is observed which can be attributed to the acoustic zone boundary modes of the metal atoms⁴⁷ in the bct lattice (owing to the higher bct phase fraction from the NPD data). The optical H vibrations from the residual hydrogen in the metal lattice can be observed as a small broad peak centred on 51 meV and also the edge of a broader peak at 111 meV which is then followed by a broad, featureless background, even at 35 K. The peak at 51 meV is consistent with in-plane modes of H occupying the O site in β-V₂H (55 meV)⁴⁷ and β-Ti_1−yV_yH_x (44 meV).⁴⁸ The higher energy band at 110 meV is also observed in β-Ti_1−yV_yH_x (111 meV) and is attributed to hydrogen occupying a T site.⁴⁹ Ikeda and Watanabe⁵⁰ note a peak at 220 meV for β-VH_0.33 which they assign to perpendicular plane modes of the O site, however the diffuse nature of the background at E > 110 meV makes this difficult to determine in the V₇₅ data.

Fig. 6 INS spectra for (a) V₇₅ 1 cycle at 5–60 K – at 11 bar, some excess hydrogen was not removed from the pipe to the sample which then crystallised next to the sample on cooling; (b) V₇₅ 10 cycles at 35 K; absorption at 46 bar P_eq and then desorption to 11 and 2 bar P_eq.

On increasing hydrogen P_eq, the peak originating from the acoustic modes of the metal atoms changes shape slightly, becoming sharper and more distinct with a section at 10 meV and another at 21 meV. This correlates well with the onset of the phase transition from bct to fcc observed in the NPD data. It is likely that these can be assigned as the transverse and longitudinal acoustic zone-boundary modes, respectively, as similar peaks are observed in the monohydrides γ-PdH and γ-CrH.⁵¹ On increasing hydrogen P_eq the peak observed at 51 meV remains at the same energy transfer but decreases in height until it is no longer observed. The peak at 111 meV increases in height initially and then also decreases. Furthermore a large peak increases in height at 148 meV and the overall background level of the data decreases. In keeping with the NPD data, the large peak centred on 148 meV can be attributed to transverse optical modes from hydrogen located on the T site of the fcc phase. Therefore at intermediate hydrogen P_eq, the co-existence of peaks can be attributed to the co-existence of the bct and fcc phases, as is observed in the NPD data.

In both the 1 cycle and 10 cycle data the large peak centred at 148 meV peak appears to be split into two peaks (139 and 157 meV). The splitting increases with hydrogen P_eq and also results in an asymmetrical shape. A similar effect has been observed in a number of d-block hydrides including TiH,⁵² δ-TiH,⁵³ NbH_x,⁵⁴ VH,¹³ TaH_0.1,⁵⁰ and Ti_0.1V_0.9H₁ alloy⁴⁸ where it is attributed to distortion of the tetrahedral sites. Specifically in NbH_x the distorted T site has D_2d point group symmetry rather than the regular tetrahedral T_d, thus yielding an A mode at 108 meV and an E mode at 164 meV. However, the splitting may also be due to dispersion effects. Hauer et al. observe a 2 : 1 asymmetrical peak shape which the authors attribute to the coexistence of non-equivalent hydrogen sites rather than hydrogen–hydrogen coupling after investigation using isotopic dilution.⁵⁴ The effect of coupling was assessed for the V₇₅ samples by removal of some hydrogen and addition of deuterium (Fig. S3, ESI†). Addition of deuterium to the V₇₅ samples after partially desorbing the hydrogen (P_eq H₂ desorption ∼2 bar, P_eq D₂ absorption ∼7 bar) causes a narrowing of the peaks, resulting in a much better defined peak at 110 meV. In the all-hydrogen material the inequivalent protons arising from a range of distorted site geometries will result in a large number of modes. Many of these will occur at very similar transition energies with considerable coupling between the modes, resulting in broad peaks. The effect of isotopic dilution is to shift many of the modes and also to remove the mechanical coupling (by virtue of the difference in mass) between oscillators. The isolated proton then behaves as a mass defect and the transition energy is that of an isolated oscillator, with an ideal width of the instrumental resolution at that energy transfer. As there is no pronounced shift in peak position, this corroborates the presence of distorted T sites causing the peak splitting, rather than dispersion. The observation of peaks at 120, 140, 157 and 167 meV (of which the first and the last are a shoulder and tail) at high hydrogen equilibration pressures in these data corroborates the complete conversion of the bct phase to fcc but suggests that the local structure is more complicated than the average structure from the NPD data. The tail at ∼160 meV towards higher energies is also observed in a number of d-block monohydrides including MoH and CrH monohydrides where the main peak is attributed to transverse optical modes, while the tail is “assumed to arise from longitudinal optical modes which show significant dispersion due to long range repulsive H–H interaction”.⁵⁵

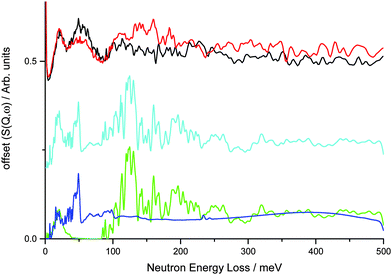
This was investigated further using DFT calculations within CASTEP. A simple model of the V₇₅ bct phase at 6 bar during absorption using a 2 × 2 × 2 expansion of the unit cell from the NPD data and assuming that all the metal atoms are vanadium generates an INS spectrum that is a poor fit to the INS data, particularly at larger energy transfers (Fig. 7). At very low energy transfers the motion of the metal atoms in the calculated INS spectrum is consistent with the observed band for the 1 and 10 cycle samples across the hydrogen loadings. This simple model for the bct phase shows a broad band centred at 50 meV (also observed in the INS data at low hydrogen P_eq) which is due to the translational motion along the ab plane of the H situated on ideal geometry O_z sites, thus corroborating the assignment from the literature. However, this model does not account for the second broad feature centred at 110 meV.

Fig. 7 Offset experimental INS data for V₇₅ 1 cycle 1 × 10⁻⁶ bar (black) and 3 bar (red) H₂P_eq, and DFT calculated INS spectra for 2 × 2 × 2 V-only cell with hydrogen and metal atoms on special positions (dark blue) and 4 × 4 × 4 Ti₁₀Cr₁₀V₇₅Mo₅ supercell with hydrogen and metal atom positions disordered (green). A combination of the 2 models is shown in light blue and is the best representation of the experimental data.

A more complex model involving a 4 × 4 × 4 supercell with randomly generated element distribution of the correct atomic ratio shows this broad band is due to the motion of H atoms on disordered sites that are of distorted octahedral and tetrahedral geometry. Distorted tetrahedral coordination is observed for M–H bond distances of 1.7–2.0 Å, although if much larger M–H distances are included (2.6–2.8 Å) the sites can be considered as distorted octahedra. The NPD data, which provides information about the average structure obtained from elastic interactions of the neutrons with the nuclei across a long range ordered arrangement of atoms in a structure, shows (by Rietveld refinement) the average position of the hydrogen to be on the O_z site. INS combined with DFT, however, provides information about the motion of the atoms from which their local structure can be inferred. The DFT calculations from the 4 × 4 × 4 supercell indicate that hydrogen is mainly disordered within the ab plane across the O_z site, thus giving rise to a band at 110 meV and suggesting that the distorted tetrahedral site 8j is occupied. The presence of hydrogen in the tetrahedral site is supported by a study by Asano et al.²⁶ who note that the addition of Mo promotes hydrogen occupancy of the distorted tetrahedral site rather than the O_z site as the Mo reduces the size of the O_z site. Calculation of the average positions of the hydrogen atoms from the 4 × 4 × 4 supercell, however, shows that they are closest to the O_z site which is in keeping with the average position from the NPD data. Combination of the two models produces the best representation of the data, suggesting clustering of the metal atoms with different local environments in different areas of the alloy. Indeed, evidence of clustering has been observed in vanadium rich V–Ti alloys^24,56 and Ti–Cr–Mo alloys,⁵⁷ while Cr and Mo have been reported to be evenly distributed in Cr/Mo–V alloys.^25,26

On comparison of the INS spectra for the V₂₀ 1 cycle and V₇₅ 1 cycle samples at hydrogen P_eq of 1 × 10⁻⁶ bar a small shift to higher energies is observed in the peak positions of the metal atom motions from 22 meV in V₇₅ to 24 meV in V₂₀ (Fig. 8) In addition, the peak due to the hydrogen in the O_z site in the bct phase observed at 51 meV in V₇₅ is observed at 59 meV in V₂₀. The shift in the peak positions to higher energies indicates stronger M–H interactions in the V₂₀ sample. As these data are from the degassed samples, the M–H interactions observed are predominantly from the trapped H found in the bct phase. The shift to higher energies is therefore in keeping with the observation of hydrogen trapping during cycling of the V₂₀ sample. This shift is even more significant as V₂₀ contains more atoms to the right hand side of the periodic table (45 : 55 left : right) than V₇₅ (85 : 15 left : right) and therefore would be predicted to have weaker M–H interactions; atoms to the right hand side of the periodic table are more efficient at screening the core charge of the metal atom from the hydrogen atoms, thus yielding a less steep hydrogen potential well and a weaker interaction.⁵⁵

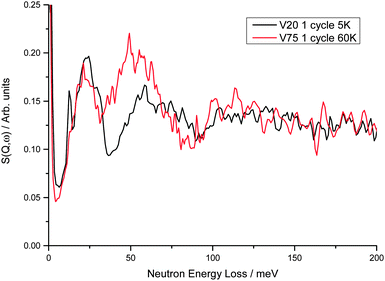Fig. 8 Comparison of V₇₅ and V₂₀ 1 cycle degassed samples at 60 K and 5 K respectively (at these temperatures the difference in the spectra owing to temperature is negligible). Peaks observed at 22 and 51 meV in V₇₅ are observed at 24 and 59 meV in V₂₀. The small but sharp peak at 12.7 meV observed in V₂₀ is barely seen in the V₇₅ spectrum at low hydrogen P_eq but increases in size with increasing hydrogen P_eq (Fig. 6). From DFT calculations of the 4 × 4 × 4 supercell, this peak originates from the anti-phase motion of the hydrogen and metal atoms along the b axis.

On increasing hydrogen P_eq for the V₂₀ 1 and 10 cycle samples, peaks are observed similar to those in the V₇₅ samples (Fig. 9). Although less well-defined, the peak at 59 meV arising from the hydrogen motion in the bct phase is observed to initially increase at low hydrogen P_eq (1 × 10⁻⁶ bar < P_eq ≤ 10 bar) and then decrease as the strong peaks from the hydrogen in the T site of the fcc phase increase. In the V₂₀ samples, the fcc phase peaks are broader (the full-width half maximum of the 150 meV peak is ∼50 meV for the V₂₀ samples compared to ∼35 meV for the V₇₅ samples), and the peak shape is much less defined. This, coupled with the broader, ill-defined peaks observed for the bct phase, indicates that the V₂₀ sample contains a greater range of hydrogen site energies (and therefore a wider range of distorted site geometries) than is observed in the V₇₅ sample. Furthermore the slight shift in the position of the fcc T site peaks to lower energies (V₇₅ = 149 meV, V₂₀ = 144 meV), indicates weaker M–H interactions in the fcc phase of the V₂₀ samples which contribute to a higher dissociation pressure, as is observed in the V₂₀ samples.

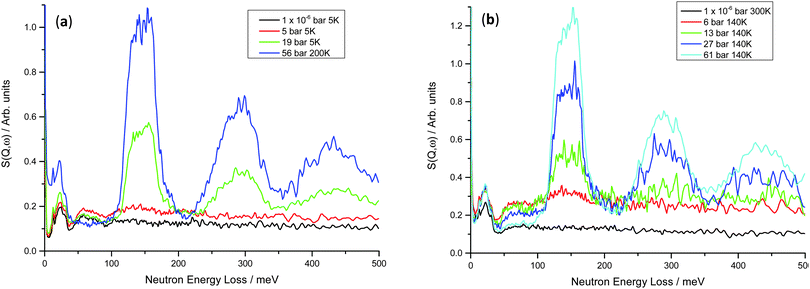Fig. 9 INS spectra for (a) V₂₀ 1 cycle at 5–200 K – the rise at low energy transfers for the 56 bar hydrogen P_eq is due to the higher collection temperature; (b) V₂₀ 10 cycles at 140–300 K – the 1 × 10⁻⁶ bar hydrogen P_eq dataset shows less intensity owing to the higher collection temperature (see Fig. S2, ESI†).

Conclusions

NPD has been used to determine that the bulk of the hydrogen stored in V₇₅ at high hydrogen P_eq is in the T sites of the fcc phase. At lower hydrogen P_eq the fcc phase converts (reversibly) to the bct phase in which the hydrogen atoms, on average, mainly occupy the distorted octahedral O_z site. On degassing the sample, a small amount of hydrogen was found to remain in the O_z site of the bct phase. This is in keeping with the PC isotherm data and suggests that the residual hydrogen that remains in the sample, thus reducing capacity on cycling, is trapped in the O_z site of the bct phase. The breadth of the peaks in the XRD and NPD data indicate a more complex structure than is described by the average structure from the Rietveld refinement and this is corroborated by the INS data. From the INS data and the DFT calculations, the local structure has been found to be more complex, suggesting clustering of the metal atoms with some areas of the sample following a more ordered structure than others. Disorder of the metal atoms and the hydrogen atoms illustrated in one of the DFT models indicates the T sites around the O_z sites can also be occupied (although not simultaneously with the O_z sites owing to spatial constraints) thus giving rise to the higher energy bands seen in the INS data at low hydrogen P_eq. Averaging of this disordered structure yields the hydrogen atoms placed closest to the O_z site, thus corroborating the NPD data.

The INS data also shows that the M–H interactions are stronger in the V₂₀ sample than in V₇₅, thus resulting in increased hydrogen trapping on cycling as is observed in the V₂₀ sample. Hydrogen trapping in the V₂₀ sample also results in the frustrated precipitation of the fcc phase on increasing hydrogen pressure in V₂₀, while the V₇₅ sample completely converts to the fcc phase, and has little residual H on cycling. These results show that in order to improve the properties of Ti–Cr–V–Mo alloys for hydrogen storage in a hydrogen tank, an optimum alloy component ratio will be required whereby the combination of strong M–H interactions and the number of lattice defects (or amount of disorder) induce an increase in the dissociation pressure, but not so much as to dramatically reduce the hydrogen capacity on cycling.

Acknowledgements

The authors would like to thank the STFC ISIS Facility for beamtime on GEM and TOSCA, and Kazutoshi Miwa and Masakazu Aoki (TOYOTA CRDL).

Notes and references

1. D. J. C. Mackay, Sustainable energy-without the hot air, UIT Cambridge Ltd, Cambridge, 2009.
2. International Energy Authority, Energy Technology Perspectives 2012 Pathways to a Clean Energy System – Executive Summary, 2012.
3. J. Yang, A. Sudik, C. Wolverton and D. J. Siegel, Chem. Soc. Rev., 2010, 39, 656–675.
4. L. H. Rude, T. K. Nielsen, D. B. Ravnsbæk, U. Bösenberg, M. B. Ley, B. Richter, L. M. Arnbjerg, M. Dornheim, Y. Filinchuk, F. Besenbacher and T. R. Jensen, Phys. Status Solidi A, 2011, 208, 1754–4773.
5. T. K. Nielsen, F. Besenbacher and T. R. Jensen, Nanoscale, 2011, 3, 2086–2098.
6. C. Liu, F. Li, L.-P. Ma and H. M. Cheng, Adv. Mater., 2010, 22, E28–E62.
7. P. P. Edwards, V. L. Kuznetsov, W. I. F. David and N. P. Brandon, Energy Policy, 2008, 36, 4356–4362.
8. L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358.
9. N. Takeichi, H. Senoh, T. Yokota and H. Tsuruta, Int. J. Hydrogen Energy, 2003, 28, 1121–1129.
10. T. Matsunaga, M. Kon, K. Washio, T. Shinozawa and M. Ishikiriyama, Int. J. Hydrogen Energy, 2009, 34, 1458–1462.
11. Y. Kojima, Y. Kawai, S. Towata, T. Matsunaga, T. Shinozawa and M. Kimbara, J. Alloys Compd., 2006, 419, 256–261.
12. Y. Fukai, The Metal-Hydrogen System: Basic Bulk Properties, Springer-Verlag, New York, 1993.
13. D. K. Ross, in Topics in Applied Physics: Hydrogen in Metals III, Properties and Applications, ed. H. Wipf, Springer-Verlag, Berlin Heidelberg, 1997, vol. 73, pp. 153–214.
14. T. Schober and H. Wenzl, in Topics in Applied Physcis: Hydrogen in Metals II, Application-Oriented Properties, ed. G. Alefeld and J. Völkl, Springer-Verlag, Berlin Heidelberg, 1978, vol. 29, pp. 11–71.
15. S. Ukita, H. Ohtani and M. Hasebe, Mater. Trans., 2008, 49, 2528–2533.
16. H. Wipf, Phys. Scr., 2001, T94, 43.
17. S. Orimo, F. Kimmerle and G. Majer, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094307.
18. J. M. Rowe, K. Skold, H. E. Flotow and J. J. Rush, J. Phys. Chem. Solids, 1971, 32, 41–54.
19. J. Luo, H.-B. Zhou, Y.-L. Liu, L.-J. Gui, S. Jin, Y. Zhang and G.-H. Lu, J. Phys.: Condens. Matter, 2011, 23, 135501.
20. S. Aboud and J. Wilcox, J. Phys. Chem. C, 2010, 114, 10978–10985.
21. V. V. Sumin, Phys. Solid State, 1997, 39, 19–22.
22. E. H. Sevilla and R. M. Cotts, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6813–6820.
23. D. Pine and R. Cotts, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 641–647.
24. S. Tanaka and H. Kimura, Mater. Trans., JIM, 1979, 20, 647–658.
25. K. Asano, S. Hayashi, Y. Nakamura and E. Akiba, J. Alloys Compd., 2012, 524, 63–68.
26. K. Asano, S. Hayashi, Y. Nakamura and E. Akiba, J. Alloys Compd., 2010, 507, 399–404.
27. T. Tamura, T. Kazumi, A. Kamegawa, H. Takamura and M. Okada, J. Alloys Compd., 2003, 356–357, 505–509.
28. K. Kamazawa, M. Aoki, T. Noritake, K. Miwa, J. Sugiyama, S. Towata, M. Ishikiriyama, S. K. Callear, M. O. Jones and W. I. F. David, Adv. Energy Mater., 2013, 3, 39–42.
29. E. Nishibori, M. Takata, K. Kato, M. Sakata, Y. Kubota, S. Aoyagi, Y. Kuroiwa, M. Yamakata and N. Ikeda, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467–468, 1045–1048.
30. S. Morishita, Y. Kondo, Y. Ohya, S. Towata and K. Abe, J. Chem. Soc. Jpn., 1999, 6, 369–374.
31. A. A. Coelho, TOPAS: General Profile and Structure Analysis Soft, 2007.
32. D. Colognesi, M. Celli, F. Cilloco, R. J. Newport, S. F. Parker, V. Rossi-Albertini, F. Sacchetti, J. Tomkinson and M. Zoppi, Appl. Phys. A: Mater. Sci. Process., 2002, 74, S64.
33. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
34. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
35. K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114.
36. Accelrys Software Inc., 2013.
37. A. J. Ramirez-Cuesta, Comput. Phys. Commun., 2004, 157, 226.
38. T. Kajitani and M. Hirabayashi, Z. Phys. Chem., 1985, 145, 27–42.
39. Y. Noda, T. Kajitani, M. Hirabayashi and S. Sato, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41, 1566–1571.
40. A. J. Maeland, T. R. P. Gibb Jr. and D. P. Schumacher, J. Am. Chem. Soc., 1961, 83, 3728–3729.
41. H. L. Yakel, Acta Crystallogr., 1958, 11, 46–51.
42. C. A. Snavely and D. A. Vaughan, J. Am. Chem. Soc., 1949, 71, 313–314.
43. B. Nowak and M. Minier, J. Less–Common Met., 1984, 101, 245–258.
44. V. V. Sumin, H. Wipf, B. Coluzzi, A. Biscarini, R. Campanella, G. Mazzolai and F. M. Mazzolai, J. Alloys Compd., 2001, 316, 189–192.
45. C. Schönfeld, R. Hempelmann, D. Richter, T. Springer, A. J. Dianoux, J. J. Rush, T. J. Udovic and S. M. Bennington, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 853–865.
46. E. Gray, T. Blach and C. Buckley, J. Alloys Compd., 1999, 293–295, 57–61.
47. J. J. Rush and H. E. Flotow, J. Chem. Phys., 1968, 48, 3795–3804.
48. T. Ueda, S. Hayashi, Y. Nakai and S. Ikeda, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 5725–5731.
49. R. Hempelmann, D. Richter, O. Hartmann, E. Karlsson and A. Wäppling, J. Chem. Phys., 1980, 90, 1935.
50. S. Ikeda and N. Watanabe, J. Phys. Soc. Jpn., 1987, 56, 565–576.
51. V. E. Antonov, A. I. Beskrovnyy, V. K. Fedotov, A. S. Ivanov, S. S. Khasanov, A. I. Kolesnikov, M. K. Sakharov, I. L. Sashin and M. Tkacz, J. Alloys Compd., 2007, 430, 22–28.
52. R. Khoda-Bakhsh and D. Ross, J. Phys. F: Met. Phys., 1982, 12, 15–24.
53. I. O. Bashkin, A. I. Kolesnikov and E. G. Ponyatovsky, High Pressure Res., 1995, 14, 91.
54. B. Hauer, R. Hempelmann, T. Udovic, J. Rush, E. Jansen, W. Kockelmann, W. Schaeffer and D. Richter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 11115–11124.
55. A. I. Kolesnikov, V. E. Antonov, V. K. Fedotov, G. Grosse, A. S. Ivanov and F. E. Wagner, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 316–317, 158–161.
56. R. C. Brouwer, J. Rector, N. Koeman and R. Griessen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3546–3559.
57. K. Iwase, T. Kamiyama, Y. Nakamura, K. Mori, M. Yonemura, S. Harjo, T. Ishigaki and E. Akiba, Mater. Trans., 2006, 47, 271–274.

---

Footnote

† Electronic supplementary information (ESI) available: Information regarding refinement of diffraction data; table of lattice parameters for V₇₅ from XRD data; unit cells for Bains transformation; effect of temperature on INS spectra for V₂₀ across various hydrogen P_eq; INS spectra of isotopic substitution in V₇₅; unit cells for DFT models. See DOI: 10.1039/c4cp01666a

---