¹ J _CH couplings in Group 14/IVA tetramethyls from the gas-phase NMR and DFT structural study: a search for the best computational protocol

Abstract

Four tetramethyl compounds EMe₄ (E = C, Si, Ge, and Pb) were studied by high-resolution NMR spectroscopy in gaseous and liquid states at 300 K. Extrapolation of experimental vapor-phase C–H J-couplings to a zero-pressure limit permitted determining the ¹J_0,CHs in methyl groups of their nearly isolated molecules. Theoretical predictions of the latter NMR parameters were also performed in a locally dense basis sets/pseudopotential (Sn, Pb) approach, by applying a few DFT methods pre-selected in calculations of other gas-phase molecular properties of all these species and SnMe₄ (bond lengths, C–H stretching IR vibrations). A very good agreement theory vs. experiment was achieved with some computational protocols for all five systems. The trends observed in their geometry and associated coupling constants (¹J_CHs, ²J_HHs) are discussed and rationalized in terms of the substituent-induced rehybridization of the methyl group (treated as a ligand) carbon, by using Bent's rule and the newly proposed, theoretically derived values of the Mulliken electronegativity (χ) of related atoms and groups. All these χ data for the Group-14/IVA entities were under a lot of controversy for a very long time. As a result, the recommended χ values are semi-experimentally confirmed for the first time and only a small correction is suggested for χ(Ge) and χ(GeMe₃).

---

1 Introduction

High-resolution nuclear magnetic resonance (NMR) spectroscopy is undoubtedly the most valuable technique for determining the structure and motion of molecules in all states of aggregation. Among various NMR parameters, magnetic shieldings σ (or related chemical shifts, δ) and scalar spin–spin coupling constants [hereafter referred to as J-couplings or J_XYs] are the most important physical observables. Nowadays, first-principles calculations of the latter NMR data are available and published for many objects.^1–4 But their performance is not as straightforward as predicting the σ data. As viewed from the classical (nonrelativistic) Ramsey theory of J_XYs,⁵ there are four interactions between nuclear spins in molecules that can contribute to an indirect J-coupling, i.e., the Fermi contact (FC), spin–dipole (SD), paramagnetic spin–orbit (PSO), and diamagnetic spin–orbit (DSO) term. Although, in most cases, the FC contribution dominates the isotropic J value, none of these terms can be a priori excluded in any reliable J_XY calculation.^1–4 Moreover, a more advanced relativistic approach is needed for J-couplings embracing heavier elements of the 5th and higher rows of the periodic table.^4,6 Fortunately, the impact of such atoms (e.g., beyond Kr) on J_XYs that do not directly involve these nuclei is small unless a heavy nucleus is located directly in the coupling path.^3,4 Currently, density-functional theory (DFT) computations seem to be the most promising in J evaluations for small and medium-sized molecules, such as, e.g., various organo-derivatives of tin⁷ and lead. It is obvious that all theoretical calculations may be verified only when accurate experimental data are accessible. The most valuable slices of such data come from the gas-phase studies, because results of this kind are not obscured by bulk effects arising from the surrounding medium and molecular effects coming from specific interactions.

In this paper we present experimental results from the vapor-phase measurements of ¹J_CH couplings for a complete set of tetramethyl derivatives of the main Group-14/IVA elements, namely, 2,2-dimethylpropane (neopentane, CMe₄), tetramethylsilane (TMS, SiMe₄), tetramethylgermane (GeMe₄), tetramethyltin (SnMe₄), and tetramethyllead (PbMe₄). Among all these isostructural systems EMe₄, where the central element E = C to Pb, only the Sn derivative was studied in such a way very recently.⁸ All species were analyzed by means of 500 MHz ¹H NMR spectra taken for their gaseous mixtures with krypton (Kr), xenon (Xe), sulfur hexafluoride (SF₆), nitrous oxide (N₂O), and carbon dioxide (CO₂) used as buffer gases. Indirect ¹J_CH couplings, evaluated from the ¹³C satellite lines of related methyl group signals, were then extrapolated to zero-pressure limit.⁹ Such a procedure leads to determining the ¹J₀,_CHs practically free from solvent effects. The latter experimental data were subsequently used for verification of related NMR J^theor_CHs predicted with various locally dense basis sets (LDBS)^10–13/effective core potential (ECP, for Sn and Pb) approaches, by using a few pre-selected DFT-level treatments. All these two-step protocols were a priori tested in computations of other gas-phase properties of these objects EMe₄, such as bond lengths and C–H stretching infrared (IR) vibrations. A general methodology of quite accurate calculations of the geometries and spectroscopic properties of these organoelement compounds was established in this way. Related ¹J_CHs were also measured for neat (pure liquid) samples. A consideration of such NMR data brings up the magnitude of the gas-to-solution effects on the one-bond ¹³C–¹H J-coupling. Finally, the impact of the change in a central E atom on J_XYs in the attached methyl groups (treated as ligands) is discussed in terms of Bent's rule, new theoretical values of the Mulliken electronegativity of atoms (χ_a) or functional groups (χ_g), and distortion of a tetrahedral symmetry around the methyl carbons in all analyzed molecules. These latter efforts also targeted a semi-empirical verification of the newly determined χ values mentioned above, being under considerable controversy for a very long time.

Four crucial and inseparable issues were addressed in this work: (i) a highly reliable representation of a molecular geometry of all compounds EMe₄, (ii) adequate calculations of ¹J_CHs and ²J_HHs operative in these isostructural model systems, (iii) interpretation of the trends in J_XY values observed for the species EMe₄ in terms of changes in the molecular shape and net charge on their methyl carbons (reflected by the recent Mulliken electronegativities of attached groups), and (iv) experimental NMR data-based validation of these electronegativity data for all five Group 14/IVA elements and related EMe₃ substituents. As far as we know, such a comprehensive internally consistent structure- and NMR-oriented investigation of the title systems has not yet been published.

2 Experimental details

2,2-Dimethylpropane (neopentane, Merck-Schuchardt, 98%) from a lecture bottle with a liquefied gas, tetramethylsilane (TMS, Aldrich, ≥99.9%), tetramethylgermane (Aldrich, 98%) and tetramethyllead (Aldrich, 65 wt% solution in xylene) from a glass container, were used without further purification. As reported in detail elsewhere,^{6,8,9b,14–16} gaseous samples were obtained by condensation of the studied compound and pure commercially available solvent gas (Kr, Xe, or SF₆) transferred from the calibration part of our vacuum line. The solute gas, EMe₄, was applied in a small concentration (∼0.005 mol L⁻¹, pressure ∼100 Torr) and was mixed with different quantities of gaseous solvent (from ∼0.2 to ∼1.5 mol L⁻¹).

One-dimensional ¹H NMR spectra were recorded at 300 K on a Varian INOVA FT-NMR spectrometer operating at the 500.6075 MHz proton Larmor frequency. The FID acquisition time was set to 2 s and a spectral width from 400 to 1000 Hz was applied. ¹J_CH couplings were directly evaluated in Hz as differences between the outside ¹³C satellites of methyl group signals. Liquid TMS was always used as an external NMR chemical-shift reference standard.

3 Computational details

All electronic structure ‘gas-phase’ calculations, i.e., for isolated vibration-free objects at 0 K in vacuum, were performed applying the Gaussian 09 suite of programs,¹⁷ by starting with the tetrahedral models of EMe₄ systems. The hybrid B3LYP functional as implemented in the Gaussian code was employed,¹⁸ because its use has been found suitable for a large variety of previous computations, including Sn and Pb containing species.^7,19–21 This exchange–correlation density functional has been one of the more successful tools for predicting different magnetic properties of organic systems.^1,18,22–25 The threshold and convergence parameters were tightened in all geometry optimizations (carried out by taking advantage of the T_d symmetry) and frequency calculations by specifying ‘Int = UltraFine’, ‘SCF = VeryTight’, and ‘Opt = VeryTight’ for numerical integration grids and convergence criteria in Gaussian;¹⁶ the former two keywords were also used in subsequent single-point NMR predictions. Moreover, the five pure d-functions have been mainly applied (5D option), see also Table S1 (ESI†). The corresponding vibrational wavenumbers, ω_is, were computed analytically at the same theory level in a rigid rotor-harmonic oscillator approximation. These data were also applied to verify that all structures, localized as stationary points on pertinent Born–Oppenheimer energy hypersurfaces, represent real global minima (NImag = 0). Finally, a gauge-including atomic orbital (GIAO) formalism²⁶ was employed to ensure the gauge independence of related calculated J_XYs. Several pre-selected functional/basis set combinations were used as DFT protocols at two stages. A locally dense basis sets (LDBS) approach,^10–13 was applied in the vast majority of calculations. In addition, simulations of the impact of nonpolar molecules of CCl₄ and C₆H₆ on the geometry and NMR response properties of species EMe₄ were performed in an improved equilibrium solvation protocol²⁷ of the polarizable continuum model of solvation (IEF-PCM).²⁸

Thus, in the first step of a ground-state-geometry optimization, a centrally situated E atom was best represented by an economical def2-TZVPP²⁹ (hereafter referred to as A) or def2-TZVPPD³⁰ (B) basis set of triple-ζ valence quality, while the small double-ζ Gaussian-type orbitals (GTOs), that is, 6-31G(d,p) (C), 6-31+G(d,p) (D) or 6-31+G(2df,p) (E) bases,¹⁷ were applied to the C and H atoms in the methyl groups. The usage of basis sets C and D for analogous organometallics was found as a fully sufficient approach.^19,20 The aug-cc-pVTZ (C,³¹ Si,³² Ge³³) and aug-cc-pVTZ-PP (Sn and Pb)³⁴ (F) basis sets were also a priori tested for the E atom, but with rather worse results. In these A, B, and F bases an all-electron description concerns C, Si, and Ge—however, the innermost orbitals of Sn and Pb are represented by small-core quasi-relativistic pseudopotentials in an effective core potential (ECP) approximation.⁷ In turn, five other basis sets were exploited for C and H in the second computational step, instead of the Pople style bases mentioned above, namely, IGLO-II (G), IGLO-III (H), aug-cc-pVTZ-J (I), pcJ-2 (J), and pcJ-3 (K). The former two Huzinaga-type atomic basis sets³⁵ modified by Kutzelnigg and coworkers,^36,37 also known as HII and HIII bases,^38–41 have been widely used for calculations of NMR properties;^36–45e.g., the compact basis set G of polarized triple-ζ valence quality consists of [9s5p1d]/(5s4p1d) C and [5s1p]/(3s1p) H functions in the [primitive]/(contracted GTOs) notation.⁴¹ The latter aug-cc-pVTZ-J⁴⁶ and pcJ-n bases²³ were specifically developed for J calculations. As for the E atoms, the following basis sets of quadruple-ζ valence quality were used for the J_CH prediction: def2-QZVPP²⁹ (L), def2-QZVPPD³⁰ (M), (aug-)cc-pVQZ (C,³¹ Si,³² Ge³³) and (aug-)cc-pVQZ-PP (Sn and Pb)³⁴ [N and O (augmented)].

In addition, a few runs were conducted in order to verify the adopted methodology. In one series, the B3LYP functional was applied, at both computational steps, in conjunction with the all-electron basis sets G available for C–Sn. Moreover, owing to some reported²² disadvantages of B3LYP in ¹J_CH calculations, two other density functionals were used, i.e., PBE⁴⁷ and PBE0,⁴⁸ in a PBE/I(C,H),L(E)//PBE0/E(C,H),A(E) approach⁴⁹ similar to that employed for hydrocarbons.²²

On the whole, 15 different basis sets A–O were used in conjunction with related DFT functionals in the two computational steps; for their application in 14 different B3LYP/basis sets combinations tested to obtain the best results, see Table S1 (ESI†). All atomic orbitals inaccessible within Gaussian¹⁷ were downloaded from the EMSL base (ver. 1.2.2)⁵⁰ and applied in their standard forms with optimized general contractions. The only exceptions were G orbitals for the Ge and Sn atoms, created by O. Malkina and V. G. Malkin, taken from an earlier release of the StoBe package.⁵¹ Such Sn basis has been used very recently.⁵² The only results from two most suitable procedures [i.e., B3LYP/G(C,H),L(E)//B3LYP/C(C,H),A(E) and, especially, B3LYP/G(C,H),M(E)//B3LYP/C(C,H),B(E) (henceforth called protocol I and II, respectively)] are discussed in depth, for the sake of brevity. An employment of a basis set J instead of G in both of the above protocols (referred to as approach I-pcJ-2 and II-pcJ-2, respectively) leads to similar or slightly worse results. Generally, the use of IGLO-II (G) in the second step was found the most reliable and efficient protocol of the DFT NMR calculations presented here. The relative computer time required for a single-point in vacuo B3LYP-prediction of J-couplings in Ge(Me)₄ with the use of basis sets G, H, J, and K was determined as 1.0, 1.9, 4.7, and 34.4, respectively.

4 Results and discussion

In the gaseous phase, nuclear spin–spin coupling constants are modified by pairwise interactions between the coexisting molecules and by additional multiple interactions. At a constant temperature, the appropriate equation for a measured one-bond heteronuclear X, Y J-coupling value in a binary mixture of two gases, i.e., a solute gas (A) and buffer gas (B), is expressed as

J_XY = J₀,_XY + J_AA,_XY × ρ_A + J_AB,_XY × ρ_B +… (1)

where J₀,_XY is the J-coupling between the nuclei X and Y at a zero-density limit, whereas couplings J_AA,_XY × ρ_A and J_AB,_XY × ρ_B are solely due to intermolecular effects coming from binary collisions of the A–A and A–B molecules, respectively. Usually, the density of a solute gas A (ρ_A) is kept sufficiently low and so the above relation, eqn (1), is simplified to a linear equation of the form (eqn (2))

J_XY = J₀,_XY + J_AB,_XY × ρ_B (2)

valid in a middle range of pressures,^9a as the term J_AA,_XY × ρ_A can be safely ignored if only micrograms of solute A are present in the gas-phase solution. Usually, this approximation is additionally verified when at least two different gaseous solvents (buffers) are carefully used in the same apparatus and J₀,_XYs obtained by extrapolation remain the same within an experimental error. It is usually assumed that an averaged value of the parameter J₀,_XY derived in this way is very close to its in vacuo value for an isolated solute molecule.

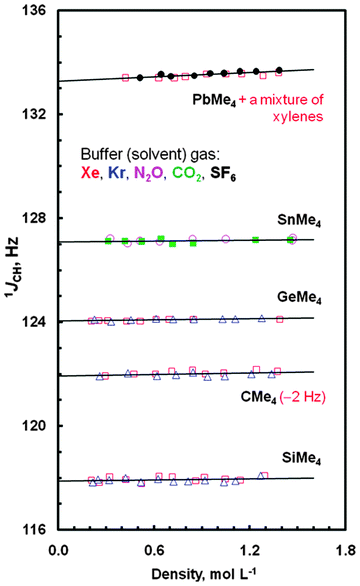
In this work, one-bond J_CH couplings between constituent atoms of the methyl groups (treated as ligands surrounding the centrally situated E atoms) in species EMe₄ were measured with good accuracy. Also their determination was made with very high precision, because the methyl group ¹H NMR signals of all these systems were flanked by sharp lines of more or less symmetrically disposed ¹³C satellites separated by J_CHs. The J₀,_CH values obtained from the extrapolation of such experimental data points to a zero density of the buffer gas are summarized in Table 1, where intermolecular effects on such couplings are also listed. As can be easily seen in Fig. 1, J_CHs are affected by different buffer gases in different ways. The greatest concentration dependence of ¹³C–¹H J-couplings was found for PbMe₄; J_AB,_CH > 200 Hz mL mol⁻¹. Related J_CH values measured for the neat samples of all tetramethyls are also given in Table 1, together with such data reported for liquids or solutions.^53–55 Inspection of this table shows a small difference ΔJ_CH = J_CH(neat) − J_0,CH,av(gas) slowly growing from CMe₄ to PbMe₄, which may be recognized as a modulation of the J₀,_CH coupling—a solvent independent characteristic of the solute molecule—induced by the surrounding medium. Indeed, there is good, R² = 0.9948, expected in view of ref. 24, quasi-linear correlation ΔJ_CH = f[2(ε − 1)/(2ε + 1)] between the J data and the values of the relative permittivity (formerly called dielectric constant, ε) of three normally liquid tetramethyls,⁵⁶ accounted via the reaction field function (Fig. S1, ESI†); unfortunately, the value of ε for PbMe₄ is not available in the literature. The above observation is also in line with the finding that the solvent induced change in the ¹J_CH coupling in a given solvent depends on the J value itself.²⁴

Table 1 Experimental NMR ¹J_CH data for gaseous mixtures, liquids, and solutions of the species EMe₄

Solute gas (A)	Solvent gas (B)	J 0,CH [Hz]	J AB,CH [Hz mL mol^−1]	J 0,CH,av [Hz]	J CH(neat)^c [Hz]	ΔJCH^c^,^d [Hz]	J CH for neat,^e solution in C6H6^f or CCl4^g [Hz]
a Density dependence of J(CH); see eqn (2). b Weighted averages. c This work. d Differences [J(CH)neat − J0(CH)av]. e Ref. 53b. f Ref. 54. g Ref. 55. h Measured for a liquid at vapor pressure of ∼2 atm. i Ref. 8. j For 65 wt% solution in xylene.
CMe4	Kr	123.95(5)	23(59)	123.93(4)	124.06(1)^h	0.13(5)	124.5(1)^e, 124.3^f, 124.0(2)^g
	Xe	123.92(6)	163(63)
SiMe4	Kr	117.88(5)	52(67)	117.88(4)	118.15(2)	0.27(6)	118.2(1)^e, 118.2^f, 117.8(2)^g
	Xe	117.88(7)	99(83)
GeMe4	Kr	124.05(2)	76(30)	124.05(1)	124.40(1)	0.35(2)	124.0(4)^e, 124.4^f, 124.6(2)^g
	Xe	124.05(1)	53(21)
SnMe4^i	CO2	127.12(8)	32(10)	127.13(5)	127.62(2)	0.49(7)	127.2(1)^e, 127.7^f, 127.8(2)^g
	N2O	127.13(7)	64(10)
PbMe4	SF6	133.28(4)	314(42)	133.29(3)	134.07(2)^j	0.78(5)^j	134.0(2)^e, 134.2^f, 134.3(2)^g
	Xe	133.31(5)	205(52)

---

Fig. 1 Dependence of the ¹J_CH data in compounds EMe₄ on the density of solvent gases at 300 K (□ – Xe, △ – Kr, ○ – N₂O, ■ – CO₂, ● – SF₆). The data points for CMe₄ are shown with the (−2 Hz) vertical shift, for clarify.

The foregoing vapor-phase J₀,_CHs and related liquid/solution data were subsequently compared with the high-quality computational results on J_CHs in all five species EMe₄ obtained for the first time. It is well-known that the Fermi-contact (FC) contribution to this type of J-couplings is a dominating term.¹ Furthermore, this contribution is very sensitive to geometry and an applied calculational protocol (basis-set size and inclusion of the electron-correlation, in particular), while the SD, PSO, and DSO terms are less sensitive to these factors.^1,38 Hence, special efforts were made in choosing a suitable DFT treatment. The use of experimental geometries often employed in J calculations on small molecules^39,57 was discarded at the beginning, because our aim was to elaborate an accurate and cheap (from the viewpoint of calculation time) methodology available for other similar organic/organometallic species. Accordingly, only a few pre-selected computational approaches were used here.

4.1 Selection of a two-step computational protocol

In the first stage, reliable equilibrium ground-state geometries of tetramethyls of all members of the periodic table Group 14/IVA were modeled, while in the second estimations of their NMR spectroscopic parameters were made at a higher theory level, on the optimized geometries. The same DFT-level approach had to always be used for all objects, so that such computed J_XYs are comparable and mutually consistent. The presence of heavy atoms in SnMe₄ and PbMe₄ forced the use of quasi-relativistic effective core potentials (ECPs) to describe their innermost orbitals. Recent results²¹ on several diatomics demonstrate that the B3LYP functional combined with a mixture of LANL08d⁵⁸ (as an ECP) for Sn and Pb, and of a triple-ζ 6-311G(d,p) basis set for H and C atoms provides a sensible compromise between accuracy and computational cost. But an application of def2-TZVP²⁹ instead of LANL08d was capable of predicting some molecular properties of these species slightly more accurately.²¹ As a consequence, only a few sufficiently flexible basis sets were tested and used in this work, for which the ECP approximation is fully consistent with an associated all-electron treatment available for the whole carbon group elements, i.e., atoms C through Pb.

It is well known that NMR parameters depend critically on the electron density in the nuclear regions which may not be accurately modeled by the ECPs.¹ However, we were mainly interested in the reliable evaluation of J_XYs within the methyl groups around E atoms. Hence, our approach was fully compatible with the ECP-based studies on NMR properties of organic ligands linked to the metal atoms.⁵⁹ Thus, all J_CHs in species EMe₄ were calculated with Gaussian 09 using the GIAO formalism coupled with B3LYP, as this DFT protocol was found suitable for many similar computations performed previously.^1,18,24

Generally, a locally dense basis sets (LDBS) method^10–13 was applied. However, in the geometry optimization step, this idea was employed in a manner opposite to that of the originally formulated one by Chesnut et al.¹⁰i.e., the E atom was described by the large (locally dense) basis set for best reproducing the E–C bond distances. Indeed, some problems with the choice of basis sets were reported for predicting the E–H bond lengths in Group-14/IVA tetrahydrides.⁶⁰ The LDBS approach was successfully used in the calculations of many molecular properties including NMR chemical shifts¹⁰ and J_XYs.^12,13 Thus, fully balanced basis functions of the same level were employed here for the C and H atoms of methyl groups, that is, double-zeta split-valence Pople's bases and more extended Huzinaga–Kutzelnigg-type IGLO-II (or IGLO-III) atomic orbitals in our first and second step, respectively. The former compact basis set was widely adapted for calculating the NMR response of many different tin-containing species.^38,42,52 It is also known that a subsequent use of IGLO sets at the geometries B3LYP-optimized in conjunction with double-ζ Pople's bases leads to adequate prediction of the experimental J_CH couplings.^41,43–45

Let us consider our results on some interatomic distances in five molecules of EMe₄. All such geometric data obtained by a pre-selected DFT protocol II are collected in Table S2 (ESI†); for the plot, related statistics and Cartesian coordinates of all these species, see Fig. S2 and S8–S10 (ESI†), respectively. An inspection of Table S2 (ESI†) reveals an excellent agreement (R² = 0.9998) with the experimental r_g bond lengths from an electron diffraction analysis of vapor-phase samples,^61–65 while perfect consistency (R² = 0.9999) was found for the carefully examined CMe₄.⁶¹ But such r_g data⁶⁵ for PbMe₄ seem likely to be underestimated, especially for the Pb⋯H distance. Obviously, there is some dissimilarity in the physical meaning of these two quantities, i.e., thermally averaged r_gs measured for vibrating species at room temperature vs. equilibrium r_es computed for motionless objects at 0 K. But their ratio is approximately constant over a wide distance range as these geometric parameters are related by the equation r_e ≅ r_g − 3au²/2,⁶⁶ where a and u are an associated Morse anharmonicity constant and a root-mean-square vibration amplitude for a related atom pair, respectively. A very good agreement (R² = 0.9993) was also achieved between our C–E distances and those B3LYP-optimized within a relativistic elimination of small components (RESC) approach⁶⁷ (ESI,† Table S2). Surprisingly, the greatest difference between such r_e data is found for SiMe₄. Some shortening of the C–E bond lengths was, however, found in a relativistic DFT study on less sterically crowded molecules H–EMe₃ possessing the post-d main-group central atom Ge–Pb.⁶⁸

Very good conformity was also found (R² = 0.9994 and 0.9998 for the protocols I and II, respectively) in comparison of in vacuo computed antisymmetric C–H IR stretchings, ω_as(CH₃), and their vapor-phase experimental counterparts, ν_as(CH₃), determined by the same researchers,⁶⁹ see Table S3 and Fig. S3 (ESI†). Unexpectedly, two such values were stated⁶⁹ for CMe₄ but only one compatible with the other independently reported⁷⁰ values of this fundamental. The present calculations supported these one-value results. So, the problem of a relation between two types of molecular parameters recurs, which is commonly overcome with linear scaling theoretical data, using the equation ν = λ × ω^71,72 or ν = a + b × ω.⁷² A better agreement obtained in the approach II also justifies a modification of the basis set A to B.³⁰ The aforementioned findings confirmed our belief that the computed T_d symmetric geometries of the title tetramethyls are sufficiently accurate, especially those found with protocols I and II. Hence, all subsequent predictions of their NMR spectroscopic properties based on such molecular structures should also be reliable.

4.2 DFT calculation results on ¹J_CHs

At this point, we present our gas- and solution-phase computational results on the total values of J_CHs in five molecules EMe₄ obtained with approaches I and II, including their partitioning into all four Ramsey contributions with dominant FC term participation as expected;^1–4,6,25 see Table 2 and Fig. S4 (as its extended version, ESI†). The J values denoted as CCl₄ or C₆H₆ are from the implicit solvent IEF-PCM^27,28 simulations mimicking solvation of solutes EMe₄ by molecules of carbon tetrachloride or benzene. A typical approach taking into account the scaling theoretical results according to the measured J data was used for assessing the J^theor_XY = f(J^exp_XY) correlations, as in our previous works^44,45,73 and in line with a recent benchmarking study.²⁵ Generally, a fairly good agreement with an experiment was found (R² = 0.9847, 0.9879, 0.9845, 0.9840, 0.9892, and 0.9930 for the approaches I, II, I-pcJ-2, II-pcJ-2, II-C₆H₆, and II-CCl₄, respectively). The only one outlying data point for CMe₄ was at first glance a considerable surprise in consideration of the relative simplicity of J_CH-coupling predictions for hydrocarbons (vide infra). The best linear four-point plot J^theor_CH = f(J_0,CH) for gaseous samples is shown in Fig. 2. In either case, i.e., using IGLO-II vs. IGLO-III or pcJ-2 vs. pcJ-3, the better conformity in the second computational step was found with the basis set of smaller size. This suggests a fortuitous cancellation of calculational errors on the geometry and NMR spectroscopic properties occurring with the use of smaller basis sets.³ On the other hand, a little difference (1.1 Hz, protocol II) between the gas-phase experimental data for CMe₄ and its predicted ¹J_CH value is considerably smaller than e.g., the 6–7 Hz discrepancy obtained at a similar theory level for some strained carbon atoms.⁴¹ An omission of the CMe₄ point gives perfect relationships with R² of 0.9999, 0.9999, 0.9997, 0.9997, 0.9995, and 0.9999, respectively. In this case, a slope of 1.036 and an intercept of −5.34 Hz [or only −0.34 Hz, after the +5Hz arbitral correction for a zero-point vibrational (ZPV) contribution to the C–H ¹J-couplings^22,25,40] was found for the best approach II, close to the ideal values of unity and zero. Hence, one can infer that J₀,_CHs [or J_CH(CCl₄)s] and pertinent J^theor_CHs are perfectly correlated for the four remaining tetramethyls. The use of the recommended PBE/I(C,H),L(E)//PBE0/E(C,H),A(E) protocol²² afforded R² of 0.9702 and 0.9998 after exclusion of CMe₄. Even worse results were found in the all-electron B3LYP/G//B3LYP/G approach available for the E atoms from C to Sn; R² of only 0.9456 and 0.9965 (without CMe₄). In view of the latter finding, the employment of the LDBS approach is fully justified.

Table 2 ¹ J _CH couplings for the species EMe₄ computed^a in vacuum and in CCl₄ solution, with their decomposition into all four Ramsey terms, [Hz]

Compd	Medium	FC	SD	PSO	DSO	Total J^theor
a Protocol II, and II-CCl4 was applied, respectively.
CMe4	Gas	119.70	0.18	0.92	0.73	121.52
	CCl4	119.67	0.18	0.92	0.73	121.50
SiMe4	Gas	114.25	0.29	1.46	0.68	116.68
	CCl4	114.24	0.29	1.46	0.68	116.67
GeMe4	Gas	120.70	0.33	1.13	0.98	123.13
	CCl4	120.67	0.33	1.13	0.98	123.10
SnMe4	Gas	124.15	0.39	1.21	0.63	126.38
	CCl4	124.08	0.39	1.22	0.63	126.31
PbMe4	Gas	130.51	0.44	1.10	0.57	132.62
	CCl4	130.41	0.44	1.11	0.57	132.53

---

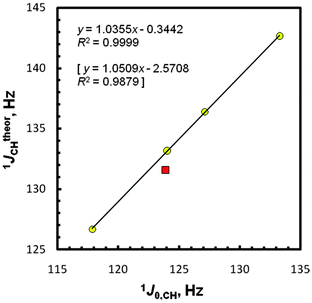Fig. 2 Correlation between (+5 Hz corrected) ¹J_CH computed (protocol II) and extrapolated ¹J_0,CH values.The statistics for the five-point plot with the CMe₄ data (■) are in brackets.

It is worth mentioning that our PCM calculations for CCl₄ solutions failed to reproduce the observed trends, because they predict a slight decrease of J_CHs vs. J₀,_CHs, from −0.00₉ Hz (Si) to −0.09₅ Hz (Pb) in the I-CCl₄ data and from −0.01₂ Hz (Si) to −0.08₈ Hz (Pb) in II-CCl₄ [Table S4 (ESI†)], in contradiction to a small increase accessed experimentally (Table 1); protocol II again turned out to be a better tool, however. A lot more remarkable is the ‘abnormal’ position of the CMe₄ data point on the plot J^theor_CH = f(J_0,CH), see Fig. 2. This observation, apparently not fulfilling a ‘periodic correlation’, was made many years ago for liquid/solution samples of all five tetramethyls,^53–55 but was only tentatively rationalized by (a) the effectiveness of an E–C orbital overlap^53a or (b) the C–H bond rehybridization.⁵⁴ The usage of the latter factor as an only criterion was criticized for molecules with the possible impact of electronegativity.⁷⁴ The most probable explanation of this irregularity will be given afterwards (vide infra).

The next crucial data shown in Table 2 relates to spin–dipole (SD) contributions to the total values of J^theor_CHs in five systems EMe₄. In this instance, our data fulfilled the expected ‘periodic correlation’, at first sight. Thus, the increase of this generally small term was found as one goes down the periodic table from CMe₄ (0.18 Hz) to PbMe₄ (0.44 Hz), regardless of the computation level used. Such finding can be explained by a gradual change in the central E atom which modulates interactions of a nuclear magnetic moment with an electron spin within the methyl groups in question. An increase of the SD term with electronegativity is known for the directly coupled nuclei,^38,57 including ¹J_EHs in tetrahydrides EH₄ (E = C to Sn).³⁸ To gain further information, various correlations were considered, using the newly proposed values of atomic Mulliken electronegativities (χ_as) and group electronegativities (χ_gs) of the EMe₃ substituents attached to the methyl carbons in species EMe₄versus the SD term magnitudes. All these χ_a and χ_g values (Table 3) were theoretically determined by Giju et al.⁶⁸ with the inclusion of relativistic effects. In the cited work, an issue of the controversial electronegativity of the Group 14/IVA elements and, especially, related EMe₃ substituents is discussed in details, but without experimental evidence of the correctness of these novel χ data. The NMR results considered in the present paper afforded such possibility for the first time (see also below). Thus, for the SD term values mentioned above the best least squares regression line (R² = 0.997) was really found with the recent χ_gs, but again after omission of the CMe₄ outlier. The plot with this bounding point is shown in Fig. 3. Obviously, any linear correlation embracing the SD terms of five species EMe₄ does not exist.

Table 3 Selected computed^a or experimental structural, spectroscopic^b and Mulliken electronegativity data^c for all species EMe₄ and their constituent units

Compd	∠ECH (gas) [°]	∠HCH (gas) [°]	∠HCH (CCl4) [°]	^2 J ^theorHH (CCl4) [Hz]	^2 J ^expHH (CCl4)^b [Hz]	χ a for the E atom^c^,^d^,^e [eV]	χ g for the EMe3 group^c^,^e [eV]
a Protocol II, and II-CCl4 was applied, respectively. b Ref. 55. c Ref. 68. d χ a for the H atom = 7.26 eV, ref. 68. e The proposed corrected value is in parenthesis, see the text.
CMe4	111.07	107.83	107.85	−11.93	−12.56	6.73	4.15
SiMe4	111.46	107.41	107.46	−13.47	−14.05	4.96	3.80
GeMe4	110.86	108.05	108.09	−12.36	−12.96	4.71 (∼4.54)	3.85 (∼3.88)
SnMe4	110.51	108.41	108.47	−12.12	−12.37	4.31	3.95
PbMe4	109.48	109.46	109.52	−10.68	−10.94	3.85	4.04

---

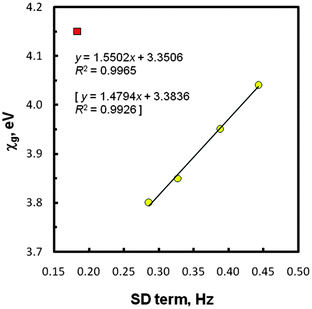Fig. 3 Group electronegativity vs. SD term (protocol II) values; the CMe₄ point (■) was omitted. The statistics with χ_g corrected for GeMe₄ (3.88 eV) are in brackets.

4.3 Discussion of observed trends

As seen in Tables S2 and S3 (ESI†) as well as Fig. S2 and S3 (ESI†), some ‘periodic tendencies’ in the geometry and infrared properties of EMe₄ are clearly shown. Indeed, related interatomic distances and, especially, C–H stretching IR frequencies change monotonically. It should be highlighted that differences in the computed tetrahedral-like geometry around the methyl carbon atoms in these species agree with Bent's model of isovalent hybridization.^75–78 According to this concept, in a molecule with inequivalent R groups, smaller bond angles are formed between the electronegative R groups since a central atom tends to direct the spⁿ-hybridized orbitals of greater p character towards its more electronegative R substituents. Based on the foregoing χ_g data of the groups attached to the methyl carbons (Table 3), it is clear that the fractional s character of a carbon 2s orbital forming the C–H bond in species EMe₄ follows the order Si < Ge < Sn < Pb, exactly the same as is observed from the ¹J_CH data. Thus, an ‘abnormally large’ J-value found for CMe₄ as an outlier (vide supra) is rationalized now to some degree, because such C–H couplings depend mainly on the FC interactions occurring for s electrons.^54,74

In order to discuss the gas-phase J₀,_CH-couplings in terms of χ_as and χ_g values,⁶⁸ two series of these data were considered for the SD terms as previously; the point due to CMe₄ was always found to be a strongly outlying one. In this case, a better four-point regression line plot was found for χ_as; R² = 0.963 (Fig. 4) vs. R² = 0.950 for χ_gs (Fig. S4, ESI†). It was also of interest to see how strong other linear relationships expected for compounds EMe₄ are, i.e., ¹J₀,_CH = f(²J_HH), ∠HCH = f(²J_HH), χ_a = f(²J_HH), and χ_g = f(²J_HH). The ²J_HHs = 6.51 × ²J_DHs (provided that there is no primary isotope effect on the J values) for species E(CH₂D)₄ in CCl₄ solution⁵⁵ and our PCM computed HCH bond angles were used accordingly (Table 3). The corresponding plots reflecting mutually consistent correlations (R² = 0.994, 0.996, 0.973, and 0.957, respectively), again after omission of CMe₄, are shown in Fig. S5–S8 (ESI†). Thus, the 2° opening of the HCH angle on going from Si to Pb causes an increase in the ²J_HH value (from −14.05 to −10.94 Hz)⁵⁵ and an increase in the s character of the C–H carbon spⁿ-hybridized bonding orbitals, as expected. All the above data dealing with Mulliken electronegativities, based on a combination of experimental and DFT results, seem to prove the legitimacy of the newly reported χ_a and χ_g values.⁶⁸ As far as we know, such χ data for this type of Group-14/IVA entities are confirmed for the first time. The analysis of the five plots [Fig. 3 and 4, Fig. S4, S7 and S8 (ESI†)] suggests, however, the need for a decrease of χ_a to ∼4.54 eV and increase of χ_g to ∼3.88 eV for Ge and –GeMe₃, respectively, because there is 0.989 ≤ R² ≤ 0.999 for the above correlations with the use of these corrected χ values.

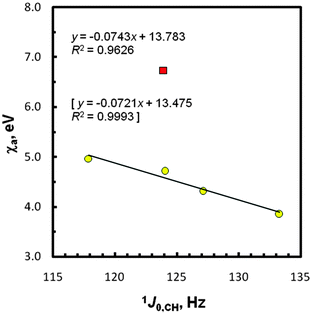Fig. 4 Correlation between the atom electronegativity and ¹J_0,CH data; the CMe₄ point (■) was omitted. The statistics with χ_a corrected for Ge (4.54 eV) are in brackets.

Finally, let us come back to some geometric parameters predicted for molecules EMe₄ (Table 3). It is worth noting that all changes in their ECH and HCH bond angles also follow the trends anticipated from Bent's rule;^75–78 the influence of the simulated ‘solvation’ by the molecules of CCl₄ or C₆H₆ on the geometry is negligible. Indeed, such angles found for CMe₄, being close in magnitude to those for GeMe₄, reproduce the relation J_CH(C) ≤ J_CH(Ge) very well and so excellently explain the ‘abnormal’ position of the CMe₄ data point in Fig. 2. Furthermore, the C–H distance in this object is in between those found for SiMe₄ (the longest length, the greatest p character) and GeMe₄. It seems that the computed geometry around all five methyl carbons in species EMe₄ is mainly dependent on the C–E distance, which forces a large modification of the methyl group shape. Indeed, its strongly ‘stretched’ geometry, most distorted from the regular tetrahedron (∠ECH = 111.46°, ∠HCH = 107.41°) was found for SiMe₄ with the shortest C–E bond length; Table 3 and Table S2 (ESI†). In contrast, a fully relaxed, practically idealized tetrahedral coordination was computed for the methyl carbons in PbMe₄ possessing the longest C–E distance. Hence, the greatest J₀,_CH coupling in this compound is attributable in part to a relatively small difference in χ_gs of its carbon substituents (H, PbMe₃) and to the greatest s character of the C–H bond among all tetramethyls under study.

In view of the foregoing facts, the ‘abnormal’ couplings ¹J_CH and ²J_HH in CMe₄, discussed here via related outlying data points, are attributable to the shortest C–E distance and greatest electronegativity of its E atom (or –EMe₃ group) which characterize this molecule. On the contrary, there is a monotonic increase in the C–E distance for all four remaining tetramethyls (E = Si to Pb), associated with a diminished internal steric congestion around the E atom, and an increase in the pertinent values of χ_a and χ_g on going down a Group 14/IVA. As a result, their ¹J_CH couplings follow the observed Si < Ge < Sn < Pb sequence. The case of the system CMe₄ is significantly different in this respect and that is the most probable origin of the aforesaid ‘anomalies’ in its molecular NMR response properties.

5 Conclusions

This investigation affords experimental one-bond C–H J-couplings in tetramethyl species EMe₄ (E = C to Pb) in vapor and liquid states. Such gas-phase J_0,CHs, obtained as J values extrapolated to a zero-pressure limit, are only slightly different from the J_CHs measured for liquids. The former data show linear dependence on the density of the gaseous solvents used. The present study also demonstrates that current DFT protocols allow for a successful prediction of the experimental NMR J-couplings and other molecular properties as well as for their interpretation in terms of electronic and geometric structure. From the computational results on the title compounds it is concluded that: (1) Reliable geometries of all these molecules can be obtained applying the B3LYP functional in the LDBS approach which consists in the use of a def2-TZVPPD basis set for a central E atom (ECPs for Sn and Pb) and 6-31G(d,p) for the ligand (methyl group) atoms; this procedure can also be proposed for other structurally similar systems. (2) Subsequent LDBS calculations of J_CHs, carried out with an IGLO-II basis sets for the C and H atoms and def2-QZVPPD for the E atoms (protocol II), afforded J values in good agreement with the experiment. (3) The use of pcJ-2 instead of IGLO-II gives a similar or worse result, but at the expense of computation time. (4) All four Ramsey contributions to J_CHs in compounds EMe₄ were computed with the Fermi-contact term being dominant participant. (5) Strong linear correlations were shown between the SD terms, J₀,_CHs, and J_HHs vs. recently reported Mulliken electronegativities (χs) of the E atoms and EMe₃ groups, excluding the CMe₄ case. (6) These χ values were positively verified for the first time, however a small correction of χ_a (Ge) and χ_g for –GeMe₃ is proposed. (7) Predicted alterations in the C–E distance and bond angles around the methyl carbons in species EMe₄ in conjunction with χ_gs of their substituents and Bent's rule permitted an explanation of the trends observed in experimental ¹J_CHs and ²J_HHs in terms of the gradual changes in the s character of carbon spⁿ-hybridized orbitals forming the C–H bonds. (8) The ‘abnormal’ molecular NMR properties of CMe₄ discussed above appear to result from the shortest C–E bond length and the greatest electronegativity of its E atom and EMe₃ group among all tetramethyls under study.

Note added in proof

Some growth of resemblance of the Mulliken electronegativity values to those determined for corresponding Sn(IV) entities,⁶⁸ suggested here for the χ(Ge) and χ(GeMe₃) data, is in line with the recent calculational results⁸⁰ showing that electrophilicity and nucleophilicity values are quite similar for identically substituted germylenes and stannylenes, i.e., the divalent Ge(II) and Sn(II) analogues of carbenes.

Acknowledgements

R.B.N. thanks the Academic Computer Centre CYFRONET (AGH – University of Science and Technology, Kraków, Poland) for access to the Gaussian 09 software (computational grant MNiSW/SGI3700/UŁódzki/057/2010).

References

1. T. Helgaker and M. Pecul, in Spin–Spin Coupling Constants with HF and DFT Methods in Calculation of NMR and EPR Parameters: Theory and Applications, ed. M. Kaupp, M. Bühl and V. G. Malkin, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2004, pp. 101–121.
2. L. B. Krivdin and R. H. Contreras, Annu. Rep. NMR Spectrosc., 2007, 61, 133–245.
3. T. Helgaker, M. Jaszuński and M. Pecul, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 53, 249–268.
4. Y. Yu. Rusakov and L. B. Krivdin, Russ. Chem. Rev. (Engl. Transl.), 2013, 82, 99–130.
5. N. F. Ramsey, Phys. Rev., 1953, 91, 303–307.
6. A. Antušek, D. Kędziera, K. Jackowski, M. Jaszuński and W. Makulski, Chem. Phys., 2008, 352, 320–326.
7. For a recent review see: S. R. Whittleton, R. J. Boyd and T. B. Grindley, in Computational Methods for Organotin Compounds in Tin Chemistry: Fundamentals, Frontiers, and Applications, ed. M. Gielen, A. Davies, K. Pannell and E. Tiekink, J. Wiley & Sons Ltd., Chichester, 2008, pp. 269–283.
8. W. Makulski, J. Mol. Struct., 2012, 1017, 45–50.
9. (a) K. Jackowski, Int. J. Mol. Sci., 2003, 4, 135–142; (b) K. Jackowski and M. Jaszuński, Concept. Magn. Reson. A, 2007, 30, 246–260.
10. D. B. Chesnut and K. D. Moore, J. Comput. Chem., 1989, 10, 648–659.
11. G. A. DiLabio, J. Phys. Chem. A, 1999, 103, 11414–11424 and references therein.
12. M. Sanchez, P. F. Provasi, G. A. Aucar and S. P. A. Sauer, Adv. Quantum Chem., 2005, 48, 161–183.
13. D. M. Reid, R. Kobayashi and M. A. Collins, J. Chem. Theory Comput., 2014, 10, 146–152.
14. M. Wilczek, W. Koźmiński and K. Jackowski, Chem. Phys. Lett., 2002, 358, 263–270.
15. W. Makulski, J. Mol. Struct., 2008, 872, 81–86.
16. W. Makulski, J. Mol. Struct., 2013, 1036, 168–173.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT 06492, USA, 2010, 23-Sep-2011.
18. J. R. Cheeseman, G. W. Truck, T. A. Keith and M. J. Frisch, J. Chem. Phys., 1996, 104, 5497–5509 and references cited therein.
19. S. R. Whittleton, R. J. Boyd and T. B. Grindley, J. Phys. Chem. A, 2006, 110, 5893–5896.
20. C. Gourlaouen, O. Parisel and J.-P. Piquemal, Chem. Phys. Lett., 2009, 469, 38–42.
21. P. Matczak, Comput. Theor. Chem., 2012, 983, 25–30.
22. T. W. Keal, T. Helgaker, P. Sałek and D. J. Tozer, Chem. Phys. Lett., 2006, 425, 163–166.
23. F. Jensen, Theor. Chem. Acc., 2010, 126, 371–382.
24. A. A. Shahkhatuni, A. B. Sahakyan, A. G. Shahkhatuni, S. S. Mamyan and H. A. Panosyan, Chem. Phys. Lett., 2012, 542, 56–61.
25. J. S. Fabián, J. M. García de la Vega, R. Suardíaz, M. Fernández-Oliva, C. Pérez, R. Crespo-Otero and R. H. Contreras, Magn. Reson. Chem., 2013, 51, 775–787.
26. K. Wolinski, J. F. Hilton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 and references therein.
27. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
28. J. Tomasi, B. Mennucci and E. Cancès, THEOCHEM, 1999, 464, 211–226.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
30. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
31. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023.
32. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371.
33. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 1999, 110, 7667–7676.
34. K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112.
35. S. Huzinaga, Approximate Atomic Wave Approximate Atomic Functions. I, II. Technical Report, University of Alberta, Edmonton, AB, Canada, 1971.
36. M. Schindler and W. Kutzelnigg, J. Chem. Phys., 1982, 76, 1919–1933.
37. W. Kutzelnigg, U. Fleischer and M. Schindler, in The IGLO-Method: Ab-initio Calculation and Interpretation of NMR Chemical Shifts and Magnetic Susceptibilities in Deuterium and Shift Calculation NMR – Basic Principles and Progress, ed. P. Diehl, E. Fluck, H. Günther, R. Kosfeld and J. Seelig, Springer-Verlag, Berlin, 1991, vol. 23, pp. 165–262.
38. O. Malkina, D. R. Salahub and V. G. Malkin, J. Chem. Phys., 1996, 105, 8793–8800.
39. M. Pecul, M. Jaszuński and J. Sadlej, Chem. Phys. Lett., 1999, 305, 139–146.
40. T. A. Ruden, O. B. Lutnæs, T. Helgaker and K. Ruud, J. Chem. Phys., 2003, 118, 9572–9581.
41. H. Dodziuk, M. Jaszuński and W. Schilf, Magn. Reson. Chem., 2005, 43, 639–646.
42. R. Vivas-Reyes, F. De Proft, M. Biesemans, R. Willem and P. Geerlings, J. Phys. Chem. A, 2002, 106, 2753–2759.
43. A. Wu, D. Cremer, A. A. Auer and J. Gauss, J. Phys. Chem. A, 2002, 106, 657–667.
44. S. Leśniak, A. Chrostowska, D. Kuc, M. Maciejczyk, S. Khayar, R. B. Nazarski and Ł. Urbaniak, Tetrahedron, 2009, 65, 10581–10589.
45. R. B. Nazarski, B. Pasternak and S. Leśniak, Tetrahedron, 2011, 67, 6901–6916.
46. P. F. Provasi, G. A. Aucar and S. P. A. Sauer, J. Chem. Phys., 2001, 115, 1324–1334.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 . Erratum: Phys. Rev. Lett., 1997, 78, 1396.
48. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169.
49. Throughout this work we follow the standard convention that w/x//y/z denotes a calculation with the method w and base x on a geometry optimized with the method y and base z, which was extended here for specifying the two basis-set partitions separated with comma.
50. EMSL Basis Set Exchange Library. http://https://bse.pnl.gov/bse/portal.
51. Orbital basis set, auxiliary functions and pseudopotentials for StoBe (Stockholm-Berlin version of deMon, a DFT molecule/cluster package). Dec. 2000. Database created by K. Hermann (The Fritz Haber Institute of the Max Planck Society, Berlin). Accessed on 27 June, 2006.
52. P. Matczak, Comput. Theor. Chem., 2013, 1013, 7–14.
53. (a) R. S. Drago and N. A. Matwiyoff, J. Organomet. Chem., 1965, 3, 62–69; (b) A. W. Douglas, J. Chem. Phys., 1966, 45, 3465.
54. F. J. Weigert, M. Winokur and J. D. Roberts, J. Am. Chem. Soc., 1968, 90, 1566–1569 and references therein.
55. M. J. Lacey, C. G. Macdonald, A. Pross, J. S. Shannon and S. Sternhell, Aust. J. Chem., 1970, 23, 1421–1429.
56. S. Geer and R. A. Holroyd, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 5043–5046.
57. J. S. Fabián, E. Díez, J. M. García de la Vega and R. Suardíaz, J. Chem. Phys., 2008, 128, 084108.
58. L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031.
59. M. Kaupp, V. G. Malkin and O. L. Malkina, in NMR of Transition Metal Compounds in Encyclopedia of Computational Chemistry, ed. P. v. R. Schleyer, J. Wiley & Sons Ltd., Chichester, 1998, vol. 3, pp. 1857–1866.
60. K. G. Dyall, P. R. Taylor, K. Faegri, Jr. and H. Partridge, J. Chem. Phys., 1991, 95, 2583–2594.
61. L. S. Bartell and W. F. Bradford, J. Mol. Struct., 1977, 37, 113–126.
62. A. R. Campanelli, F. Ramondo, A. Domenicano and I. Hargittai, Struct. Chem., 2000, 11, 155–160.
63. E. Csákvári, B. Rozsondai and I. Hargittai, J. Mol. Struct., 1991, 245, 349–355.
64. M. Nagashima, H. Fuji and M. Kimura, Bull. Chem. Soc. Jpn., 1973, 46, 3708–3711.
65. T. Oyamada, T. Iijima and M. Kimura, Bull. Chem. Soc. Jpn., 1971, 44, 2638–2642.
66. B. Beagley, J. J. Monaghan and T. G. Hewitt, J. Mol. Struct., 1971, 8, 401–411.
67. W. Lie, D. G. Fedorov and K. Hirao, J. Phys. Chem. A, 2002, 106, 7057–7061.
68. K. T. Giju, F. De Proft and P. Geerlings, J. Phys. Chem. A, 2005, 109, 2925–2936.
69. H. Bürger and S. Biedermann, Spectrochim. Acta, Part A, 1972, 28, 2283–2286.
70. K. Shimizu and H. Murata, Bull. Chem. Soc. Jpn., 1957, 30, 487–491.
71. I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887.
72. Z. A. Fekete, E. A. Hoffmann, T. Körtvélyesi and B. Penke, Mol. Phys., 2007, 105, 2597–2605.
73. R. B. Nazarski, Phosphorus, Sulfur, and Silicon, 2009, 184, 1036–1046.
74. D. M. Grant and W. M. Litchman, J. Am. Chem. Soc., 1965, 87, 3994–3995.
75. H. A. Bent, Chem. Rev., 1961, 61, 275–311.
76. J. E. Huheey, Inorg. Chem., 1981, 20, 4033–4035.
77. A. E. Reed and P. v. R. Schleyer, J. Am. Chem. Soc., 1990, 112, 1434–1445.
78. Glossary of Terms Used in Theoretical Organic Chemistry (IUPAC Recommendations 1999) prepared for publication by V. I. Minkin, Pure Appl. Chem., 1999, 71, 1919–1981.
79. E. A. Skorupska, R. B. Nazarski, M. Ciechańska, A. Jóźwiak and A. Kłys, Tetrahedron, 2013, 69, 8147–8154.
80. L. Broeckaert, P. Geerlings, A. Růžička, R. Willem and F. De Proft, Organometallics, 2012, 31, 1605–1617.

---

Footnotes

† Electronic supplementary information (ESI) available: Tables S1–S9 and Fig. S1–S8. See DOI: 10.1039/c4cp01596g

‡ Physical image vs. molecular structure relation, Part 18. For Part 17, see ref. 79.

---