Site-selective adsorption of phthalocyanine on h-BN/Rh(111) nanomesh

Abstract

Experiment and computer simulations were conducted in order to study the adsorption of the phthalocyanine molecules H₂Pc and CuPc on the h-BN/Rh(111) nanomesh. We combine STM investigations with the exploration of the potential energy surface as resulting from density functional theory calculations. Both approaches indicate a pronounced adsorption selectivity in the so called pore regions of the h-BN nanomesh, whereas the adsorption energy landscape in the pore turns out to be very shallow. This is seen by the inability to image the molecule stably at 77 K by scanning tunneling microscopy. Understanding the nature of the binding by rationalizing the site-selectivity and the mobility of the molecules is quite a challenge for both experiment and theory. In particular, we observe that the choice of the functional in the DFT description is crucial to be able to discriminate among adsorption sites that are very close in energy and to resolve low energy barriers. Our study reveals how the shape of the corrugated h-BN layer is the dominant factor that determines the subtle features of the potential energy surface for the adsorption of phthalocyanine.

---

Introduction

Aromatic macrocycles based on the porphyrin system are promising candidates for applications in a variety of fields like solar cells and fuel cells devices, and more general in the design of materials for nanotechnologies.^1–3 Thanks to their thermal stability and semiconducting properties, metal-substituted phthalocyanines (MPc) molecules have been already used for various technical applications like gas sensors, electronic, and optical devices, including dye sensitized solar cell.^4–7 Many previous studies have been carried out for a better understanding of the interaction of metal free phthalocyanine (H₂Pc) and MPc molecules with the supporting surfaces and with other co-adsorbed molecules.^2,8–14 It has been observed that on anisotropic metallic surface, like (110) surfaces of fcc lattices, MPc molecules tend to adsorb with one of their molecular axes along the close-packed direction.¹⁵ Density functional theory (DFT) calculations¹⁶ of CoPc adsorbed on Cu(111) surface also indicate that the two isoindole-like units perpendicular to the close-packed direction of the metal substrate interact stronger with the Cu(111) surface compared to the other two isoindole-like units.

Exploiting the intrinsic electronic, optic and spintronic properties of novel low-dimensional molecular materials requires that the electronic coupling with the supporting substrate is kept as low as possible. In this context, metal-supported ultra thin insulating films have attracted great interest as substrates to study the intrinsic properties of organic and inorganic nanostructures.^17–21 A single layer of hexagonal boron nitride (h-BN) on metal single crystal surfaces is a particularly versatile substrate system, where the choice of the metal can tune the structural and electronic properties of the h-BN layer.^22–24,27 Site specific adsorption and characterization of electronically decoupled nanostructures on such substrates have been already achieved by adsorbing molecules,^28,34,60 atoms and clusters.^25,26,61

On Rh(111), a highly corrugated nanomesh (NM) is formed, consisting of regions with strong interaction, so-called pores, separated by suspended wire regions, where the h-BN–Rh(111) interaction is weaker. Consequently, the NM structure is the superstructure given by the 0.25 nm h-BN lattice and the network of pores with a lattice constant of 3.2 nm.^27–30 The theoretical studies on the NM have in general reported good agreement with experiment, providing that a large enough system is employed to represent the superstructure, which consists of 13 × 13 h-BN units on 12 × 12 Rh(111) units, and that a proper DFT setup is used, including corrections for the dispersion interactions.^23,31–34 In particular, scanning tunnelling microscopy (STM) simulations within the Tersoff–Hamann approximation,³⁵ employing the revPBE functional³⁶ and the Grimme D3 correction,³⁷ reproduce the topography with a corrugation of about 0.8 Å and a corresponding modulation of the electrostatic potential of about 0.5 eV, in good agreement with experiment.³⁸ Though, shape and size of the pore of the simulated STM topography present some differences if compared to the high atomic resolution STM images. This remark is noteworthy, as the size of the pore and the property of the rim are expected to play an important role on preferred site, orientation, and mobility of adsorbates.

For the h-BN/Rh(111) NM it has been shown by Xe adsorption/desorption experiments that the preferential adsorption in the pore regions is due to the electrostatic surface potential modulation and modifications of the Rh–Xe interaction between wires and pores.^25,26 The detailed origin of the pore specific adsorption of organic molecules, instead, has not yet been explored. In the present work, we investigate the adsorption of the H₂Pc and CuPc molecules, which, with a molecular diameter of about 1.5 nm, fit well in the 2 nm-pore of the NM. We start with a new assessment of the NM structure, looking at the detailed features at the rim and the corresponding shape of the pore. To this purpose, we show high resolution imaging of the sample and compare with DFT calculations performed with different functionals. The central part of this study reports results on the adsorption properties of H₂Pc and CuPc on the NM. The pronounced adsorption selectivity in the pore regions and the substrate effects on the molecular properties are discussed. Combining experiment and theory, a picture of the potential energy surface implying the observed orientation distribution and the mobility of the adsorbate is proposed.

Methods

Experimental method

The experiments have been carried out in a commercial low-temperature STM (OMICRON LT-STM) with a base pressure in the 5 × 10⁻¹¹ mbar range. STM experiments are performed either at liquid nitrogen (LN2) temperature of 77 K or liquid Helium (LHe) temperature of 5 K. The Rh(111) single crystal has been prepared by repeated cycles of argon ion sputtering and annealing. Initial preparation of the crystal consisted of repeated sputtering and annealing cycles with the following parameters: Ion energy of 1 keV, sputter time of 1–1.5 h and annealing to 810 °C for 1–1.5 h. At later stages, sputtering time and annealing times are reduced to 30 min, with the sputtering energy lowered to 500 eV for the last preparation step.

The h-BN monolayer is grown by thermal decomposition of borazine (B₃N₃H₆) on the hot Rh(111) surface. The growth uses standard procedures with typical parameters: Rh(111) temperature of 810 °C, borazine partial pressure of 1 × 10⁻⁷ mbar and growth time of 12 min. (i.e., 54 Langmuir of borazine exposure).

The H₂Pc and CuPc molecules were purchased from SIGMA-ALDRICH in sublimation grade (99%). Both molecules were thermally evaporated from quartz crucibles using a commercial Knudsen-type evaporator (KENTAX). Prior to deposition the evaporator has been carefully out-gassed and the evaporation rate has been calibrated using a quartz-crystal microbalance (QCM). Typical deposition rates are around 3–5 Å min⁻¹ for a source temperature of 275–300 °C. It needs to be stressed that the thickness stated here is dependent on the setting of the QCM electronics and cannot be taken directly as a real thickness of the molecular layer. The evaporation has been carried out within some tens of seconds for a sub-monolayer coverage onto the substrate kept at room temperature.

Theoretical method

DFT^39,40 calculations are performed with the CP2K package⁴¹ using a hybrid Gaussian and plane wave scheme.^42,43 The model for the NM is constituted of a 13 × 13 h-BN layer and a four-layer 12 × 12 Rh slab, which corresponds to the unit cell. For the adsorbate–substrate systems, the H₂Pc molecule is added above the h-BN monolayer, for a total of 972 atoms. Periodic boundary conditions are always applied. The Goedecker–Teter–Hutter pseudopotentials^44–46 are employed for all atomic kinds to represent the atomic cores. In particular, 9 valence electrons are explicitly considered for Rh, 3 for B, 5 for N, 4 for C. Molopt basis set⁴⁷ are employed for all the elements. A short range [2s1p2d] basis set for Rh and double zeta short range basis sets with polarization are employed otherwise. The choice of pseudopotentials and basis set has been assessed in previous works.^23,38,48 Regarding the choice of the exchange–correlation functional, we observe that equivalent qualitative pictures are obtained with different models. However, some differences at the quantitative level may arise and become important to distinguish among states very close in energy. In our previous DFT studies of the NM,^23,31,38 we used revPBE-D2/D3, a revised version⁴⁹ of the Perdew, Burke, and Ernzerhof⁵⁰ (PBE) GGA functional supplemented by the D2⁵¹ or D3³⁷ version of Grimme's dispersion correction. In the present work, we reconsider the details of the pore shape and size and how these are related to phenomena (adsorption) for which the dispersion interactions are expected to play an important role. We report the results for two other functionals that account for the dispersion interactions including a nonlocal term, the vdW-DF⁵² and the PBE-rVV10.^53,54 The vdW-DF functional consists of a semilocal component based on revPBE for the exchange part and the local density approximation for the correlation. The dispersion term consists of a double integral of the density, which makes it nonlocal. The PBE-rVV10 functional is composed of the PBE⁵⁰ functional and the nonlocal dispersion term rVV10⁵⁴ (rVV10 is a revised version of the functional VV10 of Vydrov and Van Voorhis⁵³). This type of nonlocal van der Waals functionals are available in the CP2K package.^55,56 Their implementation is based on the efficient method proposed by Román-Pérez and Soler.⁵⁷ In the case of h-BN/Rh(111), the computational cost of such a nonlocal van der Waals functional is about 25% more than for standard GGAs.

The simulated STM images are generated according to the Tersoff–Hamann approximation.^35,58 More details can be found in ref. 38.

Results and discussions

h-BN/Rh(111): the shape of the pore

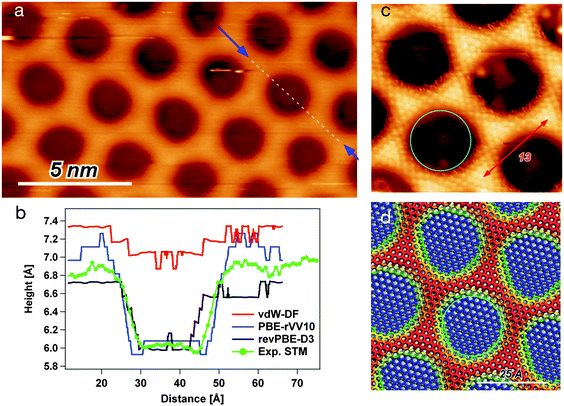
In order to achieve high atomic resolution imaging of the NM, it is necessary to decrease the sample bias to a few mV and to increase the setpoint current. This results in a close distance between tip and sample and consequently a higher resolution. The drawback is that also the interaction with the sample is increased, which can lead to distortions in the STM image, especially on the wire regions (popping of the mesh). On the other hand, high negative biases are expected to deliver the most reliable topographic information for the h-BN/Rh(111) NM. Fig. 1(a) shows a STM image taken at a bias potential of −3 V and a constant current of 2 nA. The darker circles correspond to pore regions, while the brighter areas constitute the wire. In order to quantify the corrugation of the iso-current surface and the pore region size, the height profile has been measured along the [21] direction of the h-BN (i.e. [−211] direction with regard to the Rh(111) substrate), as indicated by the dashed line running over one pore. The recorded profile is reported in panel (b) of the same figure (green line).

Fig. 1 (a) STM image at −3 V bias and 2 nA. The arrows indicate the path of the height profile. (b) Comparison between experimental height profile (green, along the [21] direction) and DFT results, where the black line is obtained for revPBE-D3, the red line for vdW-DF, and the blue line for PBE-rVV10. The experimental data have been off-set to be consistent with the pore level of the PBE-rVV10 and revPBE-D3 profiles, which present same pore's height. The zero height of the calculated structure is set at the position of the topmost Rh layer of the Rh(111) slab. (c) Experimental STM image (−1.16 V/32 pA). (d) Height color map of the B and N atoms (d_z), measured relative to the average height of the topmost Rh layer in the h-BN/Rh(111) NM model obtained with the PBE-rVV10 functional. Blue d_z < 2.4 (pore), red d_z > 3.7 (wire), green to orange in between (rim).

Due to the differences in the electronic structure of pore and wire, the interaction with adsorbates changes significantly going from one to the other. Thereby, the pore might be defined as the region where the interactions of the substrate with an adsorbate are stronger. The STM image shown in Fig. 1(c) has been obtained in the presence of an adsorbate. This seems to be under the tip on the wire regions, allowing to image with atomic resolution at very mild tunneling parameters, i.e., high tunneling resistance and low tip–sample interaction forces. On the contrary, the adsorbate is flicked off on the pore regions, as it is indicated by the noisy borders of the pore. Unfortunately, the nature of the adsorbate that was responsible for this imaging mode is not known. Nevertheless, we obtain an interaction image, where the pore regions are the ones where the adsorbate no longer stays between tip and sample. The red arrow shows the distance of 13 h-BN unit cells counted along the wire atoms, thus nicely verifying the (13 × 13)/(12 × 12) superstructure of the h-BN/Rh(111) NM. The turquoise circle shows the 21.5 Å pore diameter. It can be seen that the interaction pore diameter seems to be even larger of the order of 25 Å.

The revPBE-D3 results are in many respects in nice agreement with experiment.²³ Within this model, the flat h-BN area that we identify with the pore, laying at less than 2.5 Å from the Rh surface, exclusively involves those BN pairs with N atom at Rh-top site, or very close to it. Here, the BN bond is elongated up to 1.48 Å. This suggests that the interaction with the substrate inducing the BN stretching is effective only with an almost perfect (N-top, B-fcc) registry. The resulting shape of the pore is an elongated hexagon (not circular) covering less than 30% of the whole NM unit cell. The amount of the allowed distortion and the strength of the interaction with the substrate are determined by the balance between the semi-local XC term and the attractive dispersion correction. By applying other exchange and correlation functionals including a nonlocal dispersion term, we indeed found that the shape of the pore strongly depends on the combination of semilocal contribution and dispersion correction.

Table 1 reports some energetic and structural parameters that characterize the NM model as optimized with the three considered functionals, i.e., revPBE-D3, PBE-rVV10, and vdW-DF. A striking difference is observed in the vdW-DF structure. The minimum height of h-BN over the metal, in the pore region, is about 3.3 Å, while the wire is at about 4 Å. Hence, the structural corrugation is smaller than 1 Å. The resulting almost flat and freestanding h-BN suggests a bad balance between the rigidity of BN bonds and the strength of the interaction with the metal. The corrugation profiles along the [21] direction are reported in the ESI.† From the electronic charge distribution of the optimized structure, the STM image for a bias potential of −1 eV has been simulated, and the profile of the iso-current surface along the diagonal is reported in red in Fig. 1(b). The direct comparison to the experimental curve shows that the simulated STM topography is not in good agreement. The reduced effect of the interaction with the metal is also evident from the small and negative distortion energy of the layer, E^corr_BN. The negative sign is explained by the fact that the lattice constant for the adsorbed h-BN is 2.481 Å, i.e., smaller than the equilibrium lattice constant 2.51 Å. Hence, the overall bond length for the flat layer is contracted, and the modulation of the height allows a relaxation of the BN bonds. The actual interaction energy between h-BN and substrate is calculated as

E_int = E_h-BN/Rh − E_h-BN − E_Rh,

where the subsystems energies, E_h-BN and E_Rh, are obtained at the fixed geometries of the full system.

Table 1 E ^corr_BN [in meV/(BN pair)]: corrugation energy computed as difference between corrugated and flat 13 × 13 h-BN at the lattice constant of the NM. E_int (in eV): interaction energy between Rh and h-BN. Δz^max_Rh, Δz^max_B, and Δz^max_N (in Å): corrugation in the z-coordinate of the topmost Rh layer, the B sublattice, and the N sublattice, respectively. N^pore_N and N^wire_N: number of N atoms belonging to pore and wire, respectively

	revPBE-D3	PBE-rVV10	vdW-DF
E ^corrBN	29	60	−3
E int	−51	−50	−17
Δz^maxRh	0.09	0.16	0.08
Δz^maxB	1.17	2.33	0.89
Δz^maxN	1.06	2.28	0.90
N ^poreN	48 (28%)	77 (45%)	27 (16%)
N ^wireN	97 (57%)	49 (29%)	81 (48%)

---

The other two models give binding strengths that significantly overcome the energy cost for the corrugation of the layer and the elongation of the BN bonds within the pore. Where the registry is (N-top, B-fcc), the h-BN layer lays at about 2.2 Å from the Rh surface. This happens only for registries very close to (N-top, B-fcc) in the case of revPBE-D3. With PBE-rVV10, instead, a larger number of BN pairs, including pairs that are not precisely in optimal registry, are found to lay close to the metal and exhibit a stretched bond length (up to 1.48 Å). As parameter to measure the size of the pore, we count the number of N (or B) atoms below the average height of the h-BN layer. For revPBE-D3, atoms belong to pore if below 2.5 and to wire if above 3 Å. For PBE-rVV10, the height criteria are set at 2.4 and 3.7 Å, while for vdW-DF are at 3.3 and 3.8 Å, respectively. It turns out that the flat pore area obtained with PBE-rVV10 is the largest. The rim is still formed by about three atomic rows. However, since more BN pairs are elongated, the remaining part of the layer is pushed higher and it is not anymore a flat plateau, but a curved surface. It finally amounts to a pore to wire ratio of 1.6, closer to the experimental estimate. These differences translate into a larger distortion energy of the h-BN in the PBE-rVV10 model. Nonetheless, the interaction energy, which is dominated by the binding of the BN pairs of the pore to the Rh atoms at the surface, is almost the same as the one computed for the revPBE-D3 model. The inspection of the electronic structure through the projected density of states (PDOS) confirms the similarity between the PBE-rVV10 and the revPBE-D3 models in the strongly interacting region. In both cases, we observe the characteristic splitting of the N-p band of the PDOS at about 6 eV below the Fermi energy (PDOS are reported in ESI†).

For a more direct comparison to experiment, we computed the STM topography with a bias potential of −1 eV. The resulting contrast images are reported in the ESI,† while the profiles along the NM unit cell diagonal are shown in Fig. 1(b). The depth of the pore estimated as the mean wire height minus the mean pore depth, results in 0.88 Å over the experimental profile, 0.37 Å for the vdW-DF model, 0.66 Å for the revPBE-D3 model, and 1.05 Å for the PBE-rVV10 model. The (d) panel of Fig. 1 reports the top view of the NM structure obtained with the PBE-rVV10 model, where the color map represents the height of the B and N atoms above the metal. The overdrawn turquoise circle has the same diameter as the one marking the pore on the experimental topography ((c) panel) and it fits quite nicely onto the optimized model. In summary, the PBE-rVV10 functional seems to reproduce rather accurately the h-BN/Rh(111) NM. In particular, the agreement with experiment on width and depth of the pore regions seems to be better than with other tested functionals. On the other hand, the electronic structure properties agree with the UPS measurements of Corso et al.²⁷ at least as good as verified from the revPBE-D3 model.

H₂Pc and CuPc on h-BN/Rh(111): adsorption geometry

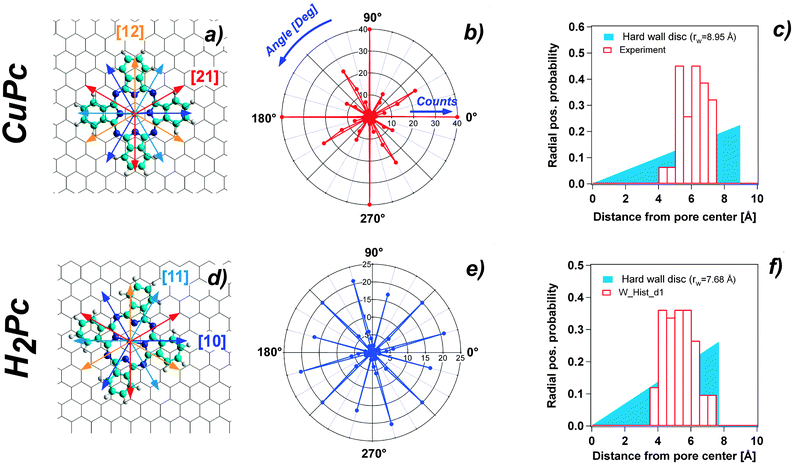
The adsorption properties of H₂Pc and CuPc in sub monolayer coverage have been investigated by STM. We observe for both molecules the pronounced adsorption selectivity in the pore regions. At 77 K the molecules cannot be imaged in a stable manner. There are clear indications that the molecules can move among the stable adsorption sites within one pore. However, they are never found on the wire regions and can also not be pushed there by the STM tip. Fig. 2(a) and (c) show 5 K STM images of H₂Pc and CuPc adsorbed on the NM. At this temperature, the molecules are immobile and it is possible to perform a statistical analysis of the specific orientation and position. All molecules are adsorbed in the NM pores, with a characteristic tendency to be positioned off the pore center. However, for both molecules a few orientations turn out to be accessible. Since the h-BN lattice shows a 3-fold symmetry, the [10] and [11] directions are inequivalent. In STM it is not possible to distinguish these directions (as well as the [21] and [12]), therefore they will be treated as equivalent. We define two possible high-symmetry orientations for CuPc and H₂Pc with respect to the honeycomb lattice of h-BN, considering the molecules as four-fold symmetric, although they are two-fold symmetric. The two observed non-equivalent orientations are indicated in Fig. 2 by arrows of two different colors. The yellow arrow corresponds to the orientation where the molecule has one leg along the [10] direction and the other leg necessarily along the [12] direction. The three configurations obtained by 30° rotation correspond to equivalent orientations with respect to the substrate lattice. We call this the A orientation. The cyan arrow corresponds to the orientation of the molecule rotated by 15° as compared to the previous one. Also in this case, three possible equivalent orientations are obtained rotating by 30°. In the following, this is called orientation B.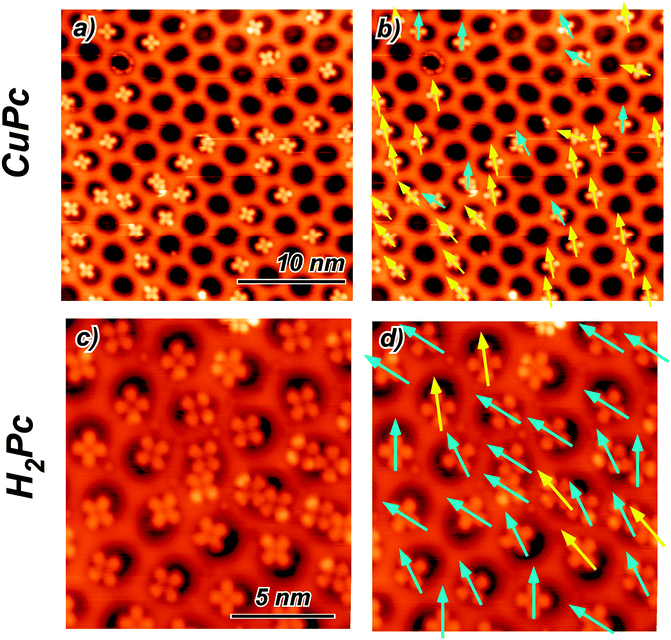

Fig. 2 (a) Constant current STM image of CuPc at 5 K adsorbed on the h-BN NM (U_S = −0.525 V; I_C = 18 pA). (b) Same image as in (a) with the arrows indicating the orientation direction of the molecules. (c) Constant current STM image of H₂Pc at 5 K adsorbed on the h-BN NM (U_S = −0.580 V; I_C = 26 pA). (d) Same image as in (b) with the arrows indicating the molecule orientation. The color of the arrows in (b) and (d) classifies the two predominant high symmetry orientations (see text and Fig. 3(a) and (d)).

All imaged molecules can be assigned to be either in the A or in the B configuration. The ratio for the CuPc case is 31 : 9 (yellow 77% : cyan 23%). From a larger sample of angles, a similar picture emerges with a ratio 111 : 17 (yellow 86% : cyan 14%). According to the Boltzmann factor this ratio at 5 K would correspond to an energy difference in the order of 1 meV. This estimation needs to be taken with very much care, as it neglects the kinetics of the cooling down process. However, it is an indication for a rather small energy difference between the A and the B orientation. Also the H₂Pc molecules can adopt both orientations. The predominant orientation in this case is B, as shown in Fig. 2(d).

Ball and stick schemes that exemplify the two orientations with respect to the h-BN lattice are displayed in panel (a) and (d) of Fig. 3. The polar plots show the statistical analysis of the orientation distribution. The data represent the histogram of the molecule orientations measured from 0° to 90°, with a bin width of 3°, and 4 times rotated by 90° due to the symmetry of the molecules.

Fig. 3 (a) Model structure on the Pc molecule (central Cu respectively H₂ not shown) oriented in the [21]-direction of the h-BN lattice denoted as orientation A. (b) Polar-plot of the orientation occurrence of CuPc on the NM at 5 K. (c) Probability distribution of the radial off-center position of the CuPc in the NM pores at 5 K. The solid shaded wedge shows the random distribution in a circular hard wall potential. (d) Same as (a) but showing the B orientation which is 15° rotated off the [21]-direction. (e) Same as (b) for H₂Pc at 5 K. (f) Same as (c) for H₂Pc at 5 K.

Another clear indication from the recorded STM images is that both molecules adsorb in a preferred off-center site, irrespective of their orientation. The lobe of the molecule closer to the rim appears typically brighter than the other three, which are, instead, accommodated inside the pore. We define the off-centering as the distance of the molecule center to the pore center. The statistical distribution evaluated for CuPc gives an average off-center distance of 5.97 Å with a standard deviation of 0.78 Å (see Fig. 3 panel (c)). Also in the case of H₂Pc the pore specific adsorption with preferential off-center position is corroborated. The average distance of the distribution is 5.12 Å, with a standard deviation equal to 0.9 Å (Fig. 3 panel (f)). The statistical significance of the off-center position is evidenced by the comparison to the random distribution case in a circular hard wall potential shown as solid colored wedge in Fig. 3(c) and (f). The radius of the disc is adapted in both cases to yield the same average radial position as the experimentally measured one.

Adsorption energy. From the experimental side we can make no real quantitative statements on the adsorption strength or the energy barriers between different adsorption sites. The quantification of effects like orientation and off-centering, as well as better understanding of the interactions leading to adsorption site selectivity, are provided by DFT-based electronic structure calculations. We carried out several structure optimizations of H₂Pc adsorbed at the NM, comparing different possible adsorption sites. We selected H₂Pc as model system, since it has a simpler electronic structure than the spin polarized CuPc. We expect that the results obtained for H₂Pc are transferable to the case of CuPc. The first set of simulations are basic structure optimizations starting from different initial position of the molecule. A complete exploration of all sites and orientations is not feasible, due to the excessive computational costs (more details in ESI†). We selected a few starting configurations based on the experimental indications. The results reported in the following are obtained for six different starting configurations: H₂Pc centered at the pore center with both orientations A and B (poreA and poreB), one configuration with the molecule center over the wire (wire), and three off-center configurations. The off-center positions are generated by centering one isoindole group at the pore center and then choosing the molecule orientation. Two are with the legs of the molecule oriented along [21] and [10], offA1 and offA2, rotated by 60° one with respect to the other. The last one is generated from offA1 by rotating by 15°, offB1 (Fig. 4).

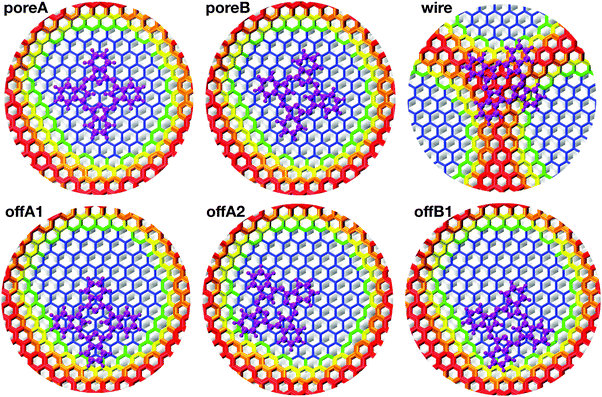Fig. 4 Top view of Pc adsorbed on the NM at the six different adsorption sites. The color map is assigned according to the height over the Rh(111) slab. The atoms of the h-BN lattice are colored according to the height color map described in the caption of Fig. 1(d). The atoms of H₂Pc are all magenta.

All structure optimizations converge to configurations that are relatively close to the initial geometry, suggesting that the potential energy landscape is shallow and offers a multitude of possible stable adsorption sites. The resulting adsorption energies reported in Table 2 agree pretty well with the experimental observation. The adsorption energy E_ads is computed as

E_ads = E_pc/NM − E^opt_pc − E^opt_NM, (1)

where E_pc/NM is the energy of the optimized complex, E^opt_pc of the molecule optimized in gas phase, and E^opt_NM of the optimized bare NM. More negative values indicate stronger binding. The adsorption over the wire turns out to be the least stable configuration, followed by the two pore centered sites. The most stable configurations are the off-center ones, and the lowest energy is assigned to the offB1 site. Also reported in the table are the two contributions to the adsorption energy, the neat DFT term E_DFT and the dispersion correction as computed from the nonlocal term of the PBE-rVV10 functional, E_dis. For all the structures, the binding strength is dominated by the dispersion contribution, whereas the neat DFT term at this distance is positive, i.e. repulsive. The three off-center configurations are characterized by the largest attraction energy coming from the dispersion term. Among them, the offA2 turns out to have also the largest repulsive DFT contribution, thus resulting less stable than offA1 and offB1. This can be explained by the shorter distances between molecule and h-BN in the vicinity of the rim for the off-center molecules. E_nm and E_pc are the distortion energy of the NM and of H₂Pc, respectively. These are computed by comparing the energy of each subsystem in the geometry of the complex to the energy of its optimized geometry. In all cases, the geometrical change of both subsystems is rather limited, confirming that the interaction is mainly attributed to dispersion forces and polarization of the electronic charge. The molecule remains flat inside the pore, as indicated by the standard deviation of the height σ_hC from its average . 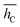On the wire, the lobes bend along the curvature of the rim, resulting in a σ_hC of 0.44 Å and a larger E_pc of 0.056 eV. The structure of the off-center molecule has only one isoindole ring bending upward, along the rim curvature. This deviation from planarity results in a E_pc between 0.02 and 0.03 eV and it is in agreement with the experimental STM images, which often show a brighter lobe of the molecule close to the rim.

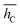Table 2 Pc adsorption at the NM with PBE-rVV10: total adsorption energy E_ads and the two separated contributions, DFT and dispersion. Distortion energies of NM and Pc, E_nm and E_pc. Average height of C atoms over Rh(111), , and its std. deviation σ_hC. Energies are in eV, average distance and deviation in Å

Adsorption site	poreA	poreB	wire	offA1	offA2	offB1
E ads	−4.065	−3.91	−2.837	−4.246	−4.234	−4.258
E DFT	0.343	0.315	0.646	0.389	0.708	0.411
E dis	−4.408	−4.282	−3.483	−4.635	−4.938	−4.669
E nm	0.041	0.041	0.089	0.050	0.021	0.073
E pc	0.011	0.010	0.059	0.024	0.018	0.030
	5.47	5.51	7.13	5.50	5.49	5.52
σ h C	0.03	0.01	0.44	0.12	0.09	0.14

---

We have studied the same six configurations also using the revPBE-D3 model, where the pore turns out to be smaller in size. All 6 structures turn out to be stable, and preference for a in-pore adsorption is confirmed also in this case. However, the hierarchy between centered and off-center configurations is inverted, being the former about 0.1 eV lower in energy. By a closer analysis, these results can be attributed to a secondary effect of the smaller pore area. Indeed, computing the adsorption energy with the same revPBE-D3 functional, but choosing the NM optimized with the PBE-rVV10 functional, the same hierarchy as reported in Table 2 is recovered.

Electronic effects. The charge density difference maps (see the ESI† for more details) show that the interaction has a relatively small effect on the molecular electronic structure and no chemical bonding is formed between molecule and substrate. The observed charge redistribution is a clear indication of the polarization of the molecule. In order to quantify this effect, we have computed the molecular dipole moment. For the adsorbed molecule, this can be done by assigning localized molecular orbitals either to H₂Pc or to the substrate, which in the present case is a simple operation thanks to the absence of covalent bonding. As expected, we observe a significant increase of the dipole component in the direction perpendicular to the surface. The μ_z component for the poreA configuration results 5.10 Debye, 5.37 Debye for the offA1 configuration, and 5.39 Debye for offB1. This corresponds to the displacement of the center of mass of the electronic charge towards the substrate. Even more interesting is the change in the μ_y component, i.e., along the [21] direction, for the same configurations. In the case of poreA, μ_y is not null but still small, −0.27 Debye. The increase is more important and in the opposite direction for both offA1, +1.34 Debye, and offB1, 3.34 Debye. This effect suggests a rearrangement of the electronic clouds towards the center of the pore and away from the rim. This has to be related to the gradient of the electrostatic potential, which is present at the rim and is induced by the modulation of the electronic properties of the h-BN across the NM. The maximum electrostatic potential gradient (i.e. the electric field), due to the work function difference between pore and wire regions, at the pore rim of the NM can be estimated to be below 1 V nm⁻¹. With this assumption, the electrostatic contribution to the adsorption energy μ·E for the off center configurations should remain below 80 meV, considering the induced dipole moment along y. This means that the electrostatic component is not the dominant part of the adsorption anisotropy between “pore” and “off”, which amounts to some 200 meV.

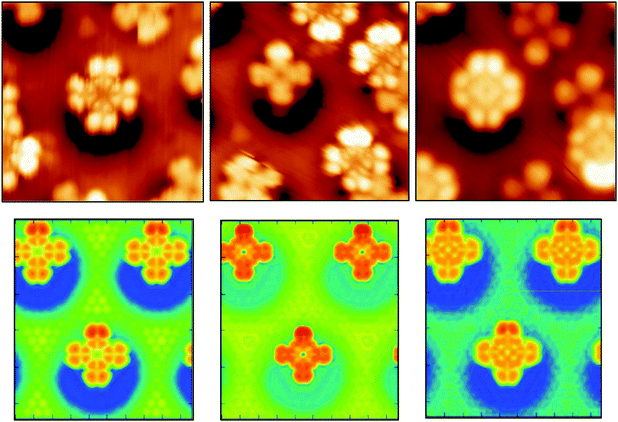
In spite of the polarization, the molecular orbitals are not strongly perturbed by the interaction with the substrate, as it is suggested by the very small distortion energies E_pc. The PDOS on N atoms and on C atoms computed for the offA1 configuration are very similar to the PDOS obtained in gas phase (see ESI†). For the adsorbed molecule, the orbital corresponding to the HOMO in gas phase is about 1.2 eV below the Fermi energy, while the LUMO is only 0.2 eV above. Hence, the molecular HOMO–LUMO gap of about 1.4 eV is maintained. The STM images in Fig. 5 (top panels) show different morphological aspects of the molecule by changing the bias potential, i.e., −2 eV, −1 eV, and +1 eV, respectively. The simulated STM images shown in the same figure reproduce the experimental morphological changes. From the PDOS, we know that with a bias potential of −2 eV the molecular HOMO orbital is imaged, whereas the bias potential of +1 eV shows the LUMO. Indeed, the obtained STM images at −2 eV and +1 eV bias potential closely resemble the shapes of the HOMO and LUMO orbitals, respectively, as computed for H₂Pc in gas phase (see ESI†). This also confirms that the structure of the molecular orbitals is not significantly perturbed by the interaction with the substrate.

Fig. 5 Top panels: experimental STM images of one molecule adsorbed at an off-center pore site obtained by different bias potentials. Left V_b = −2 eV, middle V_b = −1 eV, right V_b = +1 eV. Bottom panels: simulated STM images of the offA1 optimized structure, also obtained with the same three bias potentials.

The middle STM image, taken at −1 eV, is a clear cut cross shape, since it results from imaging in the HOMO–LUMO gap. It has also been observed that the energetic position of the HOMO orbital can vary of more than 1 eV if more than one molecule share the same pore.

Mobility of H₂Pc in the pore of the NM

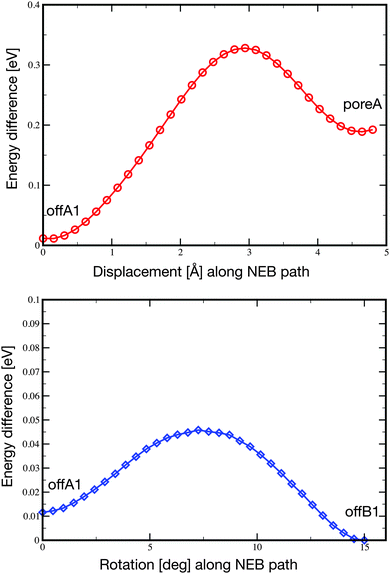
Pc is only weakly adsorbed on the NM and cannot be imaged stably anymore at 77 K. At this temperature, the molecules are pushed around in the pore during the STM scanning. Depending on the tip condition and tunneling parameters, the images at 77 K can become very blurred due to the mobility of the molecules in the pore. However, despite their mobility, the molecules are not pushed out of the pores.

In order to characterize the mobility of the molecule within the pore, we carried out the optimization of two minimum energy pathways using the nudged elastic band technique.⁵⁹ One pathway follows the movement of the molecule from the offA1 adsorption site to the poreA1, which corresponds to a displacement along the [21] axis of about 4.8 Å. The second simulated pathway follows the rotation by 15° of the molecule from the offA1 site to the offB1 site. In both cases, we initialized the pathway with a set of 32 intermediate configurations obtained from the linear interpolation between the two known minimum energy configurations. The resulting NEB minimum energy pathways turn out to be quite close to the linear interpolations given as initial guess. Namely, the molecule moves smoothly between the two minima, while the substrate barely changes. The final energy profiles are reported in Fig. 6. As expected, both energy barriers are quite small, in agreement with the high mobility of the molecule observed at temperatures higher than 5 K. However, the displacement from offA1 to poreA goes over a barrier of 0.32 eV, which is one order of magnitude larger than the barrier separating the two off-center positions (0.034 eV).

Fig. 6 Energy profile obtained by the optimization of the minimum energy pathway by NEB calculations. Top: pathway connecting the offA1 configuration to the poreA, obtained by displacing the molecule along the [21] axis. Bottom: pathway connecting the offA1 configuration to the offB1, obtained with a rotation by 15°. Notice that the scales in the two plots are different.

Summary and conclusions

The adsorption properties of the CuPc and H₂Pc molecules on the h-BN/Rh(111) NM surface have been studied by means of STM experiment and DFT theoretical simulations. The STM images have revealed that both the CuPc and H₂Pc molecules adsorb in a off-center position, i.e., the center of the molecule does not coincide with the center of the pore but is shifted by more than 5 Å. The preference for this off-center position is clearly evidenced by the statistical analysis of the radial distribution of the molecule positions in the pore and further corroborated by the observation of mobile molecules at 77 K. In the later case, the molecules switch from one off-center position to the opposite one during the STM scanning without observation of an intermediate state in the pore center. For all sub monolayer coverage (<0.2 molecules per nm²) of H₂PC and CuPc, no adsorption on the wire sections of the NM surface could be observed and also in the case of mobile molecules at 77 K the molecules only moved within the pores, but never left it. The decoupling of Pc molecules from the metallic substrate by the BN layer allowed observing constant current STM images of the molecule dominated by the contributions of the frontier orbitals of the Pc molecules. The energetic position of the HOMO and LUMO orbitals were rigidly shifted between different molecules within a range of about 1 eV, without a clear systematic on molecule position in the pore or orientation.

The DFT study confirms the experimental indication that the molecule substrate interaction is weak and the molecule adsorbs preferentially in the pore. The off-center position is significantly more stable than the centered one, with an adsorption energy difference of 0.2 eV, which is sufficient to discriminate among the two cases (at least at the low temperature of the experiment). Additionally, the energy differences among the off-center positions with different orientation are one order of magnitude smaller and, indeed, even at 5 K, several orientations have been observed in the STM images. One important result of this work is related to the subtle role played by the combination of exchange and correlation functionals to discriminate the very small energy differences. It turns out that a better agreement in the shape and size of the pore, allows a more accurate balance between electrostatic and dispersion terms of the interaction, which finally results in the right energetics. A portion of the potential energy surface underlying the motion of the molecule within the pore has also been calculated. The estimate of the energy barriers for translational and rotational displacements of the molecule are also in agreement with the experimental observation.

The research leading to these results has received funding from the Swiss University Conference through the High Performance and High Productivity Computing (HP2C) Program and from the Swiss National Science Foundation (Grant No. CRSI20_122703). Generous computational resources from the Swiss National Supercomputer Center (CSCS) and the University of Zurich are gratefully acknowledged. O.G. and T.D. would like to thank the Swiss National Science Foundation for financial support (Grant SNF-200021_149627).

References

1. Y. Suzuki, M. Hietschold and D. Zahn, Appl. Surf. Sci., 2006, 252, 5449.
2. Z. H. Cheng, L. Gao, Z. T. Deng, N. Jiang, Q. Liu, D. X. Shi, S. X. Du, H. M. Guo and H.-J. Gao, J. Phys. Chem. C, 2007, 111, 9240.
3. K. Nilson, J. Ahlund, M. Shariati, E. Gothelid, P. Palmgren, J. Schiessling, S. Berner, N. Martensson and C. Puglia, J. Phys. Chem. C, 2010, 114, 12166.
4. M. F. Craciun, S. Rogge and A. F. Morpurgo, J. Am. Chem. Soc., 2005, 127, 12210.
5. N. Papageorgiou, E. Salomon, T. Angot, J.-M. Layet, L. Giovanelli and G. Le Lay, Prog. Surf. Sci., 2004, 77, 139.
6. B. C. O'Regan, I. López-Duarte, M. V. Martínez-Díaz, A. Forneli, J. Albero, A. Morandeira, E. Palomares, T. Torres and J. R. Durrant, J. Am. Chem. Soc., 2008, 130, 2906.
7. G. de la Torre, C. G. Claessens and T. Torres, Chem. Commun., 2007, 2000.
8. S. H. Chang, S. Kuck, J. Brede, L. Lichtenstein, G. Hoffmann and R. Wiesendanger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 233409.
9. B. W. Heinrich, C. Iacovita, T. Brumme, D.-J. Choi, L. Limot, M. V. Rastei, W. A. Hofer, J. Kortus and J.-P. Bucher, J. Phys. Chem. Lett., 2010, 1, 1517.
10. A. Sperl, J. Kr oger and R. Berndt, Angew. Chem., Int. Ed., 2011, 50, 5294.
11. M. G. Betti, P. Gargiani, C. Mariani, R. Biagi, J. Fujii, G. Rossi, A. Resta, S. Fabris, S. Fortuna, X. Torrelles, M. Kumar and M. Pedio, Langmuir, 2012, 28, 13232.
12. N. Tsukahara, K.-i. Noto, M. Ohara, S. Shiraki, N. Takagi, Y. Takata, J. Miyawaki, M. Taguchi, A. Chainani, S. Shin and M. Kawai, Phys. Rev. Lett., 2009, 102, 167203.
13. M. Moors, A. Krupski, S. Degen, M. Kralj, C. Becker and K. Wandelt, Appl. Surf. Sci., 2008, 254, 4251.
14. J. Luder, B. Sanyal, O. Eriksson, C. Puglia and B. Brena, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 45416.
15. E. Rauls, W. Schmidt, T. Petram and K. Wandelt, Surf. Sci., 2012, 606, 1120.
16. R. Cuadrado, J. I. Cerdá, Y. F. Wang, G. Xin, R. Berndt and H. Tang, J. Chem. Phys., 2010, 133, 154701.
17. J. Repp, G. Meyer, S. Stojkovic, A. Gourdon and C. Joachim, Phys. Rev. Lett., 2005, 94, 026803.
18. C. Villagomez, T. Zambelli, S. Gauthier, A. Gourdon, S. Stojkovic and C. Joachim, Surf. Sci., 2009, 603, 1526.
19. C. Hirjibehedin, C. Lutz and A. Heinrich, Science, 2006, 312, 1021.
20. J. Repp, G. Meyer, F. Olsson and M. Persson, Science, 2004, 305, 493.
21. I. Swart, T. Sonnenleitner and J. Repp, Nano Lett., 2011, 11, 1580.
22. R. Laskowski, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045409.
23. J. Gómez Díaz, Y. Ding, R. Koitz, A. P. Seitsonen, M. Iannuzzi and J. Hutter, Theor. Chem. Acc., 2013, 132, 1350.
24. F. Schulz, R. Drost and P. Liljeroth, ACS Nano, 2013, 7, 11121.
25. H. Dil, J. Lobo-Checa, R. Laskowski, P. Blaha, S. Bernen, J. Osterwalder and T. Greber, Science, 2008, 319, 1824.
26. R. Widmer, D. Passerone, T. Mattle, H. Sachdev and O. Groening, Nanoscale, 2010, 2, 502.
27. M. Corso, W. Auwärter, M. Muntwiler, A. Tamai, T. Greber and J. Osterwalder, Science, 2004, 303, 217.
28. S. Berner, M. Corso, R. Widmer, O. Groening, R. Laskowski, P. Blaha, K. Schwarz, A. Goriachko, H. Over, S. Gsell, M. Schreck, H. Sachdev, T. Greber and J. Osterwalder, Angew. Chem., Int. Ed., 2007, 46, 5115.
29. R. Laskowski, P. Blaha, T. Gallauner and K. Schwarz, Phys. Rev. Lett., 2007, 98, 106802.
30. R. Laskowski and P. Blaha, J. Phys.: Condens. Matter, 2008, 20, 064207.
31. Y. Ding, M. Iannuzzi and J. Hutter, Chimia, 2011, 65, 256.
32. H. P. Koch, R. Laskowski, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155404.
33. H. F. Ma, T. Brugger, S. Berner, Y. Ding, M. Iannuzzi, J. Hutter, J. Osterwalder and T. Greber, ChemPhysChem, 2010, 11, 399.
34. H. F. Ma, Y. Ding, M. Iannuzzi, T. Brugger, S. Berner, J. Hutter, J. Osterwalder and T. Greber, Langmuir, 2012, 28, 15246.
35. J. Tersoff and D. R. Hamann, Phys. Rev. Lett., 1983, 50, 1998.
36. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
38. Y. Ding, M. Iannuzzi and J. Hutter, J. Phys. Chem. C, 2011, 115, 13685.
39. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
40. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
41. CP2K version 2.5. CP2K is freely available from, http://www.cp2k.org.
42. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477.
43. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103.
44. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703.
45. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641.
46. M. Krack, Theor. Chem. Acc., 2005, 114, 145.
47. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
48. Y. Ding, M. Iannuzzi and J. Hutter, J. Phys.: Condens. Matter, 2012, 24, 445002.
49. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
51. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
52. M. Dion, H. Rydberg, E. Schr oder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401; M. Dion, H. Rydberg, E. Schr oder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2005, 95, 109902.
53. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
54. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108(R).
55. R. Sabatini, E. K uc ukbenli, B. Kolb, T. Thonhauser and S. de Gironcoli, J. Phys.: Condens. Matter, 2012, 24, 424209.
56. F. Tran and J. Hutter, J. Chem. Phys., 2013, 138, 2014103; F. Tran and J. Hutter, J. Chem. Phys., 2013, 139, 039903.
57. G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
58. J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805.
59. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978.
60. Y. Y. Ding, M. M. Iannuzzi and J. J. Hutter, J. Phys.: Condens. Matter, 2012, 24, 445002,  DOI:10.1088/0953-8984/24/44/445002.
61. F. D. Natterer, F. Patthey and H. Brune, Phys. Rev. Lett., 2012, 109, 066101,  DOI:10.1103/PhysRevLett.109.066101.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp01466a

---