Gas-phase electrophilic aromatic substitution mechanism with strong electrophiles explained by ab initio non-adiabatic dynamics

Abstract

Ab initio non-adiabatic dynamics is used to monitor the attack of CH₃⁺ to benzene. The results show that in the gas phase the reaction is ultrafast and is governed by a single electron transfer producing a radical pair.

---

The substitution of aromatic hydrocarbon molecules, ArH, with electrophilic agents, E⁺, is one of the most studied organic reactions due to the implications of ArHE⁺ adducts from astrochemistry to biophysics.^1,2 According to the Ingold–Hughes mechanism,³ a σ-complex is the key step⁴ to this product. However, a number of different molecular mechanisms leading to the σ-complex have been discussed in the last few decades. Those include the early formation of a π-complex⁵ (see (1) in Fig. 1), a single electron transfer (ET) from the aromatic substrate to the electrophile to form a radical ion pair⁶ (2), and a combination of both schemes (3), where a π-complex is preceding the radical pair,⁷ which then leads to the σ-complex. All these mechanisms assume a ground state reaction – a true fact for weak electrophiles.⁸ In contrast, for strong ones, i.e. in general for all electrophiles whose electron affinity is higher than the ionization potential of the aromat, the gas phase reactants (ArH + E⁺) can represent an electronically excited state of the whole reaction system, and a conical intersection is required to initiate substitution in the ground state.^8,9

Fig. 1 Proposed mechanisms for electrophilic aromatic substitutions.

The purpose of this paper is to find out which of these reaction mechanisms is operative in the gas phase. As a case study, we present for the first time the detailed direct molecular dynamics of the strong electrophile CH₃⁺ for its facial, or broadside, attack on a benzene molecule incorporating all necessary electronically excited states. We employ ab initio non-adiabatic surface hopping molecular dynamics to study the attack of non-rotating CH₃⁺ to benzene, PhH. This reaction has been previously studied using quantum chemistry¹⁰ and molecular dynamics¹¹ in the ground state. Both studies concluded that a face-centered π-complex is not formed in the gas phase. However, excited states and the possibility of ET were not considered. Using a static analysis of potential energy surfaces based on complete active space self-consistent field (CASSCF)¹² calculations, Xu et al. showed⁸ that the PhH + CH₃⁺ reaction does start on an electronically excited state (see Fig. 2). Furthermore, they suggested that a conical intersection is a critical point en route to the final σ-complex discriminating the polar path via a π-complex (1) and the ET path (2) (see Fig. 1). But which path is really preferred is not elucidated in that paper. While previous studies are enlightening, a comprehensive mechanism can only be obtained by a dynamical study including excited states. The aim of this paper is to discern among all proposed mechanisms and, additionally, give important insights into the time-resolved evolution of the methyl cation – benzene intermediates and products.

Fig. 2 Proposed structures for gas phase aromatic substitution with strong electrophiles. The distance between the methyl cation carbon atom and the center of mass of the benzene molecule CM^B is denoted by r. CI stands for conical intersection.

The dynamic simulations have been done including the lowest four electronic singlet states. Potential energies, gradients and wavefunction overlaps for the full system (cation plus benzene) are computed on-the-fly at the CASSCF level of theory (see ESI† for more details). A total of 246 trajectories were simulated, each describing a direct facial attack of a non-rotating methyl cation towards the center of mass of the benzene molecule, CM^B (for more details see ESI†). While this scenario is rather idealistic in terms of a real bimolecular collision, we believe that, based on the proposed [PhH–CH₃]⁺-complex structures (see Fig. 2), the chosen collision vector is the most effective when studying the ET process, while leaving out the effect of rotational modes of either benzene or the methyl cation and intentionally neglecting other collision vectors such as a side attack. The initial conditions for both the methyl cation and benzene were represented by a Wigner distribution around their respective vibrational normal modes in the electronic ground state, so that each trajectory started with the vibrational energy equivalent to the quantum-mechanical zero-point energy, which amounts to ca. 2 eV.

To understand the nature of the potential energy surfaces, it is informative to calculate one-dimensional potential curves along the reaction coordinate (r in Fig. 2), while keeping the rest of the degrees of freedom frozen. As it can be seen in Fig. 3(a), the ground state, S₀, and the first excited state, S₁, are asymptotically degenerated due to the symmetry of the benzene π orbitals. The entry channel, i.e. where the reaction starts, corresponds to the second excited state, S₂. These potentials can also be plotted such that the character of the associated wavefunction is preserved (Fig. 3(b)). Then the entry channel corresponds to the [PhH CH₃⁺] state (blue) and this potential crosses with that of the degenerated [PhH˙⁺ ˙CH₃]_deg state (yellow) where one electron has been taken from the benzene, PhH, by the electrophile, CH₃. The pair of E states is only degenerate asymptotically but the degeneracy will be lifted during the dynamics due to e.g. vibrations. The crossing point between the entry channel and the ground state correlates with a conical intersection between three states that connects the ET and π-complex paths, leading to the radical pair and the π-complex, respectively. Note that the local minimum of the π-complex in this one-dimensional potential is actually a transition state of second order in full dimensions.^8,11

Fig. 3 MS-CASPT2 potential energy curves (see ESI†) for the three lowest electronic singlet states ordered according to energy (a) and according to the character of the wavefunction (b). CI and π_TS stand for conical intersection and π-complex transition state, respectively.

Dynamical simulations are required to unravel the path followed by the reaction. All simulated trajectories show a fast ET and are thereby considered reactive. However, only 63% are successful and lead to the stable formation of a σ-complex while 37% are reflected from the benzene plane and are labelled unsuccessful. In general, excess kinetic energy can either be redistributed in the internal degrees of freedom or can lead to re-dissociation of the [PhH–CH₃]⁺ complex, determining the branching ratio. We believe that in this case the branching ratio is of purely statistical nature and can be associated to the energy flux in the internal degrees of freedom of the system,¹³ depending on the initial condition of each trajectory.

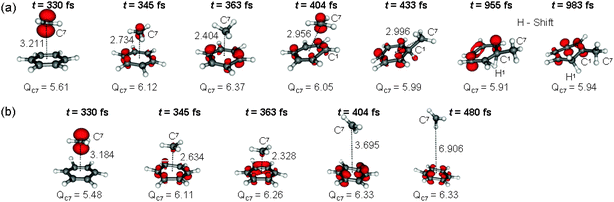
Snapshots of a representative trajectory for each case are shown in Fig. 4. At each time step, ET is visualized by plotting the density of the hole (compared to the neutral species), thereby localizing the positive charge of the system (see ESI† for details). Additionally, the Mulliken charge of the methyl carbon, Q_C⁷, is given for each snapshot. Note that a number of methods exist to describe the electronic distributions in terms of atomic charges and therefore, different definitions of ET can be defined, see e.g.ref. 14.

Fig. 4 Time evolution of the nuclear motion and hole density (positive charge) of a representative trajectory forming a σ-complex (a) and reflecting from the benzene plane (b). Distances are given in Å. Mulliken charge of the methyl carbon C⁷, Q_C⁷, is given in e.

In both trajectories the methyl cation is approaching the benzene with the positive charge located in the p orbital of the methyl cation carbon – as expected from the entry channel (t = 330 fs). Between 330 and 345 fs the system passes through the three-state conical intersection and hops to one of the [PhH˙⁺ ˙CH₃] states while charge transfer takes place. This process is found in all the trajectories, unambiguously indicating that the path for the electrophilic aromatic substitution in PhH + CH₃⁺ is mediated by a very fast single ET. Up to t = 363 fs the methyl radical follows its momentum towards the benzene ring, but from here, the two trajectories differ. While in (a) the methyl group keeps approaching, in (b) it recoils. In (a), at t = 404 fs the methyl gains back some positive charge while redirecting its momentum to eventually form a σ-bond (t = 433 fs). After complete formation of the σ-bond, isomerization of an arenium ion occurs by shifting a hydrogen (denoted as H₁) to another position in the aromatic ring (t = 955 fs and t = 983 fs). H-shifts in arenium ions have been reported to have very low barriers.^10,11 In (b), the methyl radical is reflected from the benzene plane, leaving a benzene radical cation behind (t = 404 fs and t = 480 fs). Also in this case, ET has occurred although no stable σ-complex is formed.

Fig. 2 shows the most relevant structures observed in the dynamics. 1 is the reactant, i.e. the methyl cation carbon is not bonded to any other carbon atom. In the σ-complex, 2, the methyl cation carbon is bonded to one carbon of the benzene ring. When the methyl cation carbon is bonded to two carbons a bridged side-π structure, 3, is formed. 4 depicts the situation where one benzene carbon binds to two hydrogens in the σ-complex, on the way to H-shift. Monitoring these structures in time allows identifying the reaction paths. The corresponding connectivities are defined with bond distance thresholds of C–C less than 2.10 Å and C–H less than 1.55 Å. Unsuccessful trajectories can proceed from 1 to 1 directly, or via2 or 3, that is, reflecting but forming a “hot” σ-complex on the way. A stable σ-complex implies the transition from 1 to 2, either directly, or via3, i.e. forming a σ-complex via a side-π-structure. A CH₃-shift is described as a transition from 2 to 3 to 2′, and a H-shift is a transition from 2 to 4.

The details of the dynamics involved in the successful and unsuccessful trajectories are presented in Fig. 5. Panels (a) and (g) show the time-dependent spectrum of the distance r, correlating with the number of trajectories at certain r values. It is interesting that both sets of trajectories go through the conical intersection before forming a stable σ-complex or reflecting. Panel (b) shows that the formation of the bond between the methyl and the benzene is not selective. An average C⁷–C¹ of ca. 1.4 Å indicates bond formation at C¹, ca. 2.8 Å represents bonding to C² or C³, and ca. 4.0 Å represents bonding to C⁴, C⁵ or C⁶. Panels (c) and (i) show the relative number of trajectories encountering the structures 1–4 in time. Note that the relative populations of Fig. 5(c) do not add up to 1 because combined 1/2/3 + 4 structures are also possible. Initially, all trajectories start with 1. At t = 375 fs (panel c) there is a rapid increase of the number of trajectories forming a σ-complex (2), although ca. 22% form a side-π structure (3) before forming the single bonded σ-complex. Once the σ-complex is established (after t = 420 fs) rapid H-shifts occur (4). This process stops between t = 550 fs and t = 700 fs, while CH₃-shifts happen, as seen by the increasing number of non-bonded (1) and doubly bonded (3) methyl structures while single bonded (2) methyl trajectories decrease. The CH₃-shifts are also nicely illustrated in the same time range in panel (b), where the methyl carbon changes positions on the benzene ring. Within the unsuccessful trajectories (panel i), 37% form a “hot” σ-bond (2) or side-π-structure (3), while the remaining 63% is reflected without forming any bond.

Fig. 5 Time-dependent (td) properties of successful (a–f) and unsuccessful (g–l) trajectories. (a) and (g) td-spectrum of r. (b) and (h) td-spectrum of the distance between the methyl carbon and C¹ of benzene. (c) and (i) Accumulated relative amounts of geometries 1–4. (d) and (j) td adiabatic state population in the S₀, S₁ and S₂ states depicted in Fig. 3(a). (e) and (k) td-spectrum and average of the Mulliken charge at the methyl carbon C⁷, Q_C⁷. The inset shows the average in the trajectories reflecting and those forming a “hot” σ-bond. (f) and (l) Expected value of the potential energy of a trajectory.

The ET process from the benzene to the methyl group is best monitored by the population analysis of the involved states sketched in Fig. 3(a), see Fig. 5 panels (d) and (j). The ET takes place sharply around t = 340 fs, before any bond is formed. Note that 90% of the population transfer takes place through two areas of two-state intersections (S₂/S₁ and S₁/S₀), instead of directly from S₂ to S₀, which accounts for the remaining 10%. The predominance of the former mechanism can also be inferred from the number of hops plotted in Fig. 6. At the S₁/S₀ and S₂/S₁ hopping geometries the energy difference between the involved states accounts for ca. 0.3 eV, indicating that the hopping event takes place very close to the conical intersections, while the energy difference from S₂ to S₀ is larger. The increase in the Mulliken charge at the methyl carbon, both in the successful (e) and unsuccessful (k) trajectories, nicely correlates with the occurrence of an ultrafast ET. As the methyl cation is capturing an electron from the benzene the charge of the methyl carbon is increased by 1e. Subsequently, the methyl carbon forms a σ-bond (Fig. 5e) with the benzene cation. In that case, the positive charge is delocalized over the whole aromat + CH₃ and the Mulliken charge at the C⁷ decreases by 0.2–0.3e (averaged over all trajectories). A similar process takes place in the reflected trajectories (Fig. 5(k)).

Fig. 6 Number of S₂/S₁, S₁/S₀ and S₂/S₀ hops for the trajectories forming a σ-complex (a) and reflecting (b).

Fig. 5(f) and (l) show the expectation value of the potential energy of a trajectories relative to the ground state energy at far r distances. The initial zero-point energy amounts to ca. 2 eV, hence, in the beginning, the trajectories possess a potential energy of 3.3 eV. As the methyl cation is approaching the center of mass of benzene, the potential energy decreases as expected from the topology of the potential energy profiles (recall Fig. 3). Accordingly, during the approach, the system gains kinetic energy until t = 400 fs. According to panel (f), the formation of the σ-complex requires to overcome a potential barrier of about 1 eV (t = 470 fs). In view of the large amount of internal kinetic energy, this barrier can be easily surmounted and for practical purposes, it does not represent an obstacle – in agreement with previous studies^10,11 that claimed that the formation of the σ-complex occurs barrierless. It can also be argued that the barrier observed here is a result of the momentum gained after the approach of the methyl group, which leads to structures where the r distance is much smaller than the one for the corresponding π_TS structure, and hence, creating a pseudo barrier as the methyl is moving back to a benzene carbon. The oscillations in the potential energy after 400 fs reflect the excess kinetic energy of the system, which is responsible for the rapid H- and CH₃-shifts observed during the formation of the σ-complex. Barriers of 0.4 eV for the H-shift process were calculated by Ishikawa and coworkers¹¹ in the ground state. Furthermore, from Fig. 5(f), we can retrieve a binding energy of about 2.9 eV for the formation of a stable σ-complex. This value is in good agreement with those obtained from optimized ground state structures and energies reported in ref. 10 and 11. In the unsuccessful trajectories (panel l) most of the kinetic energy leads to re-dissociation and the rest gets internally redistributed after the collision.

Conclusions

The obtained results show that the formation of the σ-complex in electrophilic aromatic substitutions with strong electrophiles is an excited state process undergoing an ultrafast single ET mediated by a three-state conical intersection. These conclusions have general importance for modeling interactions between carbocations and aromatic systems in the gas phase. Within our ideal case study, we aimed at studying the ET process during the EAS reaction based on previously proposed and optimized π- and σ-complexes. As an outlook, rotating CH₃⁺ facial as well as side attacks could be simulated in order to give further insight into the formation of the σ-complex of this gas-phase EAS reaction. In solution, the [PhH CH₃⁺] state is expected to stabilize, annihilating the conical intersection and turning the reaction into a ground state process. In future work the interaction with weak electrophiles and the effect of solvation can be investigated.

Acknowledgements

We thank the Deutsche Forschungsgemeinschaft (GO-1059/7-3) for financial support and the Vienna Scientific Cluster (VSC) for generous computational time.

References

1. R. Taylor, Electrophilic Aromatic Substitution, Wiley, New York, 1990.
2. (a) J. McMurry, Organic Chemistry, Brooks/Cole, Pacific Grove, CA, 3rd edn, 1992; (b) J. March, Advanced Organic Chemistry: Reactions, Mechanisms, and Structures, John Wiley & Sons, New York, 3rd edn, 1988, p. 447.
3. C. K. Ingold, Structure and Mechanisms in Organic Chemistry, Cornell Univ. Press, Ithaka, 2nd edn, 1986.
4. S. R. Gwaltney, S. V. Rosokha, M. Head-Gordon and J. K. Kochi, J. Am. Chem. Soc., 2003, 125, 3273.
5. (a) M. J. S. Dewar, J. Chem. Soc., 1946, 406, 777; (b) M. J. S. Dewar, Nature, 1954, 176, 784; (c) G. A. Olah, Acc. Chem. Res., 1971, 4, 240; (d) G. A. Olah, R. Malhotra and S. C. Narang, Nitration Methods and Mechanisms, VCH, New York, 1989.
6. (a) L. Perrin, J. Am. Chem. Soc., 1977, 99, 5516; (b) J. K. Kochi, Acc. Chem. Res., 1992, 25, 39; (c) E. K. Kim, T. M. Bockman and J. K. Kochi, J. Am. Chem. Soc., 1993, 115, 3091 and references therein.
7. P. M. Esteves, J. W. M. Carneiro, S. P. Cardoso, A. G. H. Barbosa, K. K. Laali, G. Rasul, G. K. S. Prakash and G. A. Olah, J. Am. Chem. Soc., 2003, 125, 4836.
8. X. Xu, S. Zilberg and Y. Haas, J. Phys. Chem. A, 2010, 114, 4924.
9. Z. Chen and Y. Mo, J. Chem. Theory Comput., 2013, 9, 4428.
10. P. C. Miklis, R. Ditchfield and T. A. Spencer, J. Am. Chem. Soc., 1998, 120, 10482.
11. Y. Ishikawa, H. Yilmaz, T. Yanai, T. Nakajima and K. Hirao, Chem. Phys. Lett., 2004, 396, 16.
12. B. O. Roos, Adv. Chem. Phys., 1987, 69, 399.
13. M. E. Corrales, V. Loriot, G. Balerdi, J. González-Vázquez, R. de Nalda, L. Banares and A. H. Zewail, Phys. Chem. Chem. Phys., 2014, 16, 8812.
14. F. A. La Porta, T. C. Ramalho, R. T. Santiago, M. V. J. Rocha and E. F. F. da Cunha, J. Phys. Chem. A, 2011, 115, 824.

---

Footnote

† Electronic supplementary information (ESI) available: Computational details. See DOI: 10.1039/c4cp01456a

---