Open Access Article
Open Access ArticleAcidity constants of lumiflavin from first principles molecular dynamics simulations†
Murat
Kılıç
and
Bernd
Ensing
*
Van't Hoff Institute for Molecular Science, University of Amsterdam, Science Park 904, 1098 XH, Amsterdam, The Netherlands. E-mail: B.Ensing@uva.nl; Web: http://molsim.chem.uva.nl
First published on 29th July 2014
Abstract
We have computed the free energy profiles of the deprotonation reactions of lumiflavin in the semiquinone and fully reduced oxidation states using constrained DFT-based molecular dynamics simulations. In the semiquinone state, the N5 nitrogen atom and the N1 nitrogen atom can become protonated. We find, in agreement with experiment, that the N5 site is the predominant proton acceptor in the semiquinone state, although the computed pKa value is somewhat smaller than the experimental number. The computed pKa for the N1 protonation in the fully reduced state is in good agreement with the experimental number. We employ two different, commonly used, reaction coordinates based on the distances between the proton and the donor and acceptor atoms. Further improvement of the accuracy of this type of pKa calculations may require development of more advanced reaction coordinates that go beyond the description of only the first proton transfer step from a donor atom to a first solvation shell water molecule.
1 Introduction
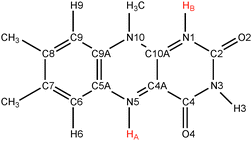
Flavins such as flavin adenine dinucleotide (FAD) and flavin mononucleotide (FMN) are common cofactors that play a key role in a wide variety of enzyme catalysed oxidation and reduction reactions. They can accept up to two electrons in either a single step or in two distinct one-electron transfer reactions. Flavins can also act as proton donors or acceptors. The electron and proton transfer reactions are coupled—the acidity constants depend on the redox state of the flavin and, vice versa, the reduction potentials are a function of the pH. Moreover, both the electron and proton affinities of the flavin are modulated by their protein or solvent environment, which underlies the versatile flavochemistry observed in nature.The structural motif of flavins is a three-ring isoalloxazine moiety with a side group attached to the nitrogen (N10) atom in the middle ring (see Fig. 1). Three other nitrogen atoms can accept or donate a proton depending on the oxidation state of the flavin. The acidity and redox properties of flavins have been subject of study since the 1930s1 using potentiometric methods,2 pulse radiolysis,3,4 NMR,5 and UV/Vis spectroscopy.3,5 The acidity constants (pKa's) and reduction potentials are therefore experimentally well-established, despite the complexity due to the intrinsic coupling of the redox and protonation reactions and the fact that the intermediate semiquinone radical is rather unstable with a formation constant of K = [FMNsq]2/([FMNox][FMNred]) ≈ 10−3.6Fig. 2 illustrates schematically the different redox and protonation states of flavins. In the oxidised state, only the N3 atom is protonated with an associated pKa of about 10.3. One-electron reduction of the neutral flavin leads to the anionic radical semiquinone state, or to the neutral semiquinone when simultaneously a proton is accepted at the N5 position. For riboflavin and FMN, the pKa of the semiquinone is estimated to be about 8.3–8.55.2,3,6 The second one-electron reduction leads to the anionic hydroquinone state, or again a neutral state when accompanied with a second protonation, this time at the N1 atom. The pKa of the riboflavin and FMN hydroquinone are estimated to be 6.25 and 6.72 respectively.2
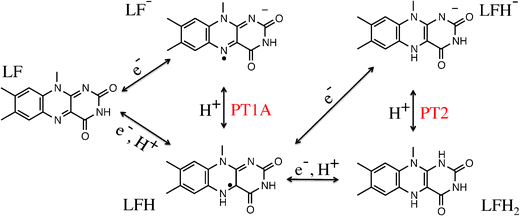 | ||
| Fig. 2 Lumiflavin (LF) can exist in several oxidation and protonation states. Electron and proton transfer reactions are indicated by arrows. | ||
Computational studies have the advantage that the electron and proton transfer processes can be decoupled by computing the reaction free energy of the proton (or electron) transfer reaction at a fixed oxidation (or protonation) state. Truhlar and coworkers have computed the redox and acidity properties of several flavins using density functional theory (DFT) and a continuum description of the aqueous solvent.7,8 For a series of lumiflavin compounds with different substituents at the C7 and C8 positions, they found reduction potentials and pKa values in good agreement with experiment, with the exception of the pKa of 1.5 for the dimethyl species in the fully reduced state, which is much smaller than the experimental value of 6.5. DFT-based molecular dynamics (DFT-MD) simulations using explicit solvent require fewer empirical parameters such as the cavity radii and the dielectric constant, and more importantly, they allow for study of the role of the molecular environment in the charge transfer process. However, sampling of the solvent configurations is computationally demanding at the DFT-MD level of theory. And secondly, the calculation of the transfer free energy requires an advanced sampling method, such as free energy perturbation9,10 or constrained molecular dynamics.11–13
We have recently studied14 the two one-electron reduction reactions of lumiflavin (LF) in aqueous solution using DFT-MD simulations. Lumiflavin is one of the smallest flavin members, in which the N10 side-chain is a methyl group as depicted in Fig. 1. We used a free energy perturbation approach15,16 that relates the redox potential to the average energy required to add (or subtract) an electron to the system, i.e. the vertical gap energy. Computation of the pKa is somewhat more involved because the proton, treated as a classical particle, has a position that should be chosen in an efficient way such that the configurations are physically relevant.10,17,18 We therefore use constrained molecular dynamics,11,19 to calculate the potential of mean force of the protonation reaction as a function of a well-chosen reaction coordinate, from which the pKa is obtained.20
In this work, we study the proton transfer (PT) reactions at the N1 and N5 lumiflavin nitrogen atoms in the semiquinone and fully reduced oxidation states. In the semiquinone state, the protonation takes place at the N5 nitrogen, which we label PT1A as indicated in Fig. 2. However, we can also measure the pKa of the N1 site in the semiquinone state (labeled PT1B). The third reaction is the protonation of the N1 site in the fully reduced state (PT2), in which case the N5 site is considered already protonated.
In the following, we first briefly review the method to calculate the pKa using constrained DFT-MD simulation and provide the details of our model. Next, the computed free energy profiles for the proton transfer reactions and the resulting pKa values for the different flavin protonation sites are discussed. We have computed the free energy profiles twice using the two most commonly used reaction coordinates for proton transfer reactions. A suggestion is made on how these reaction coordinates can be further improved.
2 Methods
2.1 Calculation of pKa from constrained dynamics
The acidity constant is related to the difference in the Helmholtz free energy, ΔA, between the protonated and deprotonated states of the molecule as: | (1) |
 | (2) |
The accuracy of the resulting free energy profile of the reaction depends crucially on how well the chosen reaction coordinate describes the reaction mechanism. For a proton transfer reaction, this choice of a reaction coordinate is complicated by the fact that after the proton has made its initial jump from the donor molecule to a nearby solvent water molecule to form a hydronium ion, another proton of this ion may make the next jump to a water molecule in the second coordination shell, and so forth. Previous work has therefore focussed mainly on the first step, the breaking of the initial donor–proton bond, thereby neglecting the changes in free energy that may occur when the charge-separation proceeds beyond the contact-ion pair distance. The good agreement of previous results with experiment so far indicates that the missing contributions are small.
Here, we use two different types of reaction coordinates. The first coordinate is a function that estimates the coordination number, nc, of the number of hydrogens within a distance d0 of the donor nitrogen atom:
 | (3) |
The second reaction coordinate type that we use includes also the distance of the proton to the accepting water molecule oxygen:
| Δd = d(N–H) − d(OW–H). | (4) |
That is, Δd is the difference between the distance of the proton to the donating flavin nitrogen and the distance of the proton to the accepting water oxygen. Its value is negative in the protonated state, zero when the proton is exactly equidistant from the donor and acceptor atoms, and positive in the deprotonated state. The advantage of using this coordinate is that we can also generate a series of simulations starting from the deprotonated state. This deprotonated state was constructed from a simulation of (deprotonated) lumiflavin in water by adding a proton to a water molecule that was hydrogen bonded to the flavin nitrogen atom. Subsequently, this system was equilibrated while maintaining the hydrogen bond using the Δd constraint and an additional coordination number restraint on the hydronium ion oxygen. This restraint worked as a repulsive harmonic wall to avoid that either of the other two hydronium hydrogens would escape to a nearby water molecule. The wall potential on this coordination number was zero as long as its value was larger than 1.6. After equilibration with this additional restraint, we performed the production simulations both without and with the restraint. The former results are the most interesting and are discussed hereafter, whereas the results obtained with the additional restraint on the proton accepting water molecule are provided in the ESI.† By performing a constrained MD series starting from the equilibrated protonated state (forward series) as well as from the equilibrated deprotonated state (reverse series), we can assess whether omitted (solvent) degrees of freedom from the reaction coordinate cause hysteresis effects (see for an discussion of such hysteresis e.g.ref. 21).
2.2 Computational details
All electronic structure calculations and ab initio molecular dynamics simulations were performed using DFT with the Perdew–Burke–Ernzerhof (PBE)22 exchange–correlation functionals and Grimme's D3 van der Waals correction23 as implemented in the CP2K program (version 2.4).24,25 The CP2K program is based on a hybrid Gaussian and plane wave scheme, in which the wave functions are expanded using a Gaussian basis set, and an auxiliary basis of plane waves is employed to expand the density.26 We used pseudopotentials of the Goedecker–Teter–Hutter (GTH) type, based on the parametrization of Hartwigsen–Goedecker–Hutter27,28 and adapted for the DFT. A split valence Gaussian basis set designed specifically for these pseudopotentials,25 of double-ζ quality and one set of polarisation functions (DZVP), was employed for all atoms including hydrogen. The auxiliary plane wave basis expansion was cutoff at 300 Ry.The system of aqueous LF contained one LF molecule and 102 water molecules in a periodic cubic unit cell with an edge of 15.148 Å. The DFT-based molecular dynamics simulations used the Born–Oppenheimer method with a time step of 0.5 fs in the canonical (NVT) ensemble. The CSVR (Canonical Sampling through Velocity Rescaling)29 thermostat was used to maintain a constant temperature of T = 300 K. The systems were equilibrated for at least 5 ps, after which at least 5 ps of constraint simulation was performed at each reaction coordinate value parameter for analysis.
To assess the quality of the PBE functional, we performed a series of benchmark calculations of the proton transfer reactions in the gas-phase using the Gaussian-09 program.30 The molecular geometries were computed at the PBE/6-31g(d,p) level, which were subsequently used to compare the deprotonation energies between different functionals using a 6-311G(2d,p) basis set. The results are compiled in Table 1, together with the B3LYP31–33 and M06-L34 results of Bhattacharyya et al.7 Comparing the results using the PBE functional, which is a first generation GGA functional, with the hybrid-GGA B3LYP, the meta-GGA M06-L, and the meta-hybrid-GGA M06-2X, we note small differences of 1–2 kcal mol−1. Note in particular that the PBE difference between the PT1A and PT2 reactions is somewhat larger (2.6 kcal mol−1) than that for the other functionals, B3LYP (1.2), M06-2X (0.0), and M06-L (1.4). Instead, the difference between PT1B and PT2 is very similar for all functionals, PBE (7.6), B3LYP (7.9), M06-2X (8.6), M06-L (7.9). The latter leads us to conclude that there is no indication that the PBE GGA functional shows a systematic deviation for the deprotonation reactions in the semiquinone radical state (PT1A and PT1B) compared to the closed shell state (PT2). For our flavin simulations in aqueous solution, we augment the PBE functional with the a posteriori van der Waals correction by Grimme.
3 Results and discussion
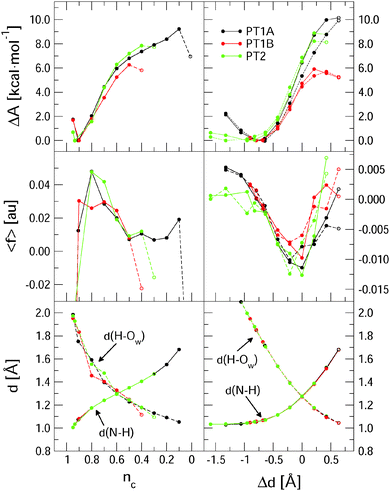
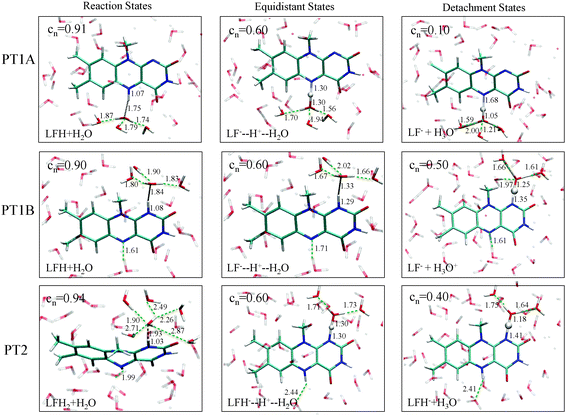
Fig. 3 summarises the main results from the constrained DFT-MD simulations that we performed to compute the pKa values of lumiflavin. The different colours represent the three proton transfer reactions that we focussed on: the (de-) protonation in the semiquinone state at the N5 atom (black lines labeled PT1A) and at the N1 atom (red lines, PT1B), and the (de-) protonation in the fully reduced state at the N1 atom (green lines; PT2). The top panels show the free energy profiles as a function of the coordination number reaction coordinate (eqn (3)) at the left side, and using the distance–difference coordinate (eqn (4)) in the right panels. These profiles where obtained by integration of the measured mean force of constraint (see eqn (2)), which are shown in the middle panels.In the top-left panel, the free energy profiles show a minimum in the protonated state at a reaction coordinate value of nc = 0.9 and increase when the proton is moved away from the flavin by decreasing nc. The bottom panel shows the average d(N–H) and d(H–OW) bond distances, which are close to respectively 1.1 Å and 1.8 Å in the protonated state as the proton forms a hydrogen bond with the nearby water molecule. For each of the three proton transfer reactions, a snapshot of this initial protonated state is shown in Fig. 4 at the left.
Decreasing the nc reaction coordinate carries the proton from the flavin toward the nearest water molecule as seen from the increasing d(N–H) distance and the decreasing d(H–OW) distance. This happens in a similar manner for all three proton transfer reactions, crossing the equidistant state at nc = 0.6. The three free energy profiles show also a similar increase, but reach different final maxima. The last data point is drawn with an open circle to indicate that in that simulation a spontaneous second proton transfer was observed that carried the hydronium ion into the second coordination shell, after which we stopped the simulation. The free energy profiles should thus be interpreted as the work required to carry the proton from the flavin up to the reaction coordinate value at which the proton escapes barrierless into the solvent. This escape occurs earliest for PT1B at a free energy barrier of 6.2 kcal mol−1 and at the latest for PT1A at 9.1 kcal mol−1. These free energies, together with the pKa values computed using eqn (1), are compiled in Table 2.
| Proton transfer | ΔA | pKa | |||
|---|---|---|---|---|---|
| n c | Δd | n c | Δd | exp. | |
| PT1A: LFH → LF− + H+ | 9.1 | 9.4 | 6.7 | 6.9 | 8.5 |
| PT1B: LFH → LF− + H+ | 6.2 | 5.6 | 4.5 | 4.1 | — |
| PT2: LFH2 → LFH− + H+ | 7.8 | 8.5 | 5.7 | 6.2 | 6.5 |
The free energy profiles as a function of the distance–difference reaction coordinate, shown at the right in Fig. 3, show the same trend for the escape barriers of the three proton transfer reactions. As explained in the method section, with this reaction coordinate, we are also able to perform the series of constraint simulations starting from the deprotonated state, which results in the profiles shown by the dotted lines. The hysteresis between the forward and reverse reaction profiles is most likely due to small differences in the solvent reorganisation that is not controlled by these simple reaction coordinates. The effect is the largest for the PT1A reaction, resulting in an overestimated deprotonation free energy of 10.0 kcal mol−1 for the forward reaction compared to an underestimated protonation free energy of 8.8 kcal mol−1 in the reverse direction.
Although we cannot estimate the amount of hysteresis in the case of the coordination number reaction coordinate, we should of course expect a similar overestimate for the deprotonation free energy, due to the solvent reorganisation lagging behind. Nevertheless, these free energies are smaller (in the cases of PT1A and PT2) than those computed using the Δd coordinate, even though we could correct the latter numbers for the hysteresis effect by taking the average of the forward and reverse estimates (see Table 2). The main difference between the nc and Δd reaction coordinates is that nc is effectively only a function of the distance between the proton and the donating nitrogen atom, whereas Δd incorporates also the distance between the proton and the accepting water oxygen. Not controlling the d(H–OW) with nc leads to larger variation in the average distance of the accepting water to the leaving proton as is seen in the bottom-left panel of Fig. 3 by comparing the three d(H–OW) curves at the early stage of the deprotonation reaction (i.e. at nc ≈ 0.9–0.7). Note how a further away water oxygen (e.g. the red dot at nc = 0.9, or the black and green dots at nc = 0.8, or the green dot at nc = 0.7) corresponds to a larger average force of constraint shown in the middle-left panel. Note also that in the nc case the largest absolute force is measured at the early stages of the deprotonation, so that the steepest part of the free energy curve is around nc = 0.8, whereas for the Δd coordinate the largest constraint force is seen near the equidistant state, so that the ΔA curve is the steepest around Δd = 0. A third difference seen in the behaviour of the nc and Δd reaction coordinates is seen in the last stage of the deprotonation reaction. Using the nc coordinate, the average constraint force remains positive, i.e. pushing the system back toward the protonated state, until the proton escapes into the solution. Instead, when using the Δd coordinate, the constraint force tends back to zero, which results in a free energy curve that shows a maximum, as expected when reaching a transition state barrier. This indicates that in the latter case, the proton escape occurs close to the actual free energy barrier, whereas in the case of the nc coordinate the proton may escape prematurely depending on a random fluctuation of the distance between the proton and the accepting water molecule.
The final state of the system is different for each of the three proton transfer reactions, irrespective of the reaction coordinate used in the constraint simulations. For PT1A, the hydronium ion remains close to the N5 site, simply hopping back and forth between first and second shell water molecules through an Eigen–Zundel–Eigen mechanism. In one simulation, using the nc coordinate constraint at 0.1, the proton was seen to be accepted by the lumiflavin O4 atom for most of the simulation. For PT1B, in all simulations in which the proton escapes (i.e. at nc ≤ 0.4 or Δd ≥ 0.6 Å) the hydronium ion did not remain close to the N1 donor atom for more than a picosecond, but moved via several Grotthus-like hops along a wire of hydrogen bonds in the water solvent to terminate at the lumiflavin N5 atom (or that of a periodic copy of the lumiflavin molecule). And finally, for PT2 the hydronium ion would also travel away from the N1 atom but in this case remain far away from the lumiflavin molecule, at a distance apparently only limited by the size of the system box.
The pKa values computed from the deprotonation free energy barriers using the two different reaction coordinates are in fair agreement with each other (see Table 2). Compared to the experimental numbers, we see good agreement for the PT2 case, but a significant underestimation for the PT1A pKa. Similar to previous pKa calculations using the same approach,13,36–38 we estimate the accuracy of the employed methodology to be within 1 pKa unit. The discrepancy for the PT1A pKa between our computed value and the experimental number is most likely due to a systematic underestimation of the free energy barrier due to the limited range of the employed reaction coordinates. As described above, in the PT1A case the hydronium ion remains near the N5 protonation site when the maximum range of either the nc or Δd reaction coordinate is reached. This indicates that the actual free energy barrier to separate the hydronium ion from the semiquinone anion is larger than we can compute with these types of reaction coordinates.
An interesting approach to compensate for the missing part of the free energy profile beyond the transition state is based on the reversible work theorem,39 which relates the proton–conjugate base radial distribution function, g(d), to a free energy profile as
| g(d) = exp[−ΔA(d)/kBT], | (5) |
 | (6) |
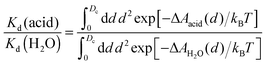 | (7) |
For the PT1B, we find a value of 4.1 using the Δd coordinate. To our knowledge, the experimental pKa of the N1 site in the semiquinone state is unknown (Land and Swallow measured 2.3 and 8.3 for the semiquinone pKa's using pulse radiolysis, however here the first number refers most likely to the N1 pKa while the N5 site is protonated3). Similar to the PT2 case, our simulations captured the PT1B deprotonated including the escape of the proton into the solvent, so that we expect a similarly good accuracy. This allows us to estimate the relative propensity, K, for the protonation of the N1 site versus the N5 site in the semiquinone state,
| HN5 + N1− ↔ N5− + HN1, | (8) |
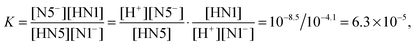 | (9) |
4 Conclusions
Using the method of constrained DFT-based molecular dynamics simulation, we have studied the (de-) protonation of the prototypical flavin named lumiflavin in aqueous solution. In the semiquinone state, the N1 and the N5 nitrogen atoms can act as proton acceptors, whereas in the fully reduced oxidation state, only the N1 site is available for protonation.We employed two different reaction coordinates in the constrained simulations to compute the deprotonation free energy profiles, from which the pKa values were obtained. The first reaction coordinate was functionalised as the coordination number of the number of hydrogens around the nitrogen atom, and thus effectively only considered the distance between the proton and the donor atom. The second reaction coordinate included also the distance from the proton to the accepting water oxygen atom, by taking the difference between the two distances. The latter reaction coordinate allowed us to estimate systematic errors due to omitted solvent degrees of freedom in these simple reaction coordinates, by measuring the hysteresis in the free energy profiles between the forward deprotonation and the backward protonation reactions. This hysteresis effect was found to be relatively small. Secondly, we noted that omission of the distance of the proton to the accepting water molecule in the first reaction coordinate leads to larger fluctuations in the measured force of constraint and free energy profile.
In the semiquinone state, the N5 nitrogen is the predominant protonation site as expected, however the computed pKa of 6.9 (using the distance difference reaction coordinate) was smaller than the experimental number of 8.5. We attribute this to the fact that the current reaction coordinates do not control the deprotonation reaction beyond the second coordination shell of the donor molecule. This problem did not play a role in the deprotonation of the N1 site in the semiquinone and fully reduced oxidation states. In the first case the proton spontaneously diffused through the solvent toward the N5 site, whereas in the fully reduced case the hydronium ion remained as far from the lumiflavin as possible in the limited simulation system. The pKa of the reduced lumiflavin was found to be 6.2 in good agreement with the experimental number of 6.5.
Acknowledgements
The work was financially supported by NWO (The Netherlands Organisation for Scientific Research) through a Vidi grant of BE.References
- L. Michaelis, M. P. Schubert and C. V. Smythe, J. Biol. Chem., 1936, 116, 587–607 CAS.
- R. Draper and L. Ingraham, Arch. Biochem. Biophys., 1969, 125, 802 CrossRef.
- E. Land and A. Swallow, Biochemistry, 1969, 8, 2117–2125 CrossRef CAS.
- R. Anderson, Biochim. Biophys. Acta, 1983, 722, 158–162 CrossRef CAS.
- S. Ghisla, P. Macheroux and F. Müller, Flavins and flavoproteins, proceedings of the 10th internat. symposium, 1991, pp. 27–32.
- S. G. Mayhew, Eur. J. Biochem., 1999, 265, 698–702 CrossRef CAS.
- S. Bhattacharyya, M. Stankovich, D. G. Truhlar and J. Gao, J. Phys. Chem. A, 2007, 111, 5729–5742 CrossRef CAS PubMed.
- M. North, S. Bhattacharyya and D. G. Truhlar, J. Phys. Chem. B, 2010, 114, 14907–14915 CrossRef CAS PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420 CrossRef CAS PubMed.
- M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238 RSC.
- E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Chem. Phys. Lett., 1989, 156, 472–477 CrossRef CAS.
- B. Trout and M. Parrinello, Chem. Phys. Lett., 1998, 288, 343 CrossRef CAS.
- M. Sprik, Chem. Phys., 2000, 258, 139–150 CrossRef CAS.
- M. Kılıç and B. Ensing, J. Chem. Theory Comput., 2013, 9, 3889–3899 CrossRef.
- A. Warshel, J. Phys. Chem., 1982, 86, 2218–2224 CrossRef CAS.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928–3938 CrossRef CAS PubMed.
- J. Cheng, M. Sulpizi and M. Sprik, J. Phys. Chem., 2009, 131, 154504 CrossRef PubMed.
- J. Cheng and M. Sprik, J. Chem. Theory Comput., 2010, 6, 880–889 CrossRef CAS.
- W. K. Den Otter and W. J. Briels, J. Chem. Phys., 1998, 109, 4139 CrossRef CAS PubMed.
- M. Sprik, Faraday Discuss., 1998, 110, 437–445 RSC.
- B. Ensing, E. J. Meijer, P. E. Blöchl and E. J. Baerends, J. Phys. Chem. A, 2001, 105, 3300 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- CP2K developers group, http://cp2k.berlios.de.
- J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS PubMed.
- G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–487 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Phys. Chem. A, 2007, 126, 014101 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ã. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian-09 Revision D.01, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- S. Ghisla and V. Massey, Biochem. J., 1986, 239, 1–12 CAS.
- J. Davies, N. L. Doltsinis, A. Kirby, C. D. Roussev and M. Sprik, J. Am. Chem. Soc., 2002, 124, 6594 CrossRef CAS PubMed.
- N. L. Doltsinis and M. Sprik, Phys. Chem. Chem. Phys., 2010, 5, 2612–2618 RSC.
- L. Bernasconi, E. Baerends and M. Sprik, J. Phys. Chem. B, 2006, 110, 11444 CrossRef CAS PubMed.
- D. Chandler, Introduction to modern statistical mechanics, Oxford University Press, New York, 1987 Search PubMed.
- I. Ivanov, B. Chen, S. Raugei and M. L. Klein, J. Phys. Chem. B, 2006, 110, 16365–16371 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The supporting information contains a comparison of the free energy profiles of the three proton transfer reactions using the Δd coordinate with and without an additional restraint on the proton accepting water molecule and radial distribution functions of the solvent environment around the donating lumiflavin site and the accepting water molecule. See DOI: 10.1039/c4cp01450b |
| This journal is © the Owner Societies 2014 |