Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic control of Förster energy transfer in a photonic environment
Frank
Schleifenbaum
,
Andreas M.
Kern
,
Alexander
Konrad
* and
Alfred J.
Meixner
*
Universität Tübingen, Institut für Physikalische und Theoretische Chemie, Auf der Morgenstelle 18, 72076 Tübingen, Germany. E-mail: x@uni-tuebingen.de; Fax: +49-7071-29-5490; Tel: +49-7071-29-76
First published on 1st May 2014
Abstract
In this study, the effect of modified optical density of states on the rate of Förster resonant energy transfer between two closely-spaced chromophores is investigated. A model based on a system of coupled rate equations is derived to predict the influence of the environment on the molecular system. Due to the near-field character of Förster transfer, the corresponding rate constant is shown to be nearly independent of the optical mode density. An optical resonator can, however, effectively modify the donor and acceptor populations, leading to a dramatic change in the Förster transfer rate. Single-molecule measurements on the autofluorescent protein DsRed using a λ/2-microresonator are presented and compared to the theoretical model's predictions. The observed resonator-induced dequenching of the donor subunit in DsRed is accurately reproduced by the model, allowing a direct measurement of the Förster transfer rate in this otherwise inseparable multichromophoric system. With this accurate yet simple theoretical framework, new experiments can be conceived to measure normally obscured energy transfer channels in complex coupled quantum systems, e.g. in photovoltaics or light harvesting complexes.
1 Introduction
Since the early work of Förster,1 the interaction between closely spaced fluorescent molecules via dipole–dipole coupling (fluorescence/Förster resonant energy transfer, FRET) has been a topic of great interest.2–9 The efficiency of the energy transfer depends on the spectral overlap between the emission of the donor chromophore and the absorption of the acceptor chromophore as well as on the distance and the mutual orientation of their respective transition dipole moments. While it is easily possible to design and prepare synthetic FRET-pairs and study the optical properties of the individual chromophores separately, this is not possible for many biological molecules such as the red fluorescent protein DsRed from the Discosoma reef coral. DsRed is known to form tetramers consisting of two different types of subunits containing a chromophore exhibiting fluorescence emission either in the green or red spectral regime.10–12 These spectral properties along with the steric composition as derived from X-ray data suggest a non-radiative Förster energy transfer within a tetrameric unit which has indeed been experimentally proven by different spectroscopic approaches using single molecule and ensemble techniques.2,11,13,14 However, it is not possible to separate the tetramers into functional monomers by chemical or biochemical means to make the isolated chromophoric species addressable for further investigation.A promising approach to spectrally isolate individual chromophoric subunits in biological FRET-systems is to modify the local photonic mode characteristics and density by using a λ/2-microresonator. We have previously demonstrated the optical confinement effect on both the fluorescence spectrum and the emission rate of single (synthetic) dye molecules by embedding them in a transparent polymer between two planar silver mirrors separated by half of the emission wavelength.15,16 The influence of the modified photonic mode density on a system consisting of coupled molecular dipole emitters is theoretically well described17–22 and several experimental demonstrations on the ensemble level have been reported to date.23–26
In this article, we report the first investigation of the autofluorescent protein DsRed embedded in a λ/2-microresonator by steady-state and time resolved spectroscopy down to the single molecule level. We use a novel microresonator design that allows coupling the fluorescence of individual chromophores to on- and off-axis cavity modes while maintaining physiological conditions for the embedded biomolecules. We show that, in this way, it is possible to spectrally isolate the two coupled chromophoric subunits of DsRed without destroying the composition of the tetrameric protein complex.
2 Rate equation model
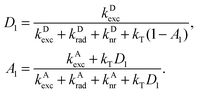
To study the effect of a photonic environment on a FRET-coupled system, we introduce a rate equation model describing the energetic processes of the system. Shown in Fig. 1, this model comprises two three-level subsystems D and A representing the donor and acceptor molecules, respectively. Each subsystem X (X = D, A) can be excited at the rate X0kexc = X0Jσ, where X0 is the probability to find the subsystem in its electronic ground state, kexc is the excitation rate constant, J is the incident illumination photon flux at the absorption wavelength and σ is the corresponding absorption cross section. Optical excitation of X0 leads to a vibronic level in the first electronically excited state X1′ which thermally relaxes rapidly within some picoseconds to X1, from which it may decay nonradiatively or radiatively at the rates X1knr and X1krad, respectively. Here, knr and krad are the nonradiative and radiative decay rate constants, respectively. In addition, the subsystems D and A are coupled via the nonradiative channel representing Förster resonant energy transfer, described by the rate constant kT as a measure of the dipole–dipole coupling strength. This Förster transition rate is defined as the probability per time interval that an acceptor molecule is transferred from its ground state A0 to its electronically excited state A1 by absorbing a photon of the optical near-field of the donor chromophore with state D1. The transition rate is then given by D1A0kT.The population probability dynamics for the excited states D1 and A1 of the subsystems can be written by a system of coupled differential equations,
| Ḋ1 = kDexcD0 − [kDrad + kDnr + kTA0]D1, |
| Ȧ1 = [kAexc + kTD1]A0 − [kDrad + kDnr + ]A1, | (1) |
 | (2) |
When placed in a modified photonic environment, e.g. a resonant cavity, the parameters in eqn (2) can change. First, the intensity of the incident light can be enhanced or suppressed when the cavity is excited on or off resonance, varying the incident photon flux J and thus kexc. With the intensity enhancement factor Fexc = I(r)/Ifs(r) denoting the incident intensity at the position r of the quantum system in a photonic environment compared to free space, the modified excitation rate constant can be expressed as kexc = Fexckexc,fs.
Second, the radiative decay rate constant krad is proportional to the local density of optical states (LDOS) ρ corresponding to the transition energy. In a photonic background, ρ is a function of space and the emitter's orientation and can vary by many orders of magnitude, dramatically changing the behavior of the coupled quantum system. Introducing the LDOS enhancement factor Frad = ρ(r)/ρfs(r) induced by the photonic environment at the position of the emitter, the radiative decay rate constant can be expressed as krad = Fradkrad,fs. The value Frad is also known as the Purcell factor.
Finally, the Förster transfer rate constant kT can be influenced by the photonic background as well. While FRET is a nonradiative process, often described as a near-field dipole–dipole interaction, it is nevertheless influenced by modifications to the electromagnetic field: if a photonic system enhances the donor dipole's near-field, it will equally enhance the induced dipole moment in the acceptor, thus increasing the FRET speed. The photonic enhancement FT = |ED(rA)|2/|EDfs (rA)|2 of the donor's dipole field intensity at the position of the acceptor compared to free space thus also describes the enhancement of the FRET channel, kT = FTkT,fs, assuming that there is no change in polarization.
The radiative and FRET enhancement factors can be conveniently computed given the photonic system's electromagnetic response in the form of its dyadic Green's function G. This 3 × 3-tensorial function describes the electric field at an arbitrary position r′ induced by a single dipole emitter in the photonic system,
| E(r′) = ω2μ(r)G(r′,r)·p. | (3) |
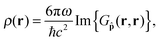 | (4) |
![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) =
= ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) ·G·
·G·![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) and
and ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) = p/|p| is a unit vector in the direction of the emitter's dipole moment. In free space, eqn (4) results analytically in ρfs(r) = ω2/(ℏc3); the LDOS is then homogeneous and isotropic. With eqn (4), the radiative enhancement factor can then be written as
= p/|p| is a unit vector in the direction of the emitter's dipole moment. In free space, eqn (4) results analytically in ρfs(r) = ω2/(ℏc3); the LDOS is then homogeneous and isotropic. With eqn (4), the radiative enhancement factor can then be written as | (5) |
 | (6) |
The dyadic Green's function G can be obtained using a number of analytical or numerical approaches. For the simple case of an ideal Fabry–Pérot microresonator, analytical calculations have been presented.27 For more complex resonator geometries including multiple layers and interfaces, the transfer matrix method (TMM) provides a quasi-analytical solution. For arbitrary photonic systems, numerical methods such as the finite-difference time-domain (FDTD)28 or surface integral equation (SIE)29 approach may be required for satisfactory results.
2.1 λ/2-Microresonator
Due to the simple geometry of a λ/2-microresonator, its electromagnetic response can be calculated analytically.27 The angular dependence of its modes' resonances limits the Purcell factor of a planar Fabry–Pérot-type resonator to at most Frad = 3, even for perfectly reflecting mirrors. Emission inhibition, on the other hand, can be very effective, reaching values of nearly Frad ≈ 0. The size of a λ/2-microresonator is on the order of the emitted light's wavelength, thus only the far field of an embedded emitter can populate its modes: as the near field's amplitude decays with R−3, it will have nearly vanished even before reaching the resonator's mirrors for the first time. A comparison of a dipole emitter's far field to its near field shows that the intensity of the far field which is only one wavelength λ away is more than 8 orders of magnitude weaker than that of the near field at a distance of λ/100. One can thus see that even a large resonant enhancement of the cavity modes will have only a minuscule effect on the FRET rate constant kT.Changes in the FRET rate D1A0kT in a λ/2-microresonator will therefore not be caused by a change in the rate constant, but instead by the changes in the donor and acceptor populations D1 and A0, respectively.30 In particular, efficient emission inhibition of the donor's emission wavelength can effectively increase its excited state population D1, leading to an increase in FRET. Similarly, inhibiting acceptor fluorescence can lead to a depletion of the ground state population A0, preventing Förster transfer.
3 Experimental results
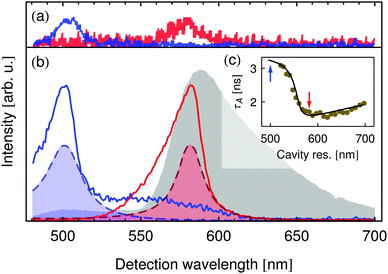
To observe the effects predicted by our model, we experimentally studied the fluorescence of a Förster-coupled system in a λ/2-microresonator. As a FRET system, we chose the autofluorescent protein DsRed, a complex molecule containing two spectrally isolated chromophoric subunits with fluorescence maxima at 505 nm and 580 nm, respectively. These two subunits can couple nonradiatively, allowing energy to be transferred from the energetically higher subunit to the lower subunit via FRET. The gray shaded area in Fig. 2(b) shows the free-space emission spectrum of DsRed when illuminated at 473 nm, clearly displaying the two fluorescence peaks.The photonic background in our study was defined by a λ/2 Fabry–Pérot microresonator enclosing the DsRed molecules. A schematic diagram of the sample-microresonator system is shown in Fig. 3. While one of the resonator's mirrors is flat, the other is minimally curved with a radius of R = 150 mm. This curvature is slight enough that the mirrors can still be assumed to be parallel, yet causes a well-defined variation in the mirror separation L(x,y) in the resonator plane. The longitudinal resonance wavelength can thus be tuned by scanning the detection point across the resonator.
The blue and red solid lines in Fig. 2(b) show the fluorescence spectra of DsRed in the microresonator for two different mirror separations L. The corresponding white-light transmission spectra, indicating the resonator's longitudinal resonances for the two mirror separations, are shown by the shaded dashed lines of the same color. The amplitudes of these spectra are not shown to scale but magnified to aid interpretation. Immediately, one can see that by choosing the correct resonance wavelength, one emission peak can be greatly enhanced while the other is nearly completely suppressed. For the blue curve, the normally dominant peak at 580 nm is so effectively suppressed by the resonator that it is visible only as a slight hump on the blue peak's flank. For the red curve, the off-resonance peak at 505 nm has completely disappeared. In both curves, the resulting peaks are asymmetric, showing a steep flank on the red side and a slow roll-off on the blue side. This is typical for emitters in a λ/2-resonator as the longitudinal resonance wavelength also corresponds to the resonator's cutoff wavelength: light with a wavelength longer than the longitudinal resonance cannot populate any mode in the resonator. Shorter wavelengths, however, can populate off-axis modes which are no longer parallel to the z-axis but which can nevertheless be collected by the high NA of the used objective.
The spectra of single DsRed tetramers shown in Fig. 2(a) in blue (donor resonat) and red (acceptor resonat) illustrate that the influence of the resonator on transfer coupled systems is observable even on the single particle level. This enables a precise control and study of individual chromophores within one distinct transfer coupled complex, whose optical properties may vary by i.e. induced environmental influences. To verify that the influence of the resonator on the molecules' emission spectra is indeed an effect of their varied emission rates and not simply a filtering of the emitted light, the acceptor fluorescence lifetime τA was studied as a function of the cavity resonance wavelength, viz. Fig. 2(c). The points show measured lifetimes and the curve is a calculation using the transfer matrix method (TMM) assuming a free-space fluorescence lifetime of τArad,fs = 6.7 ns and an emission quantum yield of ΦArad,fs = 25.2%. The dramatic change in the measured lifetime agrees perfectly with the calculation's prediction. The red and blue arrows indicate the two resonator configurations at which the spectra in Fig. 2(b) were recorded, corresponding to the cases of inhibition (blue) and enhancement (red) of strong acceptor emission.
To study the resonator's effect quantitatively and to verify the rate-equation model presented above, we study the resonator-induced dequenching of the donor chromophore: when the resonator is tuned to the emission peak at 505 nm, Fig. 2(b) shows that besides amplifying the donor emission, the acceptor fluorescence is effectively suppressed. If the quantum yield of the acceptor chromophore is sufficiently high, the lifetime of the A1 state will then be considerably increased. From eqn (1) one follows that an excited acceptor choromophore cannot participate in FRET and so this decay channel is lost to the donor. The resulting shift in the relative transition efficiency causes an increase in donor emission intensity compared to acceptor fluorescence. Fig. 4 shows the donor-to-acceptor fluorescence ratios for DsRed in a microresonator tuned to 505 nm (circles) and in free space (triangles), measured for increasing excitation power. In free space, this ratio remains in the order of 0.5 for all illumination power. With the acceptor fluorescence suppressed by the resonator, however, the donor dominates the fluorescence by a ratio of up to 10/1 in the measured range.
Typically, this behavior is difficult to observe in free space, since, on the one hand, the fluorescence lifetime of a typical acceptor dye is rather short and, on the other hand, the fluorescence lifetime of a typical (unquenched) donor, being in the same range, is too long. Hence, the acceptor has already relaxed to the ground state while the donor is still excited, allowing for another energy transfer which quenches the emission of the donor. However, using a microresonator system, it is possible to precisely adjust the radiative rates of the respective chromophores. Thus, one can significantly shorten the lifetime of the donor chromophore while the lifetime of the acceptor chromophore is lengthened.
One might argue that the larger D/A fluorescence ratio in the resonator is simply due to the fact that the donor fluorescence is enhanced and the acceptor fluorescence is suppressed by the resonator, even without a change in the FRET efficiency. This static effect, however, should not depend on the illumination power Pexc. In fact, the effect of static fluorescence enhancement can be observed for Pexc → 0. The modified fluorescence speed krad thus causes a change from fD/fA ≈ 0.5 to fD/fA ≈ 2.0, while the illumination-dependent modification of the FRET efficiency increases the ratio to fD/fA ≈ 10.
The dynamic behavior observed in the measurement is accurately reproduced by the rate equation model presented in this paper. The blue line in Fig. 4 shows the donor-to-acceptor fluorescence ratio D1kDrad/(A1kArad) predicted by our model for decay efficiencies Φx = kx/ktot given in Table 1. These values correspond to excited state fluorescence lifetimes of 2.8 ns and 2.6 ns for the uncoupled donor and acceptor, respectively, with fluorescence quantum yields (without FRET) of 18.1% and 25.2%. The FRET rate constant kT then corresponds to a value of 2.1 GHz, in agreement with previously measured data.31 With these values, the model's predictions are in excellent agreement with our experimental results.
| Chromophore | Φ rad,fs (%) | Φ nr,fs (%) | Φ T,fs (%) |
|---|---|---|---|
| Donor | 2.6 | 11.8 | 85.6 |
| Acceptor | 25.2 | 74.8 | — |
Having confirmed the accuracy of our model, we can now explore the parameter space of the studied system. In Fig. 5, we plot the donor-to-acceptor fluorescence ratio (red surface, left scale) and the FRET efficiency,
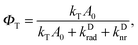 | (7) |
 | ||
| Fig. 5 Simulated D/A ratio (red surface) and FRET efficiencies (green surface) for different resonator widths d and excitation power Pexc. | ||
Many interesting features can be observed in this representation. First, one can see that the large increase in the D/A fluorescence ratio is only possible if the resonator is tuned to the correct wavelength. A large enhancement can be seen if the acceptor fluorescence is effectively inhibited while allowing, or even enhancing, donor emission. For larger L, both donor and acceptor emissions are allowed, and so the D/A ratio is similar to that in free space (cf. triangles in Fig. 4). For very small L, both donor and acceptor emissions are suppressed. While the D/A ratio is not strongly enhanced in this case, it shows a saturation onset at very low power Pexc. This is due to the fact that, with fluorescence being inhibited, Förster transfer plays the dominant role in the energy dynamics of the coupled system. As the resonator modes prevent the acceptor from decaying radiatively, the resulting FRET inhibition is clearly visible already at very low power. Finally, one can see that the FRET efficiency ΦT varies greatly across the shown parameter space. Depending on the incident power, tuning the resonator mirrors allows us to reduce the FRET efficiency between 50% and 75%. It should be pointed out that this is not a modification of the FRET rate constant kT as per the factor FT (here, FT = 1), as the resonator is not capable of sufficiently modifying the near field of the donor dipole. Much more, it is an active modification of the other transition parameters D1 and A0, allowing us to selectively change the rate and efficiency of the Förster transfer.
Acknowledgements
Financial support from the German Research Council (DFG) for ME1600/13-1 is gratefully acknowledged.References
- T. Förster, Intermolecular energy migration and fluorescence, Ann. Phys., 1948, 2, 55–75 CrossRef.
- T. A. Schüttrigkeit, U. Zachariae, T. von Feilitzsch, J. Wiehler, J. von Hummel, B. Steipe and M. E. Michel-Beyerle, Picosecond time-resolved fret in the fluorescent protein from discosoma red (wt-dsred), ChemPhysChem, 2001, 5, 325–328 CrossRef.
- S. Brasselet, E. J. G. Peterman, A. Miyawaki and W. E. Moerner, Single-molecule fluorescence resonant energy transfer in calcium concentration dependent cameleon, J. Phys. Chem. B, 2000, 104, 3676–3682 CrossRef CAS.
- J. Hofkens, M. Cotlet, T. Vosch, P. Tinnefeld, K. D. Weston, C. Ego, A. Grimsdale, K. Müllen, D. Beljonne, J. Luc Brédas, S. Jordens, G. Schweitzer, M. Sauer and F. C. de Schryver, Revealing competitive Förster-type resonance energy-transfer pathways in single bichromophoric molecules, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(23), 13146–13151 CrossRef CAS PubMed.
- E. B. van Munster and T. W. Gadella, Fluorescence lifetime imaging microscopy (flim), Adv. Biochem. Eng./Biotechnol., 2005, 95, 143–175 CrossRef PubMed.
- E. A. Jares-Erijman and T. M. Jovin, Fret imaging, Nat. Biotechnol., 2003, 21(11), 1387–1395 CrossRef CAS PubMed.
- A. A. Deniz, T. Laurence, G. S. Beligere, M. Dahan, A. B. Martin, D. S. Chemla, P. E. Dawson, P. G. Schultz and S. Weiss, Single molecule protein folding: diffusion Förster energy transfer studies of the denaturation of chymotrypsin inhibitor 2, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 5179–5184 CrossRef CAS PubMed.
- R. Gronheid, J. Hofkens, F. Köhn, T. Weil, E. Reuther, K. Müllen and F. C. de Schryver, Intramolecular forster energy transfer in dendritic systems at the single molecule level, J. Am. Chem. Soc., 2002, 124, 2418–2419 CrossRef CAS PubMed.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Kluwer Academic, New York, 2nd edn, 1999 Search PubMed.
- G. Baird, D. Zacharias and R. Tsien, Biochemistry, mutagenesis, and oligomerization of dsred, a red fluorescent protein from coral, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(22), 11984–11989 CrossRef CAS PubMed.
- B. Lounis, J. Deich, F. I. Rosell, S. G. Boxer and W. E. Moerner, Photophysics of dsred, a red fluorescent protein, from the ensemble to the single-molecule level, J. Phys. Chem. B, 2001, 105, 5048–5054 CrossRef CAS.
- M. Matz, A. Fradkov, Y. Labas, A. Savitsky, A. Zaraisky, M. Markelov and S. Lukyanov, Fluorescent proteins from non-bioluminescent anthozoa species, Nat. Biotechnol., 1999, 17, 969–973 CrossRef CAS PubMed.
- C. Blum, V. Subramaniam, F. Schleifenbaum, F. Stracke, B. Angres, A. Terskikh and A. J. Meixner, Single molecule fluorescence spectroscopy of mutants of the discosoma red fluorescent protein dsred, Chem. Phys. Lett., 2002, 362, 355–361 CrossRef CAS.
- F. Schleifenbaum, Energy transfer in the red fluorescent protein DsRed in confined optical fields, Life Sciences, Rhombos, Berlin, 2008, vol. 3 Search PubMed.
- M. Steiner, F. Schleifenbaum, C. Stupperich, A. V. Failla, A. Hartschuh and A. J. Meixner, Microcavity-controlled single-molecule fluorescence, ChemPhysChem, 2005, 6, 2190–2196 CrossRef CAS PubMed.
- M. Steiner, F. Schleifenbaum, C. Stupperich, A. V. Failla, A. Hartschuh and A. J. Meixner, A new microcavity design for single molecule detection, J. Lumin., 2006, 119(120), 167–172 CrossRef PubMed.
- G. S. Agarwal and S. D. Gupta, Microcavity-induced modification of the dipole-dipole interaction, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57(1), 667–670 CrossRef CAS.
- M. J. A. Dood, J. Knoester, A. Tip and A. Polman, Förster transfer and the local optical density of states in erbium doped silica, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1151021 Search PubMed.
- S. D. Druger, S. Arnold and L. M. Folan, Theory of enhanced energy transfer between molecules embedded in spherical dielectric particles, J. Chem. Phys., 1987, 87(5), 2649–2659 CrossRef CAS PubMed.
- T. Kobayashi, Q. Zheng and T. Sekiguchi, Resonant dipole-dipole interaction in a cavity, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52(4), 2835–2846 CrossRef CAS.
- P. T. Leung and K. Young, Theory of enhanced energy transfer in an aerosol particle, J. Chem. Phys., 1988, 89(5), 2894–2899 CrossRef CAS PubMed.
- A. C. Pineda and D. Ronis, Classical model for energy transfer in microsperical droplets, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52(5), 5178–5194 CrossRef CAS.
- P. Andrew and W. L. Barnes, Förster energy transfer in an optical microcavity, Science, 2000, 290, 785–788 CrossRef CAS.
- W. L. Barnes and P. Andrew, Energy transfer under control, Nature, 1999, 400, 505–506 CrossRef CAS PubMed.
- M. Hopmeier, W. Guss, M. Deussen, E. O. Göbel and R. F. Mahrt, Enhanced dipole-dipole interaction in a polymer microcavity, Phys. Rev. Lett., 1999, 82(20), 4118–4121 CrossRef CAS.
- A. Konrad, A. L. Trost, S. Skandary, M. Hussels, A. J. Meixner, N. V. Karapetyan and M. Brecht, Manipulating the excitation transfer in Photosystem I using a Fabry–Perot metal resonator with optical subwavelength dimensions, Phys. Chem. Chem. Phys., 2014, 16, 6175–6181 RSC.
- G. Bjork, On the spontaneous lifetime change in an ideal planar microcavity-transition from a mode continuum to quantized modes, IEEE J. Quantum Electron., 1994, 30(10), 2314–2318 CrossRef CAS.
- A. Taflove and S. C. Hagness, Computational Electrodynamics: The Finite-Difference Time-Domain Method, Artech House, Boston, 2nd edn, 2000 Search PubMed.
- A. M. Kern and O. J. F. Martin, Surface integral formulation for 3D simulations of plasmonic and high permittivity nanostructures, J. Opt. Soc. Am. A, 2009, 26(4), 732–740 CrossRef.
- C. Blum, N. Zijlstra, A. Lagendijk, M. Wubs, A. P. Mosk, V. Subramaniam and W. L. Vos, Nanophotonic control of the forster resonance energy transfer efficiency, Phys. Rev. Lett., 2012, 109(20), 203601 CrossRef.
- F. Schleifenbaum, Energy transfer in the red fluorescent protein DsRed in confined optical fields, Phd thesis, 2008 Search PubMed.
| This journal is © the Owner Societies 2014 |