Thermodynamics of 4,4′-stilbenedicarboxylic acid monolayer self-assembly at the nonanoic acid–graphite interface

Abstract

A direct calorimetric measurement of the overall enthalpy change associated with self-assembly of organic monolayers at the liquid–solid interface is for most systems of interest practically impossible. In previous work we proposed an adapted Born–Haber cycle for an indirect assessment of the overall enthalpy change by using terephthalic acid monolayers at the nonanoic acid–graphite interface as a model system. To this end, the sublimation enthalpy, dissolution enthalpy, the monolayer binding enthalpy in vacuum, and a dewetting enthalpy are combined to yield the total enthalpy change. In the present study the Born–Haber cycle is applied to 4,4′-stilbenedicarboxylic acid monolayers. A detailed comparison of these two aromatic dicarboxylic acids is used to evaluate and quantify the contribution of the organic backbone for stabilization of the monolayer at the nonanoic acid–graphite interface.

---

Introduction

Supramolecular self-assembly is an ubiquitous approach for the bottom-up fabrication of functional nanostructures. As a foundation for a targeted and efficient fabrication it is important to study and understand the mechanisms and driving forces of supramolecular self-assembly.^1–4 Two-dimensional surface supported self-assembly has attracted special interest due to both conceptual and analytical advantages. On the one hand, surfaces provide an interface and support for these nanostructures, an important prerequisite for applications in sensorics, catalysis, and organic electronics.^5–7 On the other hand, it is relatively straightforward to characterize surface-supported monolayers in real space by high resolution Scanning Probe Microscopy.^8–11

Owing to the high relevance for applications and the ease of preparation, a great part of self-assembly research is focused on the liquid–solid interface.^12,13 A number of experiments have demonstrated major influences of the liquid phase on both the thermodynamics and kinetics of interfacial self-assembly.^14–17 For instance, in comparison to the vacuum–solid interface, desorption barriers are considerably lowered, giving rise to vertical mobility of the building blocks. Consequently, self-assembly at liquid–solid interfaces is highly dynamic, and many systems represent the thermodynamically most favourable structure corresponding to the lowest Gibbs free energy.^{8,10,11,18,19} Accordingly, thermodynamical approaches were successfully applied to understand monolayer structure selection and formation processes. The driving force for self-assembly is a gain in free energy, i.e. ΔG = ΔH − TΔS < 0. Thus, for a fundamental understanding of self-assembly, a quantitative assessment of ΔG is inevitable. For the most part, binding enthalpy is gained by forming more and stronger bonds in the self-assembled structure, while entropy is reduced because the building blocks lose degrees of freedom. However, notable contributions to free energy can also arise from desolvation and dewetting processes, and are normally associated with an enthalpic cost and an entropic gain.

A common approach to theoretically determine the thermodynamically most stable structure depending on the solute concentration is based on the equality of the chemical potentials in solution and within the monolayer in thermodynamical equilibrium. By using established concepts for the concentration dependence of the chemical potential, e.g. ideal or regular solutions, the free energy of competing monolayer structures can be evaluated and compared. This approach was successfully employed to explain the concentration dependent transition from a densely packed to a porous polymorph²⁰ or the emergence of different bimolecular phases.¹⁴ Recently De Feyter et al. extended this approach by using the concentration dependence of the transition temperature of a structural phase transitions as additional experimental input for a thermodynamical model that yields monolayer enthalpies and entropies.²¹ Alternatively, the monolayer free energy can be assessed by a separate evaluation of ΔH and ΔS,^15,16 whereby ΔH can be obtained from simulations. Since most molecules of interest for monolayer self-assembly at the liquid–solid interface are relatively large, molecular mechanics (MM) or molecular dynamics (MD) are often the methods of choice. MM and MD simulations have been successfully applied to a wide range of systems.^{14–16,22–25} These simulations, however, neglect the supernatant liquid phase and remain limited to the quantification of lattice energies. Moreover, both MD and Monte Carlo (MC) simulations are valuable tools for understanding monolayer formation and selection processes.^25–29 For MC appropriate modelling of the intermolecular interactions is crucial, since the outcome is extremely sensitive to simulation parameters. On the other hand, MD as an atomistic simulation technique, does not require mapping of the molecular building blocks onto a model, but sensitively depends on parameters of the underlying force field. A disadvantage of MD is its comparatively large computational cost, limiting both system size and simulation time spans.

Apart from MD and to some degree MM simulations, most theoretical approaches rely on precise structural data as experimental input.^14–16,24 At the liquid–solid interface these data are typically acquired by STM, and especially monolayer structures of larger compounds with recognizable geometric shape can be resolved with high precision. An unsolved simulation challenge arises for porous monolayers due to possible coadsorption of solvent molecules within the pores.^14,15,21 Unfortunately, in most cases these solvent molecules cannot be discerned in STM images, hence no structural data is available for a theoretical assessment of the associated non-negligible enthalpy contribution.

Equilibrium approaches, however, are only appropriate if the experimental structure represents the thermodynamically most stable structure. Especially for larger molecules or strongly interacting surfaces, self-assembly can also become kinetically hindered, resulting in the emergence of metastable phases.¹⁷ For such systems, it is advisable to check whether an irreversible conversion from a possible metastable to a more stable phase can be induced by providing additional thermal energy.^30,31 This does not require exceptional instrumentation, as it can straightforwardly be done by simple ex situ heating.

On the experimental side, Microflow Calorimetry (MFC) is an important, if not the only experimental technique to measure heats of adsorption directly.³² MFC was similarly applied to monolayer adsorption on graphitic surfaces. The main advantage is its integral character, i.e. the measured enthalpy inherently contains all individual contributions. However, solvent desolvation and dewetting can lead to relatively large positive enthalpy contributions, and the resulting overall enthalpy change can be rather small,⁴ thus limiting the accuracy or even applicability of MFC.

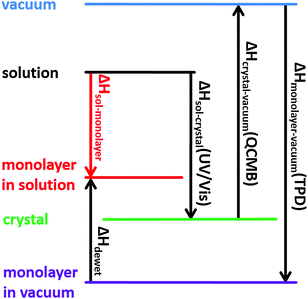
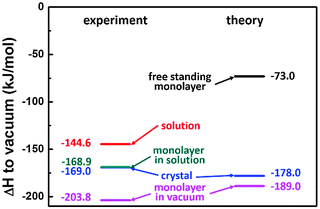
In previous work we have introduced an adapted Born–Haber cycle to deduce the overall enthalpy change for self-assembly of interfacial monolayers.⁴ Since it can become intricate to measure the enthalpy difference between molecules in solution and within the monolayer directly, we suggested an indirect assessment via measuring the enthalpy differences between defined and accessible reference states. The scheme in Fig. 1 shows how the Born–Haber cycle is constructed from the sublimation enthalpy, the dissolution enthalpy, and the binding energy of molecules within the monolayer in vacuum at the vacuum–solid interface. These required enthalpies can be measured. At the liquid–solid interface an additional contribution from solvent dewetting has to be considered.

Fig. 1 Scheme of the Born–Haber cycle. The overall enthalpy change for molecules from solution into the adsorbed monolayer (ΔH_{sol-monolayer}, red arrow) is obtained from the enthalpy differences between crystal and solution (ΔH_{crystal→sol}), crystal and vacuum (ΔH_{crystal→vacuum}), and monolayer in vacuum and an isolated molecule in vacuum (ΔH_{monolayer→vacuum}). The label “monolayer in vacuum” in the figure refers to the monolayer at the solid–vacuum interface, and the label “monolayer in solution” to the monolayer at the solid–solution interface, respectively. The effect of solvent dewetting is taken into account by a dewetting enthalpy (ΔH_dewet). To each of the enthalpies the corresponding experimental technique for its assessment is given. Labels in the figure: UV/Vis – ultraviolet/visible absorption spectroscopy; QCMB – quartz crystal microbalance; TPD – temperature programmed desorption.

In addition, we have shown that also MM and MD simulations can yield accurate and reliable figures for these enthalpies, provided that the resonance enhanced strength of two-fold cyclic hydrogen bonds between carboxylic acids is taken into account by an appropriately modified force field.³³ This perfect agreement sets the basis for hybrid Born–Haber cycles, where either theoretical or experimental enthalpy values are used, depending on which is more easily accessible. For instance, a theoretical evaluation of dissolution enthalpies by MD is computationally expensive since large system sizes and long simulation times are required, whereby the error bars still remain rather high. On the other hand, an experimental determination by measuring the solubility as a function of temperature is relatively straightforward. Binding energies of molecules within a monolayer can in principle be measured by temperature programmed desorption (TPD). However, the experiments are rather time consuming and require molecules that are thermally stable for sublimation. On the contrary, MM calculations of the monolayer binding energy based on structural data from STM experiments are rather efficient and computationally inexpensive.

In the present study we utilize the method proposed in ref. 4 to evaluate the thermodynamics of 4,4′-stilbenedicarboxylic acid (SDA) monolayer self-assembly (cf. inset in Fig. 2 for structure) at the nonanoic acid–graphite interface. Similar to previously studied terephthalic acid (TPA), SDA is a dicarboxylic acid, however, with an extended aromatic backbone, consisting of two phenyl rings interconnected by an ethenyl unit. In this respect it is interesting to quantify the influence of the extended aromatic system on the overall enthalpic stabilization. In the following, each individual enthalpy contribution to the Born–Haber cycle is discussed separately and eventually combined to yield the overall enthalpy change. This can then be compared to the entropy cost of self-assembly, as estimated by using a partition scheme based on established methods. To quantify the influence of polyaromatic systems it is also instructive to compare the thermodynamics of SDA monolayer self-assembly to previously studied TPA.

Fig. 2 STM images of SDA monolayer at the nonanoic acid–graphite interface: (a) overview image 61.5 × 61.5 nm², I = 60 pA, V_sample = 300 mV; (b) high resolution image (6.5 × 6.5 nm², I = 80 pA, V_sample = 250 mV). The unit cell is indicated by the white lines, corresponding to A = (16.1 ± 0.1) Å, B = (7.5 ± 0.1) Å, γ = 52° ± 1°. SDA molecules are depicted to scale in the overlay.

Methods

Experimental

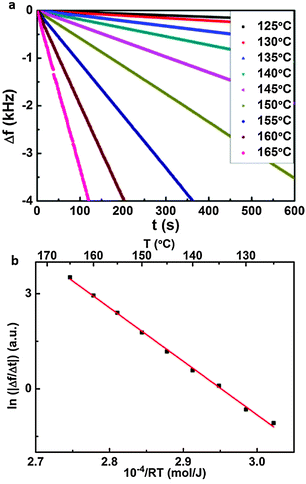
SDA and 1-nonanoic acid (9A) were obtained from ABCR and Sigma Aldrich and used without further purification. STM experiments were carried out with a home-built instrument driven by a commercial ASC500 controller from attocube systems AG. Approximately 40 μL of solution were applied on a freshly cleaved graphite sample. A rimmed sample holder was used in order to avoid concentration changes caused by spilling. Images were acquired directly at the liquid–solid interface with a mechanically cut PtIr (90/10) tip immersed into the liquid.

The sublimation enthalpy was determined by using a home-built Knudsen cell with an integrated Quartz Crystal Microbalance (QCMB) (1.4 cm crystal diameter and 6 MHz nominal eigenfrequency).³⁴ The shift of resonant frequency (Δf) which is proportional to the effusion rate was measured vs. time for different crucible temperatures. For all temperatures, the slope in Δf vs. t curves is constant, indicating the validity of the chosen approach.³⁴

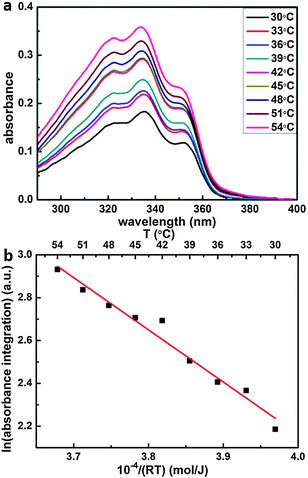
The enthalpy of dissolution was determined from temperature dependent measurements of SDA solubility in 9A by means of UV-Vis absorption spectroscopy (USB4000 Miniature Fiber Optic Spectrometer from Ocean Optics with an ISS-UV/VIS light source, and a Hellman 100-QS quartz glass cuvette; 10 mm optical path length). To this end, the cuvette was heated with two sideways mounted Peltier elements and the temperature was measured with a thermocouple in the cuvette and kept constant with a temperature controller (Eurotherm 2416). Spectra of pure 9A solvent at the respective temperatures were used as reference. According to Lambert–Beer's law, the absorbance of saturated solutions is proportional to the solubility. UV-Vis absorption spectra of SDA exhibit three clear absorption bands centered at 320 nm, 335 nm, and 350 nm due to n–π* and π–π* transitions as expected for aromatic compounds with double bonds. Since there is no interference with absorption of the 9A solvent in this spectral range, temperature dependent UV-Vis absorption spectroscopy is an appropriate method to quantify the enthalpy of dissolution.

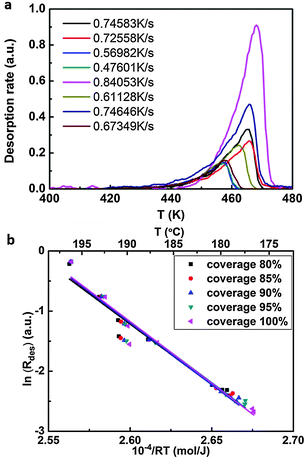
TPD experiments were performed in ultra-high vacuum. Monolayers were first deposited onto a graphite surface by thermal sublimation, and subsequently desorbed by linearly ramping the substrate temperature in time. Simultaneously, SDA desorption rates were recorded by a quadrupole mass-spectrometer positioned close to the graphite surface and set to a mass of 179 amu. Eight sets of experiments were performed with different heating rates ranging from 0.48 K s⁻¹ to 0.84 K s⁻¹. The complete analysis method was used to calculate the enthalpy of desorption, since no a priori assumptions neither on the desorption order nor on the underlying desorption mechanism are required.³⁵

Computational

Theoretical enthalpy values were obtained by MM and MD calculations using the MM3 force field.^36–38 For molecules like SDA, the strength of hydrogen bonds is significantly enhanced by resonance assisted hydrogen bonding (RAHB) due to delocalisation of the electron density across the π-system of the C=O in carboxylic groups.^39,40 The MM3 force field was modified accordingly to obtain accurate enthalpy values for hydrogen bonds: hydrogen-bond parameters ε_H⋯O = 33.4 kJ mol⁻¹ and R_H⋯O = 2.05 Å reproduce the density-functional theory (B3LYP functional, 6-31G(d) basis set, counterpoise-corrected) values of the hydrogen bond energy of the carboxylic acid dimer (−66.9 kJ mol⁻¹ for TPA as model system) and the TPA–TPA distance in the dimer (9.64 Å).

The theoretical binding enthalpy of SDA in bulk crystals was calculated in two steps. Firstly, STM results were used as a starting point to optimise the theoretical lattice parameters A, B, and γ for the 2D lattice. Based on these values the lattice parameters C, α, and β were varied until the lowest-energy 3D structure of SDA was obtained.

Adsorption energies were calculated for an SDA molecule on a large (800 C atoms) hydrogen-terminated graphene sheet, for a regular grid of the molecule's positions and azimuthal orientations.

Results and discussion

Monolayer structure

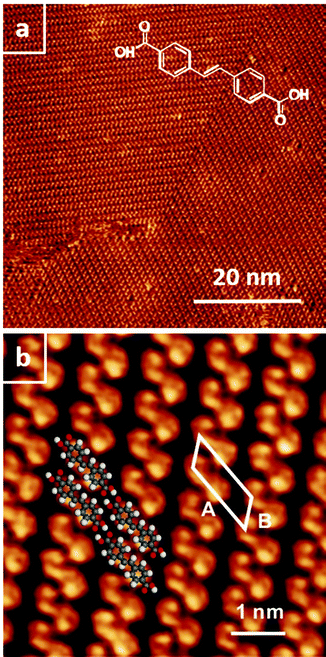
At the nonanoic acid–graphite interface SDA self-assembles into long-range ordered monolayers with low defect density and large domain size, an overview STM image is depicted in Fig. 2(a). Owing to the high stability of the monolayer, submolecular details can routinely be resolved by STM, a representative image is shown in Fig. 2(b). The structure contains one molecule per unit cell. Precise lattice parameters of A = (16.1 ± 0.1) Å, B = (7.5 ± 0.1) Å, γ = 52° ± 1° and the corresponding superstructure matrix were obtained from split images (cf. ESI†). The experimental lattice parameters and the orientation to the graphite substrate are perfectly reproduced by a commensurate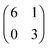 superstructure, corresponding to A = 16.13 Å, B = 7.38 Å, γ = 52.4°. Commensurability of the SDA monolayer is in accord with the absence of a Moiré pattern, i.e. a large scale STM contrast modulation due to inequivalent adsorption sites, as typically observed for incommensurate superstructures on graphite.^41,42 From the STM contrast single SDA molecules can be unambiguously identified. As indicated by the overlay to Fig. 2(b), SDA molecules are interconnected into 1D chains by two-fold cyclic hydrogen bonds between their carboxylic groups. The 2D monolayer structure is comprised of a densely packed arrangement of 1D hydrogen bonded chains, most likely stabilized by weaker interchain C–H⋯O hydrogen bonds. This precise assessment of the monolayer structure facilitates a detailed comparison with the geometry optimized structure from MM calculations (vide infra).

Born–Haber cycle

To obtain a precise value of the total enthalpy change of SDA monolayer self-assembly, we propose an adapted Born–Haber cycle as introduced in previous work using the dicarboxylic acid terephthalic acid (TPA) as a model system.⁴ The basic idea is to combine sublimation enthalpy, dissolution enthalpy, and the binding enthalpy of SDA in the monolayer to derive a precise value for the enthalpy difference between molecules dissolved in solution and incorporated into the monolayer. Additional contributions from the solvent are taken into account by a dewetting enthalpy. The proposed Born–Haber cycle is depicted in Fig. 1. Enthalpy differences between crystal and vacuum, monolayer and vacuum, crystal and solution are measured by the experimental techniques described in the experimental section, the results are presented in the following.

Binding enthalpy of monolayer on graphite with respect to vacuum

The binding enthalpy of SDA in the monolayer on graphite with respect to isolated molecules in vacuum ΔH_{monolayer→vacuum} was determined by temperature programmed desorption (TPD) experiments. Samples with monolayer coverage were prepared by sublimation of SDA from a Knudsen cell onto graphite with a crucible temperature of 190 °C and a deposition time of ∼20 min. TPD experiments were carried out by heating with a linear temperature ramp, applying different heating rates. Individual desorption spectra are depicted in Fig. 3(a). The experiments were evaluated with the complete analysis method, the corresponding results are shown in Fig. 3(b) and yield a monolayer binding enthalpy of −(203.8 ± 9.1) kJ mol⁻¹. This energy includes both SDA–SDA interactions in the monolayer and SDA adsorption energy on graphite.

Fig. 3 Temperature programmed desorption of SDA from graphite: (a) desorption rate vs. surface temperature for different heating rates; (b) corresponding plots at different monolayer coverages obtained from a complete analysis. The enthalpy of desorption derived from linear fitting of the obtained plots amounts to +(203.8 ± 9.1) kJ mol⁻¹.

The monolayer binding energy was also theoretically assessed by MM calculations with a modified MM3 force field as described in the computational section. These MM calculations also allow for a partition of the total binding energy into molecule–molecule and molecule–substrate interactions, thereby providing deeper insights into the relative strengths and interplay of these interactions. To evaluate substrate influences on the monolayer structure, first a free standing SDA monolayer comprised of densely packed hydrogen bonded chains was optimized, resulting in a SDA binding energy of −82.7 kJ mol⁻¹. The corresponding lattice parameters of A = 16.00 Å, B = 8.15 Å, γ = 49.7° are already close to those of the experimental commensurate superstructure (16.1 Å, 7.38 Å, 52.4°). Consequently, the lattice parameters of the free-standing SDA monolayer which are controlled only by molecule–molecule interactions can be maintained upon adsorption on graphite with only slight adjustments. Hence, the SDA monolayer can easily realize the energetic advantage of a commensurate superstructure on the graphite surface, where each molecule can occupy its preferred adsorption site. Additional MM calculations showed that constraining the SDA lattice to the experimental values of the commensurate superstructure reduces the binding energy to −73.0 kJ mol⁻¹, i.e. causes an energy penalty of +9.7 kJ mol⁻¹.

The molecule–substrate interaction was evaluated by optimizing a single SDA molecule on graphite. Different sites within the graphite unit cell and azimuthal orientations were probed on a regular grid. The geometry of SDA permits similar adsorption sites for both phenyl rings on graphite, and the highest and lowest binding energy configurations correspond to AB (highest binding) and AA (lowest binding) stacking with corresponding adsorption energy values of −116.4 kJ mol⁻¹ and −115.2 kJ mol⁻¹, respectively. The energy difference between the most favourable and least favourable adsorption site may be somewhat underestimated in these calculations: for comparison, the diffusion barrier for benzene on graphite calculated with MM3 is 0.004 eV,⁴ while this property was experimentally measured to be 0.017 + 0.012 eV.⁴³ The value of the energy minimum is likely to be more reliable than the energy barrier.

However, the commensurate superstructure corresponds to a different orientation of SDA on graphite (Fig. 4), where the phenyl rings are not ideally stacked on graphite. In the actual orientation the adsorption energy is still large, but the range between maximum and minimum is smaller (only between −116.0 and −115.8 kJ mol⁻¹). The calculated total binding energy of SDA in a monolayer on graphite is obtained as the sum of molecule–molecule and molecule–substrate interactions (in the adsorption configuration that corresponds to the experimental commensurate structure, Fig. 4) and amounts to −189.0 kJ mol⁻¹, in quantitative agreement with the TPD experiment.

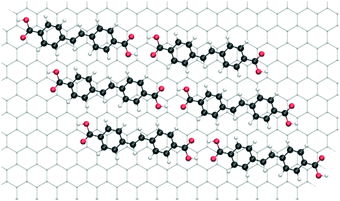Fig. 4 Model of the lowest energy SDA monolayer structure based on the experimental commensurate superstructure.

Sublimation enthalpy

The sublimation enthalpy ΔH_{crystal→vacuum} is derived from temperature dependent measurements of the effusion rate in high vacuum by means of a Quartz Crystal Microbalance (QCMB).³⁴ The shift of resonant frequency Δf vs. time t is depicted in Fig. 5(a) for nine different crucible temperatures in a range from 125 °C to 165 °C. The slope corresponds to the effusion rate, which is constant for a given crucible temperature. The effusion rate is proportional to the saturated vapour pressure of SDA at the respective crucible temperature, accordingly ΔH_{crystal→vacuum} can be derived from the slope in a Van't Hoff plot. As shown in Fig. 5(b) the corresponding Van't Hoff plot is perfectly linear, resulting in a value of ΔH_{crystal→vacuum} = +(169.0 ± 2.8) kJ mol⁻¹.

Fig. 5 Measurement of the SDA effusion rate from a Knudsen-cell by a Quartz Crystal Microbalance: (a) resonant frequency shift Δf vs. time t traces for crucible temperatures from 125 °C up to 165 °C; (b) corresponding Van't Hoff plot; each dataset in (a) is represented by one data point. From the slope a sublimation enthalpy of +(169.0 ± 2.8) kJ mol⁻¹ is deduced.

For a theoretical evaluation of ΔH_{crystal→vacuum} the crystal structure is required. An experimentally determined crystal structure is unfortunately not available for SDA. However, by analogy with crystal structures from other carboxylic acids,^44,45 it can be safely assumed that both carboxylic groups of SDA take part in two-fold cyclic hydrogen bonds, and SDA molecules, most likely, form 2D layers. To evaluate the contribution of these hydrogen bonds, MM calculations of 1D hydrogen bonded SDA chains were performed, resulting in a binding energy of −67.0 kJ mol⁻¹. To obtain a theoretical estimate of ΔH_{crystal→vacuum} a hypothetic SDA crystal structure was constructed as a stacked arrangement of 2D monolayers. MM geometry optimization results in a triclinic structure with one molecule per unit cell and lattice parameters of a = 16.0 Å, b = 7.9 Å, c = 4.3 Å, α = 132°, β = 73°, γ = 131°. The full geometry optimization of the bulk structure has not affected the intrachain spacing of SDA within the hydrogen bonded chains, but resulted in a slight change of the interchain spacing as compared to a pure 2D structure. The binding enthalpy of SDA in this hypothetic structure of −178.0 kJ mol⁻¹ is nevertheless in excellent agreement with the experimental value. Comparison of the total binding energy with that of the 1D chain, i.e. the contribution from the intermolecular hydrogen bonds, reveals a contribution of ∼100 kJ mol⁻¹ of additional intermolecular interactions, as the weak interchain hydrogen bonds and van der Waals interactions both within and between 2D layers of SDA. Interestingly, for the large SDA molecule the strength of van der Waals forces in the 3D structure already exceeds the strong two-fold hydrogen bonds.

Dissolution enthalpy

The enthalpy of dissolution ΔH_{crystal→sol} was derived from measurements of SDA solubility in 9A as a function of temperature in the range 30 °C to 54 °C by UV-Vis absorption spectroscopy. Single UV-Vis absorption spectra of saturated solutions for different temperatures are depicted in Fig. 6(a). The absorbance increases with increasing temperature, indicating an endothermic process. For the corresponding Van't Hoff plot in Fig. 6(b) the spectra were integrated between λ = 290 nm–400 nm, and the slope corresponds to an endothermic dissolution enthalpy of +(24.4 ± 1.5) kJ mol⁻¹. For comparison, the binding energy of a two-fold cyclic hydrogen bonded carboxylic acid dimer is in the range of −67.8 kJ mol⁻¹, as determined from IR absorption spectra of benzoic acid.⁴⁰ Since the experimental dissolution enthalpy is smaller than the binding enthalpy of two-fold carboxylic acid groups, we conclude that solvated SDA molecules bind to two 9A solvent molecules by two-fold hydrogen bonds. As outlined above, the computational cost of a theoretical solvation enthalpy determination by MD is relatively high, while the error bars are quite large, we thus use the experimental value for the Born–Haber cycle.

Fig. 6 SDA solubility measurements in 9A as a function of temperature: (a) UV-Vis absorption spectra of saturated SDA in 9A solutions obtained at different temperatures, (b) corresponding Van't Hoff plot; the integral absorbance for each temperature was obtained from the spectra in (a) by integration between λ = 290 nm–400 nm. The derived enthalpy of dissolution is +(24.4 ± 1.5) kJ mol⁻¹.

Dewetting enthalpy

Larger fatty acids are solvents with a high affinity to graphite. Accordingly, the formation of stable ordered solvent monolayers can be observed and has to be considered in the overall enthalpy balance. The 9A monolayer structure consists of an interdigitated dense packing of hydrogen bonded dimers.⁴⁶ Consequently, self-assembly of a solute monolayer requires prior desorption of this stably adsorbed solvent monolayer. The associated enthalpy cost of dewetting is very difficult to assess: on the experimental side, because it cannot directly be measured; on the theoretical side because the required system size renders a thorough calculation computationally very challenging, and their results not easily tractable. Albeit it is known that 9A forms quasi-static ordered monolayers on graphite,⁴ additional complications arise due to the fact that the precise thickness of the interfacial solvent layer, i.e. contributions from second and third layers, and its precise structure are not known.

Both the initial ordered 9A solvent and the subsequently self-assembled SDA solute monolayers are in direct contact with the supernatant liquid 9A. Stable adsorption of a second 9A monolayer on top of a 9A or SDA monolayer has never been observed by STM measurements. The particularly strong interaction between alkane tails and graphite is indispensable for the stabilization of 9A monolayers. Consequently, neither the ordered 9A nor the SDA monolayer provides a suitable template for stable adsorption of a second 9A layer. In order to estimate the dewetting enthalpy, it is assumed that the interaction energy per unit area of the respective monolayers with liquid 9A, i.e. the interface tensions, are comparable within the experimental error of this approach, and the structures of the second, third and further solvent layers are approximately similar both above SDA and above 9A monolayers. Therefore, when comparing SDA and 9A interfacial monolayers, the energies of these near-interface layers would cancel out. Accordingly, for dewetting only the first 9A monolayer needs to be taken into account.

Based on this simplifying assumption, the enthalpy contribution from desorption of the first 9A monolayer into the liquid is evaluated from two contributions: (i) the enthalpy difference between 9A on graphite and in vacuum, and (ii) the evaporation enthalpy, i.e. the enthalpy difference between 9A in vacuum and liquid. According to MM simulations the desorption enthalpy of 9A from graphite into vacuum amounts to ΔH(9A)_{graphite→vacuum} = +107.5 kJ mol⁻¹,⁴ in good agreement with TPD experiments.³⁴ The evaporation enthalpy amounts to ΔH(9A)_{liquid→vacuum} = +82.4 kJ mol⁻¹.⁴⁷ Consequently, the enthalpy difference between adsorbed and liquid 9A corresponds to ΔH(9A)_{graphite→liquid} = + 25.1 kJ mol⁻¹. Yet, desorption of the first 9A monolayer is also associated with a favourable entropic contribution to the total free energy. A reasonable estimate can be obtained from the entropy of melting, i.e. the transition from crystalline to liquid 9A. Since 9A molecules are fully immobilized and constrained to a specific orientation and conformation both in the crystal and in the monolayer, the entropies of 9A are comparable within the accuracy of this approach. The entropy of melting corresponds to +69.4 J mol⁻¹ K⁻¹,⁴⁸ consequently, for dewetting a 9A monolayer, the entropic contribution to the free energy −TΔS at room temperature corresponds to −20.7 kJ mol⁻¹. Accordingly, ΔG for formation of an ordered 9A monolayer at the liquid–graphite interface is only −4.4 kJ mol⁻¹, or, in other words, the 9A monolayer is thermodynamically not very stable. This provides evidence that only the first monolayer of solvent on graphite is stable, because the enthalpic stabilization in a second layer would be inferior and would not be able to compensate the entropy cost of trapping 9A into a quasi-static structure.

In order to use the dewetting enthalpy for the Born–Haber cycle, a renormalization to the number of SDA molecules becomes necessary. The renormalization factor is obtained from the area per molecule ratio of SDA and 9A, respectively. The 9A monolayer structure on graphite is known from both X-ray and neutron diffraction, resulting in an area per 9A molecule of 67.9 Ų.⁴⁶ Based on the commensurate superstructure, the area per SDA molecule amounts to 94.3 Ų. Accordingly, the dewetting enthalpy ΔH_dewet of 9A per SDA molecule corresponds to +34.9 kJ mol⁻¹.

Total binding energy and entropy

All individual enthalpy values are summarized in Fig. 7. Combination according to the scheme depicted in Fig. 1 results in a value for the total enthalpy change of −24.3 kJ mol⁻¹ for SDA monolayer self-assembly on graphite from 9A solution.

Fig. 7 Results for the Born–Haber cycle for SDA with respect to vacuum, i.e. with respect to free single molecule: left side represents the experimental results; right side represents the theoretical results.

To understand the thermodynamics of self-assembly it is also instructive to contrast the enthalpy gain with the entropy cost. The entropy of immobilizing molecules from solution depends on the concentration and increases with increasing dilution. Accordingly, a critical concentration exists, below which monolayer self-assembly becomes thermodynamically unfavourable. This critical concentration can be determined experimentally in a dilution series and for SDA monolayer self-assembly from 9A a value of (4.1 ± 0.3) μmol L⁻¹ was found. The amount of SDA in solution at the critical concentration still exceeds the number of SDA molecules required for monolayer coverage by approximately a factor of 4. At the critical concentration ΔG = 0, accordingly TΔS = ΔH and a direct comparison between enthalpy and entropy becomes feasible.

To evaluate the entropic cost of self-assembly, a partition scheme is used similarly to our previous study on TPA.⁴ First, contributions from rotational and translational entropy are considered and estimated by approaches from statistical mechanics as proposed by Whitesides and coworkers.⁴⁹ For the translational entropy the Sackur–Tetrode equation is used. Since it was originally conceived for the gas phase, the solvent is taken into account by referring the concentration to the free volume of the solvent. The results are summarized in Table 1, details of the entropy calculation are given in the ESI.†

Table 1 Contributions of rotational and translational entropy to the free energy for unsolvated SDA molecules, 9A dimers, and hydrogen bonded complexes of SDA and two 9A solvent molecules at 298 K. All in kJ mol⁻¹

	−TΔStrans	−TΔSrot	−TΔStot
SDA	+67.4	+41.3	+108.7
9A–SDA–9A	+70.3	+49.4	+119.7
9A–9A	+34.7	+43.8	+78.5

---

Similar to previously studied TPA, −TΔS (the entropy contribution to ΔG associated with adsorption of a single unsolvated SDA molecule) of +108.7 kJ mol⁻¹ notably exceeds the enthalpy gain. However, as also indicated by the relatively small dissolution enthalpy, SDA molecules are solvated by 9A molecules in solution. Accordingly, a plausible model for SDA adsorption from 9A is the release of SDA from 9A–SDA–9A complex and subsequent formation of a hydrogen bonded 9A–9A dimer. This desolvation has profound consequences for the entropy balance, since both translational and rotational entropy of the 9A–SDA–9A complex are fully lost, whereas translational and rotational entropy of the 9A–9A dimer are regained, resulting in a reduced entropy cost of +41.2 kJ mol⁻¹. The total entropy contribution to free energy of +12.5 kJ mol⁻¹ is obtained by adding the entropy cost of SDA adsorption to the entropy gain of dewetting (−28.7 kJ mol⁻¹, normalized to the number of SDA molecules), in good quantitative agreement with the total enthalpy gain of −24.3 kJ mol⁻¹.

Conclusion and summary

A previously proposed adapted Born–Haber cycle was employed to assess the total enthalpy change of self-assembly of SDA monolayers on graphite from 9A solution. A direct comparison between experimental and theoretical values of the binding energies in the monolayer again demonstrated the suitability of MM calculations with suitably parametrised force fields for carboxylic acids on graphite. In addition, the theoretical and experimental sublimation enthalpies came out similar, even though the actual SDA crystal structure was not available. This suggests that the theoretically predicted SDA crystal structure closely corresponds to the real SDA crystal structure; an alternative explanation for this agreement in sublimation enthalpies is that the van der Waals contribution is not very sensitive to the exact arrangement of SDA molecules, as long as the packing densities are comparable.

The overall enthalpy change of SDA monolayer self-assembly as deduced from the Born–Haber cycle of −24.3 kJ mol⁻¹ slightly exceeds the entropic cost of +12.5 kJ mol⁻¹ at the critical concentration. Besides the summation of experimental errors, neglect of conformational entropy and inaccuracies of the rather simple free volume approximation can be possible key factors for uncertainties in the entropic contribution. On the other hand, inaccuracies in the enthalpy assessment, especially in the rather crude model of the dewetting enthalpy may also account for the overall relatively small deviation.

Since the original motivation of this study was to reveal the influence of the extended aromatic system of SDA on the thermodynamical stability of the monolayer, it is instructive to compare the Gibbs free energy of SDA monolayer self-assembly to previously studied TPA, i.e. the influence of the extra phenyl ring on total enthalpy and entropy change. The sublimation enthalpy of TPA is +127.2 kJ mol⁻¹, i.e. about ∼42 kJ mol⁻¹ smaller than that of SDA. Yet, the binding energy of TPA molecules in the adsorbed (unsolvated) monolayer is −140 kJ mol⁻¹, i.e. already ∼64 kJ mol⁻¹ weaker than that of SDA. From this direct comparison it can be concluded that the second phenyl ring of SDA increases this molecule's binding energy on graphite almost 50% more than the binding energy in the crystal. In other words, the extended aromatic system of SDA leads to a significant increase of the adsorbed monolayer binding energy.

The second important factor that determines the solution-monolayer equilibrium is the energy of the solute in solution. The dissolution enthalpy of TPA in 9A is +12.8 kJ mol⁻¹, whereas that of SDA is almost twice as large. Since in both cases the dissolution enthalpy is positive, i.e. dissolution is endothermic, a high value for SDA means that this molecule in solution is less stable, and crystallization (or monolayer formation) of SDA from solution is more favourable than in the case of TPA. This additionally enhances the enthalpic stabilization of the interfacial SDA monolayer.

For the overall entropy change differences between TPA and SDA are less pronounced: −TΔS_tot amounts to +3.4 kJ mol⁻¹ for TPA⁴ as compared to +12.5 kJ mol⁻¹ for SDA. The logarithmic dependences of both translational and rotational entropy on the mass and principal moments of inertia – which both increase with size of the molecule – result in sublinear increases of entropies with molecular size.

Both the enthalpic aspects – the stronger adsorption on graphite and the more endothermic dissolution of SDA – and the scaling behaviour of the entropy cost contribute to the comparatively high thermodynamic stability of SDA monolayers, as experimentally expressed in a low critical concentration required for SDA monolayer formation ((4.1 ± 0.3) μmol L⁻¹, i.e. more than an order of magnitude lower than for TPA (120 ± 15) μmol L⁻¹).

In summary, we show that Born–Haber cycles are efficient work horses to evaluate the thermodynamics of monolayer self-assembly at the liquid–solid interface. The excellent agreement between theoretical and experimental monolayer binding energies once more demonstrates the feasibility of hybrid Born–Haber cycles. The Achilles' heel of this approach is the semi-theoretical evaluation of the dewetting enthalpy which at this point necessarily relies on plausible assumptions. Contributions from the dewetting enthalpy become particularly important when solvents with high affinity to the surface are used, e.g. solvents with long aliphatic tails on graphite. In this respect, combination of MFC with the proposed Born–Haber cycle might offer a way to further develop methods for the reliable assessment of dewetting enthalpies: the overall enthalpy change including contributions from dewetting could be measured with high precision by MFC. Comparison with a Born–Haber cycle of the unsolvated monolayer, i.e. without considering dewetting, can thus indirectly yield an experimental value for the dewetting enthalpy that can be used for benchmarking with theoretical estimates. Moreover, an experimental determination of the critical temperature above which the monolayers become thermodynamically unstable would be a further valuable building block towards a fully consistent picture of the thermodynamics of interfacial self-assembly.

Acknowledgements

The Nanosystems-Initiative-Munich (NIM) Cluster of Excellence and the Chinese Scholarship Council are gratefully acknowledged for funding. The Warwick Centre for Scientific Computing is acknowledged for providing computing resources.

Notes and references

1. J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1990, 29, 1304–1319.
2. J. M. Lehn, Rep. Prog. Phys., 2004, 67, 249–265.
3. A. Datta and S. K. Pati, Chem. Soc. Rev., 2006, 35, 1305–1323.
4. W. Song, N. Martsinovich, W. M. Heckl and M. Lackinger, J. Am. Chem. Soc., 2013, 135, 14854–14862.
5. W. Knoll, M. Zizlsperger, T. Liebermann, S. Arnold, A. Badia, M. Liley, D. Piscevic, F. J. Schmitt and J. Spinke, Colloids Surf., A, 2000, 161, 115–137.
6. L. Piot, F. Silly, L. Tortech, Y. Nicolas, P. Blanchard, J. Roncali and D. Fichou, J. Am. Chem. Soc., 2009, 131, 12864.
7. M. Wilms, P. Broekmann, C. Stuhlmann and K. Wandelt, Surf. Sci., 1998, 416, 121–140.
8. S. De Feyter and F. C. De Schryver, Chem. Soc. Rev., 2003, 32, 139–150.
9. L.-J. Wan, Acc. Chem. Res., 2006, 39, 334–342.
10. J. Elemans, S. B. Lei and S. De Feyter, Angew. Chem., Int. Ed., 2009, 48, 7298–7332.
11. M. Lackinger and W. M. Heckl, Langmuir, 2009, 25, 11307–11321.
12. L. C. Giancarlo and G. W. Flynn, Acc. Chem. Res., 2000, 33, 491–501.
13. D. M. Cyr, B. Venkataraman and G. W. Flynn, Chem. Mater., 1996, 8, 1600–1615.
14. L. Kampschulte, T. L. Werblowsky, R. S. K. Kishore, M. Schmittel, W. M. Heckl and M. Lackinger, J. Am. Chem. Soc., 2008, 130, 8502–8507.
15. R. Gutzler, T. Sirtl, J. F. Dienstmaier, K. Mahata, W. M. Heckl, M. Schmittel and M. Lackinger, J. Am. Chem. Soc., 2010, 132, 5084–5090.
16. J. F. Dienstmaier, K. Mahata, H. Walch, W. M. Heckl, M. Schmittel and M. Lackinger, Langmuir, 2010, 26, 10708–10716.
17. A. Bellec, C. Arrigoni, G. Schull, L. Douillard, C. Fiorini-Debuisschert, F. Mathevet, D. Kreher, A. J. Attias and F. Charra, J. Chem. Phys., 2011, 134, 124702.
18. B. A. Friesen, A. Bhattarai, U. Mazur and K. W. Hipps, J. Am. Chem. Soc., 2012, 134, 14897–14904.
19. L. Bouteiller, in Hydrogen Bonded Polymers, ed. W. Binder, Springer Berlin Heidelberg, 2007, vol. 207, pp. 79–112.
20. S. B. Lei, K. Tahara, F. C. De Schryver, M. Van der Auweraer, Y. Tobe and S. De Feyter, Angew. Chem., Int. Ed., 2008, 47, 2964–2968.
21. M. O. Blunt, J. Adisoejoso, K. Tahara, K. Katayama, M. Van der Auweraer, Y. Tobe and S. De Feyter, J. Am. Chem. Soc., 2013, 135, 12068–12075.
22. G. Eder, S. Kloft, N. Martsinovich, K. Mahata, M. Schmittel, W. M. Heckl and M. Lackinger, Langmuir, 2011, 27, 13563–13571.
23. M. Lackinger, S. Griessl, L. Kampschulte, F. Jamitzky and W. M. Heckl, Small, 2005, 1, 532–539.
24. C. Meier, M. Roos, D. Kunzel, A. Breitruck, H. E. Hoster, K. Landfester, A. Gross, R. J. Behm and U. Ziener, J. Phys. Chem. C, 2010, 114, 1268–1277.
25. S. Uemura, R. Tanoue, N. Yilmaz, A. Ohira and M. Kunitake, Materials, 2010, 3, 4252–4276.
26. N. Martsinovich and A. Troisi, J. Phys. Chem. C, 2010, 114, 4376–4388.
27. J. Adisoejoso, K. Tahara, S. Lei, P. Szabelski, W. Rżysko, K. Inukai, M. O. Blunt, Y. Tobe and S. De Feyter, ACS Nano, 2011, 6, 897–903.
28. U. K. Weber, V. M. Burlakov, L. M. A. Perdigão, R. H. J. Fawcett, P. H. Beton, N. R. Champness, J. H. Jefferson, G. A. D. Briggs and D. G. Pettifor, Phys. Rev. Lett., 2008, 100, 156101.
29. S. Lei, K. Tahara, K. Müllen, P. Szabelski, Y. Tobe and S. De Feyter, ACS Nano, 2011, 5, 4145–4157.
30. C. Marie, F. Silly, L. Tortech, K. Müllen and D. Fichou, ACS Nano, 2010, 4, 1288–1292.
31. T. Sirtl, W. Song, G. Eder, S. Neogi, M. Schmittel, W. M. Heckl and M. Lackinger, ACS Nano, 2013, 7, 6711–6718.
32. A. J. Groszek, Proc. R. Soc. London, Ser. A, 1969, 314, 473–498.
33. N. Martsinovich and A. Troisi, J. Phys. Chem. C, 2010, 114, 4376–4388.
34. R. Gutzler, W. M. Heckl and M. Lackinger, Rev. Sci. Instrum., 2010, 81, 015108.
35. A. M. Dejong and J. W. Niemantsverdriet, Surf. Sci., 1990, 233, 355–365.
36. J. W. Pinder and F. M. Richards, J. Comput. Chem., 1987, 8, 1016–1024.
37. J. H. Lii and N. L. Allinger, J. Comput. Chem., 1998, 19, 1001–1016.
38. N. L. Allinger, Y. H. Yuh and J. H. Lii, J. Am. Chem. Soc., 1989, 111, 8551–8566.
39. G. Gilli, V. Bertolasi, V. Ferretti and P. Gilli, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 564–576.
40. G. Allen, J. G. Watkinson and K. H. Webb, Spectrochim. Acta, 1966, 22, 807–814.
41. C. Kendrick, A. Kahn and S. R. Forrest, Appl. Surf. Sci., 1996, 104, 586–594.
42. U. Mazur, K. W. Hipps and S. L. Riechers, J. Phys. Chem. C, 2008, 112, 20347–20356.
43. H. Hedgeland, P. Fouquet, A. P. Jardine, G. Alexandrowicz, W. Allison and J. Ellis, Nat. Phys., 2009, 5, 561–564.
44. S. Lifson, A. T. Hagler and P. Dauber, J. Am. Chem. Soc., 1979, 101, 5111–5121.
45. B. H. Meier, F. Graf and R. R. Ernst, J. Chem. Phys., 1982, 76, 767–774.
46. A. K. Bickerstaffe, N. P. Cheah, S. M. Clarke, J. E. Parker, A. Perdigon, L. Messe and A. Inaba, J. Phys. Chem. B, 2006, 110, 5570–5575.
47. S. P. Verevkin, J. Chem. Eng. Data, 2000, 45, 953–960.
48. R. C. F. Schaake, J. C. van Miltenburg and C. G. de Kruif, J. Chem. Thermodyn., 1982, 14, 763–769.
49. M. Mammen, E. I. Shakhnovich, J. M. Deutch and G. M. Whitesides, J. Org. Chem., 1998, 63, 3821–3830.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp01147c

---