 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pressure dependent OH yields in the reactions of CH3CO and HOCH2CO with O2
C. B. M.
Groß
,
T. J.
Dillon†
and
J. N.
Crowley
*
Max-Planck-Institut für Chemie, 55128 Mainz, Germany. E-mail: john.crowley@mpic.de
First published on 28th April 2014
Abstract
OH-formation in the reactions of CH3CO (R1) and HOCH2CO (R4) with O2 was studied in He, N2 and air (27 to 400 mbar) using OH-detection by laser induced fluorescence (LIF). 248 nm laser photolysis of COCl2 in the presence of CH3CHO or HOCH2CHO was used as source of the acyl radicals CH3CO and HOCH2CO. The LIF-system was calibrated in back-to-back experiments by the 248 nm laser photolysis of H2O2 as OH radical precursor. A straight-forward analytical expression was used to derive OH yields (α) for both reactions. A Stern–Volmer-analysis results in α1b−1(N2) = 1 + (9.4 ± 1.7) × 10−18 cm3 molecule−1 × [M], α1b−1(He) = 1 + (3.6 ± 0.6) × 10−18 cm3 molecule−1 × [M] and α4b−1(N2) = 1 + (1.85 ± 0.38) × 10−18 cm3 molecule−1 × [M]. Our results for CH3CO are compared to the previous (divergent) literature values whilst that for HOCH2CO, for which no previous data were available, provide some insight into the factors controlling the yield of OH in these reactions.
1 Introduction
Acetyl radicals (CH3CO) play an important role in atmospheric chemistry. Important sources of acetyl radicals are the photolysis of acetone in the upper troposphere and the reaction of acetaldehyde with OH in the troposphere. The hydroxyl-substituted hydroxy acetyl radicals (HOCH2CO) are formed in the reaction of OH with glycol aldehyde (HOCH2CHO). The only significant reaction of acetyl and hydroxy acetyl radicals in the atmosphere is with O2, forming (mainly) peroxy radicals. Accompanying peroxy radical formation, (R1) displays a second reaction pathway forming OH and an organic by-product. The branching ratio (α) for formation of OH increases from small values (<2%) at standard pressure to unity at pressures close to zero.1,2| CH3CO + O2 + M → CH3C(O)O2 + M | (R1a) |
| →OH + c-CH2C(O)O | (R1b) |
Reaction (R1) is considered to proceed via an excited peroxy radical CH3C(O)O2# that is either stabilised by collisions with the bath gas molecules M or decomposes to form OH.2–9 This is illustrated in reaction Scheme 1 (R = CH3). The pressure dependence of α thus originates from the competition between the pressure- and bath gas-dependent quenching rate [M] × kM and the pressure-independent decomposition rate kD. A kinetic (Stern–Volmer) analysis of the reaction scheme leads to eqn (1) which can be used to parameterise α:
 | (1) |
Although OH yields are low at pressures typical for the troposphere, (R1b) has an indirect impact on atmospheric chemistry because of its occurrence in laboratory experiments. The OH product of (R1b) has, for example, been used as spectroscopic marker for CH3CO formation in the determination of photo-dissociation quantum yields for acetone,10 an important source of HOx radicals and PAN (CH3C(O)O2NO2) in the upper troposphere.11,12 Recent studies on the yield of OH in the reaction between CH3C(O)O2 and HO2 observed OH from (R1).13 The title reaction will also have occurred in and potentially impacted on the results of studies of PAN formation in (R2) at low pressures where the yield of OH is large.
| CH3C(O)O2 + NO2 + M ↔ CH3C(O)O2NO2 + M | (R2) |
For example, in their study of PAN formation, Bridier et al.14 generated CH3CO radical in the presence of O2 to examine the kinetics of the reaction of CH3C(O)O2 + NO2(R2) at pressures down to 20 mbar. As the results of the present publication show, at such pressures 18% of CH3CO reacting with O2 forms OH instead of CH3C(O)O2. Data recorded at low pressure by Bridier et al. might thus be subject to systematic error since reaction channel (R1b) was not known to take place in 1991.
 | ||
| Scheme 1 Generalised mechanism for the reactions of CH3CO (R = CH3) and HOCH2CO (R = HOCH2) with O2. | ||
The reaction of CH3C(O)O2 with HO2(R3), which competes with (R2) at low NOx levels,15 has drawn considerable interest in recent years.13,16–18 Its main reaction channel (R3a) preserves a HOx species (HOx is OH + HO2) and an organic radical and is hence radical-propagating, which helps sustain atmospheric oxidation capacity.
| CH3C(O)O2 + HO2 → CH3C(O)O + OH + O2 | (R3a) |
| → CH3C(O)O2H + O2 | (R3b) |
| → CH3C(O)OH + O3 | (R3c) |
In experiments on (R3), CH3C(O)O2 and HO2 are usually generated by reaction of Cl atoms with CH3CHO and CH3OH in air involving intermediate generation of CH3CO and CH2OH radicals. Therefore, OH-generation influences the initial [CH3C(O)O2]/[HO2]-ratio in these experiments. In product studies that do not allow for an experimental separation between different OH-formation routes, (R1b) must be well known so that discrimination between OH formed in (R1b) and (R3a), respectively, is possible.
In the present work we employ a new experimental approach to quantify the pressure-dependence of the OH forming channels (R1b) and (R4b) of the reactions of O2 with CH3CO and its OH-substituted analogue HOCH2CO.
| HOCH2CO + O2 + M → HOCH2C(O)O2 + M | (R4a) |
| → OH + ⋯ | (R4b) |
We assume that, for reaction (R4), the same pathways are available as in (R1), i.e. competition between peroxy-radical formation and OH (see Scheme 1, R = HOCH2). The formation of the peroxy radical, its UV-absorption spectrum and its reaction with HO2 will be subject of a future publication from this group.
Throughout this work the branching ratios of the OH-forming reaction channels are defined as follows: k1b/k1 = α1b and k4b/k4 = α4b.
2 Experimental
2.1 Experimental set-up
The experiments detailed in this publication were performed using the pulsed laser photolysis-laser induced fluorescence (PLP-LIF) apparatus that has been described previously19,20 and only a short description is given here. Experiments were conducted in a 500 cm3 reactor at room temperature. The pressure was monitored with a capacitance manometer, and gas flow rates were selected such that a fresh gas sample was available for photolysis at each laser pulse. Reactions were performed at pressures between 27 and 400 mbar in nitrogen and helium bath gases with added O2 or in air.Reactions were initiated by the 248 nm photolysis of H2O2 (8–12 × 1014 molecule cm−3) or COCl2 (3–11 × 1015 molecule cm−3) using an excimer laser (Lambda Physik). Laser fluences of 39–55 mJ cm−2 per pulse resulted in formation of 0.3–0.5 × 1012 OH radicals cm−3 or 1–5 × 1012 Cl-atoms cm−3. Two absorption cells located upstream of the reactor enabled on-line concentration measurements of the reactants at 185 nm and 214 nm. The optical path-lengths of the absorption cells are l185 = 43.8 cm and l214 = 34.8 cm.
Fluorescence from OH was detected by a photomultiplier tube shielded by a 309 nm interference filter and a BG 26 glass cut-off filter. The frequency doubled emission from a Nd-YAG-pumped dye laser (Quantel, Lambda Physik) was used to excite the A2Σ(ν = 1) ← X2Π(ν = 0), Q11 (1) transition of OH at 281.997 nm.
2.2 Chemicals
Liquid samples of CH3CHO (Roth, ≥99.5%) were degassed by repeated evacuation, and stored in a blackened glass bulb as ∼1% mixture in N2. HOCH2CHO was prepared during the experiments from its dimer (Sigma-Aldrich) by heating the solid sample to 50–75 °C and eluting gaseous HOCH2CHO by a continuous flow of N2. COCl2 (Fluka, >99%) was stored in a stainless steel canister as ∼4% mixture in N2 or He. H2O2 (AppliChem, 50%) was concentrated in vacuum to >80% and used as liquid sample. He (Westfalen, 99.999%), N2 (Westfalen, 99.999%) and O2 (Westfalen, 99.999%) were used as supplied.3 Results
3.1 Experimental approach
We performed back-to-back experiments in reaction mixtures containing either H2O2 or COCl2 as photolytic sources of OH radicals or Cl atoms. Addition of CH3CHO or HOCH2CHO to the COCl2 experiments converted Cl atoms into CH3CO or HOCH2CO, which reacted with O2 to form OH. This allowed us to compare OH formation via title reactions (R1b) and (R4b) directly with OH production from H2O2-photolysis, a well-characterized source of OH radicals. Formation of acyl radicals by the reaction of Cl atoms with CH3CHO (ΔH = −58 kJ mol−1)18 or HOCH2CHO (ΔH = −49 kJ mol−1)18,21 are exothermic processes and the nascent fragments are expected to be vibrationally and rotationally hot. Assuming an energy transfer efficiency of 300 cm−1 per collision with N2, hot CH3CO would be deactivated within 16 collisions, ensuring that, at the high pressures of bath gases used in this study, acetyl should, to a good approximation, be thermalized before reaction with O2 takes place. Experiments in which N2 was mixed with 1% O2 yielded the same results as those with 21% O2, so that no evidence was obtained for reaction of non-thermalised CH3CO with O2. Even in the experiments in He (presumably a less efficient energy transfer medium that N2) no dependence of the OH-yield on O2 partial pressure was obtained. We note also that the existence of a direct channel for OH-formation from excited CH3CO and O2 is considered unlikely.9| H2O2 + hν (248 nm) → 2OH | (R5) |
Quasi-instantaneous photolytic OH-formation and subsequent OH loss via(R6) result in a mono-exponential decay of [OH] that was recorded by OH-LIF.
| OH + H2O2 → HO2 + H2O | (R6) |
The LIF-signal is proportional to [OH] and was fitted by eqn (2) where fcal is a calibration factor that quantifies the sensitivity of the LIF-system.
| LIF(t) = fcal × [OH](t) = sOH × e−aOH·t | (2) |
| [OH](t) = [OH]0 × e−k6′·t | (3) |
Combining eqn (2) and (3) we get:
| fcal·[OH]0 = sOH | (4) |
In back-to-back experiments, H2O2 was replaced by COCl2 and an acyl radical source (CH3CHO or HOCH2CHO). Photolysis of COCl2 generates Cl atoms with a quantum yield of 2.23,24
| COCl2 + hν (248 nm) → 2Cl + CO | (R7) |
Reaction of Cl with CH3CHO (R8) forms CH3CO with a yield very close to unity (k8 = 8.0 × 10−11 cm3 molecule−1 s−1).17
| Cl + CH3CHO → CH3CO + HCl | (R8) |
OH formation in reaction (R1b) and its main loss via reaction (R9) are both resolved on the time-scale of our experiments and a bi-exponential time-dependence of the LIF-signal is observed (k9 = 1.5 × 10−11 cm3 molecule−1 s−1).17,18
| OH + CH3CHO → CH3CO + H2O | (R9a) |
| → CH2CHO + H2O | (R9b) |
Reaction with OH generates mainly CH3CO (α9a = 0.95) which is accounted for in the analytical expression of the [OH] time evolution presented below. Only 5% of the OH formed in (R1) is thus converted via(R9b) into CH2CHO. Even if CH2CHO were converted with unity yield into OH radicals, this would result in a maximum overestimation of no more than 5% in the value of α1b.
Measured LIF-profiles were analysed using eqn (5).
 | (5) |
 | (6) |
In this expression, k8′ = [CH3CHO] × k8, k9′ = [CH3CHO] × k9 and [Cl]0 is the Cl-concentration initially formed by photolysis. Conditions were chosen such that reaction (R1) was 5.2–250 times faster than (R8), and 28–1300 times faster than (R9) and thus fast on the experimental time-scale of ∼1 ms. Combining eqn (5) and (6) we get:
| α1bfcal [Cl]0 = sCl | (7) |
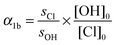 | (8) |
This assumes that fluorescence quenching is dominated by the bath gas and that the contribution of reactants is negligible so that switching between H2O2 and COCl2/aldehyde does not change the detection sensitivity to OH. The experiments performed in He, which is a weak quencher of OH-fluorescence, are the most likely to be influenced, should this not be the case. In Section 3.3 we show however that such quenching effects did not have a measurable effect on the results obtained.
The initial concentrations [OH]0 and [Cl]0 were calculated from [H2O2] and [COCl2], the respective 248 nm cross sections and the number of photons per photolysis pulse nPhot. We then derive:
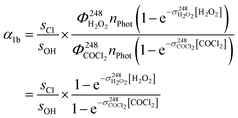 | (9) |
Since the laser intensity remained stable (within ∼1%) during back-to back experiments, nPhot cancels out as do the quantum yields of OH formation  and Cl formation
and Cl formation  that both equal 2. The precursor concentrations [H2O2] and [COCl2] were calculated from the respective optical depths
that both equal 2. The precursor concentrations [H2O2] and [COCl2] were calculated from the respective optical depths  and
and  measured at 214 nm in a separate absorption cell (see Section 2.1).
measured at 214 nm in a separate absorption cell (see Section 2.1).
 | (10) |
HOCH2CHO was used as acyl radical precursor in experiments for the determination of α4b. Reaction of Cl atoms with HOCH2CHO (R10) forms HOCH2CO with a yield of α10a = 0.65 (k10 = 7.5 × 10−11 cm3 molecule−1 s−1).25,26 Reaction of HOCHCHO with O2(R11), is not known to form OH.25,26
| Cl + HOCH2CHO → HOCH2CO + HCl | (R10a) |
| → HOCHCHO + HCl | (R10b) |
| HOCHCHO + O2 → HC(O)CHO + HO2 | (R11) |
Reaction with HOCH2CHO (R12) is the main OH loss channel in these experiments.
| OH + HOCH2CHO → HOCH2CO + H2O | (R12a) |
| → HOCHCHO + H2O | (R12b) |
Reaction with OH generates HOCH2CO with a higher yield (α12a = 0.80) than reaction with Cl. Based on this kinetic scheme, one again expects a bi-exponential time profile of [OH] that can be analysed by eqn (5). The temporal evolution of [OH] is described by the integrated rate law (11) which was derived analytically assuming reaction (R4) to be fast compared to reactions (R10) and (R12) and that [HOCH2CHO] was not significantly depleted during the experiments.
 | (11) |
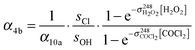 | (12) |
 ,
,  , sOH and sCl, the absorption cross sections of COCl2 and H2O2 at 214 nm and 248 nm and the branching ratio α10a.
, sOH and sCl, the absorption cross sections of COCl2 and H2O2 at 214 nm and 248 nm and the branching ratio α10a.
 | (13) |
Similarly, eqn (12) becomes
 | (14) |
This allows us to separate statistical errors, i.e. reading errors or uncertainties in the determinations of sOH and sCl which are small, from the systematic errors originating from uncertainties in literature values of the absorption cross sections and, in the case of α4b, the branching ratio α10a = 0.65 ± 0.05.25 To reduce systematic error, absorption cross sections were taken from literature sources that specify values for both wavelengths used in this work. Values for H2O2 were taken from Vaghjiani et al.,27 values for COCl2 were taken from Meller et al. whose data are published in the MPI-Mainz UV/VIS Spectral Atlas28 ( ,
,  and
and  all values given in units of 10−20 cm2 molecule−1).
all values given in units of 10−20 cm2 molecule−1).
3.2 CH3CO + O2 (N2/O2)
Back-to-back PLP-LIF-experiments on (R1) were performed at pressures between 133 and 270 mbar of N2 or at 27 and 270 mbar of air. Fig. 1 shows a pair of OH-LIF time profiles recorded at 133 mbar in N2. Both OH-profiles display the expected kinetics and were analysed using eqn (2) or (5), respectively. Although this work was not performed to re-measure the rate-coefficients of reactions (R8) and (R9), we did derive them from the fit-parameters and the respective [CH3CHO] as a check of our experimental approach. We obtained k8 = (7.4 ± 1.1) × 10−11 cm3 molecule−1 s−1, and k9 = (1.8 ± 0.2) × 10−11 cm3 molecule−1 s−1 where the uncertainties represent statistical errors (2σ) in the fit-parameters only. [CH3CHO] was determined barometrically and carries an additional uncertainty of ∼20%. Our values are, within these uncertainties, in accordance with the currently recommended literature values of k8,Lit = (8.0+1.4−1.2) × 10−11 cm3 molecule−1 s−1, and k9,Lit = (1.5 ± 0.2) × 10−11 cm3 molecule−1 s−1.17,18 | ||
| Fig. 1 OH-LIF profiles measured in back-to-back experiments in 133 mbar of N2 bath gas with 1% O2. The solid lines are fits to expressions (2) and (5). | ||
Fig. 2 shows the results of all single experiments as a plot of the reciprocal of α1b against [M]. A linear regression of the data resulted in (all errors statistical, 2σ)
| α1b−1(N2) = (0.55 ± 1.81) + (9.52 ± 0.72) × 10−18 cm3 molecule−1 [M] |
As expected3,5,29 the intercept is 1 within statistical uncertainty. We then re-fitted the data using eqn (1), i.e. we performed another linear regression with the intercept being fixed to 1 (thick solid line in Fig. 2). From this we obtain  (error statistical only, 2σ). We applied eqn (13) to incorporate the systematic uncertainties (2σ) and derive a final value of
(error statistical only, 2σ). We applied eqn (13) to incorporate the systematic uncertainties (2σ) and derive a final value of 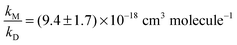 . In Fig. 2 these error margins are represented by thin solid lines.
. In Fig. 2 these error margins are represented by thin solid lines.
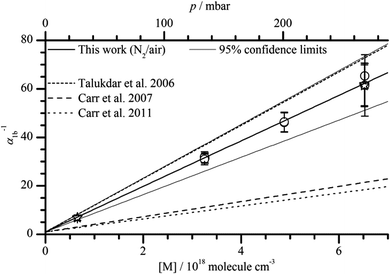 | ||
| Fig. 2 Plot of α1b−1versus bath gas number density [M] at 296 K. Talukdar et al. (2006).34 Carr et al. (2007).3 Carr et al., (2011).2 The stars represent data obtained in air, the circles represent data obtained in a mixture of oxygen (1%) in N2. | ||
We note that the data show no dependence on the O2 concentration and that values of α1b determined in air would be higher if CH3CO were not thermalized and if there were an additional OH-formation route via CH3CO# + O2. This observation rules out a significant contribution of hot acetyl radicals.
3.3 CH3CO + O2 (He)
Back-to-back PLP-LIF-experiments on (R1) were performed at pressures between 33 and 400 mbar of He. From the fit-parameters and the respective [CH3CHO] we derived k8 = (7.6 ± 0.4) × 10−11 cm3 molecule−1 s−1, and k9 = (1.9 ± 0.1) × 10−11 cm3 molecule−1 s−1 where the uncertainties represent statistical errors (2σ) in the fit-parameters, only. As described above, [CH3CHO] was determined from barometric and mass flow readings and carries an additional uncertainty of ∼20%. These values are, within combined uncertainties, in accordance with the currently recommended literature values.
Fig. 3 shows the results of all experiments performed in He with an addition of 2.7 (or 1.3) mbar of O2 as a plot of the reciprocal of α1b against He number density [M]. For the experiments with 2.7 mbar O2, a linear regression of the data resulted in (all errors statistical, 2σ)
| α1b−1(He) = (2.13 ± 0.35) + (3.52 ± 0.19) × 10−18 cm3 molecule−1 [M] |
The two data points obtained using 1.3 mbar of O2 reveal the expected trend, slightly enhanced yields (but a similar slope) due to the quenching effect of O2. With 2.7 mbar of O2 we expect α1b−1 to approach 1.6 ± 0.11 (the value we derive from  -value for N2 and air) at zero pressure. Within the statistical uncertainties the intercept (2.13 ± 0.35) is however slightly higher than this. In the experiments in He, the main contribution to OH-fluorescence quenching is O2 and not the H2O2 and CH3CHO and Cl2CO reactants. The fact that the two datasets obtained with different O2 concentrations are in good agreement, supports this.
-value for N2 and air) at zero pressure. Within the statistical uncertainties the intercept (2.13 ± 0.35) is however slightly higher than this. In the experiments in He, the main contribution to OH-fluorescence quenching is O2 and not the H2O2 and CH3CHO and Cl2CO reactants. The fact that the two datasets obtained with different O2 concentrations are in good agreement, supports this.
 | ||
| Fig. 3 Plot of α1b−1 against bath gas number density [M] or pressure. Data were recorded in He with addition of 1.3 mbar (stars) or 2.7 mbar (circles) of O2. Note that the literature data are plotted with an intercept of 1.6 to take into account the effect of quenching by O2 (see text for details). Blitz et al. (2002).4 Talukdar et al. (2006).34 Kovács et al. (2007).6 Carr et al. (2007).3 Carr et al. (2011).2 | ||
We therefore re-fitted the data using eqn (1), i.e. we performed another linear regression with the intercept being fixed to 1.6 (thick solid line in Fig. 3). From this we derived 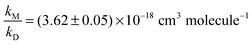 (error statistical only, 2σ). We applied eqn (13) to incorporate the systematic uncertainties (2σ) and derived a final value of
(error statistical only, 2σ). We applied eqn (13) to incorporate the systematic uncertainties (2σ) and derived a final value of  . In Fig. 3 these error margins are represented by thin solid lines.
. In Fig. 3 these error margins are represented by thin solid lines.
3.4 HOCH2CO + O2 (N2/O2)
Back-to-back PLP-LIF-experiments using HOCH2CHO as acyl radical precursor were performed at pressures between 33 and 269 mbar in N2 or air. Fig. 4 shows a pair of OH-LIF time profiles recorded at 133 mbar in N2 which were fitted using eqn (2) or (5), respectively. As a check for possible error sources of our experimental approach, we derived the rate-coefficients of reactions (R10) and (R12) from the fit-parameters and the respective [HOCH2CHO], we get k10 = (6.6 ± 0.3) × 10−11 cm3 molecule−1 s−1, and k12 = (1.0 ± 0.2) × 10−11 cm3 molecule−1 s−1 where the uncertainties represent statistical errors (2σ) in the fit-parameters, only. [HOCH2CHO] was derived by measuring its absorption at 185 nm using a literature value for the absorption cross section of HOCH2CHO (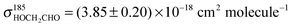 )30 and carries an additional uncertainty of ∼10%. Our values are, within combined uncertainties, in accordance with the currently recommended literature values of k10,Lit = (7.6 ± 1.5) × 10−11 cm3 molecule−1 s−1,26 and k12,Lit = (0.80+0.33−0.23) × 10−11 cm3 molecule−1 s−1.17,18
)30 and carries an additional uncertainty of ∼10%. Our values are, within combined uncertainties, in accordance with the currently recommended literature values of k10,Lit = (7.6 ± 1.5) × 10−11 cm3 molecule−1 s−1,26 and k12,Lit = (0.80+0.33−0.23) × 10−11 cm3 molecule−1 s−1.17,18
 | ||
| Fig. 4 OH-LIF profiles measured in back-to-back experiments at 133 mbar of N2 bath gas containing 2.7 mbar of O2. The solid lines are fits using equations (2) and (5). | ||
Fig. 5 shows the results of all single determinations of α4b plotted as α4b−1 against [M]. Except for the data measured at the lowest pressure of 33 mbar, the values for α4b determined in air are slightly higher than those measured in nitrogen. We therefore evaluated data recorded in N2 or air separately to check if the final results differ within their statistical uncertainties. A linear regression of the data obtained in N2 gave (all errors statistical, 2σ)
| α4b−1(N2) = (1.23 ± 0.42) + (1.78 ± 0.26) × 10−18 cm3 molecule−1 [M] |
A linear regression of the data obtained in air resulted in (all errors statistical, 2σ)
| α4b−1(air) = (1.24 ± 0.43) + (1.55 ± 0.19) × 10−18 cm3 molecule−1 [M] |
Assuming that (R4b) forms OH with unity yield at pressures approaching 0 mbar, we expect the intercept to be unity in air which, within statistical uncertainty, is the case. In the N2-experiments a constant amount of 2.7 mbar of O2 was added. Thus, at [M] = 0 molecule cm−3 we expect α4b−1 to approach ∼1.1, i.e. the value we derived using [M] = 6.5 × 1016 molecule cm−3 and 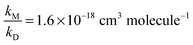 . This is also confirmed by the data. In both cases we performed linear regressions according to eqn (1), with the intercept being fixed to 1.1 for the data recorded in N2, and to unity for the air-data. We derived
. This is also confirmed by the data. In both cases we performed linear regressions according to eqn (1), with the intercept being fixed to 1.1 for the data recorded in N2, and to unity for the air-data. We derived  (solid black line in Fig. 5) for the data recorded in nitrogen and
(solid black line in Fig. 5) for the data recorded in nitrogen and  (dashed black line) for the data recorded in air (errors are statistical, 2σ). Within combined uncertainties measurements in nitrogen and air resulted in the same values of
(dashed black line) for the data recorded in air (errors are statistical, 2σ). Within combined uncertainties measurements in nitrogen and air resulted in the same values of  and, accordingly, α4b.
and, accordingly, α4b.
The slightly larger α4b-values observed at higher pressures in air are potentially due to experimental scatter. Our data do not however allow us to completely rule out the existence of an additional, O2-dependent OH-source as the cause. Therefore, we decided to rely exclusively on the data recorded in N2 (with 1–10% of O2 added) which would be less impacted by such an additional OH-source. Doing so we commit a maximum error of 7% in α4b compared to values derived from all data. The fact that the data obtained at a fixed O2-to-N2 ratio of 21%, but at various pressures (and thus at different O2 concentrations), display no significant deviation from the expected behaviour, suggests that an additional OH forming channel that is dependent on the O2 partial pressure is not significant. Incorporation of systematic uncertainties (2σ), results in a final value of  . The error margins that also enclose the data recorded in air are presented in Fig. 5 by thin solid lines.
. The error margins that also enclose the data recorded in air are presented in Fig. 5 by thin solid lines.
Our studies on OH formation in the reactions of CH3CO (R1) and HOCH2CO (R4) with O2 reveal a strong dependence of the yield on substituents, with  for (R4) a factor of 5 smaller than for (R1). Under the assumption that the collisional quenching of both activated peroxy radicals proceeds at a similar rate this large difference can be attributed to a more efficient decomposition of HOCH2C(O)O2# compared to CH3C(O)O2#. This may be rationalized in terms of a more favourable reaction pathway in which the hydroxyl group of HOCH2C(O)O2 enables formation of a six-membered transition state as illustrated in Scheme 2 in which highly stable products (formaldehyde and CO2) are formed along with OH.
for (R4) a factor of 5 smaller than for (R1). Under the assumption that the collisional quenching of both activated peroxy radicals proceeds at a similar rate this large difference can be attributed to a more efficient decomposition of HOCH2C(O)O2# compared to CH3C(O)O2#. This may be rationalized in terms of a more favourable reaction pathway in which the hydroxyl group of HOCH2C(O)O2 enables formation of a six-membered transition state as illustrated in Scheme 2 in which highly stable products (formaldehyde and CO2) are formed along with OH.
 | ||
| Scheme 2 Possible transition state for OH formation in (R4b). | ||
4 Comparison with literature
4.1 CH3CO + O2
Several experimental studies have reported OH formation via(R1b) in N2, O2 and He.2–6Table 1 and Fig. 2 and 3 summarise the -values from these studies as well as those from our work. Note that in Fig. 3 the literature data are plotted with an intercept of 1.6 to take into account the presence of O2 in our experiments at extrapolated zero mbar of He.
-values from these studies as well as those from our work. Note that in Fig. 3 the literature data are plotted with an intercept of 1.6 to take into account the presence of O2 in our experiments at extrapolated zero mbar of He.
| M | This work | Tyndall (1997) | Blitz (2002) | Talukdar (2006) | Kovács (2007) | Carr (2007) | Carr (2011) | Groß (2014) | |
|---|---|---|---|---|---|---|---|---|---|
| Tyndall (1997),5 Blitz (2002),4 Talukdar (2006),34 Kovács (2007),6 Carr (2007),3 Carr (2011),2 Groß (2014).13a Units of 10−18 cm3 molecule−1.b The cited value is based on a correction from G. S. Tyndall that was published by Carr et al.3c Value obtained by applying eqn (1) to the data of Kovács et al.6d Value derived from a single experiment at 233 mbar in N2/O2. | |||||||||
| CH3CO | |||||||||
k
M/kD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
N2 | 9.4 ± 1.7 | (5.9)b | 11.0 ± 2.5 | 3.59 ± 0.60 | 2.67 ± 1.40 | (∼9)d | ||
| He | 3.6 ± 0.6 | 1.06 ± 0.05 | 4.3 ± 1.0 | 3.9 ± 0.6c | 1.31 ± 0.51 | 1.63 ± 0.54 | |||
| Ratio N2/He | 2.6 | 2.6 | 2.7 | 1.6 | |||||
| HOCH2CO | |||||||||
k
M/kD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
N2 | 1.85 ± 0.38 | |||||||
Tyndall et al.5 studied the reaction of Cl atoms with CH3CHO by irradiation of Cl2–CH3CHO-mixtures in N2 or O2 in environmental chambers and analysed the reaction mixtures by infra-red absorption spectroscopy. They found a pressure-dependence of the apparent rate coefficient of (R8) when the experiments were performed in O2 but none for the measurements in N2. The value measured in O2 increased if the experimental pressure was decreased; at 1.6 mbar the apparent rate coefficient was 2.7 times higher than that derived in N2. The authors attributed these findings to OH formation in (R1b). Thus, they did not directly detect OH, but their kinetic and product studies provided strong evidence for OH formation. The  -value shown in Table 1 was derived by Carr et al.3 based on a personal communication with Tyndall et al.5
-value shown in Table 1 was derived by Carr et al.3 based on a personal communication with Tyndall et al.5
Blitz et al.4 used the 248 nm pulsed laser photolysis of CH3C(O)CH3 in He to generate CH3CO and used OH-LIF for the detection of hydroxyl radicals formed in (R1b) at pressures between 13–533 mbar. Calibration of the LIF-system was achieved by fixing α1b at zero pressure to unity, which neglects to take into account the fact that the acetyl radical yield is pressure dependent as a significant (but variable) fraction thermally decomposes to CH3 and CO, at least in nitrogen bath gas.31–33 Blitz et al. could thus have underestimated the value of KM/KD by about 16%.3
Talukdar et al.34 used different photolytic schemes (photolysis of acetone, Cl + CH3CHO and OH + CH3CHO) for CH3CO generation coupled to OH-LIF to investigate OH-formation or modification of OH kinetics due to (R1) at experimental pressures between 27–800 mbar in He, N2 and O2. The resulting  values are in good agreement with our results.
values are in good agreement with our results.
Kovács et al.6 used two low-pressure fast discharge flow tubes (operated at pressures between 1.3 and 11 mbar in helium) that were equipped with LIF or resonance fluorescence detection of OH radicals. CH3CO was formed by reacting CH3CHO with OH that was generated from H and NO2, or from F and H2O. The authors compared decay rates of OH radicals with or without O2 present in the reaction mixture. We applied eqn (1) to the α1b-data provided by Kovács et al. to derive a value of  that is in good agreement with those presented by Talukdar et al. and this work.
that is in good agreement with those presented by Talukdar et al. and this work.
Carr et al.3 used the 248 nm pulsed laser photolysis of CH3C(O)OH to generate prompt OH and CH3CO radicals in equal amounts. Detection of OH radicals was achieved by OH-LIF. Experiments were restricted to pressures of <138 mbar of He, or <34 mbar of N2. The approach is self-calibrated since it allows comparison of prompt OH formed in the photolysis step to OH formed from acetyl + O2 and thus requires only separation of the LIF signal into prompt and slow components. Errors in the separation of prompt and slower OH contributions would thus affect α1b two-fold and would be manifest at higher pressures of N2 where the yield of OH is small. The resulting value for  agrees well with the previous one of Blitz et al. from the same lab but accordingly differs by a factor of ∼3 from our values.
agrees well with the previous one of Blitz et al. from the same lab but accordingly differs by a factor of ∼3 from our values.
Carr et al.2 photolysed acetone at 248 nm to form CH3CO and used OH-LIF detection. The resulting OH time profiles were fitted by a bi-exponential equation similar to the one presented here. Relative values of α1b were measured in the pressure range of 7–400 mbar and based on an absolute scale by setting α1b at 0 mbar to unity. Data were corrected by 25–35% for a pressure-dependence23,31 in the CH3CO yield of acetone photolysis. In their N2-experiments the authors needed to make an additional correction since they observed a decrease of LIF-sensitivity at elevated pressures. The correction factors were derived in separate experiments by measuring OH-formation from 248 nm photolysis of t-butylhydroperoxide at the same pressure.
Although not a detailed study of the OH yield in the title reaction, we recently published data on OH formation in the reaction of HO2 with CH3C(O)O2 (ref. 13) and also observed (in this case “unwanted”) OH-formation via(R1b). This work was conducted in a different apparatus and used a different CH3CO-formation scheme (355 nm-pulsed photolysis of CH3CHO–CH3OH–Cl2–O2–N2-mixtures). OH was detected by an OH-LIF-unit that was calibrated by measuring OH from the reaction of HO2 with NO. In spite of the different experimental approach we could accurately simulate the OH signals due to reaction (R1b) with the OH yield presented in the current work (see Fig. 8 in Groß et al.13). Use of α from the more recent publication of Carr et al.2 would have resulted in an overestimation of initial OH-formation by a factor of 3.
Our results are in good agreement with those of Talukdar et al.34 and Kovács.6 We cannot explain the differences between our work and that of Blitz et al.4 and Carr et al.2,3 but we highlight the fact that no correction needs to be applied to our data.
In Table 1 we also show the ratio of the respective  values in N2 and He bath gases. From our data we derive a value of 2.6 which is in agreement with those of Talukdar et al. (2.7) and the 2007 study of Carr et al. 2007 (2.6). From the 2011 dataset of Carr et al. we derive a lower value of 1.6.
values in N2 and He bath gases. From our data we derive a value of 2.6 which is in agreement with those of Talukdar et al. (2.7) and the 2007 study of Carr et al. 2007 (2.6). From the 2011 dataset of Carr et al. we derive a lower value of 1.6.
4.2 HOCH2CO + O2
Butkovskaya et al.35 investigated the OH-initiated oxidation of HOCH2CHO in a turbulent flow reactor at 267 mbar of N2. A chemical ionisation mass spectrometer was used to detect OH and derive a yield of α4b = 22%. This high yield may reflect the fact that Butkovskaya et al.35 were unaware that the reaction of HOCH2C(O)O2 with HO2 (formed at a yield of 20% from OH + HOCH2CHO in the presence of O2) forms OH with a yield of ∼70%.16,36OH formation has also been observed37 in the reaction of O2 with CH3OCO, which is isomeric with HOCH2CO. Similar to (R4), OH-formation is accompanied by CH2O and CO2 by-products. The value of  reported, (7.4 ± 1.9) × 10−18 cm3 molecule−1, is four times larger than our value for HOCH2CO. Given that the products of decomposition are identical the difference must be related to energetic differences in the transition state leading to dissociation.
reported, (7.4 ± 1.9) × 10−18 cm3 molecule−1, is four times larger than our value for HOCH2CO. Given that the products of decomposition are identical the difference must be related to energetic differences in the transition state leading to dissociation.
5 Conclusion
We determined the pressure-dependence of the OH-forming branching ratios α1b of reaction (R1a) and α4b reaction (R4b) using a novel experimental approach. The values for α1b are in accordance with some earlier studies6,34 but clearly differ from those from the Leeds group2–4 that derive much higher OH yields. Our data for α4b show that hydroxylation of CH3CO enhances OH-formation in the reaction with O2 by approximately a factor of five.Acknowledgements
We thank Jim Burkholder (National Oceanic and Atmospheric Administration, Boulder, CO) for sending us a copy of a poster “Determination of the OH Radical Yield in the CH3CO + O2 + M Reaction” presented at the 19th International Symposium on Gas Kinetics in 2006. C. B. M. G. thanks the International Max Planck Research School for Atmospheric Chemistry and Physics for financial support.References
- G. S. Tyndall, T. A. Staffelbach, J. J. Orlando and J. G. Calvert, Int. J. Chem. Kinet., 1995, 27, 1009–1020 CrossRef CAS.
- S. A. Carr, D. R. Glowacki, C.-H. Liang, M. T. Baeza-Romero, M. A. Blitz, M. J. Pilling and P. W. Seakins, J. Phys. Chem. A, 2011, 115, 1069–1085 CrossRef CAS PubMed.
- S. A. Carr, M. T. Baeza-Romero, M. A. Blitz, M. J. Pilling, D. E. Heard and P. W. Seakins, Chem. Phys. Lett., 2007, 445, 108–112 CrossRef CAS PubMed.
- M. A. Blitz, D. E. Heard and M. J. Pilling, Chem. Phys. Lett., 2002, 365, 374–379 CrossRef CAS.
- G. S. Tyndall, J. J. Orlando, T. J. Wallington and M. D. Hurley, Int. J. Chem. Kinet., 1997, 29, 655–663 CrossRef.
- G. Kovács, J. Zádor, E. Farkas, R. Nádasdi, I. Szilágyi, S. Dóbé, T. Bérces, F. Márta and G. Lendvay, Phys. Chem. Chem. Phys., 2007, 9, 4142–4154 RSC.
- J. Lee, C.-J. Chen and J. W. Bozzelli, J. Phys. Chem. A, 2002, 106, 7155–7170 CrossRef CAS.
- H. Hou, A. Li, H. Hu, Y. Li, H. Li and B. Wang, J. Chem. Phys., 2005, 122, 224304 CrossRef PubMed.
- A. Maranzana, J. R. Barker and G. Tonachini, Phys. Chem. Chem. Phys., 2007, 9, 4129–4141 RSC.
- M. A. Blitz, D. E. Heard, M. J. Pilling, S. R. Arnold and M. P. Chipperfield, Geophys. Res. Lett., 2004, 31, L06111 Search PubMed.
- H. B. Singh, M. Kanakidou, P. J. Crutzen and D. J. Jacob, Nature, 1995, 378, 50–54 CrossRef CAS.
- S. A. McKeen, T. Gierzak, J. B. Burkholder, P. O. Wennberg, T. F. Hanisco, E. R. Keim, R.-S. Gao, S. C. Liu, A. R. Ravishankara and D. W. Fahey, Geophys. Res. Lett., 1997, 24, 3177–3180 CrossRef CAS.
- C. B. M. Groß, T. J. Dillon, G. Schuster, J. Lelieveld and J. N. Crowley, J. Phys. Chem. A, 2014, 118, 974–985 CrossRef PubMed.
- I. Bridier, F. Caralp, H. Loirat, R. Lesclaux, B. Veyret, K. H. Becker, A. Reimer and F. Zabel, J. Phys. Chem., 1991, 95, 3594–3600 CrossRef CAS.
- G. J. Phillips, N. Pouvesle, J. Thieser, G. Schuster, R. Axinte, H. Fischer, J. Williams, J. Lelieveld and J. N. Crowley, Atmos. Chem. Phys., 2013, 13, 1129–1139 CrossRef CAS.
- D. Taraborrelli, M. G. Lawrence, J. N. Crowley, T. J. Dillon, S. Gromov, C. B. M. Groß, L. Vereecken and J. Lelieveld, Nat. Geosci., 2012, 5, 190–193 CrossRef CAS.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2006, 3625–4055 CrossRef CAS.
- M. Ammann, R. A. Cox, J. N. Crowley, M. E. Jenkin, A. Mellouki, M. J. Rossi, J. Troe and T. J. Wallington, IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation, 2014, http://iupac.pole-ether.fr/index.html.
- T. J. Dillon, M. E. Tucceri and J. N. Crowley, Phys. Chem. Chem. Phys., 2006, 8, 5185–5198 RSC.
- T. J. Dillon, A. Horowitz and J. N. Crowley, Chem. Phys. Lett., 2007, 443, 12–16 CrossRef CAS PubMed.
- A. Galano, J. R. Alvarez-Idaboy, M. E. Ruiz-Santoyo and A. Vivier-Bunge, J. Phys. Chem. A, 2005, 109, 169–180 CrossRef CAS PubMed.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738 CrossRef CAS.
- V. Khamaganov, R. Karunanandan, A. Horowitz, T. J. Dillon and J. N. Crowley, Phys. Chem. Chem. Phys., 2009, 11, 6173–6181 RSC.
- C. Maul and K.-H. Gericke, Int. Rev. Phys. Chem., 1997, 16, 1–79 CrossRef CAS.
- H. Niki, P. D. Maker, C. M. Savage and M. D. Hurley, J. Phys. Chem., 1987, 91, 2174–2178 CrossRef CAS.
- C. Bacher, G. S. Tyndall and J. J. Orlando, J. Atmos. Chem., 2001, 39, 171–189 CrossRef CAS.
- G. L. Vaghjiani and A. R. Ravishankara, J. Geophys. Res.: Atmos., 1989, 94, 3487–3492 CrossRef CAS.
- H. Keller-Rudek, G. K. Moortgat, R. Sander and R. Sörensen, Earth Syst. Sci. Data, 2013, 5, 365–373 CrossRef.
- J. V. Michael, D. G. Keil and R. B. Klemm, J. Chem. Phys., 1985, 83, 1630–1636 CrossRef CAS PubMed.
- R. Karunanandan, D. Hölscher, T. J. Dillon, A. Horowitz, J. N. Crowley, L. Vereecken and J. Peeters, J. Phys. Chem. A, 2007, 111, 897–908 CrossRef CAS PubMed.
- V. Khamaganov, R. Karunanandan, A. Rodriguez and J. N. Crowley, Phys. Chem. Chem. Phys., 2007, 9, 4098–4113 RSC.
- H. Somnitz, T. Ufer and R. Zellner, Phys. Chem. Chem. Phys., 2009, 11, 8522–8531 RSC.
- B. Rajakumar, T. Gierczak, J. E. Flad, A. R. Ravishankara and J. B. Burkholder, J. Photochem. Photobiol., A, 2008, 199, 336–344 CrossRef CAS PubMed.
- R. K. Talukdar, M. E. Davis, L. Zhu, A. R. Ravishankara and J. B. Burkholder, 19th International Symposium on Gas Kinetics, Orleans, France, 2006 Search PubMed.
- N. I. Butkovskaya, N. Pouvesle, A. Kukui and G. Le Bras, J. Phys. Chem. A, 2006, 110, 13492–13499 CrossRef CAS PubMed.
- C. B. M. Groß, Fachbereich Chemie der Johannes-Gutenberg-Universität Mainz, Kinetische Studien zur OH-Bildung über die Reaktionen von HO2 mit organischen Peroxyradikalen, PhD thesis, 2013.
- J. C. Hansen, Y. Li, C. M. Rosado-Reyes, J. S. Francisco, J. J. Szente and M. M. Maricq, J. Phys. Chem. A, 2003, 107, 5306–5316 CrossRef CAS.
Footnote |
| † Present address: Department of Chemistry, University of York, York, YO10 5DD, UK. |
| This journal is © the Owner Societies 2014 |

