 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High DNP efficiency of TEMPONE radicals in liquid toluene at low concentrations†
Nikolay
Enkin
,
Guoquan
Liu
*,
Igor
Tkach
and
Marina
Bennati
*
Max-Planck Institute for Biophysical Chemistry, Am Fassberg, 37077 Göttingen, Germany. E-mail: guoquan.liu@mpibpc.mpg.de; marina.bennati@mpibpc.mpg.de
First published on 20th March 2014
Abstract
We show that at low concentrations (≤5 mM) TEMPONE radicals in liquid toluene exhibit higher DNP efficiency than in water. In spite of reduced coupling factors, the improved DNP performance in toluene results from favourable saturation and leakage factors, as determined by pulse electron–electron double resonance (ELDOR) and NMR relaxation, respectively. The extracted coupling factors at 0.35 Tesla support theoretical predictions of the Overhauser mechanism.
Dynamic nuclear polarization (DNP) is an emerging technique to enhance NMR signals and thus to improve the sensitivity or the contrast of NMR/MRI signals. In a DNP experiment, paramagnetic species, the so-called polarizers, transfer their spin polarization to hyperfine coupled nuclei when subjected to microwave irradiation. Over the last decade, the method has been extensively developed in different laboratories for NMR applications at high magnetic fields.1–7
In liquids, DNP is governed by the Overhauser mechanism,8 in which the enhancement is proportional to the gyromagnetic ratios of the electron and the interacting nuclear spin (γe/γn), the coupling factor ξ, the leakage factor f and the saturation factor s:9,10
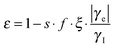 | (1) |
Recently, DNP with nitroxides in non-aqueous solvents, such as toluene16,17 or benzene,18 has been reconsidered by taking advantage of instrumental developments at different magnetic fields and progress in analysis. These non-polar solvents might be particularly attractive to host more complex organic polarizers and have the great advantage of low dielectric losses, which attenuate microwave heating. The latter facilitates mechanistic studies, which are critically dependent on temperature, and allows for the use of sample sizes close to standard NMR tubes. In the recent studies on nitroxides in toluene17 and hexane,18 large negative 1H-NMR enhancements of the solvent on the order of or even higher than those in nitroxide–water have been observed. In the toluene study a different behavior of the ring and methyl 1Hs was observed, however, a precise determination of coupling factors was hampered by the uncertainty about the saturation factor. Subsequently, a new theoretical approach was proposed to compute DNP coupling factors by combining MD simulations with analytical calculations of spectral densities at different magnetic fields.19,20 Particularly, these studies provided predictions for the site-specific DNP enhancements of different toluene 1Hs based on the molecular shape and dynamics. The same studies questioned the use of classical models21 in liquid DNP to determine atomistic parameters, such as the distance of the closest approach between the polarizer and the solvent. Nevertheless, experimental coupling factors are still missing in support of this study.
In this communication we present DNP experiments with 15N- and 2H-labelled TEMPONE (4-Oxo-TEMPO) in toluene solutions at 0.35 Tesla and an electron Larmor frequency of 9 GHz. This frequency is interesting for DNP in liquid state because of the large achievable enhancements and the possibility to combine it with high frequency NMR detection within a shuttle spectrometer.22 We are able to distinguish two kinds of 1H in toluene, i.e. the ring and the methyl 1Hs. We find that DNP enhancements in toluene as compared to water are significantly larger in the low concentration regime (≤5 mM) but reach similar maximum values at higher concentrations. The finding is investigated by electron–electron double resonance (ELDOR) and NMR to independently determine the saturation and the leakage factors.
In Fig. 1a we display representative room-temperature 1H-14 MHz NMR spectra of degassed toluene doped with 5 mM TEMPONE-D-15N. Two peaks can be resolved with a separation of about 70 Hz, corresponding to 5 ppm, which are consistent with the resonances of the ring and the methyl 1H of toluene. After irradiation by microwave (mw), on-resonant with the radical EPR absorption (low-field hyperfine line), the NMR signal is enhanced by more than two orders of magnitude. We note that the polarizer concentration here is significantly lower than that usually reported in DNP experiments in liquids (20–100 mM). The DNP enhancements εring and εmethyl were determined to be −159 and −137 with an error of approx. ±5% from the first point of the free induction decay (ESI†). The enhancement does not further increase with the radical concentration (Fig. 1b). A comparison with the enhancement of water under similar conditions of mw irradiation (B1 ≈ 3 G) shows that DNP enhancements of toluene are substantially higher at low concentrations; however, they reach slightly lower maximum values εmax at high concentrations.
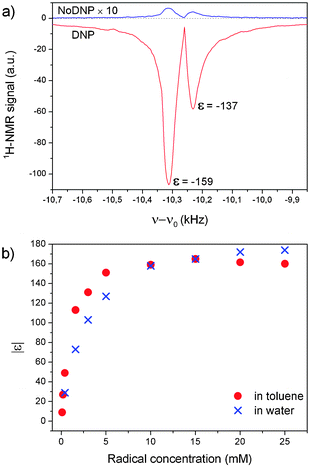 | ||
| Fig. 1 (a) 1H NMR spectra of toluene doped with 5 mM TEMPONE-D-15N at 14 MHz. (b) Concentration dependence of DNP enhancements (from maximum of εFID) of TEMPONE-D-15N in toluene and in water. Experimental details for toluene: samples degassed by three freeze–pump–thaw cycles, volumes of 20 μL, 1 or 8 scans for DNP measurements, 128 scans for Boltzmann measurements, Pmw ≈ 3 W, tirrad. = 2–30 s depending on the concentration. For aqueous samples: non-degassed, V = 0.6 μL, 64 scans for DNP measurements and 1024 scans for Boltzmann measurements, tirrad = 1–5 s. Details of the experimental set up are given in ref. 23 and in the ESI.† | ||
Before analysing the observed enhancements, heating effects during mw irradiation need to be carefully examined. An increase in sample temperature leads to higher coupling factors and consequently higher enhancements.24 According to previous DNP studies, heating effects were observed in water solutions at 9 GHz if the sample was exposed to the electric field of the microwaves.23,25–27 Heating effects are usually manifested through lengthening of the build-up time of the DNP signal (Tbuildup), which is otherwise determined by the relaxation rate of the detected nucleus in the presence of the polarizer (T1n).28 For all samples in this study, the filling height amounted to ≤5 mm, according to the homogeneity of the B1 mw field in the dielectric resonator along the z-axis.23 The inner diameter (ID) of the tube was optimized by measurements of the DNP build-up times and comparison with nuclear T1n. For toluene sample tubes with an ID of 3 mm, Tbuildup for both 1H types was found to be similar (within a 10% error limit) to T1n measured independently from inversion recovery (Table 1).
| Concentration (mM) | ε | T buildup (s) | T 1n (s) | f | T 2e (ns) | s 2,max | s eff | ξ | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H ring | H m | H ring | H m | H ring | H m | H ring | H m | H ring | H m | ||||
| a Calculated from Tbuildup. b From EPR line width, Fig. S3 (ESI). | |||||||||||||
| 0.2 | 32 | 18 | 12.1 | 8.9 | 10.7 | 7.4 | 0.34 | 0.24 | 171 | 0.18 | 0.59 | 0.25 | 0.21 |
| 0.4 | 58 | 34 | 8.0 | 6.4 | — | — | 0.51a | 0.34a | 152 | 0.34 | 0.67 | 0.26 | 0.23 |
| 1.6 | 124 | 94 | 3.3 | 3.1 | 3.2 | 3.2 | 0.80 | 0.67 | 98 | 0.66 | 0.83 | 0.28 | 0.26 |
| 5.0 | 159 | 137 | 1.2 | 1.3 | 1.4 | 1.6 | 0.91 | 0.84 | 48 | 0.84 | 0.92 | 0.29 | 0.26 |
From T1n we could also evaluate the leakage factors f according to the definition:
 | (2) |
 are the spin–lattice relaxation rates of the toluene 1Hs in the presence and absence of the radical, respectively.24 The diamagnetic contribution amounted to 0.06 s−1 for the ring and 0.1 s−1 for the methyl protons, in agreement with the values reported in ref. 17. The leakage factors from eqn (2) are listed in Table 1. The ring protons exhibit slightly larger leakage factors f compared to the methyl protons at all concentrations, which is consistent with previous results obtained at 3.4 Tesla.17 A comparison with the leakage factors in water indicates that the larger Rdia of water (0.33 s−1) is responsible for reducing f in water as compared to toluene (Fig. S1, ESI†).
are the spin–lattice relaxation rates of the toluene 1Hs in the presence and absence of the radical, respectively.24 The diamagnetic contribution amounted to 0.06 s−1 for the ring and 0.1 s−1 for the methyl protons, in agreement with the values reported in ref. 17. The leakage factors from eqn (2) are listed in Table 1. The ring protons exhibit slightly larger leakage factors f compared to the methyl protons at all concentrations, which is consistent with previous results obtained at 3.4 Tesla.17 A comparison with the leakage factors in water indicates that the larger Rdia of water (0.33 s−1) is responsible for reducing f in water as compared to toluene (Fig. S1, ESI†).
The concentration dependence of the DNP enhancements of TEMPONE-D-15N in toluene (Fig. 1b) suggests similar coupling factors as in water but a peculiar behaviour of the saturation factor. To clarify this point, pulsed ELDOR was applied to directly measure the effective saturation of both nitroxide lines seff when only one EPR line was excited by microwaves.29 Preconditions for this dual frequency experiment are the detection of the radical FID as well as the capability to pump and detect both EPR lines within the EPR resonator. For a separation of ∼60 MHz of the 15N nitroxide hyperfine lines (Fig. S3, ESI†), the experiment is well feasible at 9 GHz within the band width of a standard overcoupled dielectric resonator. On the other hand, the detection of an EPR-FID depends on T2, which usually shortens at higher concentrations due to concentration dependent relaxation contributions (exchange and dipolar couplings). For TEMPONE in toluene, detection of the FID was possible only at concentrations up to about 5 mM.
The EPR-FID intensity as a function of the frequency of the saturation pulse is depicted in Fig. 2. When the saturation pulse was resonant with the detection frequency, a complete drop in the FID signal was achieved at all concentrations (up to 5 mM). This corresponds to a full saturation (s1 = 1) of the excited EPR line. A second drop in FID was visible when the saturation pulse became resonant with the second hyperfine transition. This reduction in FID directly corresponds to the saturation factor of the coupled hyperfine line (s2).29–31 The effective saturation factor seff of the total EPR spectrum is then the average of s1 and s2, i.e. seff = (s1 + s2)/2. To correlate s2 and seff as determined by ELDOR with seff of DNP in eqn (1), one should perform both experiments at comparable microwave excitation fields. On the other hand, the saturation factor of the coupled hyperfine line reaches a maximum value s2,max, when the excited line is saturated (s1 = 1).29 The condition s1 = 1, which is well satisfied in the ELDOR experiment (Fig. 2), was tested in the DNP setup by recording the intensity of the excited EPR transition as a function of the microwave power (Fig. S2, ESI†). For P ∼ 3 W, saturation s1 close to unity was achieved at the investigated concentrations. Therefore, the saturation factors from Fig. 2a can be used to calculate seff,max for DNP (Table 1). Fig. 2b illustrates a comparison of s2,max of TEMPONE-D-15N in toluene and in water (data for water from ref. 29). The former increases rapidly with the radical concentration and it is larger than that in water at comparable concentrations.
 | ||
| Fig. 2 (a) EPR-FID intensity of the high-field hf line of TEMPONE-D-15N as a function of the frequency of the saturating (pump) pulse. Exp. details: detection is 30 MHz off resonance on the high field side to minimize simultaneous excitation of the low field line; t (π/2) = 16 ns; t (pump) = 1 μs. B1 ∼2–3 G. Error due to ringing was ≤10%. (b) Concentration dependence of s2,max. Saturation data for water are from ref. 29. Red and black traces are calculated according to eqn (3) for toluene and water samples, respectively. T1e for water is 298 ns.29 | ||
Saturation factors seff,max > 0.5 of TEMPONE in water have been previously attributed to the effect of Heisenberg exchange between the spin states of the two hyperfine lines according to:29
 | (3) |
| i1,2 = A1,2e−2wet ± B1,2e−(2we + 2wn + ωex)t | (4) |
 | ||
| Fig. 3 Recovery curves and fits of the FID in EPR and ELDOR polarization recovery measurements at 1.6 mM TEMPONE-D-15N in toluene. Experimental setup and conditions are similar to those given in Fig. 2. | ||
With the availability of all factors in eqn (1) except ξ, we were then able to determine the coupling factors for the ring and methyl 1H of toluene doped with TEMPONE at 0.35 T. This value was calculated at each concentration and is listed in Table 1. As expected, ξ is independent of the radical concentration within the error limit and averages to 0.27 and 0.24 for the ring and the methyl 1Hs, respectively.¶ The error is estimated to be ±0.025 (about 10%) and is larger at lower concentrations due to the weaker S/N ratio. However, the error in trend (difference between the average ξ of the two 1H types) is much less, as seen from the data in Table 1. Therefore the difference between the ξs is significant.
The magnitude of ξ for the 1Hs of toluene is less than that of the water protons (ξwater = 0.3329) using the same radical polarizer. One might not exclude a priori that the observed ξ results from counteracting scalar and dipolar relaxation mechanisms, although the dipolar mechanism is reportedly dominant for 1H. If pure dipolar relaxation is dominated by a single correlation function, the coupling factor can be estimated from the nuclear relaxation rates:9
 | (5) |
Our results reveal a difference in the coupling factors between the ring and methyl protons that has not been inferred to date experimentally due to the lack of information about the saturation behaviour. In a previous 94 GHz/3 T study on TEMPOL/toluene,17 larger DNP enhancements of the ring protons were observed but attributed to a favourable leakage factor. The present results are mechanistically significant as the obtained coupling factors are in excellent agreement with recent theoretical predictions19 (ξtheorring = 0.268; ξtheormethyl = 0.25 at 9.6 GHz mw frequency) performed using a sophisticated combination of MD simulations and analytical expressions of spectral densities for dipolar relaxation in the TEMPOL/toluene system. The MD trajectories allowed to capture the dynamics of the polarizer and the solvent within the short interaction range (<1 nm) and to extract appropriate dipolar correlation functions. The larger ξtheor of the ring protons was found to be associated to a larger radial density distribution at the closest possible distance to the electron spin of the nitroxide group. The agreement between our experiment and theory at this level of atomistic details is encouraging and opens up new prospects for the application of DNP to investigate molecular dynamics.
Conclusions
DNP experiments with TEMPONE in toluene at 0.35 T revealed that large signal enhancements (ε ≥ 100) could be achieved at low polarizer concentrations (c ≤ 5 mM), which makes this solvent attractive for future developments and applications of DNP. The high DNP performance was rationalized by investigating the different parameters of the Overhauser equation. Most importantly, the saturation behaviour of the EPR line in toluene turned out to be very efficient due to a Heisenberg exchange coupling rate that is larger than that in water by a factor of ≥2. Knowledge of the saturation factor permitted us to evaluate the DNP coupling factors for the different protons of toluene that provide insight into the DNP mechanism at the atomistic level. Our results support a recent theoretical MD investigation, by which the coupling factors in toluene reflect the detailed motion of the solvent protons around the atoms bearing the electron spin.Acknowledgements
We would like to thank Giacomo Parigi and Deniz Sezer for discussion. We acknowledge financial support from the Max Planck Society and the COST Action TD1103 (European Network on Hyperpolarization). NE acknowledges the Graduate School for Neurosciences, Biophysics and Molecular Biosciences in Göttingen (GGNB) for financial support.Notes and references
- T. Maly, G. T. Debelouchina, V. S. Bajaj, K. N. Hu, C. G. Joo, M. L. Mak-Jurkauskas, J. R. Sirigiri, P. C. A. van der Wel, J. Herzfeld, R. J. Temkin and R. G. Griffin, J. Chem. Phys., 2008, 128, 052211 Search PubMed.
- J. H. Ardenkjaer-Larsen, B. Fridlund, A. Gram, G. Hansson, L. Hansson, M. H. Lerche, R. Servin, M. Thaning and K. Golman, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163 CrossRef CAS PubMed.
- P. Höfer, G. Parigi, C. Luchinat, P. Carl, G. Guthausen, M. Reese, T. Carlomagno, C. Griesinger and M. Bennati, J. Am. Chem. Soc., 2008, 130, 3254–3255 CrossRef PubMed.
- R. G. Griffin and T. F. Prisner, Phys. Chem. Chem. Phys., 2010, 12, 5737–5740 RSC.
- J. G. Krummenacker, V. P. Denysenkov, M. Terekhov, L. M. Schreiber and T. F. Prisner, J. Magn. Reson., 2012, 215, 94–99 CrossRef CAS PubMed.
- C. Y. Cheng and S. I. Han, Annu. Rev. Phys. Chem., 2013, 64, 507–532 CrossRef CAS PubMed.
- Q. Z. Ni, E. Daviso, T. V. Chan, E. Markhasin, J. Sudheer, T. M. Swager, R. J. Temkin, J. Herzfeld and R. G. Griffin, Acc. Chem. Res., 2013, 46, 1933–1941 CrossRef CAS PubMed.
- A. W. Overhauser, Phys. Rev., 1953, 92, 411–415 CrossRef CAS.
- D. Hausser and D. Stehlik, Adv. Magn. Reson., 1968, 3, 79–139 Search PubMed.
- W. Müller-Warmuth and K. Meise-Gresch, Adv. Magn. Reson., 1983, 11, 1–45 Search PubMed.
- M. Bennati, I. Tkach and M. T. Türke, in Electron paramagnetic resonance, ed. B. Gilbert, Royal Society of Chemistry, Cambridge, 2011, pp. 155–182 Search PubMed.
- M. D. Lingwood and S. Han, Annu. Rep. NMR Spectrosc., 2011, 73, 83–126 CrossRef CAS.
- C. Griesinger, M. Bennati, H. M. Vieth, C. Luchinat, G. Parigi, P. Höfer, F. Engelke, S. J. Glaser, V. Denysenkov and T. F. Prisner, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 64, 4–28 CAS.
- N. M. Loening, M. Rosay, V. Weis and R. G. Griffin, J. Am. Chem. Soc., 2002, 124, 8808–8809 CrossRef CAS PubMed.
- K. Tateishi, M. Negoro, A. Kagawa and M. Kitagawa, Angew. Chem., Int. Ed., 2013, 52, 13307–13310 CrossRef CAS PubMed.
- G. J. Krüger, W. Müller-Warmuth and R. Van Steenwinkel, Z. Naturforsch., A: Astrophys. Phys. Phys. Chem., 1966, 21, 1224–1230 Search PubMed.
- E. V. Kryukov, M. E. Newton, K. J. Pike, D. R. Bolton, R. M. Kowalczyk, A. P. Howes, M. E. Smith and R. Dupree, Phys. Chem. Chem. Phys., 2010, 12, 5757–5765 RSC.
- O. Neudert, C. Mattea, H. W. Spiess, S. Stapf and K. Muennemann, Phys. Chem. Chem. Phys., 2013, 15, 20717–20726 RSC.
- D. Sezer, Phys. Chem. Chem. Phys., 2013, 15, 526–540 CAS.
- D. Sezer, Phys. Chem. Chem. Phys., 2014, 16, 1022–1032 RSC.
- L. P. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017–4025 CAS.
- A. Krahn, P. Lottmann, T. Marquardsen, A. Tavernier, M. T. Turke, M. Reese, A. Leonov, M. Bennati, P. Höfer, F. Engelke and C. Griesinger, Phys. Chem. Chem. Phys., 2010, 12, 5830–5840 RSC.
- M. T. Türke, I. Tkach, M. Reese, P. Höfer and M. Bennati, Phys. Chem. Chem. Phys., 2010, 12, 5893–5901 RSC.
- M. Bennati, C. Luchinat, G. Parigi and M.-T. Türke, Phys. Chem. Chem. Phys., 2010, 12, 5902–5910 RSC.
- M. Gafurov, V. Denysenkov, M. J. Prandolini and T. F. Prisner, Appl. Magn. Reson., 2012, 43, 119–128 CrossRef CAS.
- P. Neugebauer, J. G. Krummenacker, V. P. Denysenkov, G. Parigi, C. Luchinat and T. F. Prisner, Phys. Chem. Chem. Phys., 2013, 15, 6049–6056 RSC.
- J. M. Franck, A. Pavlova, J. A. Scott and S. Han, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 74, 33–56 CrossRef CAS PubMed.
- M. T. Türke and M. Bennati, Appl. Magn. Reson., 2012, 43, 129–138 CrossRef PubMed.
- M. T. Türke and M. Bennati, Phys. Chem. Chem. Phys., 2011, 13, 3630–3633 RSC.
- J. S. Hyde, J. C. W. Chen and J. H. Freed, J. Chem. Phys., 1968, 48, 4211–4226 CrossRef CAS PubMed.
- M. T. Türke, G. Parigi, C. Luchinat and M. Bennati, Phys. Chem. Chem. Phys., 2012, 14, 502–510 Search PubMed.
- B. L. Bales and M. Peric, J. Phys. Chem. B, 1997, 101, 8707–8716 CrossRef CAS.
- J. D. Currin, Phys. Rev., 1962, 126, 1995 CrossRef CAS.
- C. Riplinger, J. P. Y. Kao, G. M. Rosen, V. Kathirvelu, G. R. Eaton, S. S. Eaton, A. Kutateladze and F. Neese, J. Am. Chem. Soc., 2009, 131, 10092–10106 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The DNP setup, evaluation of enhancements, comparison of leakage factors in toluene and water, power and concentration dependence of the TEMPONE CW-EPR line in toluene, EPR and ELDOR recovery curves at 0.1 and 3 mM TEMPONE concentrations, an estimate of exchange coupling from the EPR line width. See DOI: 10.1039/c4cp00854e |
| ‡ T1e was also measured at 0.1 and 3 mM TEMPONE concentrations, as displayed in Fig. S4 (ESI†). Values were found to be distributed within the error limit given in the text, likely due to the slightly different oxygen content. |
| § This is not always valid and has to be verified from case to case. A comparative estimate of ωex obtained from the EPR line broadening is reported in Fig. S5 (ESI†). The value of Kx = (4.3 ± 0.5) × 109 s−1 M−1 is within the error limit as given in the text. However, determination from line broadening seems to be less accurate. |
| ¶ The coupling factor at low concentrations is likely to be underestimated due to insufficient irradiation time. We did not use longer irradiation times to avoid heating in the resonator and in the sample. |
| This journal is © the Owner Societies 2014 |
