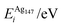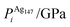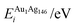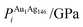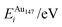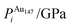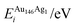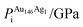Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Segregation effects on the properties of (AuAg)147†
A. L.
Gould
*a,
C. J.
Heard
b,
A. J.
Logsdail
*c and
C. R. A.
Catlow
ac
aRutherford Appleton Laboratory, Harwell Oxford Didcot, Oxon, OX11 0FA, UK. E-mail: a.gould@ucl.ac.uk
bSchool of Chemistry, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
cKathleen Lonsdale Materials Chemistry, 20 Gordon Street, London, WC1H 0AJ, UK. E-mail: a.logsdail@ucl.ac.uk
First published on 15th April 2014
Abstract
AuAg nanoclusters are promising supported co-catalysts for photocatalytic hydrogen reduction. However, beyond the quantum regime (N > 100) little is known about how the electronic properties of these nanoparticles are affected by chemical ordering. We investigate the effects of chemical ordering on the properties of 147-atom cuboctahedral AuAg nanoclusters, using empirical potentials coupled with an atomic-swap basin-hopping search to optimise the elemental distribution, with the lowest energy arrangements then reminimised using Density Functional Theory (DFT). Force-field calculations show Au atoms preferentially occupy sub-surface positions in the bimetallic structures, which results in the formation of a pseudo-onion structure for Ag-rich compositions. At the DFT-level, however, an Ag core surrounded by an Au shell (Ag@Au) is energetically favoured, as electron density can be drawn more readily when Au atoms are positioned on the nanocluster surface, thus resulting in a partial negative charge. Core@shell configurations are analogous to structures that can be chemically synthesised, and further detailed electronic analysis is discussed in the context of nanocluster applications to co-catalysed photocatalysis.
1. Introduction
Supported metal nanoparticles (nanoclusters) can enhance heterogeneous catalysis in comparison to isolated supports or nanoclusters,1,2 with the structure of the nanocluster greatly influencing catalytic performance.3 Recently, nanoclusters have been used successfully as co-catalysts for photocatalytic reactions on semiconducting substrates, using both visible and ultraviolet light sources.4 Two distinct physical processes are thought to occur in the synthesis routes: for visible-light (2–3 eV), surface plasmon resonances result in the direct injection of electrons from the nanocluster into the semiconductor conduction band,5 whereas for UV radiation (3–103 eV), direct excitation of electrons from the valence band of the semiconductor to the conduction band occurs, with nanoclusters then acting as an electron trap for the excited states, thus extending the photocatalytic lifetime.6Bimetallic nanoclusters (“nanoalloys”) have garnered much recent interest, as the combination of two metallic species can result in favourable synergistic effects, and lower production costs.7 The introduction of a second metal, however, significantly complicates the nanocluster structure, as there is a range of possible chemical arrangements for the two elements. The three most common chemical orderings are mixed nanoalloys, segregated subclusters and core@shell segregated nanoalloys.8,9 The quantity of different chemical arrangements, or “homotops”,10,11 for a bimetallic nanocluster ANABNB is defined as:
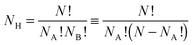 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 alloy systems, although symmetric equivalence in the chemical arrangements can be used to simplify analysis.13
1 alloy systems, although symmetric equivalence in the chemical arrangements can be used to simplify analysis.13
In general, the geometric preferences of nanoclusters depend strongly on factors such as the atomic size, electronegativity and electronic charge for the constituent species.14,15 Compact, non-crystalline structures often form for small nuclearities (N), minimising surface area at the expense of increased internal strain due to the non-optimal internal interatomic distances.16 Strain energy is generally proportional to cluster volume, so the non-crystalline structures become energetically unfavourable at large N, instead forming more bulk-like arrangements where the strain energy is reduced. For bimetallic systems, atomic size mismatch between species can play an important role in the reduction of the structure-induced strain energy.17 If atomic size mismatch is large, the overall strain energy can be reduced for non-crystalline structures by placing the smaller atoms inside the nanoalloy, as observed for Ag–Ni, Ag–Cu and Au–Cu.14
Previous studies have highlighted three prominent high symmetry structures for nanoclusters: the icosahedron (Ih), the Ino-decahedron (I-Dh) and the cuboctahedron (CO); each of which form closed shell geometries at equivalent N.18,19 Small clusters favour the Ih, where minimisation of the surface energy takes precedence over strain contributions.20 I-Dh has less internal strain than Ih, and is therefore favoured at larger N. CO is a face-centred cubic (FCC) fragment and therefore has the lowest internal strain of these geometries (arising in nanoclusters due to surface contractions). However, it has the largest surface/volume ratio, and thus is favoured at sizes tending to the bulk (N → ∞).16
Geometrically complete atomic shells are achieved at the same nuclearities for Ih, I-Dh and CO, and are referred to as “magic numbers” due to the particularly high geometric stabilities encountered.21 Equivalent electronic stability is achieved for “magic numbers” of electrons when the total number of valence electrons results in a complete valence shell (1s2, 2s2, 2p6,…). These magic clusters are of experimental interest as their high stability results in monodisperse systems, and the clusters can therefore be identified as particularly strong peaks in mass spectra, indicative of their greater stability with respect to dissociation when compared to neighbouring sizes.22
AuAg nanoalloys are of recent interest as they have been shown to improve catalytic activity for CO and H2 oxidation,23 and reduce production costs.24 However, they are a complex system to study as the mismatch in atomic size is small, and coupled with their significantly differing electronegativities (2.54 for Au and 1.93 for Ag25), the formation of alloys during chemical synthesis is common. An appreciable degree of charge transfer may occur between the elements, due to the differing electronegativities, which can affect atomic radii and mitigates against the stability of chemical arrangements such as core@shell.17 Experimental synthesis of core@shell structural arrangements, however, has been demonstrated as feasible due to kinetic trapping.26–29
To discuss the thermodynamic stability of AuAg nanoclusters, we need to consider the bulk properties of Au and Ag. The homogeneous bond lengths are very similar: 2.889 and 2.884 Å for Ag and Au, respectively,30 meaning that there is minimal size mismatch between the two atomic species, and thus a minimal strain-induced driving force for segregation. However, the surface energy of Ag is less than that of Au (78 and 97 meV Å−2 respectively31), which would favour surface segregation of Ag atoms. The cohesive energy of Ag is also lower than that of Au: 2.95 eV atom−1 compared to 3.81 eV atom−1, respectively,32 which implies preferential segregation of Au atoms towards a nanocluster core, where they will have a higher coordination.33
Previous computational work has thoroughly investigated the structural preferences for small Au34–38 and Ag39–43 nanoclusters, however AuAg is less well studied. Higher-level DFT calculations for small AuAg nanoalloys (N ≤ 10 atoms37) have shown a preference for topologies that maximise the number of Au–Ag interactions, allowing for improved charge transfer between the two metallic species.44,45 In these small clusters the adopted chemical order can induce further charge transfer than initially expected, as found by Chen et al. for (AuAg)13.33 Bonačić-Koutecký observed planar structures were favoured for Au4Ag4 and Ag8, due to dominant s-orbital bonding, whilst the favoured arrangement of Au8 is less clear; Bonačić-Koutecký found 3D structures, attributed to the participation of d electrons,46 whereas Heiles et al. determined Au8 to be planar.45
Larger nanoalloys (10 ≤ x ≤ 100 atoms) favour structures that have an Ag-enriched surface and an Au-enriched core, as calculated using a combined empirical potentials and DFT approach,47–50 although a recent basin-hopping study by Cerbelaud et al., using an empirical potential that incorporates charge transfer effects, finds that Au atoms on the nanoalloy surface are energetically favourable and in better agreement with equivalent DFT calculations up to N = 201.51 Most recently, the kinetic ordering in 55-atom icosahedral AuAg clusters were investigated by Calvo et al.,52 using discrete-path sampling with empirical potentials. Inversion of core@shell structures from Au@Ag to Ag@Au required compositional rearrangement (rather than diverse atomistic mechanisms) in two stages; firstly the migration of many atoms, breaking icosahedral symmetry, followed by the introduction of vacancies. Spontaneous reordering under ambient conditions was determined to be very unlikely, due to an overall forward (backward) energy barrier of 2.74 (0.62) eV.
For N < 100, the properties of the clusters are often governed by quantum effects where “every atom counts”; however, the electronic properties of larger clusters (N > 100) should become more consistent with variation in N, and so observations made for large N may be extrapolated for comparison with even larger experimental clusters. Therefore, in this work we examine the energetically favourable chemical ordering for different AuAg nanoclusters beyond the quantum regime, using a representative 147-atom CO. The chemical orderings were optimised (with respect to the energy of the nanocluster) for various stoichiometries using semi-empirical potentials with atomic-swap searches, and the lowest energy structures have then been reminimised at the DFT-level, and reanalysed. By determining the most stable and/or the most catalytically suitable arrangements, particular morphologies may be proposed for experimental synthesis in the highlighted photocatalytic applications.
2. Theoretical methods
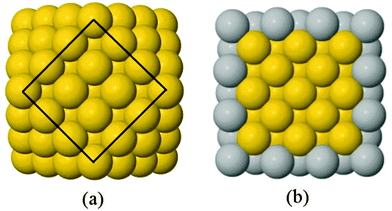
A 147-atom CO nanocluster [Fig. 1(a)] was created using mathematical constructs. Starting with pure Ag147, the Au content was systematically increased until the final composition reached Au147. The optimisation of chemical ordering was investigated for Au147−nAgn, where n = 1, 13, 55, 73, 92, 134 and 146. Our choices of n are such that the ratios of Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au allow geometric “magic number” [n = 13, 55, 92, 134] core@shell arrangements to be formed [Fig. 1(b)]. We also investigated 1
Au allow geometric “magic number” [n = 13, 55, 92, 134] core@shell arrangements to be formed [Fig. 1(b)]. We also investigated 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 alloys [n = 73] and atomically doped systems [n = 1, 146].
1 alloys [n = 73] and atomically doped systems [n = 1, 146].
2.1 The Gupta potential
To improve computational feasibility we have used semi-empirical potentials in our initial searches for optimal chemical ordering; the potentials are fitted to an assumed functional form that reproduces bulk properties. The Gupta potential, commonly used to model interatomic interactions for metallic systems,53 has previously been successful applied to problems of a similar nature to ours.54–56 It is derived from the second moment approximation to tight-binding theory, where atoms are modelled as rigid ions, and electrons are allowed to ‘hop’ between.57 The truncated form consists of an attractive many body (Vmi) and a repulsive pair (Vri) term, obtained by summing over all N atoms, to give a total energy: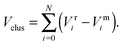 | (2) |
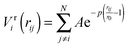 | (3) |
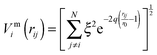 | (4) |
| Parameter | A/eV | r 0/Å | ξ/eV | p | q |
|---|---|---|---|---|---|
| Au–Au | 0.2061 | 2.8843 | 4.036 | 10.229 | 1.790 |
| Au–Ag | 0.15445 | 2.8864 | 3.5875 | 10.5785 | 1.484 |
| Ag–Ag | 0.1028 | 2.8885 | 3.139 | 10.928 | 1.178 |
2.2 Basin-hopping algorithm
Searches for the optimal chemical ordering of the nanocluster were performed using the basin-hopping (BH) algorithm as implemented in the software package GMIN.58 More explicitly, the atomic swap functionality was used exclusively, rather than full basin-hopping, where two atoms are randomly selected, and their coordinates are interchanged. By using just the atomic-swap functionality, we ensure that the starting CO structure is maintained throughout.For each chemical composition we have investigated, a 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-iteration search was performed, with between 0 and 147 atomic random swaps at each step, and the new chemical arrangement then energetically reminimised. The geometry and energies of the lowest energy structures were stored throughout. In all cases, there was no variation in the lowest energy arrangements near to the final iterations of the search, and thus the number of iterations, and atomic swaps, were deemed to be sufficiently converged.
000-iteration search was performed, with between 0 and 147 atomic random swaps at each step, and the new chemical arrangement then energetically reminimised. The geometry and energies of the lowest energy structures were stored throughout. In all cases, there was no variation in the lowest energy arrangements near to the final iterations of the search, and thus the number of iterations, and atomic swaps, were deemed to be sufficiently converged.
2.3 Density functional theory (DFT)
The lowest energy structures were reminimised using DFT, as implemented by the projector-augmented wave method (PAW).59 Grid-based PAW (GPAW) uses a real-space grid, transforming the wavefunctions at the core to a smooth pseudo-wavefunction.60 The transformation [T] is specified by a set of all-electron partial waves, a set of pseudo partial waves, and a set of projector functions. The projector functions are what join (or augment) together the two solutions at a certain radius.61 Both Au and Ag have 11 valence electrons in our setup, and we used converged grid spacings of 0.18 for the numerical representation of the wavefunctions, and vacuum regions of 6 Å around the nanocluster, thus ensuring that no spurious energies or cut-off artefacts were encountered. For the geometry optimisations, convergence was achieved when the forces on all atoms were reduced below 0.01 eV Å−1.We have used the generalized gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE) exchange–correlation functional,62 with the residual minimisation method, direct inversion in iterative subspace (RMM-DIIS) for spin-polarized calculations throughout. The calculations included 1617 explicit valence electrons and the initial magnetic moment (μ) of the nanocluster was set to 1, to account for a single unpaired electron. During the calculations, however, μ was allowed to relax dynamically, and tended towards μ = 0 in all cases; this observation was supported by the spin contamination, 〈S2〉, which also tended to 0. This resultant singlet state is an artefact of the DFT method, but the overall effect on geometry, energy and charge density was found to be negligible, due to the delocalised “metallic” nature of the wavefunction at the Fermi Energy (EF). This was verified by performing fixed-spin DFT calculations, with μ = 1, on the final geometries, for which the difference in energy compared to the spin-paired results was less than 0.4 meV per atom, and consistent in sign for each combinatorial arrangement.
2.4 Energetic analysis
In order to relate the differing stoichiometric compositions of our fixed-size bimetallic clusters, there are several methods of energetic analysis. The simplest observable is the binding energy, Eb:63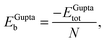 | (5) |
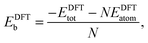 | (6) |
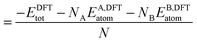 | (7) |
The excess energy, Eexc, is useful as it highlights the energetic difference between the bulk and nanocluster of interest, and is defined as a function of composition thus:63
| EGuptaexc = EGuptatot − NA(Ecoh,A) − NB(Ecoh,B) | (8) |
| EDFTexc = EDFTtot − NA(Ecoh,A) − NB(Ecoh,B) | (9) |
E exc can be related to the number of surface atoms within a structure, inferring the excess energy of the nanocluster is related to the energy required to create the nanocluster surfaces. The ratio of Eexc to the number of surface atoms, approximated as N2/3, is written as:64,65
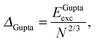 | (10) |
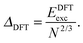 | (11) |
However, when comparing clusters of the same size but of differing compositions, ΔGupta and ΔDFT can become biased as metals with larger cohesive energies result in clusters with larger excess energies. Thus, an unbiased alternative is ΔGupta147, where EGuptab is subtracted instead of the bulk cohesive energies:66,67
 | (12) |
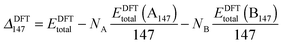 | (13) |
2.5 Chemical ordering
The extent of mixing (chemical order parameter), σ, may be defined as:68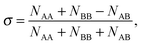 | (14) |
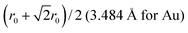 . σ = 1 indicates complete separation, σ ≈ 0 for disordered mixing, and σ < 0 indicates more ordered mixing, such as layering and onion-like configurations.68
. σ = 1 indicates complete separation, σ ≈ 0 for disordered mixing, and σ < 0 indicates more ordered mixing, such as layering and onion-like configurations.68
3. Results and discussion
3.1 Chemical ordering for atomically doped systems
Pure monometallic nanoclusters were created, and the geometries minimised with respect to the energy. EGuptab and EDFTb were calculated as 3.547 and 2.993 eV for Au, respectively; and 2.670 and 2.526 eV for Ag, respectively, highlighting significantly reduced bond strengths at the DFT level.The most elementary combination of the two elements is to introduce a single dopant atom of a secondary species into the monometallic clusters, replacing one of the original atoms. We have investigated occupation of all the possible dopant sites for a single Au atom substituted into Ag147, which results in a composition of Au1Ag146, and also repeated the opposite process for Ag included in Au147 to give Au146Ag1, with the results presented in Tables 2 and 3.
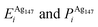 , respectively. The change in pressure and energy are given as ΔPi and ΔEi, respectively. For the site descriptions the notation surf. and subsurf. are used for surface and subsurface sites, respectively
, respectively. The change in pressure and energy are given as ΔPi and ΔEi, respectively. For the site descriptions the notation surf. and subsurf. are used for surface and subsurface sites, respectively
| ΔEGuptatot/eV | Site description | ΔEi/eV | ΔPi/GPa | ΔEDFTtot/eV | Δqi | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (a) | 0.000 | Vertex, subsurf. | −2.255 | −1.596 | −3.268 | −1.536 | −1.013 | 0.060 | 0.089 | 0.203 |
| (b) | 0.124 | Edge, subsurf. | −2.927 | 4.815 | −3.316 | −2.759 | −0.388 | −7.573 | 0.111 | 0.198 |
| (c) | 0.161 | Centre of (111), surf. | −2.927 | 4.841 | −3.112 | −7.807 | −0.184 | −12.648 | 0.055 | 0.256 |
| (d) | 0.167 | Centre of (100), subsurf. | −2.628 | −4.759 | 3.333 | −3.856 | −0.705 | 0.902 | 0.069 | 0.210 |
| (e) | 0.228 | Edge, surf. | −2.961 | 3.985 | −2.932 | −4.710 | 0.028 | −8.695 | 0.042 | 0.311 |
| (f) | 0.250 | Centre of cluster | −2.866 | 9.768 | −3.338 | 2.121 | −0.471 | −7.647 | 0.083 | 0.259 |
| (g) | 0.262 | Edge, two-layers subsurf. | −2.866 | 9.655 | −3.349 | 0.141 | −0.482 | −9.515 | 0.038 | 0.269 |
| (h) | 0.269 | Centre of (100), surf. | −2.960 | 4.062 | −3.056 | −7.177 | −0.096 | −11.239 | 0.036 | 0.294 |
| (i) | 0.309 | Vertex, surf. | −2.208 | −1.589 | −2.710 | −3.185 | −0.502 | −1.596 | 0.000 | 0.341 |
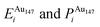 , respectively. The change in pressure and energy are given as ΔPi and ΔEi, respectively. For the site descriptions the notation surf. and subsurf. are used for surface and subsurface sites, respectively
, respectively. The change in pressure and energy are given as ΔPi and ΔEi, respectively. For the site descriptions the notation surf. and subsurf. are used for surface and subsurface sites, respectively
| ΔEGuptatot/eV | Site description | ΔEi/eV | ΔPi/GPa | ΔEDFTtot/eV | Δqi | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (j) | 0.000 | Centre of (100), surf. | −3.778 | 5.521 | −3.031 | −5.297 | 0.747 | −10.818 | 0.137 | −0.243 |
| (k) | 0.020 | Edge, two-layers subsurf. | −3.709 | 5.730 | −3.373 | 16.749 | 0.336 | 11.019 | 0.113 | −0.218 |
| (l) | 0.067 | Edge, surf. | −3.778 | 5.427 | −2.911 | −3.546 | 0.867 | −8.973 | 2.592 | −0.077 |
| (m) | 0.067 | Vertex, surf. | −3.181 | −12.140 | −2.670 | −2.716 | 0.512 | 9.424 | 2.258 | −0.075 |
| (n) | 0.078 | Centre of cluster | −3.709 | 5.895 | −3.349 | 21.960 | 0.360 | 16.065 | 0.148 | −0.141 |
| (o) | 0.114 | Centre of (111), surf. | −3.759 | 3.280 | −3.105 | 0.305 | 0.654 | −2.975 | 0.095 | −0.278 |
| (p) | 0.118 | Centre of (100), subsurf. | −3.501 | −11.874 | −3.358 | 15.527 | 0.143 | 27.401 | 0.031 | −0.275 |
| (q) | 0.149 | Edge, subsurf. | −3.759 | 3.244 | −3.345 | 19.194 | 0.414 | 15.950 | 0.000 | −0.284 |
| (r) | 0.298 | Edge, subsurf. | −3.181 | −12.147 | −3.277 | 27.914 | −0.096 | 40.060 | 0.017 | −0.234 |
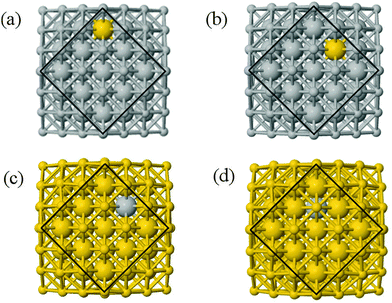
We performed calculations initially using the Gupta potentials. For Au1Ag146, the lowest energy configuration (Emin) is with the dopant Au atom occupying a subsurface vertex site, as shown in Fig. 2(a), with the next lowest energy arrangement (Emin−1) being the Au atom occupying a subsurface site below an edge [Fig. 2(b)]. Positioning of the Au dopant on (c) the (111) surface and (e) edge sites are greater in energy, implying reduced stability when the Au atom is on the surface (EGuptatot = 0.161 and 0.228 eV, respectively). Given the lower surface energy and weaker binding of Ag compared to Au, these observations are understandable as the Au atom favours occupation of a highly coordinated site. For each dopant site, i, the local atomic energy at the dopant positions (Ei) is given in Table 2 for the pure cluster and Au1Ag146, as well as the relative change in energy as a result of doping at each of these sites (ΔEi). A decrease in energy is observed for most single dopant configurations (i.e. ΔEi < 0 eV), due to the increased strength of the Au–Ag interactions, with the exception being ΔEi = 0.028 eV for a surface edge.
In contrast, when substituting an Ag atom into Au147 to form Au146Ag1, the positioning of the Ag atom on the surface is energetically favoured. Emin is arranged with the Ag dopant occupying a site on the (100) face, whereas for Emin−1 the Ag atom occupies a slightly off centre site within the cluster [Fig. 2(c) and (d)]. ΔEi > 0 eV, i.e. endothermic, for most Au146Ag1 arrangements, and thus it is not energetically favourable to introduce a single Ag atom, with ΔEi values between 0.143 and 0.867 eV (Table 3). The only exception to this is for (r) in Table 3, where Ag is occupying a subsurface edge position.
To ascertain the possible causes of preferred dopant positioning, we calculated the local atomic pressure Pi for each dopant site using the Gupta potentials. Pi is defined as:
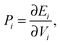 | (15) |
The results of our calculations are listed in Tables 2 and 3 for Au1Ag146 and Au146Ag1, respectively. For Emin(Au1Ag146), ΔPi = 0.060 GPa, however, for Emin−1(Au1Ag146), where the Au occupies a sub-surface site below an edge, ΔPi = −7.573 GPa, and is accompanied by a corresponding decrease in bond lengths from the Au dopant to surface Ag (0.02–0.03 Å), and an increase in bond lengths from the Au dopant to other subsurface Ag (0.02–0.03 Å). ΔPi also varies dramatically for Au146Ag1 depending on the site occupied by the dopant Ag: ΔPi < 0 for Emin, yet ΔPi > 0 for Emin−1. In general, ΔPi decreases for doping of Ag147 with Au, and increases when doping Au147 with Ag, however there is a large variation in values, and thus it is difficult to correlate preferred positioning of the dopant atoms with the partial pressure encountered at each structural site.
Each atomically-doped system was reminimised using DFT, resulting in considerable reordering of the nanocluster energetics when compared to the semi-empirical potentials, as shown in Fig. 3. [DFT minima images are given in the ESI,† Fig. S1.] For Au1Ag146, the lowest energy DFT arrangement (EDFTmin) is for the Au dopant to occupy a vertex position on the surface of the nanocluster, with the next lowest energy configuration (EDFTmin−1) being the occupation of a (100) surface site, with an energy difference of 0.036 eV between the two arrangements (Table 2). This is in stark contrast to the Gupta potential, where positioning of the Au atom in a subsurface site is energetically beneficial.
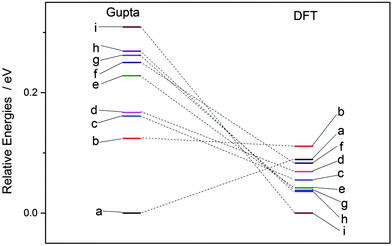 | ||
| Fig. 3 Energetic reordering of Au1Ag146, where a–i represent differing dopant positions, as given in Table 2. In general, the energetic competition between isomers is closer at the DFT level than Gupta. | ||
Similarly, for Au146Ag1, the DFT calculations result in reordering of the most stable chemical arrangements (Table 3). EDFTmin positions the Ag dopant in a subsurface edge site, and EDFTmin−1 places Ag also occupying a subsurface site, below a (100) surface, with an energy difference between the two of only 0.031 eV. These preferred chemical arrangements are again very different from the results of the Gupta potential, with the cohesive and surface energies seemingly less influential to the most stable chemical arrangements. The energetic reordering for the different chemical arrangements may therefore be attributed to alternative properties such as the partial charging of the dopant atom (Δqi), which are not considered when using the semi-empirical potentials. To minimise electronic repulsion within monometallic nanoclusters, electrons tend to migrate to the surface, which may result in a negative partial charge on the vertex, edge and face atoms.69 However, in bimetallic systems other factors can be influential, such as the electronegativities of the composite species, and charge transfer can influence the final shape and properties of the nanoalloy. Analysis of atomic charges were performed on each nanocluster using Bader analysis,70 and the 147-atomic sites were analysed according to their structural position: face, edge, vertex or core, as given in Table 5. For both of the pure systems charge accumulates at the surface (Δq > 0 e), and charge depletion occurs in the core (Δq <0 e), implying electron migration to the surface sites. The order of partial atomic charges for Ag147 are: Δqvertex > Δqedge > Δqface, whereas for Au147 they are: Δqvertex > Δqface > Δqedge. For both pure nanoclusters the least coordinated atomic sites (i.e. vertices) accumulate the greatest charge.
| Structure | ΔEGuptab/eV | ΔEDFTb/eV |
|---|---|---|
| Au13Ag134 | 0.027 | 0.001 |
| Au55Ag92 | 0.015 | 0.016 |
| Au92Ag55 | 0.003 | −0.019 |
| Au134Ag13 | 0.050 | 0.002 |
| Structure | σ | Δqcore | Δqface | Δqedge | Δqvertex |
|---|---|---|---|---|---|
| Ag147 | 1.000 | −0.030 | 0.014 | 0.007 | 0.072 |
| Au1Ag146 | 0.964 | −0.018 | 0.004 | 0.001 | 0.067 |
| Au13Ag134 | 0.539 | 0.035 | −0.012 | −0.026 | −0.025 |
| Au13@Ag134 | 0.745 | −0.015 | −0.007 | 0.009 | 0.052 |
| Au55Ag92 | 0.021 | 0.143 | −0.087 | −0.091 | −0.064 |
| Au55@Ag92 | 0.309 | 0.077 | −0.070 | −0.055 | 0.046 |
| Au74Ag73 | −0.036 | 0.117 | −0.119 | −0.090 | 0.143 |
| Au92Ag55 | 0.064 | 0.088 | 0.154 | −0.019 | 0.083 |
| Ag55@Au92 | 0.309 | −0.129 | 0.062 | 0.079 | 0.110 |
| Au134Ag13 | 0.655 | 0.013 | −0.080 | 0.030 | 0.034 |
| Ag13@Au134 | 0.745 | −0.043 | 0.014 | 0.018 | 0.085 |
| Au146Ag1 | 0.964 | −0.045 | 0.003 | 0.028 | 0.086 |
| Au147 | 1.000 | −0.050 | 0.017 | 0.022 | 0.089 |
In comparison, for the atomically doped Au1Ag146 system, Au atoms universally undergo charge accumulation, with the lowest energy structures also having the highest Δqi for the dopant atom (0.341 and 0.294 for EDFTmin and EDFTmin−1, respectively). Improved stability of dopants is noted when the Au atom occupies a surface site at the DFT-level, and thus we conclude that there is a relationship between dopant coordination and the maximisation of Δqi.
Complementary to the Au1Ag146 analysis, in Au146Ag1 the Ag atoms undergo charge depletion (−0.284 and −0.275 for EDFTmin and EDFTmin−1, respectively), whilst the majority of Au surface atoms accumulate charge. The results from DFT calculations again correlate widely with Δqi, except for arrangement (o) in Table 3. Additionally, we highlight improved stability of the Ag dopant when occupying subsurface sites, and therefore a balance between Δqi and atomic coordination exists.
In general, the presence of a single dopant atom lowers Eexc of the cluster (ESI,† Table S1), with minor distortions to bond lengths (<1%). Structurally, the Gupta potentials favour occupation of subsurface sites by Au atoms in Au1Ag146, whilst DFT methods prefer Au atoms occupying surface positions. No clear trend was observed for Ag atoms in Au146Ag1 using the Gupta potentials, but occupation of subsurface positions for Ag atoms are favoured by DFT methods. The dominating factor in determining the DFT relative total energy (EDFTtot) appears to be Δqi. However, with the preferential positioning of Au being surface, and Ag being subsurface, we note that there is a correlation between both the atomic coordination and electron transfer. Though there is no clear connection between energetic ordering and the minimisation of ΔPi, this is perhaps unsurprising given the similar atomic radii of Au and Ag. Furthermore, we were able to highlight that charge accumulation and depletion occurred for Au and Ag dopant atoms respectively, as is perhaps expected given their differing electronegativities.
3.2 Chemical ordering for AunAg147−n nanoalloys
For a greater quantity of secondary species n, and thus a more complex ordering landscape, basin-hopping searches using the Gupta potential are performed to gain optimised chemical ordering. A preference for alloy arrangements is observed in the lowest energy structures, with a maximised number of Au–Ag interactions, and therefore larger EGuptab. Experimentally, alloy arrangements can result in compromised rather than enhanced catalytic abilities, and thus the combination of two metals does not always produce a desirable synergistic effect.71 For this reason, the controlled synthesis of core@shell structures is of great interest, and so we utilised the layered structure of the CO to create core@shell arrangements with complete shells of varying thickness, thus enabling comparison of the properties for core@shell chemical arrangements to the alloy arrangements.In the structures identified as lowest energy from the basin-hopping searches, there are alloy arrangements with Au atoms preferentially occupying sub-vertex positions within the nanoalloys (Fig. 4). This shows some correlation with recent work by Bochicchio et al.72 on size-mismatched systems, where the dopant atom relieves the pressure in the subvertex position. However, we have already highlighted in Section 3.1 that positioning of Au atoms in sub-vertex lattice sites leads only to the reduction of interatomic bond distances and the formation of more (stronger) Au–Ag interactions for AuAg nanoclusters. The subsurface positions are fully occupied by Au dopants for n = 13 or larger, which results in a sub-layer of Au atoms and a triple-layered chemical ordering (Ag@Au@Ag) in exceptional cases; this is particularly apparent for the 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92 ratio of Au
92 ratio of Au![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ag (ESI,† Fig. S2). As Au content is increased beyond 55 atoms, gold atoms then begin to also occupy the surface sites. σ is above 0 in all cases, which indicates that disordered mixing is preferred over ordered mixing.
Ag (ESI,† Fig. S2). As Au content is increased beyond 55 atoms, gold atoms then begin to also occupy the surface sites. σ is above 0 in all cases, which indicates that disordered mixing is preferred over ordered mixing.
Overall, EGuptab increases linearly with increasing Au content, from 2.669 eV (Ag147) up to 3.541 eV (Au147), in line with Vegard's law (Fig. 5).73,74 This is unsurprising given the bond strengths at the Gupta level are: Au–Au (2.82 eV) > Au–Ag (1.81 eV) > Ag–Ag (1.36 eV), with values in parentheses given for the dimer pairs. The core@shell arrangements have similar energies to the alloy arrangements, as shown in Table 4, however at the Gupta-level all alloy arrangements are lower in energy. The same linear trend for EDFTb is apparent when the energies of the lowest-energy alloys are recalculated using DFT, as presented in Fig. 5 and Table S1 of the ESI.† Dimer bond strengths are Au–Au (2.68 eV) > Au–Ag (2.57 eV) > Ag–Ag (2.16 eV) in this case, and so the energetic ordering of bonds does not change. Importantly, we note that the core@shell arrangement for Ag55@Au92 has a lower DFT energy than the alloy equivalent, whereas all other core@shell arrangements are higher in energy than the alloy chemical orderings. In general, the energy difference between the core@shell and alloy structures is not large [≤0.05 eV (Gupta) and ≤0.02 eV (DFT)], as highlighted in Table 4; and as mentioned previously, restructuring from core@shell geometries requires a great deal of energy (>2 eV), and thus if segregated structures are formed initially, the chemical ordering would be relatively stable under ambient conditions, and in the absence of surface reactions.
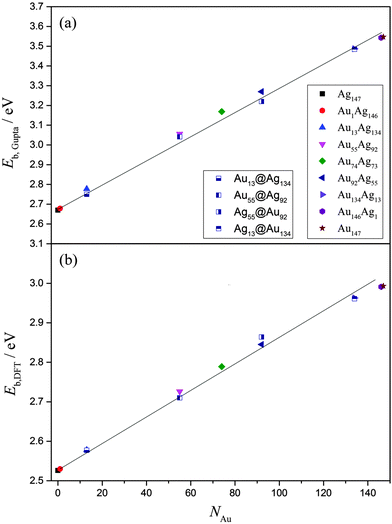 | ||
| Fig. 5 (a)EGuptab and (b) EDFTb as a function of Au content, NAu. The lines are given as a guide to the eye. A key to the symbols is also provided in (a). | ||
The propensity of (AuAg)147 to prefer an alloy arrangement at the Gupta level is confirmed when comparing EGuptab with σ (ESI,† Fig. S3). Ag55@Au92 has a greater value of σ than the alloy arrangement, Au92Ag55, as expected for a more segregated arrangement, yet has a lower EGuptab; the observation is made for Au55Ag92 in comparison to Au55@Ag92. At the DFT-level, Au55@Ag92 again has a lower EDFTb in comparison to the corresponding alloy, however Ag55@Ag92 has a higher EDFTb than its corresponding alloy, showing that DFT favours the Ag@Au arrangement for the 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92 ratio. We note, however, that the energy differences are too small to make the same generalisations for the 13
92 ratio. We note, however, that the energy differences are too small to make the same generalisations for the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 ratio.
134 ratio.
The energetic preference, at the DFT level, for Au surface segregation may be due to the improved charge transfer to Au atoms if they are the outermost species in the nanocluster, as discussed in Section 3.1; the electrons will naturally migrate to the surfaces to increase their degrees of freedom. Therefore, we have examined the extent of charge transfer occurring within each nanoalloy and core@shell structure presented.
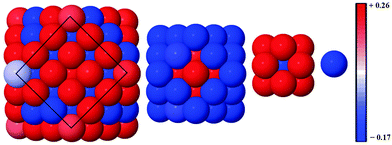
Alloy arrangements exhibit disordered mixing (σ ≈ 0), yet have the greatest changes in charge (Δq) when Ag is the dominant element in the composition: for instance, Δqface is greater for both Au13Ag134 (0.012) and Au55Ag92 (0.087) in comparison to the core@shell equivalents, Au13@Ag134 (0.007) and Au55@Ag92 (0.070), as a greater number of surface Au–Ag interactions exist between the surface Ag and subsurface Au atoms (Table 5). Further analysis of the onion-like Au55Ag92 structure shows there is a combination of both charge depletion and charge accumulation at the surface, but in the sub-surface Au shell (42 atoms) charge accumulation occurs, and the inner Ag core (13 atoms) is charge depleted, as shown in Fig. 6. Whilst most of the core@shell structures favour charge accumulation at the surface, the degree of charge transfer is determined by whether Au or Ag occupies the surface layer of the nanocluster. Alloy arrangements exhibit a trade-off between the additional electronic degrees of freedom at the surface and the contrasting electronegativities of Au and Ag: Au13Ag134 exhibits this compromise, with charge accumulation only occurring at the Ag vertices, with any remaining Ag atoms undergoing charge depletion; within the sub-surface Au there is charge accumulation. All the core@shell structures exhibit charge accumulation at the vertices. Au55@Ag92 undergoes charge depletion on faces and edges (Δqface = −0.070, Δqedge = −0.055), whilst the inverse structure, Ag55@Au92, has considerable charge accumulation at the surface (Δqface = 0.062, Δqedge = 0.079). Au13@Ag134 and Ag13@Au134 also exhibit similar behaviour to a lesser extent, with charge accumulation only on the vertices for the Ag shell, but Δqedge and Δqvertex > 0 for the Au shelled nanoclusters. This variation is perhaps due to the differing electronegativities of Ag (1.93) and Au (2.54), and thus charge transfer occurs from Ag to Au.
In summary, all nanoclusters experience charge accumulation at the lowest coordination sites in the nanocluster, irrespective of chemical ordering. Core@shell systems illustrate a greater change in atomic partial charges, as shown when comparing 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92 systems to the 13
92 systems to the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 systems, due to the segregation of chemical species. In general, charge accumulates on Au, whereas charge depletes from Ag, in the alloys and core@shell arrangements, similar to our observations for single dopants.
134 systems, due to the segregation of chemical species. In general, charge accumulates on Au, whereas charge depletes from Ag, in the alloys and core@shell arrangements, similar to our observations for single dopants.
3.3 Stability of AunAg147−n nanoalloys
We have discussed the properties of core@shell and energetically favourable alloy chemical arrangements for AunAg147−n. Attention is needed, however, to the relative stability of the different compositions, and chemical orderings, with respect to the pure nanoclusters, as agglomeration and chemical reactivity may occur in experimental environments, which would alter the structure and stoichiometry of the nanoclusters. Therefore, we plot ΔGupta147 and ΔDFT147 as a function of NAu in Fig. 7(a) and (b), respectively, with the most stable chemical arrangements positioned at the minima.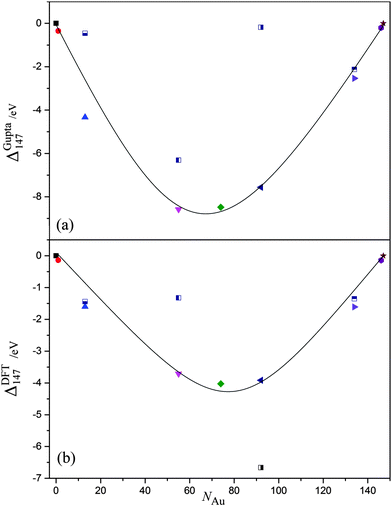 | ||
| Fig. 7 (a) ΔGupta147 and (b) ΔDFT147 as a function of Au content, NAu. The black line is given as a guide to the eye; symbols are the same as given in Fig. 5. | ||
For the semi-empirical calculations, Au55Ag92 has the lowest ΔGupta147, and may therefore be considered the most stable structure with respect to the formation of surfaces, which are approximated as N2/3 in eqn (10) and (11). In general, ΔGupta147 follows a ‘U-shaped’ trend with increasing NAu, but Ag55@Au92 is a clear anomaly to this trend. As mentioned previously in Section 3.2, an Ag core is not thermodynamically favourable, due to low Ag–Ag bond strength and high Au surface energies, thus resulting in lower stability for Ag55@Au92.
The stability of Au55Ag92 may be attributed to the Ag@Au@Ag arrangement that the alloy takes: Au–Ag interactions are maximised, and there is a corresponding reduction in the (weaker) Ag–Ag bonds. Nonetheless, the stability is not entirely dependent on the number of Au–Ag bonds, as Au74Ag73 is less stable despite having more Au–Ag interactions [σ(Au92Ag55) = 0.064, σ(Au74Ag73) = −0.036]. The difference is that Au55Ag92 has more surface Ag atoms, and thus there is an overall balance at the Gupta level between reducing surface energies and increasing binding energies. Of the core@shell systems, Au55@Ag92 has the lowest ΔGupta147 as it maximises the number of Au–Ag interactions, and has a thermodynamically favourable Au core. Au13@Ag134 has fewer Au–Ag interactions, thus lowering the stability of this arrangement.
In contrast, Ag55@Au92 has the lowest ΔDFT147 as calculated at the DFT-level, by an energy of ∼2.5 eV, which is surprising given that thermodynamic considerations would favour an Ag shell. The next most stable structure, Au92Ag55, has the same stoichiometry but more Au–Ag bonds, adopting an Ag@Au@Au/Ag configuration, where the outermost shell is an alloyed layer of both Au and Ag atoms [σ(Ag55@Au92) = 0.309, σ(Au92Ag55) = 0.064]. The energetic preference of Ag55@Au92 for DFT may be attributed to the Au surface being able to draw electron density from the Ag atoms more readily than if Au atoms were positioned internally; we have seen from the single dopant calculations for DFT methods in Section 3.1 that an Au atom prefers to be at the surface. Thus, as electrons migrate to the surface of the cluster due to the increased degrees of electronic freedom available, it also follows that Au would benefit from greater charge transfer when positioned at the surface. We find, therefore, that overall stability is not only a case of maximisation of Au–Ag bonds and minimising surface energies of the nanocluster through specific chemical ordering, but a compromise of the ease at which Au can gain electrons. For DFT, the latter observable is prevalent in determining ΔDFT147.
In summary, the stability of a nanoalloy at the Gupta-level is determined through a balance of maximising Au–Ag interactions and minimising the surface energy – it is more favourable to have a greater proportion of the surface atoms as Ag rather than Au. However, when reminimised using DFT, the stability of the nanocluster is also dependent on maximal charge transfer from Ag to Au, and thus an Au shell is more favourable than initially thought due to the increased degrees of electronic freedom at the surface.
3.4 Electronic properties
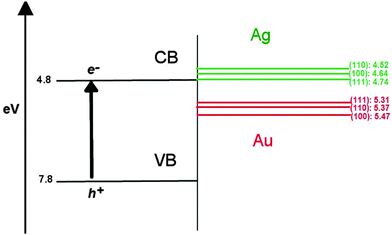
In the context of using these AuAg nanoclusters as semiconductor-supported co-catalysts in photocatalytic reactions, such as the reduction of hydrogen, it is known that the introduction of a co-catalyst results in a shift of the EF towards the conduction band (CB) of the semiconductor, indicating improved reductive ability.75 The possibility of screening suitable nanoclusters through a band alignment procedure, where the density of states (DOS) of the nanocluster are aligned against the band structure of the support, as illustrated in Fig. 8 using the work functions of different bulk Au and Ag surfaces (given in Table 6), is therefore possible.76 Au may exhibit better catalytic activity than Ag in this context, due to the greater work function of ∼5.4 eV compared to ∼4.6 eV, respectively; this places EF of Au below the conduction band minimum (CBM) of popular semiconducting supports such as TiO2, which would allow an electron to “drop” in energy should it transfer from the oxide conduction band to the unoccupied states of the nanocluster. Ag, however, would require an overpotential for the same electron transfer to occur, as EF of Ag is above the TiO2 CBM, making Ag less likely to accumulate photo-excited electrons and contribute to H reduction.| Surface | Φ Ag | Φ Au |
|---|---|---|
| (100) | 4.64 | 5.47 |
| (110) | 4.52 | 5.37 |
| (111) | 4.74 | 5.31 |
For an electron to be transferred to the co-catalyst from a semiconductor, the unoccupied surface d-orbitals of the nanocluster must be readily accepting of, and lower in energy than the photo-excited electrons in the CB of the support. If there were no unoccupied d-orbitals available on the nanocluster surface, tunnelling of electrons would allow occupation of states on core atoms, though the probability of this decays exponentially with depth from the surface. So, for trapping of photo-excited electrons to occur, it is more favourable for surface atoms to have a positive partial charge, otherwise the process is dependent on electron tunnelling.
By this proposition, our observations in Section 3.2 imply that Au@Ag would most favour the acceptance of photo-excited electrons, due to the positive partial charges on the vertex and edge sites of the nanocluster surface. However, from the concept of work function alignment introduced in Fig. 8, one would expect Ag@Au to be more suitable, as an Au shell would lead to a lower EF, and thus more energetically accessible states for an additional incoming electron. In order to address these topics, we have examined the DOS profiles of all systems, specifically the d-orbitals, which we have decomposed into projected contributions from core and shell atoms, and considered the position of the unoccupied d-orbitals with respect to EF.
E F for Au147 and Ag147 is calculated as −4.830 eV and −3.996 eV, respectively, matching the difference between bulk Au and Ag in Table 6. Fig. 9(a) shows Ag147 has less unoccupied d-orbitals on the surface atoms than Au [Fig. 9(b)], and when analysed alongside the high EF one would hypothesise that Ag147 would be unsuitable for use in co-catalysed photocatalytic reactions. Au147 has more unoccupied d-states than Ag147 at EF, but the difference is so small that one would not expect this alone to account for the reported catalytic activity observed in experiments.4 However, the proximity of EF for Au147 to the CBM of both rutile and anatase could account for any enhanced activity, especially when one considers surface effects on the electronic structure of the support, such as upward band-bending. Introduction of a single Ag atom, to form Au146Ag1, results in negligible increases in the d-orbital contributions at EF, by 0.16 states, whereas the introduction of a single Au atom to Ag147 results in the reverse effect for Au1Ag146. Furthermore, the DOS profile for Au74Ag73 appears to be an average of the composite species, with EF also positioned at an intermediate value of −4.335 eV.
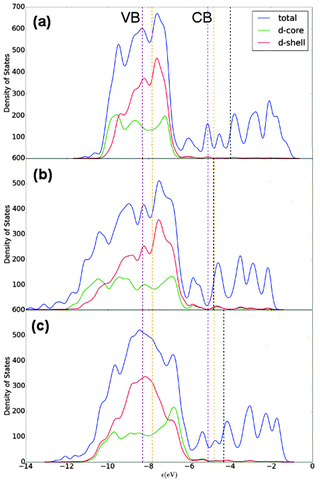 | ||
| Fig. 9 Density of states (DOS) profiles for (a) Ag147, (b) Au147 and (c) Au74Ag73. A key is provided. EF is given as a black dotted line, with the valence band maximum (VBM) and conduction band minimum (CBM) in purple and orange for anatase and rutile TiO2, respectively.77 A Gaussian broadening of 0.05 eV has been used on the electronic states. | ||
Alloy structures marginally increase the quantity of unoccupied d-states at EF, in comparison to their corresponding core@shell arrangements (with the exception of Au13Ag134/Au13@Ag134), as illustrated in the ESI† (Fig. S4 and S5). For instance, Au55Ag92 has 10.06 unoccupied d-states (d-core and d-shell) at EF, in comparison to 8.89 for Au55@Ag92. There is a greater quantity of unoccupied d-states at EF for Au92Ag55 than for Ag55@Au92 (13.91 vs. 11.5 d-orbitals at EF). Decomposing the number of unoccupied d-orbitals into core and shell contributions shows that Ag55@Au92 has a greater number of unoccupied d-orbitals in the shell than Au55@Ag92 (11.13 vs. 2.71 at EF). The same trend is observed for the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 ratios, where Ag13@Au134 has 8.61 d-orbital states just above EF, and Au13@Ag134 has only 3.13, respectively.
134 ratios, where Ag13@Au134 has 8.61 d-orbital states just above EF, and Au13@Ag134 has only 3.13, respectively.
Despite the differences in available d-orbitals between core@shell and alloy arrangements being marginal, a noticeable shift in EF is also observed: for core@shell structures EF is closest to that of the shell species in all cases – for instance, EF for Au55@Ag92 is −4.039 eV whilst for Ag147EF is −3.966 eV (ESI,† Table S1).
In summary, the differences in EF for monometallic species replicate bulk differences, and for single dopant systems minimal changes occur to the electronic structure of the system; Furthermore, Au74Ag73 displays properties that are an average of the two pure systems. Core@shell structures offer more desirable features than the alloy nanoclusters for co-catalysed photocatalysis, with a greater number of available unoccupied d-orbitals close to EF and marginally greater numbers of unoccupied d-orbitals were observed for Ag@Au compositions than for Au@Ag; however, the change in d-orbitals for bimetallic nanoclusters is still very low for all compositions investigated and thus further work is necessary to understand the successful photocatalytic applications of these nanoclusters.
4. Conclusions
We have presented a thorough examination of the optimised chemical orderings for cuboctahedral (AuAg)147 nanoalloys, with the aim being to highlight thermodynamically stable structures and to discuss their desirable properties for photocatalytic applications. In general, alloy structures are more thermodynamically stable at the Gupta level, as these maximise Au–Ag interactions. Au was found to favourably occupy sub-vertex positions within the alloy nanoclusters, as this maximises stronger Au–Ag interactions. This effect leads to onion-like structures forming, e.g. Ag@Au@Ag, as seen previously for AuPd.78 However, at the DFT-level, Au atoms are instead found to favour surface sites, with Ag55@Au92 being the most energetically favourable investigated. This may be attributed to the fact that the Au atoms can draw electron density more easily when positioned in the geometric shell, as electrons will naturally migrate towards the surface. The difference in binding energies between alloy and core@shell structures at equivalent stoichiometries is small, and thus both structures can be assumed to be energetically stable. Charge transfer between core@shell arrangements is of an interfacial nature, and thus influences from the core are more pronounced for thin shells, allowing for co-catalyst design. From thermodynamic arguments, Au is favoured at the core, and Ag at the surface in core@shell structures, due to the differing surface and cohesive energies. However, at the DFT-level, Bader analysis shows that Au@Ag results in electron depletion at the surface, and overall instability compared to Ag@Au, and further analysis is needed to understand if this effect would result in alternative alloy arrangements at the DFT level of theory.Electronic properties were examined for the applicability of different chemical orderings to co-catalysed photocatalysis, however none of the structures investigated display desirable properties as encountered for systems such as AuPd.79,80 At best, a shift in EF is observed for (AuAg)147 as a result of combining the two metals, indicative of a capability to extend the lifetime of photo-excited electrons beyond that which is found for isolated Ag147 nanoclusters. EF of bimetallic systems is closest to that of the shell species in all cases. Despite the lack of unoccupied d-orbitals in the structures investigated, the experimental photocatalytic activity could be fine-tuned through pre-treatment experimental processes such as surface oxidation and is subject to on-going investigation.
Acknowledgements
We are grateful to R. Ferrando, C. A. Downing and N. Dimitratos for their input and advice. The authors acknowledge financial support from EPSRC (EP/I030662/1) and (EP/K038419/1) and Diamond Light Source, (as well as computational resources from Research Complex at Harwell and the Catalysis Hub). The work presented here made use of IRIDIS High Performance Computing facility provided via the Centre for Innovation (CfI). Via our membership of the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/L00202), this work made use of the facilities of HECToR, the UK's national high-performance computing service, which is provided by UoE HPCx Ltd at the University of Edinburgh, Cray Inc. and NAG Ltd, and funded by the Office of Science and Technology through EPSRC's High End Computing Programme.Notes and references
- A. Abad, A. Corma and H. García, Chem. – Eur. J., 2008, 14, 212–222 CrossRef CAS PubMed.
- D. I. Enache, D. W. Knight and G. J. Hutchings, Catal. Lett., 2005, 103, 43–52 CrossRef CAS.
- G. A. Somorjai and J. Y. Park, Top. Catal., 2008, 49, 126–135 CrossRef CAS PubMed.
- A. Primo, A. Corma and H. García, Phys. Chem. Chem. Phys., 2011, 13, 886–910 RSC.
- C. Gomes Silva, R. Juárez, T. Marino, R. Molinari and H. García, J. Am. Chem. Soc., 2010, 133, 595–602 CrossRef PubMed.
- M. Jakob, H. Levanon and P. V. Kamat, Nano Lett., 2003, 3, 353–358 CrossRef CAS.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- D. Mott, N. T. B. Thuy, Y. Aoki and S. Maenosono, Philos. Trans. R. Soc., A, 2010, 368, 4275–4292 CAS.
- S. Nishimura, A. T. N. Dao, D. Mott, K. Ebitani and S. Maenosono, J. Phys. Chem. C, 2012, 116, 4511–4516 CAS.
- J. Jellinek and E. B. Krissinel, Chem. Phys. Lett., 1996, 258, 283–292 CAS.
- J. Jellinek, Theory of atomic and molecular clusters: with a glimpse at experiments, Springer, 1999 Search PubMed.
- F. Pittaway, L. O. Paz-borbo, R. L. Johnston, H. Arslan, R. Ferrando, C. Mottet, G. Barcaro and A. Fortunelli, J. Phys. Chem., 2009, 113, 9141–9152 CAS.
- M. T. Oakley, R. L. Johnston and D. J. Wales, Phys. Chem. Chem. Phys., 2013, 15, 3965–3976 RSC.
- A. Rapallo, G. Rossi, R. Ferrando, A. Fortunelli, B. C. Curley, L. D. Lloyd, G. M. Tarbuck and R. L. Johnston, J. Chem. Phys., 2005, 122, 194308 CrossRef PubMed.
- V. Moreno, J. Creuze, F. Berthier, C. Mottet, G. Tréglia and B. Legrand, Surf. Sci., 2006, 600, 5011–5020 CAS.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856 CAS.
- G. Rossi, R. Ferrando, A. Rapallo, A. Fortunelli, B. C. Curley, L. D. Lloyd and R. L. Johnston, J. Chem. Phys., 2005, 122, 194309 CrossRef PubMed.
- T. P. Martin, Phys. Rep., 1996, 273, 199–241 CrossRef CAS.
- G. A. Somorjai, B. Chaudret, P. Serp and K. Philippot, Nanomaterials in Catalysis, John Wiley & Sons, 2012 Search PubMed.
- J. Doye and D. Wales, J. Chem. Soc., Faraday Trans., 1997, 93, 4233–4243 RSC.
- M. M. Mariscal, O. A. Oviedo and E. P. M. Leiva, Metal Clusters and Nanoalloys: From Modeling to Applications, Springer, New York, 2012 Search PubMed.
- W. de Heer, Rev. Mod. Phys., 1993, 65, 611–676 CAS.
- T. Déronzier, F. Morfin, M. Lomello and J.-L. Rousset, J. Catal., 2014, 311, 221–229 CrossRef PubMed.
- C. Wang, H. Yin, R. Chan, S. Peng, S. Dai and S. Sun, Chem. Mater., 2009, 21, 433–435 CrossRef CAS.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics 2012-2013, CRC press, 2012 Search PubMed.
- L. Lu, H. Wang, Y. Zhou, S. Xi, H. Zhang, J. Hu and B. Zhao, Chem. Commun., 2002, 144–145 RSC.
- R. T. Tom, A. S. Nair, N. Singh, M. Aslam, C. L. Nagendra, R. Philip, K. Vijayamohanan and T. Pradeep, Langmuir, 2003, 19, 3439–3445 CrossRef CAS.
- S. Anandan, F. Grieser and M. Ashokkumar, J. Phys. Chem. C, 2008, 112, 15102–15105 CAS.
- H.-L. Jiang, T. Akita, T. Ishida, M. Haruta and Q. Xu, J. Am. Chem. Soc., 2011, 133, 1304–1306 CrossRef CAS PubMed.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22 CrossRef CAS.
- B. C. Curley, G. Rossi, R. Ferrando and R. L. Johnston, Eur. Phys. J. D, 2007, 43, 53–56 CrossRef CAS.
- C. Kittel and P. McEuen, Introduction to solid state physics, Wiley, New York, 1996, vol. 7 Search PubMed.
- F. Chen and R. L. Johnston, Acta Mater., 2008, 56, 2374–2380 CAS.
- I. L. Garzón, K. Michaelian, M. R. Beltrán, A. Posada-Amarillas, P. Ordejón, E. Artacho, D. Sánchez-Portal and J. M. Soler, Phys. Rev. Lett., 1998, 81, 1600 CrossRef.
- G. Bravo-Pérez, I. L. Garzón and O. Novaro, THEOCHEM, 1999, 493, 225–231 Search PubMed.
- N. T. Wilson and R. L. Johnston, Eur. Phys. J. D, 2000, 12, 161–169 CrossRef CAS.
- J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 35418 CrossRef.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867 CrossRef CAS PubMed.
- V. Bonačić-Koutecký, M. Boiron, J. Pittner, P. Fantucci and J. Koutecký, Eur. Phys. J. D, 1999, 9, 183–187 Search PubMed.
- M. N. Huda and A. K. Ray, Eur. Phys. J. D, 2003, 22, 217–227 CrossRef CAS.
- M. N. Huda and A. K. Ray, Phys. Rev. A, 2003, 67, 13201 CrossRef.
- X. Yang, W. Cai and X. Shao, J. Phys. Chem. A, 2007, 111, 5048–5056 CrossRef CAS PubMed.
- A. Desireddy, B. E. Conn, J. Guo, B. Yoon, R. N. Barnett, B. M. Monahan, K. Kirschbaum, W. P. Griffith, R. L. Whetten and U. Landman, Nature, 2013, 501, 399–402 CrossRef CAS PubMed.
- G. F. Zhao and Z. Zeng, J. Chem. Phys., 2006, 125, 014303 CrossRef CAS PubMed.
- S. Heiles, A. J. Logsdail, R. Schäfer and R. L. Johnston, Nanoscale, 2012, 4, 1109–1115 RSC.
- V. Bonačić-Koutecký, J. Burda, R. Mitrić, M. Ge, G. Zampella and P. Fantucci, J. Chem. Phys., 2002, 117, 3120 CrossRef PubMed.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371 CrossRef CAS.
- L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Chem. Phys., 2008, 128, 134517 CrossRef PubMed.
- M. Zhang and R. Fournier, THEOCHEM, 2006, 762, 49–56 CrossRef CAS PubMed.
- F. Chen, B. C. Curley, G. Rossi and R. L. Johnston, J. Phys. Chem. C, 2007, 111, 9157–9165 CAS.
- M. Cerbelaud, R. Ferrando, G. Barcaro and A. Fortunelli, Phys. Chem. Chem. Phys., 2011, 13, 10232–10240 RSC.
- F. Calvo, A. Fortunelli, F. Negreiros and D. J. Wales, J. Chem. Phys., 2013, 139, 111102 CrossRef CAS PubMed.
- R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265 CrossRef CAS.
- F. Chen and R. L. Johnston, Appl. Phys. Lett., 2008, 92, 023112 CrossRef PubMed.
- A. J. Logsdail and R. L. Johnston, RSC Adv., 2012, 2, 5863–5869 RSC.
- A. J. Logsdail, Z. Y. Li and R. L. Johnston, Phys. Chem. Chem. Phys., 2013, 15, 8392–8400 CAS.
- O. K. Andersen and O. Jepsen, Phys. Rev. Lett., 1984, 53, 2571–2574 CrossRef CAS.
- D. Wales and J. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 35109 Search PubMed.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. A. Hansen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- R. Ismail and R. L. Johnston, Phys. Chem. Chem. Phys., 2010, 12, 8607–8619 RSC.
- C. L. Cleveland and U. Landman, J. Chem. Phys., 1991, 94, 7376 CrossRef CAS PubMed.
- J. Uppenbrink and D. J. Wales, J. Chem. Phys., 1992, 96, 8520 CrossRef CAS PubMed.
- L. O. Paz-Borbón, R. L. Johnston, G. Barcaro and A. Fortunelli, J. Phys. Chem. C, 2007, 111, 2936–2941 Search PubMed.
- G. Rossi and R. Ferrando, J. Phys.: Condens. Matter, 2009, 21, 084208 CrossRef CAS PubMed.
- F. Aguilera-Granja, A. Vega, J. Rogan, X. Andrade and G. García, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224405 CrossRef.
- X. Ma, Y. Dai, M. Guo, Y. Zhu and B. Huang, Phys. Chem. Chem. Phys., 2013, 15, 8722–8731 RSC.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef PubMed.
- J. Sinzig, U. Radtke, M. Quinten and U. Kreibig, Z. Phys. D: At., Mol. Clusters, 1993, 26, 242–245 CrossRef CAS.
- D. Bochicchio, F. Negro and R. Ferrando, Comput. Theor. Chem., 2013, 1021, 177–182 CrossRef CAS PubMed.
- L. Vegard, Z. Phys. A: At. Nucl., 1921, 5, 17–26 CAS.
- L. Vegard, Z. Kristallogr., 1928, 67, 239–259 Search PubMed.
- N. Lopez and J. K. Nørskov, J. Am. Chem. Soc., 2002, 124, 11262–11263 CrossRef CAS PubMed.
- V. Pfeifer, P. Erhart, S. Li, K. Rachut, J. Morasch, J. Bro, P. Reckers, T. Mayer, S. Ru, A. Zaban, M. Sero, J. Bisquert, W. Jaegermann and A. Klein, J. Phys. Chem. Lett., 2013, 4, 4182–4187 CrossRef CAS.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave and I. P. Parkin, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- D. Ferrer, D. A. Blom, L. F. Allard, S. Mejía, E. Pérez-Tijerina and M. José-Yacamán, J. Mater. Chem., 2008, 18, 2442–2446 RSC.
- N. Dimitratos, J. A. Lopez-Sanchez, D. Morgan, A. F. Carley, R. Tiruvalam, C. J. Kiely, D. Bethell and G. J. Hutchings, Phys. Chem. Chem. Phys., 2009, 11, 5142–5153 RSC.
- J. Pritchard, L. Kesavan, M. Piccinini, Q. He, R. Tiruvalam, N. Dimitratos, J. A. Lopez-Sanchez, A. F. Carley, J. K. Edwards, C. J. Kiely and G. J. Hutchings, Langmuir, 2010, 26, 16568–16577 CrossRef CAS PubMed.
Footnote |
† Electronic supplementary information (ESI) available: Figure of geometrically decomposed atomic arrangement for Au13Ag134 and Au55Ag92 alloys; table of the differences in Eb and Eexc for all investigated systems, along with EF; plot of EGuptab and EDFTb against σ; plots of the DOS for alloy and core@shell structures with varying Ag![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Au ratios. See DOI: 10.1039/c4cp00753k Au ratios. See DOI: 10.1039/c4cp00753k |
| This journal is © the Owner Societies 2014 |