Excited states of protonated DNA/RNA bases†
Matias
Berdakin
a,
Géraldine
Féraud
b,
Claude
Dedonder-Lardeux
b,
Christophe
Jouvet
*b and
Gustavo A.
Pino
*a
aINFIQC (CONICET – Universidad Nacional de Córdoba) Dpto. de Fisicoquímica – Facultad de Ciencias Químicas – Centro Láser de Ciencias Moleculares – Universidad Nacional de Córdoba, Ciudad Universitaria, X5000HUA Córdoba, Argentina. E-mail: gpino@fcq.unc.edu.ar
bCNRS, Aix Marseille Université, Physique des Interactions Ioniques et Moléculaires (PIIM): UMR-7345, 13397 Marseille, France. E-mail: Christophe.jouvet@univ-amu.fr
First published on 28th March 2014
Abstract
The very fast relaxation of the excited states to the ground state in DNA/RNA bases is a necessary process to ensure the photostability of DNA and its rate is highly sensitive to the tautomeric form of the bases. Protonation of the bases plays a crucial role in many biochemical and mutagenic processes and it can result in alternative tautomeric structures, thus making important the knowledge of the properties of protonated DNA/RNA bases. We report here the photofragmentation spectra of the five protonated DNA/RNA bases. In most of the cases, the spectra exhibit well resolved vibrational structures, with broad bands associated with very short excited state lifetimes. The similarity between the electronic properties, e.g. excitation energy and very short excited state lifetimes for the canonical tautomers of protonated and neutral DNA bases, suggests that the former could also play an important role in the photostability mechanism of DNA.
1. Introduction
Understanding the response of the DNA/RNA bases to UV radiation is critical since their photochemistry constitutes a fundamental step in radiation-induced DNA/RNA damage and very likely it has also played an important role in prebiotic chemistry.1 In the recent years, experimental and theoretical groups have been working extensively and settling benchmark results to disentangle the intrinsic properties of these building blocks of life in the gas phase. These studies have been recently reviewed in three complete papers.1–3The neutral DNA bases are structurally rich given that they can exist in many tautomeric forms. However, nature has chosen those structures (the canonical forms), shown in Fig. 1, that allow for a precise recognition between C (cytosine) and G (guanine) through three H-bonds and between T (thymine) or U (uracil) and A (adenine) through a double H-bond, to guarantee the preservation of the genetic information encoded in the DNA molecule. The excited state lifetimes of DNA bases depend strongly on their tautomeric form, the canonical tautomers being those with the shortest excited state lifetimes, which is considered to be the natural photoprotection mechanism of DNA.1–3
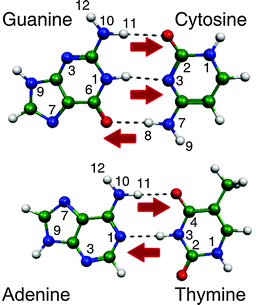 | ||
| Fig. 1 Watson–Crick (WC) structures of the DNA base pairs. The red arrows indicate possible protonation sites of canonical tautomers through a proton transfer reaction within the WC pair. | ||
DNA bases are susceptible to protonation through proton transfer or other reaction mechanisms.4,5 The protonation processes are important because alternative tautomeric structures of the DNA bases can be formed. The existence of such non-canonical tautomers could induce longer excited state lifetimes1–3 or development of mutations in the nucleic acid replication because the H-bonding structure changes leading to failures in the recognition process.5–10
An excited state proton/hydrogen transfer reaction in the Watson–Crick (WC) GC pair has been identified by Sobolewski and Domcke11 as one of the most important deactivation pathways of the photoexcited pair in the gas phase. Therefore, in a bottom-up strategy to build up a whole photochemical and photophysical model of DNA, understanding the structure of protonated DNA bases, their tautomeric forms, stability and the effects of protonation on the excited state lifetime and absorption spectra is of imperative relevance to calibrate the calculations with experimental results. However, very few detailed studies have been conducted on these protonated bases5–7,12–14 compared with the numerous studies performed on the neutral species.1–3
We performed a detailed study of the electronic spectroscopy of the five cold protonated DNA/RNA bases (CH+, TH+, UH+, GH+ and AH+) by means of photofragmentation spectroscopy in a cold ion trap that allows getting information about their excitation energies and excited state lifetimes. Structural assignment is obtained with ab initio calculations in the ground and excited states.
2. Methodology
2.a. Experiment
The electronic spectra of the protonated aromatic DNA/RNA bases were obtained via parent ion photofragment spectroscopy in a cryogenically-cooled quadrupole ion trap (Paul Trap from Jordan TOF Products, Inc.).15 The setup is similar to the one developed in several groups based on the original design by Wang and Wang.16–18 The protonated ions are produced in an electrospray ionization source built at Aarhus University.19 At the exit of the capillary, ions are trapped in an octopole trap for 90 ms. They are extracted by applying a negative pulse of ca. 50 V and are further accelerated to 190 V by a second pulsed voltage just after the exit electrode. This time sequence of pulsed voltages produces ion packets with a duration between 500 ns and 1 μs. The ions are driven by a couple of electrostatic lenses toward the Paul trap biased at 190 V so that the ions enter the trap gently avoiding fragmentation induced by collisions. A mass gate placed at the entrance of the trap allows selecting the parent ion. The Paul trap is mounted on the cold head of a cryostat (Coolpak Oerlikon) connected to a water-cooled He compressor. Helium as a buffer gas is injected into the trap using a pulsed valve (General Valve) triggered 1 ms before the ions enter the trap as previously reported by Kamrath et al.17 The ions are trapped and thermalized at a temperature between 20 and 50 K through collisions with the cold buffer gas (see ESI†). The ions are kept in the trap for several tens of ms before the photodissociation laser is triggered. This delay is necessary to ensure thermalization of ions and efficient pumping of the He buffer gas from the trap to avoid collision induced dissociation of the ions during the extraction towards the 1.5 m long time-of-flight mass spectrometer. After laser excitation, the ions are stored in the trap for a delay that can be varied between 20 and 90 ms before extraction to the TOF mass spectrometer. The complete mass spectrum is recorded on a micro channel plate (MCP) detector with a digitizing storage oscilloscope interfaced to a PC. The photofragment yield spectrum of each detected ion is normalized to the parent ion signal and the laser power.The photo-dissociation laser is an OPO laser from EKSPLA, which has a 10 Hz repetition rate, 10 ns pulse width, a resolution of 10 cm−1 and a scanning step of 0.02 nm. The laser is shaped to a 1 mm2 spot to fit the entrance hole of the trap and the laser power is around 20 mW in the UV spectral region.
2.b. Calculations
Ab initio calculations have been performed using the TURBOMOLE program package,20 making use of the resolution-of-the-identity (RI) approximation for the evaluation of the electron-repulsion integrals.21 The equilibrium geometries of the protonated species in their ground states (S0) have been determined at the MP2 (Møller–Plesset second order perturbation theory) level. Vertical excitation energies of the lowest excited singlet states have been determined at the RI-ADC(2)(second order Algebraic Diagrammatic Construction) level.22 Due to numerous conical intersections between the nπ* and ππ* states, the excited state optimization is not straightforward and has failed in many systems as shown already for protonated adenine.12,13 Calculations were performed with the correlation-consistent polarized valence double-zeta (cc-pVDZ or aug-cc-pVDZ) basis set.23 The vibrations in the ground and excited states have been calculated for the enol/1H–2H24 tautomer of protonated cytosine and the electronic spectra simulated using the Pgopher software25 for Franck Condon analysis.3. Results
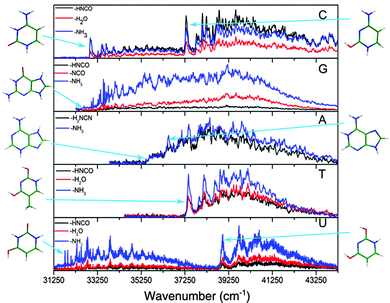
The spectra of all the cold protonated DNA/RNA bases are presented in Fig. 2. The laser has been scanned at a lower energy up to 410 nm but no signal was detected below the bands shown here.For all the protonated molecules, the fragments observed in these experiments are the same as those observed in collision induced dissociation (CID) or in infrared multi-photon dissociation (IRMPD): NH3 loss, H2O loss and HNCO/H2NCN loss, which means that very likely these fragments come from dissociation in the ground state following internal conversion (IC). Internal conversion following UV excitation (e.g. 310 nm) leads to the production of ions in the S0 state with 4 eV (32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) of vibrational excitation, which is above the dissociation threshold of all the systems studied in this work. This allows us to ignore the possibility of missing some transitions due to low dissociation yield.
000 cm−1) of vibrational excitation, which is above the dissociation threshold of all the systems studied in this work. This allows us to ignore the possibility of missing some transitions due to low dissociation yield.
Most of the bands are very broad except those of GH+ in the low energy region of the spectrum for which the width of the vibrational bands is limited by the laser bandwidth and the rotational contour (12 cm−1) and the low energy band system of UH+, which has only slightly broader bandwidths (19 cm−1).
In the case of the protonated pyrimidine bases, for CH+ and UH+ clearly two band systems (hereafter called the blue and red systems according to their absorption region) are observed, which might be due to two electronic states or two isomers. However, only one system is observed for TH+ in the (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250–44
250–44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250) cm−1 spectral range, while the low resolution spectra in the (33
250) cm−1 spectral range, while the low resolution spectra in the (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330–30
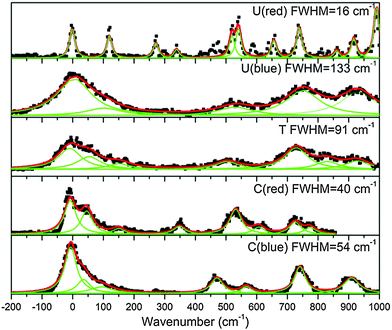
330–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300) cm−1 spectral region did not show any transition associated with TH+ (see ESI†) An enlarged view of the spectra near the band origins for the protonated pyrimidine bases is shown in Fig. 3. The broad character of the vibrational bands is noticeable except for the red system of UH+. Although it has to be taken with caution, the widths of the bands were fitted by a Lorentzian function to extract excited state lifetimes using the uncertainty principle, and the validity of this assumption will be discussed in Section 4.a.
300) cm−1 spectral region did not show any transition associated with TH+ (see ESI†) An enlarged view of the spectra near the band origins for the protonated pyrimidine bases is shown in Fig. 3. The broad character of the vibrational bands is noticeable except for the red system of UH+. Although it has to be taken with caution, the widths of the bands were fitted by a Lorentzian function to extract excited state lifetimes using the uncertainty principle, and the validity of this assumption will be discussed in Section 4.a.
An enlarged view of the spectra near the band origin for the protonated purine bases is depicted in Fig. 4. Protonated guanine shows a well resolved spectrum with narrow bands (FWHM = 12 ± 2 cm−1). Protonated adenine presents two band systems composed of a very broad absorption band on the red part of the spectrum and a group of broad peaks starting at 1000 cm−1 to the blue of the origin of the red band. It must be noticed that for the very broad part of the spectrum in the low energy region, the intensity of the two fragments (m/z 94 (–H2NCN) and 119 (–NH3)) is the same whereas for the blue band system the –NH3 fragment is more intense than the –H2NCN fragment, indicating the existence of two electronic states or isomers. The excited state lifetimes for GH+ and the blue band system of AH+ obtained from the fit of the bandwidth are also reported in Table 1.
| Protonated base | Measured FWHM (cm−1) | Estimated lifetimes (fs) |
|---|---|---|
| a The width of the bands in protonated guanine (<1 cm−1) and in protonated uracil red system (16 ± 5 cm−1) corresponds to the Lorentzian bandwidth of a Voigt profile, given a Gaussian function (FWHM = 12 cm−1) that represents the convolution of the rotational contour and the laser bandwidth. For the protonated uracil red system, the bands are only slightly larger than the guanine bands so that the lifetime may be longer than 330 fs. | ||
| Uracil red systema | 16 ± 5 | ≥330 |
| Uracil blue system | 133 ± 15 | 40 ± 20 |
| Thymine | 91 ± 20 | 58 ± 20 |
| Cytosine red system | 40 ± 10 | 133 ± 20 |
| Cytosine blue system | 54 ± 10 | 98 ± 20 |
| Adenine blue system | 177 ± 20 | 30 ± 20 |
| Guaninea | <1 | >5000 |
4. Analysis and discussion
4.a. Determination of the excited state lifetimes
The excited state lifetimes have been estimated from the widths of the bands fitted by Lorentzian functions as can be seen in Fig. 3, except for GH+ and UH+ (red) that were fitted to Voigt profiles to account for the rotational contour and the laser Gaussian bandwidth (12 cm−1) convolution. The fitting of the other spectra gives the same Lorentzian bandwidth independent of fitting to Voigt or Lorentzian profiles.The relationship between the Lorentzian bandwidth and the excited state lifetime is given by the uncertainty principle, which can be written as:
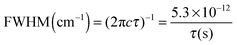 | (1) |
For the red band system of UH+ (Fig. 3) as well as for GH+ (Fig. 4) that present a well resolved narrow vibrational structure, no low frequency progressions (lower than 100 cm−1) are observed. Therefore, there are no reasons to expect low vibrational frequency progressions blended into a spectral background of the other bases for which very broad bands are observed.
The ground state vibrational frequencies were calculated for all the protonated bases and the lowest frequencies corresponding to out-of-plane modes are in the order of 200 cm−1. At the low temperature of the experiment, the vibrational modes of the electronic ground state are not excited. Thus, the band broadening is not expected to be due to hot band sequences. Under the assumption that the excited state frequencies are in the same range as the ground state frequencies (200 cm−1), any vibrational progression in low frequency modes would have been easily separated in the absence of lifetime broadening, as in the case of the red system of UH+ or of GH+. It is thus reasonable to assume that the bandwidths are intrinsic and that lifetimes can be deduced.
The estimated lifetimes are listed in Table 1 and are found between 30 fs and 100 fs (±50 fs) for most of the species except for GH+ and the red band system of UH+ that shows only a small broadening compared to GH+, and should have a lifetime longer than a few hundreds of femtoseconds.
We do not observe a large change of the broadening of the bands with the excess energy in contrast with other systems such as neutral adenine, for which a few bands are well resolved at low energy and a continuous absorption is observed at higher energy indicating a shorter lifetime.26,27 In protonated bases, the non-radiative processes leading to the fast decays are present on the 0–0 transition and do not change drastically at least for the first 1000 cm−1 above the origin. At higher energy the spectra become structure-less but this is most probably due to spectral congestion.
It is worth noting that the short excited state lifetime determined here corresponds to the ππ* excited state lifetime. These lifetimes do not give direct information on the rate of the dissociation process that leads to the photofragments detected. The photofragmentation takes place most likely in the electronic ground state, following fast IC as in the case of neutral DNA bases, which is expected to be the main deactivation pathway associated with the ππ* excited state lifetime.
In the gas phase isolated system, IC produces highly vibrationally excited ions for which one possibility for energy dissipation is the unimolecular dissociation. However, in bulk systems, the major energy dissipation mechanism is vibrational relaxation through energy transfer to the solvent and the environment or even IVR to the whole DNA molecule, insuring the stability of the molecule.1–4
4.b. Tautomer assignment
Generally for neutral and protonated aromatic molecules, geometry optimization of the first excited state at the ADC(2) level leads to adiabatic transition energies in very good agreement with experimental values, the mean error being around ±0.2 eV.15,28–32 In the present study, it was possible to optimize only the excited state of the most stable isomer of CH+ (the enol/1H–2H tautomer). The calculated adiabatic transition is 4.62 eV, in very good agreement with the experimental value of the origin of the blue system (4.63 eV), being within the usual 0.2 eV (even much smaller in this case). For this case, the assignment of the spectrum seems quite certain (see below A. CytosineH+).As a general trend, the excited state optimization process for aromatic molecules (neutral or protonated) leads to a stabilization of ca. 0.5 eV compared to the vertical excitation energy (Evert).15,28–32 In the case of the enol/1H–2H tautomer of CH+, Evert is 5.15 eV and the stabilization is expected to lead to an adiabatic transition energy Ead = Evert − 0.5 eV = 4.65 eV in very good agreement with the experimental value (4.63 eV) and the calculated adiabatic transition energy (4.62 eV). Therefore, the empirical rule:
| Eexp = Evert − (0.5 ± 0.3 eV) | (2) |
The calculated vertical excitation energies together with the experimental transition energies and the difference δ = (Evert − 0.5) − Eexp for the main tautomers are summarized in Table 2.
| Protonated base | Tautomer | Experimental transition Eexp | ππ* calculated vertical transition, Evert | E vert − 0.5 | δ = (Evert − 0.5) − Eexp | S0 (eV) |
|---|---|---|---|---|---|---|
| a Taken from ref. 12. | ||||||
| Cytosine |
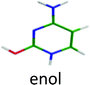
|
4.63 | 5.15 | 4.65 | 0.02 | 0.00 |
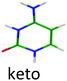
|
4.08 | 4.38 | 3.88 | −0.20 | 0.07 | |
| Thymine |
|
4.64 | 5.07 | 4.57 | −0.07 | 0.00 |
|
Not observed | 4.05 | 3.55 | × | 0.17 | |
| Uracil |
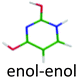
|
4.83 | 5.44 | 4.94 | 0.11 | 0.00 |
|
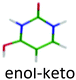
3.90 | 4.39 | 3.89 | −0.01 | 0.08 | |
| Guanine |
|
4.05 | 4.41 | 3.91 | −0.14 | 0.00 |
| Adenine |
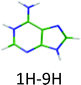
|
4.54 | 4.83a | 4.33 | −0.21 | 0.00 |
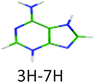
|
4.40 | 4.80a | 4.30 | −0.10 | 0.02 | |
For this tautomer the excited state optimization was possible and the calculated adiabatic transition of 4.62 eV is in very good agreement with the experimental value of the blue band system (4.63 eV). The blue band system (Fig. 1) is thus assigned to enol/1H–2H tautomer. For this tautomer, the ground and excited state frequencies have been calculated and the spectrum can be satisfactorily simulated as shown in Fig. 5. The lowest out-of plane frequency is calculated to be 95 cm−1 in the excited state and is only very weakly active with one quantum (ν1 not visible in Fig. 5) and more active with 2 quanta (2ν1 visible in Fig. 5). The agreement between the simulated spectrum and the experimental one is very good, showing active modes which are mainly in-plane modes. Only the mode observed at +950 cm−1 is missing in the simulation.
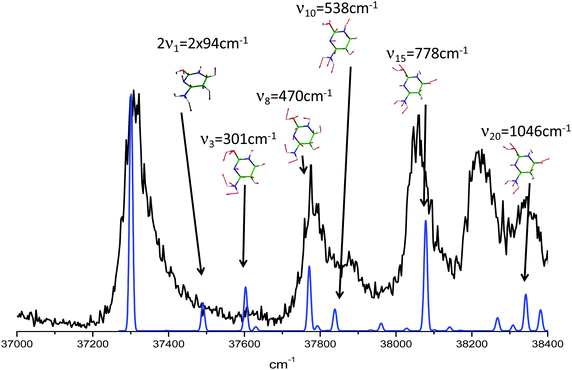 | ||
| Fig. 5 In black the enol/1H–2H tautomer of cytosineH+ experimental spectrum. In blue the calculated spectrum. Above each transition the vibrational mode involved for each calculated band. | ||
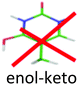
For the second isomer keto/1H–3H, also characterized by IR-MPD spectroscopy,5,7 the ππ* optimization leads to a crossing with a nπ* state through the NH2 rotation. Thus, the excited state optimization was not successful and the adiabatic energy of the ππ* cannot be obtained. However, taking into account the ground state energy and the calculated vertical energy, the assignment of the electronic spectrum of the red band system to the keto/1H–3H tautomer can be quite ascertained. Both tautomers have short excited state lifetimes (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 cm−1) and another system starting at higher energy (+0.15 eV) is composed of a broad vibrational progression with the first band at 273 nm (4.54 eV = 36
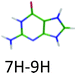
460 cm−1) and another system starting at higher energy (+0.15 eV) is composed of a broad vibrational progression with the first band at 273 nm (4.54 eV = 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630 cm−1). In fact, three ground state tautomers have been calculated to lie within less than 0.1 eV and their vertical electronic excitation energies are also within 0.1 eV,12 thus the empirical rule (eqn (2)) cannot be used unambiguously. The state-of-the-art ab initio calculations have already been performed by Marian et al.,12 thus we did not perform any calculation for this system but just compared with previous calculations. In the ground state the 1H–9H tautomer is the most stable one, followed by the 3H–7H and the 3H–9H tautomers at 0.02 eV and 0.08 eV above the energy of the 1H–9H tautomer, respectively.
630 cm−1). In fact, three ground state tautomers have been calculated to lie within less than 0.1 eV and their vertical electronic excitation energies are also within 0.1 eV,12 thus the empirical rule (eqn (2)) cannot be used unambiguously. The state-of-the-art ab initio calculations have already been performed by Marian et al.,12 thus we did not perform any calculation for this system but just compared with previous calculations. In the ground state the 1H–9H tautomer is the most stable one, followed by the 3H–7H and the 3H–9H tautomers at 0.02 eV and 0.08 eV above the energy of the 1H–9H tautomer, respectively.
The 3H–9H tautomer can probably be ruled out since its absorption lies in the 320 nm region13 and, taking into account the ion trap temperature and the ground state energies, the population of this species is expected to be very low.
The other two tautomers (1H–9H and 3H–7H) have very similar vertical electronic transition energies at 4.83 eV and 4.80 eV, respectively. The energy gap between the two first ππ* states of each of these two tautomers is around 0.2–0.3 eV larger than the observed energy gap between the two experimental electronic transitions. Thus one can probably assign the two systems to different tautomers.
In the low energy system the intensity of the m/z = 94 and m/z = 119 fragments arising from H2NCN and NH3 loss are the same whereas on the higher energy band system the m/z 119 fragment becomes more intense than m/z 94. Very likely, this difference arises from the different structures of the tautomers responsible for each absorption band and this argument can be used to assign the spectra.
The H2NCN fragment can be produced by direct fragmentation of the 3H–7H tautomer while in the case of the 1H–9H tautomer the formation of this fragment would require a subsequent H atom loss or a previous rearrangement of the structure. In any case, the rate of production of the H2NCN fragment from 1H–9H tautomer is expected to be lower than that from the 3H–7H tautomer and then its branching ratio should also be lower. Then, we can assume that the higher energy band system is due to the 1H–9H tautomer, while the lower energy system is due to the 3H–7H tautomer. Nevertheless, an unambiguous assignment would require additional work such as IR-UV spectroscopy. Both tautomers have very short excited state lifetimes (Table 1).
4.c. Lifetimes of protonated tautomers
The keto/1H–3H and the enol/1H–2H tautomers of CH+ and the 1H–9H tautomer of AH+ can be obtained by a proton transfer (PT) reaction in the canonical WC structures (Fig. 1). We observed short excited state lifetimes for these tautomers. However, the 7H–9H tautomer of GH+ (long excited state lifetime) and the enol–enol/2H–4H tautomer of TH+ (short excited state lifetime) cannot be produced by a PT reaction within the CG and TA WC base pairs, respectively. Therefore, the electronic properties of the canonical CH+ and AH+, which are biologically significant, are expected to be relevant for the DNA photostability. In line with the results obtained for neutral isolated DNA/RNA bases, for which the biologically most relevant forms exhibit the shortest excited state lifetimes,1–3 the same rule seems to hold for the protonated bases. Canonical CH+ and AH+ have short excited state lifetimes, while the excited state lifetime of the non-canonical GH+ tautomer is longer by at least three orders of magnitude.The excited states of the WC bases pairs also have very short lifetimes, a property that is related to photostability of DNA.34,35 The processes at play have been the subject of many investigations1–3,11,34–38 but it is not so easy to get a unified mechanism since there are many possible deactivation pathways, which have not all been explored.
The similarity between the electronic properties e.g.: excitation energy and very short excited state lifetimes for canonical tautomers of the neutral and protonated DNA bases, reported here, suggests that the latter could also play an important role in the photostability mechanisms of DNA. Thus this paper provides a complete set of data that can be used as an experimental benchmark for theoretical excited state dynamics calculations.
5. Conclusions
We have presented here a complete set of experimental data concerning the excited states of the protonated DNA/RNA bases. When the comparison with a neutral homologue can be done the electronic transition energies do not change drastically between neutral and protonated species. In contrast, the excited state lifetime of the protonated species seems to be very short except for guanine and one uracil tautomer. This challenges theoretical calculations and these results are benchmarks for testing ab initio methods, in particular to identify the non-radiative processes. However standard excited state calculations constitute a good tool to allow identification of tautomers.‡ In this paper, since the excited state lifetimes are extracted from vibrational broadening, the values can neither describe possible non-exponential decays nor variation of these lifetimes with the excess energy. Thus a femtosecond pump–probe experiment would be highly desirable.Acknowledgements
This work was supported by ECOS-MinCyT cooperation program (A11E02) the ANR Research Grant (ANR2010BLANC040501), FONCyT, CONICET and SeCyT-UNC. We acknowledge the use of the computing facility cluster GMPCS of the LUMAT federation (FR LUMAT 2764).Notes and references
- K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342 CrossRef CAS.
- C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- H. Saigusa, J. Photochem. Photobiol., C, 2006, 7, 197–210 CrossRef CAS PubMed.
- D. Tuna, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2014, 118, 122–127 CrossRef CAS PubMed.
- J. Y. Salpin, S. Guillaumont, J. Tortajada, L. MacAleese, J. Lemaire and P. Maitre, ChemPhysChem, 2007, 8, 2235–2244 CrossRef CAS PubMed.
- J. M. Bakker, R. K. Sinha, T. Besson, M. Brugnara, P. Tosi, J. Y. Salpin and P. Maitre, J. Phys. Chem. A, 2008, 112, 12393–12400 CrossRef CAS PubMed.
- J. M. Bakker, J. Y. Salpin and P. Maitre, Int. J. Mass Spectrom., 2009, 283, 214–221 CrossRef CAS PubMed.
- L. D. Williams and B. Ramsay Shaw, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 1779–1783 CrossRef CAS.
- N. Russo, M. Toscano, A. Grand and F. Jolibois, J. Comput. Chem., 1998, 19, 989–1000 CrossRef CAS.
- S. Y. Han, S. H. Lee, J. Chung and H. B. Oh, J. Chem. Phys., 2007, 127, 245102 CrossRef PubMed.
- A. L. Sobolewski and W. Domcke, Phys. Chem. Chem. Phys., 2004, 6, 2763–2771 RSC.
- C. Marian, D. Nolting and R. Weinkauf, Phys. Chem. Chem. Phys., 2005, 7, 3306–3316 RSC.
- N. R. Cheong, S. H. Nam, H. S. Park, S. Ryu, J. K. Song, S. M. Park, M. Pérot, B. Lucas, M. Barat, J. A. Fayeton and C. Jouvet, Phys. Chem. Chem. Phys., 2011, 13, 291–295 RSC.
- S. Øvad Pedersen, K. Støchkel, C. Skinnerup Byskov, L. Munksgaard Baggesen and S. Brøndsted Nielsen, Phys. Chem. Chem. Phys., 2013, 15, 19748–19752 RSC.
- I. Alata, J. Bert, M. Broquier, C. Dedonder, G. Feraud, G. Grégoire, S. Soorkia and C. Jouvet, J. Phys. Chem. A, 2013, 117, 4420–4427 CrossRef CAS PubMed.
- X. B. Wang and L. S. Wang, Rev. Sci. Instrum., 2008, 79, 073108 CrossRef PubMed.
- M. Z. Kamrath, R. A. Relph, T. L. Guasco, C. M. Leavitt and M. A. Johnson, Int. J. Mass Spectrom., 2010, 300, 91–98 CrossRef PubMed.
- C. M. Choi, H. J. Kim, J. H. Lee, W. J. Shin, T. O. Yoon, N. J. Kim and J. Heo, J. Phys. Chem. A, 2009, 113, 8343–8350 CrossRef CAS PubMed.
- J. U. Andersen, H. Cederquist, J. S. Forster, B. A. Huber, P. Hvelplund, J. Jensen, B. Liu, B. Manil, L. Maunoury, S. Brøndsted Nielsen, U. V. Pedersen, J. Rangama, H. T. Schmidt, S. Tomita and H. Zettergren, Phys. Chem. Chem. Phys., 2004, 6, 2676–2681 RSC.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- C. Hattig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef CAS PubMed.
- J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS PubMed.
- We use the notation 1H–2H to indicate the hydrogen and proton positions on nitrogen numbered 1 and on the oxygen linked to carbon 2 (see Fig. 1 for atom numbering).
- C. M. Western, PGOPHER, a Program for Simulating Rotational Structure. V 7.0.101, PGOPHER, a Program for Simulating Rotational StructureWestern, University of Bristol, http://pgopher.chm.bris.ac.uk Search PubMed.
- N. J. Kim, G. Jeong, Y. S. Kim, J. Sung, S. K. Kim and Y. D. Park, J. Chem. Phys., 2000, 113, 10051–10055 CrossRef CAS PubMed.
- M. Miyazaki, H. Kang, C. M. Choi, N. S. Han, J. K. Song, N. J. Kim and M. Fujii, J. Chem. Phys., 2013, 139, 124311 CrossRef PubMed.
- I. Alata, D. Dedonder, M. Broquier, E. Marceca and C. Jouvet, J. Am. Chem. Soc., 2010, 132, 17483–17489 CrossRef CAS PubMed.
- G. A. Pino, A. N. Oldani, E. Marceca, M. Fujii, S.-I. Ishiuchi, M. Miyazaki, M. Broquier, C. Dedonder and C. Jouvet, J. Chem. Phys., 2010, 133, 124313 CrossRef CAS PubMed.
- G. Gregoire, C. Jouvet, C. Dedonder and A. L. Sobolewski, J. Am. Chem. Soc., 2007, 129, 6223–6231 CrossRef CAS PubMed.
- G. A. Pino, I. Alata, C. Dedonder, C. Jouvet, K. Sakota and H. Sekiya, Phys. Chem. Chem. Phys., 2011, 13, 6325–6331 RSC.
- M. C. Capello, M. Broquier, C. Dedonder-Lardeux, C. Jouvet and G. A. Pino, J. Chem. Phys., 2013, 138, 054304 CrossRef PubMed.
- A. K. Chandra, M. T. Nguyen and T. Uchimaru, J. Phys. Chem. A, 1999, 103, 8853–8860 CrossRef CAS.
- A. Abo-Riziq, L. Grace, E. Nir, M. Kabelac, P. Hobza and M. S. De Vires, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 20–23 CrossRef CAS PubMed.
- T. Schultz, E. Samoylova, W. Radloff, I. V. Hertel, A. L. Sobolewski and W. Domcke, Science, 2004, 306, 1765–1768 CrossRef CAS PubMed.
- E. Nir, K. Kleinermanns and M. S. de Vries, Nature, 2000, 408, 949–951 CrossRef CAS PubMed.
- C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 074316 CrossRef PubMed.
- D. Nachtigallová, H. Lischka, J. J. Szymczak, M. Barbatti, P. Hobza, Z. Gengeliczki, G. Pino, M. P. Callahan and M. S. de Vries, Phys. Chem. Chem. Phys., 2010, 12, 4924–4933 RSC.
- G. Féraud, C. Dedonder-Lardeux, C. Jouvet, Y. Inokuchi, T. Haino, R. Sekiya and T. Ebata, J. Phys. Chem. Lett., 2014, 5, 1236–1240 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00742e |
| ‡ We also confirmed recently the identification of different tautomers of protonated uracil with a new UV-UV hole-burning spectroscopy.39 |
| This journal is © the Owner Societies 2014 |