Electrolyte layering at the calcite(104)–water interface indicated by Rb⁺- and Se(VI) K-edge resonant interface diffraction

Abstract

Calcite–water interface reactions are of major importance in various environmental settings as well as in industrial applications. Here we present resonant interface diffraction results on the calcite(104)–aqueous solution interface, measured in solutions containing either 10 mmol L⁻¹ RbCl or 0.5 mmol L⁻¹ Se(VI). Results indicate that Rb⁺ ions enter the surface adsorbed water layers and adsorb at the calcite(104)–water interface in an inner-sphere fashion. A detailed analysis based on specular and off-specular resonant interface diffraction data reveals three distinct Rb⁺ adsorption species: one 1.2 Å above the surface, the second associated with surface adsorbed water molecules 3.2 Å above the surface, and the third adsorbed in an outer-sphere fashion 5.6 Å above the surface. A peak in resonant amplitude between L = 1.5 and L = 3.0 is interpreted as signal from a layered electrolyte structure. The presence of a layered electrolyte structure seems to be confirmed by data measured in the presence of Se(VI).

---

1 Introduction

Calcite, the most stable CaCO₃ polymorph at standard conditions,¹ is ubiquitous in natural environments. Calcite surface reactions play a major role in natural systems as well as in many industrial applications. During the past decades a vast number of studies elucidated various aspects of calcite–water interface phenomena including: surface speciation,^2–5 dissolution and precipitation,^6–8 surface adsorption of heavy metals or organics,^9–13 and coprecipitation or structural incorporation of environmentally relevant trace elements.^14–20 A fundamental understanding of the molecular structure of the calcite–water interface, and its relation to interface reactivity may provide a basis to explain many of the observed interfacial phenomena.

Numerous experimental^2,3,21–27 and theoretical^28–31 studies investigate the molecular interface structure, mostly focusing on the structure of the calcite(104) surface (relative to the calcite crystal structure in hexagonal coordinates³²), which is often assumed to be the most abundant and relevant surface displayed on natural as well as on synthetic calcite crystals grown at ambient conditions.³ There appears to be agreement that the structure of the calcite(104) surface is largely determined by the bulk crystal structure. Breaking of bonds upon formation of the surface leads to minor relaxations of calcium and carbonate ions from their bulk structural positions.^2,3,21–23 According to most recent investigations such relaxations may reach up to 4–6 monolayers deep into the crystal structure.²¹ In aqueous environments broken bonds are partially saturated by two layers of adsorbing water molecules.^3,21–23,30 A recent direct comparison between X-ray reflectivity data and molecular dynamics (MD) simulations³³ showed that the ability of simulations to predict calcite surface relaxation in contact with water is not yet satisfactory. Most recently we have shown that the relaxation of the calcite surface layers in contact with aqueous solution agrees intriguingly well with the expected response of an ionic dielectric on the surface potential as predicted from surface complexation modelling.^3,34 This indicates that surface relaxation might be a polarization response of the calcite structure close to the surface to the calcite surface potential. As surface charging effects are not yet usually considered in atomistic modelling, this finding offers a likely explanation for the inability of MD simulations to precisely predict calcite surface relaxation.

In a recent publication Ricci et al.³⁵ showed that, using advanced AFM techniques, it is possible to visualize single background electrolyte cations (Na⁺ and Rb⁺) adsorbed within the Stern layer at the calcite(104) surface. Ricci et al. show that the observation of Na⁺ within the Stern layer is in agreement with MD simulations. At the same time MD predicts that anions (Cl⁻) and divalent, more strongly hydrated cations like Ca²⁺, remain beyond the two strongly bonded surface water layers during interaction with the calcite surface.

In a previous surface diffraction study³ we could not evidence any significant changes in crystal truncation rod (CTR) profiles induced by changes in the aqueous contact solution composition. Therefore we concluded that ions other than OH⁻ and H⁺, likely adsorb beyond the two surface adsorbed water layers in an outer-sphere fashion. Concentration levels of Na⁺ in the contact solutions during CTR measurements in that study were in the range from 2 mmol L⁻¹ to 100 mmol L⁻¹. The contrast on the CTR profiles created by varying amounts of surface adsorbed Na⁺ ions was apparently below the detection limit of the method.

Here we present a new surface diffraction investigation of the calcite(104)–water interface, in which we specifically probe the structural position of background electrolyte ions at the calcite–water interface by means of resonant interface diffraction. Resonant interface diffraction is understood here as an extension of the resonant anomalous X-ray reflectivity (RAXR) method^36,37 to three dimensions. RAXR puts special emphasis on the specular (00L) CTR and the surface normal direction. The relation between the two methods is similar to that of the non-resonant analogues surface diffraction and X-ray reflectivity.

As probes for the electrolyte structure at the interface, we choose ions which we assume to show no specific interactions with the calcite surface. As a cation we choose Rb⁺ as an analogue for Na⁺, which is of major relevance in natural systems and has been used as background electrolyte cation in many previous studies. The alkali metal cation Rb⁺ is chemically very similar to Na⁺. The major difference is the larger ionic radius of Rb⁺, 152 pm, compared to Na⁺, 102 pm³⁸ (note that the hydrated radii 149 pm and 102 pm,³⁹ respectively, are very similar). This leads to a lower charge density at the Rb⁺ surface and consequently to weaker hydration; −275 kJ mol⁻¹ hydration free energy of Rb⁺ compared to −365 kJ mol⁻¹ hydration free energy of Na⁺.³⁹ Rb⁺ is usually considered a structure breaking ion whereas Na⁺ is considered as intermediate with respect to its effect on water ordering.⁴⁰ The obvious advantage of Rb⁺ over Na⁺ in the context of X-ray spectroscopic techniques is its higher K-edge energy (Rb 1s-energy 15.200 keV). This enables in situ investigation of Rb⁺ ions at the calcite–water interface through a thin layer of liquid. Similar measurements are not feasible with Na⁺ (Na 1s-energy 1.0708 keV). Furthermore the higher number of electrons in Rb⁺ (36 compared to 10 in Na⁺) increases its effect on the non-resonant X-ray scattering signal.

The choice of the anion might be less obvious. Hexavalent selenium forms divalent selenate (Se(VI)O₄²⁻) anions in aqueous solution. We prefer selenium over the more obvious halogen ions because compared to chloride (Cl 1s-energy 2.822 keV) the 1s-energy of Se at 12.658 keV is in a suitable range. The halogen anion with a similar 1s-energy, Br⁻ (Br 1s-energy 13.474 keV), is prone to beam damage in intense X-ray light.^41,42 Previous experiments have shown that selenate neither adsorbs at the calcite surface in significant amounts nor can it be incorporated into the calcite structure,³⁴ unless it is co-precipitated with calcite at high levels of supersaturation and fast growth rates.⁴³ Selenate shows neither any effect on the calcite zetapotential, nor any significant influence on calcite dissolution³⁴ and growth.⁴⁴

2 Experimental details

Solution preparation

Aqueous solutions used in this study are prepared from MilliQ-water (18.2 MΩ cm, <2 ppb dissolved organic carbon) and reagent grade chemicals. Prior to use, solutions are pre-equilibrated with calcite (calcium carbonate Merck Suprapure) and atmospheric CO₂ (log₁₀(p(CO₂)) = −3.44) using a similar method as previously reported.³ Pre-equilibration proceeds until the pH expected according to thermodynamic modelling using PhreeqC⁴⁵ and the Nagra/PSI thermodynamic database⁴⁶ is reached, which usually takes some days or weeks. After pre-equilibration the calcium carbonate powder is removed by filtration, using 0.45 μm Millipore filter membranes.

For the Rb⁺ experiments 10 mmol L⁻¹ RbCl are added to the solution prior to pre-equilibration. The corresponding equilibrium composition is: pH 8.3, ionic strength = 12 mmol L⁻¹, c(Rb⁺) = 10 mmol L⁻¹, c(Ca²⁺) = 0.6 mmol L⁻¹, c(inorganic carbon) = 1.2 mmol L⁻¹, including c(CO₃²⁻) = 0.013 mmol L⁻¹. At these conditions we expect the zetapotential of calcite to be about neutral/slightly positive.³

For the Se(VI) experiments 0.5 mmol L⁻¹ Na₂SeO₄, 70 mmol L⁻¹ HCl, and 30 mmol L⁻¹ NaCl are added to the solution prior to pre-equilibration. The corresponding equilibrium composition is: pH 7.5, ionic strength = 140 mmol L⁻¹, c(SeO₄²⁻) = 0.5 mmol L⁻¹, c(Ca²⁺) = 35 mmol L⁻¹, c(inorganic carbon) = 0.29 mmol L⁻¹, including c(CO₃²⁻) = 7.6 × 10⁻⁴ mmol L⁻¹. At these conditions we expect the zetapotential of calcite to be positive, ca. 10 mV³.

Crystal preparation

For the surface diffraction experiments, calcite single crystals are freshly cleaved from optically clear Iceland Spar crystals from Mexico Chihuahua purchased from Ward's Natural Science. Directly after cleavage a clear flawless crystal platelet (ca. 1 mm × 6 mm × 6 mm) is mounted on the diffractometer. The crystal is covered by an 8 μm thick Kapton window and brought in contact with solution as quickly as possible to minimize the possibility of contamination with adventitious carbon.

Surface diffraction measurements

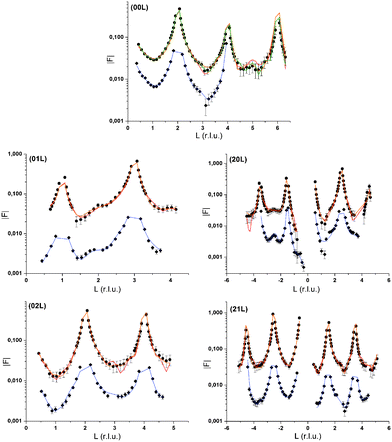
Surface diffraction measurements are performed at the GeoSoilEnviroCARS undulator beamline, 13IDC, at the Advanced Photon Source (APS) in Argonne as previously described.³ As before, we use a thin film cell in order to investigate the mineral water interface in situ through a ca. 2 μm thick layer of water.

For the non-resonant CTR measurements the energy is switched to a value significantly below the absorption edge of the element of interest in the resonant investigation. In the Rb⁺ system CTRs are measured at 14.5 keV. In the Se(VI) system CTRs are measured at 12.2 keV. In each system we measure seven CTRs. CTR data are shown in Fig. 1 together with model calculations. Integration of image data is performed using the tdl software package (http://https://github.com/xraypy/tdl). Note that coordinates used to measure non-resonant and resonant surface diffraction data refer to a pseudo-orthorhombic surface unit cell as used in our previous study.³ “Calcite(104)” is used here as a proper name. The “(104) surface” is described by the (001) vector according to the surface unit cell.

Fig. 1 CTR data measured at the calcite(104)–water interface in the presence of 10 mmol L⁻¹ RbCl in solution (black circles) and in the presence of 0.5 mmol L⁻¹ Se(VI) (grey diamonds). Model calculations are depicted as lines. Three model curves are shown for the Rb⁺-data. The orange line corresponds to the model including one Rb⁺-surface species, 1Rb. The red curve corresponds to the model including 3Rb⁺-surface species and a layered Rb⁺ structure, 3Rb+L. The green line in the 00L CTR represents a variation of the 3Rb+L model including Cl⁻ counter ions. The model in the presence of Se(VI) is depicted as a blue line. Rb⁺ and Se(VI) datasets are offset along the y-axis for clarity.

Resonant anomalous dispersion terms

In order to analyse the resonant interface diffraction scans it is necessary to know a priori the resonant anomalous dispersion terms f′(E) and f′′(E) of the resonant elements.³⁶ We use resonant anomalous dispersion terms calculated for the bare atoms after Cromer–Liberman⁴⁷ using the HEPHAESTUS software⁴⁸ in a range of ±500 eV around the absorption edges as reference values. Experimental f′′(E) functions are measured as X-ray absorption spectra in transmission mode on 0.1 molar aqueous solutions of RbCl and Na₂SeO₄, respectively. A differential Kramers–Kronig transformation^49,50 is applied to obtain experimental f′(E). Cromer–Liberman and experimental f′(E) and f′′(E) functions for Rb⁺ and Se(VI) are shown in the ESI,† Fig. S1.

Resonant interface diffraction

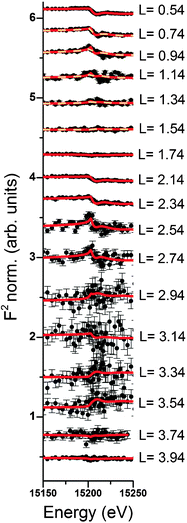
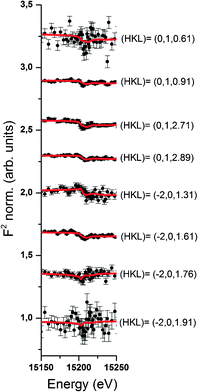
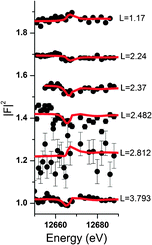
Resonant interface diffraction data are measured on the same samples in the same configuration as non-resonant CTRs. For each resonant interface diffraction scan, the energy of the incident X-ray beam is scanned about ±500 eV around the absorption edge of the resonant element at a fixed position in reciprocal space.

Along the specular CTR resonant scans are recorded at regular intervals of 0.2 L units, starting from L = 0.54 to L = 3.94. For Rb⁺, off-specular resonant scans are recorded along the 01 L and the −20 L rods at regular intervals of 0.3 L units. Additional scans are inserted at intermediate L values at which a clearly detectable resonant signal was expected. Integration of the image data is again performed using the tdl software package (http://https://github.com/xraypy/tdl). Only resonant scans having a resonant signal clearly distinguishable from noise are considered for data analysis. For measurement of resonant data in the presence of the dilute (0.5 mmol L⁻¹) Se(VI) solution, this criterion is only fulfilled for six resonant scans. The data measured in the relatively concentrated (10 mmol L⁻¹) RbCl solution is of much higher quality and 25 resonant scans could be considered for structure analysis. Resonant interface diffraction data used for structure analysis are shown in Fig. 2, 3 (Rb⁺), and 4 (Se(VI)), along with best fit model calculations. The resonant data measured on Rb⁺ allow the analysis of the interface structure with a spatial resolution in z of: Δz = 1.5 Å. Data are sensitive to a z-range up to 15 Å above and below the surface (for details on these values see ESI†).

Fig. 2 Resonant interface diffraction scans measured along the specular CTR (H = K = 0) at the calcite(104) face in contact with a solution containing 10 mmol L⁻¹ Rb⁺ around the Rb 1s-energy at 15.2 keV. Data (black dots) are shown along with best fit model calculations (lines). Thick red lines correspond to the full 3Rb+L model including three different interfacial Rb⁺ species and a layered Rb⁺ structure. The simplified model including only one Rb⁺ species (1Rb) is indicated as dashed yellow line in specular scans from L = 0.74 to L = 1.54. Scans are offset along the y-axis for clarity.

Fig. 3 Resonant interface diffraction scans measured along the off-specular CTRs at the calcite(104) face in contact with a solution containing 10 mmol L⁻¹ Rb⁺ around the Rb 1s-energy at 15.2 keV. Data (black dots) are shown along with best fit model calculations (3Rb+L, lines). Scans are offset along the y-axis for clarity.

Fig. 4 Resonant interface diffraction scans measured around the Se 1s energy at 12.658 keV along the specular CTR at the calcite(104) face in contact with a solution containing 0.5 mmol L⁻¹ Se(VI). Note that the Se absorption edge is shifted to 12.664 keV due to the hexavalent oxidation state of Se(VI). Data (black dots) are shown along with best fit model calculations (red lines). Scans are offset along the y-axis for clarity.

Data analysis

A new “python interface structure refinement” software is developed to model non-resonant and resonant interface diffraction data. Especially in cases as here, where resonant atoms are the heaviest in the interface structure, the resonant element distribution, as derived from the resonant data, has a big impact on the non-resonant CTR model as well. Structure factors from the non-resonant model are, however, a prerequisite to calculating resonant structure factors. Therefore, the development of an interface model based on resonant and non-resonant data is a highly iterative process, which can be tackled best using a program that allows to handle both kinds of data and provides means to switch easily between the refinement of the two kinds of data. The python interface structure refinement code is specifically developed for this purpose and available with the tdl software package at http://https://github.com/xraypy/tdl.

The functions used to model non-resonant CTR data are based on those in the ROD software.⁵¹ The interface structure model is optimized to minimize the objective function χ² = Σ_i(|F_obs|_i − |F_calc|_i)²/σ²(|F_obs|)_i, where |F_obs| are measured structure factors, |F_calc| are calculated structure factors, and σ²(|F_obs|) are the standard deviations associated with the measured structure factors. The Nelder–Mead Simplex minimization algorithm⁵² is applied to minimize χ², and to optimize structural parameters.

The structure models refined in this study contain four layers of calcite, as previously suggested.²¹ Carbonate ions are treated as rigid bodies, which can be translated and rotated.²² Bond valence constraints are applied to keep bond-valence sums⁵³ of the atoms in the first calcite monolayer within ±10% of the ion valence and within ±5% of the ion valence in the second monolayer beneath the surface. A new feature in the python interface structure refinement code allows to refine anisotropic Debye–Waller parameters. In this study, anisotropic Debye–Waller parameters, described by U-tensors, are applied in the two topmost calcite monolayers, for adsorbed water oxygen atoms (note that adsorbed water is modelled by considering only the oxygen atom of the water molecule, because hydrogen atoms are largely invisible in X-ray diffraction) and for adsorbed resonant atoms in the case of Rb⁺. All other atoms are described by isotropic thermal vibrations (U₁₁ = U₂₂ = U₃₃, U₁₂ = U₁₃ = U₂₃ = 0). A layered water profile⁵⁴ is included to describe the effect of bulk water on specular surface scattering.

The approach to model resonant interface diffraction data follows closely the equations laid out by Park et al.³⁶ Whenever necessary, equations are adjusted to allow the treatment of a three dimensional structure and off-specular as well as specular resonant interface diffraction data. Resonant amplitude, A_R, and phase, P_R are derived from individual resonant scans based on model derived non-resonant structure factors along with a linear background using the Levenberg–Marquardt least squares optimization routine provided with scientific python (SciPy). In the case of the Rb⁺ data, where a sufficient number of resonant scans at regular intervals are available, A_R and P_R can be used for straightforward Fourier synthesis of the electron density distribution associated with Rb⁺ at the interface.³⁶ The result of the Fourier synthesis may serve as guidance where to include Rb⁺ into the interface model. Model refinement on resonant data is again performed using the Nelder–Mead-Simplex minimization algorithm.

One new model feature for resonant data analysis, which appeared to be necessary to achieve a satisfactory description of the data measured on Rb⁺ and Se(VI), is a layered electrolyte model. This model assumes that the resonant element forms a semi-infinite layered structure, similar to the above mentioned layered water structure,⁵⁴ starting at a height z₀ above the surface and showing constant layering with a layer distance, d. This layered electrolyte structure is assumed to show periodicity only in the z direction. Therefore, it influences only the specular CTR and resonant data along the specular CTR. Details on the layered electrolyte model are given in the ESI.†

3 Results and discussion

Non-resonant CTR data

Three interface models will be presented. Two models, labelled in the following 1Rb and 3Rb+L, describe data recorded in the presence of Rb⁺. The Se(VI) model describes data recorded in the presence of Se(VI). The agreement between the non-resonant CTR data and interface model calculations is generally very good. The normalized quality of fit parameter χ_norm² = 1/(n − p)χ², where χ² is as defined above, n is the number of data points, and p is the number of adjustable parameters in the model, is smaller than two for all models and datasets (cf.Fig. 1). This may give us some confidence that the non-resonant structure factors used to obtain resonant structure factors are reliable. The number of non-resonant data points is 363 for the Rb⁺ data and 188 for the Se(VI) data. The models generally confirm the findings of our previous study.³ The atomic scale structure of the calcite(104)–water interface is largely determined by the bulk crystal structure of calcite. Going from the bulk to the surface, atoms relax increasingly from their structural positions and exhibit increasing thermal vibration in the four topmost calcite monolayers (ML). Two layers of interfacial water are structurally associated with the calcite surface. Oxygen atoms of the first water layer lie 2.55 to 2.64 Å above surface calcium atoms, while oxygen atoms of the second water layer lie above outward oriented oxygen atoms of surface carbonate ions, 2.97 to 3.16 Å above the surface. The z-positions of these water layers are significantly different from those in our previous study, with the oxygen atoms of the first water layer being around 0.25 Å further away from the surface, while the second water layer is around 0.17 Å closer to the surface. This may be due to the introduction of a layered water structure above the two layers of adsorbed water, which was not included in the our previous interfacial model. The water structure is in agreement with a slightly distorted octahedral environment of the surface calcium ion, and the bond valence sums of the surface atoms correspond to the expected valences within the accepted tolerance of 10%. In comparison to our previous study,³ inclusion of four adjustable calcite ML into the model, and refinement of anisotropic thermal vibration parameters in the first two ML and for adsorbed ions and water molecules, improved the ability of the models to reproduce the CTR data drastically.

Rb⁺ at the calcite(104)–water interface

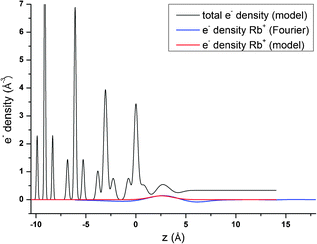
Resonant amplitude and phase values, A_R and P_R, extracted from the specular resonant interface diffraction scans in Fig. 2, are shown in Fig. 5. To interpret the A_R and P_R data let us first turn to the simplified 1Rb model, including only one Rb⁺ adsorption species. In this model the Rb⁺ distribution is adjusted to fit specular resonant interface diffraction scans in the L range from L = 0.74 to L = 1.54. A_R and P_R according to the 1Rb model are shown as thin dashed lines in Fig. 5. The 1Rb model fit to the original data is shown as dashed yellow lines in Fig. 2. Data in this L-range predict a simple smooth distribution of Rb⁺ at the interface, that can be satisfactorily described by a single inner-sphere adsorbed Rb⁺ species. In Fig. 6 the Rb⁺ electron density distribution projected onto the surface normal derived from Fourier synthesis (blue line) is compared to the Rb⁺ distribution according to the 1Rb model (red line). The total electron density distribution according to the 1Rb CTR model is shown as thin black line. For this simple model the Fourier synthesis agrees very well with the fit model; the description of the five resonant scans by the model is good as well, χ_norm² = 3.3. There are two symmetry equivalent Rb⁺ adsorption sites per surface unit cell, linked by the glide plane symmetry along the a-axes of the surface unit cell.³ According to the 1Rb model each of them is occupied by 0.21 Rb⁺ ions, which are located 2.61 Å above the surface and show a very wide distribution (U₃₃ = 1.56 Ų). Note that for parameters fitted to resonant data we report as many digits as we consider significant. For details how uncertainties are estimated please refer to the ESI.†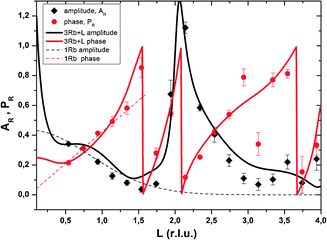

Fig. 5 Resonant amplitude (A_R, black diamonds) and phase (P_R, red circles) values extracted from the specular Rb K-edge resonant interface diffraction scans. The original data are shown in Fig. 2. Experimental values are shown along with model calculated A_R and P_R. 1Rb – thin dashed lines and 3Rb+L – thick solid lines.

Fig. 6 Projection of electron density onto the surface normal. Electron density related to Rb⁺ according to Fourier synthesis (blue line) and according to the adjusted 1Rb model (red line) is shown along with the total electron density distribution according to the 1Rb CTR model (thin black line).

In order to obtain the 1Rb CTR model fit in Fig. 1 the lateral position and the lateral thermal vibration parameters and cross terms of the inner-sphere Rb⁺ species are adjusted to optimize the description of the CTR data. The off-specular resonant data cannot be satisfactorily described using just one Rb⁺ adsorption species. Nevertheless, the simple 1Rb model allows us to draw one first conclusion, which is rather surprising with respect to our previous CTR study on the calcite(104)–water interface.³ In our previous work we did not see a significant effect of changes in the solution composition on the CTR data. Therefore, we concluded that all ions other than H⁺ or OH⁻ adsorb at the calcite–water interface beyond the two surface adsorbed water layers. The 1Rb model, however, clearly demonstrates that Rb⁺ ions enter the two adsorbed water layers. Even though the finding of inner-sphere adsorbed Rb⁺ at the calcite(104)–water interface was surprising to us, it is in very good agreement with the recent AFM study by Ricci et al.³⁵ The surface coverage with Rb⁺ measured by resonant interface diffraction agrees remarkably well with the concentration of Na⁺ in the b-plane predicted by our Basic-Stern surface complexation model,³ which would at similar solution conditions correspond to about 0.3 ML.

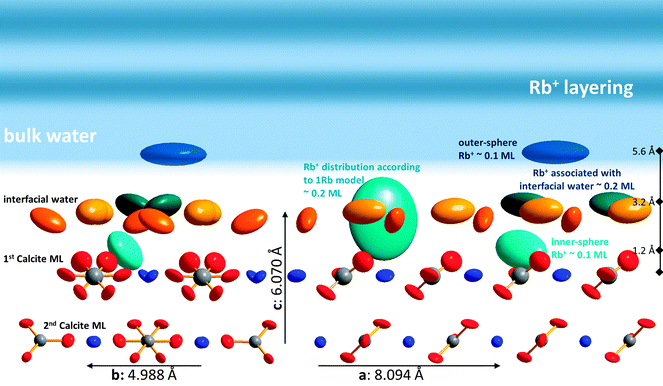
Of course it is not sufficient to limit resonant data interpretation to five resonant scans, when many more good quality scans are available. However, if all resonant data are included, the Rb⁺ structure above the surface appears highly complex. When the L-range of resonant scans is increased the direct space spatial resolution increases. This results in a splitting of the broad distribution of Rb⁺ above the surface in the 1Rb model into three separate Rb⁺ adsorption species. Three separate adsorption species seems a lot at a first glance, but this number is confirmed by the fact that the inclusion of three Rb⁺ adsorption species into the 3Rb+L model is necessary in order to obtain a satisfactory description of the off-specular resonant data (cf.Fig. 3); any simpler model fails to get the phases of the off-specular resonant scans even qualitatively right. The positions of the Rb⁺ adsorption species at the calcite(104)–water interface are depicted in Fig. 7. An inner-sphere species with a coverage of 0.1 ML is located 1.2 Å above the surface. The lateral position of this Rb⁺ adsorption species is close to the oxygen atoms of the surface carbonate ions and at maximum distance from the two neighbouring surface calcium ions, which seems reasonable. The second Rb⁺ adsorption species is the main species with a coverage of 0.2 ML. It is located inside the two adsorbed water layers, 3.2 Å above the surface. Considering that, according to our previous Basic-Stern surface complexation model, the water molecules above the surface calcium atoms are to a large degree (∼30%) deprotonated,³⁴ this site appears a likely adsorption site as well. Finally there is an outer-sphere Rb⁺ species 5.6 Å above the surface with an occupancy of 0.1 ML. The vertical position of this species is associated with the onset of the layered bulk water profile. Still, this species appears to have a distinct lateral position, because it significantly affects the description of the off-specular resonant data. We do not intend to measure the precise distances between adsorbed Rb⁺ species and the calcite surface atoms. The CTR models represent the average distribution of electron density at the interface. The local structure around an adsorbed ion may be different from the averaged interface structure obtained from the CTR model.

Fig. 7 Schematic representation of the calcite(104)–water interface structure in the presence of Rb⁺. Vibrational ellipsoids show 50% probability regions (Ca – blue, O – red, C – grey, oxygen of the 1st water layer – orange, oxygen of the 2nd water lay layer – yellow, Rb – different shades of turquoise). The calcite(104)–water interface is shown from two perspectives, the left side shows a projection along the x-axes, the right side shows a projection along the y-axes of the pseudo-orthorhombic surface unit cell. Both perspectives contain the Rb⁺ adsorption species according to the 3Rb+L model. The right image additionally contains the Rb⁺ species corresponding to the 1Rb model. The layered bulk water structure is indicated in light blue and the layered Rb⁺ structure according to the 3Rb+L model in dark blue.

The peak in the resonant amplitude (A_R) parameter observed along the specular CTR between L = 1.5 and L = 3 (cf.Fig. 5) can by no means be described with a simple structure containing an inner-sphere and one or two outer-sphere species. The only obvious way to reproduce this peak with a structural model is by a layered Rb⁺ structure, as explained in the ESI.† Therefore, a layered Rb⁺ structure is included in the 3Rb+L model. Structural parameters are: φ₀ = 0.37, K = 0.0, z₀ = 1.4 (=8.4 Å), d_z = 0.49 (=2.97 Å), U₀ = 0.2 Ų and U_bar = 0.1 Ų. (φ₀: first layer occupancy, K: occupancy decay factor, z₀: first layer z-position, d_z: layer spacing, U₀: first layer thermal vibration, and U_bar: increase of thermal vibrations with consecutive layers. For details on these parameters as well as for an illustration of the effect of a layered structure on A_R, as a rationale behind our interpretation, please refer to the ESI.†)

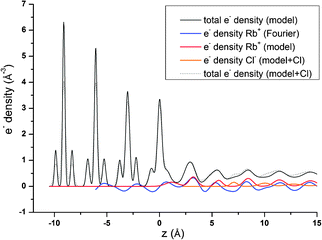
Fig. 8 shows that the layered electrolyte structure (red line) included in the 3Rb+L model is also evident in the Fourier synthesis based on all resonant scans along the specular CTR (blue line). The effect of the layered structure on the total electron density distribution is enormous. This is due to the high value of φ₀ and the fact that the best adjustment could be achieved for K = 0. φ₀ = 0.37 (=0.19 ML) corresponds to an interfacial Rb⁺ concentration of approximately 5 mol L⁻¹ opposed to a Rb⁺ concentration in the bulk solution of 0.01 mol L⁻¹. K = 0 indicates a constant concentration in the layered structure and can only be explained by assuming that a high Rb⁺ concentration prevails in the z-range that the resonant data are sensitive to (up to about 15 Å above the surface), followed by a drop in concentration to the bulk value at a distance beyond that region.

Fig. 8 Projection of electron density onto the surface normal. Electron density related to Rb⁺ according to Fourier synthesis (blue line) and according to the adjusted 3Rb+L model (red line) is shown along with the total electron density distribution according to the 3Rb+L CTR model (thin black line). Also shown is the result of a model of the specular CTR data including Cl⁻ as counter ions located between the Rb-layers. The thin dashed black line shows the total electron density distribution according to the 3Rb+L model including Cl⁻ and the orange line shows the Cl⁻ contribution.

These results indicating a layering of the electrolyte and a high Rb⁺ concentration persistent within a z-range previously thought to represent the onset of the diffuse layer, are certainly unexpected and need further confirmation. The layering however, is an effect which is frequently observed in MD simulations (e.g., ref. 35, 55 and 56). It is usually not as pronounced as according to the 3Rb+L model, but this difference might be due to the absence of a net surface charge in common theoretical interface models. Previous results based on experimental X-ray photoelectron spectroscopy (XPS) on hematite (001)⁵⁷ report that a layered electrolyte (NaCl in that case) structure may be induced upon interaction between a crystal surface and an electrolyte. In the XPS work, the authors state that the formation of dihydro-halite (NaCl·2H₂O) induced by the hematite(001) surface might be a likely explanation for the observed effect, and would explain the features observed in XPS spectra. Formation of a hydro-RbCl structure at room temperature induced by the calcite(104) surface might be an interesting option to explain the layered Rb⁺ structure. Unfortunately, there is no structural data available for any hydrated RbCl phase analog to dihydro-halite.

We are rather convinced that we may rule out explanations for the observed layering, which involve incorporation of Rb⁺ into the calcite structure. Even though evaporation of equilibrium contact solution through the 8 μm Kapton window of the thin film cell during measurements is likely⁵⁸ and this may induce calcite growth at the sample surface, incorporation of Rb⁺ into growing calcite is unexpected from a crystal chemical perspective¹⁴ and attempts to fit the peak between L = 1.5 and 3 as Rb⁺ incorporation into Ca²⁺ lattice positions resulted in poor fits. Furthermore, we minimize evaporation by flushing the top of the Kapton window with water saturated Helium gas during the measurements. Nevertheless, for future resonant interface diffraction experiments it might be worth considering to perform the measurements in a transmission cell,⁵⁸ in order to completely rule out evaporation artefacts.

The elevated Rb⁺ concentration (0.19 ML per layer or about 5 mol L⁻¹) in the z-range between 8.4 Å above the surface and ≥15 Å above the surface is another unexpected observation. It is not in agreement with our previous Basic Stern surface complexation model.³ According to this model, there is a relatively low permanent negative potential (−440 mV to −580 mV in the pH range from 7.5 to 9.7) in the 0-plane. The 0-plane is assumed to be located between the surface and the first layer of adsorbed water at ∼1.5 Å above the surface. The negative charge originates from deprotonation of surface water molecules. The Basic Stern model assumes this low 0-plane potential is very effectively screened by adsorption of counter ions in the b-plane, located beyond the two surface adsorbed water layers, ∼4–6 Å above the surface. As described above, the amount of inner-sphere adsorbed Rb⁺ derived from the resonant surface diffraction data agrees roughly with the amount of Na⁺ expected to be adsorbed in the b-plane according to the Basic-Stern model. The location of the Rb⁺ within the layers of adsorbed water is, however, not as expected, questioning the distinction between 0-plane and b-plane adsorption used in the model. It is well known, that the Gouy–Chapman model breaks down at high diffuse layer potentials. This may provide an explanation for the elevated Rb⁺ concentration between 4 Å and 15 Å above the surface. Let us assume that the potential at the onset of the diffuse layer is underestimated by the Basic-Stern model, either because the absolute 0-plane potential is even lower than assumed or because the screening of the potential due to counter ion adsorption is overestimated by the model (i.e. the Stern layer capacitance is overestimated). E.g. in a scenario in which the potential at the onset of the diffuse layer is −200 mV, the Rb⁺ coverage at the onset of the diffuse layer would be expected above one ML (∼1.7 ML). Even if we average the Gouy–Chapman concentration profile over a z-range, corresponding to one layer of the layered Rb⁺ structure (2.97 Å), the expected occupancy in this layer remains unrealistically high (∼0.8 ML). A tentative explanation of the elevated Rb⁺ concentration between 4 Å and ≥15 Å above the surface could therefore involve a low diffuse layer potential with a corresponding amount of counter ions distributed over an larger z-range. This agrees nicely with the concept of a condensed layer as proposed by Kilic et al.⁵⁹ for electrode surfaces at large applied voltages (cf.Fig. 2 in ref. 59).

One obvious question that arises from our results indicating a layering of Rb⁺ above the surface: where are the counter anions in this structure and at which concentration do they appear? Unfortunately, we have no specific information about the distribution of the most abundant counter anions, Cl⁻. Nevertheless, CTRs result from diffraction on the total electron density distribution at the interface and should therefore contain information about all chemical species present at the interface. The 3Rb+L model successfully describes the CTR data, even if it does not include Cl⁻. To test any effect inclusion of Cl⁻ counter ions might have on the CTR model, we refined an interface model based on the 3Rb+L model but including Cl atoms between the layers of Rb⁺. The parameters defining the Rb⁺ ions in the structure are kept constant, the other parameters are adjusted to give an optimal fit to the specular (00L) CTR. The resulting fit is shown as a green line in Fig. 1. The corresponding total electron density distribution and the Cl⁻-distribution are shown as a thin black dashed line and orange line in Fig. 8, respectively. The inclusion of Cl⁻ into the model leads to a near perfect fit to the specular CTR and the resulting structure seems physically reasonable. Cl⁻ ions are intercalated between the Rb⁺ layers with about equal surface coverage of 0.15 to 0.2 ML, compared to the Rb⁺ coverage of 0.19 ML (=φ₀/2). Although this result is intriguing, it should not be interpreted as evidence for the Cl⁻ distribution. The CTR model contains many adjustable parameters and it is not surprising that the addition of parameters increases the ability of the model to describe the data.

From the surface complexation modelling perspective, an explanation of alternating Rb⁺ and Cl⁻ layers is not straight forward, but might be possible if complex interface models involving e.g. the hypernetted chain equation⁶⁰ are considered. On the other hand, in the scenario of low diffuse layer charge, where the layered Rb⁺ structure might correspond to a “condensed” counter-ion layer,⁵⁹ anions between the Rb⁺ layers would not be expected.

Se(VI)O₄²⁻ at the calcite(104)–water interface

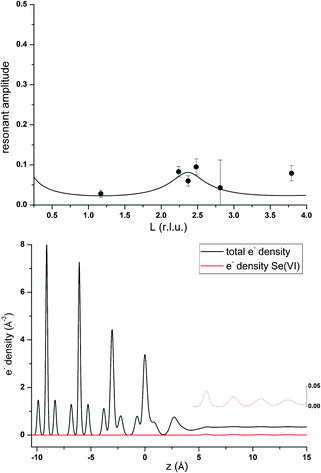
Some further experimental support that anions might also be affected by electrolyte layering at the calcite(104)–water interface comes from the data measured in the presence of Se(VI). Unfortunately the quality of the Se(VI) data is not satisfactory. Since Se(VI) shows no specific interaction with the calcite(104) surface, and due to the low concentration used in the Se(VI) experiment (0.5 mmol L⁻¹), the resonant signal was weak in this experiment. Nevertheless, a peak in A_R around L = 2.4 is apparent in the resonant Se(VI) data. This can be explained by a model including only a layered Se(VI) structure starting beyond the surface adsorbed water layers. The corresponding resonant data and model calculations are shown in Fig. 4. The resonant amplitude as a function of L and the corresponding electron density distribution projected onto the surface normal are shown in Fig. 9.

Fig. 9 Upper image: resonant amplitude, A_R, as a function of specular momentum transfer. Lower image: electron density distribution projected onto the surface normal. The total electron density distribution as obtained from the CTR model is shown in black, the electron density distribution related to Se is shown in red. The small inset shows a magnification of Se electron density distribution.

Due to the poor data quality obtained in the Se(VI) experiment, caution is advised when interpreting the Se(VI) model. Nevertheless, the Se(VI) model shows some intriguing parallels to the 3Rb+L model. Parameters of the best fit layered Se(VI) structure are: φ₀ = 0.04, K = 0.0, z₀ = 0.93 (=5.65 Å), d = 0.42 (=2.52 Å). z₀, the height of the first Se-layer above the surface, coincides exactly with the height of the outer-sphere adsorbed Rb⁺ above the surface. This might indicate that the height of the onset of the layered structure or outer-sphere adsorbed ions is independent of the electrolyte, and that the first layer contains cations as well as anions. φ₀ = 0.04 and K = 0.0 corresponds to a concentration of ∼0.7 mol L⁻¹ Se(VI) in the layered structure, which remains constant in the region the resonant data are sensitive to. This means that the concentration gradient is the same as in the 3Rb+L model, and the increase of the interfacial concentration over the bulk concentration is of the same order of magnitude (∼10³). In fact it is about a factor of 3 higher, which might be due to the divalent charge of Se(VI)O₄²⁻ as opposed to the monovalent Rb⁺. The interlayer distance between consecutive Se layers (2.52 Å) is smaller compared to the 3Rb+L model (2.97 Å). The smaller layer distance could be attributed to the fact that the Se(VI) data are measured in the presence of NaCl as background electrolyte, where the Na⁺ cations are smaller compared to Rb⁺ (hydrated ionic radii are 102 pm and 149 pm, respectively³⁹).

4 Conclusions

The python interface structure refinement software (http://https://github.com/xraypy/tdl) developed in the framework of this study proved to be a useful tool for the analysis of non-resonant and resonant interface diffraction data.

Data and models presented demonstrate the amount of element specific information on mineral–solution interface structures that can be obtained by resonant interface diffraction or related methods like RAXR.^36,37 In order to model the electrolyte structure above a surface, the element specific information, including resonant amplitudes and phases, is invaluable.

Within the z-range resonant data are sensitive to (∼15 Å above and below the surface in this study) we identify Rb⁺ ions, which enter the two layers of structurally bound surface water and adsorb at the calcite(104) face in an inner-sphere fashion, even based on a very much simplified model (1Rb).

Considering all resonant scans (3Rb+L model), the Rb⁺ structure above the surface appears complex, including three distinct adsorption sites. One minor species (0.1 ML) 1.2 Å above the surface is in direct contact with the calcite surface atoms. The main species (0.2 ML) is associated with the two surface water layers and is located 3.2 Å above the surface. The third species has again a lower occupancy (0.1 ML) and corresponds to outer-sphere adsorbed Rb⁺. Its distance to the surface (5.6 Å) is associated with the onset of the layered bulk water profile. Resonant interface diffraction scans measured along the off-specular CTRs indicate that all of these adsorption species have distinct lateral positions relative to the calcite surface structure.

A peak in the resonant amplitude between L = 1.5 and L = 3.0 is interpreted as signal from a layered electrolyte structure, starting 8.4 Å above the surface and showing an interlayer distance of 2.97 Å. The occupancy of the layers in this structure (0.19 ML) corresponds to a high interfacial Rb⁺ concentration of about 5 mol L⁻¹. Resonant scans recorded in the presence of Se(VI) can be interpreted as a layered Se(VI) structure above the two surface adsorbed water layers, with remarkable parallels to the layered Rb⁺ structure, concerning the height of the layered structure above the surface and the increase of the interfacial concentration relative to the concentration in the bulk solution.

The structural interpretation that Rb⁺ adsorption species enter the structurally bound surface water layers seems sound and is obvious even from model independent Fourier synthesis. This finding confirms recent AFM results.³⁵ It does, however, not agree with our previous Basic Stern surface complexation model.³ Accordingly, this model will need to be adjusted.

The layering of the electrolyte structure, the high concentration in this layered structure, and the observed concentration profile with constant layer occupancy in the first 15 Å above the surface pose fundamental questions. At a first glance it seems difficult to reconcile these observations with the classical idea of an electric double layer. It may, however, be brought into agreement with the concept of a condensed layer as proposed for highly charged electrode surfaces.⁵⁹ Similar layering effects appear in MD simulations,^35,55,56 and layered structures have been previously proposed based on XPS data.⁵⁷ The layered structures seem to be consistent for both Rb⁺ and Se(VI) data.

Certainly, further studies will be necessary to corroborate our observations and interpretations concerning the layering of the electrolyte. If the electrolyte layering will be verified, these results might have significant impact on interface chemistry.

Acknowledgements

We gratefully acknowledge financial support from the German Federal Ministry for Education and Research (BMBF) and the German Research Foundation (DFG) through the collaborative Project (CP) RECAWA within the research and development program “Geotechnologien”. Financial support from the European Union's European Atomic Energy Community's (Euratom) Seventh Framework Program FP7-Fission-2010 under grant agreement number 269688 (CP-SKIN), and from the German Federal Ministry of Economics and Technology (BMWi) under grant agreement number 02 E 10800 (CP-VESPA), is acknowledged. Data presented here were collected at GeoSoilEnviroCARS (Sector 13), Advanced Photon Source (APS), Argonne National Laboratory. GeoSoilEnviroCARS is supported by the National Science Foundation – Earth Sciences (EAR-1128799) and Department of Energy – Geosciences (DE-FG02-94ER14466). Use of the Advanced Photon Source was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.

Notes and references

1. L. N. Plummer and E. Busenberg, Geochim. Cosmochim. Acta, 1982, 46, 1011–1040.
2. P. Fenter, P. Geissbuhler, E. DiMasi, G. Srajer, L. B. Sorensen and N. C. Sturchio, Geochim. Cosmochim. Acta, 2000, 64, 1221–1228.
3. F. Heberling, T. P. Trainor, J. Lützenkirchen, P. Eng, M. A. Denecke and D. Bosbach, J. Colloid Interface Sci., 2011, 354, 843–857.
4. O. S. Pokrovsky and J. Schott, Environ. Sci. Technol., 2002, 36, 426–432.
5. S. L. S. Stipp, Geochim. Cosmochim. Acta, 1999, 63, 3121–3131.
6. A. E. Nielsen, J. Cryst. Growth, 1984, 67, 289–310.
7. E. Ruiz-Agudo, C. V. Putnis, L. J. Wang and A. Putnis, Geochim. Cosmochim. Acta, 2011, 75, 3803–3814.
8. H. H. Teng, P. M. Dove and J. J. De Yoreo, Geochim. Cosmochim. Acta, 2000, 64, 2255–2266.
9. L. W. Cheng, P. F. Lyman, N. C. Sturchio and M. J. Bedzyk, Surf. Sci., 1997, 382, L690–L695.
10. C. E. Cowan, J. M. Zachara and C. T. Resch, Geochim. Cosmochim. Acta, 1990, 54, 2223–2234.
11. E. J. Elzinga, C. D. Tait, R. J. Reeder, K. D. Rector, R. J. Donohoe and D. E. Morris, Geochim. Cosmochim. Acta, 2004, 68, 2437–2448.
12. F. Heberling, B. Brendebach and D. Bosbach, J. Contam. Hydrol., 2008, 102, 246–252.
13. A. A. Rouff, E. J. Elzinga and R. J. Reeder, Environ. Sci. Technol., 2006, 40, 1792–1798.
14. E. Curti, Appl. Geochem., 1999, 14, 433–445.
15. S. D. Kelly, E. T. Rasbury, S. Chattopadhyay, A. J. Kropf and K. M. Kemner, Environ. Sci. Technol., 2006, 40, 2262–2268.
16. L. Z. Lakshtanov and S. L. S. Stipp, Geochim. Cosmochim. Acta, 2004, 68, 819–827.
17. M. Marques Fernandes, M. Schmidt, T. Stumpf, C. Walter, D. Bosbach, R. Klenze and T. Fanghänel, J. Colloid Interface Sci., 2008, 321, 323–331.
18. R. J. Reeder, E. J. Elzinga, C. D. Tait, K. D. Rector, R. J. Donohoe and D. E. Morris, Geochim. Cosmochim. Acta, 2004, 68, 4799–4808.
19. A. J. Tesoriero and J. F. Pankow, Geochim. Cosmochim. Acta, 1996, 60, 1053–1063.
20. F. Heberling, M. A. Denecke and D. Bosbach, Environ. Sci. Technol., 2008, 42, 471–476.
21. P. Fenter and N. C. Sturchio, Geochim. Cosmochim. Acta, 2012, 97, 58–69.
22. P. Geissbuhler, P. Fenter, E. DiMasi, G. Srajer, L. B. Sorensen and N. C. Sturchio, Surf. Sci., 2004, 573, 191–203.
23. U. Magdans, X. Torrelles, K. Angermund, H. Gies and J. Rius, Langmuir, 2007, 23, 4999–5004.
24. K. Voitchovsky, J. J. Kuna, S. A. Contera, E. Tosatti and F. Stellacci, Nat. Nanotechnol., 2010, 5, 401–405.
25. S. L. Stipp, J. Hochella and F. Michael, Geochim. Cosmochim. Acta, 1991, 55, 1723–1736.
26. F. Ohnesorge and G. Binnig, Science, 1993, 260, 1451–1456.
27. J. Schutte, P. Rahe, L. Troger, S. Rode, R. Bechstein, M. Reichling and A. Kuhnle, Langmuir, 2010, 26, 8295–8300.
28. D. Aquilano, M. Calleri, E. Natoli, M. Rubbo and G. Sgualdino, Mater. Chem. Phys., 2000, 66, 159–163.
29. S. Kerisit and S. C. Parker, J. Am. Chem. Soc., 2004, 126, 10152–10161.
30. P. Raiteri, J. D. Gale, D. Quigley and P. M. Rodger, J. Phys. Chem. C, 2010, 114, 5997–6010.
31. A. Villegas-Jimenez, A. Mucci and M. A. Whitehead, Langmuir, 2009, 25, 6813–6824.
32. S. A. Markgraf and R. J. Reeder, Am. Mineral., 1985, 70, 590–600.
33. P. Fenter, S. Kerisit, P. Raiteri and J. D. Gale, J. Phys. Chem. C, 2013, 117, 5028–5042.
34. F. Heberling, D. Bosbach, J.-D. Eckhardt, U. Fischer, J. Glowacky, M. Haist, U. Kramar, S. Loos, H. S. Müller, T. Neumann, C. Pust, T. Schäfer, J. Stelling, M. Ukrainczyk, V. Vinograd, M. Vučak and B. Winkler, Appl. Geochem., 2014, 45, 158–190.
35. M. Ricci, P. Spijker, F. Stellacci, J.-F. Molinari and K. Voïtchovsky, Langmuir, 2013, 29, 2207–2216.
36. C. Park and P. A. Fenter, J. Appl. Crystallogr., 2007, 40, 290–301.
37. C. Park, P. A. Fenter, K. L. Nagy and N. C. Sturchio, Phys. Rev. Lett., 2006, 97, 016101.
38. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
39. Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999.
40. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370.
41. P. C. Rieke, D. R. Baer, G. E. Fryxell, M. H. Engelhard and M. S. Porter, J. Vac. Sci. Technol., A, 1993, 11, 2292–2297.
42. V. Olieric, E. Ennifar, A. Meents, M. Fleurant, C. Besnard, P. Pattison, M. Schiltz, C. Schulze-Briese and P. Dumas, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2007, 63, 759–768.
43. R. J. Reeder, G. M. Lamble, J. F. Lee and W. J. Staudt, Geochim. Cosmochim. Acta, 1994, 58, 5639–5646.
44. F. Renard, G. Montes-Hernandez, E. Ruiz-Agudo and C. V. Putnis, Chem. Geol., 2013, 340, 151–161.
45. D. L. Parkhurst and C. A. J. Appelo, User's guide to PhreeqC (Version 2), US Geological Survey, Denver, 1999.
46. W. Hummel, U. Berner, E. Curti, F. J. Pearson and T. Thoenen, Radiochim. Acta, 2002, 90, 805–813.
47. D. T. Cromer and D. Liberman, J. Chem. Phys., 1970, 53, 1891–1898.
48. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
49. K. Ohta and H. Ishida, Appl. Spectrosc., 1988, 42, 952–957.
50. M. Newville, J. O. Cross, B. Ravel, L. B. Sorensen, C. E. Bouldin and Y. Yacoby, J. Phys. IV, 1997, 7, 759–760.
51. E. Vlieg, J. Appl. Crystallogr., 2000, 33, 401–405.
52. J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313.
53. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244.
54. P. Fenter and N. C. Sturchio, Prog. Surf. Sci., 2004, 77, 171–258.
55. M. Machesky, D. Wesolowski, J. Rosenqvist, M. Predota, L. Vlcek, M. Ridley, V. Kohli, Z. Zhang, P. Fenter, P. T. Cummings, S. Lvov, M. Fedkin, V. Rodriguez-Santiago, J. Kubicki and A. Bandura, Langmuir, 2011, 27, 4585–4593.
56. D. Spagnoli, D. J. Cooke, S. Kerisit and S. C. Parker, J. Mater. Chem., 2006, 16, 1997–2006.
57. A. Shchukarev, J. F. Boily and A. R. Felmy, J. Phys. Chem. C, 2007, 111, 18307–18316.
58. S. S. Lee, P. Fenter and C. Park, J. Synchrotron Radiat., 2013, 20, 125–136.
59. M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 75, 021502.
60. J. Rasaiah, Chem. Phys. Lett., 1970, 7, 260–264.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00672k

---